lesson 8 3 problem solving solving right triangles answer key

8.3.1Pythagorean Theorem

Standard 8.3.1.

Use the Pythagorean Theorem to solve problems involving right triangles.

For example : Determine the perimeter of a right triangle, given the lengths of two of its sides. 

Another example : Show that a triangle with side lengths 4, 5 and 6 is not a right triangle.

Determine the distance between two points on a horizontal or vertical line in a coordinate system. Use the Pythagorean Theorem to find the distance between any two points in a coordinate system.

Informally justify the Pythagorean Theorem by using measurements, diagrams and computer software.

Essential Understandings/Ideas:

In this learning progression the essential idea is for students to use the Pythagorean Theorem as a tool in problem solving.  In this progression, we start with the basic relationship of the side lengths of a triangle and move to giving students situations in which they can classify triangles as acute, obtuse, and right.  The focus then becomes the right triangle and the Pythagorean Theorem.  It is necessary for them to build a right triangle and use the Pythagorean Theorem to solve the problem. 

Initial experiences with Pythagorean Theorem should be CONCRETE by actually finding areas of squares off of each side length and recognizing the relationship between the three squares.  This way, students can understand that the theorem is about math objects and their relationship, not just an equation to memorize.  The key is developing the understanding of why and how the Pythagorean Theorem is true. Learning is focused on determining distances in right triangle situations. Students will understand the relationship between side lengths of a right triangle and the area of the squares built from those side lengths.  Students will understand that the relationship for a RIGHT triangle is a 2 + b 2 = c 2 . Students should also explore the relationship that occurs when the triangles are acute to discover a 2 + b 2  is greater than c 2 and obtuse triangles have a relationship where a 2 + b 2 is less than c 2 .  This will help students understand and apply the idea that the CONVERSE of the Pythagorean Theorem is also true. (NCTM Grade 8 FOCAL POINTS.  p.71, 72)

Students will then use the relationship of a 2 + b 2 = c 2 for RIGHT triangles to find missing side lengths and find distances that they cannot "measure."   The focus is applying this understanding and using the Pythagorean Theorem as a tool to solve problems.  This will require students to draw a right triangle to model a situation and find the distance between two points on a coordinate grid.  This is the essential learning that students need in order to understand and develop the distance formula on the coordinate grid.

All Standard Benchmarks - with codes:

8.3.1.1  Use the Pythagorean Theorem to solve problems involving right triangles.

For example:  Determine the perimeter of a right triangle, given the lengths of two of its sides.  Another example:  Show that a triangle with side lengths 4, 5, and 6 is not a right triangle.

8.3.1.2  Determine the distance between two points on a horizontal or vertical line in a coordinate system.  Use the Pythagorean Theorem to find the distance between any two points in a coordinate system.

8.3.1.3  Informally justify the Pythagorean Theorem by using measurements, diagrams and computer software.

Benchmark Group A

For example:  Determine the perimeter of a right triangle, given the lengths of two of its sides.     

Another example:  Show that a triangle with side lengths 4, 5, and 6 is not a right triangle.

What students should know and be able to do [at a mastery level] related to these benchmarks:

• Use the Pythagorean Theorem to find side lengths of a RIGHT triangle.
• If any two side lengths of a RIGHT triangle are known, the length of the third side can be found by using the Pythagorean Theorem.
• Draw a right triangle to model a situation in which it is difficult to measure one of the distances involved and then use the Pythagorean Theorem to solve.
• Students will be able to use the Pythagorean Theorem to determine the length of the shortest line between two points "as the crow flies" on a coordinate grid.
• Given three side lengths of a triangle, students can determine if the triangle is a right triangle using the converse of the Pythagorean theorem
• Use irrational numbers to represent lengths.

Work from previous grades that supports this new learning includes:

• Use positive exponents specifically when the exponent is 2 (squaring)
• Use square roots
• Find the area of regular and irregular shapes using grid/dot paper
• Classify and interpret rational numbers
• Interpret and estimate irrational numbers (this isn't from another grade but important to learn within this standard or before?)
• Know how to solve for a variable by "undoing"
• Use variables to represent lengths.
• Properties of a right triangle.
• Understand order of operations when solving an equation
• Plot ordered pairs on a coordinate grid.
• Classify angles and triangles as acute, right, and obtuse.
• "Students have an understanding of similarity of geometric relationships. The relationships between the lengths within the object are preserved and use scale factor to solve problems for example, finding lengths in similar figures, distances on maps, and so on..." NCTM Grade 8 Focal Points, p. 50

NCTM Standards:

• create and critique inductive and deductive arguments concerning geometric ideas and relationships, such as congruence, similarity, and the Pythagorean relationship.
• use geometric models to represent and explain numerical and algebraic relationships;

8G7  Apply the Pythagorean Theorem to determine unknown side lengths in right triangles in real-world and mathematical problems in two and three dimensions.

8G8  Apply the Pythagorean Theorem to find the distance between two points in a coordinate system.

8G6  Explain a proof of the Pythagorean Theorem and its converse. 

Misconceptions

Student Misconceptions and Common Errors:

• Students often miss the idea that this works for only RIGHT triangles. It is important for students to explore the relationships of the areas of the side length of non-right triangles to clarify that a 2 + b 2 = c 2 is only true for right triangles.
• Students will make the mistake of just adding the side lengths (a + b = c)
• Students will do a 2 + b 2 = c and forget to take the square root of c 2 to find the length of the hypotenuse.
• Students will sometimes substitute the hypotenuse in for a or b instead of c in the equation.
• When finding a length of a segment drawn on dot paper, students count the dots instead of length in units.

In the Classroom:

According to NCTM Principles and Standards for School Mathematics , "Technology is essential in teaching and learning mathematics; it influences the mathematics that is taught and enhances students' learning" (NCTM 2000, p. 11). Interactive Web sites can help students to explore dynamic demonstrations of the Pythagorean relationship. In addition, visual and dynamic demonstrations can help students to analyze and explain mathematical relationships.

Teacher:  All right students, today we are going to go outside to see if you can discover a very important "rule" in mathematics.  Your group will need a tape measure, one of these 5 foot sticks, and a paper and pencil to record your data.  When you get outside I need each group to lean the stick against a wall and measure the distance the bottom of the stick is away from the wall and how far the stick went up the wall.  Let's set up a table on our paper before we go outside to record our data..  How can we best organize this data?

Student:  Ok, we have two measurements we are getting so let's make two columns.

Student:  No, I think we will have three measurements.  Looks like we will be making a triangle so we have three sides.  One will just always be 5 feet.

Teacher:  That is correct, technically we will have three lengths that we will be working with. And as always you should try to be very precise with your measurements.  Your groups will need to collect data for a variety of position lengths and then see if you can see a relationship between the three lengths that you have.

(Go outside to gather data, or just use a wall in the classroom if weather is not permitting.)

Student:  We have collected our data but we can't seem to find a pattern, although we did notice that as the bottom length gets smaller the top length gets larger.

Student: We noticed that too.  We also noticed that none of the lengths that we measured were ever larger than 5.

Teacher:  Good observations and both will always be true.   Does anyone remember why none of the measured lengths will be 5 or larger?

Student:  Aren't we working with a right triangle here?

Student:  Yeah, we are.  Wasn't there a special name for the side opposite from the right angle?  I can't remember the name but I remember that it has to be the longest length in the triangle.

Student: I remember, it was called the hypotenuse and the other two sides, the ones we are measuring, are called the legs.

Teacher:  That is correct.  But now we need to try and look for a relationship between the side lengths.   Did anyone measure lengths on the ground that were integers?

Student:  We did 1 foot on the bottom.

Teacher:  And what did you come up with?

Student:  About $4\frac{7}{8}$ feet.

Teacher:  Good - Ok, how about anyone else?

Student:  We measured 3 feet on the bottom.

Teacher:  Ok, stop right there.  If you do not have this position of your stick on your paper you need to measure it right now and see what the other length measures.

Student:  We got 4 feet.  Would it also work if we measured 4 feet on the bottom? Yep, we got three feet on the wall.  It's like we are just flipping the triangle.

Teacher:   That is correct.  Ok, now in your groups see if you can find the relationship with the lengths. 

Student:  I see it, we have 3 feet, 4 feet, and 5 feet.  Just add 1.

Student:  But that didn't work for 1 feet, $4\frac{7}{8}$ feet, and 5 feet.

Student:  Oh yeah, it should probably work for all lengths.

Teacher:  (If a few groups haven't found the relationship yet have them draw a right triangle and then give the hint to draw the squares off of each side length and examine the area).

Student:  Oh, I think we found something.

Student:  I think we did too.

Teacher:  Ok group 1, tell us what you found.

Student:  We found that if you draw squares off of each side length and found the areas there was a pattern.  The areas of the two squares on the legs added together equal the area of the square on the hypotenuse.

Student:  Well that's not what our group found.  Our group noticed that if you take each of the lengths of the legs and square them they add to get the hypotenuse length squared.

Student:  Aren't those the same thing?

Teacher: Let's examine it with this drawing.  What do you think?

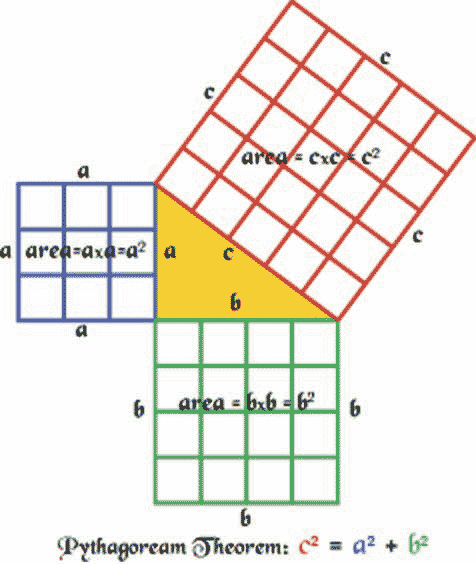
Student:  They are the same thing.  When we found what the side length squared was it was the same thing the other group did when they found the area of the square. 

Teacher:  And you guys discovered a well known mathematical theorem known as the Pythagorean Theorem.  If the leg lengths of a right triangle are a and b and the hypotenuse is c , then a 2 + b 2 = c 2 or (leg) 2 + (leg) 2 = (hypotenuse) 2 .  Another way to think about the Pythagorean Theorem is the areas of the squares drawn off the legs added together is equal to the area of the square drawn off the hypotenuse.

Student:  I have heard someone say a 2 + b 2 = c 2 but I've never known what they meant.

Teacher:  Well, now you do, and we will go back inside and start applying what we have learned with the Pythagorean Theorem to other examples.

*Side note:  A teacher could also look at the relationship of the side lengths when the 5 foot stick is placed against an object (a tree, or other leaning object) that is not perpendicular and therefore does not have a 90 degree angle.  This activity will lead into discovering the converse of the Pythagorean Theorem.

Teacher Notes:

• It is essential for students to make the squares and draw the pictures that represent this relationship. This is the concrete connection to this abstract idea. Making this connection will help students to avoid misconceptions like a + b = c or a 2 +b 2 =c . Students also need to develop the practice of checking the reasonableness of their answers. For example, the hypotenuse needs to be the longest side, or if the leg lengths are 3 and 4, the hypotenuse cannot be 25. This check will help students realize the misconception that a 2 +b 2 =c .
• Sometimes math books complicate the situation by writing the Pythagorean Theorem in a second form with subtraction when finding one of the legs. This may lead students to believe that there are two formulas for the Pythagorean Theorem, when really it is just a second equivalent form of the basic equation.
• The focus is on the relationship among the side lengths and NOT the measurements themselves ( NCTM Focal Points 8 p.68).
• "Measurement formulas allow us to rely on measurements that are simpler to access to calculate measurements that are more complicated to access" (Good Questions, Great Ways to Differentiate Mathematics Instruction. p.105).
• The Pythagorean Theorem is the building block of the distance formula. However, this standard is not focused on the distance formula. Requiring students to use the distance formula is not necessary and often confusing to the student if they can find the distance using the Pythagorean Theorem. Once the Pythagorean Theorem is fully developed, having students make connections to the distance formula may be a good extension activity.
• This is a logical place to teach students about rational versus irrational numbers. Although it is not in this benchmark, students need to have an understanding of irrational numbers and square roots in order to make sense of their answers.

Instructional Resources:

• Triangles of Squares : This is an interactive lesson that has students explore the relationship of the squares of the sides of triangles to determine if the triangle is acute, obtuse, or right.The lesson itself is available as a download at the bottom of this resources page.
• PYTHAGOREAN PUZZLE : This is an interactive lesson that has students explore the proof of the Pythagorean Theorem by cutting out squares and triangles and "puzzling" them together to show that the smaller areas add to be the larger area. The puzzel itself is available as a download at the bottom of this resources page.
• Students further explore square roots using the diagonals of rectangles. Using measurement, students will discover a method for finding the diagonal of any rectangle when the length and width are known, which leads to the Pythagorean Theorem. http://illuminations.nctm.org/LessonDetail.aspx?ID=L684
• http :// www . nctm . org / standards / content . aspx ? id =26776
• OnMATH 2008 Volume 6 "The Pythagorean Theorem: Going Beyond a 2 +b 2 =c 2 " by Dr. Katrina Piatek-Jimenez
• Going beyond the formula for the Pythagorean Theorem

This lesson provides students with an opportunity to explore the relationships of the squares off of the sides of a variety of triangles not just right triangles.  These conditions allow students to really focus in on the relationship of the areas rather than just memorizing the formula.  It is a great exploration that uncovers the converse of the Pythagorean Theorem as well.  It includes a technology extension exploration with Cabri II Plus.  There is also an extension to use with gifted students looking at the area of shapes other than squares off the sides of the triangle.  This activity allows students to connect the geometric meaning to the algebraic formula of the Pythagorean Theorem.

Additional Instructional Resources:

• The Pythagorean Theorem relates the lengths of the three sides of a right triangle. In the investigation on this web page, you will learn more about the Pythagorean Theorem and see whether or not it works for triangles that are not right triangles. http://www.keymath.com/x24555.xml
• Good resource for PROOF From NCTM FOCAL POINTS GRADE 8 p.70

•   These two videos are a great way for students to see the proof in action with water pouring into the squares built off each side.

Water proof of the Pythagorean Theorem Not the Pythagorean Theorem ( Water proof too )

• Science of NFL football - The Pythagorean Theorem http://www.nbclearn.com/portal/site/learn/nfl/cuecard/51220/
• Animated proof of the Pythagorean Theorem; use website to show students many of the proofs.   http://www.usna.edu/MathDept/mdm/pyth.html

Title:  A Right Triangle with Squares

Students make a square tool and use the tool to investigate the Pythagorean Theorem and its converse with Geometry Sketchpad.   http://www.keypress.com/x5596.xml

•   Great "real world" connection to Pythagorean Theorem!  http :// www . aimsedu . org / resources / video / index . html
• Ellis, J. " What's your angle, Pythagoras ?" Picture book. 
• Board game that can be used as review.  Some of the questions involving 45,45,90 and 30,60,90 might not apply.  Another review could be students creating their own game card questions to use.   http://www.glencoe.com/sec/math/t_resources/gamezone/pdfs/mac3_04/class_ch03.pdf
• Webquest = http :// zunal . com / webquest . php ? w =30275
• Interactive video from PBS. http://www.asset.asu.edu/new/mathactive/lessons/149/look.swf
• Professor R. Smullyan in his book 5000 B . C . and Other Philosophical Fantasies tells of an experiment he ran in one of his geometry classes. He drew a right triangle on the board with squares on the hypotenuse and legs and observed the fact the the square on the hypotenuse had a larger area than either of the other two squares. Then he asked, "Suppose these three squares were made of beaten gold, and you were offered either the one large square or the two small squares. Which would you choose?" Interestingly enough, about half the class opted for the one large square and half for the two small squares. Both groups were equally amazed when told that it would make no difference.   (Section pulled from http://www.cut-the-knot.org/pythagoras/index.shtml )

Pythagorean Theorem: It is a theorem that states a relationship that exists in any right triangle. If the lengths of the legs in the right triangle are a and b and the length of the hypotenuse is c, we can write the theorem as the following equation:

a 2 +b 2 =c 2

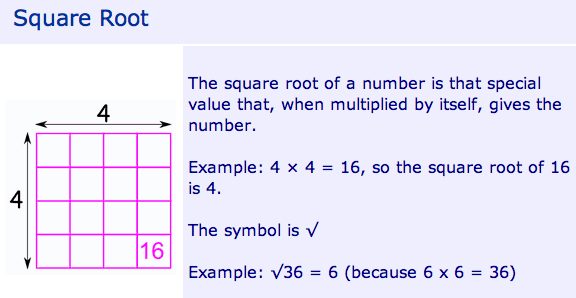
square root: A divisor of a quantity that when squared gives the quantity. For example, 5 is a square root of 25 because 5 × 5 = 25. Another square root of 25 is -5 because (-5) × (-5) = 25. The +5 is called the principle square root of 25.

hypotenuse:  In a right triangle, the side opposite to the right angle.

perfect square:  A number that is the square of a whole number. For example, 9 is a perfect square since 3 is a whole number and 3 × 3 = 3 2 = 9 .

Pythagorean Triple:  A set of three non-zero whole numbers, a , b , and c , such that a 2 + b 2 = c 2 .   There are infinitely many Pythagorean triples. Some examples are: (3, 4, 5) ; (11, 60, 61) ; (5, 12, 13) .

right triangle: A triangle with one right angle.

rational number:  A number that can be written as $\frac{a}{b}$ where a and b are integers, with b not equal to 0.

converse: The converse of a statement is formed by switching the hypothesis and the conclusion. For example, the Pythagorean Theorem only works for right triangles.  So if given three side lengths and the angles are unknown, students can determine that it is a right triangle if the Pythagorean Theorem works.

irrational number:  A number whose decimal form is non-terminating and non-repeating. Irrational numbers cannot be written in the form a/b, where a and b are integers. So all numbers that are not rational are irrational.  For example, pi or the square root of a non square number.  However, students can make their own irrational numbers like .1001000100001000001... or .112123123412345...

leg of a right triangle:  Either of the two shorter sides of a right triangle. These two sides together form the right angle in the right triangle.

distance formula: Given the two points ( x 1 , y 1 ) and ( x 2 , y 2 ), the distance between these points is given by the following formula (The Distance Formula is a variant of the Pythagorean Theorem):

Professional Learning Communities:

  Reflection - Critical Questions regarding the teaching and learning of these benchmarks

• How does the Pythagorean Theorem connect to student understanding of irrational numbers?  How can students be helped to make this connection?
• How can teachers help students make the connection between the distance formula and the Pythagorean Theorem and not teach them as two separate entities?
• What evidence exists that students grasp the concrete meaning of the Pythagorean Theorem rather than just memorizing the formula?  
• Understanding the Pythagorean Relationship Using Interactive Figures   This link provides teachers with an opportunity to look at a computer-generated model showing the proof.  Reflection questions are included for teachers to discuss.  

From NCTM Principles and Standards.

 Materials:

Tilted Squares , Irrational Numbers , and the Pythagorean Theorem Article from NCTM Mathematics Teaching in the Middle School, August 2009. Volume 15, Issue 1, pg. 57 (note: Membership in NCTM is required to access this resource).

References:

AIMS Education Foundation .  Triangles of Squares and Pythagorean Puzzle.

Focal Points Grade 8, NCTM .

Small, M. Good Questions: Great Ways to Differentiate Mathematics Instruction (NCTM) .

Website includes 9 multiple choice questions with answer key; also includes some converse questions. ( http://www.quantiles.com/ )

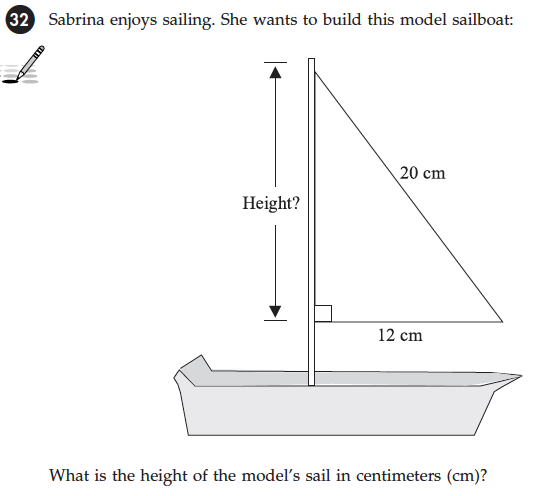
FCAT 2006 Mathematics Released Test  2006 Florida Department of Education (gridded response item).

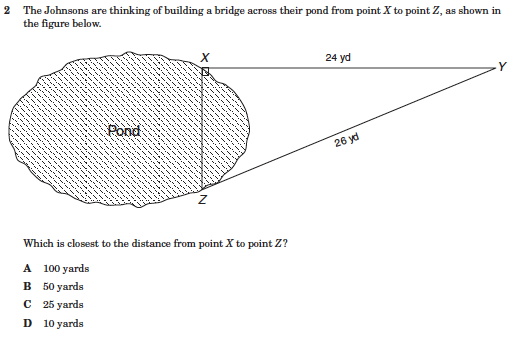
TAKS (Texas Assessment of Knowledge and Skills) Mathematics, Grade 8, 2010 released items.

#17 from MN Math MCA grade 8 item sampler

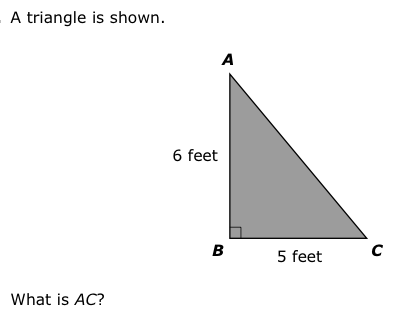
 #24 from MN Math MCA grade 8 item sampler

5.   A boat sets sail from an island located at (4, 12) on a map.  Its destination is the boat landing located at (6, 2).  What is the shortest distance that the boat will travel?  (Differentiated question - What is the shortest distance the boat will travel if each unit on the grid is 0.5 mile?  ANS  5.1 mi)        

6.   Given three side lengths of a triangle, determine if the triangle is a right, acute, or obtuse triangle.

a)  2ft, 4ft, 5 ft                        b) 6 in, 8in, 10in          c) 10m, 5m, 10m

correct answers: a) obtuse       b) right       c) acute

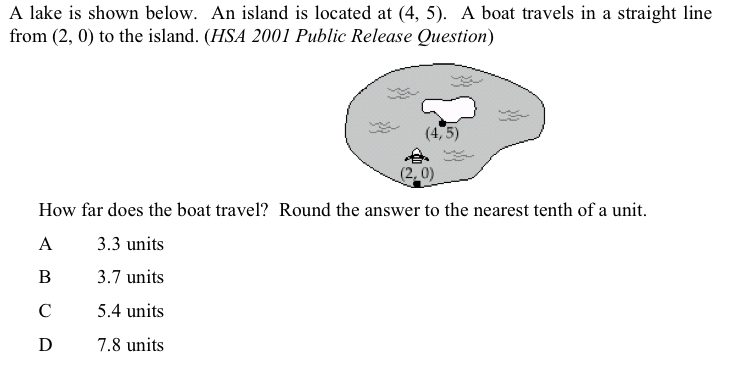
7.   A lake is shown below.  An island is located at (4,5).  A boat travels in a straight line from (2,0) to the island.  ( HSA 2001 Public Release Question )

8.   A diagram of a baseball field is shown below.  The infield is a square that measures 90 feet on each side ( HSA 2001 Public Release Question )

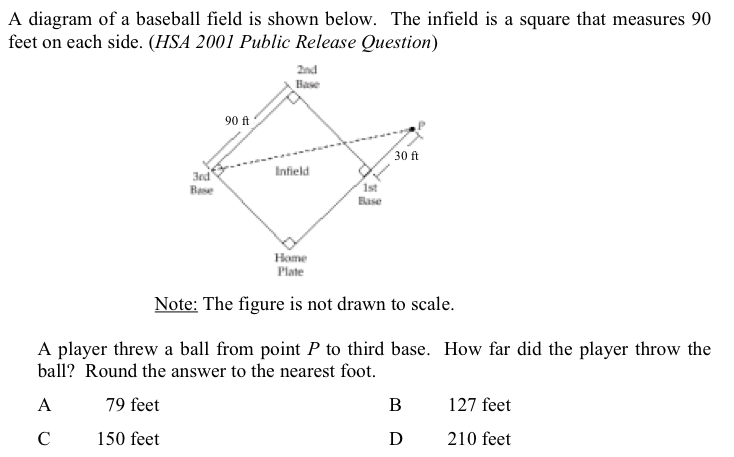
Correct answer:  C

9.   Jill wants to plant flowers in a triangular plot.  She has three lengths of plastic garden edging that measure 8 feet, 15 feet, and 17 feet.  Determine whether these pieces form a right triangle.  Explain. 

Correct answer:  Yes.  Sample explanation:  Because 8 2 + 15 2 = 17 2 , the pieces fit together to form a right triangle by the converse of the Pythagorean Theorem

Differentiation

Struggling Students:

• Encourage students to keep drawing the squares off the side lengths to reinforce the concrete. It's not necessary to make them use just the formula. (This is good for ALL students!)
• When teaching Pythagorean Theorem, hands-on activities involving math manipulatives are typically helpful to ELL students because the lesson involves multiple learning modalities and does not require a student to rely solely upon his/her ability to understand verbal instruction.
• Rewrite word problems using fewer and easier words so that ESL students can practice both math and language skills without being stuck on what a particular phrase or word means as they read the problem. Keep the sentences short and to the point. Take out extra detail that is not needed to convey the gist of the problem.
• Using a graphic organizer is a powerful strategy for helping all students and it especially helps English Language Learners with organizing and remembering information.  Because graphic organizers arrange details in a visual form, they help students retain concepts. a graphic organizer for Pythagorean Theorem

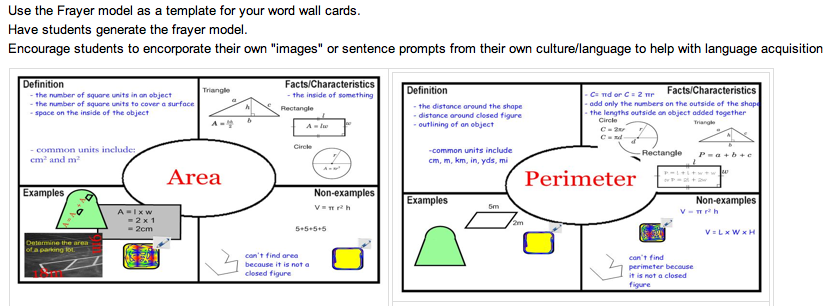
The image above was taken from: http :// math - on - the - move . wikispaces . com / ELL + Math

• Lesson from OnMATH: Online Journal of School Mathematics NCTM website.  Pythagorean Theorem: Connecting Interactive Websites by Cheng-Yao Lin. (2006-2007, Volume 5 Number 1)
• Pythagorean Interactive Proof Lesson

This lesson focus is on different proofs of the Pythagorean Theorem from different cultures.  There is a brief history about the Pythagorean Theorem and then it links you to multiple interactive websites that illustrate and animate the different proofs. The technology of this is important.

Some possible extensions of this lesson (from the proof lesson above) include the following:

• Consider a n + b n = c n , n > 2. Does this formula work just like the Pythagorean Theorem? Can you find an interactive Web site with a proof of this theorem?
• Consider the converse of the Pythagorean Theorem and generalize the theorem to shapes other than triangles.
• Can you find the Pythagorean Theorem in everyday life? What real world applications of Pythagorean Theorem are there? How about finding the distance from one corner of a class room to all the other corners of a classroom; use concrete, practical/realistic, introduction into three dimensions.
• One side of a right triangle is 5 units long. What could the other sides be? (Open question).
• Math Tools book, p.237-238. "Go Fly a Kite" choice activities for gifted.
• Teach simplifying radicals.
• Derive the distance formula .
• Special Triangles 30-60-90 and 45-45-90.
• Parachute activity   (only the reflection questions at the end are leveled).

Parents/Admin

Administrative/Peer Classroom Observation:

Parent Resources:

• http :// www . mathsisfun . com / pythagoras . html
• http :// www . regentsprep . org / Regents / math / ALGEBRA / AT 1/ Pythag . htm  

Related Frameworks

• 8.3.1.1 Pythagorean Theorem
• 8.3.1.2 Distance & the Pythagorean Theorem
• 8.3.1.3 Justify the Pythagorean Theorem

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

8.3: Right Triangle Trigonometry

• Last updated
• Save as PDF
• Page ID 143156

• The NROC Project

Learning Objectives

• Find the missing lengths and angles of a right triangle.
• Solve applied problems using right-triangle trigonometry.

Introduction

Suppose you have to build a ramp and don’t know how long it needs to be. You know certain angle measurements and side lengths, but you need to find the missing pieces of information.

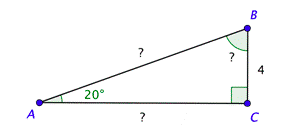
There are six trigonometric functions, or ratios, that you can use to compute what you don’t know. You will now learn how to use these six functions to solve right-triangle application problems.

Solving Right Triangles

Determining all of the side lengths and angle measures of a right triangle is known as solving a right triangle. Let’s look at how to do this when you’re given one side length and one acute angle measure. Once you learn how to solve a right triangle, you’ll be able to solve many real world applications, such as the ramp problem at the beginning of this lesson, and the only tools you’ll need are the definitions of the trigonometric functions, the Pythagorean Theorem, and a calculator.

Example \(\PageIndex{2}\)

Problem: You need to build a ramp with the following dimensions. Solve the right triangle shown below. Use the approximations \(\sin 20^{\circ} \approx 0.342\) and \(\tan 20^{\circ} \approx 0.364\), and give the lengths to the nearest tenth.

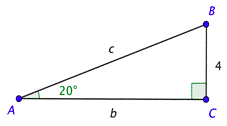
Remember that the acute angles in a right triangle are complementary, which means their sum is \(90^{\circ}\). Since \(m \angle A=20^{\circ}\), it follows that \(m \angle B=90^{\circ}-20^{\circ}=70^{\circ}\).

You can use the definition of sine to find \(c\). Substitute the measure of the angle on the left side of the equation and use the triangle to set up the ratio on the right. Solving the equation and rounding to the nearest tenth gives you \(c \approx 11.7\).

\(\begin{array}{c} \sin 20^{\circ}=\frac{\text { opposite }}{\text { hypotenuse }} \\ 0.342 \approx \frac{4}{c} \\ c(0.342) \approx 4 \\ c \approx \frac{4}{0.342} \approx 11.695 \end{array}\)

In a similar way, you can use the definition of tangent and the measure of the angle to find \(b\). Solving the equation and rounding to the nearest tenth gives you \(b \approx 11.0\).

\(\begin{array}{c} \tan 20^{\circ}=\frac{\text { opposite }}{\text { adjacent }} \\ 0.364 \approx \frac{4}{b} \\ 0.364 b \approx 4 \\ b \approx \frac{4}{0.364} \approx 10.989 \end{array}\)

The ramp needs to be 11.7 feet long.

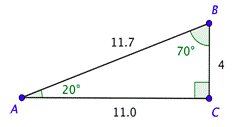
In the problem above, you were given the values of the trigonometric functions. In the next problem, you’ll need to use the trigonometric function keys on your calculator to find those values.

Example \(\PageIndex{3}\)

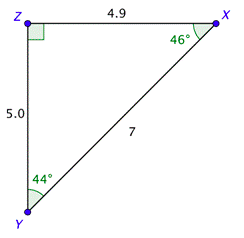
Problem: Solve the right triangle shown below. Give the lengths to the nearest tenth.

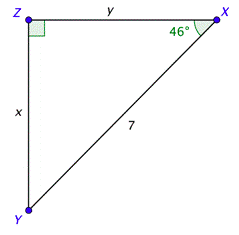
The acute angles are complementary, which means their sum is \(90^{\circ}\). Since \(\text { Since } m \angle X=46^{\circ}\), it follows that \(m \angle Y=90^{\circ}-46^{\circ}=44^{\circ}\).

You can use the definition of sine to find \(x\). Use your calculator to find the value of \(\sin 46^{\circ}\) and the triangle to set up the ratio on the right. Solving the equation and rounding to the nearest tenth gives you \(x \approx 5.0\).

\(\begin{array}{c} \sin 46^{\circ}=\frac{\text { opposite }}{\text { hypotenuse }} \\ 0.72 \approx \frac{x}{7} \\ 7(0.72) \approx x \\ 5.04 \approx x \end{array}\)

To find \(y\), you can either use another trigonometric function (such as cosine) or you can use the Pythagorean Theorem. Solving the equation and rounding to the nearest tenth gives you \(y \approx 4.9\).

\(\begin{array}{c} 5.0^{2}+y^{2} \approx 7^{2} \\ 25+y^{2} \approx 49 \\ y^{2} \approx 24 \\ y \approx \sqrt{24} \\ y \approx 4.899 \end{array}\)

We now know all three sides and all three angles. Their values are shown in the drawing.

Sometimes you may be given enough information about a right triangle to solve the triangle, but that information may not include the measures of the acute angles. In this situation, you will need to use the inverse trigonometric function keys on your calculator to solve the triangle.

Example \(\PageIndex{4}\)

Problem: Solve the right triangle shown below, given that \(\tan N =\frac{5}{4}\). Find the exact side lengths and approximate the angles to the nearest degree.

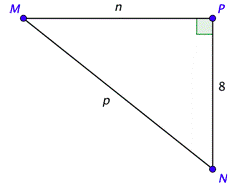
You are not given an angle measure, but you can use the definition of tangent to find the value of \(n\).

Use the ratio you are given on the left side and the information from the triangle on the right side. Cross-multiply and solve for \(n\).

\(\begin{aligned} \tan N &=\frac{\text { opposite }}{\text { adjacent }} \\ \frac{5}{4} &=\frac{n}{8} \\ 40 &= 4 n \\ n &=10 \end{aligned}\)

Use the Pythagorean Theorem to find the value of \(p\).

\(\begin{array}{c} 10^{2}+8^{2}=p^{2} \\ 100+64=p^{2} \\ 164=p^{2} \\ \sqrt{164}=p \end{array}\)

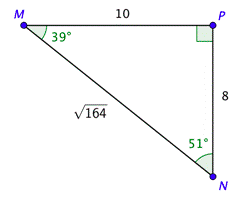
We can use the triangle to find a value of the tangent and the inverse tangent key on your calculator to find the angle that yields that value. Rounding to the nearest degree, \(\angle M\) is approximately \(39^{\circ}\), \(M \approx 39^{\circ}\). Subtract \(39^{\circ}\), from \(90^{\circ}\) to get \(N \approx 51^{\circ}\).

\(\begin{array}{c} \tan M=\frac{8}{10}=0.8 \\ M=\tan ^{-1} 0.8 \\ M \approx 38.7^{\circ} \end{array}\)

Try It \(\PageIndex{1}\)

What is the value of \(x\) to the nearest hundredth?

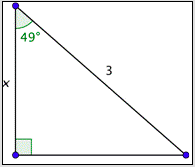
• 4.57. Incorrect. You probably set up the ratio incorrectly, equating \(\cos 49^{\circ}\) and \(\frac{3}{x}\). A correct way to set up the equation is \(\cos 49^{\circ}=\frac{x}{3}\). The correct answer is 1.97.
• 1.97. Correct. One way to set up a correct equation is to use the definition of cosine. This will give you \(\cos 49^{\circ}=\frac{x}{3}\). The solution to this equation is: \(x=3 \cdot \cos 49^{\circ} \approx 3 \cdot(0.656)=1.968\). This rounds to 1.97.
• 0.90. Incorrect. You probably set up the correct equation, \(\cos 49^{\circ}=\frac{x}{3}\), and solved it correctly. However, your calculator was not set to degrees. The correct answer is 1.97.
• 0.22. Incorrect. You may have correctly set up your equation as \(\cos 49^{\circ}=\frac{x}{3}\), but then incorrectly solved it as \(x=\frac{\cos 49^{\circ}}{3}\). The correct answer is 1.97.

Using Trigonometry in Real-World Problems

There are situations in the real world, such as building a ramp for a loading dock, in which you have a right triangle with certain information about the sides and angles, and you wish to find unknown measures of sides or angles. This is where understanding trigonometry can help you.

Example \(\PageIndex{5}\)

Problem: Ben and Emma are out flying a kite. Emma can see that the kite string she is holding is making a \(70^{\circ}\) angle with the ground. The kite is directly above Ben, who is standing 50 feet away. To the nearest foot, how many feet of string has Emma let out?

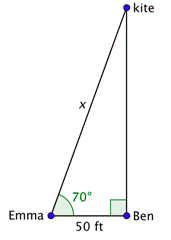
We want to find the length of string let out. It is the hypotenuse of the right triangle shown.

Since the 50-foot distance measures the adjacent side to the \(70^{\circ}\) angle, you can use the cosine function to find \(x\).

\(\cos 70^{\circ}=\frac{50}{x}\)

Solve the equation for \(x\). Use a calculator to find a numerical value. The answer rounds to 146.

\(\begin{array}{c} x \cdot \cos 70^{\circ}=50 \\ x=\frac{50}{\cos 70^{\circ}} \\ x=\frac{50}{0.342 \ldots} \\ x=146.19 \ldots \end{array}\)

Emma has let out approximately 146 feet of string.

In the example above, you were given one side and an acute angle. In the next one, you’re given two sides and asked to find an angle. Finding an angle will usually involve using an inverse trigonometric function. The Greek letter theta, \(\theta\), is commonly used to represent an unknown angle. In this example, \(\theta\) represents the angle of elevation.

Example \(\PageIndex{6}\)

Problem: A wheelchair ramp is placed over a set of stairs so that one end is 2 feet off the ground. The other end is at a point that is a horizontal distance of 28 feet away, as shown in the diagram. What is the angle of elevation to the nearest tenth of a degree?

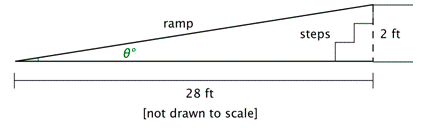
The angle of elevation is labeled \(\theta ^{\circ}\) in the diagram. The lengths given are the sides opposite and adjacent to this angle, so you can use the tangent function to find \(\theta\).

You want to find the measure of an angle that gives you a certain tangent value. This means that you need to find the inverse tangent. Remember that you have to use the keys 2ND and TAN on your calculator. Look at the hundredths place to round to the nearest tenth.

\(\begin{aligned} \tan \theta^{\circ} &=\frac{2}{28} \\ \tan \theta^{\circ} &=\frac{1}{14} \\ \theta^{\circ} &=\tan ^{-1}\left(\frac{1}{14}\right) \\ \theta &=4.0856 \ldots \end{aligned}\)

The angle of elevation is approximately \(4.1^{\circ}\).

Sometimes the right triangle can be part of a bigger picture.

Try It \(\PageIndex{2}\)

A guy wire is attached to a telephone pole 3 feet below the top of the pole, as shown below. The guy wire is anchored 14 feet from the telephone pole and makes a \(64^{\circ}\) angle with the ground. How high up the pole is the guy wire attached? Round your answer to the nearest tenth of a foot.

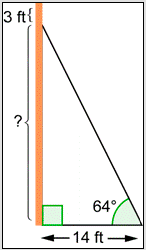
• \(14 \cdot \sin 64^{\circ} \approx 12.6 \text { feet }\)
• \(14 \cdot \tan 64^{\circ} \approx 28.7 \text { feet }\)
• \(14 \cdot \tan 64^{\circ}+3 \approx 31.7 \text { feet }\)
• \(\frac{14}{\cos 64^{\circ}} \approx 31.9 \text { feet }\)
• \(14 \cdot \sin 64^{\circ} \approx 12.6 \text { feet }\). Incorrect. You may have been confused as to which ratio corresponds to which trigonometric function. You need to solve the equation \(\tan 64^{\circ}=\frac{x}{14}\), where \(x\) represents the vertical distance from the base of the telephone pole up to where the guy wire is attached. The correct answer is \(14 \cdot \tan 64^{\circ} \approx 28.7 \text { feet }\).
• \(14 \cdot \tan 64^{\circ} \approx 28.7 \text { feet }\). Correct. Let \(x\) represent the vertical distance from the base of the telephone pole up to where the guy wire is attached. Then \(\tan 64^{\circ}=\frac{x}{14}\). Solving this equation for \(x\) gives you \(x=14 \cdot \tan 64^{\circ} \approx 28.7 \text { feet }\).
• \(14 \cdot \tan 64^{\circ}+3 \approx 31.7 \text { feet }\). Incorrect. It looks like you set up and solved the correct equation to find the unknown length. However, you misread the problem. When you added the 3 you found the height of the entire pole. The correct answer is \(14 \cdot \tan 64^{\circ} \approx 28.7 \text { feet }\).
• \(\frac{14}{\cos 64^{\circ}} \approx 31.9 \text { feet }\). Incorrect. It looks like you set up and solved an equation to find the length of the wire (the hypotenuse of the triangle). You need to solve the equation \(\tan 64^{\circ}=\frac{x}{14}\), where \(x\) represents the vertical distance from the base of the telephone pole up to where the guy wire is attached. The correct answer is \(14 \cdot \tan 64^{\circ} \approx 28.7 \text { feet }\).

There are many ways to find the missing side lengths or angle measures in a right triangle. Solving a right triangle can be accomplished by using the definitions of the trigonometric functions and the Pythagorean Theorem. This process is called solving a right triangle. Being able to solve a right triangle is useful in solving a variety of real-world problems such as the construction of a wheelchair ramp.

Chapter 8: Right Triangles and Trigonometry

• Chapter Readiness Quiz
• Chapter Test
• Math in Motion
• Standardized Test Practice
• Vocabulary Review

The resource you requested requires you to enter a username and password below:

Please read our Terms of Use and Privacy Notice before you explore our Web site. To report a technical problem with this Web site, please contact the site producer .

Lesson 8: Solve for Unknown Angles—Angles in a Triangle

Related documents

Study collections

Add this document to collection(s).

You can add this document to your study collection(s)

Add this document to saved

You can add this document to your saved list

Suggest us how to improve StudyLib

(For complaints, use another form )

Input it if you want to receive answer

Sine and Cosine in the Same Right Triangle

8.1: Which One Doesn’t Belong: Four Triangles (5 minutes)

CCSS Standards

Building On

• HSG-SRT.C.6

Routines and Materials

Instructional Routines

• Which One Doesn’t Belong?

This warm-up prompts students to compare four triangles. It gives students a reason to use language precisely (MP6). It gives the teacher an opportunity to hear how students use terminology and talk about characteristics of the items in comparison to one another. 

Arrange students in groups of 2–4. Display the triangles for all to see. Give students 1 minute of quiet think time and then time to share their thinking with their small group. In their small groups, ask each student to share their reasoning why a particular item does not belong, and together find at least one reason each item doesn't belong.

Student Facing

Which one doesn’t belong?

Student Response

For access, consult one of our IM Certified Partners .

Activity Synthesis

Ask each group to share one reason why a particular item does not belong. Record and display the responses for all to see. After each response, ask the class if they agree or disagree. Since there is no single correct answer to the question of which one does not belong, attend to students’ explanations and ensure the reasons given are correct.

During the discussion, ask students to explain the meaning of any terminology they use. Also, press students to defend unsubstantiated claims.

If not mentioned by students, remind the class that trigonometry only works with right triangles.

8.2: Twin Triangles (15 minutes)

• HSG-SRT.C.7
• MLR8: Discussion Supports

Required Materials

• Scientific calculators

In this partner activity, students take turns writing and solving trigonometric equations. As students trade roles explaining their thinking and listening, they have opportunities to explain their reasoning and critique the reasoning of others (MP3). This allows students to continue to practice applying trigonometry while simultaneously generating data for a compare/contrast activity. By comparing the two columns, students will notice the triangles are congruent since the angles given are complementary. The discussion will culminate in a conjecture that \(\sin(\theta)=\cos(90 - \theta)\) which students will prove in the next activity.

Arrange students in pairs or groups of 4. Tell half the group to work on column A while the other half of the group works on column B.

Your teacher will assign you to either Column A or Column B. Find the value of the variable for the problems in your column.

Compare your solutions with your group's solutions. Why did you get the same answers to different problems?

Ask students to share any equations they used and record each response for all to see.

A1:  \(\cos(41)=\frac{7}{x}\)

B1:  \(\sin(49)=\frac{7}{x}\)

A2:  \(\sin(65)=\frac{y}{6}\)

B2:  \(\cos(25)=\frac{y}{6}\)

A3:  \(\sin(50)=\frac{8}{z}\)

B3:  \(\cos(40)=\frac{8}{z}\)

Ask students to share the reasons they came up with for all the answers being the same. Discuss that each row is the same triangle because all the triangles have one right angle and the other two angles are complementary. So each row of equations is saying the same thing but from different perspectives. Cosine and sine have a special relationship, one students already explored before they knew the names cosine or sine. Ask students to think back to any conjectures they made while building the right triangle table. Discuss until students agree on a precise conjecture such as, “The sine of any acute angle is equal to the cosine of the complementary angle.”

“Mathematicians often use Greek letters to represent angles. Theta,  \(\theta\) , is a Greek letter we use frequently in trigonometry. What other Greek letters do you know?” ( \(\pi, \alpha\) . . .)

“Let’s write the conjecture you just came up with using theta: \(\sin(\theta)=\cos(90 - \theta)\) . In the next activity you will prove this conjecture.”

8.3: Explain the Co-nnection (15 minutes)

• Tools for creating a visual display

Students will take the examples from the previous activity and generalize them into a proof of \(\sin(\theta)=\cos(90 - \theta)\) . Monitor for groups that create displays that communicate their mathematical thinking clearly, contain an error that would be instructive to discuss, or organize the information in a way that is useful for all to see.

During the lesson synthesis students will use this equation and generate more examples to explore the relationship between cosine and sine further by determining which angles cause sine to be less than cosine, equal to cosine, or greater than cosine.

Arrange students in groups of 2–4. Provide each group with tools for creating a visual display. Clarify that they will be writing a draft individually first, before they work as a group to write a convincing argument.

• Draw a diagram that will help you explain why \(\sin(\theta)=\cos(90 - \theta)\) .
• Explain why \(\sin(\theta)=\cos(90 - \theta)\) .

Discuss your thinking with your group. If you disagree, work to reach an agreement.

Create a visual display that includes:

• A clearly-labeled diagram.
• An explanation using precise language.

Are you ready for more?

• Make a conjecture about the relationship between \(\tan(\theta)\) and \(\tan(90-\theta)\) .
• Prove your conjecture.

Anticipated Misconceptions

If students struggle prompt them to draw a right triangle and label one of the acute angles  \(\theta\) . Ask them what is the measure of the other acute angle. ( \(90-\theta\) ) Then prompt students to label the sides with any variables.

Select groups to share their visual displays. Encourage students to ask questions about the mathematical thinking or design approach that went into creating the display. Here are questions for discussion, if not already mentioned by students:

• How can you clearly connect the explanation to the diagram? (label the parts, draw arrows, use phrases such as 'adjacent leg')
• What type of triangle does this equation work for? (only right triangles)

Lesson Synthesis

Give students a few minutes to respond to the prompt: “Use the visual displays and any other resources available to find values of \(\theta\) where:

\(\sin(\theta)<\cos(\theta)\)

• \(\sin(\theta)=\cos(\theta)\)

\(\sin(\theta)>\cos(\theta)\)

How does this relate to the equation \(\sin(\theta)=\cos(90 - \theta)\) ?"

Students should notice: 

• \(\sin(\theta)<\cos(\theta)\)  if  \(\theta<45\)
• \(\sin(\theta)=\cos(\theta)\)  if  \(\theta=45\)
• \(\sin(\theta)>\cos(\theta)\)  if  \(\theta>45\)

Invite students to share their thinking. (We know  \(\sin(\theta)=\cos(90 - \theta)\)  so if we also want  \(\sin(\theta)=\cos(\theta)\) that means  \(\theta=90-\theta\) . The only solution to \(\theta=90-\theta\) is 45 degrees. That's because 45 degrees is complementary to itself.)

Display sketches of triangles to solidify that, for example,  \(\sin(\theta)<\cos(\theta)\) when \(\theta<45\) because when the angle is small the opposite leg will be shorter than the adjacent leg. So,  \(\sin(\theta)=\frac{\text{short leg}}{\text{hypotenuse}}\) ,  \(\cos(\theta)=\frac{\text{long leg}}{\text{hypotenuse}}\)

\(\sin(\theta)=\cos(\theta)\) ​​​​​​

8.4: Cool-down - Cosine’s Complement (5 minutes)

Student lesson summary.

In previous lessons, we recalled that any right triangle with acute angles of 25 and 65 degrees was similar to any other right triangle with these same acute angles. Revisiting these triangles, we notice that the sine of 25 degrees is equal to the cosine of 65 degrees, and the cosine of 25 degrees is equal to the sine of 65 degrees.

Looking at a general right triangle, the angles can be written as 90, \(\theta\) , and \(90-\theta\) . Mathematicians often use Greek letters to represent angles. For instance,  \(\theta\) is a Greek letter we use frequently in trigonometry.

Geometry: Common Core (15th Edition)

By charles, randall i., chapter 8 - right triangles and trigonometry - 8-3 trigonometry - practice and problem-solving exercises - page 510: 11, work step by step, update this answer.

You can help us out by revising, improving and updating this answer.

After you claim an answer you’ll have 24 hours to send in a draft. An editor will review the submission and either publish your submission or provide feedback.

• Texas Go Math
• Big Ideas Math
• Engageny Math
• McGraw Hill My Math
• enVision Math
• 180 Days of Math
• Math in Focus Answer Key
• Math Expressions Answer Key
• Privacy Policy

Eureka Math Grade 8 Module 3 Lesson 14 Answer Key

Engage ny eureka math 8th grade module 3 lesson 14 answer key, eureka math grade 8 module 3 lesson 14 example answer key.

Eureka Math Grade 8 Module 3 Lesson 14 Exercise Answer Key

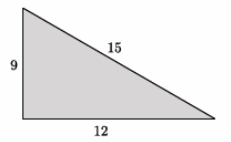
Eureka Math Grade 8 Module 3 Lesson 14 Exit Ticket Answer Key

Question 2. Do the lengths 5, 9, and 14 form a right triangle? Explain. Answer: No, the lengths of 5, 9, and 14 do not form a right triangle. If they did, then the equation 5 2 +9 2 =14 2 would be a true statement. However, the left side equals 106, and the right side equals 196. Therefore, these lengths do not form a right triangle.

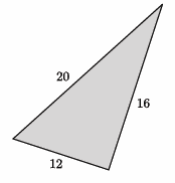
Eureka Math Grade 8 Module 3 Lesson 14 Problem Set Answer Key

Students practice using the converse of the Pythagorean theorem and identifying common errors in computations.

Leave a Comment Cancel Reply

You must be logged in to post a comment.