what is fluency reasoning and problem solving in maths

Mastery-Aligned Maths Tutoring

“The best thing has been the increase in confidence and tutors being there to deal with any misunderstandings straight away."

FREE daily maths challenges

A new KS2 maths challenge every day. Perfect as lesson starters - no prep required!

Fluency, Reasoning and Problem Solving: What This Looks Like In Every Maths Lesson

Neil Almond

Fluency reasoning and problem solving have been central to the new maths national curriculum for primary schools introduced in 2014. Here we look at how these three approaches or elements of maths can be interwoven in a child’s maths education through KS1 and KS2. We look at what fluency, reasoning and problem solving are, how to teach them, and how to know how a child is progressing in each – as well as what to do when they’re not, and what to avoid.

The hope is that this blog will help primary school teachers think carefully about their practice and the pedagogical choices they make around the teaching of reasoning and problem solving in particular.

Before we can think about what this would look like in practice however, we need to understand the background tothese terms.

What is fluency in maths?

Fluency in maths is a fairly broad concept. The basics of mathematical fluency – as defined by the KS1 / KS2 National Curriculum for maths – involve knowing key mathematical facts and being able to recall them quickly and accurately.

But true fluency in maths (at least up to Key Stage 2) means being able to apply the same skill to multiple contexts, and being able to choose the most appropriate method for a particular task.

Fluency in maths lessons means we teach the content using a range of representations, to ensure that all pupils understand and have sufficient time to practise what is taught.

Read more: How the best schools develop maths fluency at KS2 .

What is reasoning in maths?

Reasoning in maths is the process of applying logical thinking to a situation to derive the correct problem solving strategy for a given question, and using this method to develop and describe a solution.

Put more simply, mathematical reasoning is the bridge between fluency and problem solving. It allows pupils to use the former to accurately carry out the latter.

Read more: Developing maths reasoning at KS2: the mathematical skills required and how to teach them .

What is problem solving in maths?

It’s sometimes easier to start off with what problem solving is not. Problem solving is not necessarily just about answering word problems in maths. If a child already has a readily available method to solve this sort of problem, problem solving has not occurred. Problem solving in maths is finding a way to apply knowledge and skills you have to answer unfamiliar types of problems.

Read more: Maths problem solving: strategies and resources for primary school teachers .

We are all problem solvers

First off, problem solving should not be seen as something that some pupils can do and some cannot. Every single person is born with an innate level of problem-solving ability.

Early on as a species on this planet, we solved problems like recognising faces we know, protecting ourselves against other species, and as babies the problem of getting food (by crying relentlessly until we were fed).

All these scenarios are a form of what the evolutionary psychologist David Geary (1995) calls biologically primary knowledge. We have been solving these problems for millennia and they are so ingrained in our DNA that we learn them without any specific instruction.

Why then, if we have this innate ability, does actually teaching problem solving seem so hard?

Mathematical problem solving is a  learned skill

As you might have guessed, the domain of mathematics is far from innate. Maths doesn’t just happen to us; we need to learn it. It needs to be passed down from experts that have the knowledge to novices who do not.

This is what Geary calls biologically secondary knowledge. Solving problems (within the domain of maths) is a mixture of both primary and secondary knowledge.

The issue is that problem solving in domains that are classified as biologically secondary knowledge (like maths) can only be improved by practising elements of that domain.

So there is no generic problem-solving skill that can be taught in isolation and transferred to other areas.

This will have important ramifications for pedagogical choices, which I will go into more detail about later on in this blog.

The educationalist Dylan Wiliam had this to say on the matter: ‘for…problem solving, the idea that pupils can learn these skills in one context and apply them in another is essentially wrong.’ (Wiliam, 2018)So what is the best method of teaching problem solving to primary maths pupils?

The answer is that we teach them plenty of domain specific biological secondary knowledge – in this case maths. Our ability to successfully problem solve requires us to have a deep understanding of content and fluency of facts and mathematical procedures.

Here is what cognitive psychologist Daniel Willingham (2010) has to say:

‘Data from the last thirty years lead to a conclusion that is not scientifically challengeable: thinking well requires knowing facts, and that’s true not simply because you need something to think about.

The very processes that teachers care about most—critical thinking processes such as reasoning and problem solving—are intimately intertwined with factual knowledge that is stored in long-term memory (not just found in the environment).’

Colin Foster (2019), a reader in Mathematics Education in the Mathematics Education Centre at Loughborough University, says, ‘I think of fluency and mathematical reasoning, not as ends in themselves, but as means to support pupils in the most important goal of all: solving problems.’

In that paper he produces this pyramid:

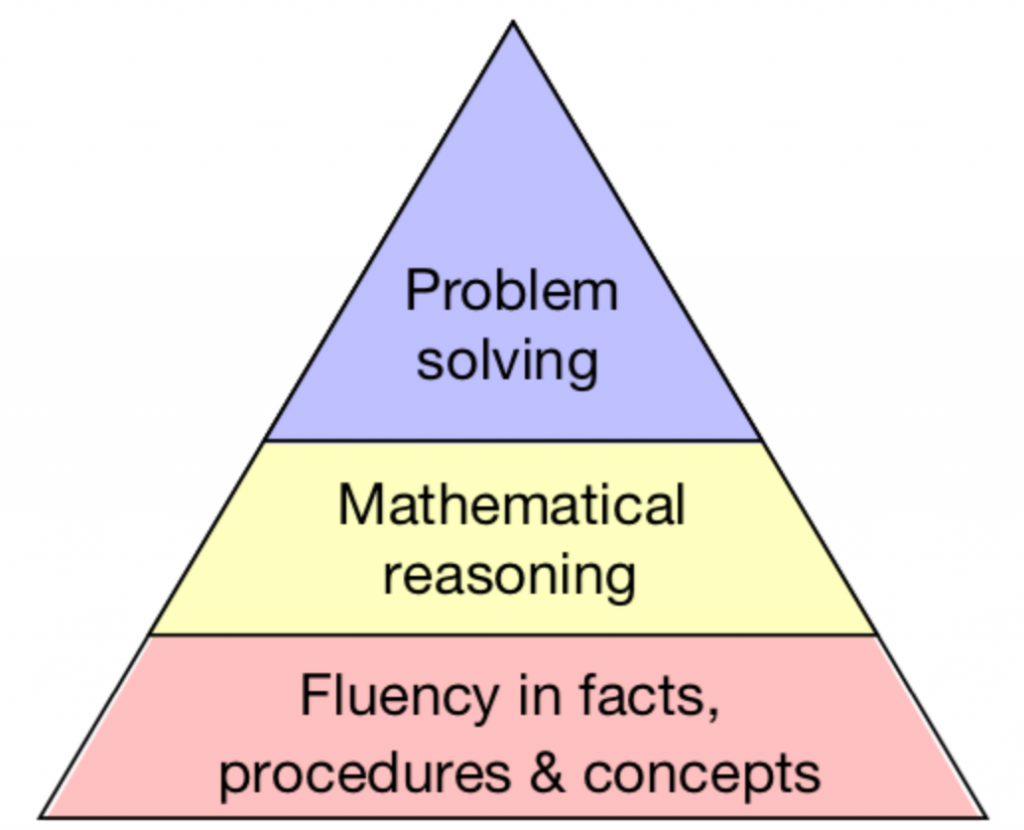
This is important for two reasons:

1)    It splits up reasoning skills and problem solving into two different entities

2)    It demonstrates that fluency is not something to be rushed through to get to the ‘problem solving’ stage but is rather the foundation of problem solving.

In my own work I adapt this model and turn it into a cone shape, as education seems to have a problem with pyramids and gross misinterpretation of them (think Bloom’s taxonomy).

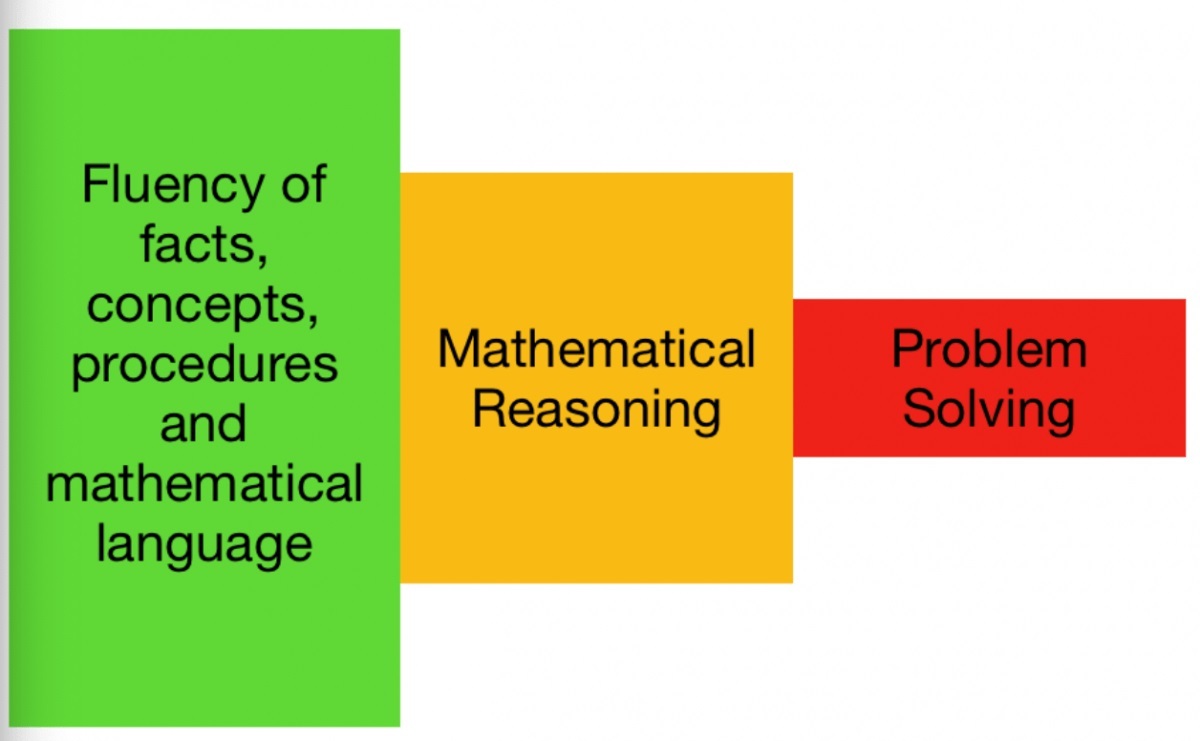
Notice how we need plenty of fluency of facts, concepts, procedures and mathematical language.

Having this fluency will help with improving logical reasoning skills, which will then lend themselves to solving mathematical problems – but only if it is truly learnt and there is systematic retrieval of this information carefully planned across the curriculum.

Performance vs learning: what to avoid when teaching fluency, reasoning, and problem solving

I mean to make no sweeping generalisation here; this was my experience both at university when training and from working in schools.

At some point schools become obsessed with the ridiculous notion of ‘accelerated progress’. I have heard it used in all manner of educational contexts while training and being a teacher. ‘You will need to show ‘ accelerated progress in maths ’ in this lesson,’ ‘Ofsted will be looking for ‘accelerated progress’ etc.

I have no doubt that all of this came from a good place and from those wanting the best possible outcomes – but it is misguided.

I remember being told that we needed to get pupils onto the problem solving questions as soon as possible to demonstrate this mystical ‘accelerated progress’.

This makes sense; you have a group of pupils and you have taken them from not knowing something to working out pretty sophisticated 2-step or multi-step word problems within an hour. How is that not ‘accelerated progress?’

This was a frequent feature of my lessons up until last academic year: teach a mathematical procedure; get the pupils to do about 10 of them in their books; mark these and if the majority were correct, model some reasoning/problem solving questions from the same content as the fluency content; set the pupils some reasoning and word problem questions and that was it.

I wondered if I was the only one who had been taught this while at university so I did a quick poll on Twitter and found that was not the case.

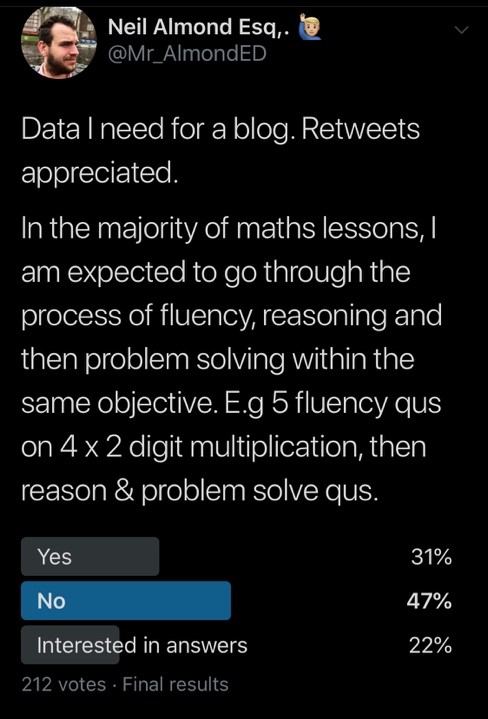
I know these numbers won’t be big enough for a representative sample but it still shows that others are familiar with this approach.

The issue with the lesson framework I mentioned above is that it does not take into account ‘performance vs learning.’

What IS performance vs learning’?

The premise is that performance in a lesson is not a good proxy for learning.

Yes, those pupils were performing well after I had modeled a mathematical procedure for them, and managed to get questions correct.

But if problem solving depends on a deep knowledge of mathematics, this approach to lesson structure is going to be very ineffective.

As mentioned earlier, the reasoning and problem solving questions were based on the same maths content as the fluency exercises, making it more likely that pupils would solve problems correctly whether they fully understood them or not.

Chances are that all they’d need to do is find the numbers in the questions and use the same method they used in the fluency section to get their answers – not exactly high level problem solving skills.

Teaching to “cover the curriculum” hinders development of strong problem solving skills.

This is one of my worries with ‘maths mastery schemes’ that block content so that, in some circumstances, it is not looked at again until the following year (and with new objectives).

The pressure for teachers to ‘get through the curriculum’ results in many opportunities to revisit content just not happening in the classroom.

Pupils are unintentionally forced to skip ahead in the fluency, reasoning, problem solving chain without proper consolidation of the earlier processes.

As David Didau (2019) puts it, ‘When novices face a problem for which they do not have a conveniently stored solution, they have to rely on the costlier means-end analysis.

This is likely to lead to cognitive overload because it involves trying to work through and hold in mind multiple possible solutions.

It’s a bit like trying to juggle five objects at once without previous practice. Solving problems is an inefficient way to get better at problem solving.’

Third Space's Ultimate Guide to Problem Solving Techniques

Download our free guide to problem solving techniques and get a head start on ensuring learning over performance!

Fluency and reasoning – Best practice in a lesson, a unit, and a term

By now I hope you have realised that when it comes to problem solving, fluency is king. As such we should look to mastery maths based teaching to ensure that the fluency that pupils need is there.

The answer to what fluency looks like will obviously depend on many factors, including the content being taught and the year group you find yourself teaching.

But we should not consider rushing them on to problem solving or logical reasoning in the early stages of this new content as it has not been learnt, only performed.

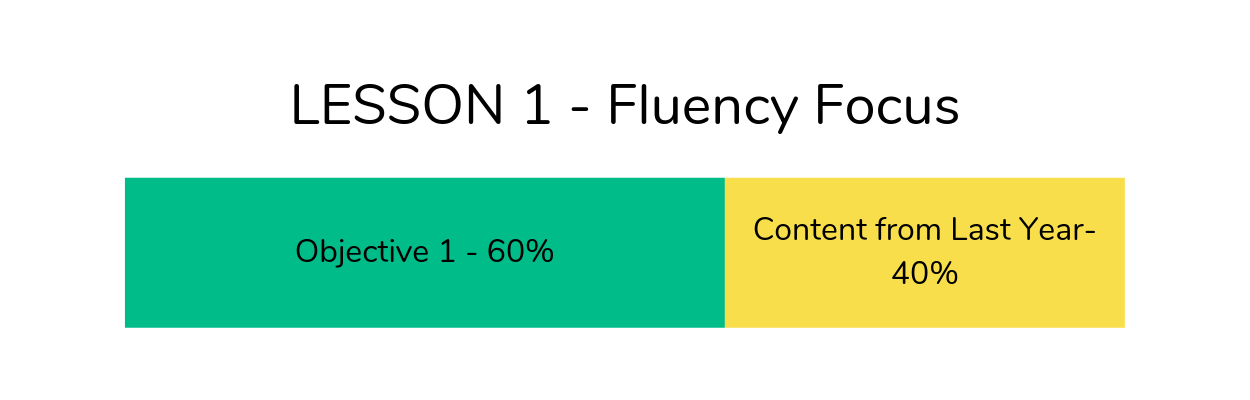
I would say that in the early stages of learning, content that requires the end goal of being fluent should take up the majority of lesson time – approximately 60%. The rest of the time should be spent rehearsing and retrieving other knowledge that is at risk of being forgotten about.

This blog on mental maths strategies pupils should learn in each year group is a good place to start when thinking about the core aspects of fluency that pupils should achieve.

Little and often is a good mantra when we think about fluency, particularly when revisiting the key mathematical skills of number bond fluency or multiplication fluency. So when it comes to what fluency could look like throughout the day, consider all the opportunities to get pupils practicing.

They could chant multiplications when transitioning. If a lesson in another subject has finished earlier than expected, use that time to quiz pupils on number bonds. Have fluency exercises as part of the morning work.

Read more: How to teach times tables KS1 and KS2 for total recall .

What about best practice over a longer period?

Thinking about what fluency could look like across a unit of work would again depend on the unit itself.

Look at this unit below from a popular scheme of work.

They recommend 20 days to cover 9 objectives. One of these specifically mentions problem solving so I will forget about that one at the moment – so that gives 8 objectives.

I would recommend that the fluency of this unit look something like this:

LY = Last Year

This type of structure is heavily borrowed from Mark McCourt’s phased learning idea from his book ‘Teaching for Mastery.’

This should not be seen as something set in stone; it would greatly depend on the needs of the class in front of you. But it gives an idea of what fluency could look like across a unit of lessons – though not necessarily all maths lessons.

When we think about a term, we can draw on similar ideas to the one above except that your lessons could also pull on content from previous units from that term.

So lesson one may focus 60% on the new unit and 40% on what was learnt in the previous unit.

The structure could then follow a similar pattern to the one above.

Best practice for problem solving in a lesson, a unit, and a term 

When an adult first learns something new, we cannot solve a problem with it straight away. We need to become familiar with the idea and practise before we can make connections, reason and problem solve with it.

The same is true for pupils. Indeed, it could take up to two years ‘between the mathematics a student can use in imitative exercises and that they have sufficiently absorbed and connected to use autonomously in non-routine problem solving.’ (Burkhardt, 2017).

Practise with facts that are secure

So when we plan for reasoning and problem solving, we need to be looking at content from 2 years ago to base these questions on.

Now given that much of the content of the KS2 SATs will come from years 5 and 6 it can be hard to stick to this two-year idea as pupils will need to solve problems with content that can be only weeks old to them.

But certainly in other year groups, the argument could be made that content should come from previous years.

You could get pupils in Year 4 to solve complicated place value problems with the numbers they should know from Year 2 or 3. This would lessen the cognitive load, freeing up valuable working memory so they can actually focus on solving the problems using content they are familiar with.

Read more: Cognitive load theory in the classroom

Increase complexity gradually.

Once they practise solving these types of problems, they can draw on this knowledge later when solving problems with more difficult numbers.

This is what Mark McCourt calls the ‘Behave’ phase. In his book he writes:

‘Many teachers find it an uncomfortable – perhaps even illogical – process to plan the ‘Behave’ phase as one that relates to much earlier learning rather than the new idea, but it is crucial to do so if we want to bring about optimal gains in learning, understanding and long term recall.’  (Mark McCourt, 2019)

This just shows the fallacy of ‘accelerated progress’; in the space of 20 minutes some teachers are taught to move pupils from fluency through to non-routine problem solving, or we are somehow not catering to the needs of the child.

When considering what problem solving lessons could look like, here’s an example structure based on the objectives above.

Fluency, Reasoning and Problem Solving should NOT be taught by rote 

It is important to reiterate that this is not something that should be set in stone. Key to getting the most out of this teaching for mastery approach is ensuring your pupils (across abilities) are interested and engaged in their work.

Depending on the previous attainment and abilities of the children in your class, you may find that a few have come across some of the mathematical ideas you have been teaching, and so they are able to problem solve effectively with these ideas.

Equally likely is encountering pupils on the opposite side of the spectrum, who may not have fully grasped the concept of place value and will need to go further back than 2 years and solve even simpler problems.

In order to have the greatest impact on class performance, you will have to account for these varying experiences in your lessons.

Read more: 

• Maths Mastery Toolkit : A Practical Guide To Mastery Teaching And Learning
• Year 6 Maths Reasoning Questions and Answers
• Get to Grips with Maths Problem Solving KS2
• Mixed Ability Teaching for Mastery: Classroom How To
• 21 Maths Challenges To Really Stretch Your More Able Pupils
• Maths Reasoning and Problem Solving CPD Powerpoint
• Why You Should Be Incorporating Stem Sentences Into Your Primary Maths Teaching

DO YOU HAVE STUDENTS WHO NEED MORE SUPPORT IN MATHS?

Every week Third Space Learning’s specialist online maths tutors support thousands of students across hundreds of schools with weekly online 1 to 1 maths lessons designed to plug gaps and boost progress.

Since 2013 these personalised one to 1 lessons have helped over 150,000 primary and secondary students become more confident, able mathematicians.

Learn how the programmes are aligned to maths mastery teaching or request a personalised quote for your school to speak to us about your school’s needs and how we can help.

Related articles

Maths Problem Solving: Engaging Your Students And Strengthening Their Mathematical Skills

Free Year 7 Maths Test With Answers And Mark Scheme: Mixed Topic Questions

What Is A Number Square? Explained For Primary School Teachers, Parents & Pupils

What Is Numicon? Explained For Primary School Teachers, Parents And Pupils

FREE Guide to Maths Mastery

All you need to know to successfully implement a mastery approach to mathematics in your primary school, at whatever stage of your journey.

Ideal for running staff meetings on mastery or sense checking your own approach to mastery.

Privacy Overview

• Big Ideas Login
• Request a Sample

Mathematical Fluency: What Is It and Why Does It Matter?

• Judy Hickman

Let’s address fluency in math by defining what fluency is, why it matters, and how the three stages of fluency are defined by Florida in the B.E.S.T. Standards for Mathematics.

What is mathematical fluency.

“When we are fluent in a language, we can respond and converse without having to think too hard. The language comes naturally, and we do not use up space in our brain thinking about what word to use. Fluency comes from using the language in multiple settings, from trying things out, and failing and trying again.” – Dr. Nic, Creative Maths  

This approach to fluency in any language applies to the language of mathematics, too.

In mathematics, fluency builds on a foundation of conceptual understanding, strategic reasoning, and problem-solving to achieve automaticity. Students connect conceptual understanding (Stage 1) with strategies and methods (Stage 2) and use the methods in a way that makes sense to them (Stage 3) .

When students go through these stages to build fluency, they gain an understanding of the operations and the strategies and methods in their toolbox for solving them, and they become strategic thinkers who can efficiently compute arithmetic.

Fluency is often misunderstood as being able to quickly compute basic math facts, regardless of conceptual understanding, otherwise known as memorization. But being fluent in mathematics is more than memorization, accuracy, and speed.

Accuracy goes beyond memorizing a procedure to get the right answer; it involves understanding the meaning of the procedure, applying it carefully, and checking to see if the answer makes sense. Emphasizing speed can discourage flexible thinking. True fluency is built when students are permitted to stop, think, and use strategies that make sense to efficiently solve a problem.

Why is mathematical fluency important?

By building fluency in math, students can efficiently use foundational skills to solve deeper, more meaningful problems that they encounter in the world around them. Fluency contributes to success in the math classroom and in everyday life.

For example, math fluency is useful for:

• adding scores while playing a game
• using mental math to decide the best buy while shopping at a grocery store
• estimating a percent when determining a tip for a delivery driver
• and so much more!

Throughout everyday life, fluent math thinkers use strategies and methods that they understand to efficiently compute operations and check that their answers are reasonable.

“While being fluent with math facts doesn’t make word problems easy, it does reduce the number of cognitive resources needed to tackle the computation portion of the process, allowing those resources to be allocated to other components of the process.” – Differentiated Teaching

3 Stages of Fluency Defined by Florida’s B.E.S.T. Standards for Mathematics

Let’s examine the three stages of fluency as defined by Florida’s B.E.S.T Standards for Mathematics .

Stage 1: Exploration

• Students investigate arithmetic operations to increase understanding by using manipulatives, visual models, and engaging in rich discussion.
• Models help build on prior learning and make connections between concepts.
• Exercises classified as Stage 1 will prompt students to use a model to solve.

Stage 2: Procedural Reliability

• Students utilize skills from the exploration stage to develop an accurate, reliable method that aligns with the student’s understanding and learning style.
• Students may need the teacher’s help to choose a method, and they are learning how to use a method without help.
• Students choose any method to solve problems independently. Then students are asked to describe their method to ensure that they understand the method and why it works.

Stage 3: Procedural Fluency

• Students build on their conceptual understanding from Stages 1 and 2 and use an efficient and accurate procedure to compute an operation, including the standard algorithms.
• Students are no longer asked to describe their method because they are proving that they can solve accurately and without assistance.

Note: E mbedded within Stages 1-3 is Automaticity . Automaticity is the ability to act according to an automatic response which is easily retrieved from long-term memory. It usually results from repetition and practice.

How do math programs and curriculum incorporate fluency?

When looking for a new math curriculum, districts should consider math programs that use a variety of models (Stage 1) and strategies (Stage 2) as well as standard algorithms (Stage 3) to teach math.

Practice problems should encourage the use of various methods to solve problems as well as student explanations of the methods they choose to use (Stage 2). Student exploration, collaboration, and peer discussion will also aid students in the development of their mathematical thinking.

Programs that integrate foundational mathematical thinking and reasoning skills will help students become mathematical thinkers who can strategically choose efficient methods to solve problems.

By acquiring mathematical fluency, students will have a greater cognitive capacity to solve more complex problems in the real world.

Related Articles

Understanding florida's mathematical thinking and reasoning (mtr) standards.

Topics: Florida , MTR

You are using an outdated browser. Please upgrade your browser to improve your experience.

Here’s Why Mathematical Fluency is Critical For Problem-Solving and Reasoning

In summary: Mathematical fluency skills help students think faster and more clearly, giving them the energy, attention and focus to tackle complex problem-solving and reasoning questions.

The future needs problem-solvers with reasoning skills. But as education shifts its focus to the critical and creative angle of mathematics problems, we can’t lose sight of the abilities and skills that make this thinking possible:  mathematical fluency .

We’ve covered mathematical fluency in another article ( What is mathematical fluency? ), but here’s the TL;DR version:

Mathematical fluency is the ability to quickly and accurately recall mathematical facts and concepts. It’s made up of 5 key parts – accuracy, flexibility and appropriate response, efficiency, automaticity, and number sense. 

Fluency builds the foundations students use to tackle more complex, multi-step questions in problem-solving and reasoning activities, and it’s crucial to their success. Here’s why:

Mathematical fluency saves energy

Students have only so much energy. You’ll have noticed this before and after lunch breaks. The same principles apply when it comes to problem-solving and reasoning activities.

Let’s say your PSR activity has five steps, and each one of them has four or five problems to solve. The more energy students spend on figuring out those smaller questions, the less they’ll have when it comes to critically and creatively tackling the whole question.

Further, when students aren’t succeeding at one part of a larger problem, it can make the entire activity seem like an overwhelming exercise.

If we’re to look at a student’s brain, those with high fluency skills would have efficient neural pathways, meaning there’s less energy spent and less time is taken for the question to be received and for the answer to be found.

The good news is that these neural pathways are strengthened with repeated exercise, like with any learned behaviour.

By getting students to practice fluency, you’re strengthening the mind muscles they need to do heavier lifting and for longer.

Fluency saves time

Hand-in-hand with saving energy, fluency saves time for students, and this has two distinct benefits: it helps students stay focused on the logical progression of problems and perform better on tests.

Focus  – In a multi-step problem that asks students to use several approaches (like a mix of geometry, algebra, fractions and so on), being able to recall or solve the minutiae with little or no effort keeps them from losing focus on their logical progression.

It’s like being on a hike where you’re expected to find your food and water, camp, and mountain climb – if you’re stuck focusing on each step and breathing in and out, you probably won’t feel much like setting up a tent or getting your ropes and climbing gear in order.

Better test-taking  – Tests have time limits and they’re stressful. Fluency alleviates these pressures; first, by enabling students to attempt to complete more questions, and by getting around the roadblocks of basic computations (like counting on fingers, writing down, working out or reaching for the calculator).

Math fluency builds confidence and reduces mathematics anxiety

Motivation, engagement and progress all rely on students’ confidence that they can complete tasks. For students with mathematics anxiety (the feeling of being overwhelmed or paralysed by mathematics), this is especially important.

Strong fluency allows students to work and see success independently, growing their sense of autonomy and confidence, and helping them see whole problems as small, achievable steps.

It’s like any kind of sporting competition or arts performance; the drilled basics allow the athlete or artist to work on more complicated movements and strategies and prepares them mentally for big events.

In this case, our events are tests, problem-solving, or being introduced to new concepts and material.

Download printable worksheets for math fluency Explore resources

Early mathematical fluency is an indicator of later success

Students who have better fluency in their early education are likely to perform better as they enter secondary school. But it goes further than that  – mathematically fluent early learners see significant gains in their mathematics achievements later on .

We can make educated guesses for why this is – the pace of education and the progressive complexity of mathematics means that those who don’t develop strong fluency early will have a harder time keeping up.

This is especially true when it comes to problem-solving and reasoning.

Preparing students early with fact fluency gives them the tools they need to take on the harder problems they’ll inevitably face in their secondary schooling. If we don’t, it’s like throwing an entry-level karate student into the ring with a black belt master – they won’t have the strategy, reflex or thinking to take them on.

Mathematical fluency prepares students for the problem-solving future

It’s hard to imagine what the future careers of our students will look like. But judging by the push into an automatic world, we can almost guarantee they’ll need three key things to be successful:

• The ability to understand and manipulate data
• Critical thinking skills that will allow them to act strategically and tactically
• Creative thinking skills that enable them to approach problems in a variety of ways

How to reinforce your students’ mathematical fluency

We recommend three things:

Playing mathematics games

Practice requires repetition, and repetition is fun when it’s gamified. But games have a few further benefits:

• They encourage thinking about mathematics on a strategic level
• They need less teacher input and encourage autonomous learning
• They build students computational fluency
• They connect the classroom environment to the home learning environment

Daily mathematics fluency activities

Mathematics skills become strong when they’re done regularly. After a concept has been introduced, you should look to have activities planned to cement students’ knowledge until you’re confident they can work on it or use it independently.

Give students time to discover

Plan lessons that allow students time to discover number patterns, structures, and concepts and test them out in different situations to see if what they discovered works. This builds autonomy and gives students the chance to reflect on their learning.

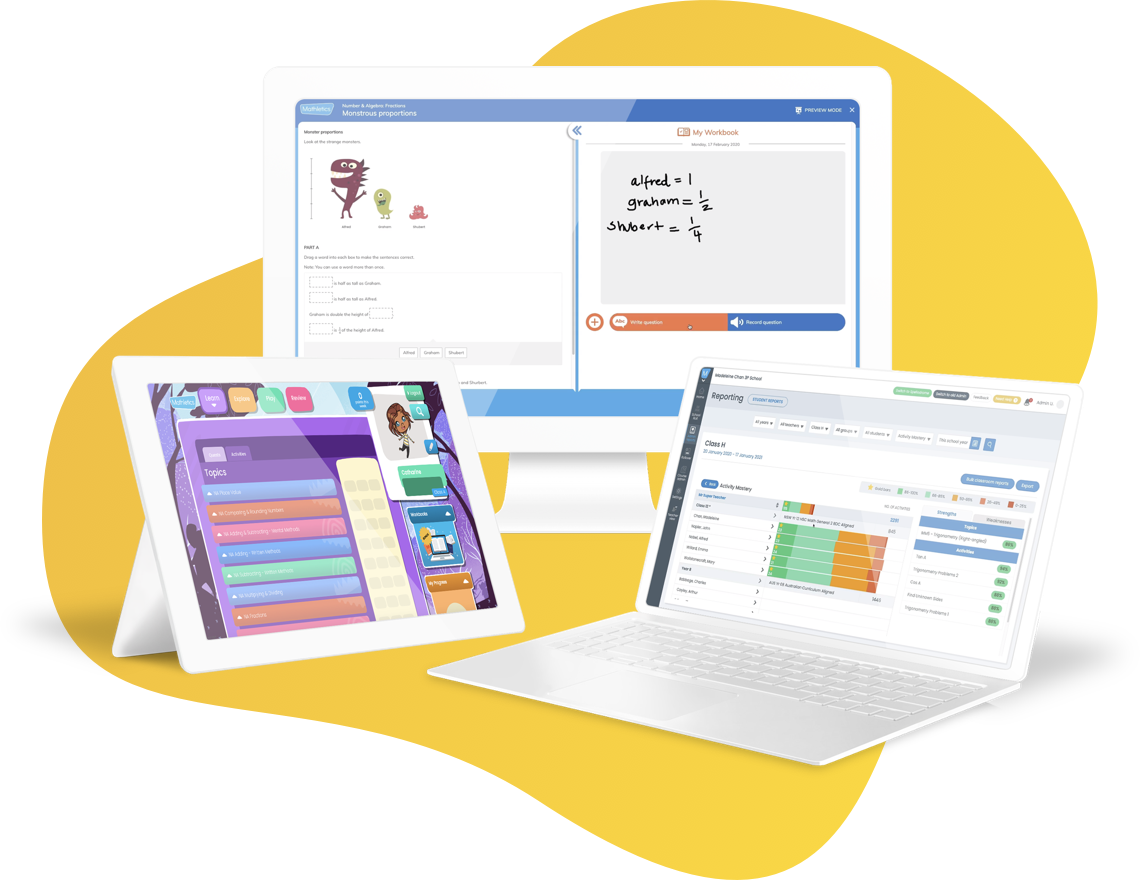
Develop mathematical fluency, problem-solving, and reasoning with our award-winning programs

You might like....

• Topical and themed
• Early years
• Special needs
• Schools directory
• Resources Jobs Schools directory News Search

Fluency, reasoning and problem solving in primary maths

Primary maths, australia and new zealand, tes resources team.

Develop fluency, reasoning and problem solving within any topic as part of a mastery approach

The skills of fluency, reasoning and problem solving are well-known to all primary maths teachers. In mastery teaching , they play an essential role in helping pupils to gain a deeper understanding of a topic. But what does this look like in practice?

For more information on mastery, check out this  handy introduction .

Firstly, problem solving is at the heart of mastering maths. While there is nothing new about using problem-solving questions to consolidate understanding, mastery gets teachers to rethink the traditional lengthy word-problem format. Instead, problem-solving questions are often open-ended, with more than one right answer. 

Problem solving is an important skill for all ages and abilities and, as such, needs to be taught explicitly. It is therefore useful to have challenges like these at the end of every lesson.

Secondly, verbal reasoning demonstrates that pupils understand the maths. Talk is an integral part of mastery as it encourages students to reason, justify and explain their thinking. This is tricky for many teachers who are not used to focusing on verbal reasoning in their maths lessons. You might, for example, get young learners to voice their thought processes. Older students could take part in class debates, giving them the space to challenge their peers using logical reasoning.

Introducing scaffolded sentence structures when talking about maths gives pupils the confidence to communicate their ideas clearly, before writing them down. A mastery classroom should never be a quiet classroom.

Finally, fluency, reasoning and problem solving underpins the deepening of understanding. Fluency alone doesn’t give students the chance to delve deeper into the mathematics. They may well be able to answer the questions, but can they also justify their answer or explore other possibilities?

Typically, teachers start new topics by developing fluency in order to give learners confidence with the skill. However, sometimes starting with a problem-solving question – eg, Prove that 4+3=7 – deepens understanding sooner. How? Pupils have to be reliant on resources they’ve used elsewhere, such as concrete manipulatives and pictorial representations, to help them explain the maths.

When planning, try not to get hung up on whether an activity focuses on either reasoning or problem solving as often it is a combination. Instead, turn your attention to using these types of questions to secure fluency and ensure that all children move beyond it into a world of deeper understanding.

Fluency, reasoning and problem solving in your classroom

Embedding these concepts into your everyday teaching can take time so patience is key! Mastery specialists recommend being more fluid with your planning and investing more time in making resources that will allow you to be reactionary to progress made in the lessons.

We’ve hand-picked these useful ideas to get you started:

This blog post was written with grateful thanks to Jenny Lewis, Primary Maths Specialist at the White Rose Maths Hub, and Helen Williams, Director of Primary at Mathematics Mastery, for their insights.

Want to know more about primary maths mastery? Check out our collection of free resources, quality assured by mastery experts and helpfully mapped by topic to year groups and learning objectives.

You are using an outdated browser. Upgrade your browser today or install Google Chrome Frame to better experience this site.

• Professional learning

Teach. Learn. Grow.

Teach. learn. grow. the education blog.

Why it’s important to support fluency in mathematics

The idea of fluency is big in K–12 mathematics education. However, there is not a clear, shared meaning of the word. In fact, if you were to ask educators to define “fluency” in the context of learning mathematics, you would probably get a dozen different answers.

I encourage you to stop reading this post and think about fluency. Go ahead and pause for a moment. This post can wait. What do you believe fluency in math education is?

What fluency is when we’re talking about math?

Sometimes educators think about fluency as getting the right answer quickly. Sometimes, it’s about accurately performing a standard algorithm efficiently or remembering facts. But there is much more to it.

Fluency demands  thinking about mathematical procedures  with efficiency, accuracy, flexibility, and appropriateness. Being fluent means that students can choose among methods and strategies to solve contextual and mathematical problems, that they understand and are able to explain their approaches, and that they are able to produce accurate answers efficiently.

It helps to also define what I mean by “efficiency,” “accuracy,” “flexibility,” and “appropriateness”:

• “Efficiency” is the ways in which students carry out strategic procedural plans easily, keep track of sub-problems, and make use of intermediate results to solve a problem
• “Accuracy” means students reliably produce the correct answer
• “Flexibility” refers to students knowing more than one approach, being able to choose a viable strategy, and using one method to solve and another method to double-check their work
• “Appropriateness” means students know when to apply a particular procedure

An example: The role of fluency in understanding fractions

Simply memorizing facts and procedures does not a fluent student make. According to research done by the  Rational Number Project , students who only memorize will experience challenges in making sense of math. This is especially true when students begin to learn about fractions and operations with fractions. And, even more specifically, difficulty with operations with fractions often stems from a lack of a robust understanding of the idea of a fraction.

For example, children have difficulty internalizing that the symbol for a fraction represents a single entity. When asked if 2/3 is one or two numbers, many children will say that the symbol represents two numbers. When students consider 2/3 as two numbers, then it makes sense that they would try to treat them like whole numbers. For example, when students add two fractions by adding the numerators and then denominators, they are interpreting the symbols as four numbers, not two. Many errors with fractions can be traced to students’ lack of mental images for the quantity a symbol represents.

Students who have not fully developed fluency with fractions often have difficulty ordering fractions, since ordering fractions is more complex than ordering whole numbers. Comparing 1/4 and 1/6, for example, conflicts with children’s whole number ideas. Six is greater than four, but 1/4 is greater than 1/6. With fractions, more can mean less. In contrast, 3/5 is greater than 2/5 because three of the same-size parts are greater than two of the same-size parts. In this case, more implies more.

Being able to order plays an important part in estimating fraction addition and subtraction. Ideally when a student adds 1/4 and 1/3, they should be able to reason, from their mental images of the symbols, that a) the answer is greater than 1/2, but less than one, and b) 2/7 is an unreasonable answer because it is less than 1/2.

Understanding fraction equivalence is not as simple as it may seem. Some children have difficulty noting equivalence from pictures.

Imagine a circle partitioned into fourths with one of those fourths partitioned into three equal parts. Some children may be unable to agree that 3/12 equals 1/4, even though they can see that the two sections of the circle are the same size. Children can struggle to remove the extra lines drawn in the fourth that’s partitioned into three equal parts. But that is just what must be done to understand fraction equivalence from a picture.

All of these challenges related to a foundational understanding of the idea of a fraction can lead to the difficulties children have with fraction addition and subtraction. These difficulties come from asking students to operate on fractions before they have a strong conceptual understanding of these new numbers.

Fluency involves getting answers as well as thinking about reasons, providing explanations, and communicating thinking clearly.

How asking—and answering—“why” can improve mathematical fluency

To help students gain fluency in math, it’s important to help them explore and understand why.

Consider the following problem: 2/3 x 3/4. Most readers will likely be able to compute the correct answer mentally (the answer is 1/2). It is important to be able to get this answer but also to explain how it makes sense. When working with students on a problem like this one, consider asking them questions like these:

• Why does 2/3 x 3/4 equal 1/2?
• Both 2/3 and 3/4 are bigger than 1/2. Why does multiplying produce a number smaller than the two numbers being multiplied?
• Why do we multiply the numerators and the denominators?

Again, both the answer and the explanation of how the answer makes sense are important.

Why does 2/3 x 3/4 equal 1/2? Because when we multiply fractions, we multiply the numerators and the denominators:

• 2/3 x 3/4 = (2 x 3)/(3 x 4)
• 2 x 3 = 6 and 3 x 4 = 12, so (2 x 3)/(3 x 4) = 6/12

Why does multiplying produce a number smaller than the two numbers multiplied? It helps to begin by thinking about the second part of our equation, 3/4, since that’s the larger number.

What does 3/4 look like? Picture a rectangle.

3 non-negotiables for differentiation in the math classroom

4 ways to engage students with writing in math class

That’s not how I learned it! 4 ways to help your child with “new math”

Helping students grow

Students continue to rebound from pandemic school closures. NWEA® and Learning Heroes experts talk about how best to support them here on our blog, Teach. Learn. Grow.

See the post

Put the science of reading into action

The science of reading is not a buzzword. It’s the converging evidence of what matters and what works in literacy instruction. We can help you make it part of your practice.

Get the guide

Support teachers with PL

High-quality professional learning can help teachers feel invested—and supported—in their work.

Read the article

STAY CURRENT by subscribing to our newsletter

You are now signed up to receive our newsletter containing the latest news, blogs, and resources from nwea..

Oxford Education Blog

The latest news and views on education from oxford university press., the role of reasoning in supporting problem solving and fluency.

A recent webinar with Mike Askew explored the connection between reasoning, problem solving and fluency. This blog post summaries the key takeaways from this webinar.

Using reasoning to support fluency and problem solving 

You’ll probably be very familiar with the aims of the National Curriculum for mathematics in England: fluency, problem-solving and reasoning. An accepted logic of progression for these is for children to become fluent in the basics, apply this to problem-solving, and then reason about what they have done. However, this sequence tends towards treating reasoning as the icing on the cake, suggesting that it might be a final step that not all children in the class will reach. So let’s turn this logic on its head and consider the possibility that much mathematical reasoning is in actual fact independent of arithmetical fluency.

What does progress in mathematical reasoning look like?

Since we cannot actually ‘see’ children’s progression in learning, in the way we can see a journey’s progression on a SatNav, we often use metaphors to talk about progression in learning. One popular metaphor is to liken learning to ‘being on track’, with the implication that we can check if children going in the right direction, reaching ‘stations’ of fluency along the way. Or we talk about progression in learning as though it were similar to building up blocks, where some ideas provide the ‘foundations’ that can be ‘built upon’. 

Instead of thinking about reasoning as a series of stations along a train track or a pile of building blocks, we can instead take a gardening metaphor, and think about reasoning as an ‘unfolding’ of things. With this metaphor, just as the sunflower ‘emerges’ from the seed, so our mathematical reasoning is contained within our early experiences. A five-year-old may not be able to solve 3 divided by 4, but they will be able to share three chocolate bars between four friends – that early experience of ‘sharing chocolate’ contains the seeds of formal division leading to fractions. 1  

Of course, the five-year-old is not interested in how much chocolate each friend gets, but whether everyone gets the same amount – it’s the child’s interest in relationships between quantities, rather than the actual quantities that holds the seeds of thinking mathematically.  

The role of relationships in thinking mathematically

Quantitative relationships.

Quantitative relationships refer to how quantities relate to each other. Consider this example:

I have some friends round on Saturday for a tea party and buy a packet of biscuits, which we share equally. On Sunday, I have another tea party, we share a second, equivalent packet of the biscuits. We share out the same number of biscuits as yesterday, but there are more people at the table. Does each person get more or less biscuits? 2

Once people are reassured that this is not a trick question 3 then it is clear that if there are more people and the same quantity of biscuits, everyone must get a smaller amount to eat on Sunday than the Saturday crowd did. Note, importantly, we can reason this conclusion without knowing exact quantities, either of people or biscuits. 

This example had the change from Saturday to Sunday being that the number of biscuits stayed the same, while the number of people went up. As each of these quantities can do three things between Saturday and Sunday – go down, stay the same, go up – there are nine variations to the problem, summarised in this table, with the solution shown to the particular version above. 

Before reading on, you might like to take a moment to think about which of the other cells in the table can be filled in. (The solution is at the end of this blog).

It turns out that in 7 out of 9 cases, we can reason what will happen without doing any arithmetic. 4 We can then use this reasoning to help us understand what happens when we do put numbers in. For example, what we essentially have here is a division – quantity of biscuits divided between number of friends – and we can record the changes in the quantities of biscuits and/or people as fractions:

So, the two fractions represent 5 biscuits shared between 6 friends (5/6) and 5 biscuits shared between 8 (5/8). To reason through which of these fractions is bigger we can apply our quantitative reasoning here to see that everyone must get fewer biscuits on Sunday – there are more friends, but the same quantity of biscuits to go around. We do not need to generate images of each fraction to ‘see’ which is larger, and we certainly do not need to put them both over a common denominator of 48.  We can reason about these fractions, not as being static parts of an object, but as a result of a familiar action on the world and in doing so developing our understanding of fractions. This is exactly what MathsBeat does, using this idea of reasoning in context to help children understand what the abstract mathematics might look like.

Structural relationships : 

By   structural relationships,   I mean   how we can break up and deal with a quantity in structural ways. Try this:

Jot down a two-digit number (say, 32) Add the two digits (3 + 2 = 5) Subtract that sum from your original number (32 – 5 = 27) Do at least three more Do you notice anything about your answers?

If you’ve done this, then you’ll probably notice that all of your answers are multiples of nine (and, if like most folks, you just read on, then do check this is the case with a couple of numbers now).

This result might look like a bit of mathematical magic, but there must be a reason.

We might model this using three base tens, and two units, decomposing one of our tens into units in order to take away five units. But this probably gives us no sense of the underlying structure or any physical sensation of why we always end up with a multiple of nine.

If we approach this differently, thinking about where our five came from –three tens and two units – rather than decomposing one of the tens into units, we could start by taking away two, which cancels out.

And then rather than subtracting three from one of our tens, we could take away one from each ten, leaving us with three nines. And a moment’s reflection may reveal that this will work for any starting number: 45 – (4 + 5), well the, five within the nine being subtracted clears the five ones in 45, and the 4 matches the number of tens, and that will always be the case. Through the concrete, we begin to get the sense that this will always be true.

If we take this into more formal recording, we are ensuring that children have a real sense of what the structure is: a  structural sense , which complements their number sense. 

Decomposing and recomposing is one way of doing subtraction, but we’re going beyond this by really unpacking and laying bare the underlying structure: a really powerful way of helping children understand what’s going on.

So in summary, much mathematical reasoning is independent of arithmetical fluency.

This is a bold statement, but as you can see from the examples above, our reasoning doesn’t necessarily depend upon or change with different numbers. In fact, it stays exactly the same. We can even say something is true and have absolutely no idea how to do the calculation. (Is it true that 37.5 x 13.57 = 40 x 13.57 – 2.5 x 13.37?)

Maybe it’s time to reverse the logic and start to think about mathematics emerging from reasoning to problem-solving to fluency.

Mike Askew:  Before moving into teacher education, Professor Mike Askew began his career as a primary school teacher. He now researches, speaks and writes on teaching and learning mathematics. Mike believes that all children can find mathematical activity engaging and enjoyable, and therefore develop the confidence in their ability to do maths. 

Mike is also the Series Editor of  MathsBeat , a new digitally-led maths mastery programme that has been designed and written to bring a consistent and coherent approach to the National Curriculum, covering all of the aims – fluency, problem solving and reasoning – thoroughly and comprehensively. MathsBeat’s clear progression and easy-to-follow sequence of tasks develops children’s knowledge, fluency and understanding with suggested prompts, actions and questions to give all children opportunities for deep learning. Find out more here .

You can watch Mike’s full webinar,  The role of reasoning in supporting problem solving and fluency , here . (Note: you will be taken to a sign-up page and asked to enter your details; this is so that we can email you a CPD certificate on competition of the webinar). 

Solution to  Changes from Saturday to Sunday and the result

 1 If you would like to read more about this, I recommend Lakoff, G., & Núñez, R. E. (2000). Where mathematics comes from: How the embodied mind brings mathematics into being. Basic Books.

2 Adapted from a problem in: Lamon, S. (2005). Teaching Fractions and Ratios for Understanding. Essential Content Knowledge and Instructional Strategies for Teachers, 2nd Edition. Routledge.

3 Because, of course in this mathematical world of friends, no one is on a diet or gluten intolerant!

4 The more/more and less/less solutions are determined by the actual quantities: biscuits going up by, say, 20 , but only one more friend turning up on Sunday is going to be very different by only having 1 more biscuit on Sunday but 20 more friends arriving. 

Share this:

One thought on “ the role of reasoning in supporting problem solving and fluency ”.

Hi Mike, I enjoyed reading your post, it has definitely given me a lot of insight into teaching and learning about mathematics, as I have struggled to understand generalisations and concepts when dealing solely with numbers, as a mathematics learner. I agree with you in that students’ ability to reason and develop an understanding of mathematical concepts, and retain a focus on mathematical ideas and why these ideas are important, especially when real-world connections are made, because this is relevant to students’ daily lives and it is something they are able to better understand rather than being presented with solely arithmetic problems and not being exposed to understanding the mathematics behind it. Henceforth, the ideas you have presented are ones I will take on when teaching: ensuring that students understand the importance of understanding mathematical ideas and use this to justify their responses, which I believe will help students develop confidence and strengthen their skills and ability to extend their thinking when learning about mathematics.

Comments are closed.

Building fluency through problem solving

Editor’s Note:

This is an updated version of a blog post published on January 13, 2020.

Problem solving builds fluency and fluency builds problem solving. How can you help learners make the most of this virtuous cycle and achieve mastery?

Fluency. It’s so important that I have written not one , not two , but three blog posts on the subject. It’s also one of the three key aims for the national curriculum.

It’s a common dilemma. Learners need opportunities to apply their knowledge in solving problems and reasoning (the other two NC aims), but can’t reason or solve problems until they’ve achieved a certain level of fluency.

Instead of seeing this as a catch-22, think of fluency and problem solving as a virtuous cycle — working together to help learners achieve true mastery.

Supporting fluency when solving problems

Fluency helps children spot patterns, make conjectures, test them out, create generalisations, and make connections between different areas of their learning — the true skills of working mathematically. When learners can work mathematically, they’re better equipped to solve problems.

But what if learners are not totally fluent? Can they still solve problems? With the right support, problem solving helps learners develop their fluency, which makes them better at problem solving, which develops fluency…

Here are ways you can support your learners’ fluency journey.

Don’t worry about rapid recall

What does it mean to be fluent? Fluency means that learners are able to recall and use facts in a way that is accurate, efficient, reliable, flexible and fluid. But that doesn’t mean that good mathematicians need to have super-speedy recall of facts either.

Putting pressure on learners to recall facts in timed tests can negatively affect their ability to solve problems. Research shows that for about one-third of students, the onset of timed testing is the beginning of maths anxiety . Not only is maths anxiety upsetting for learners, it robs them of working memory and makes maths even harder.

Just because it takes a learner a little longer to recall or work out a fact, doesn’t mean the way they’re working isn’t becoming accurate, efficient, reliable, flexible and fluid. Fluent doesn’t always mean fast, and every time a learner gets to the answer (even if it takes a while), they embed the learning a little more.

Give learners time to think and reason

Psychologist Daniel Willingham describes memory as “the residue of thought”. If you want your learners to become fluent, you need to give them opportunities to think and reason. You can do this by looking for ways to extend problems so that learners have more to think about.

Here’s an example: what is 6 × 7 ? You could ask your learners for the answer and move on, but why stop there? If learners know that 6 × 7 = 42 , how many other related facts can they work out from this? Or if they don’t know 6 × 7 , ask them to work it out using facts they do know, like (5 × 7) + (1 × 7) , or (6 × 6) + (1 × 6) ?

Spending time exploring problems helps learners to build fluency in number sense, recognise patterns and see connections, and visualise — the three key components of problem solving.

Developing problem solving when building fluency

Learners with strong problem-solving skills can move flexibly between different representations, recognising and showing the links between them. They identify the merits of different strategies, and choose from a range of different approaches to find the one most appropriate for the maths problem at hand.

So, what type of problems should you give learners when they are still building their fluency? The best problem-solving questions exist in a Goldilocks Zone; the problems are hard enough to make learners think, but not so hard that they fail to learn anything.

Here’s how to give them opportunities to develop problem solving.

Centre problems around familiar topics

Learners can develop their problem-solving skills if they’re actively taught them and are given opportunities to put them into practice. When our aim is to develop problem-solving skills, it’s important that the mathematical content isn’t too challenging.

Asking learners to activate their problem-solving skills while applying new learning makes the level of difficulty too high. Keep problems centred around familiar topics (this can even be content taught as long ago as two years previously).

Not only does choosing familiar topics help learners practice their problem-solving skills, revisiting topics will also improve their fluency.

Keep the focus on problem solving, not calculation

What do you want learners to notice when solving a problem? If the focus is developing problem-solving skills, then the takeaway should be the method used to answer the question.

If the numbers involved in a problem are ‘nasty’, learners might spend their limited working memory on calculating and lose sight of the problem. Chances are they’ll have issues recalling the way they solved the problem. On top of that, they’ll learn nothing about problem-solving strategies.

It’s important to make sure that learners have a fluent recall of the facts needed to solve the problem. This way, they can focus on actually solving it rather than struggling to recall facts. To understand the underlying problem-solving strategies, learners need to have the processing capacity to spot patterns and make connections.

The ultimate goal of teaching mathematics is to create thinkers. Making the most of the fluency virtuous cycle helps learners to do so much more than just recall facts and memorise procedures. In time, your learners will be able to work fluently, make connections, solve problems, and become true mathematical thinkers.

Jo Boaler (2014). Research Suggests that Timed Tests Cause Math Anxiety. Teaching Children Mathematics , 20(8), p.469.

Willingham, D. (2009). Why don’t students like school?: A Cognitive Scientist Answers Questions About How the Mind Works and What It Means for Your Classroom. San Francisco: Jossey-Bass.

Gill Knight

Browse by Topic

Your teaching practice.

Boost your teaching confidence with the latest musings on pedagogy, classroom management, and teacher mental health.

Maths Mastery Stories

You’re part of a growing community. Get smart implementation advice and hear inspiring maths mastery stories from teachers just like you.

Teaching Tips

Learn practical maths teaching tips and strategies you can use in your classroom right away — from teachers who’ve been there.

Classroom Assessment

Identify where your learners are at and where to take them next with expert assessment advice from seasoned educators.

Your Learners

Help every learner succeed with strategies for managing behaviour, supporting mental health, and differentiating instruction for all attainment levels.

Teaching Maths for Mastery

Interested in Singapore maths, the CPA approach, bar modelling, or number bonds? Learn essential maths mastery theory and techniques here.

Deepen your mastery knowledge with our biweekly newsletter

By clicking “Accept All” , you agree to the storing of cookies on your device to enhance site navigation, analyze site usage and assist in our marketing efforts.

Developing mathematical fluency: comparing exercises and rich tasks

• Open access
• Published: 26 September 2017
• Volume 97 , pages 121–141, ( 2018 )

Cite this article

You have full access to this open access article

• Colin Foster   ORCID: orcid.org/0000-0003-1648-7485 1  

22k Accesses

26 Citations

59 Altmetric

Explore all metrics

Achieving fluency in important mathematical procedures is fundamental to students’ mathematical development. The usual way to develop procedural fluency is to practise repetitive exercises, but is this the only effective way? This paper reports three quasi-experimental studies carried out in a total of 11 secondary schools involving altogether 528 students aged 12–15. In each study, parallel classes were taught the same mathematical procedure before one class undertook traditional exercises while the other worked on a “mathematical etude” (Foster International Journal of Mathematical Education in Science and Technology , 44 (5), 765–774, 2013b ), designed to be a richer task involving extensive opportunities for practice of the relevant procedure. Bayesian t tests on the gain scores between pre- and post-tests in each study provided evidence of no difference between the two conditions. A Bayesian meta-analysis of the three studies gave a combined Bayes factor of 5.83, constituting “substantial” evidence (Jeffreys, 1961 ) in favour of the null hypothesis that etudes and exercises were equally effective, relative to the alternative hypothesis that they were not. These data support the conclusion that the mathematical etudes trialled are comparable to traditional exercises in their effects on procedural fluency. This could make etudes a viable alternative to exercises, since they offer the possibility of richer, more creative problem-solving activity, with comparable effectiveness in developing procedural fluency.

Similar content being viewed by others

Word problems in mathematics education: a survey

Lieven Verschaffel, Stanislaw Schukajlow, … Wim Van Dooren

Retrieval Practice Consistently Benefits Student Learning: a Systematic Review of Applied Research in Schools and Classrooms

Pooja K. Agarwal, Ludmila D. Nunes & Janell R. Blunt

Research on early childhood mathematics teaching and learning

Camilla Björklund, Marja van den Heuvel-Panhuizen & Angelika Kullberg

Avoid common mistakes on your manuscript.

1 Introduction

Attaining fluency in key mathematical procedures is essential to students’ mathematical development (Department for Education [DfE], 2013 ; National Council of Teachers of Mathematics [NCTM], 2014 ; Truss, 2013 ). Being secure with important mathematical procedures gives students increased power to tackle more complicated mathematics at a more conceptual level (Codding, Burns, & Lukito, 2011 ; Foster, 2013b , 2016 ), since automating skills frees up mental capacity for being creative (Lemov, Woolway, & Yezzi, 2012 , p. 36). Devising ways to support the development of robust fluency with mathematical procedures is currently a focus of attention. For example, in England the national curriculum for mathematics emphasises procedural fluency as the first stated aim (DfE, 2013 ), and the current “mastery” agenda stresses “intelligent practice” as a route to simultaneously developing procedural fluency and conceptual understanding (Hodgen, 2015 ; National Association of Mathematics Advisors [NAMA], 2016 ; National Centre for Excellence in the Teaching of Mathematics [NCETM], 2016 ).

However, a focus on procedural fluency is sometimes seen as a threat to reform approaches to the learning of mathematics, which emphasise sense making through engagement with rich problem-solving tasks (Advisory Committee on Mathematics Education [ACME], 2012 ; Office for Standards in Education [Ofsted], 2012 ). In a technological age, in which calculators and computers can perform mathematical procedures quickly and accurately, it may be argued that teaching problem solving should be prioritised over practising procedures. It may also be that an excessive focus on basic procedures fails to kindle students’ interest in mathematics and could be linked to students, especially girls, not choosing to pursue mathematics beyond a compulsory phase (Boaler, 2002 ). Nevertheless, in a high-stakes assessment culture, where procedural skills are perceived to be the most straightforward ones to assess, the backwash effect of examinations is likely to lead to schools and teachers feeling constrained to prioritise the development of procedural fluency over these other aspects of learning mathematics (Foster, 2013c ; Ofsted, 2012 ; Taleporos, 2005 ).

In this context, it has been suggested that a mathematics task genre of etudes might be capable of addressing procedural fluency at the same time as offering a richer experience of learning mathematics (Foster, 2013b , 2014 ). Etudes are mathematics tasks in which extensive practice of a well-defined mathematical procedure is embedded within a rich mathematical problem (Foster, 2013b ). Such tasks aim to generate plentiful practice incidentally as learners tackle a rich, open-ended problem. East Asian countries which perform well in large-scale international assessments such as the Programme for International Student Assessment (PISA) and the Trends in International Mathematics and Science Study (TIMSS) are thought to succeed in emphasising mathematical fluency without resorting to low-level rote learning of procedures (Askew et al., 2010 ; Fan & Bokhove, 2014 ; Leung, 2014 ).

There have been many attempts to design tasks that incorporate meaningful practice (Kling & Bay-Williams, 2015 ) or exploit systematic variation (NAMA, 2016 ) to address fluency goals within deeper and more thought-provoking contexts. Not only might this lead to greater interest and motivation for students (Li, 1999 ), it is conceivable that it could assist in the development of procedural fluency by to some extent shifting students’ focus away from the details of the procedure, perhaps thereby aiding automation. From the point of view of being economical with students’ learning time, Hewitt ( 1996 ) described the generation of purposeful practice by subordinating the role of practice to a component of a larger mathematical problem. In this way, attention is placed not on the procedure being performed but instead on the effect of its use on a desired goal (Hewitt, 2015 ).

Mathematical etudes draw on these intentions to situate procedural practice within rich, problem-solving tasks. Although anecdotally etudes have been very favourably received by mathematics teachers, and appear to be popular with students, it is not known whether or not they are as effective as traditional exercises at developing procedural fluency. While etudes might be expected to offer other advantages, such as greater engagement and opportunities for creative problem solving and exploration, it is not known whether this comes at a cost of effectiveness in narrow terms of developing procedural fluency. It seems possible that diverting students’ attention away from the details of carrying out a procedure and onto some wider mathematics problem could hinder their immediate progress in procedural fluency. However, on the contrary, problem-solving aspects of an etude could potentially focus students on the details of a procedure in a way that supports development of fluency. So this paper investigates whether or not etudes are as effective as exercises for developing students’ procedural fluency.

2 Mathematical etudes

2.1 background.

Procedural fluency involves knowing when and how to apply a procedure and being able to perform it “accurately, efficiently, and flexibly” (NCTM, 2014 , p. 1). The Mathematical Etudes Project Footnote 1 aims to devise creative ways to help learners of mathematics develop their fluency in important mathematical procedures. It might be supposed that any varied diet of rich problem-solving tasks would automatically generate plentiful opportunities for students to gain practice in a multitude of important mathematical procedures, and that this would be a natural way for procedural fluency to be addressed in the curriculum. However, a rich, open-ended task may be approached in a variety of ways (Yeo, 2017 ), and, where a choice of approaches is possible, students may be drawn to those which utilise skills with which they are already familiar and comfortable. In this way, areas of weakness may remain unaddressed. For example, a student lacking confidence with algebra may be able to solve a mathematical problem successfully using numerical trial and improvement approaches, or perhaps by drawing an accurate graph. From the point of view of problem solving, selecting to use tools with which one is already competent is an entirely appropriate strategy, but if algebraic objectives were central to why the teacher selected the task, then the task has failed pedagogically. In this way, an open-ended task cannot necessarily be relied on to focus students’ attention onto a specific mathematical procedure. Even if it does succeed in doing this, it may not generate sufficient practice of the particular technique to develop the desired fluency, since a broader problem is likely to contain other aspects which also demand the student’s time and attention.

For this reason, an etude cannot simply be a problem which provides an opportunity for students to use the desired procedure; it must place that procedure at the centre of the students’ activity and force its repeated use. Success with the task must be contingent on repeated accurate application of the desired procedure. The Mathematical Etudes Project has developed numerous practical classroom tasks which embed extensive practice of single specified mathematical procedures within rich problem-solving contexts (Foster, 2011 , 2012a , b , 2013a , b , d , 2014 , 2015a ). It is whether such tasks are as effective as traditional exercises in developing fluency or not that is the subject of this research.

The term “etude” is borrowed from music, where an etude is “originally a study or technical exercise, later a complete and musically intelligible composition exploring a particular technical problem in an esthetically satisfying manner” (Encyclopaedia Britannica, 2007 ). Originally, etudes were intended for private practice, rather than performance, but later ones sought to achieve the twin objectives of satisfying an audience in concert as well as working as an effective tool for the development of the performer’s fluency. This latter sense inspires the idea of a mathematical etude, which is defined as a mathematics task that embeds “extensive practice of a well-defined mathematical technique within a richer, more aesthetically pleasing mathematical context” (Foster, 2013b , p. 766). In musical etudes, such as those by Chopin, the self-imposed constraint of focusing on (normally) a single specific technique may contribute to the beauty of the music.

The idea of practising a basic skill in the context of more advanced skills is common in areas such as sport (Willingham, 2009 , p. 125), and has been used within mathematics education. For example, Andrews ( 2002 ) outlined “a means by which practice could be embedded within a more meaningful and mathematically coherent activity” (p. 16). Boaler advised that it is best to “learn number facts and number sense through engaging activities that focus on mathematical understanding rather than rote memorization” (Boaler, 2015 , p. 6), and many have argued that algorithms do not necessarily have to be learned in a rote fashion (Fan & Bokhove, 2014 ). Watson and De Geest ( 2014 ) described systematic variation of tasks for the development of fluency, and it is known that, to be effective, practice must be purposeful, and systematically focused on small elements, and that feedback is essential (Ericsson & Pool, 2016 ). The challenge is to devise mathematics tasks which do this within a rich context.

The three etudes trialled in the studies described in this paper will now be discussed. Two of these etudes address solving linear equations in which the unknown quantity appears on both sides (studies 1 and 2), and the third etude concerns performing an enlargement of a given shape on a squared grid with a specified positive integer scale factor (study 3).

2.2 Linear equations etudes

The first two etudes described focus on solving linear equations. Both are intended to generate practice at solving linear equations in which the unknown quantity appears on both sides.

2.2.1 Expression polygons etude

In this etude, students are presented with the diagram shown in Fig. 1 , called an expression polygon (Foster, 2012a , 2013a , 2014 , 2015a ). Each line joining two expressions indicates that they are equated, and the initial task for students is to solve the six equations produced, writing each solution next to the appropriate line. For example, the top horizontal line joining x  + 5 to 2 x  + 2 generates the equation x  + 5 = 2 x  + 2, the solution to which is x  = 3, so students write 3 next to this line. In addition to recording their solutions on the expression polygon, a student could write out their step-by-step methods on a separate piece of paper.

Expression polygons etude. (Taken from Foster, 2015a )

Having completed this, the students will obtain the solutions 1, 2, 3, 4, 5 and 6. The pattern is provocative, and students typically comment on it (Foster, 2012a , 2015a ). This leads naturally to a challenge: “Can you make up an expression polygon of your own that has a nice, neat set of solutions?” Students make choices over what they regard as “nice” and “neat”. They might choose to aim for the first six even numbers, first six prime numbers, first six squares or some other significant set of six numbers. Regardless of the specific target numbers chosen, the experimentation involved in producing their expression polygon is intended to generate extensive practice in solving linear equations. Working backwards from the desired solution to a possible equation, and modifying the numbers to make it work, necessitates unpicking the equation-solving process, which could contribute to understanding of and facility with the procedure. Students are expected to attend more to the solutions obtained than they would when working through traditional exercises, where the answers typically form no pattern and are of no wider significance than that individual question. As students gain facility in solving equations, they focus their attention increasingly on strategic decisions about which expressions to choose. They might even go on to explore what sets of six numbers may be the solutions of an expression polygon, or experiment with having five expressions rather than four, for instance. In this way, the task is intended to self-differentiate through being naturally extendable (Foster, 2015a , b ).

2.2.2 Devising equations etude

2.3 enlargements etude.

In this third etude, which addresses the topic of performing an enlargement of a given shape, students are presented with the diagram shown in Fig. 2 , containing a right-angled isosceles triangle on a squared grid. The task is to find the locus of all possible positions for a centre of enlargement such that, for a scale factor of 3, the image produced lies completely on the grid. Students can generally find, without too much difficulty, one centre of enlargement that will work, but finding all possible points is demanding and may entail reverse reasoning from the possible image vertex positions to those of the original triangle. Further extensions are possible by considering different starting shapes, different positions of the starting shape on the grid and different scale factors. In all of this work, the enlargement procedure is being practised extensively within a wider investigative context.

Enlargement etude grid. (Taken from Foster, 2013d )

2.4 Summary

Each of the three etudes described above is intended to generate extensive opportunities for practising a single specified procedure within a rich problem-solving context. However, although etudes might be anticipated to have benefits for students in terms of greater engagement and creative problem solving, it is not known how effective they are in comparison with the standard approach of traditional exercises in the narrow objective of developing students’ procedural fluency. It might be thought that incorporating other aspects beyond repetition of the desired procedure might to some extent diminish the effectiveness of a task for developing students’ procedural fluency. However, the opposite could be the case if the problem-solving context to some extent directs students’ attention away from the performance of the procedure and onto conceptual aspects, leading to greater automation. Consequently, the research question for these studies is: Are etudes as effective as traditional exercises at developing students’ procedural fluency or not?

In these exploratory studies, it is important to emphasise that a choice was made to compare etudes and exercises only in very narrow terms of procedural fluency. While it is likely that etudes offer other, harder-to-measure benefits for students, such as providing opportunities for creative, open-ended, inquiry-based exploration and problem solving, unless they are at least about as good as traditional exercises at developing students’ procedural fluency, it is unlikely, in a high-stakes assessment culture, that schools and teachers will feel able to use them regularly as an alternative. Traditional exercises are widely used by teachers not because they are perceived to be imaginative and creative sets of tasks but because they are believed to work in the narrow sense of developing fluency at necessary procedures. If there were some other way to achieve this, that did not entail the tedium of repetitive drill, it would presumably be preferred—provided that it were equally effective at the main job. For this reason, in these studies the focus was entirely on the effect of etudes on procedural fluency. Rather than trying to measure the plausible but more nebulous ways in which etudes might be superior, in this first exploratory set of studies it was decided to focus solely on the question of the effectiveness of etudes for the purpose of developing procedural fluency.

3 Study 1: Expression polygons

The aim of this study was to investigate whether a particular etude (“Expression polygons”, see Section 2.2.1 ) is as effective as traditional exercises at developing students’ procedural fluency in solving linear equations, relative to the alternative hypothesis that the etude and the exercises are not equally effective.

A quasi-experimental design was used, with pairs of classes at the same school assigned to either the intervention (the etude) or control (traditional exercises) condition. Data was collected across one or two lessons, in which students in the intervention group tackled an etude while those in the control group worked through as many traditional exercises as possible in the same amount of time. Pre- and post-tests were administered at the beginning and end of the lesson(s).

A classical t test on the gain scores (post-test − pre-test) would be suitable for detecting a statistically significant difference between the two groups; however, within the paradigm of null hypothesis significance testing, failure to find such a difference would not constitute evidence for the null hypothesis of no difference—it would simply be inconclusive (Dienes, 2014 ). No evidence of a difference is not evidence of no difference. This is because failure to detect a difference might be a consequence of an underpowered study, which might have been able to detect a difference had a larger sample size (or more sensitive test) been used. For this reason, it is necessary to use a Bayesian approach for these studies, in order to establish how likely is the hypothesis of no difference between the two treatments (etude and traditional exercises) in terms of gain in procedural fluency, relative to the alternative hypothesis that there is a difference. Thus, Bayesian t tests were carried out on the gain scores obtained in each study, as described below.

3.1.1 Instrument

The “Expression polygons” etude (Foster, 2012a , 2013a , 2015a ) discussed in Section 2.2.1 was used for the intervention groups, and the control groups were provided with traditional exercises and asked to complete as many as possible in the same amount of time (see Fig. 3 for both), normally around 20 min. The exercises consisted of linear equations in which the unknown appears on both sides, leading to small integer solutions. Pre- and post-tests were designed (Fig. 4 ), each consisting of four equations of the same kind as those used in the exercises. In this way, it was hoped that any bias in the focus of the tests would be toward the control group (exercises), since the matching between the exercises and the post-test was intended to be as close as possible. Each test was scored out of 4, with one mark given for the correct solution to each equation. The post-test included a space at the end for open comments, asking students to write down “what you think about the work you have done on solving equations”. This question was intended to capture students’ perceptions of the two different tasks.

Study 1 materials: expression polygons etude (intervention) and traditional exercises (control)

Study 1 pre-test and post-test

3.1.2 Participants

Schools were recruited through a Twitter request for help, and schools A, B and C (Table 1 ) took part in this study. These schools were a convenience sample, spanning a range of sizes and composition. In most schools in England, mathematics classes are set by attainment, and this was the case for schools A and B, while school C used mixed attainment classes. In all of the schools, teachers were asked to:

choose two similar classes (e.g. Year 8 or 9 parallel sets) who you are teaching to solve linear equations with the unknown on both sides (e.g. equations like 7 x  − 1 = 5 x  + 3). In these materials, all the solutions are whole numbers, but some may be negative.

A total of 241 mathematics students from Years 8 and 9 (age 12–14) participated. Forty-eight students’ pre- and post-tests could not be matched, either because they were not present for one of them or (for the vast majority) because they did not put their name clearly on the test. These students’ tests were excluded from the analysis, leaving N  = 193. The large number of tests which could not be matched here was mainly due to the fact that in one particular class (20 students) none of the students wrote their names on either of their tests, and so none of the data from this class could be used.

3.1.3 Administration

Teachers were asked to use the materials with a pair of “parallel” classes across one or preferably two of the students’ normal mathematics lessons. Allocation was at class level, and schools were responsible for choosing pairs of classes that they regarded as similar, which were normally a pair from the same Year group which were setted classes at the same level (e.g., both set 3 out of 6). In most cases, the same teacher taught both classes, so as to minimise teacher effects.

Pre- and post-tests were administered individually in the same amount of time and until most students had finished (normally about 10 min. for each). Both classes were then taught by the teacher how to solve linear equations with the unknown on both sides. Teachers were asked to teach both classes “as you would normally, in the same way, and for approximately the same amount of time”. Following this, the control class received traditional exercises (Fig. 3 ), with the expectation that the number of questions would be more than enough for the time available (normally about 20 min.) and that students would not complete all of them, which generally proved to be the case. The intervention group received the “Expression polygons” etude (Fig. 3 ). Teachers were advised that “It is important that [the students] go beyond solving the six equations and spend some time generating their own expression polygons (or trying to).” Teachers were asked to allow the two classes the same amount of time to work on these tasks: “however much time you have available and feel is appropriate; ideally at least a whole lesson and perhaps more”. It is estimated that this was generally about 20–30 min. During this phase, teachers were asked to help both classes as they would normally, using their professional judgement as to what was appropriate, so that the students would benefit from the time that they spent on these tasks. Then the post-test was administered in the same way as the pre-test.

3.2 Results

The mean and standard deviation of the scores for both conditions at pre- and post-test, along with mean gain scores calculated as the mean of (post-test − pre-test) for each student, are shown in Table 2 and Fig. 5 . The similarity of the mean scores on the pre-test is reassuring regarding the matching of the parallel classes. A Bayesian t test was carried out on the gain scores, using the BayesFactor Footnote 2 package in R , comparing the fit of the data under the null hypothesis (the etude is as effective as the traditional exercises) and the alternative hypothesis (the etude and the exercises are not equally effective). A Bayes factor B indicates the relative strength of evidence for two hypotheses (Dienes, 2014 ; Rouder, Speckman, Sun, Morey, & Iverson, 2009 ), and means that the data are B times as likely under the null hypothesis as under the alternative. With a Cauchy prior width of .707, an estimated Bayes factor (null/alternative) of 1.03 was obtained, indicating no reason to conclude in favour of either hypothesis. (Conventionally, a Bayes factor between 3 and 10 represents “substantial” evidence [Jeffreys, 1961 ].) Prior robustness graphs for all of the Bayesian analyses described in this paper are included in the Appendix . In this case, calculation indicates that an exceptionally wide Cauchy prior width of more than 2.39 would be needed in order to obtain a “substantial” (Jeffreys, 1961 ) Bayes factor. The 95% credible interval Footnote 3 for the standardised effect size was [− .545, .005].

Study 1 results. (Error bars indicate ± 1 standard error)

Students’ comments on the study were few and generally related to the teaching episode rather than the etude or exercises. Insufficient responses meant that analysis of students’ perceptions of the two tasks was not possible.

3.3 Discussion

Such an inconclusive result does not allow us to say that either the exercises or the etude is superior in terms of developing procedural fluency, and neither does it allow us to say that there is evidence of no difference. Scrutiny of the students’ work suggested that in the time available many had engaged only superficially with the etude, whereas students in the control group had generally completed many exercises. It is possible that the style of the etude task was unfamiliar and/or that students were unclear regarding what they were supposed to do. For this reason, it was decided to devise a new etude to address the same topic of linear equations, one that it was hoped would be easier for students to understand and more similar in style to tasks that they might be familiar with. This etude formed the basis of study 2.

4 Study 2: Devising equations

The aim of this study was to investigate whether a different etude (“Devising equations”, see Section 2.2.2 ) is as effective as traditional exercises at developing students’ procedural fluency in solving linear equations, relative to the alternative hypothesis that the etude and the exercises are not equally effective.

The same quasi-experimental design was used as in study 1, with pairs of classes at the same school assigned to either the intervention (the “Devising equations” etude, see Section 2.2.2 ) or control (traditional exercises).

4.1.1 Instrument and administration

This time the intervention group received the “Devising equations” etude, as described in Section 2.2.2 (see Fig. 6 ). The control group received the same set of traditional exercises as used in study 1 (see Fig. 3 ) and were asked to complete as many as possible in the same amount of time as given to the etudes group. The same pre- and post-tests were used as in study 1 (see Fig. 4 ). Administration was exactly as for study 1, except that this time the only advice given to teachers regarding the etude was that students should “generate and solve their own equations”.

Study 2 “Devising equations” task

4.1.2 Participants

Schools were again recruited through a Twitter request. Schools D, E, F, G and H (Table 1 ) took part, all of which used attainment setting for mathematics. Teachers were again asked to choose parallel classes, and a total of 213 mathematics students from Years 8 and 9 (age 12–14) participated. This time, 19 students’ pre- and post-tests could not be matched, because students did not always put their names on their tests, leaving N  = 194.

4.2 Results

Results are shown in Table 3 and Fig. 7 . As in study 1, a Bayesian t test was carried out on the gain scores (Dienes, 2014 ; Rouder et al., 2009 ), with a Cauchy prior width of .707, this time giving a Bayes factor (null/alternative) of 5.92. This means that the data are nearly six times as likely under the null hypothesis (the etude is as effective as the traditional exercises) as under the alternative hypothesis (the etude and the exercises are not equally effective). Conventionally, a Bayes factor between 3 and 10 represents “substantial” evidence (Jeffreys, 1961 ). The prior robustness graph (see Appendix ) indicates that any Cauchy prior width of more than .317 would have led to a Bayes factor of at least 3, which suggests that this finding is robust. The 95% credible interval for the standardised effect size was [−.326, .233].

Study 2 results. (Error bars indicate ± 1 standard error)

Again, students’ comments were insufficiently plentiful or focused on the task to enable an analysis.

4.3 Discussion

Study 2 provides substantial evidence that there is little difference across one or two lessons between the effect on students’ procedural fluency of using traditional exercises or the “Devising equations” etude. Examination of students’ work showed a much greater engagement with this etude than with the “Expression polygons” one used in study 1, as evidenced by far more written work, so it is plausible that the effect of this etude might consequently have been stronger and, in this case, was closely matched to that of the exercises.

In an attempt to extend the bounds of generalisability of this finding, a third study was conducted, using the enlargements etude discussed in Section 2.3 , in order to see whether a similar result would be obtained in a different topic area.

5 Study 3: Enlargements

The aim of this study was to investigate whether a third etude (“Enlargements”, see Section 2.3 ) is as effective as traditional exercises at developing students’ procedural fluency in a different (geometric) topic area: performing an enlargement of a given shape on a squared grid with a specified positive integer scale factor. As before, the alternative hypothesis was that the etude and the exercises are not equally effective.

The same quasi-experimental design was used as in studies 1 and 2, with pairs of parallel classes in each school assigned to either the intervention (this time the “Enlargements” etude) or control (traditional exercises) condition.

5.1.1 Instrument and administration

The “Enlargements” etude (Foster, 2013d ) discussed in Section 2.3 was used for the intervention groups, and the control groups were provided with traditional exercises and asked to complete as many as possible in the same amount of time (see Fig. 8 for both). The exercises consisted of a squared grid containing five right-angled triangles and four given points. Each question asked students to enlarge one of the given shapes by a scale factor of 2, 3 or 5, using as centre of enlargement one of the given points. Pre- and post-tests were administered (Fig. 9 ), in which students were asked to enlarge a given triangle with a scale factor of 4 on a squared grid about a centre of enlargement marked with a dot. The pre- and post-tests were intended to be as similar as possible in presentation to the traditional exercises, again in the hope that any bias in the focus of the post-test would be in favour of the control group. As before, the post-test included a space at the end for open comments, asking students to write down “what you think about the work you have done on enlargements”. Each test was scored out of 4, with one mark for each correctly positioned vertex and one for an enlarged triangle of the correct shape, size and orientation (not necessarily position). Administration was exactly as for studies 1 and 2, except that this time teachers were asked to ensure

that the students understand that they are meant to try to find as many possible positions for the centre of enlargement as they can—perhaps even the whole region where these centres can be. Students could also go on to explore what happens if the starting triangle is in a different position, or is a different shape, or if a different scale factor is used (original emphasis).

The purpose of this was to try to ensure that the students would engage extensively with the etude and not assume that finding one viable centre of enlargement was all that was required.

Study 3 materials: enlargement etude (intervention) and traditional exercises (control)

Study 3 pre-test and post-test

5.1.2 Participants

As before, schools were recruited through a Twitter request. Schools I, J and K in Table 1 took part, all of which used attainment setting for mathematics lessons. Teachers were again asked to choose parallel classes, and a total of 151 mathematics students from Years 9 and 10 (age 13–15) participated. Year 9–10 classes were used this time, rather than Year 8–9 classes, due to teachers’ choices about suitability for this different topic. This time, only 10 students’ pre- and post-tests could not be matched, again because of missing names on some of the tests, leaving N  = 141.

5.2 Results

Analysis proceeded as before, and the results are shown in Table 4 and Fig. 10 . Again, a Bayesian t test was carried out on the gain scores (Dienes, 2014 ; Rouder et al., 2009 ), with a Cauchy prior width of .707, this time giving a Bayes factor (null/alternative) of 5.20, meaning that the data are about five times as likely under the null hypothesis (the etude is as effective as the traditional exercises) as under the alternative hypothesis (the etude and the exercises are not equally effective). Conventionally, a Bayes factor between 3 and 10 represents “substantial” evidence (Jeffreys, 1961 ). The prior robustness graph (see Appendix ) indicates that any Cauchy prior width of more than .365 would have led to a Bayes factor of at least 3, which suggests that the finding is robust. The 95% credible interval for the standardised effect size was [−.384, .257].

Study 3 results. (Error bars indicate ± 1 standard error)

Once again, student comments were too few to allow a reasonable analysis.

5.3 Discussion

Study 3 provides substantial evidence that there is no difference across one or two lessons between the effect on students’ procedural fluency of using traditional exercises or this enlargement etude. Examination of students’ work showed a lot of drawing on the sheets, with many students correctly finding the locus of all possible positions for the centre of enlargement. It may be that this greater degree of engagement (relative to study 1) could account for this etude being of comparable benefit to the exercises, as was the case in study 2.

6 General discussion

The Bayes factors obtained in these three studies were combined using the BayesFactor package in R and the meta.ttestBF Bayesian meta-analysis function. Again using a Cauchy prior width of .707, this time an estimated combined Bayes factor (null/alternative) of 5.83 was obtained (Table 5 ). This again falls within the conventionally accepted range of 3 to 10 for “substantial” evidence (Jeffreys, 1961 ). This means that, taken together, the three studies reported support the conclusion in favour of the null hypothesis that the etudes are as effective as the traditional exercises in developing students’ procedural fluency, relative to the alternative hypothesis that the etudes and the exercises are not equally effective.

The smaller Bayes factor for study 1 may have resulted from a less clearly articulated etude that was unfamiliar in style to the students, requiring a greater degree of initiative in constructing expressions than is normally expected in mathematics classrooms. If it is the case that students were less sure what was expected of them, this could explain why the etudes group carried out less equation solving here than the exercises group did. As reported above, in studies 2 and 3, a greater effort was made in the teacher instructions to explain the intentions of the task, and a greater engagement with the etudes was inferred from the quantity of written work produced.

7 Conclusion

These three exploratory studies suggest that the etudes trialled here are as effective as the traditional exercises in developing students’ procedural fluency. Consequently, for a hypothetical teacher whose sole objective was to develop students’ procedural fluency, it should be a matter of indifference whether to do this by means of exercises or etudes. Given the plausible benefits of etudes in terms of richness of experience and opportunity for open-ended problem solving and creative thinking, it may be that etudes might on balance be preferred (Foster, 2013b ).

It should be stressed that only three etudes were tested in these studies across only two mathematics topics and with students aged 12–15. Further studies using other etudes in other topic areas and with students outside this age range would be necessary to extend the generalisability of this finding. In addition, studies including delayed post-tests would be highly desirable, but were not practicable for this initial exploratory study. It would also be important to examine evidence for the hypothesised benefits of etudes beyond the narrow focus of these studies on procedural fluency. For example, it is plausible that etudes are more engaging for students, provide opportunities for students to operate more autonomously and solve problems, promote discussion and reasoning and support conceptual understanding of the mathematics. Classroom observation data, other kinds of assessments, as well as canvassing teacher and student perspectives, would be necessary to explore the extent to which this might be the case.

Caution must be exercised in interpreting these findings, since the constraints of the participating schools did not allow random allocation of students to condition (etude or exercises). Instead, schools selected pairs of “parallel” classes, generally based on level of class within the Year group (e.g., set 3 out of 6). It is reassuring that pre-test scores were generally close across the two conditions, but there remains the possibility that the parallel classes differed on some relevant factor. It should also be noted that some pre- and post-tests could not be matched, as students did not write their names on their tests, meaning that these tests had to be excluded from the data. In studies 2 and 3, the percentages of tests excluded were 9% and 7%, respectively, but in study 1 the percentage was much higher (20%). However, this was largely the result of one particular class, in which none of the students wrote their names on either test; ignoring this class, the percentage of missing data was a less severe 12%. However, these higher than desirable percentages of missing data are a reason to be cautious in interpreting these findings.

The extent of the guidance given to teachers about how to use the etudes was necessarily highly limited by the constraints of these studies. For practical reasons, the entire instructions on conducting the trials were restricted to one side of A4 paper. No professional development was involved, as these trials were carried out at a distance, and in most cases the participating schools and teachers were recruited via Twitter and contacted solely by email, and were not known personally to the researcher. It may be supposed that students would derive far greater benefit from etudes if they were deployed by teachers who had received professional development which involved prior opportunities to think about and discuss ways of working with these sorts of tasks. It remains for future work to explore this possibility.

www.mathematicaletudes.com

http://bayesfactorpcl.r-forge.r-project.org/

A credible interval is the Bayesian analogue of a frequentist confidence interval. A credible interval has the much simpler interpretation that the probability of the parameter lying in the 95% credible interval is .95. The 95% highest-density intervals were also calculated for the standardised effect size for each study, and in each case were extremely close to the 95% credible intervals, and so are not reported.

ACME. (2012). Raising the bar: Developing able young mathematicians . London: Advisory Committee on Mathematics Education. Retrieved from http://www.acme-uk.org/media/10498/raisingthebar.pdf . Accessed 23 Sep 2017.

Andrews, P. (2002). Angle measurement: An opportunity for equity. Mathematics in School , 31 (5), 16–18.

Google Scholar  

Askew, M., Hodgen, J., Hossain, S., & Bretscher, N. (2010). Values and variables: Mathematics education in high-performing countries . London: Nuffield Foundation.

Boaler, J. (2002). Experiencing school mathematics: Traditional and reform approaches to teaching and their impact on student learning . London: Routledge.

Boaler, J. (2015). Fluency without fear: Research evidence on the best ways to learn math facts . Stanford, CA: youcubed. Retrieved from https://www.youcubed.org/fluency-without-fear/ . Accessed 23 Sep 2017.

Codding, R. S., Burns, M. K., & Lukito, G. (2011). Meta-analysis of mathematic basic-fact fluency interventions: A component analysis. Learning Disabilities Research & Practice , 26 (1), 36–47.

Article   Google Scholar  

Department for Education (DfE). (2013). Mathematics programmes of study: Key stage 3: National curriculum in England . London: DfE.

Dienes, Z. (2014). Using Bayes to get the most out of non-significant results. Frontiers in Psychology , 5 , 781.

Encyclopaedia Britannica. (2007). Étude . Retrieved from https://www.britannica.com/art/etude-music . Accessed 11 Feb 2017.

Ericsson, A., & Pool, R. (2016). Peak: Secrets from the new science of expertise . New York: Houghton Mifflin Harcourt.

Fan, L., & Bokhove, C. (2014). Rethinking the role of algorithms in school mathematics: A conceptual model with focus on cognitive development. ZDM Mathematics Education , 46 (3), 481–492.

Foster, C. (2011). A picture is worth a thousand exercises. Mathematics Teaching , 224 , 10–11.

Foster, C. (2012a). Connected expressions. Mathematics in School , 41 (5), 32–33.

Foster, C. (2012b). Working without a safety net. The Australian Mathematics Teacher , 68 (2), 25–29.

Foster, C. (2013a). Connected quadratics. Teach Secondary , 2 (1), 46–48.

Foster, C. (2013b). Mathematical études: Embedding opportunities for developing procedural fluency within rich mathematical contexts. International Journal of Mathematical Education in Science and Technology , 44 (5), 765–774.

Foster, C. (2013c). Resisting reductionism in mathematics pedagogy. Curriculum Journal , 24 (4), 563–585.

Foster, C. (2013d). Staying on the page. Teach Secondary , 3 (1), 57–59.

Foster, C. (2014). Mathematical fluency without drill and practice. Mathematics Teaching , 240 , 5–7.

Foster, C. (2015a). Expression polygons. Mathematics Teacher , 109 (1), 62–65.

Foster, C. (2015b). The convergent–divergent model: An opportunity for teacher–learner development through principled task design. Educational Designer , 2 (8).

Foster, C. (2016). Confidence and competence with mathematical procedures. Educational Studies in Mathematics , 91 (2), 271–288.

Hewitt, D. (1996). Mathematical fluency: The nature of practice and the role of subordination. For the Learning of Mathematics , 16 (2), 28–35.

Hewitt, D. (2015). The economic use of time and effort in the teaching and learning of mathematics. In S. Oesterle & D. Allan (Eds.), Proceedings of the 2014 Annual Meeting of the Canadian Mathematics Education Study Group (pp. 3–23). Edmonton, Canada: University of Alberta.

Hodgen, J. (2015). Unlocking potential in our curriculum: Mastering subjects. In A. Bingham (Ed.), Lessons learned: Putting experience to work (pp. 35–44). London: Ark, King’s College London.

Jeffreys, H. (1961). The theory of probability (3rd ed.). Oxford: Oxford University Press.

Kling, G., & Bay-Williams, J. M. (2015). Three steps to mastering multiplication facts. Teaching Children Mathematics , 21 (9), 548–559.

Lemov, D., Woolway, E., & Yezzi, K. (2012). Practice perfect: 42 rules for getting better at getting better . San Francisco, CA: Jossey-Bass.

Leung, F. K. (2014). What can and should we learn from international studies of mathematics achievement? Mathematics Education Research Journal, 26 (3), 579–605.

Li, S. (1999). Does practice make perfect? For the Learning of Mathematics , 19 (3), 33–35.

National Association of Mathematics Advisors [NAMA]. (2016). Five myths of mastery in mathematics. Mathematics Teaching , 251 , 20–24.

National Centre for Excellence in the Teaching of Mathematics [NCETM] (2016). The essence of maths teaching for mastery . Retrieved from https://www.ncetm.org.uk/files/37086535/The+Essence+of+Maths+Teaching+for+Mastery+june+2016.pdf . Accessed 23 Sep 2017.

National Council of Teachers of Mathematics [NCTM]. (2014). Procedural fluency in mathematics: A position of the National Council of Teachers of Mathematics . Reston, VA: NCTM.

Office for Standards in Education [Ofsted]. (2012). Mathematics: Made to measure . London: Ofsted. Retrieved from https://www.gov.uk/government/uploads/system/uploads/attachment_data/file/417446/Mathematics_made_to_measure.pdf . Accessed 23 Sep 2017.

Rouder, J. N., Speckman, P. L., Sun, D., Morey, R. D., & Iverson, G. (2009). Bayesian t tests for accepting and rejecting the null hypothesis. Psychonomic Bulletin & Review , 16 (2), 225–237.

Taleporos, E. (2005). Consequential validity: A practitioner’s perspective. Educational Measurement: Issues and Practice , 17 (2), 20–23.

Truss, E. (2013, January 17). Education minister Elizabeth Truss speaks at the North of England Education Conference . Retrieved from https://www.gov.uk/government/speeches/education-minister-elizabeth-truss-speaks-at-the-north-of-england-education-conference . Accessed 11 Feb 2017.

Watson, A., & De Geest, E. (2014). Department-initiated change. Educational Studies in Mathematics , 87 (3), 351–368.

Willingham, D. T. (2009). Why don’t students like school: A cognitive scientist answers questions about how the mind works and what it means for the classroom . San Francisco, CA: Jossey-Bass.

Yeo, J. B. (2017). Development of a framework to characterise the openness of mathematical tasks. International Journal of Science and Mathematics Education, 15 (1), 175–191.

Download references

Author information

Authors and affiliations.

Centre for Research in Mathematics Education, School of Education, University of Nottingham, Nottingham, NG8 1BB, UK

Colin Foster

You can also search for this author in PubMed   Google Scholar

Corresponding author

Correspondence to Colin Foster .

Appendix: Prior robustness graphs for the three Bayesian analyses

Horizontal dashed lines show the conventional cut-off Bayes Factor of 3 for “substantial” evidence (Jeffreys, 1961 ).

Rights and permissions

Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.

Reprints and permissions

About this article

Foster, C. Developing mathematical fluency: comparing exercises and rich tasks. Educ Stud Math 97 , 121–141 (2018). https://doi.org/10.1007/s10649-017-9788-x

Download citation

Published : 26 September 2017

Issue Date : February 2018

DOI : https://doi.org/10.1007/s10649-017-9788-x

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Bayesian hypothesis testing
• Enlargements
• Linear equations
• Mathematics education
• Find a journal
• Publish with us
• Track your research

Advertisement

How AI mathematicians might finally deliver human-level reasoning

Artificial intelligence is taking on some of the hardest problems in pure maths, arguably demonstrating sophisticated reasoning and creativity – and a big step forward for AI

By Alex Wilkins

10 April 2024

Simon Danaher

In pure mathematics, very occasionally, breakthroughs arrive like bolts from the blue – the result of such inspired feats of reasoning and creativity that they seem to push the very bounds of intelligence . In 2016, for instance, mathematician Timothy Gowers marvelled at a solution to the cap set problem , which has to do with finding the largest pattern of points in space where no three points form a straight line. The proof “has a magic quality that leaves one wondering how on Earth anybody thought of it”, he wrote.

You might think that such feats are unique to humans. But you might be wrong. Because last year, artificial intelligence company Google DeepMind announced that its AI had discovered a better solution to the cap set problem than any human had . And that was just the latest demonstration of AI’s growing mathematical prowess. Having long struggled with this kind of sophisticated reasoning, today’s AIs are proving themselves remarkably capable – solving complex geometry problems, assisting with proofs and generating fresh avenues of attack for long-standing problems.

Can AI ever become conscious and how would we know if that happens?

All of which has prompted mathematicians to ask if their field is entering a new era. But it has also emboldened some computer scientists to suggest we are pushing the bounds of machine intelligence, edging ever closer to AI capable of genuinely human-like reasoning – and maybe even artificial general intelligence, AI that can perform as well as or better than humans on a wide range of tasks. “Mathematics is the language of reasoning,” says Alex Davies at DeepMind. “If models can…

Sign up to our weekly newsletter

Receive a weekly dose of discovery in your inbox! We'll also keep you up to date with New Scientist events and special offers.

To continue reading, subscribe today with our introductory offers

No commitment, cancel anytime*

Offer ends 2nd of July 2024.

*Cancel anytime within 14 days of payment to receive a refund on unserved issues.

Inclusive of applicable taxes (VAT)

Existing subscribers

More from New Scientist

Explore the latest news, articles and features

Chatbots can persuade conspiracy theorists their view might be wrong

Subscriber-only

AI can spot parasites in stool samples to help diagnose infections

Watch mini humanoid robots showing off their football skills, why ais that tackle complex maths could be the next big breakthrough, popular articles.

Trending New Scientist articles

What is the Hardest Subject to Teach in 2024?

Wondering about the hardest subject to teach? You’ve come to the right place!

Teaching is a noble profession, but some subjects are notoriously harder to teach than others, posing unique challenges.

From reading and writing basics in elementary school to advanced sciences and mathematics in higher education, certain topics can perplex even seasoned educators. We should know because we’ve taught in various capacities since the early 2010s!

However, with the right strategies, even the most challenging subjects can become accessible and engaging.

This guide explores the hardest subjects to teach at each educational level, from elementary to post-secondary, providing practical tips to help teachers navigate these obstacles confidently and successfully . Let’s go!

The Hardest Subject to Teach in Elementary School

Elementary school is the foundation upon which all future learning is built. It’s where young minds first encounter the fundamental concepts that will shape their academic journey.

However, even at this early stage, certain subjects can pose significant challenges for teachers.

Reading and Writing

Mastering the art of reading and writing is a monumental task for young learners. Teachers must not only introduce the intricacies of phonics, grammar, and vocabulary but also cultivate a love for literature and self-expression.

The challenge lies in catering to diverse learning styles and abilities while ensuring that no child is left behind. In addition to teaching our own child to read, we’ve also been teaching ELL students to read in English.

Tips for teaching reading and writing effectively:

• Incorporate multisensory activities that engage sight, sound, and touch to reinforce concepts. Gamification helps a lot !
• Foster a print-rich environment by displaying words, labels, and student work throughout the classroom.
• Encourage creative writing exercises that allow students to express themselves freely, building confidence and enthusiasm.

Mathematics

Math is often perceived as a daunting subject , even at the elementary level. Teachers must impart numerical skills and a deep understanding of abstract concepts like patterns, shapes, and problem-solving strategies.

Tips for teaching mathematics effectively:

• Use hands-on manipulatives and visual aids to make abstract concepts more concrete and tangible.
• Incorporate real-world examples and storytelling to demonstrate the practical applications of mathematics.
• Encourage collaborative learning and group problem-solving to foster a supportive and engaging learning environment.

Science, with its vast array of topics and concepts, can be a daunting subject for elementary STEM teachers.

From the intricacies of the natural world to the principles of physics and chemistry, educators must find ways to make these complex ideas accessible and engaging for young minds.

Tips for teaching science effectively:

• Incorporate hands-on experiments and interactive demonstrations to bring scientific concepts to life .
• Foster a sense of wonder and curiosity by encouraging students to ask questions and explore their surroundings.
• Leverage technology and multimedia resources to provide vivid illustrations and simulations of scientific phenomena.

The Hardest Subject to Teach in Middle School

As students transition from elementary to middle school, the academic landscape becomes increasingly complex. Once straightforward subjects now demand a deeper level of understanding and critical thinking.

For teachers, this period can be particularly challenging as they navigate the unique obstacles posed by certain subjects.

Algebra marks a significant shift in mathematical thinking, introducing abstract concepts and symbolic representations. Teachers must guide students through this cognitive leap , helping them grasp the underlying logic and problem-solving strategies.

Tips for teaching algebra effectively:

• Break down complex problems into smaller, manageable steps to build confidence and understanding.
• Utilize visual aids and real-world examples to make abstract concepts more relatable and tangible.
• Encourage collaborative learning and peer tutoring to foster a supportive and engaging learning environment.

Foreign Languages

Learning a new language requires mastery of grammar, vocabulary, pronunciation, and cultural nuances. We’ve been teaching English as a foreign language for years so we know how tough foreign languages can be.

Teachers must impart linguistic knowledge and cultivate an appreciation for diverse cultures and communication styles.

Tips for teaching foreign languages effectively:

• Immerse students in the target language through interactive activities, games, and multimedia resources.
• Incorporate cultural elements, such as music, art, and literature, to provide context and enrich the learning experience.
• Encourage students to practice speaking and writing regularly, providing constructive feedback and support.

Earth Science

Earth science encompasses various topics, from geology and meteorology to astronomy and environmental studies.

Teachers must navigate the complexities of these interconnected disciplines while making abstract concepts accessible to middle school students.

Tips for teaching earth science effectively:

• Leverage technology and multimedia resources to provide vivid illustrations and simulations of natural phenomena.
• Incorporate hands-on activities, such as rock and mineral identification or weather observation, to reinforce concepts.
• Encourage critical thinking and problem-solving by exploring real-world environmental challenges and potential solutions.

The Hardest Subject to Teach in High School

High school marks a pivotal stage in a student’s academic journey, where the demands of rigorous coursework and college preparation intensify.

For teachers, this level presents a unique set of challenges, particularly in subjects that require a deep understanding of complex concepts and advanced problem-solving skills.

Calculus is often regarded as the pinnacle of mathematical complexity in high school curricula. Teachers must guide students through the intricate world of limits, derivatives, and integrals, concepts that can seem abstract and counterintuitive to many learners.

Tips for teaching calculus effectively:

• Emphasize the practical applications of calculus in fields like physics, engineering, and economics to make the subject more relatable.
• Utilize visual aids, such as graphs and animations, to illustrate complex concepts and their real-world implications.
• Encourage collaborative problem-solving and peer tutoring to foster a supportive learning environment.

Physics delves into the fundamental laws that govern the universe, from mechanics and thermodynamics to electromagnetism and quantum theory.

Teachers must not only convey these intricate concepts but also cultivate a deep appreciation for the scientific method and critical thinking.

Tips for teaching physics effectively:

• Incorporate hands-on experiments and demonstrations to bring abstract concepts to life and reinforce understanding.
• Leverage technology and multimedia resources to provide vivid simulations and visualizations of complex phenomena.
• Encourage students to apply physics principles to real-world scenarios and problem-solving exercises.

Chemistry is a multifaceted discipline that combines theoretical concepts with practical laboratory work.

Teachers must navigate the intricacies of atomic structure, chemical reactions, and quantitative analysis while ensuring student safety in the lab environment.

Tips for teaching chemistry effectively:

• Utilize interactive models and simulations to visualize abstract concepts like molecular structures and chemical processes.
• Emphasize the real-world applications of chemistry in fields like medicine, environmental science, and materials science.
• Foster a culture of safety and responsibility in the laboratory, providing clear guidelines and supervision.

Advanced Foreign Languages

As students progress to advanced levels of foreign language study, the complexities of grammar, vocabulary, and cultural nuances become increasingly challenging.

Teachers must impart linguistic proficiency and cultivate a deep appreciation for the target culture and its nuances.

Tips for teaching advanced foreign languages effectively:

• Immerse students in authentic materials, such as literature, films, and news sources, to expose them to real-world language usage.
• Encourage students to converse and discuss complex topics to improve fluency and cultural understanding.
• Incorporate technology and language-learning apps to provide personalized practice and feedback.

The Hardest Subject to Teach in Post-Secondary Degree Programs

At the post-secondary level, the academic landscape becomes increasingly specialized and rigorous.

Degree programs in fields like engineering, medicine, and law demand a deep understanding of complex concepts, critical thinking skills, and the ability to apply knowledge in practical settings.

For educators, these subjects present unique challenges that require innovative teaching approaches and a commitment to excellence.

Engineering

Engineering is a multidisciplinary field that combines principles from mathematics, physics, and computer science to solve real-world problems.

Teachers must impart theoretical knowledge and also cultivate practical skills in design, analysis, and problem-solving.

Tips for teaching engineering effectively:

• Incorporate hands-on projects and simulations that mimic real-world engineering challenges, allowing students to apply their knowledge in practical settings.
• Encourage collaboration and teamwork, as engineering often involves working in cross-functional teams to tackle complex problems.
• Leverage industry partnerships and guest lectures to provide insights into current trends, technologies, and best practices in the field.

The study of medicine is a demanding and comprehensive endeavor , encompassing a vast array of subjects from anatomy and physiology to pharmacology and clinical practice.

Teachers must not only convey complex scientific concepts but also cultivate critical thinking, ethical reasoning, and compassionate patient care.

Tips for teaching medicine effectively:

• Integrate hands-on clinical experiences, such as simulations and case studies, to bridge the gap between theory and practice.
• Emphasize the importance of lifelong learning and staying up-to-date with the latest medical research and advancements.
• Foster a culture of empathy and patient-centered care, encouraging students to consider the human aspect of medicine beyond just scientific knowledge.

The study of law is a rigorous and intellectually demanding pursuit , requiring a deep understanding of legal principles, statutes, and case law.

When I was in graduate school, I took several law classes. My professor’s approach was so different from other teachers’ so he could better provide knowledge and cultivate critical thinking, analytical reasoning, and effective communication skills.

Tips for teaching law effectively:

• Incorporate case studies and legal simulations to provide practical experience in applying legal concepts and reasoning.
• Encourage debate and discussion on complex legal issues, fostering the ability to analyze multiple perspectives and arguments.
• Emphasize the importance of clear and persuasive communication, both in written and oral form, as it is essential in the legal profession.

10 Tips for Teaching Difficult Subjects

While certain subjects may inherently pose greater challenges, some strategies and techniques can help teachers navigate these complexities and make even the most daunting topics more accessible and engaging for students.

Here are some helpful tips for teaching difficult subjects effectively:

• Break it down: Deconstruct complex concepts into smaller, manageable components, allowing students to build understanding incrementally.
• Leverage visuals: Incorporate visual aids, such as diagrams, animations, and multimedia resources, to illustrate abstract ideas and make them more concrete.
• Encourage active learning: Engage students through hands-on activities, experiments, and problem-solving exercises that reinforce concepts and foster critical thinking.
• Make real-world connections: Relate subject matter to real-life applications and examples that students can relate to, demonstrating the practical relevance of the material.
• Foster collaboration: Promote collaborative learning through group projects, peer tutoring, and discussions, creating a supportive environment where students can learn from one another.
• Embrace technology: Utilize educational technology, such as interactive simulations, online resources, and learning management systems, to enhance engagement and provide personalized learning experiences.
• Differentiate instruction: Cater to diverse learning styles and abilities by offering multiple modes of instruction, from lectures and readings to multimedia presentations and hands-on activities.
• Cultivate curiosity: Encourage students to ask questions, explore their interests, and develop a genuine passion for the subject matter, fostering intrinsic motivation and lifelong learning.
• Provide ongoing feedback: Offer regular, constructive feedback to students, identifying areas for improvement and celebrating successes to support their growth and development.
• Embrace a growth mindset: Foster a classroom culture that embraces challenges, values effort, and recognizes that intelligence and abilities can be developed through perseverance and hard work.

By implementing these strategies, teachers can transform even the most challenging subjects into engaging and rewarding learning experiences, empowering students to overcome obstacles and achieve academic success.

Final Thoughts on the Hardest Subject to Teach

Teaching is a noble calling that requires dedication, patience, and a deep subject understanding. Some subjects may be more challenging, but the rewards of shaping young minds are priceless.

From elementary to higher education, each subject presents unique obstacles. However, innovative strategies, technology, and a supportive learning environment can make even the most daunting topics accessible and engaging.

Ultimately, the hardest subject to teach is not defined by complexity but by the teacher’s ability to adapt, innovate, and inspire . It showcases educators’ dedication and creativity in breaking down barriers, igniting curiosity, and empowering students.

As education evolves, every subject holds the power to transform lives . By embracing challenges and refining teaching methods, we can unlock the boundless potential of every student, one lesson at a time.

Hardest Subject to Teach: FAQs

Do you still have questions about the hardest subject to teach? Here are answers to some frequently asked questions.

What CORE Subject is the hardest to teach in general?

While the difficulty of teaching a subject can vary depending on the grade level and individual student needs, mathematics is often considered one of the most challenging core subjects to teach across all educational levels.

The abstract nature of math concepts, the requirement for logical reasoning and problem-solving skills, and the cumulative aspect of the subject can be challenging for teachers and students.

What makes a subject hard to teach?

Teaching a challenging subject involves abstract concepts, complex terms, needed background, and diverse learners. Explaining math, physics, or philosophy can be tough.

Chemistry, biology, or law terms can be hard. Math or foreign languages are challenging without the right foundation. Teaching tough subjects to diverse learners in one class is a challenge.

How can teachers make difficult subjects easier to learn?

Educators use various tools to simplify complex topics and engage learners effectively: Break down complex ideas into smaller steps. Use visuals, multimedia, and interactive tasks for improved understanding.

Encourage engagement through teamwork, interaction, and peer teaching. Connect lessons to real-world scenarios. Provide ongoing guidance, support, and opportunities for skill enhancement.

Are there any resources available to help teachers with challenging subjects?

Yes, teachers can access resources like professional development workshops, online communities, teaching materials, tech tools, and collaboration to effectively address the hardest subjects to teach.

The post What is the Hardest Subject to Teach in 2024? appeared first on The Tutor Resource .

Or search by topic

Number and algebra

• The Number System and Place Value
• Calculations and Numerical Methods
• Fractions, Decimals, Percentages, Ratio and Proportion
• Properties of Numbers
• Patterns, Sequences and Structure
• Algebraic expressions, equations and formulae
• Coordinates, Functions and Graphs

Geometry and measure

• Angles, Polygons, and Geometrical Proof
• 3D Geometry, Shape and Space
• Measuring and calculating with units
• Transformations and constructions
• Pythagoras and Trigonometry
• Vectors and Matrices

Probability and statistics

• Handling, Processing and Representing Data
• Probability

Working mathematically

• Thinking mathematically
• Mathematical mindsets
• Cross-curricular contexts
• Physical and digital manipulatives

For younger learners

• Early Years Foundation Stage

Advanced mathematics

• Decision Mathematics and Combinatorics
• Advanced Probability and Statistics

Exploring Problem Solving, Reasoning and Fluency in a Geometrical Context

Inside Triangles

How many different triangles can you draw on the dotty grid which each have one dot in the middle?

Seeing Squares

Players take it in turns to choose a dot on the grid. The winner is the first to have four dots that can be joined to form a square.

Poly Plug Rectangles

The computer has made a rectangle and will tell you the number of spots it uses in total. Can you find out where the rectangle is?

Can you each work out what shape you have part of on your card? What will the rest of it look like?

Nine-pin Triangles

How many different triangles can you make on a circular pegboard that has nine pegs?

Brush Loads

How can you arrange the 5 cubes so that you need the smallest number of Brush Loads of paint to cover them? Try with other numbers of cubes as well.

Square Corners

What is the greatest number of counters you can place on the grid below without four of them lying at the corners of a square?

Stringy Quads

This practical problem challenges you to make quadrilaterals with a loop of string. You'll need some friends to help!