lesson 12 homework page 67

Succeed Grade 5 Modules 1 & 2 | Eureka Math Virginia Edition

Eureka Math

Grade 5 Modules 1 & 2 VIRGINIA EDITION

Great Minds PBC is the creator of Eureka Math®, Wit & Wisdom®, Alexandria Plan™, and PhD Science™.

Published by Great Minds PBC. greatminds.org Copyright © 2021 Great Minds PBC. All rights reserved. No part of this work may be reproduced or used in any form or by any means—graphic, electronic, or mechanical, including photocopying or information storage and retrieval systems—without written permission from the copyright holder. Printed in the USA 10 9 8 7 6 5

ISBN 978-1-64497-958-7

Learn ♦ Practice ♦ Succeed Eureka Math® student materials for A Story of Units® (K–5) are available in the Learn, Practice, Succeed trio. This series supports differentiation and remediation while keeping student materials organized and accessible. Educators will find that the Learn, Practice, and Succeed series also offers coherent—and therefore, more effective—resources for Response to Intervention (RTI), extra practice, and summer learning.

Learn Eureka Math Learn serves as a student’s in-class companion where they show their thinking, share what they know, and watch their knowledge build every day. Learn assembles the daily classwork—Application Problems, Exit Tickets, Problem Sets, templates—in an easily stored and navigated volume.

Practice Each Eureka Math lesson begins with a series of energetic, joyous fluency activities, including those found in Eureka Math Practice. Students who are fluent in their math facts can master more material more deeply. With Practice, students build competence in newly acquired skills and reinforce previous learning in preparation for the next lesson. Together, Learn and Practice provide all the print materials students will use for their core math instruction.

Succeed Eureka Math Succeed enables students to work individually toward mastery. These additional problem sets align lesson by lesson with classroom instruction, making them ideal for use as homework or extra practice. Each problem set is accompanied by a Homework Helper, a set of worked examples that illustrate how to solve similar problems. Teachers and tutors can use Succeed books from prior grade levels as curriculum-consistent tools for filling gaps in foundational knowledge. Students will thrive and progress more quickly as familiar models facilitate connections to their current grade-level content.

Students, families, and educators: Thank you for being part of the Eureka Math® community, where we celebrate the joy, wonder, and thrill of mathematics. Nothing beats the satisfaction of success—the more competent students become, the greater their motivation and engagement. The Eureka Math Succeed book provides the guidance and extra practice students need to shore up foundational knowledge and build mastery with new material.

What is in the Succeed book? Eureka Math Succeed books deliver supported practice sets that parallel the lessons of A Story of Units®. Each Succeed lesson begins with a set of worked examples, called Homework Helpers, that illustrate the modeling and reasoning the curriculum uses to build understanding. Next, students receive scaffolded practice through a series of problems carefully sequenced to begin from a place of confidence and add incremental complexity.

How should Succeed be used? The collection of Succeed books can be used as differentiated instruction, practice, homework, or intervention. When coupled with Affirm®, Eureka Math’s digital assessment system, Succeed lessons enable educators to give targeted practice and to assess student progress. Succeed’s perfect alignment with the mathematical models and language used across A Story of Units ensures that students feel the connections and relevance to their daily instruction, whether they are working on foundational skills or getting extra practice on the current topic.

Where can I learn more about Eureka Math resources? The Great Minds® team is committed to supporting students, families, and educators with an ever-growing library of resources, available at eureka-math.org. The website also offers inspiring stories of success in the Eureka Math community. Share your insights and accomplishments with fellow users by becoming a Eureka Math Champion. Best wishes for a year filled with Eureka moments!

Jill Diniz Director of Mathematics Great Minds

Grade 5 Modules 1â&#x20AC;&#x201C;2

Contents Module 1: Place Value and Decimal Fractions Topic A: Multiplicative Patterns on the Place Value Chart Lesson 1 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Lesson 2 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Lesson 3 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13 Lesson 4 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 17 Topic B: Decimal Fractions and Place Value Patterns Lesson 5 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 21 Lesson 6 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 27 Topic C: Place Value and Rounding Decimal Fractions Lesson 7 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 31 Lesson 8 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 35 Topic D: Adding and Subtracting Decimals Lesson 9 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 39 Lesson 10 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 43 Topic E: Multiplying Decimals Lesson 11 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 51 Lesson 12 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 55 Topic F: Dividing Decimals Lesson 13 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 59 Lesson 14 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 65 Lesson 15 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 69 Lesson 16 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 73

Module 2: Multi-Digit Whole Number and Decimal Fraction Operations Topic A: Mental Strategies for Multi-Digit Whole Number Multiplication Lesson 1 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 79 Lesson 2 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 83 Topic B: The Standard Algorithm for Multi-Digit Whole Number Multiplication Lesson 3 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 87 Lesson 4 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 93 Lesson 5 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 99 Lesson 6 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 103 Lesson 7 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 107 Lesson 8 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 113 Lesson 9 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 117 Topic C: Decimal Multi-Digit Multiplication Lesson 10 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 123 Lesson 11 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 127 Lesson 12 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 133 Topic D: Measurement Word Problems with Whole Number and Decimal Multiplication Lesson 13 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 139 Lesson 14 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 143 Lesson 15 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 147 Topic E: Mental Strategies for Multi-Digit Whole Number Division Lesson 16 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 151 Lesson 17 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 157 Lesson 18 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 161 Topic F: Partial Quotients and Multi-Digit Whole Number Division Lesson 19 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 165 Lesson 20 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 169 Lesson 21 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 173 Lesson 22 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 177 Lesson 23 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 181

Topic G: Partial Quotients and Multi-Digit Decimal Division Lesson 24 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 185 Lesson 25 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 191 Lesson 26 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 195 Lesson 27 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 201 Topic H: Measurement Word Problems with Multi-Digit Division Lesson 28 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 205 Lesson 29 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 209

Grade 5 Module 1

Lesson 1 Homework Helper 5•1

A STORY OF UNITS

Note: It is common to encourage students to simply “move the decimal point” a number of places when multiplying or dividing by powers of 10. Instead, encourage students to understand that the decimal point lives between the ones place and the tenths place. The decimal point does not move. Rather, the digits shift along the place value chart when multiplying and dividing by powers of ten. Use the place value chart and arrows to show how the value of the each digit changes. 1. 4.215 × 10 = 42.15

2. 421 ÷ 100 = 4.21

Reason concretely and pictorially using place value understanding to relate adjacent base ten units from millions to thousandths.

Lesson 1 Homework Helper 5â&#x20AC;˘1

3. A student used his place value chart to show a number. After the teacher instructed him to multiply his number by 10, the chart showed 3,200.4. Draw a picture of what the place value chart looked like at first.

4. A microscope has a setting that magnifies an object so that it appears 100 times as large when viewed through the eyepiece. If a small bug is 0.183 cm long, how long will the insect appear in centimeters through the microscope? Explain how you know.

The bug will appear to be 18. 3 cm long through the microscope. Since the microscope magnifies objects 100 times, the bug will appear to be 100 times larger. I used a place value chart to show what happens to the value of each digit when it is multiplied by 100. Each digit shifts 2 places to the left.

Lesson 1: Copyright ÂŠ Great Minds PBC Virginia Edition greatminds.org/math

Lesson 1 Homework 5•1

1. Use the place value chart and arrows to show how the value of each digit changes. The first one has been done for you. a. 4.582 × 10 =

b. 7.281 × 100 =

c. 9.254 × 1,000 =

d. Explain how and why the value of the 2 changed in (a), (b), and (c).

2. Use the place value chart and arrows to show how the value of each digit changes. The first one has been done for you. a. 2.46 ÷ 10 =

b. 678 ÷ 100 =

c. 67 ÷ 1,000 =

d. Explain how and why the value of the 6 changed in the quotients in (a), (b), and (c).

Lesson 1 Homework 5â&#x20AC;˘1

3. Researchers counted 8,912 monarch butterflies on one branch of a tree at a site in Mexico. They estimated that the total number of butterflies at the site was 1,000 times as large. About how many butterflies were at the site in all? Explain your thinking, and include a statement of the solution.

4. A student used his place value chart to show a number. After the teacher instructed him to divide his number by 100, the chart showed 28.003. Draw a picture of what the place value chart looked like at first.

Explain how you decided what to draw on your place value chart. Be sure to include reasoning about how the value of each digit was affected by the division.

5. On a map, the perimeter of a park is 0.251 meters. The actual perimeter of the park is 1,000 times as large. What is the actual perimeter of the park? Explain how you know using a place value chart.

Lesson 2 Homework Helper 5â&#x20AC;˘1

1. Solve. a.

2. Solve. a. b. c. Explain how you decided on the number of zeros in the product for part (a). I visualized a place value chart. Multiplying by 100 shifts each digit in the factor 9, 647 two places to the left, so there were 2 additional zeros in the product. d. Explain how you decided where to place the decimal in the quotient for part (b). The divisor, 1, 000, has 3 zeros, so each digit in 9, 647 shifts 3 places to the right. When the digit 9 shifts 3 places to the right, it moves to the ones places, so I knew the decimal point needed to go between the ones place and the tenths place. I put the decimal between the 9 and the 6.

Lesson 2: Copyright ÂŠ Great Minds PBC Virginia Edition greatminds.org/math

Reason abstractly using place value understanding to relate adjacent base ten units from millions to thousandths.

Lesson 2 Homework Helper 5•1

3. Jasmine says that 7 hundredths multiplied by 1,000 equals 7 thousands. Is she correct? Use a place value chart to explain your answer. Jasmine is not correct. 7 ones × 1, 000 would be 7 thousands. But 0. 07 × 1, 000 = 70. Look at my place value chart.

Lesson 2 Homework 5•1

1. Solve. a. 36,000 × 10 =

e. 2.4 × 100 =

b. 36,000 ÷ 10 =

c. 4.3 × 10 =

g. 4.54 × 1,000 =

d. 4.3 ÷ 10 =

h. 3,045.4 ÷ 100 =

24 ÷ 1,000 =

2. Find the products. a. 14,560 × 10

b. 14,560 × 100 = c. 14,560 × 1,000 =

Explain how you decided on the number of zeros in the products for (a), (b), and (c).

3. Find the quotients. a. 16.5 ÷ 10 = b. 16.5 ÷ 100 = c. Explain how you decided where to place the decimal in the quotients for (a) and (b).

4. Ted says that 3 tenths multiplied by 100 equals 300 thousandths. Is he correct? Use a place value chart to explain your answer.

5. Alaska has a land area of about 1,700,000 square kilometers. Florida has a land area the size of Alaska. 10 What is the land area of Florida? Explain how you found your answer.

Lesson 3 Homework Helper 5•1

1. Write the following in exponential form. c. 100,000 =

2. Write the following in standard form. c.

643 ÷ 103 =

3. Complete the patterns.

Use exponents to name place value units, and explain patterns in the placement of the decimal point.

Lesson 3 Homework 5•1

1. Write the following in exponential form (e.g., 100 = 102). a. 1000 =

d. 100 × 10 =

b. 10 × 10 =

e. 1,000,000 =

c. 100,000 =

10,000 × 10 =

2. Write the following in standard form (e.g., 4 × 102 = 400). a. 4 × 103 =

e. 6.072 × 103 =

b. 64 × 104 =

c. 5,300 ÷ 102 =

g. 948 ÷ 103 =

d. 5,300,000 ÷ 103 =

h. 9.4 ÷ 102 =

60.72 × 104 =

3. Complete the patterns. a. 0.02

b. 3,400,000

4. After a lesson on exponents, Tia went home and said to her mom, “I learned that 104 is the same as 40,000.” She has made a mistake in her thinking. Use words, numbers, or a place value chart to help Tia correct her mistake.

5. Solve 247 ÷ 10 2 and 247 × 102. a. What is different about the two answers? Use words, numbers, or pictures to explain how the digits shift.

b. Based on the answers from the pair of expressions above, solve 247 ÷ 103 and 247 × 103.

Lesson 4 Homework Helper 5â&#x20AC;˘1

1. Convert and write an equation with an exponent.

2. Convert using an equation with an exponent.

3. The height of a cellphone is 13 cm. Express this measurement in meters. Explain your thinking. Include an equation with an exponent in your explanation.

Lesson 4: Copyright ÂŠ Great Minds PBC Virginia Edition greatminds.org/math

Use exponents to denote powers of 10 with application to metric conversions.

Lesson 4 Homework 5â&#x20AC;˘1

1. Convert and write an equation with an exponent. Use your meter strip when it helps you. a.

2 meters to centimeters

2m = 200 cm

108 centimeters to meters

2.49 meters to centimeters

50 centimeters to meters

6.3 meters to centimeters

7 centimeters to meters

In the space below, list the letters of the problems where smaller units are converted to larger units.

2 Ă&#x2014; 102 = 200

2. Convert using an equation with an exponent. Use your meter strip when it helps you. a.

4 meters to millimeters

1.7 meters to millimeters

1,050 millimeters to meters

65 millimeters to meters

4.92 meters to millimeters

3 millimeters to meters

In the space below, list the letters of the problems where larger units are converted to smaller units.

Lesson 4 Homework 5•1

3. Read each aloud as you write the equivalent measures. Write an equation with an exponent you might use to convert. a. 2.638 m

2.638 × 103 = 2,638

4. Yi Ting’s height is 1.49 m. Express this measurement in millimeters. Explain your thinking. Include an equation with an exponent in your explanation.

5. A ladybug’s length measures 2 cm. Express this measurement in meters. Explain your thinking. Include an equation with an exponent in your explanation.

6. The length of a sticky note measures 77 millimeters. Express this length in meters. Explain your thinking. Include an equation with an exponent in your explanation.

Lesson 5 Homework Helper 5â&#x20AC;˘1

1. Express as decimal numerals. a.

5 . 132 2. Express in words. a. 0.034

Thirty-four thousandths

b. 73.29 3. Write the number in expanded form using decimals and fractions.

Lesson 5: Copyright ÂŠ Great Minds PBC Virginia Edition greatminds.org/math

Name decimal fractions in expanded, unit, and word forms by applying place value reasoning.

4. Write a decimal for each of the following.

Lesson 5 Homework 5•1

1. Express as decimal numerals. The first one is done for you. a. Five thousandths

b. Thirty-five thousandths c. Nine and two hundred thirty-five thousandths d. Eight hundred and five thousandths 8

528 1000 502

h. 300 1000 2. Express each of the following values in words. a. 0.008 b. 15.062 c. 607.409

3. Write the number on a place value chart. Then, write it in expanded form using fractions or decimals to express the decimal place value units. The first one is done for you. a.

1 +4 × 1 +6 × 1 27.346 = 2 × 10 + 7 × 1+ 3 × ( 10 ) ( 100 ) ( 1000 ) or

27.346 = 2 × 10 + 7 × 1+ 3 × 0.1+ 4 × 0.01 + 6 × 0.001

4. Write a decimal for each of the following. Use a place value chart to help, if necessary. a. 3 × 10 + 5 × 1 + 2 ×

( ) +7× ( )+ 6× ( ) 1

b. 9 × 100 + 2 × 10 + 3 × 0.1 + 7 × 0.001 c.

5 × 1000 + 4 × 100 + 8 × 1 + 6 ×

( ) +5 × ( ) 1

5. At the beginning of a lesson, a piece of chalk is 4.875 inches long. At the end of the lesson, it is 3.125 inches long. Write the two amounts in expanded form using fractions. a.

At the beginning of the lesson:

At the end of the lesson:

6. Mrs. Herman asked the class to write an expanded form for 412.638. Nancy wrote the expanded form using fractions, and Charles wrote the expanded form using decimals. Write their responses.

Lesson 5 Template 5â&#x20AC;˘1

thousands through thousandths place value chart

Lesson 6 Homework Helper 5â&#x20AC;˘1

1. Show the numbers on the place value chart using digits. Use >, <, or = to compare.

2. Use the >, <, or = to compare the following.

Lesson 6: Copyright ÂŠ Great Minds PBC Virginia Edition greatminds.org/math

Compare decimal fractions to the thousandths using like units, and express comparisons with >, <, =.

3. Arrange the numbers in increasing order.

Lesson 6 Homework 5•1

1. Use >, <, or = to compare the following. a. 16.45

f. Five ones and eight tenths

Fifty-eight tenths

g. Thirty-six and nine thousandths

h. One hundred four and twelve hundredths

One hundred four and two thousandths

One hundred fifty-eight thousandths

0.58 Seven hundred three and five hundredths

j. 703.005

2. Arrange the numbers in increasing order. a. 8.08

3. Arrange the numbers in decreasing order. a. 8.508 8.58 7.5 7.058

4. James measured his hand. It was 0.17 meter. Jennifer measured her hand. It was 0.165 meter. Whose hand is bigger? How do you know?

5. In a paper airplane contest, Marcel’s plane travels 3.345 meters. Salvador’s plane travels 3.35 meters. Jennifer’s plane travels 3.3 meters. Based on the measurements, whose plane traveled the farthest distance? Whose plane traveled the shortest distance? Explain your reasoning using a place value chart.

Lesson 7 Homework Helper 5â&#x20AC;˘1

Round to the given place value. Label the number lines to show your work. Circle the rounded number. Use a place value chart to show your decompositions for each. 1. 3.27

Lesson 7: Copyright ÂŠ Great Minds PBC Virginia Edition greatminds.org/math

Round a given decimal to any place using place value understanding and the vertical number line.

Lesson 7 Homework Helper 5•1

2. Rosie’s pedometer said she walked 1.46 miles. She rounded her distance to 1 mile, and her brother, Isaac, rounded her distance to 1.5 miles. They are both right. Why?

Rosie rounded the distance to the nearest mile, and Isaac rounded the distance to the nearest tenth of a mile. 1. 46 rounded to the nearest one is 1.

1. 46 rounded to the nearest tenth is 15 tenths or 1. 5.

Lesson 7 Homework 5â&#x20AC;˘1

Fill in the table, and then round to the given place. Label the number lines to show your work. Circle the rounded number. 1. 4.3 a. Hundredths

2. 225.286 a. Hundredths

Lesson 7 Homework 5•1

a. Hundredths

b. Tenths

4. On a Major League Baseball diamond, the distance from the pitcher’s mound to home plate is 18.386 meters. a. Round this number to the nearest hundredth of a meter. Use a number line to show your work.

b. How many centimeters is it from the pitcher’s mound to home plate?

5. Jules reads that 1 pint is equivalent to 0.473 liters. He asks his teacher how many liters there are in a pint. His teacher responds that there are about 0.47 liters in a pint. He asks his parents, and they say there are about 0.5 liters in a pint. Jules says they are both correct. How can that be true? Explain your answer.

Lesson 8 Homework Helper 5â&#x20AC;˘1

1. Round the quantity to the given place value. Draw number lines to explain your thinking. Circle the rounded value on the number line.

Lesson 8: Copyright ÂŠ Great Minds PBC Virginia Edition greatminds.org/math

2. A decimal number has two digits to the right of its decimal point. If we round it to the nearest tenth, the result is 28.7. What is the maximum possible value of this decimal? Use words and the number line to explain your reasoning.

Lesson 8 Homework 5â&#x20AC;˘1

1. Write the decomposition that helps you, and then round to the given place value. Draw number lines to explain your thinking. Circle the rounded value on each number line. a. 43.586 to the nearest tenth, hundredth, and one.

b. 243.875 to nearest tenth, hundredth, ten, and hundred.

2. A trip from New York City to Seattle is 2,852.1 miles. A family wants to make the drive in 10 days, driving the same number of miles each day. About how many miles will they drive each day? Round your answer to the nearest tenth of a mile.

3. A decimal number has two digits to the right of its decimal point. If we round it to the nearest tenth, the result is 18.6. a. What is the maximum possible value of this number? Use words and the number line to explain your reasoning. Include the midpoint on your number line.

b. What is the minimum possible value of this decimal? Use words, pictures, or numbers to explain your reasoning.

Lesson 9 Homework Helper 5•1

Note: Adding decimals is just like adding whole numbers—combine like units. Study the examples below: 2 apples + 3 apples = 5 apples 2 ones + 3 ones = 5 ones

2 tens + 3 tens = 5 tens = 50

2 hundredths + 3 hundredths = 5 hundredths = 0.05 1. Solve.

Add decimals using place value strategies, and relate those strategies to a written method.

Lesson 9 Homework Helper 5â&#x20AC;˘1

2. Solve using the standard algorithm.

3. Anthony spends $6.49 on a book. He also buys a pencil for $2.87 and an eraser for $1.15. How much money does he spend altogether?

Lesson 9: Copyright ÂŠ Great Minds PBC Virginia Edition greatminds.org/math

Lesson 9 Homework 5•1

1. Solve. a. 3 tenths + 4 tenths =

b. 12 tenths + 9 tenths =

c. 3 hundredths + 4 hundredths = d. 27 hundredths + 7 hundredths = e. 4 thousandths + 3 thousandths = f.

39 thousandths + 5 thousandths =

g. 5 tenths + 7 thousandths =

hundredths hundredths =

thousandths

thousandths thousandths = thousandths

h. 4 ones 4 tenths + 4 tenths = i.

8 thousandths + 6 ones 8 thousandths =

2. Solve using the standard algorithm. a. 0.4 + 0.7 =

b. 2.04 + 0.07 =

c. 6.4 + 3.7 =

d. 56.04 + 3.07 =

e. 72.564 + 5.137 =

f. 75.604 + 22.296 =

3. Walkway Over the Hudson, a bridge that crosses the Hudson River in Poughkeepsie, is 2.063 kilometers long. Anping Bridge, which was built in China 850 years ago, is 2.07 kilometers long. a. What is the total span of both bridges? Show your thinking.

b. Leah likes to walk her dog on the Walkway Over the Hudson. If she walks across and back, how far will she and her dog walk?

4. For his parents’ anniversary, Danny spends $5.87 on a photo. He also buys a balloon for $2.49 and a box of strawberries for $4.50. How much money does he spend all together?

Lesson 10 Homework Helper 5•1

Note: Subtracting decimals is just like subtracting whole numbers—subtract like units. Study the examples below. 5 apples − 1 apple = 4 apples 5 ones − 1 one = 4 ones 5 tens − 1 ten = 4 tens 5 hundredths − 1 hundredth = 4 hundredths

1. Subtract.

Subtract decimals using place value strategies, and relate those strategies to a written method.

Lesson 10 Homework Helper 5â&#x20AC;˘1

4. A pen costs $2.57. It costs $0.49 more than a ruler. Kayla bought two pens and one ruler. She paid with a ten-dollar bill. How much change does Kayla get? Use a tape diagram to show your thinking.

Lesson 10: Copyright ÂŠ Great Minds PBC Virginia Edition greatminds.org/math

Note: Encourage your child to use a variety of strategies when solving. The standard algorithm may not always be necessary for some students. Ask them about different ways to solve the problem. Below you’ll find some alternate solution strategies that could be applied.

Lesson 10 Homework 5•1

1. Subtract. You may use a place value chart. a. 9 tenths – 3 tenths =

b. 9 ones 2 thousandths – 3 ones =

c. 4 hundreds 6 hundredths – 3 hundredths = d. 56 thousandths – 23 thousandths =

thousandths hundreds

thousandths =

hundredths hundredths

2. Solve using the standard algorithm. a. 1.8 – 0.9 =

b. 41.84 – 0.9 =

c. 341.84 – 21.92 =

d. 5.182 – 0.09 =

e. 50.416 – 4.25 =

f. 741 – 3.91 =

3. Solve. a. 30 tens – 3 tens 3 tenths

b. 5 – 16 tenths

c. 24 tenths – 1 one 3 tenths

d. 6 ones 7 hundredths – 2.3

e. 8.246 – 5 hundredths

f. 5 ones 3 tenths – 0.53

4. Mr. House wrote 8 tenths minus 5 hundredths on the board. Maggie said the answer is 3 hundredths because 8 minus 5 is 3. Is she correct? Explain.

5. A clipboard costs $2.23. It costs $0.58 more than a notebook. Lisa bought two clipboards and one notebook. She paid with a ten-dollar bill. How much change does Lisa get? Use a tape diagram to show your thinking.

Lesson 10 Template 5â&#x20AC;˘1

hundreds to thousandths place value chart (from Lesson 7)

Lesson 11 Homework Helper 5â&#x20AC;˘1

1. Solve by drawing disks on a place value chart. Write an equation, and express the product in standard form.

Lesson 11: Copyright ÂŠ Great Minds PBC Virginia Edition greatminds.org/math

Multiply a decimal fraction by single-digit whole numbers, relate to a written method through application of the area model and place value understanding, and explain the reasoning used.

2. Draw an area model, and find the sum of the partial products to evaluate each expression.

Lesson 11 Homework 5•1

1. Solve by drawing disks on a place value chart. Write an equation, and express the product in standard form. a. 2 copies of 4 tenths

b. 4 groups of 5 hundredths

c. 4 times 7 tenths

d. 3 times 5 hundredths

e. 9 times as much as 7 tenths

f. 6 thousandths times 8

2. Draw a model similar to the one pictured below. Find the sum of the partial products to evaluate each expression. a. 4 × 6.79

b. 6 × 7.49

c. 9 copies of 3.65

d. 3 times 20.175

3. Leanne multiplied 8 × 4.3 and got 32.24. Is Leanne correct? Use an area model to explain your answer.

4. Anna buys groceries for her family. Hamburger meat is $3.38 per pound, sweet potatoes are $0.79 each, and hamburger rolls are $2.30 a bag. If Anna buys 3 pounds of meat, 5 sweet potatoes, and 1 bag of hamburger rolls, what will she pay in all for the groceries?

Lesson 12 Homework Helper 5â&#x20AC;˘1

1. Choose the reasonable product for each expression. Explain your thinking in the spaces below using words, pictures, or numbers.

2. Lenox weighs 9.2 kg. Her older brother is 3 times as heavy as Lenox. How much does her older brother weigh in kilograms?

Lesson 12: Copyright ÂŠ Great Minds PBC Virginia Edition greatminds.org/math

Multiply a decimal fraction by single-digit whole numbers, including using estimation to confirm the placement of the decimal point.

Lesson 12 Homework 5•1

1. Choose the reasonable product for each expression. Explain your thinking in the spaces below using words, pictures, or numbers. a.

Lesson 12 Homework 5â&#x20AC;˘1

2. Yi Ting weighs 8.3 kg. Her older brother is 4 times as heavy as Yi Ting. How much does her older brother weigh in kilograms?

3. Tim is painting his storage shed. He buys 4 gallons of white paint and 3 gallons of blue paint. Each gallon of white paint costs $15.72, and each gallon of blue paint is $21.87. How much will Tim spend in all on paint?

4. Ribbon is sold at 3 yards for $6.33. Jackie bought 24 yards of ribbon for a project. How much did she pay?

Lesson 13 Homework Helper 5â&#x20AC;˘1

Note: The use of unit language (e.g., 21 hundredths rather than 0.21) allows students to use knowledge of basic facts to compute easily with decimals. 1. Complete the sentence with the correct number of units, and then complete the equation.

2. Complete the number sentence. Express the quotient in units and then in standard form.

Lesson 13: Copyright ÂŠ Great Minds PBC Virginia Edition greatminds.org/math

Divide decimals by single-digit whole numbers involving easily identifiable multiples using place value understanding and relate to a written method.

3. Find the quotients. Then, use words, numbers, or pictures to describe any relationships you notice between the pair of problems and their quotients.

Both problems are dividing by 5, but the quotient for part (a) is 10 times larger than the quotient for (b). That makes sense because the number we started with in part (a) is also 10 times larger than the number we started with in part (b). 4. Is the quotient below reasonable? Explain your answer.

5. A toy airplane weighs 3.69 kg. It weighs 3 times as much as a toy car. What is the weight of the toy car?

Lesson 13 Homework 5•1

1. Complete the sentences with the correct number of units, and then complete the equation. a. 3 groups of

tenths is 1.5.

b. 6 groups of

hundredths is 0.24.

c. 5 groups of

thousandths is 0.045.

0.045 ÷ 5 =

2. Complete the number sentence. Express the quotient in units and then in standard form. a. 9.36 ÷ 3 = ____________ ones÷ 3 + ____________hundredths÷ 3 = ____________ones + ____________hundredths =____________

b. 36.012 ÷ 3 = ____________ ones ÷ 3+ ____________ thousandths ÷ 3 = ____________ ones + ____________ thousandths = ____________

c. 3.55 ÷ 5 = ____________ tenths÷ 5 + ____________ hundredths÷ 5 =___________________________________ = ___________________________________

3.545 ÷ 5 = _____________________________________________________ =_____________________________________________________ = _____________________________________________________ Lesson 13: Copyright © Great Minds PBC Virginia Edition greatminds.org/math

3. Find the quotients. Then, use words, numbers, or pictures to describe any relationships you notice between each pair of problems and quotients. a. 21 ÷ 7 =

b. 48 ÷ 8 =

0.048 ÷ 8 =

4. Are the quotients below reasonable? Explain your answers. a. 0.54 ÷ 6 = 9

b. 5.4 ÷ 6 = 0.9

c. 54 ÷ 6 = 0.09

Lesson 13 Homework 5â&#x20AC;˘1

5. A toy airplane costs $4.84. It costs 4 times as much as a toy car. What is the cost of the toy car?

6. Julian bought 3.9 liters of cranberry juice, and Jay bought 8.74 liters of apple juice. They mixed the two juices together and then poured them equally into 2 bottles. How many liters of juice are in each bottle?

Lesson 14 Homework Helper 5•1

1. Draw place value disks on the place value chart to solve. Show each step using the standard algorithm.

2. Solve 15.704 ÷ 4 using the standard algorithm.

Divide decimals with a remainder using place value understanding and relate to a written method.

3. Mr. Huynh paid $85.44 for 6 pounds of cashews. What’s the cost of 1 pound of cashews?

The cost of 1 pound of cashews is $14.24.

Lesson 14 Homework 5•1

1. Draw place value disks on the place value chart to solve. Show each step using the standard algorithm. a. 5.241 ÷ 3 =

b. 5.372 ÷ 4 =

2. Solve using the standard algorithm. a. 0.64 ÷ 4 =

b. 6.45 ÷ 5 =

c. 16.404 ÷ 6 =

3. Mrs. Mayuko paid $40.68 for 3 kg of shrimp. What’s the cost of 1 kilogram of shrimp?

4. The total weight of 6 pieces of butter and a bag of sugar is 3.8 lb. If the weight of the bag of sugar is 1.4 lb, what is the weight of each piece of butter?

Lesson 15 Homework Helper 5â&#x20AC;˘1

1. Draw place value disks on the place value chart to solve. Show each step in the standard algorithm.

Lesson 15: Copyright ÂŠ Great Minds PBC Virginia Edition greatminds.org/math

Divide decimals using place value understanding, including remainders in the smallest unit.

3. Four bakers shared 5.4 kilograms of sugar equally. How much sugar did they each receive?

Each baker received 1.35 kilograms of sugar.

Lesson 15 Homework 5•1

1. Draw place value disks on the place value chart to solve. Show each step in the standard algorithm. a. 0.7 ÷ 4 = Ones

Thousandths

b. 8.1 ÷ 5 = Ones

2. Solve using the standard algorithm. a. 0.7 ÷ 2 =

b. 3.9 ÷ 6 =

d. 0.92 ÷ 2 =

e. 9.4 ÷ 4 =

3. A rope 8.7 meters long is cut into 5 equal pieces. How long is each piece?

4. Yasmine bought 6 gallons of apple juice. After filling up 4 bottles of the same size with apple juice, she had 0.3 gallon of apple juice left. How many gallons of apple juice are in each container?

Lesson 16 Homework Helper 5â&#x20AC;˘1

1. A comic book costs $6.47, and a cookbook costs $9.79.

a. Zion buys 5 comic books and 3 cookbooks. What is the total cost for all of the books?

Lesson 16: Copyright ÂŠ Great Minds PBC Virginia Edition greatminds.org/math

Solve word problems using decimal operations.

b. Zion wants to pay for the all the books with a $100 bill. How much change will he get back?

2. Ms. Porter bought 40 meters of string. She used 8.5 meters to tie a package. Then she cuts the remainder into 6 equal pieces. Find the length of each piece. Give the answer in meters.

Each piece of string is 5.25 meters. 74

Lesson 16 Homework 5â&#x20AC;˘1

Solve using tape diagrams. 1. A gardener installed 42.6 meters of fencing in a week. He installed 13.45 meters on Monday and 9.5 meters on Tuesday. He installed the rest of the fence in equal lengths on Wednesday through Friday. How many meters of fencing did he install on each of the last three days?

2. Jenny charges $9.15 an hour to babysit toddlers and $7.45 an hour to babysit school-aged children. a. If Jenny babysat toddlers for 9 hours and school-aged children for 6 hours, how much money did she earn in all?

b. Jenny wants to earn $1,300 by the end of the summer. How much more will she need to earn to meet her goal?

3. A table and 8 chairs weigh 235.68 lb together. If the table weighs 157.84 lb, what is the weight of one chair in pounds?

4. Mrs. Cleaver mixes 1.24 liters of red paint with 3 times as much blue paint to make purple paint. She pours the paint equally into 5 containers. How much blue paint is in each container? Give your answer in liters.

Grade 5 Module 2

Lesson 1 Homework Helper 5•2

1. Fill in the blanks using your knowledge of place value units and basic facts. a.

Multiply multi-digit whole numbers and multiples of 10 using place value patterns and the distributive and associative properties.

Lesson 1 Homework Helper 5â&#x20AC;˘2

2. Determine if these equations are true or false. Defend your answer using knowledge of place value and the commutative, associate, and/or distributive properties.

3. Find the products. Show your thinking.

Lesson 1 Homework 5•2

1. Fill in the blanks using your knowledge of place value units and basic facts. a. 43 × 30 Think: 43 ones × 3 tens =

43 × 30 = b. 430 × 30 Think: 43 tens × 3 tens =

430 × 30 = c. 830 × 20 Think: 83 tens × 2 tens = 166 830 × 20 = d. 4,400 × 400 hundreds ×

hundreds = 176

4,400 × 400 = e. 80 × 5,000 tens ×

thousands = 40

80 × 5,000 = 2. Determine if these equations are true or false. Defend your answer using your knowledge of place value and the commutative, associative, and/or distributive properties. a. 35 hundreds = 5 tens × 7 tens

b. 770 × 6 = 77 × 6 × 100

c. 50 tens × 4 hundreds = 40 tens × 5 hundreds

d. 24 × 10 × 90 = 90 × 2,400

3. Find the products. Show your thinking. The first row gives some ideas for showing your thinking. a. 5× 5 50 × 500 50 × 50 5 × 50 = ( 5 × 5 ) × ( 10 × 100 ) = 25 × 10 = ( 5 × 10 ) × ( 5 × 10 ) = 25 = 25, 000 = 250 = ( 5 × 5 ) × 100 = 2, 500 b. 80 × 5

c. 637 × 3

6,370 × 300

63,700 × 300

4. A concrete stepping-stone measures 20 square inches. What is the area of 30 such stones?

5. A number is 42,300 when multiplied by 10. Find the product of this number and 500.

Lesson 2 Homework Helper 5â&#x20AC;˘2

1. Round the factors to estimate the products.

Estimate multi-digit products by rounding factors to a basic fact and using place value patterns.

2. There are 6,015 seats available for each of the Radio City Rockettes Spring Spectacular dance shows. If there are a total of 68 shows, about how many tickets are available in all?

Lesson 2 Homework 5•2

1. Round the factors to estimate the products. a. 697 × 82 ≈

A reasonable estimate for 697 × 82 is b. 5,897 × 67 ≈

A reasonable estimate for 5,897 × 67 is c. 8,840 × 45 ≈

A reasonable estimate for 8,840 × 45 is

2. Complete the table using your understanding of place value and knowledge of rounding to estimate the product. Expressions a. 3,409 × 73

Rounded Factors

b. 82,290 × 240 c. 9,832 × 39 d. 98 tens × 36 tens e. 893 hundreds × 85 tens

3. The estimated answer to a multiplication problem is 800,000. Which of the following expressions could result in this answer? Explain how you know. 8,146 × 12

81,467 × 121

8,146 × 121

81,477 × 1,217

4. Fill in the blank with the missing estimate. a. 751 × 34 ≈

b. 627 × 674 ≈

c. 7,939 × 541 ≈

= 24,000 = 420,000 = 4,000,000

5. In a single season, the New York Yankees sell an average of 42,362 tickets for each of their 81 home games. About how many tickets do they sell for an entire season of home games?

6. Raphael wants to buy a new car. a. He needs a down payment of $3,000. If he saves $340 each month, about how many months will it take him to save the down payment?

b. His new car payment will be $288 each month for five years. Estimate the tot al of these payments.

Lesson 3 Homework Helper 5â&#x20AC;˘2

A STORY OF UNITS Write and interpret numerical expressions, and compare expressions using a visual model.

Lesson 3 Homework Helper

1. Draw a model. Then write the numerical expression. a. The sum of 5 and 4, doubled

3 times the difference between 42.6 and 23.9

The sum of 4 twelves and 3 sixes

Lesson 3: Copyright ÂŠ Great Minds PBC Virginia Edition greatminds.org/math

Write and interpret numerical expressions, and compare expressions using a visual model.

2. Compare the two expressions using >, <, or =.

Lesson 3 Homework 5•2

Lesson 3 Homework

1. Draw a model. Then, write the numerical expressions. a. The sum of 21 and 4, doubled

b. The sum of 21 and some number, doubled

c. 2 times the difference between 49.5 and 37.5

d. 15 times the difference between some number and 18.1

e. The difference between 9 thirty-sevens and 8 thirty-sevens

The sum of 2 twelves and 2 copies of a number

2. Write the numerical expressions in words. Then, solve. Words

The Value of the Expression

a. 10 × (2.5 + 13.5)

b. (98 − 78) × 11

c. (71 + 29) × 26

d. (50 × 2) + (15 × 2)

3. Compare the two expressions using > , < , or = . In the space beneath each pair of expressions, explain how you can compare without calculating. Draw a model if it helps you. a. 93 × (40 + 2)

(40 + 2) × 39

60 copies of a minus 1 copy of a

4. Larry claims that (14 + 12) × (8 + 12) and (14 × 12) + (8 × 12) are equivalent because they have the same digits and the same operations. a. Is Larry correct? Explain your thinking.

b. Which expression is greater? How much greater?

Lesson 4 Homework Helper 5•2

Convert numerical expressions into unit form as a mental strategy for multi-digit multiplication.

Lesson 4 Homework Helper

1. Circle each expression that is not equivalent to the expression in bold.

2. Solve using mental math. Draw a tape diagram and fill in the blanks to show your thinking. a.

19 × 25 = 19 twenty-fives

b. 21 × 32 = 21 thirty-twos

Think: 20 thirty-twos + 1 thirty-two

Think: 20 twenty-fives − 1 twenty-five = ( 20 × 25) − ( =

= ( 20 × 32) + ( 1 × 32) = 640

3. The pet store has 99 fish tanks with 44 fish in each tank. How many fish does the pet store have? Use mental math to solve. Explain your thinking. I need to find 99 forty-fours.

I know that 99 forty-fours is 1 unit of forty-four less than 100 forty-fours. I multiplied 100 × 44, which is 4, 400. I need to subtract one group of 44.

4, 400 − 44. The pet store has 4, 356 fish.

Lesson 4 Homework 5•2

Lesson 4 Homework

1. Circle each expression that is not equivalent to the expression in bold. a. 37 × 19 37 nineteens

(30 × 19) − (7 × 29)

37 × (20 − 1)

(40 − 2) × 19

(26 + 30) × (26 + 5)

(26 × 30) + (26 × 5)

35 × (20 + 60)

(34 × 8) + (34 × 9)

34 × (90 − 1)

89 thirty-fours

b. 26 × 35 35 twenty-sixes

c. 34 × 89 34 × (80 + 9)

2. Solve using mental math. Draw a tape diagram and fill in the blanks to show your thinking. The first one is partially done for you. a. 19 × 50 = __________ fifties

b. 11 × 26 = __________ twenty-sixes

Think: 20 fifties − 1 fifty

Think: _____ twenty-sixes + _____ twenty-six

= ( __________ × 50) − ( __________ × 50)

= ( __________ × 26) + ( __________ × 26)

= __________ − __________

= __________ + __________

= __________

c. 49 × 12 = __________ twelves

d. 12 × 25 = __________ twenty-fives

Think: _____ twelves − 1 twelve

Think: _____ twenty-fives + _____ twenty-fives

= ( __________ × 12) − ( __________ × 12)

= ( __________ × 25) + ( __________ × 25)

3. Define the unit in word form and complete the sequence of problems as was done in the lesson. a. 29 × 12 = 29 __________

b. 11 × 31 = 31 __________

Think: 30 __________ − 1 __________

Think: 30 __________ + 1 __________

= (30 × __________ ) − (1 × __________ )

= (30 × __________ ) + (1 × __________ )

c. 19 × 11 = 19 __________

d. 50 × 13 = 13 __________

Think: 20 __________ − 1 __________

Think: 10 __________ + 3 __________

= (20 × __________ ) − (1 × __________ )

= (10 × __________ ) + (3 × __________ )

4. How can 12 × 50 help you find 12 × 49?

5. Solve mentally. a. 16 × 99 = __________

b. 20 × 101 = __________

6. Joy is helping her father to build a rectangular deck that measures 14 ft by 19 ft. Find the area of the deck using a mental strategy. Explain your thinking.

7. The Lason School turns 101 years old in June. In order to celebrate, they ask each of the 23 classes to collect 101 items and make a collage. How many total items will be in the collage? Use mental math to solve. Explain your thinking.

Lesson 5 Homework Helper 5•2

Connect visual models and the distributive property to partial products of the standard algorithm without renaming.

Lesson 5 Homework Helper

1. Draw an area model, and then solve using the standard algorithm. Use arrows to match the partial products from the area model to the partial products in the algorithm. a.

2. Elizabeth pays $123 each month for her cell phone service. How much does she spend in a year?

Elizabeth spends $1,476 in a year for cell phone service.

Lesson 5 Homework 5•2

Lesson 5 Homework

1. Draw an area model, and then solve using the standard algorithm. Use arrows to match the partial products from the area model to the partial products in the algorithm. a. 24 × 21 = _________

b. 242 × 21 = _________

2. Solve using the standard algorithm. a. 314 × 22 = _________

b. 413 × 22 = _________

c. 213 × 32 = _________

Lesson 5 Homework 5â&#x20AC;˘2

3. A young snake measures 0.23 meters long. During the course of his lifetime, he will grow to be 13 times his current length. What will his length be when he is full grown?

4. Zenin earns $142 per shift at his new job. During a pay period, he works 12 shifts. What would his pay be for that period?

Lesson 6 Homework Helper 5•2

Connect area diagrams and the distributive property to partial products of the standard algorithm without renaming.

Lesson 6 Homework Helper

1. Draw an area model. Then, solve using the standard algorithm. Use arrows to match the partial products from your area model to the partial products in the algorithm. a.

Lesson 6 Homework Helper 5â&#x20AC;˘2

2. Desmond bought a car and paid monthly installments. Each installment was $452 per month. After 36 months, Desmond still owes $1,567. What was the total price of the car?

Lesson 6 Homework 5•2

Lesson 6 Homework

1. Draw an area model. Then, solve using the standard algorithm. Use arrows to match the partial products from your area model to the partial products in the algorithm. a. 27 × 36 ×

b. 527 × 36

2. Solve using the standard algorithm. a. 649 × 53

c. 758 × 46

b. 496 × 53

d. 529 × 48

3. Each of the 25 students in Mr. McDonald’s class sold 16 raffle tickets. If each ticket costs $15, how much money did Mr. McDonald’s students raise?

4. Jayson buys a car and pays by installments. Each installment is $567 per month. After 48 months, Jayson owes $1,250. What was the total price of the vehicle?

Lesson 7 Homework Helper 5•2

Connect area models and the distributive property to partial products of the standard algorithm with renaming.

Lesson 7 Homework Helper

1. Draw an area model. Then, solve using the standard algorithm. Use arrows to match the partial products from the area model to the partial products in the algorithm. 431 × 246 = 106, 026

2. Solve by drawing the area model and using the standard algorithm. 2,451 × 107 = 262, 257

3. Solve using the standard algorithm. 7,302 × 408 = 2, 979, 216

Lesson 7 Homework 5•2

Lesson 7 Homework

1. Draw an area model. Then, solve using the standard algorithm. Use arrows to match the partial products from your area model to the partial products in your algorithm.

a. 273 × 346

b. 273 × 306

c. Both Parts (a) and (b) have three-digit multipliers. Why are there three partial products in Part (a) and only two partial products in Part (b)?

2. Solve by drawing the area model and using the standard algorithm. a. 7,481 × 290

b. 7,018 × 209

3. Solve using the standard algorithm. a. 426 × 357

b. 1,426 × 357

c. 426 × 307

d. 1,426 × 307

4. The Hudson Valley Renegades Stadium holds a maximum of 4,505 people. During the height of their popularity, they sold out 219 consecutive games. How many tickets were sold during this time?

5. One Saturday at the farmer’s market, each of the 94 vendors made $502 in profit. How much profit did all vendors make that Saturday?

Lesson 8 Homework Helper 5•2

Fluently multiply multi-digit whole numbers using the standard algorithm and using estimation to check for reasonableness of the product.

Lesson 8 Homework Helper

1. Estimate the products first. Solve by using the standard algorithm. Use your estimate to check the reasonableness of the product. a.

4,308 × 505

2. When multiplying 809 times 528, Isaac got a product of 42,715. Without calculating, does his product seem reasonable? Explain your thinking.

Lesson 8 Homework 5•2

Lesson 8 Homework

1. Estimate the product first. Solve by using the standard algorithm. Use your estimate to check the reasonableness of the product. a. 312 × 149

b. 743 × 295

c. 428 × 637

d. 691 × 305

e. 4,208 × 606

3,068 × 523

g. 430 × 3,064

h. 3,007 × 502

254 × 6,104

≈ 300 × 100 = 30,000 312 × 149

Lesson 8 Homework 5â&#x20AC;˘2

2. When multiplying 1,729 times 308, Clayton got a product of 53,253. Without calculating, does his product seem reasonable? Explain your thinking.

3. A publisher prints 1,912 copies of a book in each print run. If they print 305 runs, the manager wants to know about how many books will be printed. What is a reasonable estimate?

Lesson 9 Homework Helper 5â&#x20AC;˘2

Fluently multiply multi-digit whole numbers using the standard algorithm to solve multi-step word problems.

Lesson 9 Homework Helper

Solve. 1. Howard and Robin are both cabinet makers. Over the last year, Howard made 107 cabinets. Robin made 28 more cabinets than Howard. Each cabinet they make has exactly 102 nails in it. How many nails did they use altogether while making the cabinets?

Lesson 9 Homework Helper 5•2

2. Mrs. Peterson made 32 car payments at $533 each. She still owes $8,530 on her car. How much did the car cost?

Mrs. Peterson’s car cost $25, 586.

Lesson 9 Homework 5•2

Lesson 9 Homework

Solve. 1. Jeffery bought 203 sheets of stickers. Each sheet has a dozen stickers. He gave away 907 stickers to his family and friends on Valentine’s Day. How many stickers does Jeffery have remaining?

2. During the 2011 season, a quarterback passed for 302 yards per game. He played in all 16 regular season games that year. a. For how many total yards did the quarterback pass?

b. If he matches this passing total for each of the next 13 seasons, how many yards will he pass for in his career?

Lesson 9 Homework 5â&#x20AC;˘2

3. Bao saved $179 a month. He saved $145 less than Ada each month. How much would Ada save in three and a half years?

4. Mrs. Williams is knitting a blanket for her newborn granddaughter. The blanket is 2.25 meters long and 1.8 meters wide. What is the area of the blanket? Write the answer in centimeters.

Soccer Field Dimensions

5. Use the chart to solve.

Minimum Length Maximum Length Minimum Width Maximum Width

FIFA Regulation (in yards) 110 120 70 80

New York State High Schools (in yards) 100 120 55 80

a. Write an expression to find the difference in the maximum area and minimum area of a NYS high school soccer field. Then, evaluate your expression.

b. Would a field with a width of 75 yards and an area of 7,500 square yards be within FIFA regulation? Why or why not?

c. It costs $26 to fertilize, water, mow, and maintain each square yard of a full size FIFA field (with maximum dimensions) before each game. How much will it cost to prepare the field for next week’s match?

Lesson 10 Homework Helper 5â&#x20AC;˘2

1. Estimate the product. Solve using an area model and the standard algorithm. Remember to express your products in standard form.

Multiply decimal fractions with tenths by multi-digit whole numbers using place value understanding to record partial products.

2. Estimate. Then, use the standard algorithm to solve. Express your products in standard form.

Lesson 10 Homework 5•2

1. Estimate the product. Solve using an area model and the standard algorithm. Remember to express your products in standard form. a. 53 × 1.2 ≈

b. 2.1 × 82 ≈

1 2 (tenths) 1 2 (tenths) × 53 × 53

2 1 (tenths) 2 1 (tenths) × 82 × 82

2. Estimate. Then, use the standard algorithm to solve. Express your products in standard form. a. 4.2 × 34 ≈

4 2 (tenths) 4 2 (tenths) × 34 × 34

b. 65 × 5.8 ≈

5 8 (tenths) 5 8 (tenths) × 65 × 65

c. 3.3 × 16 ≈

e. 73 × 2.4 ≈

d. 15.6 × 17 ≈

f. 193.5 × 57 ≈

3. Mr. Jansen is building an ice rink in his backyard that will measure 8.4 meters by 22 meters. What is the area of the rink?

4. Rachel runs 3.2 miles each weekday and 1.5 miles each day of the weekend. How many miles will she have run in 6 weeks?

Lesson 11 Homework Helper 5â&#x20AC;˘2

1. Estimate the product. Solve using the standard algorithm. Use the thought bubbles to show your thinking.

Multiply decimal fractions by multi-digit whole numbers through conversion to a whole number problem and reasoning about the placement of the decimal.

3. Use the whole number product and place value reasoning to place the decimal point in the second product. Explain how you know.

Lesson 11 Homework 5â&#x20AC;˘2

1. Estimate the product. Solve using the standard algorithm. Use the thought bubbles to show your thinking. (Draw an area model on a separate sheet if it helps you.) a.

Lesson 11 Homework 5•2

2. Solve using the standard algorithm. a. 2.03 × 13

b. 53.16 × 34

c. 371.23 × 53

d. 1.57 × 432

3. Use the whole number product and place value reasoning to place the decimal point in the second product. Explain how you know. a. If 36 × 134 = 4,824 then

36 × 1.34 =

b. If 84 × 2,674 = 224,616 then 84 × 26.74 =

c. 19 × 3,211 = 61,009 then

321.1 × 19 =

4. A slice of pizza costs $1.57. How much will 27 slices cost?

5. A spool of ribbon holds 6.75 meters. A craft club buys 21 spools. a. What is the total cost if the ribbon sells for $2 per meter?

b. If the club uses 76.54 meters to complete a project, how much ribbon will be left?

Lesson 12 Homework Helper 5â&#x20AC;˘2

1. Estimate. Then solve using the standard algorithm. You may draw an area model if it helps you.

Reason about the product of a whole number and a decimal with hundredths using place value understanding and estimation.

Estimate. Then solve using the standard algorithm.

3. Tatiana walks to the park every afternoon. In the month of August, she walked 2.35 miles each day. How far did Tatiana walk during the month of August?

Lesson 12 Homework 5•2

1. Estimate. Then, solve using the standard algorithm. You may draw an area model if it helps you. a. 24 × 2.31 ≈

b. 5.42 × 305 ≈

2. 3 1 24 ×

5. 4 2 ×3 0 5

2. Estimate. Then, solve using the standard algorithm. Use a separate sheet to draw the area model if it helps you. a. 1.23 × 21 ≈

c. 0.32 × 41 ≈

e. 6.09 × 28 ≈

g. 6.09 × 208 ≈

b. 3.2 × 41 ≈

d. 0.54 × 62 ≈

f. 6.83 × 683 ≈

h. 171.76 × 555 ≈

3. Eric’s goal is to walk 2.75 miles to and from the park every day for an entire year. If he meets his goal, how many miles will Eric walk?

4. Art galleries often price paintings by the square inch. If a painting measures 22.5 inches by 34 inches and costs $4.15 per square inch, what is the selling price for the painting?

5. Gerry spends $1.25 each day on lunch at school. On Fridays, she buys an extra snack for $0.55. How much money will she spend in two weeks?

Lesson 13 Homework Helper 5â&#x20AC;˘2

1. Solve. a. Convert years to days.

b. Convert pounds to ounces.

2. After solving, write a statement to express each conversion. a. The height of a male ostrich is 7.3 meters. What is his height in centimeters?

His height is 730 centimeters.

Use whole number multiplication to express equivalent measurements.

b. The capacity of a container is 0.3 liter. Convert this to milliliters.

The capacity of the container is 300 milliliters.

Lesson 13 Homework 5•2

1. Solve. The first one is done for you. a. Convert weeks to days.

b. Convert years to days.

6 weeks = 6 × (1 week)

7 years = ___________ × ( ___________ year)

= 6 × (7 days)

= ___________ × ( ___________ days)

= ___________ days

c. Convert meters to centimeters. 4.5 m = ___________ × ( ___________ m)

d. Convert pounds to ounces. 12.6 pounds

= ___________ × ( ___________ cm) = ___________ cm

e. Convert kilograms to grams.

f. Convert yards to inches.

2. After solving, write a statement to express each conversion. The first one is done for you. a. Convert the number of hours in a day to minutes.

b. A newborn giraffe weighs about 65 kilograms. How much does it weigh in grams?

24 hours = 24 × (1 hour) = 24 × (60 minutes) = 1,440 minutes One day has 24 hours, which is the same as 1,440 minutes.

c. The average height of a female giraffe is 4.6 meters. What is her height in centimeters?

d. The capacity of a beaker is 0.1 liter. Convert this to milliliters.

e. A pig weighs 9.8 pounds. Convert the pig’s weight to ounces.

A marker is 0.13 meters long. What is the length in millimeters?

Lesson 14 Homework Helper 5•2

1. Solve. a. Convert quarts to gallons.

b. Convert grams to kilograms.

2. After solving, write a statement to express each conversion. a. A jug of milk holds 16 cups. Convert 16 cups to pints.

16 cups is equal to 8 pints. b. The length of a table is 305 centimeters. What is its length in meters?

The table’s length is 3. 05 meters.

Use fraction and decimal multiplication to express equivalent measurements.

Lesson 14 Homework 5•2

1. Solve. The first one is done for you. a. Convert days to weeks.

b. Convert quarts to gallons. 36 quarts = ___________ × (1quart)

42 days = 42 × (1 day) = 42 × =

= ___________ ×

= ___________ gallons

=___________ gallons c. Convert centimeters to meters. 760 cm = ___________ × ( ___________ cm)

d. Convert meters to kilometers. 2,485 m = ___________ × ( ___________ m)

= ___________ × ( ___________ m)

= ___________ × (0.001 km)

= ___________ m

= ___________ km

e. Convert grams to kilograms. 3,090 g =

f. Convert milliliters to liters.

2. After solving, write a statement to express each conversion. The first one is done for you. a. The screen measures 36 inches. Convert 36 inches to feet.

b. A jug of juice holds 8 cups. Convert 8 cups to pints.

36 inches = 36 × (1 inch) = 36 ×

= 12 feet = 3 feet The screen measures 36 inches or 3 feet. c. The length of the flower garden is 529 centimeters. What is its length in meters?

d. The capacity of a container is 2,060 milliliters. Convert this to liters.

e. A hippopotamus weighs 1,560,000 grams. Convert the hippopotamus’ weight to kilograms.

The distance was 372,060 meters. Convert the distance to kilometers.

Lesson 15 Homework Helper 5â&#x20AC;˘2

1. A bag of peanuts is 5 times as heavy as a bag of sunflower seeds. The bag of peanuts also weighs 920 grams more than the bag of sunflower seeds. a. What is the total weight in grams for the bag of peanuts and the bag of sunflower seeds?

The total weight for the bag of peanuts and the bag of sunflower seeds is 1, 380 grams.

Solve two-step word problems involving measurement conversions.

Lesson 15 Homework Helper 5•2

b. Express the total weight of the bag of peanuts and the bag of sunflower seeds in kilograms.

The total weight of the bag of peanuts and the bag of sunflower seeds is 1. 38 kilograms.

2. Gabriel cut a 4 meter 50 centimeter string into 9 equal pieces. Michael cut a 508 centimeter string into 10 equal pieces. How much longer is one of Michael's strings than one of Gabriel’s?

One of Michael’s strings is 0. 8 centimeters longer than one of Gabriel’s.

Lesson 15 Homework 5•2

Solve. 1. Tia cut a 4-meter 8-centimeter wire into 10 equal pieces. Marta cut a 540-centimeter wire into 9 equal pieces. How much longer is one of Marta’s wires than one of Tia’s?

2. Jay needs 19 quarts more paint for the outside of his barn than for the inside. If he uses 107 quarts in all, how many gallons of paint will be used to paint the inside of the barn?

Lesson 15 Homework 5â&#x20AC;˘2

3. String A is 35 centimeters long. String B is 5 times as long as String A. Both are necessary to create a decorative bottle. Find the total length of string needed for 17 identical decorative bottles. Express your answer in meters.

4. A pineapple is 7 times as heavy as an orange. The pineapple also weighs 870 grams more than the orange. a. What is the total weight in grams for the pineapple and orange?

b. Express the total weight of the pineapple and orange in kilograms.

Lesson 16 Homework Helper 5•2

1. Divide. Draw place value disks to show your thinking for (a). a.

400 ÷ 10 = 40

650,000 ÷ 100

Use divide by 10 patterns for multi-digit whole number division.

Lesson 16 Homework Helper 5â&#x20AC;˘2

Lesson 16 Homework 5•2

1. Divide. Draw place value disks to show your thinking for (a) and (c). You may draw disks on your personal white board to solve the others if necessary. a. 300 ÷ 10

b. 450 ÷ 10

c. 18,000 ÷ 100

d. 730,000 ÷ 100

e. 900,000 ÷ 1,000

680,000 ÷ 1,000

2. Divide. The first one is done for you. a. 18,000 ÷ 20

b. 18,000 ÷ 200

18,000 ÷ 2,000

d. 420,000 ÷ 60

e. 420,000 ÷ 600

420,000 ÷ 6,000

g. 24,000 ÷ 30

h. 560,000 ÷ 700

450,000 ÷ 9,000

= 18,000 ÷ 10 ÷ 2 = 1,800 ÷ 2 = 900

Lesson 16 Homework 5â&#x20AC;˘2

3. A stadium holds 50,000 people. The stadium is divided into 250 different seating sections. How many seats are in each section?

4. Over the course of a year, a tractor trailer commutes 160,000 miles across America. a. Assuming a trucker changes his tires every 40,000 miles, and that he starts with a brand new set of tires, how many sets of tires will he use in a year?

b. If the trucker changes the oil every 10,000 miles, and he starts the year with a fresh oil change, how many times will he change the oil in a year?

Lesson 17 Homework Helper 5â&#x20AC;˘2

1. Estimate the quotient for the following problems.

Lesson 17: Copyright ÂŠ Great Minds PBC Virginia Edition greatminds.org/math

Use basic facts to approximate quotients with two-digit divisors.

2. A baker spent $989 buying 48 pounds of nuts. About how much does each pound of nuts cost?

Each pound of nuts costs about $20.

Lesson 17 Homework 5•2

1. Estimate the quotient for the following problems. The first one is done for you. a. 821 ÷ 41

b. 617 ÷ 23

d. 482 ÷ 52 ≈

m. 835 ÷ 89

n. 345 ÷ 72 ÷

k. 729 ÷ 81 ÷

h. 645 ÷ 69 ÷

g. 476 ÷ 81

e. 531 ÷ 48

c. 821 ÷ 39

o. 559 ÷ 11 ÷

Lesson 17 Homework 5â&#x20AC;˘2

2. Mrs. Johnson spent $611 buying lunch for 78 students. If all the lunches cost the same, about how much did she spend on each lunch?

3. An oil well produces 172 gallons of oil every day. A standard oil barrel holds 42 gallons of oil. About how many barrels of oil will the well produce in one day? Explain your thinking.

Lesson 18 Homework Helper 5â&#x20AC;˘2

1. Estimate the quotients for the following problems.

Lesson 18: Copyright ÂŠ Great Minds PBC Virginia Edition greatminds.org/math

2. Meilin has saved $4,825. If she is paid $68 an hour, about how many hours did she work?

Meilin worked about 70 hours.

Lesson 18 Homework 5•2

1. Estimate the quotients for the following problems. The first one is done for you. a. 8,328 ÷ 41

b. 2,109 ÷ 23

≈ 8,000 ÷ 40

d. 3,861 ÷ 59 ≈

2,759 ÷ 48 ≈ =

m. 6,537 ÷ 74 ≈ =

4,368 ÷ 63 ≈

n. 4,998 ÷ 48 ÷

k. 8,194 ÷ 91 ÷

9,032 ÷ 89 ≈

h. 8,432 ÷ 81 ÷

5,576 ÷ 92 ≈

g. 5,086 ÷ 73

e. 2,899 ÷ 66

c. 8,215 ÷ 38

o. 6,106 ÷ 25 ÷

Lesson 18 Homework 5â&#x20AC;˘2

2. 91 boxes of apples hold a total of 2,605 apples. Assuming each box has about the same number of apples, estimate the number of apples in each box.

3. A wild tiger can eat up to 55 pounds of meat in a day. About how many days would it take for a tiger to eat the following prey? Prey

Weight of Prey

Eland Antelope

1,754 pounds

Chital Deer

Water Buffalo

2,322 pounds

Number of Days

Lesson 19 Homework Helper 5â&#x20AC;˘2

1. Divide, and then check. a.

Lesson 19: Copyright ÂŠ Great Minds PBC Virginia Edition greatminds.org/math

Divide two- and three-digit dividends by multiples of 10 with single-digit quotients, and make connections to a written method.

2. How many groups of thirty are in two hundred twenty-four?

There are 7 groups of thirty in two hundred twenty-four.

Lesson 19 Homework 5•2

1. Divide, and then check using multiplication. The first one is done for you. a. 71 ÷ 20

d. 280 ÷ 30

e. 437 ÷ 60

Lesson 19 Homework 5â&#x20AC;˘2

2. A number divided by 40 has a quotient of 6 with a remainder of 16. Find the number.

3. A shipment of 288 reams of paper was delivered. Each of the 30 classrooms received an equal share of the paper. Any extra reams of paper were stored. After the paper was distributed to the classrooms, how many reams of paper were stored?

4. How many groups of sixty are in two hundred forty-four?

Lesson 20 Homework Helper 5â&#x20AC;˘2

1. Divide. Then check with multiplication

Lesson 20: Copyright ÂŠ Great Minds PBC Virginia Edition greatminds.org/math

Divide two- and three-digit dividends by two-digit divisors with singledigit quotients, and make connections to a written method.

Lesson 20 Homework Helper 5•2

2. A rectangular 95-square-foot vegetable garden has a length of 19 feet. What is the width of the 2 vegetable garden?

The width of the vegetable garden is 5 feet. 3. A number divided by 41 has a quotient of 4 with 15 as a remainder. Find the number.

The number is 179.

Lesson 20 Homework 5•2

1. Divide. Then, check with multiplication. The first one is done for you. a. 72 ÷ 31

b. 89 ÷ 21

c. 94 ÷ 33

d. 67 ÷ 19

e. 79 ÷ 25

f. 83 ÷ 21

Lesson 20 Homework 5â&#x20AC;˘2

2. A 91 square foot bathroom has a length of 13 feet. What is the width of the bathroom?

3. While preparing for a morning conference, Principal Corsetti is laying out 8 dozen bagels on square plates. Each plate can hold 14 bagels. a. How many plates of bagels will Mr. Corsetti have?

b. How many more bagels would be needed to fill the final plate with bagels?

Lesson 21 Homework Helper 5â&#x20AC;˘2

1. Divide. Then check using multiplication. a.

Lesson 21: Copyright ÂŠ Great Minds PBC Virginia Edition greatminds.org/math

2. How many forty-nines are in one hundred fifty-nine?

There are 3 groups of forty-nine in 159.

Lesson 21 Homework 5•2

1. Divide. Then, check using multiplication. The first one is done for you. a. 129 ÷ 21

b. 158 ÷ 37

c. 261 ÷ 49

d. 574 ÷ 82

e. 464 ÷ 58

2. It takes Juwan exactly 35 minutes by car to get to his grandmother’s. The nearest parking area is a 4-minute walk from her apartment. One week, he realized that he spent 5 hours and 12 minutes traveling to her apartment and then back home. How many round trips did he make to visit his grandmother?

3. How many eighty-fours are in 672?

Lesson 22 Homework Helper 5•2

1. Divide. Then check using multiplication. a. 874 ÷ 41

b. 703 ÷ 29

Divide three- and four-digit dividends by two-digit divisors resulting in two- and three-digit quotients, reasoning about the decomposition of successive remainders in each place value.

Lesson 22 Homework Helper 5â&#x20AC;˘2

2. 31 students are selling cupcakes. There are 167 cupcakes to be shared equally among students. a. How many cupcakes are left over after sharing them equally?

There are 12 cupcakes left over after sharing them equally.

b. If each student needs 6 cupcakes to sell, how many more cupcakes are needed?

Lesson 22: Copyright ÂŠ Great Minds PBC Virginia Edition greatminds.org/math

Lesson 22 Homework 5•2

1. Divide. Then, check using multiplication. The first one is done for you. a. 487 ÷ 21

b. 485 ÷ 15

c. 700 ÷ 21

d. 399 ÷ 31

e. 820 ÷ 42

2. When dividing 878 by 31, a student finds a quotient of 28 with a remainder of 11. Check the student’s work, and use the check to find the error in the solution.

3. A baker was going to arrange 432 desserts into rows of 28. The baker divides 432 by 28 and gets a quotient of 15 with remainder 12. Explain what the quotient and remainder represent.

Lesson 23 Homework Helper 5•2

1. Divide. Then check using multiplication. a. 4,753 ÷ 22

b. 3,795 ÷ 62

2. 1,292 balloons were shared equally among 38 students. How many balloons did each student receive?

Each student received 34 balloons.

Lesson 23 Homework 5•2

1. Divide. Then, check using multiplication. a. 9,962 ÷ 41

b. 1,495 ÷ 45

c. 6,691 ÷ 28

d. 2,625 ÷ 32

e. 2,409 ÷ 19

2. A political gathering in South America was attended by 7,910 people. Each of South America’s 14 countries was equally represented. How many representatives attended from each country?

3. A candy company packages caramel into containers that hold 32 fluid ounces. In the last batch, 1,848 fluid ounces of caramel were made. How many containers were needed for this batch?

Lesson 24 Homework Helper 5â&#x20AC;˘2

1. Divide. a.

Lesson 24: Copyright ÂŠ Great Minds PBC Virginia Edition greatminds.org/math

Divide decimal dividends by multiples of 10, reasoning about the placement of the decimal point and making connections to a written method.

2. Use place value reasoning and the first quotient to compute the second quotient. Use place value to explain how you placed the decimal point.

There are 10 times fewer groups, so there has to be 10 times more in each group.

Instead of 4 groups, there are 40 groups. That's 10 times more groups, so there must be 10 times less in each group.

Lesson 24 Homework 5•2

1. Divide. Show every other division sentence in two steps. The first two have been done for you. a. 1.8 ÷ 6 = 0.3

b. 1.8 ÷ 60 = (1.8 ÷ 6) ÷ 10 = 0.3 ÷ 10 = 0.03

c. 2.4 ÷ 8 =

d. 2.4 ÷ 80 =

e. 14.6 ÷ 2 =

g. 0.8 ÷ 4 =

h. 80 ÷ 400 =

0.56 ÷ 70 =

k. 9.45 ÷ 9 =

9.45 ÷ 900 =

14.6 ÷ 20 =

2. Use place value reasoning and the first quotient to compute the second quotient. Use place value to explain how you placed the decimal point. a. 65.6 ÷ 80 = 0.82 65.6 ÷ 8 =

b. 2.5.÷ 50 = 0.05 2.5 ÷ 5 =

c. 19.2 ÷ 40 = 0.48 19.2 ÷ 4 =

d. 39.6 ÷ 6 = 6.6 39.6 ÷ 60 =

Lesson 24 Homework 5â&#x20AC;˘2

3. Chris rode his bike along the same route every day for 60 days. He logged that he had gone exactly 127.8 miles. a. How many miles did he bike each day? Show your work to explain how you know.

b. How many miles did he bike over the course of two weeks?

4. 2.1 liters of coffee were equally distributed to 30 cups. How many milliliters of coffee were in each cup?

Lesson 25 Homework Helper 5â&#x20AC;˘2

1. Estimate the quotients.

Lesson 25: Copyright ÂŠ Great Minds PBC Virginia Edition greatminds.org/math

Use basic facts to approximate decimal quotients with two-digit divisors, reasoning about the placement of the decimal point.

2. Estimate the quotient in (a). Use your estimated quotient to estimate (b) and (c).

Lesson 25 Homework 5•2

1. Estimate the quotients. a. 3.53 ÷ 51 ≈

b. 24.2 ÷ 42 ≈

c. 9.13 ÷ 23 ≈

d. 79.2 ÷ 39 ≈

e. 7.19 ÷ 58 ≈

2. Estimate the quotient in (a). Use your estimated quotient to estimate (b) and (c). a. 9.13 ÷ 42 ≈

b. 913 ÷ 42 ≈

c. 91.3 ÷ 42 ≈

3. Mrs. Huynh bought a bag of 3 dozen toy animals as party favors for her son’s birthday party. The bag of toy animals cost $28.97. Estimate the price of each toy animal.

4. Carter drank 15.75 gallons of water in 4 weeks. He drank the same amount of water each day. a. Estimate how many gallons he drank in one day.

b. Estimate how many gallons he drank in one week.

c. About how many days altogether will it take him to drink 20 gallons?

Lesson 26 Homework Helper 5•2

1. Divide. Then check your work with multiplication. a.

48.07 ÷ 19 = 2. 53

Divide decimal dividends by two-digit divisors, estimating quotients, reasoning about the placement of the decimal point, and making connections to a written method.

2. The weight of 42 identical mini toy soldiers is 109.2 grams. What is the weight of each toy soldier?

The weight of each toy soldier is 2. 6 grams.

Lesson 26 Homework 5•2

1. Create two whole number division problems that have a quotient of 9 and a remainder of 5. Justify which is greater using decimal division.

2. Divide. Then, check your work with multiplication. a. 75.9 ÷ 22

b. 97.28 ÷ 19

c. 77.14 ÷ 38

d. 12.18 ÷ 29

3. Divide. a. 97.58 ÷ 34

b. 55.35 ÷ 45

4. Use the equations on the left to solve the problems on the right. Explain how you decided where to place the decimal in the quotient. a. 520.3 ÷ 43 = 12.1

52.03 ÷ 43 =

b. 19.08 ÷ 36 = 0.53

190.8 ÷ 36 =

5. You can look up information on the world’s tallest buildings at http://www.infoplease.com/ipa/A0001338.html. a. The Aon Centre in Chicago, Illinois, is one of the world’s tallest buildings. Built in 1973, it is 1,136 feet high and has 80 stories. If each story is of equal height, how tall is each story?

b. Burj al Arab Hotel, another one of the world’s tallest buildings, was finished in 1999. Located in Dubai, it is 1,053 feet high with 60 stories. If each floor is the same height, how much taller or shorter is each floor than the height of the floors in the Aon Center?

Lesson 27 Homework Helper 5•2

1. Divide. Check your work with multiplication. 6.3 ÷ 18

Lesson 27 Homework Helper 5â&#x20AC;˘2

2. 43.4 kilograms of raisins was placed into 31 packages of equal weight. What is the weight of one package of raisins?

Lesson 27: Copyright ÂŠ Great Minds PBC Virginia Edition greatminds.org/math

Lesson 27 Homework 5•2

1. Divide. Check your work with multiplication. a. 7 ÷ 28

b. 51 ÷ 25

c. 6.5 ÷ 13

d. 132.16 ÷ 16

e. 561.68 ÷ 28

f. 604.8 ÷ 36

2. In a science class, students water a plant with the same amount of water each day for 28 consecutive days. If the students use a total of 23.8 liters of water over the 28 days, how many liters of water did they use each day? How many milliliters did they use each day?

Lesson 27 Homework 5â&#x20AC;˘2

3. A seamstress has a piece of cloth that is 3 yards long. She cuts it into shorter lengths of 16 inches each. How many of the shorter pieces can she cut?

4. Jenny filled 12 pitchers with an equal amount of lemonade in each. The total amount of lemonade in the 12 pitchers was 41.4 liters. How many liters of lemonade would be in 7 pitchers?

Lesson 28 Homework Helper 5â&#x20AC;˘2

1. Juanita is saving for a new television that costs $931. She has already saved half of the money. Juanita earns $19.00 per hour. How many hours must Juanita work to save the rest of the money?

Lesson 28: Copyright ÂŠ Great Minds PBC Virginia Edition greatminds.org/math

Solve division word problems involving multi-digit division with group size unknown and the number of groups unknown.

2. Timmy has a collection of 1,008 baseball cards. He hopes to sell the collection in packs of 48 cards and make $178.50 when all the packs are sold. If each pack is priced the same, how much should Timmy charge per pack?

Lesson 28 Homework 5â&#x20AC;˘2

1. Mr. Rice needs to replace the 166.25 ft of edging on the flower beds in his backyard. The edging is sold in lengths of 19 ft each. How many lengths of edging will Mr. Rice need to purchase?

2. Olivia is making granola bars. She will use 17.9 ounces of pistachios, 12.6 ounces of almonds, 12.5 ounces of walnuts, and 12.5 ounces of cashews. This amount makes 25 bars. How many ounces of nuts are in each granola bar?

3. Adam has 16.45 kg of flour, and he uses 6.4 kg to make hot cross buns. The remaining flour is exactly enough to make 15 batches of scones. How much flour, in kg, will be in each batch of scones?

4. There are 90 fifth-grade students going on a field trip. Each student gives the teacher $9.25 to cover admission to the theater and for lunch. Admission for all of the students will cost $315, and each student will get an equal amount to spend on lunch. How much will each fifth grader get to spend on lunch?

5. Ben is making math manipulatives to sell. He wants to make at least $450. Each manipulative costs $18 to make. He is selling them for $30 each. What is the minimum number he can sell to reach his goal?

Lesson 29 Homework Helper 5â&#x20AC;˘2

1. Alonzo has 2,580.2 kilograms of apples to deliver in equal amounts to 19 stores. Eleven of the stores are in Philadelphia. How many kilograms of apples will be delivered to stores in Philadelphia?

1493.8 kilograms of apples will be delivered to stores in Philadelphia.

Lesson 29: Copyright ÂŠ Great Minds PBC Virginia Edition greatminds.org/math

2. The area of a rectangle is 88.4 m2. If the length is 13 m, what is its perimeter?

The perimeter of the rectangle is 39.6 meters.

Lesson 29 Homework 5â&#x20AC;˘2

Solve. 1. Michelle wants to save $150 for a trip to the Six Flags amusement park. If she saves $12 each week, how many weeks will it take her to save enough money for the trip?

2. Karen works for 85 hours throughout a two-week period. She earns $1,891.25 throughout this period. How much does Karen earn for 8 hours of work?

3. The area of a rectangle is 256.5 m2. If the length is 18 m, what is the perimeter of the rectangle?

4. Tyler baked 702 cookies. He sold them in boxes of 18. After selling all of the boxes of cookies for the same amount each, he earned $136.50. What was the cost of one box of cookies?

5. A park is 4 times as long as it is wide. If the distance around the park is 12.5 kilometers, what is the area of the park?

Credits Great Minds® has made every effort to obtain permission for the reprinting of all copyrighted material. If any owner of copyrighted material is not acknowledged herein, please contact Great Minds for proper acknowledgment in all future editions and reprints of this module.

EMBARC.Online

Topic outline, grade 5 module 3, addition and subtraction of fractions.

Topic A: Equivalent Fractions

Topic b: making like units pictorially, mid-module review, topic c: making like units numerically, topic d: further applications, end-of-module review.

Texas Go Math
Big Ideas Math
Engageny Math
McGraw Hill My Math
enVision Math
180 Days of Math
Math in Focus Answer Key
Math Expressions Answer Key
Privacy Policy

$CCSS Math Answers$

Eureka Math Grade 5 Module 1 Lesson 12 Answer Key

Engage ny eureka math 5th grade module 1 lesson 12 answer key, eureka math grade 5 module 1 lesson 12 sprint answer key.

$Eureka Math Grade 5 Module 1 Lesson 12 Sprint Answer Key 1$

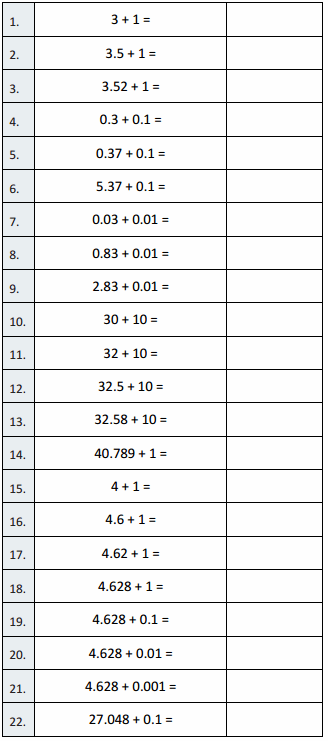
Question 1. 3 + 1 = Answer:- 4

Question 2. 3.5 + 1 = Answer:- 4.5

Question 3. 3.52 + 1 = Answer:- 4.52

Question 4. 0.3 + 0.1 = Answer:- 0.4

Question 5. 0.37 + 0.1 = Answer:- 0.47

Question 6. 5.37 + 0.1 = Answer:- 5.47

Question 7. 0.03 + 0.01 = Answer:- 0.04

Question 8. 0.83 + 0.01 = Answer:- 0.84

Question 9. 2.83 + 0.01 = Answer:- 2.84

Question 10. 30 + 10 = Answer:- 40

Question 11. 32 + 10 = Answer:- 42

Question 12. 32.5 + 10 = Answer:- 42.5

Question 13. 32.58 + 10 = Answer:- 42.58

Question 14. 40.789 + 1 = Answer:- 41.789

Question 15. 4 + 1 = Answer:- 5

Question 16. 4.6 + 1 = Answer:- 5.6

Question 17. 4.62 + 1 = Answer:- 5.62

Question 18. 4.628 + 1 = Answer:- 5.628

Question 19. 4.628 + 0.1 = Answer:- 4.728

Question 20. 4.628 + 0.01 = Answer:- 4.638

Question 21. 4.628 + 0.001 = Answer:- 4.629

Question 22. 27.048 + 0.1 = Answer:- 27.148

Question 23. 5 + 0.1 = Answer:- 5.1

Question 24. 5.7 + 0.1 = Answer:- 5.8

Question 25. 5.73 + 0.1 = Answer:- 5.74

Question 26. 5.736 + 0.1 = Answer:- 5.836

Question 27. 5.736 + 1 = Answer:- 6.736

Question 28. 5.736 + 0.01 = Answer:- 5.746

Question 29. 5.736 + 0.001 = Answer:- 5.737

Question 30. 6.208 + 0.01 = Answer:- 6.218

Question 31. 3 + 0.01 = Answer:- 3.01

Question 32. 3.5 + 0.01 = Answer:- 3.51

Question 33. 3.58 + 0.01 = Answer:- 3.59

Question 34. 3.584 + 0.01 = Answer:- 3.594

Question 35. 3.584 + 0.001 = Answer:- 3.585

Question 36. 3.584 + 0.1 = Answer:- 3.684

Question 37. 3.584 + 1 = Answer:- 4.584

Question 38. 6.804 + 0.01 = Answer:- 6.814

Question 39. 8.642 + 0.001 = Answer:- 8.643

Question 40. 7.65 + 0.001 = Answer:- 7.651

Question 41. 3.987 + 0.1 = Answer:- 4.087

Question 42. 4.279 + 0.001 = Answer:- 4.280

Question 43. 13.579 + 0.01 = Answer:- 13.589

Question 44. 15.491 + 0.01 = Answer:- 15.501

$Eureka Math Grade 5 Module 1 Lesson 12 Sprint Answer Key 3$

Question 1. 2 + 1 = Answer:- 3

Question 2. 2.5 + 1 = Answer:- 3.5

Question 3. 2.53 + 1 = Answer:- 3.53

Question 4. 0.2 + 0.1 = Answer:- 0.3

Question 5. 0.27 + 0.1 = Answer:- 0.37

Question 6. 5.27 + 0.1 = Answer:- 5.37

Question 7. 0.02 + 0.01 = Answer:- 0.03

Question 8. 0.82 + 0.01 = Answer:- 0.83

Question 9. 4.82 + 0.01 = Answer:- 4.83

Question 10. 20 + 10 = Answer:- 30

Question 11. 23 + 10 = Answer:- 33

Question 12. 23.5 + 10 = Answer:- 33.5

Question 13. 23.58 + 10 = Answer:- 33.58

Question 14. 30.789 + 1 = Answer:- 31.789

Question 15. 3 + 1 = Answer:- 4

Question 16. 3.6 + 1 = Answer:- 4.6

Question 17. 3.62 + 1 = Answer:- 4.62

Question 18. 3.628 + 1 = Answer:- 4.628

Question 19. 3.628 + 0.1 = Answer:- 3.728

Question 20. 3.628 + 0.01 = Answer:- 3.638

Question 21. 3.628 + 0.001 = Answer:- 3.629

Question 22. 37.048 + 0.1 = Answer:- 37.148

Question 23. 4 + 0.1 = Answer:- 4.1

Question 24. 4.7 + 0.1 = Answer:- 4.8

Question 25. 4.73 + 0.1 = Answer:- 4.83

Question 26. 4.736 + 0.1 = Answer:- 4.836

Question 27. 4.736 + 1 = Answer:- 5.736

Question 28. 4.736 + 0.01 = Answer:- 4.746

Question 29. 4.736 + 0.001 = Answer:- 4.737

Question 30. 5.208 + 0.01 = Answer:- 5.218

Question 31. 2 + 0.01 = Answer:- 2.01

Question 32. 2.5 + 0.01 = Answer:- 2.51

Question 33. 2.58 + 0.01 = Answer:- 2.59

Question 34. 2.584 + 0.01 = Answer:- 2.594

Question 35. 2.584 + 0.001 = Answer:- 2.585

Question 36. 2.584 + 0.1 = Answer:- 2.684

Question 37. 2.584 + 1 = Answer:- 3.584

Question 38. 5.804 + 0.01 = Answer:- 5.814

Question 39. 7.642 + 0.001 = Answer:- 7.643

Question 40. 6.75 + 0.001 = Answer:- 6.751

Question 41. 2.987 + 0.1 = Answer:- 3.087

Question 42. 3.279 + 0.001 = Answer:- 3.280

Question 43. 12.579 + 0.01 = Answer:- 12.589

Question 44. 14.391 + 0.01 = Answer:- 14.401

Eureka Math Grade 5 Module 1 Lesson 12 Problem Set Answer Key

$Eureka Math Grade 5 Module 1 Lesson 12 Problem Set Answer Key 6$

Question 2. Pedro is building a spice rack with 4 shelves that are each 0.55 meter long. At the hardware store, Pedro finds that he can only buy the shelving in whole meter lengths. Exactly how many meters of shelving does Pedro need? Since he can only buy whole-number lengths, how many meters of shelving should he buy? Justify your thinking. Answer:- Pedro wants 4 x 0.55m = 2.20m of shelving. But the hardware store provide the shelving meters only in whole numbers so he have to buy the shelving in whole number and i.e., 3m because 2.20 is very nearest to the whole number of 3m. So, he can buy the shelving in 3m.

Question 3. Marcel rides his bicycle to school and back on Tuesdays and Thursdays. He lives 3.62 kilometers away from school. Marcel’s gym teacher wants to know about how many kilometers he bikes in a week. Marcel’s math teacher wants to know exactly how many kilometers he bikes in a week. What should Marcel tell each teacher? Show your work. Answer:- Marcel says, He bikes in a week was 14km. Actual was 14.48km but he says approximate and nearest tenth of 14.48 km. Why because Marcel rides his bicycle to school and back on Tuesdays and Thursdays for to and fro 3.62 x 4 = 14.48km.

Question 4. The poetry club had its first bake sale, and they made $79.35. The club members are planning to have 4 more bake sales. Leslie said, “If we make the same amount at each bake sale, we’ll earn $3,967.50.” Peggy said, “No way, Leslie! We’ll earn $396.75 after five bake sales.” Use estimation to help Peggy explain why Leslie’s reasoning is inaccurate. Show your reasoning using words, numbers, or pictures. Answer:- The poetry club had its first bake sale, and they made $79.35 we will take a nearest whole number $80.00 this is for one bake sale. If they keep four more bake sales and gets same sale as 80.00 they will earn 80 x 5 = 400 or $79.35 x 5 = $396.75. Leslie was wrong because she had multiplied 79.35 with 50 means with 50 bake sales not with 5 bake sales.

Eureka Math Grade 5 Module 1 Lesson 12 Exit Ticket Answer Key

$Engage NY Math 5th Grade Module 1 Lesson 12 Exit Ticket Answer Key 10$

Question 2. Estimate the answer for 7.13 × 6. Explain your reasoning using words, pictures, or numbers. Answer:- 7.13 x 6 = 42.78 because 7.13 times of 6 when we multiply 7.13 with 6 we will get 42.78 as the answer (7 + 0.13) x (6) (7 x 6) + (0.13 x 6) 42 + 0.78 42.78

Eureka Math Grade 5 Module 1 Lesson 12 Homework Answer Key

$Eureka Math 5th Grade Module 1 Lesson 12 Homework Answer Key 12$

Question 2. Yi Ting weighs 8.3 kg. Her older brother is 4 times as heavy as Yi Ting. How much does her older brother weigh in kilograms? Answer:- Yi Ting weighs 8.3 kg. Her older brother is 4 times as heavy as Yi Ting. That means 8.3 x 4 = 33.2 Yi Ting’s older brother weigh in kilograms is 33.2kgs.

Question 3. Tim is painting his storage shed. He buys 4 gallons of white paint and 3 gallons of blue paint. Each gallon of white paint costs $15.72, and each gallon of blue paint is $21.87. How much will Tim spend in all on paint? Answer:- He buys 4 gallons of white paint is $15.72 x 4 = $62.88 He buys 3 gallons of blue paint is $21.87 x 3 = $65.61 Therefore, Tim spend in all on paints is $128.49.

Question 4. Ribbon is sold at 3 yards for $6.33. Jackie bought 24 yards of ribbon for a project. How much did she pay? Answer:- Ribbon sold 3 yards for $6.33 i.e., each yard costs $2.11. And Jackie bought 24 yards of ribbon for a project. That means 2.11 x 24 = 50.64 Total she pays $5.64