case study laws of motion class 11

myCBSEguide

Class 11 Physics Case...

Class 11 Physics Case Study Questions

Table of Contents

myCBSEguide App

Download the app to get CBSE Sample Papers 2023-24, NCERT Solutions (Revised), Most Important Questions, Previous Year Question Bank, Mock Tests, and Detailed Notes.

Looking for complete and comprehensive case study questions for class 11 Physics? myCBSEguide is just a click away! With extensive study materials, sample papers, case study questions and mock tests, myCBSEguide is your one-stop solution for class 11 Physics exam preparation needs. So, what are you waiting for? Log on to myCBSEguide and get started today!

What is the purpose of physics?

Physics is the study of the fundamental principles governing the natural world. It is a vital part of the scientific enterprise, providing the foundation on which other sciences are built. Physics is essential for understanding how the world works, from the smallest particles to the largest structures in the Universe. In class 11 Physics, students are introduced to the basic concepts of physics and learn about the fundamental principles governing the natural world. Class 11 Physics concepts are essential for understanding the world around us and for further study in physics and other sciences.

What are case study questions in physics?

In physics, case study questions are intended to evaluate a student’s ability to apply theoretical principles to real-life situations. These questions usually ask the student to assess data from a specific experiment or setting in order to discover what physical principles are at play. Problem-solving and critical-thinking skills are developed through case study questions, which are an important aspect of physics education.

CBSE Case Study Questions in Class 11 Physics

CBSE Class 11 Physics question paper pattern includes case study questions. Class 11 Physics case study questions assess a student’s ability to apply physics principles to real-world environments. The questions are usually focused on a situation provided in the Class 11 Physics question paper, and they demand the student to answer the problem using their physics knowledge. Class 11 Physics case study questions are an important aspect of the CBSE physics curriculum. Class 11 Physics case study questions are a useful way to assess a student’s expertise in the subject.

Sample Class 11 Physics Case Study Questions

Expert educators at myCBSEguide have created a collection of Class 11 physics case study questions. The samples of Class 11 physics case study questions are given below. Class 11 physics case study questions are designed to test your understanding of the concepts and principles of physics. They are not meant to be easy, but they should be done if you have a good grasp of the subject. So, take a look at the questions and see how you fare. Good luck!

Class 11 Physics Case Study Question 1

Read the case study given below and answer any four subparts: Potential energy is the energy stored within an object, due to the object’s position, arrangement or state. Potential energy is one of the two main forms of energy, along with kinetic energy. Potential energy depends on the force acting on the two objects.

kinetic energy
potential energy
mechanical energy
none of these
potential energy decreases
potential energy increases
kinetic energy decreases
kinetic energy increases
only when spring is stretched
only when spring is compressed
both a and b
5 × 10 4 J
5 × 10 5 J

Answer Key:

Class 11 Physics Case Study Question 2

distance between body
source of heat
all of the above
convection and radiation
(b) convection
(d) all of the above
(a) convection
(a) increase
(c) radiation

Class 11 Physics Case Study Question 3

internal energy.
1 +(T 2 /T 1 )
(T 1 /T 2 )+1
(T 1 /T 2 )- 1
1 – (T 2 / T 1 )
increase or decrease depending upon temperature ratio
first increase and then decrease
(d) 1- (T 2 / T 1 )
(b) increase
(c) constant

Class 11 Physics Case Study Question 4

It is far away from the surface of the earth
Its surface temperature is 10°C
The r.m.s. velocity of all the gas molecules is more than the escape velocity of the moon’s surface
The escape velocity of the moon’s surface is more than the r.m.s velocity of all molecules
T(H 2 ) = T(N 2 )
T(H 2 ) < T(N 2 )
T(H 2 ) > T(N 2 )

The given samples of Class 11 Physics case study questions will help Class 11 Physics students to get an idea on how to solve it. These Class 11 Physics case study questions are based on the topics covered in the Class 11 Physics syllabus and are designed to test the student’s conceptual understanding. The questions are of varying difficulty levels and cover a wide range of topics. By solving these Class 11 Physics case study questions, students will be able to develop their problem-solving skills and improve their understanding of the concepts.

Examining Class 11 Physics syllabus

Senior Secondary school education is a transitional step from general education to a discipline-based curriculum concentration. The current curriculum of Class 11 Physics takes into account the rigour and complexity of the disciplinary approach, as well as the learners’ comprehension level. Class 11 Physics syllabus has also been carefully crafted to be similar to international norms.

The following are some of the Class 11 Physics syllabus’s most notable features:

Emphasis is placed on gaining a fundamental conceptual knowledge of the material.
Use of SI units, symbols, naming of physical quantities, and formulations in accordance with international standards are emphasised.
For enhanced learning, provide logical sequencing of subject matter units and suitable placement of concepts with their links.
Eliminating overlapping concepts/content within the field and between disciplines to reduce the curricular load.
Process skills, problem-solving ability, and the application of Physics principles are all encouraged.

CBSE Class 11 Physics (Code No. 042)

myCBSEguide: A true saviour for many students

myCBSEguide has been a true saviour for many students who struggle to find resources elsewhere. It is a reliable source of information and provides students with everything they need to excel in their academics. myCBSEguide has helped many students score high marks in their exams and has been a valuable resource for their studies. Teachers recommend myCBSEguide to all CBSE students. And best of all, it’s available 24/7, so you can study at your own pace, anytime, anywhere. So why wait? Get started today and see the difference myCBSEguide can make to your studies.

Test Generator

Create question paper PDF and online tests with your own name & logo in minutes.

Question Bank, Mock Tests, Exam Papers, NCERT Solutions, Sample Papers, Notes

Competency Based Learning in CBSE Schools
Class 11 Physical Education Case Study Questions
Class 11 Sociology Case Study Questions
Class 12 Applied Mathematics Case Study Questions
Class 11 Applied Mathematics Case Study Questions
Class 11 Mathematics Case Study Questions
Class 11 Biology Case Study Questions
Class 12 Physical Education Case Study Questions

Save my name, email, and website in this browser for the next time I comment.

cbseexpert.com

Class 11 Physics Case Study Questions PDF Download

Post author: studyrate
Post published:
Post category: Physics
Post comments: 0 Comments

Class 11 Physics Case Study Questions are available here. You can read these Case Study questions by chapter for your final physics exam. Subject matter specialists and seasoned teachers created these quizzes. You can verify the right response to each question by referring to the answer key, which is also provided. To achieve high marks on your Board exams, practice these questions.

Join our Telegram Channel, there you will get various e-books for CBSE 2024 Boards exams for Class 9th, 10th, 11th, and 12th.

We are providing Case Study questions for Class 11 Physics based on the Latest syllabus. There is a total of 14 chapters included in the CBSE Class 11 physics exams. Students can practice these questions for concept clarity and score better marks in their exams.

Table of Contents

Class 11th PHYSICS: Chapterwise Case Study Question & Solution

Case study questions play a crucial role in the Class 11 Physics curriculum. They are designed to assess your understanding of various concepts and principles in real-life scenarios. These questions help you apply theoretical knowledge to practical situations, enhancing your problem-solving skills.

Case Study-Based Questions for Class 11 Physics

Case Study Based Questions on Class 11 Physics Chapter 2 Units and Measurements
Case Study Based Questions on Class 11 Physics Chapter 3 Motion in a Straight Line
Case Study Based Questions on Class 11 Physics Chapter 4 Motion in a Plane
Case Study Based Questions on Class 11 Physics Chapter 5 Laws of Motion
Case Study Based Questions on Class 11 Physics Chapter 6 Work, Energy, and Power
Case Study Based Questions on Class 11 Physics Chapter 7 System of Particles and Rotational Motion
Case Study Based Questions on Class 11 Physics Chapter 8 Gravitation
Case Study Based Questions on Class 11 Physics Chapter 9 Mechanical Properties of Solids
Case Study Based Questions on Class 11 Physics Chapter 10 Mechanical Properties of Fluids
Case Study Based Questions on Class 11 Physics Chapter 11 Thermal Properties of Matter
Case Study Based Questions on Class 11 Physics Chapter 12 Thermodynamics
Case Study Based Questions on Class 11 Physics Chapter 13 Kinetic Theory
Case Study Based Questions on Class 11 Physics Chapter 14 Waves
Case Study Based Questions on Class 11 Physics Chapter 15 Oscillations

Class 11 Physics MCQ Questions

Before the exams, students in class 11 should review crucial Physics Case Study issues. They will gain a better understanding of the kinds of Case Study questions that may be offered in Physics exams for Grade 11. These questions were created by our highly qualified faculty for standard 11 Physics based on the questions that appeared most frequently in last year’s exams. The solutions have been written in a way that will make them simple to grasp and will aid students in grade 11 in understanding the topics.

Class 11 Books for Boards

Class 11 Physics Syllabus 2024

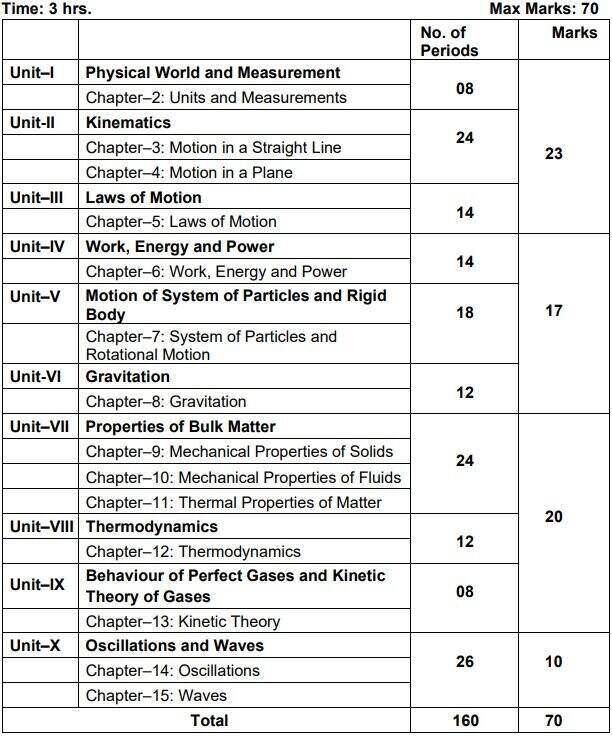
Unit I: Physical World and Measurement 08 Periods

Chapter–2: Units and Measurements

Need for measurement: Units of measurement; systems of units; SI units, fundamental and derived units. significant figures. Dimensions of physical quantities, dimensional analysis and its applications.

Unit II: Kinematics 24 Periods

Chapter–3: Motion in a Straight Line

The frame of reference, Motion in a straight line, Elementary concepts of differentiation and integration for describing motion, uniform and non-uniform motion, and instantaneous velocity, uniformly accelerated motion, velocity-time and position-time graphs. Relations for uniformly accelerated motion (graphical treatment).

Chapter–4: Motion in a Plane

Scalar and vector quantities; position and displacement vectors, general vectors and their notations; equality of vectors, multiplication of vectors by a real number; addition and subtraction of vectors, Unit vector; resolution of a vector in a plane, rectangular components, Scalar and Vector product of vectors. Motion in a plane, cases of uniform velocity and uniform acceleration projectile motion, uniform circular motion.

Unit III: Laws of Motion 14 Periods

Chapter–5: Laws of Motion

Intuitive concept of force, Inertia, Newton’s first law of motion; momentum and Newton’s second law of motion; impulse; Newton’s third law of motion. Law of conservation of linear momentum and its applications. Equilibrium of concurrent forces, Static and kinetic friction, laws of friction, rolling friction, lubrication.

Dynamics of uniform circular motion: Centripetal force, examples of circular motion (vehicle on a level circular road, vehicle on a banked road).

Unit IV: Work, Energy and Power 14 Periods

Chapter–6: Work, Energy and Power

Work done by a constant force and a variable force; kinetic energy, workenergy theorem, power. Notion of potential energy, potential energy of a spring, conservative forces: non- conservative forces, motion in a vertical circle; elastic and inelastic collisions in one and two dimensions.

Unit V: Motion of System of Particles and Rigid Body 18 Periods

Chapter–7: System of Particles and Rotational Motion

Centre of mass of a two-particle system, momentum conservation and Centre of mass motion. Centre of mass of a rigid body; centre of mass of a uniform rod. Moment of a force, torque, angular momentum, law of conservation of angular momentum and its applications. Equilibrium of rigid bodies, rigid body rotation and equations of rotational motion, comparison of linear and rotational motions. Moment of inertia, radius of gyration, values of moments of inertia for simple geometrical objects (no derivation).

Unit VI: Gravitation 12 Periods

Chapter–8: Gravitation

Kepler’s laws of planetary motion, universal law of gravitation. Acceleration due to gravity and its variation with altitude and depth. Gravitational potential energy and gravitational potential, escape velocity, orbital velocity of a satellite.

Unit VII: Properties of Bulk Matter 24 Periods

Chapter–9: Mechanical Properties of Solids

Elasticity, Stress-strain relationship, Hooke’s law, Young’s modulus, bulk modulus, shear modulus of rigidity (qualitative idea only), Poisson’s ratio; elastic energy.

Chapter–10: Mechanical Properties of Fluids

Pressure due to a fluid column; Pascal’s law and its applications (hydraulic lift and hydraulic brakes), effect of gravity on fluid pressure. Viscosity, Stokes’ law, terminal velocity, streamline and turbulent flow, critical velocity, Bernoulli’s theorem and its simple applications. Surface energy and surface tension, angle of contact, excess of pressure across a curved surface, application of surface tension ideas to drops, bubbles and capillary rise.

Chapter–11: Thermal Properties of Matter

Heat, temperature, thermal expansion; thermal expansion of solids, liquids and gases, anomalous expansion of water; specific heat capacity; Cp, Cv – calorimetry; change of state – latent heat capacity. Heat transfer-conduction, convection and radiation, thermal conductivity, qualitative ideas of Blackbody radiation, Wein’s displacement Law, Stefan’s law .

Unit VIII: Thermodynamics 12 Periods

Chapter–12: Thermodynamics

Thermal equilibrium and definition of temperature zeroth law of thermodynamics, heat, work and internal energy. First law of thermodynamics, Second law of thermodynamics: gaseous state of matter, change of condition of gaseous state -isothermal, adiabatic, reversible, irreversible, and cyclic processes.

Unit IX: Behavior of Perfect Gases and Kinetic Theory of Gases 08 Periods

Chapter–13: Kinetic Theory

Equation of state of a perfect gas, work done in compressing a gas. Kinetic theory of gases – assumptions, concept of pressure. Kinetic interpretation of temperature; rms speed of gas molecules; degrees of freedom, law of equi-partition of energy (statement only) and application to specific heat capacities of gases; concept of mean free path, Avogadro’s number.

Unit X: Oscillations and Waves 26 Periods

Chapter–14: Oscillations

Periodic motion – time period, frequency, displacement as a function of time, periodic functions and their application. Simple harmonic motion (S.H.M) and its equations of motion; phase; oscillations of a loaded spring- restoring force and force constant; energy in S.H.M. Kinetic and potential energies; simple pendulum derivation of expression for its time period.

Chapter–15: Waves

Wave motion: Transverse and longitudinal waves, speed of traveling wave, displacement relation for a progressive wave, principle of superposition of waves, reflection of waves, standing waves in strings and organ pipes, fundamental mode and harmonics, Beats.

FAQs about Class 11 Physics Case Studies

What is the best website for a case study of physics class 11 .

studyrate.in is the best website for Class 11 Physics Case Study Questions for Board Exams. Here you can find various types of Study Materials, Ebooks, Notes, and much more free of cost.

How do you write a case study question for Class 11?

The CBSE will ask two Case Study Questions in the CBSE Class 11th Maths Question Paper. Question numbers 15 and 16 will be case-based questions where 5 MCQs will be asked based on a paragraph.

Are the case study questions based on the latest syllabus?

Yes, the case study questions are curated to align with the latest Class 11 Physics syllabus.

50+ jee mains mcq questions motion in a straight line with solutions.

Physical World Notes Class 11 Physics Notes- Download PDF for JEE/NEET

Laws of Motion Notes Class 11 Physics Notes- Download PDF for JEE/NEET

The Topper Combo Flashcards

Contains the Latest NCERT in just 350 flashcards.
Colourful and Interactive
Summarised Important reactions according to the latest PYQs of NEET(UG) and JEE

No thanks, I’m not interested!

Gurukul of Excellence

Classes for Physics, Chemistry and Mathematics by IITians

Join our Telegram Channel for Free PDF Download

Case Study Questions for Class 11 Physics

Chapter 1: Physical World Chapter 2: Units and Measurements Chapter 3: Motion in a Straight Line Chapter 4: Motion in a Plane Chapter 5: Laws of Motion Chapter 6: Work, Energy, and Power Chapter 7: System of Particles and Rotational Motion Chapter 8: Gravitation Chapter 9: Mechanical Properties of Solids Chapter 10: Mechanical Properties of Fluids Chapter 11: Thermal Properties of Matter Chapter 12: Thermodynamics Chapter 13: Kinetic Theory Chapter 14: Oscillations Chapter 15: Waves

Class 11 Physics Case Study Question

Case study question class 11 physics (cbse / ncert board).

Class 11 Physics Case Study Question and Answer: CBSE / NCERT Board Class 11 Physics Case Study Question prepared by expert Physics Teacher. Students can learn Case Based Question / Paragraph Type Question for NCERT Class 11 Physics.

There are total 15 chapter Physical World, Units and Measurement, Motion in a Straight Line, Motion in a Plane, Laws of Motion, Work, Energy and Power, Systems of Particles and Rotational Motion, Gravitation, Mechanical Properties of Solids, Mechanical Properties of Fluids, Thermal Properties of Matter, Thermodynamics, Kinetic Theory, Oscillations, Waves.

For any problem during learning any Case or any doubts please comment us. We are always ready to help You.

CBSE Class 11 Physics Case Study Question

Chapter 1 Physical World,
Chapter 2 Units and Measurement,
Chapter 3 Motion in a Straight Line,
Chapter 4 Motion in a Plane,
Chapter 5 Laws of Motion
Chapter 6 Work, Energy and Power,
Chapter 7 Systems of Particles and Rotational Motion,
Chapter 8 Gravitation,
Chapter 9 Mechanical Properties of Solids,
Chapter 10 Mechanical Properties of Fluids,
Chapter 11 Thermal Properties of Matter,
Chapter 12 Thermodynamics,
Chapter 13 Kinetic Theory,
Chapter 14 Oscillations,
Chapter 15 Waves

What is Case Study Question?

Ans. At case Study there will one paragraph and on the basis of that concept some question will made. Students have to solve that question.

How many marks will have at case based question?

Most of time 5 questions will made from each case. There will 1 or 2 marks for each question.

Ye case study download kaise hyonge.

We have a strong team of experienced Teachers who are here to solve all your exam preparation doubts

Light class 8 case study questions pdf, chhattisgarh class 8 sanskrit chapter 8 solution, kerala scert class 9 physics chapter 3 laws of motion solution, new mathematics today class 5 solutions chapter 22 – unitary method.

Username or Email Address

Remember Me

NCERT Solutions
NCERT Class 11
NCERT 11 Physics
Chapter 5: Laws Of Motion

NCERT Solutions for Class 11 Physics Chapter 5 Laws of Motion

Ncert solutions class 11 physics chapter 5 – free pdf download.

* According to the CBSE Syllabus 2023-24, this chapter has been renumbered as Chapter 4.

NCERT Solutions for Class 11 Physics Chapter 5 Laws of Motion is one of the key tools to prepare Physics efficiently for the examination. The solutions of Chapter 5 Laws of Motion, are given below to help students learn new concepts in an interactive and easy way. Using NCERT Solutions will help students to get an idea about the question paper pattern and the marking scheme of the exam.

In the previous chapter, we mainly focused on the motion of a particle. We saw that uniform motion depends on velocity, whereas non-uniform motion depends on acceleration. So far, we did not give much thought to what governs the motion of bodies. Now, this becomes a basic question in the present chapter. To learn all the basic concepts covered in this chapter, NCERT Solutions for Class 11 Physics are designed with accurate and authentic information strictly based on the latest CBSE Syllabus for 2023-24 and its curriculum. Let’s have a look at NCERT laws of motion Class 11 solutions.

carouselExampleControls112

Previous Next

Access the answers to NCERT Solutions for Class 11 Physics Chapter 5 Laws of Motion

1. Give the magnitude and direction of the net force acting on

(a) a drop of rain falling down with a constant speed

(b) a cork of mass 10 g floating on water

(d) a car moving with a constant velocity of 30 km/h on a rough road

(e) a high-speed electron in space far from all material objects, and free of electric and magnetic fields.

(a) The raindrop is falling at a constant speed. Therefore, acceleration will become zero. When acceleration is zero, the force acting on the drop will become zero since F = ma.

(b) The cork is floating on water, which means the weight of the cork is balanced by the upthrust. Therefore, the net force on the cork will be zero

(d) The net force acting on the high-speed electron will be zero since the electron is far from the material objects and free of electric and magnetic fields.

2. A pebble of mass 0.05 kg is thrown vertically upwards. Give the direction and magnitude of the net force on the pebble,

(a) during its upward motion

(b) during its downward motion

(c) at the highest point where it is momentarily at rest. Do your Solutions change if the pebble was thrown at an angle of 45° with the horizontal direction? Ignore air resistance.

(a) During the upward motion of the pebble, the acceleration due to gravity acts downwards, so the magnitude of the force on the pebble is

F = mg = 0.05 kg x 10 ms -2 = 0.5 N

The direction of the force is downwards

(b) During the downward motion also the magnitude of the force will be equal to 0.5 N and the force acts downwards

(c) If the pebble is thrown at an angle of 45° with the horizontal direction, it will have both horizontal and vertical components of the velocity. At the highest point, the vertical component of velocity will be zero but the horizontal component of velocity will remain throughout the motion of the pebble. This component will not have any effect on the force acting on the pebble. The direction of the force acting on the pebble will be downwards and the magnitude will be 0.5 N because no other force other than acceleration acts on the pebble.

3. Give the magnitude and direction of the net force acting on a stone of mass 0.1 kg,

(a) just after it is dropped from the window of a stationary train

(b) just after it is dropped from the window of a train running at a constant velocity of 36 km/h

(c ) just after it is dropped from the window of a train accelerating with1 m s -2

(d) lying on the floor of a train which is accelerating with 1 m s -2 , the stone being at rest relative to the train. Neglect air resistance throughout.

(a) Mass of stone = 0.1 kg

Acceleration = 10 ms -2

Net force, F = mg = 0.1 x 10 = 1.0 N

The force acts vertically downwards

(b) The train moves at a constant velocity. Therefore, the acceleration will be equal to zero. So there is no force acting on the stone due to the motion of the train. Therefore, the force acting on the stone will remain the same (1.0 N)

(c) When the train accelerates at 1m/s 2 , the stone experiences an additional force of F’ = ma = 0.1 x 1 = 0.1 N. The force acts in the horizontal direction.

But as the stone is dropped, the force F’ no longer acts and the net force acting on the stone F = mg = 0.1 x 10 = 1.0 N. (vertically downwards).

(d) As the stone is lying on the train floor, its acceleration will be the same as that of the train.

Therefore, the magnitude of the force acting on the stone, F = ma = 0.1 x 1 = 0.1 N.

It acts along the direction of motion of the train.

4. One end of a string of length l is connected to a particle of mass m and the other to a small peg on a smooth horizontal table. If the particle moves in a circle with speed v the net force on the particle (directed towards the centre) is :

(ii) T – mv 2 /l

(iii) T + mv 2 /l

T is the tension in the string. [Choose the correct alternative].

Solution (i) T

The net force acting on the particle is T, and it is directed towards the centre. It provides the centripetal force required by the particle to move along a circle.

5. A constant retarding force of 50 N is applied to a body of mass 20 kg moving initially with a speed of 15 m s -1 . How long does the body take to stop?

Force = – 50 N (since it is a retarding force)

Mass m = 20 kg

u = 15 m s -1

Force F = ma

a = F/m = -50/20 = – 2.5 ms -2

Using the equation, v = u + at

0 = 15 + (- 2.5) t

6. A constant force acting on a body of mass 3.0 kg changes its speed from 2.0 ms -1 to 3.5 ms -1 in 25 s. The direction of the motion of the body remains unchanged. What is the magnitude and direction of the force?

Mass, m = 3.0 Kg

u = 2.0 m/s

v = 3.5 m/s

F = m [(v-u)/t] (since a = (v -u)/t )

F = 3 [ (3.5 – 2)/25] = 0.18 N

The force acts in the direction of motion of the body

7. A body of mass 5 kg is acted upon by two perpendicular forces 8 N and 6 N. Give the magnitude and direction of the acceleration of the body.

Mass, m = 5 kg

Force, F 1 = 8N and F 2 = 6N

The resultant force of the body

Acceleration, a = F/m

a = 10/ 5 = 2m/s in the direction of the resultant force

The direction of the acceleration,

tan β = 6/8 = 0.75

β = tan -1 (0.75)

β = 37 0 with 8N

8. The driver of a three-wheeler moving at a speed of 36 km/h sees a child standing in the middle of the road and brings his vehicle to rest in 4.0 s just in time to save the child. What is the average retarding force on the vehicle? The mass of the three-wheeler is 400 kg, and the mass of the driver is 65 kg.

Initial velocity, u= 36 km/h

Final velocity, v = 0

Mass of the three-wheeler, m 1 = 400 Kg

Mass of the driver, m 2 = 65 Kg

Time taken to bring the vehicle to rest = 4.0 s

Acceleration, a = v- u/t = (0 – 10)/ 4 = – 2.5 m/s

Now, F = (m 1 + m 2 )/ a = (400 + 65) x (-2.5)

= – 1162.5 N = – 1.16 x 10 3 N

The negative sign shows that the force is retarding

9. A rocket with a lift-off mass of 20,000 kg is blasted upwards with an initial acceleration of 5.0 ms -2 . Calculate the initial thrust (force) of the blast.

Mass of the rocket, m = 20000 kg = 2 x 10 4 kg

Initial acceleration = 5 ms -2

g = 9.8 m/s 2

The initial thrust (force) should give an upward acceleration of 5 ms -2 and should overcome the force of gravity.

Thus, the thrust should produce a net acceleration of 9.8 + 5.0 = 14.8 ms -2 .

Using Newton’s second law of motion, the initial thrust acting on the rocket

Thrust = force = mass x acceleration

F = 20000 x 14.8 = 2.96 x 10 5 N

10 . A body of mass 0.40 kg moving initially with a constant speed of 10 ms -1 to the north is subject to a constant force of 8.0 N directed towards the south for 30 s. Take the instant the force is applied to be t = 0, the position of the body at that time to be x = 0, and predict its position at t = -5 s, 25 s, 100 s.

Mass of the body = 0.40 kg

Initial velocity, u = 10 m/s

Force, f = -8 N (retarding force)

Using the equation S = ut + (½) at 2

(a) Position at the time t = – 5 s

The force starts acting on the body from t = 0 s

So the acceleration of the body when the time is – 5 s is 0

S 1 = (10)(-5) + (½) (0) (-5) 2 = – 50 m

(b) Position at the time t = 25 s

The acceleration of the body due to the force acting in the opposite direction

Acceleration, a = F/a = -8 /0.4 = -20 ms -2

S 2 = (10)(25) + (½) (-20) (25) 2 = – 6000 m

For the first 30 sec, the body will move under the retardation of the force, and after that, the speed will remain constant.

Therefore, distance covered in 30 sec

S 3 = (10)(30) + (½)(-20)(30 2 )

= 300 – 9000 = – 8700m

The speed after 30 sec is

v = 10 – (20 x 30) = 590 m/s

The distance covered in the next 70 sec is

S 4 = – 590 x 70 + (½) (0) (70) 2 = – 41300 m

Therefore the position after 100 sec = S 3 + S 4 = – 8700 – 41300 = – 50000m

11. A truck starts from rest and accelerates uniformly at 2.0 ms -2 . At t = 10 s, a stone is dropped by a person standing on the top of the truck (6 m high from the ground). What are the (a) velocity, and (b) acceleration of the stone at t = 11s? (Neglect air resistance.)

Initial velocity, u = 0

Acceleration, a = 2 ms -2 ,

Using equation, v = u + at, we get

v = 0 + 2 x 10 = 20 m/s

The final velocity, v = 20 m/s

At time, t = 11 sec, the horizontal component of the velocity in the absence of the air resistance remains unchanged

V x =20 m/s

The vertical component of the velocity is given by the equation

V y = u + a y t

Here t = 11 – 10 = 1s and a y = a = 10 m/s

Therefore, the resultant velocity v of the stone is

v = ( v x 2 + v y 2 )½

v = (20 2 + 10 2 ) 1/2

v = 22.36 m/s

tan θ = v y /v x = 10/20 = ½ = 0.5

θ = tan -1 (0.5 ) = 26. 56 0 from the horizontal

(b) When the stone is dropped from the truck, the horizontal force on the stone is zero. The only acceleration of the stone is that due to gravity which is equal to 10 m/s 2 and it acts vertically downwards.

12. A bob of mass 0.1 kg hung from the ceiling of a room by a string 2 m long is set into oscillation. The speed of the bob at its mean position is 1 ms -1 . What is the trajectory of the bob if the string is cut when the bob is (a) at one of its extreme positions, (b) at its mean position?

(a) When the bob is at one of its extreme positions, the velocity is zero. So, if the string is cut the bob will fall vertically downward under the force of its weight F = mg.

(b) At its mean position the bob has a horizontal velocity. If the string is cut, the bob will behave like a projectile and will fall on the ground after taking a parabolic path.

13. A man of mass 70 kg, stands on a weighing machine in a lift, which is moving

(a) upwards with a uniform speed of 10 ms -1 .

(b) downwards with a uniform acceleration of 5 ms -2 .

What would be the readings on the scale in each case?

(d) What would be the reading if the lift mechanism failed and it hurtled down freely under gravity?

Mass of the man, m = 70 kg,

g = 10 m/s 2

The weighing machine in each case measures the reaction R, i.e., the apparent weight.

(a) When the lift moves upwards with a uniform speed of 10 m/s, it’s acceleration= 0.

R = mg = 70 x 10 = 700 N

(b) Lift moving downwards with a = 5 ms -2

Using Newton’s second law of motion, the equation of motion can be written as

R = m (g – a) = 70 (10 – 5) = 350 N

R = m (g + a) = 70 (10 + 5) = 1050 N

(d) If the lift were to come down freely under gravity, downward . a = g

:. R = m(g -a) = m(g – g) = 0

The man will be in a state of weightlessness

14. Figure shows the position-time graph of a particle of mass 4 kg. What is the (a) force on the particle for t < 0, t > 4 s, 0 < t < 4 s? (b) impulse at t = 0 and t = 4 s? (Consider one-dimensional motion only).

When t＜0, the distance covered by the particle is zero. Therefore, the force on the particle is zero.

When 0＜ t ＜4s, the particle is moving with a constant velocity. Therefore, the force will be zero.

When t＞4s, the particle remains at a constant distance. Therefore, the force of the particle will be zero.

Impulse at t = 0.

Here, u = 0

v = ¾ = 0.75 m/s

Impulse= total change in momentum = mv – mu = m (v – u)

= 4 (0 – 0.75) = -3 kg m/s

Impulse at t= 4s

u = 0.75 m/s, v = 0

Impulse = m (v – u) = 4 (0 – 0.75) = -3 kg m/s

15. Two bodies of masses 10 kg and 20 kg respectively kept on a smooth, horizontal surface are tied to the ends of a tight string. A horizontal force F = 600 N is applied to (i) A, (ii) B along the direction of string. What is the tension in the string in each case?

Mass of the body A, m 1 = 10 kg

Mass of the body B, m 2 = 20 kg

Horizontal force = 600 N

Total mass of the system, m = m 1 + m 2 = 30 kg

Applying Newton’s second law of motion, we have

a = F/m = 600/30 = 20 m/s 2

(i) When the force is applied on A (10 kg)

F – T = m 1 a

T = F – m 1 a

T = 600 – (10 x 20)

= 600 – 200 = 400 N

(ii) When the force is applied on B (20 kg)

F – T = m 2 a

T = F – m 2 a

= 600 – (20 x 20) = 200 N

16. Two masses 8 kg and 12 kg are connected at the two ends of a light inextensible string that goes over a frictionless pulley. Find the acceleration of the masses and the tension in the string when the masses are released.

Smaller mass, m 1 = 8 kg

Larger mass, m 2 = 12 kg

Tension in the string = T

The heavier mass m 2 will move downwards and the smaller mass m 1 will move upwards.

Applying Newton’s second law,

For mass m 1 :

T – m 1 g = m 1 a —– (1)

For mass m2:

m 2 g – T = m 2 a ——(2)

Add (1) and (2)

(m 2 – m 1 ) g = (m 1 + m 2 ) a

a = (m 2 – m 1 ) g/ (m 1 + m 2 )

=[ (12 – 8)/(12 + 8)] x 10 = (4 /20) x 10= 2m/s

Therefore, acceleration of the mass is 2 m/s 2

Substituting this value of acceleration in equation (ii) we get

m 2 g – T = m 2 a

= 2m 1 m 2 g/(m 1 + m 2 )

T = 2 x 12 x 8 x 10/ (12 + 8)

Therefore, the tension on the string is 96 N

17. A nucleus is at rest in the laboratory frame of reference. Show that if it disintegrates into two smaller nuclei, the products must move in opposite directions.

Let m 1 , m 2 be the masses of the two daughter nuclei and v 1 ,v 2 be their respective velocities of the daughter nuclei. Let m be the mass of the parent nucleus.

Total linear momentum after disintegration = m 1 v 1 +m 2 v 2 .

Before disintegration, the nucleus is at rest. Therefore, its linear momentum before disintegration is zero.

Applying the law of conservation of momentum,

Total linear momentum before disintegration = Total linear momentum after disintegration

0 = m 1 v 1 + m 2 v 2

v 1 =-m 2 v 2 /m 1

The negative sign indicates v 1 and v 2 are in opposite directions.

18. Two billiard balls, each of mass 0.05 kg, moving in opposite directions with speed 6 ms -1 collide and rebound with the same speed. What is the impulse imparted to each ball due to the other?

Mass of each ball = 0.05 kg

Initial velocity of each ball = 6 m/s

The initial momentum of each ball before the collision

= 0.05 x 6 = 0.3 kg m/s

After the collision, the balls change in the direction of motion without a change in the magnitude of the velocity

Final momentum after collision of the first ball = – 0.05 x 6 = – 0.3 kg m/s

Final momentum after collision of the second ball = 0.3 kg m/s

Impulse imparted to the first ball = (-0.3) – (0.3) = – 0.6 kg m/s

Impulse imparted to the second ball = (0.3) – (-0.3) = 0.6 kg m/s

The two impulses are opposite in direction.

19. A shell of mass 0.020 kg is fired by a gun of mass 100 kg. If the muzzle speed of the shell is 80 ms -1 .What is the recoil speed of the gun?

Mass of the shell, m = 0.020 kg

Mass of the gun, M = 100 Kg

Speed of the shell = 80 m/s

The initial velocity of the shell and the gun is zero. So, the initial momentum of the system is zero.

Applying the law of conservation of momentum, the initial momentum is equal to the final momentum.

0 = mv – MV

Recoil speed of the gun, v = mv/M

v = (0.020 x 80)/100

v = 0.016 m/s

20. A batsman deflects a ball by an angle of 45° without changing its initial speed which is equal to 54 km/h. What is the impulse imparted to the ball? (Mass of the ball is 0.15 kg.)

Velocity of the ball = 54 km/h

The ball is deflected back such that the total angle = 45 0

The initial momentum of the ball is mucosӨ = (0.15 x 54 x 1000 x cos 22. 5)/3600

= 0.15 x 15 x 0.9239 along NO

Final momentum of the ball = mucosӨ along ON

Impulse = change in the momentum = mucosӨ – (-mucosӨ) = 2mucosӨ = 2 x 0.15 x 15 x 0.9239 = 4.16 kg.m/s

21. A stone of mass 0.25 kg tied to the end of a string is whirled round in a circle of radius 1.5 m with a speed of 40 rev./min in a horizontal plane. What is the tension in the string? What is the maximum speed with which the stone can be whirled around if the string can withstand a maximum tension of 200 N?

Mass of the stone = 0.25 kg

Radius, r = 1.5 m

Number of revolution in a second, n= 40/60 = (⅔) rev/sec

The angular velocity, ω = 2πn = 2 x 3.14 x (⅔)

The tension on the string provides the necessary centripetal force

T = 0.25 x 1.5 x [2 x 3.14 x (⅔)] 2

Maximum tension on the string, T max = 200 N

T max = mv 2 max /r

v 2 max = (T max x r)/m

= ( 200 x 1.5)/0.25 = 1200

v max = 34. 6 m/s

Therefore, the maximum speed of the stone is 34.64 m/s

22. If in problem 21, the speed of the stone is increased beyond the maximum permissible value, and the string breaks suddenly, which of the following correctly describes the trajectory of the stone after the string breaks?

(a) the stone moves radially outwards

(b) the stone flies off tangentially from the instant the string breaks

Solution: (b)

At each point of the circular motion, the velocity will be tangential. If the string breaks suddenly the stone moves in the tangential direction according to Newton’s first law of motion.

23. Explain why

(a) a horse cannot pull a cart and run in empty space

(b) passengers are thrown forward from their seats when a speeding bus stops suddenly

(d) a cricketer moves his hands backwards while holding a catch

The horse pushes the ground with a certain force when it pulls the cart. By applying the third law of motion, the ground will exert an equal and opposite reaction force upon the feet of the horse. This causes the horse to move forward. In empty space, the horse will not experience a reaction force. Therefore, the horse cannot pull the cart in empty space.
Due to inertia of motion. When a bus stops all of a sudden, the lower part of a person’s body that is in contact with the seat comes to rest suddenly but the upper part will continue to be in motion. As a result, the person’s upper half of the body is thrown forward in the direction of the motion of the bus.
When the lawnmower is pulled, the vertical component of the applied force acts upwards. This reduces the effective weight of the lawnmower. When the lawn mower is pushed, the vertical component acts in the direction of the weight of the mower. Therefore, there is an increase in the weight of the mower. So, it is easier to pull a lawnmower than to push it.
When the batsman hits the ball, the ball will have a large momentum. When he moves his hands backwards the time of impact is increased contact, so the force is reduced.

24. Figure shows the position-time graph of a particle of mass 0.04 kg. Suggest a suitable physical context for this motion. What is the time between two consecutive impulses received by the particle? What is the magnitude of each impulse?

This graph could be of a ball rebounding between two walls separated by a distance of 2 cm. The ball rebounds between the walls every 2 seconds with a uniform velocity.

Velocity = displacement/ time = (2 x 10 -2 )/2 = 0.01 m/s

Initial momentum = mu = 0.04 x 0.01 = 4 x 10 -4 kgm/s

Final momentum = mv = 0.04 x (-0.01) = – 4 x 10 -4 kgm/s

Magnitude of impulse = Change in momentum

= (4 x 10 -4 )-(- 4 x 10 -4 ) = 8 x 10 -4 kgm/s

The time between two consecutive impulses is 2 sec, so the ball receives an impulse every 2 seconds.

25. Figure shows a man standing stationary with respect to a horizontal conveyor belt that is accelerating with 1 ms -2 . What is the net force on the man? If the coefficient of static friction, between the man’s shoes and the belt is 0.2, up to what acceleration of the belt can the man continue to be stationary relative to the belt? (Mass of the man = 65 kg.)

Here acceleration of conveyor belt a = 1 ms -2 ,

Coefficient of static friction, μ s = 0.2

mass of man, m = 65 kg

Net Force = ma = 65 x 1 = 65N

This net force is due to the friction between the belt and the man

Maximum static friction = μ s N

Beyond that, the man starts moving relative to the belt as per the pseudo force

At maximum static friction

μ s N = μ s .mg = ma max

a max = μs g = 0.2 x 10 = 2 m/s 2

26. A stone of mass m tied to the end of a string is revolving in a vertical circle of radius R. The net force at the lowest and highest points of the circle directed vertically downwards are: (choose the correct alternative).

T 1 and v 1 denote the tension and speed at the lowest point. T 2 and v 2 denote corresponding values at the highest point.

Solution: (a)

The net force at the lowest point is (mg – T 1 ) and the net force at the highest point is (mg + T 2 ). Therefore option (a) is correct.

Since mg and T 1 are in mutually opposite directions at the lowest point and mg and T 2 are in the same direction at the highest point.

27. A helicopter of mass 1000 kg rises with a vertical acceleration of 15 ms -2 . The crew and the passengers weigh 300 kg. Give the magnitude and direction of

(a) force on the floor by the crew and passengers

(b) the action of the rotor of the helicopter on surrounding air

Mass of helicopter = 1000 kg

Crew and passengers weight = 300 kg

Vertical acceleration, a = 15 ms -2 and g = 10 ms -2

The total mass of the system, m i = 1000 + 300 = 1300 Kg

(a) Force on the floor of the helicopter by the crew and passengers

R – mg = ma

= m (g + a) = 300 (10 + 15) N = 7500 N

(b) Action of the rotor of the helicopter on surrounding air is due to the mass of the helicopter and the passengers.

R’ – m i g = m i a

R’ = m i (g+a)

= 1300 x (10 + 15) = 32500 N

This force acts vertically downwards

(c) Force on the helicopter due to the surrounding air is the reaction of the force applied by the rotor on the air. As action and reaction are equal and opposite, therefore, the force of reaction, F = 32500 N. This force acts vertically upwards.

28. A stream of water flowing horizontally with a speed of 15 m/s pushes out of a tube of cross-sectional area 10 -2 m 2 and hits at a vertical wall nearby. What is the force exerted on the wall by the impact of water, assuming that it does not rebound?

Speed of water flowing, v= 15 m/s

Cross-sectional area of the tube, A= 10 -2 m 2

In one second, the distance travelled is equal to the velocity v

Density of water, ρ = 1000 kgm -3

Mass of water hitting the wall per second = ρ x A x v

= 1000 kgm -3 x 10 -2 m 2 x 15 m/s = 150 kg/s

Force exerted on the wall because of the impact of water = momentum loss of water per second

= Mass x velocity

= 150 kg/s x 15 m/s = 2250 N

29. Ten one rupee coins are put on top of one another on a table. Each coin has a mass of m kg. Give the magnitude and direction of

(a) the force on the 7th coin (counted from the bottom) due to all coins above it

(b) the force on the 7th coin by the eighth coin

(a) The force on the 7th coin is due to the weight of the three coins kept above it.

Weight of one coin is mg. So the weight of three coins is 3mg

Force exerted on the 7th coin is (3mg)N and the force acts vertically downwards.

(b) The eighth coin is already under the weight of two coins above it and it has its own weight too. Hence, the force on the 7th coin due to the 8th coin will be the same as the force on the 7th coin by the three coins above it.

Therefore, the force on the 7th coin by the 8th coin is (3mg)N and the force act vertically downwards.

The total downward force on the 6th coin is 4mg

Applying Newton’s third law of motion, the 6th coin will exert a reaction force upwards. Therefore, the force exerted by the 6th coin on the 7th coin is equal to 4mg and acts in the upward direction.

30. An aircraft executes a horizontal loop at a speed of 720 km/h with its wings banked at 15°. What is the radius of the loop?

The speed of the aircraft executing the horizontal loop = 720 km/h = 720 x (5/18) = 200 m/s

The angle of banking = 15°

tanθ= v 2 /rg , we have

r = v 2 /gtanθ = (200 x 200)/(10 x tan 15 0 ) = (200 x 200)/ (10 x 0.2679)= 14931 m

31. A train runs along an unbanked circular track of radius of 30 m at a speed of 54 km/h. The mass of the train is 10 6 kg. What provides the centripetal force required for this purpose the engine or the rails? What is the angle of banking required to prevent wearing out of the rail?

Radius of the track = 30 m

Velocity of the train = 54 km/h = 54 x (5/18) = 15 m/s

Mass of the train = 10 6 kg

The required centripetal force is provided by the force of lateral friction due to the rails on the wheels of the train

The angle of banking required to prevent wearing out of the rails

tanθ= v 2 /rg = (15 x 15)/ (30 x 10) = 0.75

θ = tan -1 (0.75) = 37 0

32. A block of mass 25 kg is raised by a 50 kg man in two different ways as shown in Fig. What is the action on the floor by the man in the two cases? If the floor yields to a normal force of 700 N, which mode should the man adopt to lift the block without the floor yielding?

Mass of the block = 25 kg

Mass of the man = 50 kg

Acceleration due to gravity = 10 m/s 2

Weight of the block, F = 25 x 10 = 250 N

Weight of the man, W = 50 x 10 = 500 N

In the 1st case, the man lifts the block directly by applying an upward force of 250 N (same as the weight of the block)

According to Newton’s third law of motion, there will be a downward reaction on the floor. The action on the floor by the man.

= 500 N + 250 N = 750 N.

In the 2nd case, the man applies a downward force of 25 kg wt. According to Newton’s third law of motion, the reaction is in the upward direction.

In this case, action on the floor by the man

= 500 N – 250 N= 250 N.

Therefore, the man should adopt the second method.

33. A monkey of mass 40 kg climbs on a rope (Fig.) which can stand a maximum tension of 600 N. In which of the following cases will the rope break, when the monkey

(a) climbs up with an acceleration of 6 ms -2

(b) climbs down with an acceleration of 4 ms -2

(d) falls down the rope nearly freely under gravity

(Ignore the mass of the rope).

Mass of the monkey = 40 kg

Maximum tension the rope can withstand, T max = 600 N

(a) When the monkey climbs up with an acceleration of 6m/s2,

Tension T – mg = ma

T = m (g+a)

T = 40 (10 + 6)

Since T > Tmax, the rope will break

(b) When the monkey climbs down with the acceleration of 4m/s 2

mg – T = ma

T = mg – ma = m (g – a)

= 40 (10 – 4) = 240 N

Since T ＜T max , the rope will not break

T – mg = ma

T – mg = 0

T = mg = 40 x 10 = 400 N

(d) When the monkey falls freely, the acceleration of the monkey will be equal to the acceleration due to gravity

The equation of motion is written as

mg + T = mg

T = m(g-g) = 0

34 . Two bodies A and B of masses 5 kg and 10 kg in contact with each other rest on a table against a rigid wall (Fig.). The coefficient of friction between the bodies and the table is 0.15. A force of 200 N is applied horizontally to A. What are (a) the reaction of the partition (b) the action-reaction forces between A and B? What happens when the wall is removed? Does the Solution to (b) change, when the bodies are in motion? Ignore the difference between μ s and μ k .

Mass of the body, m A = 5 Kg

Mass of the body, m B = 10 kg

Applied Force = 200 N

Coefficient of friction between the bodies and the table μ s = 0.15

(a) The force of friction is given by the relation:

f s = μ(m A + m B )g

= 0.15 (5 + 10) x 10

= 1.5 x 15 = 22.5 N, towards left

Therefore, the net force on the partition is 200 – 22.5 = 177. 5 N rightward

According to Newton’s third law, action and reaction are in the opposite direction

Therefore, the reaction of the partition will be 177.5 N, in the leftward direction

(b) Force of friction on mass A

F A = μm A g

= 0.15 x 5 x 10 = 7.5 N leftward

The net force exerted by mass A on mass B = 200 – 7.5 = 192.5 N rightwards

An equal amount of reaction force will be applied on mass A by B, i.e., 192.5 N acting leftward

When the wall is removed, the two bodies move in the direction of the applied force

The net force acting on the moving system = 177. 5 N

The equation of motion for the system of acceleration a, can be written as

Net force = (m A + m B ) a

a = Net force/ (m A + m B )

= 177.5/ (5 + 10) = 177. 5/15 = 11. 83 m/s 2

Net force causing mass A to move

F A = m A a = 5 x 11.83 = 59. 15 N

Net force exerted by the mass A on mass B= 192.5 – 59.15= 133. 35 N

This force acts in the direction of motion. As per Newton’s third law of motion, an equal amount of force will be exerted by mass B on mass A, i.e., 133.3N, acting opposite to the direction of motion.

35. A block of mass 15 kg is placed on a long trolley. The coefficient of static friction between the block and the trolley is 0.18. The trolley accelerates from rest with 0.5 ms -2 for 20 s and then moves with uniform velocity. Discuss the motion of the block as viewed by (a) a stationary observer on the ground (b) an observer moving with the trolley.

Mass of the block = 15 kg

Coefficient of static friction between the block and the trolley, p= 0.18

Acceleration of the trolley = 0.5 m/s 2

(a) Force experienced by block, F = ma = 15 x 0.5 = 7.5 N, this force acts in the direction of motion of the trolley

Force of friction, F f = p mg = 0.18 x 15 x 10 = 27 N

Force experienced by the block will be less than the friction. So the block will not move. So, for a stationary observer on the ground, the block will be stationary.

(b) The observer moving with the trolley has an accelerated motion. He forms a non-inertial frame in which Newton’s laws of motion are not applicable. The trolley will be at rest for the observer moving with the trolley

36. The rear side of a truck is open and a box of 40 kg mass is placed 5 m away from the open end as shown in Fig. The coefficient of friction between the box and the surface below it is 0.15. On a straight road, the truck starts from rest and accelerates with 2 ms -2 . At what distance from the starting point does the box fall off the truck? (Ignore the size of the box).

Force experienced by box, F = ma = 40 x 2 = 80 N

Frictional force F f = μmg = 0.15 x 40 x 10 = 60 N

Net force = F – F f = 80 – 60 = 20 N

Backward acceleration produced in the box, a =20/40(Net Force/m)

a = 0.5 ms -2

If t is time taken by the box to travel s =5 metre and fall off the truck then from

S = ut + 1/2 at 2 `

5 = 0 x t + (½) x 0.5 t 2

t= √(5×2/0.5) = 4.47 s`

If the truck travels a distance x during this time, then again from

S = ut + 1/2 at 2

x = 0 x 4.47 + (½) x 2(4.47) 2 = 19.98 m

37. A disc revolves with a speed of 33⅓ rpm and has a radius of 15 cm. Two coins are placed at 4 cm and 14 cm away from the centre of the record. If the coefficient of friction between the coins and record is 0.15, which of the coins will revolve with the record?

Speed of revolution of the disc = 33 ⅓ rpm= 100/3 rpm= 100/ (3 x 60) rps = 5/9 rps

ω = 2πv = 2 x (22/7)x (5/9) = 220/63 rad/s

The coins revolve with the disc, the centripetal force is provided by the frictional force mv 2 /r ≤ μmg ——–(1)

As v = rω, equation (1) becomes mrω 2 /r ≤ μmg

r ≤ μg/ω 2 = (0.15 x 10)/(220/63) 2 = 12 cm

For coin A, r = 4 cm

The condition (r≤ 12) is satisfied for coin placed at 4cm, so coin A will revolve with the disc

For coin B, r = 14 cm

The condition (r≤ 12) is not satisfied for the coin placed at 14cm, so coin B will not revolve with the disc.

38. You may have seen in a circus a motorcyclist driving in vertical loops inside a ‘death well’ (a hollow spherical chamber with holes, so the spectators can watch from outside). Explain clearly why the motorcyclist does not drop down when he is at the uppermost point, with no support from below. What is the minimum speed required at the uppermost position to perform a vertical loop if the radius of the chamber is 25 m?

When the motorcyclist is at the uppermost point of the death-well, the normal reaction R on the motorcyclist by the ceiling of the chamber acts downwards. His weight mg also acts downwards. The outward centrifugal force acting on the motorcyclist is balanced by these two forces.

R + mg = mv 2 /r ———(1)

Here, v is the velocity of the motorcyclist

m is the mass of the motorcyclist and the motorcycle

Because of the balance between the forces, the motorcyclist does not fall

The minimum speed required at the uppermost position to perform a vertical loop is given by the equation (1) when R = 0

mg = mv 2 min /r

V 2 min = gr

V min = √10 x 25 = 15.8 m/s

39. A 70 kg man stands in contact against the inner wall of a hollow cylindrical drum of radius 3 m rotating about its vertical axis with 200 rev/min. The coefficient of friction between the wall and his clothing is 0.15. What is the minimum rotational speed of the cylinder to enable the man to remain stuck to the wall (without falling) when the floor is suddenly removed?

Mass of the man, m = 70 kg

Radius of the drum, r = 3 m

Coefficient of friction between the wall and his clothing, μ = 0.15

Number of revolution of hollow cylindrical drum = 200 rev/min= 200/60 = 10/3 rev/s

The centripetal force required is provided by the normal N of the wall on the man

N = mv 2 /R = mω 2 R

When the floor revolves, the man sticks to the wall of the drum. Hence, the weight of the man (mg) acting downward is balanced by the frictional force acting vertically upwards.

The man will not fall if mg ≤ limiting frictional force f e (μN)

mg ≤ μ (mω 2 R)

Therefore, for minimum rotational speed of the cylinder

ω 2 = g/Rμ = 10/(0.15 x 3) = 22. 2

ω =√22.2 = 4.7 rad/s

40. A thin circular loop of radius R rotates about its vertical diameter with an angular frequency ω. Show that a small bead on the wire loop remains at its lowermost point for ω ≤ √g / R . What is the angle made by the radius vector joining the centre to the bead with the vertically downward direction for ω = √2g/ R? Neglect friction.

Let θ be the angle made by the radius vector joining the bead and the centre of the wire with the downward direction. Let, N be the normal reaction

mg = N cosθ —–(1)

mrω 2 = Nsinθ —– (2)

(or) m (Rsinθ) ω 2 = Nsinθ

Substituting the value of N in (1)

mg = mRω 2 cosθ

(or) cos θ = g/Rω 2 ———(3)

As l cosθ I ≤ 1 the bead will remain at the lowermost point

g/Rω 2 ≤ 1 or ω ≤ √g/R

For ω = √2g/ R , equation (3) becomes

cos θ = g/Rω 2

cos θ = (g/R) (R/2g) = ½

Chapter 5 Solutions for Class 11 Physics PDF given here has answers to the questions in the textbook, along with NCERT Exemplar Problems , Worksheets, Extra questions, Short answer questions MCQs, HOTS (High Order Thinking Skills) and Important questions.

Subtopics of Class 11 Physics Chapter 5 Laws of Motion

Some of the topics and subtopics covered in the NCERT Solutions for Class 11 Physics Chapter 5 are listed below.

Chapter 5 of Class 11 Physics is an important chapter in mechanics. Numericals on the conservation of momentum are frequently asked in the exams. If all three laws of motion are well understood, students will be able to relate these laws to day-to-day activities. An ample amount of everyday practice will help you in solving the numericals easily. While practising, one can refer to the NCERT Solutions for Class 11 Laws of Motion to cross-check the right answers.

BYJU’S provides advanced study materials, CBSE notes , videos and animation that help you to understand the topic thoroughly. Our interactive teaching method helps you to remember the topic for a significant period. This will help you to score good marks in the Class 11 examinations as well as in the entrance examinations.

Disclaimer –

Dropped Topics –

Frequently Asked Questions on NCERT Solutions for Class 11 Physics Chapter 5

Why should i refer to the ncert solutions for class 11 physics chapter 5 laws of motion, what are the concepts covered in chapter 5 of ncert solutions for class 11 physics, explain the topic of law of inertia using a monohybrid cross covered in chapter 5 of ncert solutions for class 11 physics., leave a comment cancel reply.

Your Mobile number and Email id will not be published. Required fields are marked *

Request OTP on Voice Call

Post My Comment

Register with BYJU'S & Download Free PDFs

CBSE Class 11 Physics Chapter 5 Laws of motion Study Materials

NCERT Solutions Class 11 All Subjects Sample Papers Past Years Papers

Laws of Motion : Notes and Study Materials -pdf

Concepts of Laws of Motion
Laws of Motion Master File
Laws of Motion Revision Notes
Laws of Motion MindMap
NCERT Solution Laws of Motion
NCERT Exemplar Solution Laws of Motion
Laws of Motion : Solved Example 1
Laws of Motion: Solved Example 2

Law of Motion Class 11 Notes Physics Chapter 5

• Dynamics is the branch of physics in which we study the motion of a body by taking into consideration the cause i.e., force which produces the motion. • Force Force is an external cause in the form of push or pull, which produces or tries to produce motion in a body at rest, or stops/tries to stop a moving body or changes/tries to change the direction of motion of the body. • The inherent property, with which a body resists any change in its state of motion is called inertia. Heavier the body, the inertia is more and lighter the body, lesser the inertia. • Law of inertia states that a body has the inability to change its state of rest or uniform motion (i.e., a motion with constant velocity) or direction of motion by itself. • Newton’s Laws of Motion Law 1. A body will remain at rest or continue to move with uniform velocity unless an external force is applied to it. First law of motion is also referred to as the ‘Law of inertia’. It defines inertia, force and inertial frame of reference. I here is always a need of ‘frame of reference’ to describe and understand the motion of particle, lhc simplest ‘frame of reference’ used are known as the inertial frames. A frame of referent, e is known as an inertial frame it, within it, all accelerations of any particle are caused by the action of ‘real forces’ on that particle. When we talk about accelerations produced by ‘fictitious’ or ‘pseudo’ forces, the frame of reference is a non-inertial one. Law 2. When an external force is applied to a body of constant mass the force produces an acceleration, which is directly proportional to the force and inversely proportional to the mass of the body. Law 3. “To every action there is equal and opposite reaction force”. When a body A exerts a force on another body B, B exerts an equal and opposite force on A. • Linear Momentum The linear momentum of a body is defined as the product of the mass of the body and its velocity. • Impulse Forces acting for short duration are called impulsive forces. Impulse is defined as the product of force and the small time interval for which it acts. It is given by Impulse of a force is a vector quantity and its SI unit is 1 Nm. — If force of an impulse is changing with time, then the impulse is measured by finding the area bound by force-time graph for that force. — Impulse of a force for a given time is equal to the total change in momentum of the body during the given time. Thus, we have • Law of Conservation of Momentum The total momentum of an isolated system of particles is conserved. In other words, when no external force is applied to the system, its total momentum remains constant. • Recoiling of a gun, flight of rockets and jet planes are some simple applications of the law of conservation of linear momentum. • Concurrent Forces and Equilibrium “A group of forces which are acting at one point are called concurrent forces.” Concurrent forces are said to be in equilibrium if there is no change in the position of rest or the state of uniform motion of the body on which these concurrent forces are acting. For concurrent forces to be in equilibrium, their resultant force must be zero. In case of three concurrent forces acting in a plane, the body will be in equilibrium if these three forces may be completely represented by three sides of a triangle taken in order. If number of concurrent forces is more than three, then these forces must be represented by sides of a closed polygon in order for equilibrium. • Commonly Used Forces (i) Weight of a body. It is the force with which earth attracts a body towards its centre. If M is mass of body and g is acceleration due to gravity, weight of the body is Mg in vertically downward direction. (ii) Normal Force. If two bodies are in contact a contact force arises, if the surface is smooth the direction of force is normal to the plane of contact. We call this force as Normal force. Example. Let us consider a book resting on the table. It is acted upon by its weight in vertically downward direction and is at rest. It means there is another force acting on the block in opposite direction, which balances its weight. This force is provided by the table and we call it as normal force. (iii) Tension in string. Suppose a block is hanging from a string. Weight of the block is acting vertically downward but it is not moving, hence its weight is balanced by a force due to string. This force is called ‘Tension in string’. Tension is a force in a stretched string. Its direction is taken along the string and away from the body under consideration. • Simple Pulley Consider two bodies of masses m 1 and m 2 tied at the ends of an in extensible string, which passes over a light and friction less pulley. Let m 1 > m 2 . The heavier body will move downwards and the lighter will move upwards. Let a be the common acceleration of the system of two bodies, which is given by • Apparent Weight and Actual Weight — ‘Apparent weight’ of a body is equal to its ‘actual weight’ if the body is either in a state of rest or in a state of uniform motion. — Apparent weight of a body for vertically upward accelerated motion is given as Apparent weight =Actual weight + Ma = M (g + a) — Apparent weight of a body for vertically downward accelerated motion is given as Apparent weight = Actual weight Ma = M (g – a). • Friction The opposition to any relative motion between two surfaces in contact is referred to as friction. It arises because of the ‘inter meshing’ of the surface irregularities of the two surfaces in contact. • Static and Dynamic (Kinetic) Friction The frictional forces between two surfaces in contact (i) before and (ii) after a relative motion between them has started, are referred to as static and dynamic friction respectively. Static friction is always a little more than dynamic friction. The magnitude of kinetic frictional force is also proportional to normal force. • Limiting Frictional Force This frictional force acts when body is about to move. This is the maximum frictional force that can exist at the contact surface. We calculate its value using laws of friction. Laws of Friction: (i) The magnitude of limiting frictional force is proportional to the normal force at the contact surface. (ii) The magnitude of limiting frictional force is independent of area of contact between the surfaces. • Coefficient of Friction The coefficient of friction (μ) between two surfaces is the ratio of their limiting frictional force to the normal force between them, i.e., • Angle of Friction It is the angle which the resultant of the force of limiting friction F and the normal reaction R makes with the direction of the normal reaction. If θ is the angle of friction, we have • Angle of Repose Angle of repose (α) is the angle of an inclined plane with the horizontal at which a body placed over it just begins to slide down without any acceleration. Angle of repose is given by α = tan-1 (μ) • Motion on a Rough Inclined Plane Suppose a motion up the plane takes place under the action of pull P acting parallel to the plane. • Centripetal Force Centripetal force is the force required to move a body uniformly in a circle. This force acts along the radius and towards the centre of the circle. It is given by where, v is the linear velocity, r is the radius of circular path and ω is the angular velocity of the body. • Centrifugal Force Centrifugal force is a force that arises when a body is moving actually along a circular path, by virtue of tendency of the body to regain its natural straight line path. The magnitude of centrifugal force is same as that of centripetal force. • Motion in a Vertical Circle The motion of a particle in a horizontal circle is different from the motion in vertical circle. In horizontal circle, the motion is not effected by the acceleration due to gravity (g) whereas in the motion of vertical circle, the motion is not effected by the acceleration due to gravity (g) whereas in the motion of vertical circle, the value of ‘g’ plays an important role, the motion in this case does not remain uniform. When the particle move up from its lowest position P, its speed continuously decreases till it reaches the highest point of its circular path. This is due to the work done against the force of gravity. When the particle moves down the circle, its speed would keep on increasing. Let us consider a particle moving in a circular vertical path of radius V and centre o tide with a string. L be the instantaneous position of the particle such that Here the following forces act on the particle of mass ‘m’. (i) Its weight = mg (verticaly downwards). (ii) The tension in the string T along LO. We can take the horizontal direction at the lowest point ‘p’ as the position of zero gravitational potential energy. Now as per the principle of conservation of energy, From this relation, we can calculate the tension in the string at the lowest point P, mid-way point and at the highest position of the moving particle. Case (i) : At the lowest point P, θ = 0° When the particle completes its motion along the vertical circle, it is referred to as “Looping the Loop” for this the minimum speed at the lowest position must be √5gr • IMPORTANT TABLES

CBSE Class 11 Physics Chapter-5 Important Questions

1 Marks Questions

1.What is the unit of coefficient of friction?

Ans: It has no unit.

2.Name the factor on which coefficient of friction depends?

Ans: Coefficient of friction depends on the nature of surfaces in contact and nature of motion.

3.What provides the centripetal force to a car taking a turn on a level road?

Ans: Centripetal force is provided by the force of friction between the tyres and the road.

4.Why is it desired to hold a gun tight to one’s shoulder when it is being fired?

Ans: Since the gun recoils after firing so it must be held lightly against the shoulder because gun and the shoulder constitute one system of greater mass so the back kick will be less.

5.Why does a swimmer push the water backwards?

Ans: A swimmer pushes the water backwards because due to reaction of water he is able to swim in the forward direction

6.Friction is a self adjusting force. Justify.

Ans: Friction is a self adjusting force as its value varies from zero to the maximum value to limiting friction.

7.A thief jumps from the roof of a house with a box of weight W on his head. What will be the weight of the box as experienced by the thief during jump?

Ans: Weight of the box W = m (g – a) = m (g – g) = 0.

8.Which of the following is scalar quantity? Inertia, force and linear momentum.

Ans: Inertia and linear momentum is measured by mass of the body and is a vector quantity and mass is a scalar quantity.

9.Action and reaction forces do not balance each other. Why?

Ans: Action and reaction do not balance each other because a force of action and reaction acts always on two different bodies.

10.If force is acting on a moving body perpendicular to the direction of motion, then what will be its effect on the speed and direction of the body?

Ans: No change in speed, but there can be change in the direction of motion.

11.The two ends of spring – balance are pulled each by a force of 10kg.wt. What will be the reading of the balance?

Ans: The reading of the balance will be 10kgwt.

12.A lift is accelerated upward. Will the apparent weight of a person inside the lift increase, decrease or remain the same relative to its real weight? If the lift is going with uniform speed, then?

Ans: The apparent weight will increase. If the lift is going with uniform speed, then the apparent weight will remain the same as the real weight.

14. If, in Exercise 5.21, the speed of the stone is increased beyond the maximum permissible value, and the string breaks suddenly, which of the following correctly describes the trajectory of the stone after the string breaks:

(a) the stone moves radially outwards,

(b) the stone flies off tangentially from the instant the string breaks,

Ans.(b) When the string breaks, the stone will move in the direction of the velocity at that instant. According to the first law of motion, the direction of velocity vector is tangential to the path of the stone at that instant. Hence, the stone will fly off tangentially from the instant the string breaks.

2 Marks Questions

1.Give the magnitude and direction of the net force acting on

(a) A drop of rain falling down with constant speed.

(b) A kite skillfully held stationary in the sky.

Ans: (1) According to first law of motion F = 0 as a = 0 (particle moves with constant speed)

(2) Since kite is stationary net force on the kite is also zero.

4.A force is being applied on a body but it causes no acceleration. What possibilities may be considered to explain the observation?

Ans: (1) If the force is deforming force then it does not produce acceleration.

(2) The force is internal force which cannot cause acceleration.

5.Force of 16N and 12N are acting on a mass of 200kg in mutually perpendicular directions. Find the magnitude of the acceleration produced?

6.An elevator weighs 3000kg. What is its acceleration when the in the tension supporting cable is 33000N. Given that g = 9.8m/s 2 .

Ans: Net upward force on the

ElevatorF = T – mg

7.Write two consequences of Newton’s second law of motion?

Ans: (1) It shows that the motion is accelerated only when force is applied.

(2) It gives us the concept of inertial mass of a body.

8.A bird is sitting on the floor of a wire cage and the cage is in the hand of a boy. The bird starts flying in the cage. Will the boy experience any change in the weight of the cage?

Ans: When the bird starts flying inside the cage the weight of bird is no more experienced as air inside is in free contact with atmospheric air hence the cage will appear lighter.

9.Why does a cyclist lean to one side, while going along curve? In what direction does he lean?

Ans: A cyclist leans while going along curve because a component of normal reaction of the ground provides him the centripetal force he requires for turning.

He has to lean inwards from his vertical position i.e. towards the centre of the circular path.

10.How does banking of roads reduce wear and tear of the tyres?

Ans: When a curved road is unbanked force of friction between the tyres and the road provides the necessary centripetal force. Friction has to be increased which will cause wear and tear. But when the curved road is banked, a component of normal reaction of the ground provides the necessary centripetal force which reduces the wear and tear of the tyres.

12.A soda water bottle is falling freely. Will the bubbles of the gas rise in the water of the bottle?

Ans: bubbles will not rise in water because water in freely falling bottle is in the state of weight – lessens hence no up thrust force acts on the bubbles.

13.Two billiard balls each of mass 0.05kg moving in opposite directions with speed 6m/s collide and rebound with the same speed. What is the impulse imparted to each ball due to other.

Ans: Initial momentum to the ball A = 0.05(6) = 0.3 kg m/s

As the speed is reversed on collision,

final momentum of ball A = 0.05(-6) = -0.3 kg m/s

Impulse imparted to ball A = change in momentum of ball A = final momentum – initial momentum = -0.3 -0.3 = -0.6 kg m/s.

15.Explain why passengers are thrown forward form their seats when a speeding bus stops suddenly.

Ans: When the speeding bus stops suddenly, lower part of the body in contact with the seat comes to rest but the upper part of the body of the passengers tends to maintain its uniform motion. Hence the passengers are thrown forward.

Talk to our experts

1800-120-456-456

Laws of Motion Class 11 Notes CBSE Physics Chapter 4 (Free PDF Download)

Revision Notes for CBSE Class 11 Physics Chapter 4 (Laws of Motion) - Free PDF Download

If students need reference by their side for exams, they must prefer Chapter 4 physics Class 11 notes. This chapter deals with Newton’s laws of motion and its real-time application. Students are provided with proper formulas that they can directly apply to solve their queries during exams. According to the CBSE board examination pattern, students should prepare well from notes readily available on Vedantu. These Newton’s laws of motion are thoroughly understood with notes of Physics Class 11 Chapter 4. These are highly helpful if it is about solving complex problems at different levels.

Download CBSE Class 11 Physics Revision Notes 2024-25 PDF

Also, check CBSE Class 11 Physics revision notes for other chapters:

Laws of Motion Chapter-Related Important Study Materials It is a curated compilation of relevant online resources that complement and expand upon the content covered in a specific chapter. Explore these links to access additional readings, explanatory videos, practice exercises, and other valuable materials that enhance your understanding of the chapter's subject matter.

Laws of Motion Class 11 Notes Physics - Basic Subjective Questions

Section-A (1 Mark Questions)

1. Name the factor on which coefficient of friction depends?

Ans. The coefficient of friction will mainly depend upon two factors, they are as following:

1. The materials of the surfaces in contact.

2. The characteristics of the surfaces.

2. What provides the centripetal force to a car taking a turn on a level road?

Ans. The frictional force between the tyres and the road provides centripetal force.

3. Why is it desired to hold a gun tight to one's shoulder when it is being fired?

Ans. As the gun recoils after shooting, it must be held softly on the shoulder. Here the gun and the shoulder are one mass system, due to this the back kick will be reduced. A gunman must keep his weapon securely against his shoulder when shooting.

4. Why does a swimmer push the water backwards?

Ans. From the Newton's 3rd laws of motion, we know that "when one body exerts a force on the other body, the first body experiences a force equivalent in magnitude in the opposite direction of the force exerted". As a result, in order to swim ahead, the swimmer pushes water backward with his hands.

5. Friction is a self-adjusting force. Justify.

Ans. Friction is a self-adjusting force that changes in magnitude from zero to maximum to limit friction.

6. A thief jumps from the roof of a house with a box of weight W on his head. What will be the weight of the box as experienced by the thief during jump?

Ans. The thief is in free fall during the jump. Both he/she and the box will be weightless during that time. So, the weight of the box experience by the thief during the jump will be zero. So, mathematically it can be written as: Weight of the box, W=m(g-a)=m(g-g)=0.

7. Action and reaction forces do not balance each other. Why?

Ans. Because a force of action and response always operates on two separate bodies, action and reaction do not balance each other.

8. If force is acting on a moving body perpendicular to the direction of motion, then what will be its effect on the speed and direction of the body?

Ans. When a force acts in a perpendicular direction on a moving body, the work done by the force is zero. Since W = F.S cosθ, where S = 90° and cos90° = 0, therefore W = 0.

As a result, the magnitude of the body's velocity (or speed) will remain unchanged. The direction of motion of the body, however, will be altered.

9. The two ends of spring - balance are pulled each by a force of 10kg.wt. What will be the reading of the balance?

Ans. As the spring balancing is based on the tension in the spring, it reads weight. Now, if both ends are pulled by a 10kg weight, the tension is 10kg , and the reading will be 10kg .

10. A lift is accelerated upward. Will the apparent weight of a person inside the lift increase, decrease or remain the same relative to its real weight? If the lift is going with uniform speed, then?

Ans. There will be an increase in perceived weight. The apparent weight will stay the same as the true weight, if the lift moves at a constant pace.

Section-B (2 Marks Questions)

11. Give the magnitude and direction of the net force acting on

(a) A drop of rain falling down with constant speed.

(b) A kite skillfully held stationary in the sky.

Ans.

(a) As the raindrop is falling with a constant speed, so its acceleration a will be 0. As the force acting on a particle is given by F = ma, so the net force acting on the rain drop will be 0.

(b) As the kite is held stationary, so by Newton's first laws of motion, the algebraic sum of forces acting on the kite is zero.

12. Two blocks of masses m 1 , m 2 are connected by light spring on a smooth horizontal surface. The two masses are pulled apart and then released. Prove that the ratio of their acceleration is inversely proportional to their masses.

Ans. Due to inertia, the mass of the two bodies tries to expand, and the acceleration will act in the opposite direction as it shrinks. So let us assume that the F 1 and F 2 be the forces acting in opposite directions due to masses m 1 and m 2 .

Thus $F_{1}+F_{2}=0$

$m_{1}+a_{2}=m_{2}a_{2}=0$

$m_{1}+a_{1}=m_{2}a_{2}=0$

$m_{1}+a_{1}=m_{2}a_{2}$

$\dfrac{a_{1}}{a_{2}}=-\dfrac{m_{1}}{m_{2}}$

Hence the above is proved.

13. Force of 16 N and 12 N are acting on a mass of 200 kg in mutually perpendicular directions. Find the magnitude of the acceleration produced?

Ans. In the given question, we have the force of 16 N and 12 N given and they are acting on a mass of 200 kg in mutually perpendicular directions. We need to find the magnitude of the acceleration produced.

$F=\sqrt{F_{1}^{2}+F_{2}^{2}+2F_{1}F_{2}\;cos\theta }$

Since, the forces are in mutually perpendicular directions. Therefore, (θ = 90°). Hence, the force will become:

$F=\sqrt{F_{1}^{2}+F_{2}^{2}}$

Now substituting the values, we get

$F=\left ( \sqrt{(16)^{2}+(12)^{2}} \right )$

=20 N

Hence, the magnitude of the acceleration will be:

$a=\dfrac{F}{m}$

$=\dfrac{20}{200}$

$=0\cdot 1ms^{-2}$

14. An elevator weighs 3000 kg. What is its acceleration when the tension supporting cable is 33000 N. Given that g = 9.8 ms −2 .

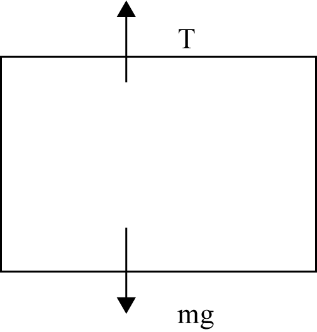
Ans. From the question, we have an elevator having the weighs given as 3000 kg. We need to find the acceleration, if the tension in the supporting cable is given as 33000 N.

Net upward force on the Elevator F is equal to $=T-ms(\vec{}F=ma)$

$\Rightarrow ma=T-mg$

$\Rightarrow T=m(a+g)$

$\Rightarrow T=33000N=3000(a+9\cdot 8)$

$a=\dfrac{33000-3000\times 9\cdot 8}{3000}$

$=1\cdot 2ms^{-2}$

15. How does banking of roads reduce wear and tear of the tyres?

Ans. When a curving road is unbanked, the centripetal force is provided by friction between the tyres and the road. Friction must be increased, resulting in wear and tear. When the curving road is banked, however, a component of the ground's natural response supplies the necessary centripetal force, reducing tyre wear and tear.

16. Two billiard balls each of mass 0.05 kg moving in opposite directions with speed 6 ms-1collide and rebound with the same speed. What is the impulse imparted to each ball due to the other?

Ans. As from the question, we have the mass of each ball given as 0.05 kg

Initial velocity of each ball will be = 6 ms -1

Magnitude of the initial momentum of each ball given as, p i = 0.3 kg ms -1

The balls alter their directions of motion after colliding, but their velocity magnitudes do not change. Final momentum of each ball given as, $p_{f}=-0\cdot 3kg\;ms^{-1}$

Each ball's impulse equals a change in the system's momentum.

$=p_{f}-p_{i}$

$=0\cdot 3-0\cdot 3=-0\cdot 6\;kg\;ms^{-1}$

The negative indication implies that the balls are receiving opposite-direction shocks.

PDF Summary - Class 11 Physics Laws of Motion Notes (Chapter 4)

A force is something that causes a body's rest or motion to alter. An interaction between two bodies is also referred to as force. Two bodies exert forces on each other even if they are not physically in contact, e.g., the electrostatic force between two charges or gravitational force between any two bodies.

It is a vector quantity having SI unit Newton (N) and dimension \[\left[ {ML{T^{--2}}} \right]\] .

Superposition of Force: When many forces are acting on a body then their resultant is obtained by the laws of vector addition:

$\overrightarrow {{F_{res.}}} = \overrightarrow {{F_1}} + \overrightarrow {{F_2}} + \overrightarrow {{F_3}} .............. + \overrightarrow {{F_n}}$

$\overrightarrow {{F_{res.}}} = \sqrt {{{\overrightarrow {{F_1}} }^2} + {{\overrightarrow {{F_2}} }^2} + 2{{\overrightarrow {{F_1}} }^{}}\overrightarrow {{F_2}} \cos {\theta ^{}}} $

$\tan \alpha = \dfrac{{{F_2}\sin \theta }}{{{F_1} + {F_2}\cos \theta }}$

The resultant of the two forces \[\overrightarrow {{F_1}} \] and \[\overrightarrow {{F_2}} \] acting at angle \[\theta \] is given by: \[\overrightarrow {{F_{res.}}} = \sqrt {{{\overrightarrow {{F_1}} }^2} + {{\overrightarrow {{F_2}} }^2} + 2{{\overrightarrow {{F_1}} }^{}}\overrightarrow {{F_2}} \cos {\theta ^{}}} \]

The resultant force is directed at an angle α with respect to force F1 where:

\[\tan \alpha = \dfrac{{{F_2}\sin \theta }}{{{F_1} + {F_2}\cos \theta }}\]

Lami’s Theorem:

If three forces F 1 , F 2 and F 3 are acting simultaneously on a body and the body is in equilibrium, then according to Lami’s theorem:

\[\dfrac{{{{\text{F}}_1}}}{{\sin (\pi - \alpha )}} = \dfrac{{{{\text{F}}_2}}}{{\sin (\pi - \beta )}} = \dfrac{{{{\text{F}}_3}}}{{\sin (\pi - \gamma )}}\] where α , β & γ are the angles opposite to the forces F 1 , F 2 & F 3 respectively.

(Image will be uploaded soon)

Basic Forces:

There are basically four types of forces: Weight, Contact force, Tension and Spring Force.

Weight: It is the force with which earth attracts a body toward itself. It is also called the gravitational force.

Contact Force: When two bodies come in contact, they exert forces on each other that are called contact forces.

Normal Force (N) : This is the contact force component that is normal to the surface. It determines how tightly two surfaces are forced together.

Frictional Force (f) : It is the component of contact force parallel to the surface. It opposes the relative motion (or attempted motion) of the two in contact surfaces.

Tension: It refers to the force exerted by the end of a taut string, rope, or chain. The direction of strain is pulling the body, whereas the natural reaction is pushing it.

Spring Force: It is the resists to change its length; the more you alter its length the harder it resists. The force exerted by a spring is given by \[F{\text{ }} = {\text{ }}--k.x\] , where x is the change in length and k is the spring constant (unit Nm -1 )

Newton's Laws of Motion:

Newton's first laws:.

If a body is at rest or in motion in a straight line, it will remain at rest or in motion unless it is acted by any external force. This is known as Law of Inertia or First laws of Newton

Inertia is the property of the inability of a body to change its position of rest or uniform motion in a straight line unless some external force acts on it.

Newton’s first laws is valid only in a frame of reference of the inertial frame, i.e., if a frame of reference is at rest or in uniform motion it is called inertial, otherwise non-inertial.

Newton's Second Laws:

According to second laws, rate of change of momentum of a body is proportional to the resultant force acting on the body, i.e.,

$F \propto \dfrac{{dp}}{{dt}}$ or $F \propto ma$

$\Rightarrow \dfrac{{dp}}{{dt}} = m\dfrac{{dv}}{{dt}}$ .

The applied resultant force causes a change in momentum in the direction of the applied resultant force is a measure of the total amount of motion in the body.

\[\vec F=\dfrac {d{\vec v}}{dt}\]

\[\Rightarrow m {\vec a}=\dfrac {{\vec P_2}-{\vec P_1}}{t}\]

The external force acting on a body can accelerate it, either by changing the magnitude of velocity or direction of velocity or both.

Special Cases:

Case 1:

If the force is parallel or antiparallel to the motion of the body, then it changes only the magnitude of $\overrightarrow v $ but not the direction. Therefore, the path will be a straight line.

If the force is acting perpendicular to the motion of body, it changes only the direction but not the magnitude of $\overrightarrow v $ . Therefore, the path will be Circular.

If the force acts at an angle θ to the motion of a body, it changes both the magnitude and direction of $\overrightarrow v $ . In this case the path of the body may be elliptical, non-uniform circular, parabolic or hyperbolic.

Newtons Third Laws:

According to this laws, for every action, there is an equal and opposite reaction. E.g. when two bodies A and B exerts a force on each other i.e. ${F_A}$ & ${F_B}$ . Then the force exerted by any of the bodies will be the same as the force exerted by another body but in opposite direction. \[{{\text{F}}_{{\text{AB}}}} = - {{\text{F}}_{{\text{BA}}}}\]

The two forces involved in any interaction between two bodies are called action and reaction.

Linear Momentum:

It is defined as the product of the mass of the body and its velocity i.e.

Linear momentum = \[mass\:\times\:velocity\]

If a body of mass $m$ is moving with a velocity $v$ , its linear momentum $\overrightarrow P $ is given by:

\[\overrightarrow P = m\overrightarrow v \]

It is a vector quantity and its direction is the same as the direction of the velocity of the body.

SI unit of linear momentum is \[kg{\text{ }}m{s^{--1}}\] and the cgs unit of linear momentum is \[g{\text{ }}cm{\text{ }}{s^{--1}}\] .

The entire change in linear momentum is used to calculate the force's impulse, which is the product of the average force during impact and the duration of the impact created during the collision.

The force which acts on bodies for short time are called impulsive forces. E.g. hitting a ball with a bat, firing a bullet with a gun etc.

An impulsive force does not remain constant instead, it varies from zero to maximum and then back to zero. Therefore, it is not possible to measure easily the value of impulsive force because it changes with time.

\[{\vec I} = {\vec F_{av}} \times {\text{t}} = {\vec p_2} -{\vec p_1}\]

Apparent Weight on a Body in a Lift

(a) When the lift is at rest, i.e. a=0:

\[mg - R = 0\]

\[\Rightarrow mg = R\]

\[R = mg(1 - \dfrac{a}{g})\]

\[{W_{app.}} = {W_o}(1 - \dfrac{a}{g})\]

\[R + mg - mg = 0\]

\[{F_{AB}}\times \Delta t = {f_{ms}} = {\mu _s}R\]

\[\angle AOC = \theta\]

\[{W_{app.}} = {W_o}\]

(b) When the lift moves upwards with an acceleration a:

\[R - mg - ma = 0\]

\[\Rightarrow R = m(g + a)\]

\[\Rightarrow R = mg(1 + \dfrac{a}{g})\]

\[{\therefore W_{app}} = {W_o}{\left ( 1 + \dfrac{a}{g} \right )}\]

\[R + ma - mg = 0\]

\[\Rightarrow R = mg(1 - \dfrac{a}{g})\]

\[\therefore {W_{app}} = {W_o}(1 - \dfrac{a}{g})\]

(d) When the lift falls freely, i.e., a = g :

\[\Rightarrow R\;=\;0\]

\[\therefore {W_{app}}\;=\;0\]

Principle of Conservation of Linear Momentum-

According to this principle, in an isolated system, the vector sum of all the system's linear momenta is conserved and is unaffected by their interactions reciprocal action and response.

Mutual forces between pairs of particles in an isolated system (i.e., a system with no external force) can thus produce changes in the linear momentum of individual particles. The linear momentum changes cancel in pairs, and the overall linear momentum remains unaltered because the mutual forces for each pair are equal and opposing. As a result, an isolated system of interacting particles' total linear momentum is conserved. This principle is a direct result of Newton's second and third laws of motion.

Consider an isolated system that consists of two bodies A and B with initial linear momenta \[{P_A}\] and \[{P_B}\] . Allow them to collide for a short time t before separating with linear momenta \[{P_{A}}'\] and \[{P_{B}}'\] , respectively.

If \[{F_AB}\] is force on A exerted by B, and \[{F_{BA}}\] is force on B exerted by A, then according to second law of newton:

\[{F_{AB}}\times \Delta t = \] Change in linear momentum of A = \[{\vec P_{A}}' - {\vec P_A}\]

\[{F_{BA}} \times \Delta t = \] Change in linear momentum of B= \[{\vec P_{B}}' - {\vec P_B}\]

Now, according to third law of newton:

\[\Rightarrow {{\text{F}}_{{\text{AB}}}} = - {{\text{F}}_{{\text{BA}}}}\]

\[\therefore\:from\:equations\:we\:get\:\]

\[\Rightarrow {{\vec P_{A}}'-{\vec P_A}}\:=\:{{\vec P_{B}}'-{\vec P_B}}\]

\[\Rightarrow {{\vec P_{A}}'+{{\vec P_B}}'}={{\vec P_{A}}+{\vec P_{B}}}\]

which shows that the total final linear momentum of the isolated system is equal to its total initial linear momentum. This proves the principle of conservation of linear momentum.

Friction is an opposing force that comes into play when one body actually moves (slides or rolls) or even tries to move over the surface of another body.

It is the force that comes into play when two surfaces come into contact with each other and oppose their relative motion.

I Frictional force is unaffected by the contact area. Because with an increase in the area of contact, the force of adhesion also increases.

When the surfaces in contact are extra smooth, the distance between the molecules of the surfaces in contact decreases, increasing the adhesive force between them. Therefore, the adhesive pressure increases, and so does the force of friction.

Types of Friction:

There are 3 types of friction: Static, Limiting and Kinetic Friction.

Static Friction- The opposing force that comes into play when one body tends to move over the surface of another body, but the actual motion has yet not started is called Static friction.

Limiting Friction - Limiting friction is the maximum opposing force that comes into play when one body is just on the verge of moving over the surface of the other body.

Kinetic Friction - Kinetic friction or dynamic friction is the opposing force that comes into play when one body is actually moving over the surface of another body.

Laws of Limiting Friction:

(i) Friction always works in the opposite direction of relative motion, making it a perverse force.

(ii) The maximum static friction force, fms (also known as limiting friction), is proportional to the normal reaction (R) between the two in contact surfaces i.e.

\[{f_{ms}} \propto R\]

(iii) The limiting friction force is tangential to the interface between the two surfaces and is determined by the kind and state of polish of the two surfaces in contact.

(iv) As long as the normal reaction stays constant, the limiting friction force is independent of the area of the surfaces in contact.

Coefficient of Static Friction:

We know that,

\[\Rightarrow {f_{ms}} = {\mu _s}R\]

Here, \[{\mu _s}\] is a constant of proportionality and is called the coefficient of static friction and its value depends upon the nature of the surfaces in contact and is usually less than unity i.e. 1 but never 0.

Since the force of static friction (f S ) can have any value from zero to maximum ( \[{f_{ms}}\] ), i.e. \[{f_s} \leqslant {f_{ms}}\] ,

Kinetic Friction :

The laws of kinetic friction are exactly the same as those for static friction. Accordingly, the force of kinetic friction is also directly proportional to the normal reaction:

\[{f_k} \propto R\]

\[\Rightarrow {f_k} = {\mu _k}R\]

Rolling Friction:

The opposing force that comes into play when a body rolls over the surface of another body is called rolling friction.

Friction caused by rolling. Consider a wheel that is rolling down a street. As the wheel travels down the road, it presses against the road's surface and is compressed slightly as shown in Fig. :

Angle of Friction:

The angle of friction between any two surfaces in contact is defined as the angle formed by the resultant of the limiting friction force F and the normal reaction direction R. It is represented by θ.

In the given fig. OA represents the normal reaction R that balances the weight mg of the body. OB represent F, the limiting force of sliding friction, when the body tends to move to the right. Complete the parallelogram OACB. Join OC. This represents the resultant of R and F. By definition, \[\angle AOC = \theta \] is the angle of friction between the two bodies in contact.

The angle of friction is determined by the nature of the materials used on the surfaces in contact as well as the nature of the surfaces themselves.

Relation Between 𝛍 and 𝛉:

In $\Delta AOC$ , $\tan \theta = \dfrac{{AC}}{{OA}} = \dfrac{{OB}}{{OA}} = \mu $$\tan \theta = \dfrac{{AC}}{{OA}} = \dfrac{{OB}}{{OA}} = \mu $

Hence, $\mu = \tan \theta $ ... (6)

(i.e.\[\mu\] is the coefficient of limiting friction )

Angle of Repose or Angle of Sliding:

The minimum angle of inclination of a plane with the horizontal at which a body placed on the plane begins to slide down is known as the angle of repose or angle of sliding.

Represented by α. Its value depends on the material and nature of the surfaces in contact.

In fig., AB is an inclined plane such that a body placed on it just begins to slide down. \[\angle BAC\:\alpha\] = angle of repose.

The various forces involved are :

weight, mg of the body,

normal reaction, R,

Force of friction F,

Now, mg can be resolved into two rectangular components: mg cosα opposite to R and mg sinα opposite to F:

$F = mg\sin \alpha $ ... (7)

$R = mg\cos \alpha $ ... (8)

Diving these two eq. we get:

$\tan \alpha = \dfrac{F}{R}$

$\Rightarrow \tan \alpha = \mu $ ... (9)

Hence coefficient of limiting friction between any two surfaces in contact is equal to the tangent of the angle of repose between them.

From (6) and (9): $\mu = \tan \alpha = \tan \theta $

Therefore $\alpha = \theta $

i.e. (Angle of friction = Angle of repose)

Methods of Changing Friction:

Some of the ways of reducing friction are:

By polishing.

By lubrication.

By proper selection of materials.

By Streamlining.

By using ball bearings.

Dynamics of Uniform Circular Motion Concept of Centripetal Force:

The force required to move a body uniformly in a circle is known as centripetal force. This force acts along the circle's radius and towards the centre.

When a body moves in a circle, the direction of motion at any given time is along the tangent to the circle. According to Newton’s first law of motion, a body cannot change its direction of motion by itself an external force is needed. This external force is called the centripetal force.

An expression for centripetal force is:

\[F = m{v^2}/r = m{\omega ^2}r\]

\[R{\text{ }}--{\text{ }}mg{\text{ }} = {\text{ }}0{\text{ }}or{\text{ }}R{\text{ }} = {\text{ }}mg \]

\[F{\text{ }} = {\text{ }}{\mu _s}{\text{ }}R{\text{ }} = {\text{ }}{\mu _s}{\text{ }}mg{\text{ }} \]

\[R{\text{ }}cos\theta = {\text{ }}mg{\text{ }} + {\text{ }}F{\text{ }}sin\theta \]

\[From\:{\text{ }}\left( 3 \right),{\text{ }}R{\text{ }}\left( {cos\theta --{\text{ }}{\mu _s}{\text{ }}sin\theta } \right){\text{ }} = {\text{ }}mg \]

On account of a continuous change in the direction of motion of the body, there is a change in velocity of the body, and hence it undergoes an acceleration, called centripetal acceleration or radial acceleration.

Centrifugal Force:

Centrifugal force is a force that arises when a body is moving actually along a circular path, by virtue of the tendency of the body to regain its natural straight-line path.

When a body is moving in a straight line centripetal force is applied on the body, it is forced to move along a circle. The body has a natural inclination to return to its normal straight-line course while moving in a circle. This tendency gives rise to a force called centrifugal force.

The magnitude of centrifugal force = $m{v^2}/r$ , which is the same as that of centripetal force, but opposite in direction i.e. The centrifugal force acts along the circle's radius, away from the centre.

Note : Centripetal and Centrifugal forces, being the forces of action and reaction act always on different bodies. E.g. when a piece of stone tied to one end of a string is rotated in a circle, centripetal force F1 is applied on the stone by the hand. Due to the stone's desire to revert to its natural straight line route, centrifugal force F2 acts on it, pulling the hand outwards.. The centripetal and centrifugal forces are shown in Fig. :

Rounding A-Level Curved Road:

When a vehicle goes around a curved road, it requires some centripetal force. The vehicle's wheels have a tendency to depart the curved path and return to the straight-line path as it rounds the curve. Force of friction between the wheels and the road opposes this tendency of the wheels. This force (friction) therefore, acts, towards the centre of the circular track and provides the necessary centripetal force.

Three forces are acting on the car, fig.

The weight of the car, mg, acting vertically downwards,

Normal reaction R of the road on the car, acting vertically upwards,

Frictional Force F, along the surface of the road, towards the centre of the turn.

As there is no acceleration in the vertical direction,

$R{\text{ }}--{\text{ }}mg{\text{ }} = {\text{ }}0{\text{ }}or{\text{ }}R{\text{ }} = {\text{ }}mg$ ...(1)

The centripetal force required for circular motion is applied along the road's surface, toward the turn's centre. As previously stated, static friction is what supplies the required centripetal force. Clearly $F \leqslant m{v^2}/r$ …(2)

where v is velocity of car and r is the radius of the curved path as,

$F{\text{ }} = {\text{ }}{\mu _s}{\text{ }}R{\text{ }} = {\text{ }}{\mu _s}{\text{ }}mg{\text{ }}$ ( ${\mu _s}$ is coefficient of static friction between the tyres and the road)

Therefore from (2),

\[\dfrac{{{\text{m}}{{\text{v}}^2}}}{{\text{r}}} \leqslant {{\mu_s}mg}\]

\[v\:\leqslant\:\sqrt{{\mu_s}rg}\]

\[\therefore {\vec v_{max}}= \sqrt{{\mu_s}rg}\] ……(3)

Therefore, the maximum velocity with which car can move without slipping is:

\[{\text{v}} = \sqrt {{\mu _{\text{s}}}{\text{rg}}} \]

Banking of Roads:

The phenomenon of raising the outer edge of the curved road above the inner edge is called banking of roads.

The maximum permissible velocity with which a vehicle can go round a level curved road without skidding depends on μ (Coefficient of friction between the tyre and the road). As a result, the frictional force is not a reliable source of the required centripetal force for the vehicle.

In Fig., OX is a horizontal line. OA is the level of the banked curved road whose outer edge has been raised.

$\angle XOA{\text{ }} = \;\theta $ = angle of banking.

Forces are acting on the vehicle as shown in Fig:

Weight mg of the vehicle acting vertically downwards.

Normal reaction R of the banked road acting upwards in a direction perpendicular to OA.

Force of friction F between the banked road and the tyres, acting along with AO. R can be resolved into two rectangular components-

R cosθ, along a vertically upward direction

R sinθ, along the horizontal, towards the centre of the curved road. F can also be resolved into two rectangular components:

(i) F cosθ, along the horizontal, towards the centre of curved road

(ii) F sinθ, along the vertically downward direction.

As there is no acceleration along the vertical direction, the net force along this direction must be zero. Therefore,

$R{\text{ }}cos\theta = {\text{ }}mg{\text{ }} + {\text{ }}F{\text{ }}sin\theta $ ……(1) If v is the vehicle's velocity on a banked circular road with radius r, then centripetal force is = $m{v^2}/r$ . This is provided by the horizontal components of R and F as shown in Fig.

Therefore, \[R\sin \theta + F\cos \theta = \dfrac{{{\text{m}}{{\text{v}}^2}}}{{\text{r}}}\] ...(2)

But F < ${\mu _s}$ R, where ${\mu _s}$ is coefficient of static friction between the banked road and the tyres. To obtain ${v_{\max }}$ , we put $F{\text{ }} = {\text{ }}{\mu _s}{\text{ }}R$ in (1) and (2)

\[{\text{R}}\cos \theta = {\text{mg}} + {\mu _{\text{s}}}{\text{R}}\sin \theta \] … (3)

And \[{\text{R}}\sin \theta + {\mu _{\text{s}}}{\text{R}}\cos \theta = \dfrac{{{\text{m}}{{\text{v}}^2}}}{{\text{r}}}\] …(4)

$From{\text{ }}\left( 3 \right),{\text{ }}R{\text{ }}\left( {cos\theta --{\text{ }}{\mu _s}{\text{ }}sin\theta } \right){\text{ }} = {\text{ }}mg$

\[{\text{R}} = \dfrac{{{\text{mg}}}}{{\cos \theta - {\mu _{\text{s}}}\sin \theta }}\] …(5)

From (4), $\quad {\text{R}}\left( {\sin \theta + {\mu _{\text{s}}}\cos \theta } \right) = \dfrac{{{\text{m}}{{\text{v}}^2}}}{{\text{r}}}$

$\operatorname{Using} (5),\dfrac{{\operatorname{mg} \left( {\sin \theta + {\mu _{\text{s}}}\cos \theta } \right)}}{{\left( {\cos \theta - {\mu _{\text{s}}}\sin \theta } \right)}} = \dfrac{{{\text{m}}{{\text{v}}^2}}}{{\text{r}}}$

$\therefore \quad {v^2} = \dfrac{{\operatorname{rg} \left( {\sin \theta + {\mu _{\text{s}}}\cos \theta } \right)}}{{\left( {\cos \theta - {\mu _{\text{s}}}\sin \theta } \right)}} = \dfrac{{\operatorname{rg} \cos \theta \left( {\tan \theta + {\mu _{\text{s}}}} \right)}}{{\cos \theta \left( {1 - {\mu _{\text{s}}}\tan \theta } \right)}}$

\[{\text{v}} = {\left[ {\dfrac{{rg\left( {{\mu _{\text{s}}} + \tan \theta } \right)}}{{\left( {1 - {\mu _{\text{s}}}\tan \theta } \right)}}} \right]^{1/2}}\] …(6)

Discussion:

If \[{\mu _s}\] = 0, i.e., if banked road is perfectly smooth, then from eqn. (51), \[{v_o} = {(rg\tan \theta )^{\dfrac{1}{2}}}\]

Even when there is no friction, this is the speed at which a banked road may be rounded. On a banked road, driving at this speed causes essentially little wear and tear tyres .

\[{v_o}^2 = {\text{ }}rg{\text{ }}\tan \theta \]

\[\Rightarrow {\overrightarrow F _{real}} + {\overrightarrow F _{pseudo}} = {m_p}{a_{P,O}}\]

\[{\overrightarrow F _{real}} - {m_p}{\overrightarrow a _o} = {m_p}{\overrightarrow a _{P,O}}\]

If speed of vehicle is less than \[{v_o}\] , frictional force will be up the slope. Therefore, the vehicle can be parked only if \[\tan \theta \leqslant {\mu _s}\] .

The average speed of vehicles passing through a road is usually banked. However, if a vehicle's speed is slightly less or more than this, the self-adjusting static friction between the tyres and the road will operate, and the vehicle will not slide.

Note that curved railway tracks are also banked for the same reason. The level of the outer rail is raised a little above the level of the inner rail while laying a curved railway track.

Bending of a Cyclist:

When a cyclist turns, he must also exert centripetal force. His weight is balanced by the usual reaction of the ground if he keeps himself vertical while spinning. In that case, he must rely on the friction between the tyres and the road to generate the required centripetal force. Because the force of friction is modest and unpredictable, relying on it is risky.

In order to avoid relying on friction to generate centripetal power, the cyclist must bend slightly inwards from his vertical position while turning. A component of normal reaction in the horizontal direction produces the required centripetal force in this way.

To calculate the angle of bending with vertical, suppose

m = mass of the cyclist,

v = velocity of the cyclist while turning,

r = radius of the circular path,

\[\theta\] = angle of bending with the vertical

In the fig. shown below the weight of the cyclist(mg) acts vertically downwards at the centre of gravity C. R is the normal reaction on the cyclist. It acts at an angle \[\theta\] with the vertical.

R can be resolved into two rectangular components: \[R\:\cos\theta\] , along the vertically upward direction,\[R\:\sin\theta\], along the horizontal, towards the centre of the circular track.

In equilibrium , \[R{\text{ }}cos\theta = {\text{ }}mg\]\[R{\text{ }}cos\theta = {\text{ }}mg\] ….(1)

\[R{\text{ }}\sin \theta = {\text{ }}m{v^2}/r\] ….(2)

Dividing (2) by (1), we get, \[\tan \theta = {\text{ }}\dfrac{{{v_{}}^2}}{{rg}}\]

For a safe turn, θ should be small, for which v should be small and r should be large i.e. Turning should be done slowly and on a greater radius track. This means, a safe turn should neither be fast nor sharp.

Pseudo Force:

\[{\overrightarrow F _{pseudo}} = - {m_p}{\overrightarrow a _0}\] If observer O is non-inertial and still wants to apply Newton's Second Law on particle P, the observer must add a "Pseudo force" to the real forces on particle P.

\[{\overrightarrow F _{real}} + {\overrightarrow F _{pseudo}} = {m_p}{a_{P,O}}\]

i.e \[{\overrightarrow F _{real}} - {m_p}{\overrightarrow a _o} = {m_p}{\overrightarrow a _{P,O}}\]

Where \[{\overrightarrow a _{P,O}}\] is acceleration of P with respect to observer O.

Laws of Motion Class 11 Notes - Free PDF Download

Free Laws of Motion Class 11 NCERT notes PDF is available online to prepare well for their exams. Different teachers have prepared this PDF with years of experience and prepared different questions after learning the CBSE question paper. These notes are significantly helpful to the students as questions are prepared with appropriate answers to different levels of questions.

Physics Class 11 Chapter 4 notes are easy to read that covers all questions asked in the exams. Thus it helps students to prepare well before their final board class. All the answers are described in a precise manner such that students need not refer anywhere else for the same. According to marks assigned, the concepts are quickly clarified, and students become aware of answering a particular question.

What Topics are Covered With Ch 4 Physics Class 11 Notes?

NCERT covers the entire syllabus as preferred by the CBSE board. Thus notes of Laws of Motion Class 11 are well prepared according to the question paper pattern designed by CBSE. These notes aid students while preparation and hence reduce their stress that comes during a hectic study schedule. These revision notes are best for self-study. Experienced teachers have prepared them according to the requirement. Below are the topics covered in physics Chapter 4 Class 11 notes:

The chapter begins with stating Dynamics, which is the study of forces and motions.

Then the first definition is covered: how to define forces?

The next concept is regarding Inertia along with its three different states.

Finally, it covers the definition of three different laws of motion along with the subtopics to prove these laws in detail. Numerical problems are also covered under this concept.

Now let us study each concept that is covered in Class 11 physics ch 4 notes.

Dynamics is defined as the term in physics, which deals with the study and knowledge about motion forces and laws.

What is Inertia? Also, Describe Its Three Different States.

If an object moves in a straight line or is at rest or in a uniform motion, it cannot change its state to another until compelled. This property is known as inertia. It is measured according to the mass of a body.

There Are Three Different Types of Inertia

Inertia of motion

Inertia of rest

Inertia of direction

Class 11 physics laws of motion notes also cover a basic definition of force and its interaction with different objects. Force is the basic pull and pushes applied to an object, whether the object is at rest or moving. We can also say that it is an interaction of one object with another, due to which an object changes its state.

On general terms, there are two different types of forces:

Constant Force

Action Force

Newton’s Laws of Motion

Newton has given three different laws of motion along with the proof to each law.

Newton’s First Law of Motion: Until you apply any external force to an object, the object will not change its state. It is basically if an object is at rest or moving uniformly in a straight line.

Also, this definition is called the Law of Inertia.

Newton’s Second Law of Motion: The net force is equivalent to the magnitude of the net force along with the direction of the applied net force.

Also, many define the second law of motion as the force directly proportional to acceleration produced while moving and the mass of the body.

\[\vec{F} = K \frac{d\bar{p}}{dt} = Km\vec{a}\]

Suppose F is the net force and m is the mass of the body, and a is the acceleration then Force is defined by the expression given above. Here, k is the constant of proportionality.

Newton’s Third Law of Motion: It is defined that if we apply a force to an object, we will experience an equal force in the opposite direction applied by the object on us.

This Law Deals With Some Other Basic Subtopics Like

Linear Momentum

Law of Conservation of Momentum

Concurrent forces and Equilibrium

Notes of Chapter 4 physics Class 11 will also cover the concept of the simple pulley, friction, actual and apparent weight, laws of friction, angle of friction, coefficient of friction, motion in a circle, and many other numerical problems associated with it.

Why Should You Choose Vedantu for Class 11 Chapter 4 Physics Notes?

Students need a definitive tool to prepare well for exams. These physics ch 4 Class 11 notes are the best way to prepare well for the exams and avoid the last-minute rush. The most difficult chapter needs basic clarification for each topic and its subtopic if you want to score good marks.

Also, students get the least time to prepare their notes. Hence, these Vedantu notes will aid them at every step to clarify their concepts. According to CBSE format, the entire content of notes of ch 4 physics Class 11 is prepared by experienced teachers. Thus students need not scroll any other website for their help.

Benefits for Taking Notes of Laws of Motions Class 11 CBSE Physics Chapter 4

The advantages of taking Laws of Motion Class 11 Notes CBSE Physics Chapter 4 in the form of a free PDF download aid students in effective learning, revision, and exam preparation, leading to improved performance in their academic journey.

Taking Laws of Motion Class 11 Notes CBSE Physics Chapter 4 in the form of a free PDF download offers several advantages to students:

Accessibility: The free PDF download of class 11 physics notes allows students to access the study material anytime, anywhere, using their preferred devices.

Comprehensive Coverage: The notes provide a concise yet comprehensive overview of the chapter, covering all the key concepts related to laws of motion.

Simplified Explanations: The notes offer simplified explanations and examples, making complex concepts easier to understand and retain.

Quick Revision: These notes serve as handy reference material for quick revision before exams, helping students recall important points and formulas.

Time-Saving: The PDF format allows students to save time in note-taking, enabling them to focus on understanding the concepts better.

Supplementary Practice : The notes often include practice questions and solutions, facilitating self-assessment and reinforcing learning.

Exam-Oriented: The notes are designed to align with the CBSE exam pattern, ensuring that students focus on topics that are relevant for the board exams.

Improved Organization: The PDF format offers an organized layout, enabling students to navigate through the notes and find specific topics easily.

Enhanced Learning: By referring to these notes, students can enhance their learning experience and perform better in exams.

Free of Cost: Accessing the notes for free eliminates any financial burden, making quality study material available to all students without any constraints.

The Laws of Motion Class 11 Notes CBSE Physics Chapter 4 in the form of a free PDF download offer a valuable resource to students pursuing physics. These comprehensive notes provide simplified explanations, examples, and practice questions, enhancing students' understanding and problem-solving skills related to motion. The convenience of accessing these notes as a PDF download allows for easy revision and quick reference during exam preparation. By utilizing these notes, students can efficiently cover the entire chapter, reinforcing their conceptual knowledge and preparing effectively for assessments. The free availability of these notes ensures equitable access to quality study material, promoting a holistic learning experience for all students.

FAQs on Laws of Motion Class 11 Notes CBSE Physics Chapter 4 (Free PDF Download)

1. A 5 kg iron sphere feels an upsurge of velocity from 2 m/s to 4 m/s. The velocity rises within the 20 s because a constant force acts on it by unchanging the direction. Find the magnitude & direction of this force.

As per the question

Mass (m) = 5 kg

Time, t = 20 s

Initial velocity, u = 2 m/s

Final velocity, v = 4 m/s

Also, F = m * a …. [1]

As, v = u + at (equation of motion)

a = (v - u) / t

Or, m [(v - u) / t] = Force

Since, a = (v – u) / t

Force = 5 [(4 – 2) / 20]

= 0.5 N (along the direction of motion)

2. What are the chief roles played by Vedantu in CBSE board exams?

Vedantu is involved in so many educational activities. It is paying attention to the quality studies for Physics also. The awareness, along with thorough solved question and answer practice papers, is very helpful to our students for the CBSE board exams.

3. Explain Newton’s law of gravitation?

If two particles possessing different masses (M and m) are mutually attracted with identical and opposite forces such as F and - F.

The relation is F = G(Mm/r 2 )

Here, r = distance between the two particles

G = the universal constant of gravitation

4. How to prepare for Chapter 4 of Class 11 Physics?

The student should make a routine allotting equal hours to every subject and following this regularly to achieve better results. Apart from this, the student should study the given chapter line by line and highlight the important points and topics to retain so that they help during the examination. After this is done, the student should refer to the NCERT solutions and solve the given exercises to attain a better practice at the type of questions that can be asked in the question paper. Consistent practice and hard work will help the student in passing with flying colours.

5. Where can I get the NCERT Solutions for Chapter 4 of Class 11 Physics?

The NCERT solutions are planned and devised to meet the demands and needs of the students. These are planned by experts, containing various exercises considering the syllabus present in the curriculum. These exercises help the student to get a strong idea and understanding of the concept and topics so that the questions asked in the question papers don't perplex them. It is advised that the students have a copy of the NCERT solutions for every subject. These can be availed easily online and practised in the comforts of the home.

6. What are the important topics covered in Chapter 4 of Physics Class 11?

The important topics that are covered in Class 11 Chapter 4 Physics are:

Laws of motion

The law of inertia

Aristotle's fallacy

Newton’s first, second and third laws of motion

Conservation of momentum

Equilibrium of a particle

Common forces in mechanics

Circular motion

Solving problems in mechanics.

All these topics are important for the student to be well versed in. To achieve this they can refer to the NCERT Solutions offered by Vedantu and these solutions can be downloaded online. The exercises that these solutions offer will help the student to grasp a stronghold of the concepts present in Chapter 4 Physics.

7. Why is it important to refer to the NCERT Solutions for Chapter 4 of Class 11 Physics?

The NCERT solutions are devised by student matter experts in order to fulfil the needs and demands of the students. These solutions have numerous exercises that the student needs to practice to retain the important concepts better. Apart from this all these exercises have detailed and explained answers that will help the student in every step of the understanding process, clearing all their doubts and confusions. These solutions also have in the previous year’s question papers that the student can practice getting an idea of how the question might be asked. Thus, practising and acing the NCERT solutions will inevitably lead the student in grabbing good grades in the exam.

8. A nucleus is at rest in the laboratory frame of reference. Show that if it disintegrates into two smaller nuclei the products must move in opposite directions.

Let m 1 and m 2 be the mass of the product respectively

Let v 1 and v 2 be the velocity respectively

Thus, the total linear momentum after disintegration becomes m 1 v 1 +m 2 v 2

But it is to be noted that before disintegration the nucleus is at rest and therefore the linear momentum before disintegration becomes zero

Thus, following the principle of conservation of linear momentum;

(image will be uploaded soon)

CBSE Study Materials for Class 11

CBSE Class 11 Physics Notes Chapter 5 Laws of Motion

Here, we have provided CBSE Class 11 Physics Notes Chapter 5 Laws of Motion. Students can view these CBSE Class 11 Physics Notes Chapter 5 before exams for better understanding of the chapter.

April 19, 2024

Table of Contents

CBSE Class 11 Physics Notes Chapter 5: Students should use the CBSE Class 11 Physics Notes Chapter 5 if they need to refer to them during an exam. The application of Newton’s laws of motion in real time is covered in this chapter. Proper formulas are given to students, which they can use immediately to solve exam questions. The CBSE board examination schedule states that students should study thoroughly using easily accessible here.

These Newton’s laws of motion are fully comprehended with the CBSE Class 11 Physics Notes Chapter 5 . These are quite beneficial while attempting to solve complicated issues on various levels.

CBSE Class 11 Physics Notes Chapter 5 PDF

To ensure they are well-prepared for their exams, Free Laws of Motion Class 11 NCERT notes PDF are available online. With years of experience, several teachers have created this PDF. They have also developed unique questions based on their understanding of the CBSE question paper. The questions in these notes are prepared with appropriate solutions for varying difficulty levels, which is a huge benefit to the students.

CBSE Class 11 Physics Notes Chapter 5

Something that modifies a body’s rest or motion is called a force. Force can also refer to an interaction between two bodies. Even when two bodies are not in direct touch, they can nonetheless exert forces on one another. Examples of these forces include the gravitational force between any two bodies and the electrostatic force between two charges.

Basic Forces

Tension, weight, contact force, and spring force are the four main categories of forces.

Weight: The force that draws a body towards the earth is known as weight. Another name for it is the gravitational force.

Touch Force: Contact forces are the forces that two bodies apply to one another when they come into touch.

The contact force component that is normal to the surface is known as the normal force (N). It establishes the force with which two surfaces are pressed together.
The portion of the contact force that is parallel to the surface is known as the frictional force (f). It resists the two in contact surfaces’ relative motion or attempted motion.

The force that a taut string, rope, or chain exerts at its end is referred to as tension. The body is pulled in the direction of strain while it is pushed naturally.

Newton’s Laws of Motion:

Newton’s first laws:.

A body that is moving or at rest in a straight line won’t change its state until an outside force acts upon it. This is referred to as the Newtonian First Law of Inertia.

A body’s inability to modify its position of rest or uniform motion in a straight line without the application of an external force is known as its inertia.

Newton’s first laws are only applicable in inertial frames of reference; that is, a frame of reference is considered inertial if it is at rest or moving uniformly; otherwise, it is considered non-inertial.

Newton’s Second Laws state that a body’s rate of change of momentum is proportionate to the force that the consequent action exerts on it.

Special Cases:

The force simply modifies the magnitude of v→, not the direction, depending on whether it is parallel or antiparallel to the body’s motion. As a result, the route will be linear.

The force simply modifies the direction of v→, not its magnitude, if it is operating perpendicular to the body’s motion. The route will be round as a result.

The force modifies the direction and amount of v→ when it acts at an angle θ to the body’s motion. In this scenario, the body’s trajectory could be hyperbolic, parabolic, elliptical, or non-uniform circular.

Linear Momentum

It can be described as the result of multiplying the body’s mass by its velocity.

The force’s impulse, which is the product of the average force at impact and the impact duration generated throughout the collision, is computed using the complete change in linear momentum.

Impulsive forces are those that have brief physical effects on bodies. For instance, using a bat to strike a ball, a rifle to fire a bullet, etc.

Instead of staying constant, an impulsive force fluctuates between zero and its maximum and vice versa. Because it varies over time, the value of impulsive force is therefore difficult to measure.

Principle of Conservation of Linear Momentum

This principle states that the vector sum of all the linear momenta in an isolated system is preserved and unaffected by the reciprocal action and response of the system’s interactions.

Thus, in an isolated system (one in which there is no external force), mutual forces between pairs of particles can result in changes in the linear momentum of individual particles. Because the mutual forces for each pair are equal and opposing, the changes in linear momentum cancel in pairs, leaving the overall linear momentum unchanged. Consequently, the total linear momentum of an isolated system of interacting particles is conserved. The second and third laws of motion established by Newton directly lead to this principle.

When one body actually moves (slides, rolls, or merely attempts to move over the surface of another body), friction—an opposing force—comes into play.

It is the force that opposes the relative motion of two surfaces when they come into contact with one another.

The contact area has no effect on frictional force. Because the force of adhesion grows as the area of contact increases.

The adhesive force between two surfaces increases when they are very smooth because the molecules on the surfaces are closer to one another. when a result, when the adhesive pressure rises, so does the frictional force.

Types of Friction

3 types of friction: Static, Limiting and Kinetic Friction.

Static Friction: Static friction is the opposing force that develops when one body seeks to move over the surface of another body without any real motion having occurred.

Limiting Friction: The greatest opposing force that is applied when one body is about to pass across the surface of the other is known as limiting friction.

Dynamic friction, also known as kinetic friction, is the opposing force that arises when two bodies are really moving across each other’s surfaces.

Coefficient of Static Friction

Rolling Friction

Rolling friction is the opposing force that arises when a body rolls across the surface of another body.

Benefits of CBSE Class 11 Physics Notes Chapter 5

The benefits of using Laws of Motion Class 11 Notes CBSE Physics Chapter 5 as a free PDF download help students learn, review, and prepare for exams more effectively, which improves their academic achievement.

Using the notes from Laws of Motion Class 11 Students can benefit from multiple advantages when they download the free PDF version of CBSE Physics Chapter 5:

Accessibility: Students can use their preferred devices to access the class 11 Physics notes study material at any time, anywhere, by downloading the notes in PDF format for free.
Extensive Coverage: The notes offer a succinct yet thorough synopsis of the chapter, encompassing all the essential ideas about laws of motion.
Simplified explanations: Complex concepts are made easier to comprehend and remember by providing examples and simplified explanations in the notes.
Time-saving: Students may concentrate on better understanding the material by taking notes in less time while using the PDF format.

CBSE Class 11 Physics Notes Chapter 5 FAQs

(a) Law 1: Everybody remains at rest or continues to move with uniform velocity unless an external force is applied to it. (c) Law 3: When a body A exerts a force on another body B, B exerts an equal and opposite force on A.

Laws of Motion Class 11 Notes CBSE Physics Chapter 5

Class 11 Physics has an important syllabus to follow. The chapters related to fundamental topics such as units, measurements, motion, work, energy, power, mechanical properties of matter, gravitation, thermodynamics, etc hold immense importance in the development of a conceptual foundation among the students.

CBSE Class 11 Physics Notes Chapter 3 Motion in a Straight Line

Entamoeba Histolytica Life Cycle

.st1{display:none} Related Articles

UP Board Solutions for Class 11 Biology Chapter 1 The Living World (जीव जगत)
CBSE Class 8 Social Science Sample Paper 2024-25 PDF Download
RD Sharma Solutions Class 10 Maths Chapter 4 Exercise 4.5 Triangles
RD Sharma Solutions Class 10 Maths Chapter 5 Exercise 5.2 Trigonometric Ratios
RD Sharma Solutions Class 10 Maths Chapter 4 Exercise 4.4 Triangles
RD Sharma Solutions Class 10 Maths Chapter 4 Exercise 4.3 Triangles
JKBOSE Date Sheet 2025 Releasing Soon for Class 10th, 12th
CBSE Class 9 Geography Notes Chapter 4 Climate PDF Download
CBSE Class 10 Syllabus 2024-25 PDF Download Subject Wise
UP Board Time Table 2025 PDF Download Soon Class 10th, 12th

Have doubts?

Our support team will be happy to assist you!

NCERT Solutions for Class 11th: Ch 5 Laws Of Motion Physics

Ncert solutions for class 11th: ch 5 laws of motion physics science.

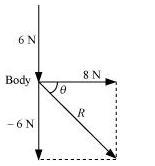
Contact Form

COMMENTS

Case Study Questions for Class 11 Physics Chapter 5 Laws of Motion
Case Study Questions: Question 1: Conservation of Momentum. This principle is a consequence of Newton's second and third laws of motion. In an isolated system (i.e., a system having no external force), mutual forces (called internal forces) between pairs of particles in the system causes momentum change in individual particles.
Class 11 Physics Case Study Questions Chapter 5 Laws of Motion
Laws of Motion Case Study Questions With Answers. Here, we have provided case-based/passage-based questions for Class 11 Physics Chapter 5 Laws of Motion. Case Study/Passage-Based Questions. Case Study 1: The first law refers to the simple case when the net external force on a body is zero. The second law of motion refers to the general ...
Class 11 Physics Case Study Questions
Class 11 Physics Case Study Question 4 Read the case study given below and answer any four subparts: ... Laws of Motion: 14: Chapter-5: Laws of Motion: Unit-IV: Work, Energy and Power: 14: 17: Chapter-6: Work, Energy and Power: Unit-V: Motion of System of Particles and Rigid Body: 18:
CBSE Case Study Questions Class 11 Physics PDF Download
Chapter-wise Solved Case Study Questions for Class 11 Physics. Chapter 1: Physical World. Chapter 2: Units and Measurements. Chapter 3: Motion in a Straight Line. Chapter 4: Motion in a Plane. Chapter 5: Laws of Motion. Chapter 6: Work, Energy, and Power. Chapter 7: System of Particles and Rotational Motion.
PDF Kendriya Vidyalaya Sanghathan Chandigarh Region Class-xi Subject ...
CLASS-XI SUBJECT-PHYSICS Chapter -5 Laws of Motion . 2 Table of Contents S.N. Content Page No. 1 Gist of chapter 3-4 2 Formulae used in chapter 5-7 3 MCQs 8-14 4 Assertion Reasoning type questions 15-17 5 Case study based question 18-22 6 Answer key 23 . 3 Gist of Chapter 1. Force: it is the push or pull which bring the change in (i) change in ...
Class 11 Physics Case Study Questions PDF Download
Case Study Based Questions on Class 11 Physics Chapter 6 Work, Energy, and Power. Case Study Based Questions on Class 11 Physics Chapter 7 System of Particles and Rotational Motion. Case Study Based Questions on Class 11 Physics Chapter 8 Gravitation. Case Study Based Questions on Class 11 Physics Chapter 9 Mechanical Properties of Solids.
Case Study Questions for Class 11 Physics
Case Study Questions for Class 11 Physics. Chapter 1: Physical World. Chapter 2: Units and Measurements. Chapter 3: Motion in a Straight Line. Chapter 4: Motion in a Plane. Chapter 5: Laws of Motion. Chapter 6: Work, Energy, and Power. Chapter 7: System of Particles and Rotational Motion. Chapter 8: Gravitation.
Case Study Questions Class 11 Physics
This document contains 4 case studies related to Newton's laws of motion. Each case study provides context and questions about key concepts like inertia, momentum, impulse, Newton's 3 laws of motion, and conservation of momentum. For case study 1, the summary discusses how Newton's 1st law explains why a book at rest on a table remains at rest, as the downward force of gravity is balanced by ...
Class 11 Physics Case Study Question Chapter 1 to 15
Case Study Question Class 11 Physics (CBSE / NCERT Board) CBSE Class 11 Physics Case Study Question. There are total 15 chapter Physical World, Units and Measurement, Motion in a Straight Line, Motion in a Plane, Laws of Motion, Work, Energy and Power, Systems of Particles and Rotational Motion, Gravitation, Mechanical Properties of Solids ...
CBSE Class 11 Physics Chapter 4
The CBSE Class 11 Physics Chapter 4 - Law of Motion covers fundamental concepts that form the basis of classical mechanics. Understanding these principles is crucial for building a strong foundation in physics. The chapter introduces Newton's laws of motion, emphasizing their application in real-world scenarios.
NCERT Solutions for Class 11 Physics Chapter 5 Laws of Motion
Access the answers to NCERT Solutions for Class 11 Physics Chapter 5 Laws of Motion. 1. Give the magnitude and direction of the net force acting on. (a) a drop of rain falling down with a constant speed. (b) a cork of mass 10 g floating on water. (c) a kite skillfully held stationary in the sky. (d) a car moving with a constant velocity of 30 ...
CBSE Class 11 Physics Chapter 5 Laws of motion Study Materials
Law of Motion Class 11 Notes Physics Chapter 5. • Dynamics is the branch of physics in which we study the motion of a body by taking into consideration the cause i.e., force which produces the motion. • Force Force is an external cause in the form of push or pull, which produces or tries to produce motion in a body at rest, or stops/tries ...
Laws of Motion
JEE Main 2022 (IIT JEE 2022). Thinking about Laws of Motion IIT JEE (Laws of Motion Class 11 IIT JEE)? IIT JEE Physics. This JEEt Lo 2022 session is about La...
NCERT Solutions for Class 11 Physics Chapter 5 Laws of Motion
Answer: (a) When the pebble is moving upward, the acceleration g is acting downward, so the force is acting downward is equal to F = mg = 0.05 kg x 10 ms -2 = 0.5 N. (b) In this case also F = mg = 0.05 x 10 = 0.5 N. (downwards). (c) The pebble is not at rest at highest point but has horizontal component of velocity.
Laws of Motion Class 11 Notes CBSE Physics Chapter 4 (PDF)
FAQs on Laws of Motion Class 11 Notes CBSE Physics Chapter 4 (Free PDF Download) 1. A 5 kg iron sphere feels an upsurge of velocity from 2 m/s to 4 m/s. The velocity rises within the 20 s because a constant force acts on it by unchanging the direction. Find the magnitude & direction of this force. As per the question.
Laws of Motion
JEE Main 2022 (IIT JEE 2022). Thinking about Friction Theory (Friction Class 11) from Laws of Motion Class 11 IIT JEE (Class 11 Physics Chapter 5)? JEE Main ...
CBSE Class 11 Physics Notes Chapter 5 Laws of Motion
Case 1: The force simply modifies the magnitude of v→, not the direction, depending on whether it is parallel or antiparallel to the body's motion. As a result, the route will be linear. Case 2: The force simply modifies the direction of v→, not its magnitude, if it is operating perpendicular to the body's motion.
Law of Motion Class 11 Notes Physics Chapter 5
Law of Motion Class 11 Notes Physics Chapter 5. • Dynamics is the branch of physics in which we study the motion of a body by taking into consideration the cause i.e., force which produces the motion. • Force. Force is an external cause in the form of push or pull, which produces or tries to produce motion in a body at rest, or stops/tries ...
NCERT Solutions for Class 11th: Ch 5 Laws Of Motion Physics
θ is the angle made by R with the force of 8 N ∴ θ = tan-1 (-6/8) = -36.87 0 The negative sign indicates that θ is in the clockwise direction with respect to the force of magnitude 8 N. As per Newton's second law of motion, the acceleration (a) of the body is given as:F = ma ∴ a = F / m = 10 / 5 = 2 ms-2 5.8. The driver of a three-wheeler moving with a speed of 36 km/h sees a child ...
CBSE Class 11-science Physics Laws of Motion
CBSE Class 11-science Physics Laws of Motion. Newton's First Law of Motion. State Newton's first law of motion. Define inertia and its relation to mass. Define and differentiate between an inertial and non inertial reference frame. Newton's Second Law of Motion. Define Momentum, Newton second law.

Class 11 Physics Case Study Questions

myCBSEguide App

What is the purpose of physics?

What are case study questions in physics?

CBSE Case Study Questions in Class 11 Physics

Sample Class 11 Physics Case Study Questions

Class 11 Physics Case Study Question 1

Class 11 Physics Case Study Question 2

Class 11 Physics Case Study Question 3

Class 11 Physics Case Study Question 4

Examining Class 11 Physics syllabus

myCBSEguide: A true saviour for many students

Related Posts

Leave a Comment

cbseexpert.com

Class 11 Physics Case Study Questions PDF Download

Class 11th PHYSICS: Chapterwise Case Study Question & Solution

Case Study-Based Questions for Class 11 Physics

Class 11 Books for Boards

Class 11 Physics Syllabus 2024

FAQs about Class 11 Physics Case Studies

How do you write a case study question for Class 11?

Are the case study questions based on the latest syllabus?

You Might Also Like

Physical World Notes Class 11 Physics Notes- Download PDF for JEE/NEET

Laws of Motion Notes Class 11 Physics Notes- Download PDF for JEE/NEET

The Topper Combo Flashcards

Case Study Questions for Class 11 Physics

Share this:

Class 11 Physics Case Study Question

CBSE Class 11 Physics Case Study Question

Leave a Reply Cancel reply

We have a strong team of experienced Teachers who are here to solve all your exam preparation doubts

NCERT Solutions for Class 11 Physics Chapter 5 Laws of Motion

Access the answers to NCERT Solutions for Class 11 Physics Chapter 5 Laws of Motion

Subtopics of Class 11 Physics Chapter 5 Laws of Motion

Frequently Asked Questions on NCERT Solutions for Class 11 Physics Chapter 5

Register with BYJU'S & Download Free PDFs

CBSE Class 11 Physics Chapter 5 Laws of motion Study Materials

Laws of Motion : Notes and Study Materials -pdf

Law of Motion Class 11 Notes Physics Chapter 5

CBSE Class 11 Physics Chapter-5 Important Questions

Laws of Motion Class 11 Notes CBSE Physics Chapter 4 (Free PDF Download)

Revision Notes for CBSE Class 11 Physics Chapter 4 (Laws of Motion) - Free PDF Download

Download CBSE Class 11 Physics Revision Notes 2024-25 PDF

Laws of Motion Class 11 Notes Physics - Basic Subjective Questions

Section-B (2 Marks Questions)

Lami’s Theorem:

Basic Forces:

Newton's Laws of Motion:

Newton's Second Laws:

Newtons Third Laws:

Linear Momentum:

Apparent Weight on a Body in a Lift

Principle of Conservation of Linear Momentum-

Types of Friction:

Laws of Limiting Friction:

Coefficient of Static Friction:

Angle of Friction:

Angle of Repose or Angle of Sliding:

Methods of Changing Friction:

Dynamics of Uniform Circular Motion Concept of Centripetal Force:

Centrifugal Force:

Rounding A-Level Curved Road:

Banking of Roads:

Discussion:

Bending of a Cyclist:

Pseudo Force:

Laws of Motion Class 11 Notes - Free PDF Download

What Topics are Covered With Ch 4 Physics Class 11 Notes?

Newton’s Laws of Motion

This Law Deals With Some Other Basic Subtopics Like

Why Should You Choose Vedantu for Class 11 Chapter 4 Physics Notes?

Benefits for Taking Notes of Laws of Motions Class 11 CBSE Physics Chapter 4

FAQs on Laws of Motion Class 11 Notes CBSE Physics Chapter 4 (Free PDF Download)

CBSE Study Materials for Class 11

CBSE Class 11 Physics Notes Chapter 5 Laws of Motion

CBSE Class 11 Physics Notes Chapter 5

Basic Forces

Newton’s Laws of Motion: