assignment problem linear programming hungarian method

Hungarian Method

The Hungarian method is a computational optimization technique that addresses the assignment problem in polynomial time and foreshadows following primal-dual alternatives. In 1955, Harold Kuhn used the term “Hungarian method” to honour two Hungarian mathematicians, Dénes Kőnig and Jenő Egerváry. Let’s go through the steps of the Hungarian method with the help of a solved example.

Hungarian Method to Solve Assignment Problems

The Hungarian method is a simple way to solve assignment problems. Let us first discuss the assignment problems before moving on to learning the Hungarian method.

What is an Assignment Problem?

A transportation problem is a type of assignment problem. The goal is to allocate an equal amount of resources to the same number of activities. As a result, the overall cost of allocation is minimised or the total profit is maximised.

Because available resources such as workers, machines, and other resources have varying degrees of efficiency for executing different activities, and hence the cost, profit, or loss of conducting such activities varies.

Assume we have ‘n’ jobs to do on ‘m’ machines (i.e., one job to one machine). Our goal is to assign jobs to machines for the least amount of money possible (or maximum profit). Based on the notion that each machine can accomplish each task, but at variable levels of efficiency.

Hungarian Method Steps

Check to see if the number of rows and columns are equal; if they are, the assignment problem is considered to be balanced. Then go to step 1. If it is not balanced, it should be balanced before the algorithm is applied.

Step 1 – In the given cost matrix, subtract the least cost element of each row from all the entries in that row. Make sure that each row has at least one zero.

Step 2 – In the resultant cost matrix produced in step 1, subtract the least cost element in each column from all the components in that column, ensuring that each column contains at least one zero.

Step 3 – Assign zeros

• Analyse the rows one by one until you find a row with precisely one unmarked zero. Encircle this lonely unmarked zero and assign it a task. All other zeros in the column of this circular zero should be crossed out because they will not be used in any future assignments. Continue in this manner until you’ve gone through all of the rows.
• Examine the columns one by one until you find one with precisely one unmarked zero. Encircle this single unmarked zero and cross any other zero in its row to make an assignment to it. Continue until you’ve gone through all of the columns.

Step 4 – Perform the Optimal Test

• The present assignment is optimal if each row and column has exactly one encircled zero.
• The present assignment is not optimal if at least one row or column is missing an assignment (i.e., if at least one row or column is missing one encircled zero). Continue to step 5. Subtract the least cost element from all the entries in each column of the final cost matrix created in step 1 and ensure that each column has at least one zero.

Step 5 – Draw the least number of straight lines to cover all of the zeros as follows:

(a) Highlight the rows that aren’t assigned.

(b) Label the columns with zeros in marked rows (if they haven’t already been marked).

(c) Highlight the rows that have assignments in indicated columns (if they haven’t previously been marked).

(d) Continue with (b) and (c) until no further marking is needed.

(f) Simply draw the lines through all rows and columns that are not marked. If the number of these lines equals the order of the matrix, then the solution is optimal; otherwise, it is not.

Step 6 – Find the lowest cost factor that is not covered by the straight lines. Subtract this least-cost component from all the uncovered elements and add it to all the elements that are at the intersection of these straight lines, but leave the rest of the elements alone.

Step 7 – Continue with steps 1 – 6 until you’ve found the highest suitable assignment.

Hungarian Method Example

Use the Hungarian method to solve the given assignment problem stated in the table. The entries in the matrix represent each man’s processing time in hours.

\(\begin{array}{l}\begin{bmatrix} & I & II & III & IV & V \\1 & 20 & 15 & 18 & 20 & 25 \\2 & 18 & 20 & 12 & 14 & 15 \\3 & 21 & 23 & 25 & 27 & 25 \\4 & 17 & 18 & 21 & 23 & 20 \\5 & 18 & 18 & 16 & 19 & 20 \\\end{bmatrix}\end{array} \)

With 5 jobs and 5 men, the stated problem is balanced.

\(\begin{array}{l}A = \begin{bmatrix}20 & 15 & 18 & 20 & 25 \\18 & 20 & 12 & 14 & 15 \\21 & 23 & 25 & 27 & 25 \\17 & 18 & 21 & 23 & 20 \\18 & 18 & 16 & 19 & 20 \\\end{bmatrix}\end{array} \)

Subtract the lowest cost element in each row from all of the elements in the given cost matrix’s row. Make sure that each row has at least one zero.

\(\begin{array}{l}A = \begin{bmatrix}5 & 0 & 3 & 5 & 10 \\6 & 8 & 0 & 2 & 3 \\0 & 2 & 4 & 6 & 4 \\0 & 1 & 4 & 6 & 3 \\2 & 2 & 0 & 3 & 4 \\\end{bmatrix}\end{array} \)

Subtract the least cost element in each Column from all of the components in the given cost matrix’s Column. Check to see if each column has at least one zero.

\(\begin{array}{l}A = \begin{bmatrix}5 & 0 & 3 & 3 & 7 \\6 & 8 & 0 & 0 & 0 \\0 & 2 & 4 & 4 & 1 \\0 & 1 & 4 & 4 & 0 \\2 & 2 & 0 & 1 & 1 \\\end{bmatrix}\end{array} \)

When the zeros are assigned, we get the following:

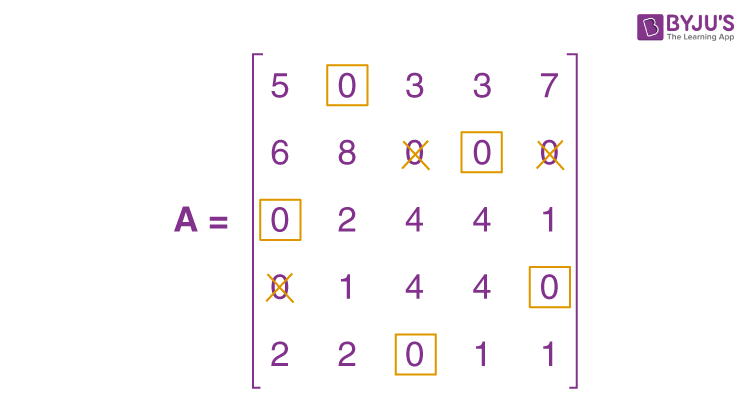
The present assignment is optimal because each row and column contain precisely one encircled zero.

Where 1 to II, 2 to IV, 3 to I, 4 to V, and 5 to III are the best assignments.

Hence, z = 15 + 14 + 21 + 20 + 16 = 86 hours is the optimal time.

Practice Question on Hungarian Method

Use the Hungarian method to solve the following assignment problem shown in table. The matrix entries represent the time it takes for each job to be processed by each machine in hours.

\(\begin{array}{l}\begin{bmatrix}J/M & I & II & III & IV & V \\1 & 9 & 22 & 58 & 11 & 19 \\2 & 43 & 78 & 72 & 50 & 63 \\3 & 41 & 28 & 91 & 37 & 45 \\4 & 74 & 42 & 27 & 49 & 39 \\5 & 36 & 11 & 57 & 22 & 25 \\\end{bmatrix}\end{array} \)

Stay tuned to BYJU’S – The Learning App and download the app to explore all Maths-related topics.

Frequently Asked Questions on Hungarian Method

What is hungarian method.

The Hungarian method is defined as a combinatorial optimization technique that solves the assignment problems in polynomial time and foreshadowed subsequent primal–dual approaches.

What are the steps involved in Hungarian method?

The following is a quick overview of the Hungarian method: Step 1: Subtract the row minima. Step 2: Subtract the column minimums. Step 3: Use a limited number of lines to cover all zeros. Step 4: Add some more zeros to the equation.

What is the purpose of the Hungarian method?

When workers are assigned to certain activities based on cost, the Hungarian method is beneficial for identifying minimum costs.

Leave a Comment Cancel reply

Your Mobile number and Email id will not be published. Required fields are marked *

Request OTP on Voice Call

Post My Comment

Register with BYJU'S & Download Free PDFs

Register with byju's & watch live videos.

• Practice Mathematical Algorithm
• Mathematical Algorithms
• Pythagorean Triplet
• Fibonacci Number
• Euclidean Algorithm
• LCM of Array
• GCD of Array
• Binomial Coefficient
• Catalan Numbers
• Sieve of Eratosthenes
• Euler Totient Function
• Modular Exponentiation
• Modular Multiplicative Inverse
• Stein's Algorithm
• Juggler Sequence
• Chinese Remainder Theorem
• Quiz on Fibonacci Numbers

Hungarian Algorithm for Assignment Problem | Set 1 (Introduction)

• For each row of the matrix, find the smallest element and subtract it from every element in its row.
• Do the same (as step 1) for all columns.
• Cover all zeros in the matrix using minimum number of horizontal and vertical lines.
• Test for Optimality: If the minimum number of covering lines is n, an optimal assignment is possible and we are finished. Else if lines are lesser than n, we haven’t found the optimal assignment, and must proceed to step 5.
• Determine the smallest entry not covered by any line. Subtract this entry from each uncovered row, and then add it to each covered column. Return to step 3.

Try it before moving to see the solution

Explanation for above simple example:

  An example that doesn’t lead to optimal value in first attempt: In the above example, the first check for optimality did give us solution. What if we the number covering lines is less than n.

Time complexity : O(n^3), where n is the number of workers and jobs. This is because the algorithm implements the Hungarian algorithm, which is known to have a time complexity of O(n^3).

Space complexity :   O(n^2), where n is the number of workers and jobs. This is because the algorithm uses a 2D cost matrix of size n x n to store the costs of assigning each worker to a job, and additional arrays of size n to store the labels, matches, and auxiliary information needed for the algorithm.

In the next post, we will be discussing implementation of the above algorithm. The implementation requires more steps as we need to find minimum number of lines to cover all 0’s using a program. References: http://www.math.harvard.edu/archive/20_spring_05/handouts/assignment_overheads.pdf https://www.youtube.com/watch?v=dQDZNHwuuOY

Similar Reads

• Mathematical

Please Login to comment...

Improve your coding skills with practice.

What kind of Experience do you want to share?

Hungarian Method Examples

Now we will examine a few highly simplified illustrations of Hungarian Method for solving an assignment problem .

Later in the chapter, you will find more practical versions of assignment models like Crew assignment problem , Travelling salesman problem , etc.

Example-1, Example-2

Example 1: Hungarian Method

The Funny Toys Company has four men available for work on four separate jobs. Only one man can work on any one job. The cost of assigning each man to each job is given in the following table. The objective is to assign men to jobs in such a way that the total cost of assignment is minimum.

This is a minimization example of assignment problem . We will use the Hungarian Algorithm to solve this problem.

Identify the minimum element in each row and subtract it from every element of that row. The result is shown in the following table.

"A man has one hundred dollars and you leave him with two dollars, that's subtraction." -Mae West

On small screens, scroll horizontally to view full calculation

Identify the minimum element in each column and subtract it from every element of that column.

Make the assignments for the reduced matrix obtained from steps 1 and 2 in the following way:

• For every zero that becomes assigned, cross out (X) all other zeros in the same row and the same column.
• If for a row and a column, there are two or more zeros and one cannot be chosen by inspection, choose the cell arbitrarily for assignment.

An optimal assignment is found, if the number of assigned cells equals the number of rows (and columns). In case you have chosen a zero cell arbitrarily, there may be alternate optimal solutions. If no optimal solution is found, go to step 5.

Use Horizontal Scrollbar to View Full Table Calculation

Draw the minimum number of vertical and horizontal lines necessary to cover all the zeros in the reduced matrix obtained from step 3 by adopting the following procedure:

• Mark all the rows that do not have assignments.
• Mark all the columns (not already marked) which have zeros in the marked rows.
• Mark all the rows (not already marked) that have assignments in marked columns.
• Repeat steps 5 (ii) and (iii) until no more rows or columns can be marked.
• Draw straight lines through all unmarked rows and marked columns.

You can also draw the minimum number of lines by inspection.

Select the smallest element (i.e., 1) from all the uncovered elements. Subtract this smallest element from all the uncovered elements and add it to the elements, which lie at the intersection of two lines. Thus, we obtain another reduced matrix for fresh assignment.

Now again make the assignments for the reduced matrix.

Final Table: Hungarian Method

Since the number of assignments is equal to the number of rows (& columns), this is the optimal solution.

The total cost of assignment = A1 + B4 + C2 + D3

Substituting values from original table: 20 + 17 + 17 + 24 = Rs. 78.

Share This Article

Operations Research Simplified Back Next

Goal programming Linear programming Simplex Method Transportation Problem

The Hungarian Method for the Assignment Problem

• First Online: 01 January 2009

Cite this chapter

• Harold W. Kuhn 9  

10k Accesses

187 Citations

11 Altmetric

This paper has always been one of my favorite “children,” combining as it does elements of the duality of linear programming and combinatorial tools from graph theory. It may be of some interest to tell the story of its origin.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

Subscribe and save.

• Get 10 units per month
• Download Article/Chapter or eBook
• 1 Unit = 1 Article or 1 Chapter
• Cancel anytime
• Available as PDF
• Read on any device
• Instant download
• Own it forever
• Compact, lightweight edition
• Dispatched in 3 to 5 business days
• Free shipping worldwide - see info

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Unable to display preview.  Download preview PDF.

Similar content being viewed by others

On weighted means and their inequalities

Constrained Variational Optimization

The Alternating Least-Squares Algorithm for CDPCA

H.W. Kuhn, On the origin of the Hungarian Method , History of mathematical programming; a collection of personal reminiscences (J.K. Lenstra, A.H.G. Rinnooy Kan, and A. Schrijver, eds.), North Holland, Amsterdam, 1991, pp. 77–81.

Google Scholar  

A. Schrijver, Combinatorial optimization: polyhedra and efficiency , Vol. A. Paths, Flows, Matchings, Springer, Berlin, 2003.

MATH   Google Scholar  

Download references

Author information

Authors and affiliations.

Princeton University, Princeton, USA

Harold W. Kuhn

You can also search for this author in PubMed   Google Scholar

Corresponding author

Correspondence to Harold W. Kuhn .

Editor information

Editors and affiliations.

Inst. Informatik, Universität Köln, Pohligstr. 1, Köln, 50969, Germany

Michael Jünger

Fac. Sciences de Base (FSB), Ecole Polytechnique Fédérale de Lausanne, Lausanne, 1015, Switzerland

Thomas M. Liebling

Ensimag, Institut Polytechnique de Grenoble, avenue Félix Viallet 46, Grenoble CX 1, 38031, France

Denis Naddef

School of Industrial &, Georgia Institute of Technology, Ferst Drive NW., 765, Atlanta, 30332-0205, USA

George L. Nemhauser

IBM Corporation, Route 100 294, Somers, 10589, USA

William R. Pulleyblank

Inst. Informatik, Universität Heidelberg, Im Neuenheimer Feld 326, Heidelberg, 69120, Germany

Gerhard Reinelt

ed Informatica, CNR - Ist. Analisi dei Sistemi, Viale Manzoni 30, Roma, 00185, Italy

Giovanni Rinaldi

Center for Operations Reserach &, Université Catholique de Louvain, voie du Roman Pays 34, Leuven, 1348, Belgium

Laurence A. Wolsey

Rights and permissions

Reprints and permissions

Copyright information

© 2010 Springer-Verlag Berlin Heidelberg

About this chapter

Kuhn, H.W. (2010). The Hungarian Method for the Assignment Problem. In: Jünger, M., et al. 50 Years of Integer Programming 1958-2008. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-540-68279-0_2

Download citation

DOI : https://doi.org/10.1007/978-3-540-68279-0_2

Published : 06 November 2009

Publisher Name : Springer, Berlin, Heidelberg

Print ISBN : 978-3-540-68274-5

Online ISBN : 978-3-540-68279-0

eBook Packages : Mathematics and Statistics Mathematics and Statistics (R0)

Share this chapter

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Publish with us

Policies and ethics

• Find a journal
• Track your research