research on chemical equation

• Science Notes Posts
• Contact Science Notes
• Todd Helmenstine Biography
• Anne Helmenstine Biography
• Free Printable Periodic Tables (PDF and PNG)
• Periodic Table Wallpapers
• Interactive Periodic Table
• Periodic Table Posters
• Science Experiments for Kids
• How to Grow Crystals
• Chemistry Projects
• Fire and Flames Projects
• Holiday Science
• Chemistry Problems With Answers
• Physics Problems
• Unit Conversion Example Problems
• Chemistry Worksheets
• Biology Worksheets
• Periodic Table Worksheets
• Physical Science Worksheets
• Science Lab Worksheets
• My Amazon Books

What Is a Chemical Equation? Definition and Examples

A chemical equation is a symbolic representation of a chemical reaction , indicating the reactants and products in a reaction and the direction in which the reaction proceeds. French chemist Jean Beguin gets credit for formulating the first chemical equation in 1615.

Here is an explanation of the types of chemical equations, the parts they contain, and examples.

Parts of a Chemical Equation

The three essential parts of a chemical equation are the reactants, the products, and the reaction arrow, but many equations contain much more information.

• Chemical Formulas : Reactants and products are written as chemical formulas , using element symbols and subscripts.
• Reactants : By convention, chemical reactions are read from left to right. The reactants are written on the left side of the equation. Drawing the chemical structures of the reactants is fine, but the usual method gives the reactant chemical formulas (e.g., H 2 , O 2 ).
• Products : Products of a chemical reaction are written on the right side of the reaction arrow.
• Reaction Arrow : The reaction arrow tells which direction the chemical reaction proceeds.
• Plus Signs : When more than one reactant or product occurs, use a plus sign (+) between them.
• Coefficients : Coefficients are numbers written in front of a chemical formula. They indicate the stoichiometry of the reactants and products, so you can see at a glance the mole ratio between them in a balanced equation. For example, in the formula 4H 2 O 2 , “4” is the coefficient. By convention, the number “1” is omitted. So, you write O 2 and not 1O 2 . Usually, coefficients are whole numbers, but sometimes you’ll see equations using fractions or decimal points.
• Subscripts : Subscripts follow the element symbol in a chemical formula, indicating how many atoms of that element are in a compound. For example, the “2” in H 2 O is a subscript.
• State of Matter : Not all chemical equations list the state of matter of reactants and products. But, when given, the state of matter follows the chemical formula of a reactant or product, enclosed within parentheses. The abbreviations for the states of matter are (s) for solid, (l) for liquid, (g) for gas, and (aq) for when a species is dissolved in aqueous solution .

Reaction Arrow in a Chemical Equation

The type of reaction arrow describes the direction in which the chemical reaction proceeds:

• The most common reaction arrow points from left to right. The symbol → means the reaction proceeds in a net forward direction, where reactants react and yield products.
• Some equations illustrate equilibrium. The symbol ⇌ indicates a condition of chemical equilibrium between the reactants and products. The reaction proceeds in both directions, with both sides of the equation acting simultaneously as reactants and products. If one arrow is shorter than the other, then the longer arrow represents the primary direction the reaction proceeds, while the shorter arrow indicates the reaction still occurs in this direction, but is not favored.
• The symbol ⇄ means that the reaction proceeds in both the forward and backward directions.
• An equal sign or = indicates a stoichiometric relationship.

Unbalanced and Balanced Chemical Equations

Chemical equations are either unbalanced or balanced.

• An unbalanced chemical equation lists the reactants and products and the direction the reaction proceeds, but does not specify a mole ratio between reactants and products. Example: H 2 + O 2 → H 2 O
• A balanced chemical equation includes coefficients before chemical formulas and indicates the stoichiometric ratio between reactants and products. A balanced chemical equation contains equal numbers and types of atoms on both sides of the reaction arrow. It is balanced for both mass and charge. Example: 2H 2 + O 2 → 2H 2 O

Ionic Chemical Equations

Ionic chemical equations indicate the net electrical charge on reactants and products. In a balanced ionic equation, the net electrical charge is the same on both sides of the reaction arrow.

Example: 2Ag + (aq) + Cr 2 O 7 2− (aq) → Ag 2 Cr 2 O 7 (s)

Note that you multiply the coefficient by the charge. In this example, there are two “+” charges for the silver ion and two “-” charges for the chromate ion. These charges cancel one another out, leaving a net neutral charge on the reactants side of the equation [2(+1) + 1(−2) = 0]. The product, silver chromate, is electrically neutral.

• Brady, James E.; Senese, Frederick; Jespersen, Neil D. (2007). Chemistry: Matter and Its Changes . John Wiley & Sons. ISBN 9780470120941.
• IUPAC (1997). “Chemical reaction equation.” Compendium of Chemical Terminology (2nd ed.) (the “Gold Book”). Oxford: Blackwell Scientific Publications. ISBN 0-9678550-9-8. doi: 10.1351/goldbook
• Marshall, Hugh (1902). “Suggested Modifications of the Sign of Equality for Use in Chemical Notation”. Proceedings of the Royal Society of Edinburgh . 24: 85–87. doi: 10.1017/S0370164600007720
• Myers, Richard (2009). The Basics of Chemistry . Greenwood Publishing Group. ISBN 978-0-313-31664-7.
• van ‘t Hoff, J.H. (1884). Études de Dynamique Chemique [Studies of chemical dynamics] (in French). Amsterdam, Netherlands: Frederik Muller & Co.

Related Posts

Chemical Equations: Using shorthand to show balanced reactions

by Robin Marks, M.A., Anthony Carpi, Ph.D.

Chemical equations are an efficient way to describe chemical reactions. This module explains the shorthand notation used to express how atoms are rearranged to make new compounds during a chemical reaction. It shows how balanced chemical equations convey proportions of each reactant and product involved. The module traces the development of chemical equations over the past four centuries as our understanding of chemical processes grew. A look at chemical equations reveals that nothing is lost and nothing is gained in a typical chemical reaction–matter simply changes form.

Imagine that you’re traveling in an exotic place and your rusty car muffler falls off. You need to find a place where you can buy a replacement, and you don’t speak the local language. Take a moment now to draw a sketch that conveys that you’re searching for a shop where you can get a new part installed. Maybe you include a car, a muffler, a storefront, and a person holding a screwdriver or other tool.

Then look at your picture: think about what kind of understanding you and the viewer need to share in order for you to convey your message. If you showed the same picture to someone 500 years ago, they’d have no idea what a car is, let alone what a muffler does or that there are people who specialize in installing them. But you and your 21st-century viewer can translate your sketch because of shared knowledge you have about cars.

Chemical equations play a similar role for people conveying messages about what happens during a chemical reaction . You probably remember that In a chemical reaction , bonds between atoms in a compound are broken, and the atoms rearrange to form new compounds, either releasing or consuming energy in the process (see our Chemical Reactions module).

As an example, let’s consider what happened to the muffler. Simply saying it rusted isn’t much of an explanation. You could say iron reacted with oxygen to produce rust. That's better, but not very precise. What, exactly, is rust? Chemically, it’s iron oxide, but iron forms many types of oxides. So we need a very specific way to express the chemical reaction that to led to our muffler’s demise.

• Writing chemistry in shorthand

That’s what chemical equations are for: they’re a type of shorthand used to precisely communicate exactly what’s happening in the reaction . In the most basic sense, a chemical equation describes the type and amount of each substance that reacts (the reactants) to form a given amount of specific substances produced (the products). Reactants will always react in proportions given in the equation. If the supply of one reactant runs out, the excess of the other will remain unreacted.

The shorthand that explains our rusty car part is this:

The number in front of an atom or molecule , which we call the coefficient, tells us the relative amounts of each substance involved in or produced by the reaction . The numbers in subscript refer specifically to the element that’s in front of them.

In other words, 4 iron atoms in the muffler reacted with 3 oxygen molecules in the air. Each of these oxygen molecules contains 2 oxygen atoms. When the chemical bonds reassemble and these reactants combine, the result is 2 molecules of a specific iron oxide that contains 2 iron atoms and 3 oxygen atoms—a.k.a rust.

Plenty of the iron in this muffler combined with oxygen in the environment, creating rust and leaving holes in the muffler where the iron has been consumed.

This equation conveys something much deeper than numbers of particles , though: it captures the centuries-long accumulation of knowledge about what our universe is made of and how matter interacts. Like an elegant poem (or like your rusty muffler drawing), a chemical equation conveys a world of complex concepts in just a few expressions.

Comprehension Checkpoint

• A brief history of the chemical equation

As our understanding of chemical processes deepened over time, chemical equations slowly became more sophisticated. Ultimately, such equations played a role in the recognition of chemistry as its own important science, separate from medicine, alchemy (which was popular in the 17th and 18th centuries), and physics.

The first known written chemical equation—which is really more of a diagram—appeared in what’s considered to be the first chemistry textbook, the Tyrocinium Chymicum (meaning “Begin Chemistry”). It was penned by French scientist and teacher Jean Beguin in Paris in 1615, and describes what Beguin observed when he heated antimony sulfide with a chloride of mercury. The mercury became vapor, leaving behind a residue of antimony oxychloride.

While Beguin’s diagram looks very different than modern chemical equations (and it isn’t entirely correct), it reflects an understanding of reactants and products in a chemical reaction .

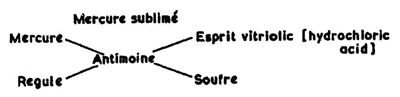
Figure 2: This drawing, from Jean Beguin’s Tyrocinium Chymicum , shows what the author believed was happening when antimony sulfide reacts with mercury chloride. The diagram conveys an understanding that a chemical reaction begins with specific reactants and produces specific products.

Beguin revealed the beginnings of an understanding of what occurs in a chemical reaction , but not an explanation of why. More than a century passed before new diagrams revealed deeper insights into the phenomena that drive reactions .

These insights came from William Cullen, who was also a teacher, and founded the chemistry department at the University of Glasgow in 1747. His hand-written lecture notes contain diagrams using arrows and letters, indicating four different types of reactions:

Figure 3: Drawings in a set of undated lecture notes written by William Cullen in the mid-18th century. Cullen developed the drawings in the hope that they would help his students better understand chemical reactions.

The diagram on the lower left described what Cullen called a “single elective attraction,” or what we now call a single replacement reaction , one that involves a single element taking the place of another element within a compound . (For more on reaction types, see our Chemical Equations module. The upper left is his diagram for a double replacement reaction, or one that involves the exchange of a component from each of two different compounds. In both cases, the reactions produce precipitates , indicated by the squiggly lines.

The two diagrams on the right relate to the dissolution of salts . The prevailing wisdom during Cullen’s time was that “elective attractions,” which we now know as charge , caused a metal in one substance to be attracted to another substance. The metals swapped places, forming either a new solid precipitate or dissolving in solution (sometimes producing a solution that displayed new properties).

While he didn’t have all the details right, Cullen’s thinking was on track, and his diagrams represent an important step toward what is now a common generic chemical equation:

We may take this simple type of equation for granted now, but at the time, it demonstrated some very perceptive ideas about what is actually happening during a chemical reaction . Remember, atoms and molecules were still not understood in Cullen’s time. It took a trio of chemists working over the next 50 years to clarify the picture that gave us the modern chemical equation. So, to grasp the idea that substances combined and were exchanged in chemical reactions is really significant.

In 1774, French chemist Antoine Lavoisier made an important observation – he noted that while substances in a chemical reaction changed form in ways described by Cullen, the mass of the system did not change. In other words, the amount of each element present remained the same, meaning that matter and mass are conserved. This is a crucial concept that will be important when we discuss balancing chemical reactions – all elements have to be fully accounted for at the start and at the end of a chemical reaction.

Around the same time as Lavosier, Joseph Proust , another Frenchman, was working extensively with copper carbonate. He found that regardless of how he changed the ratio of starting reactants – adding more copper sometimes, or more carbon or oxygen at others, the copper, carbon, and oxygen all reacted together in a constant ratio. His insight brought us the law of definite proportions: in any given compound , the elements occur in fixed ratios, regardless of their source. (Visit our module on Chemical Reactions to learn more about the work of these scientists). Again, this seems obvious to us today as we know that elements only react together in certain ways, but Proust completed his work before it was widely recognized that atoms and compounds existed.

Finally, in 1803, English chemist John Dalton tied these threads together by proposing that matter is made of atoms of unique substances that could not be created or destroyed (see our module Early Ideas about Matter for more information). He showed that each element could combine with multiple others to form different compounds , and always in whole number ratios .

This knowledge, taken together, provided the foundation for the chemical notation we use today. Chemical equations aren’t like mathematical equations, which have been around much longer. While the quantity of each element must be equal on both sides of the equation, you will never see an “equals” sign in a chemical equation. That’s because a chemical equation describes a process of change.

• Conservation of mass: a balancing act

Again, iron and oxygen combine to form a specific iron oxide. The arrow indicates that this reaction proceeds to the right as it is written, meaning that iron oxide is formed. In some cases, the reaction can also go backward, and we use a double arrow showing that some reactions go in both directions. Unfortunately for the muffler, that’s not the case here.

Now look at the equation more closely: How many iron atoms are on the reactant side (left) versus the product side (right)? How many oxygen atoms? You will see that they’re not equal as the equation is currently written.

However, we know from the law of conservation of matter that atoms can’t be created or destroyed. In other words, we can’t just get rid of an iron atom or create an oxygen atom to make the equation work. Nor can we change the subscripts in the reaction , because doing so would suggest that we are starting with a different reactant or obtaining a different product .

What we can do is adjust the numbers of reactant and product components (iron atoms and/or oxygen molecules on the left side and iron oxide molecules on the right), because doing so doesn’t imply creating or destroying matter . It’s a way of bookkeeping – in order to produce a molecule that has two iron atoms, you need to find a source of those atoms.

Let’s see how this works with the reaction that creates rust.

We already know that the numbers of each type of atom aren’t equal on each side of the reaction . To address this, we can add coefficients in front of the reactants and products to adjust the number of particles and create a balanced equation. (If there is no coefficient, it means there is only one of that type of particle.)

Let’s look at the reaction atom by atom.

Since the rust molecule has two iron atoms , we must balance the Fe atoms by adding the coefficient “2” in front of the iron atom on the reactant side, since that is the only place where iron appears on the left side of the equation. Now we have two irons on each side of the equation.

Moving on to the oxygen atoms , we find two on the left side of the equation, but three on the right side. We could mathematically balance the equation by using one and a half oxygen molecules , since each molecule is made up of two oxygen atoms. To better understand this, picture one oxygen molecule as two atoms bonded together O-O, therefore 1.5 oxygen molecules (O-O and O-O) provides three oxygen atoms:

In the real world, though, oxygen doesn’t occur in half-molecules. We can solve this conundrum by simply multiplying all the coefficients by two:

Now we have 4 atoms of iron on the left side, and 4 (2 molecules , each containing 2 iron atoms) on the right side. For oxygen, there are 6 atoms on the left side (3 molecules of 2 atoms each) and 6 on the right side (2 molecules containing 3 oxygen atoms). Now we have a balanced equation.

• Balanced equations indicate proportions
• 2 cups of flour
• 1 cup of sugar

and promises you a batch of 12 cookies. You can follow the recipe and use 2 cups of flour and 1 cup of sugar and expect 12 cookies, or you can double the recipe and use 4 cups of flour and 2 cups of sugar and expect 24 cookies (or you can triple the recipe, or half it, or so on).

Similarly, to make a “batch” of 2 rust molecules , you need 4 iron atoms and 3 oxygen molecules:

So, for every four atoms of iron and three molecules of oxygen, we get two molecules of rust. Much as you would do with a cookie recipe, you could double this: start with eight iron atoms and six oxygen molecules and make four molecules of rust. No matter how many times you multiply it, the base proportion always remains constant .

In the real world of chemistry, though, we don’t deal with individual atoms and molecules ; there are a lot more than two molecules of rust on a muffler that falls off a car. That’s where the concept of the mole comes in handy. A mole is a quantity of particles , specifically a mole is 6.022 x 10 23 particles. In other words, one mole of iron atoms contains 6.022 x 10 23 atoms. Four moles of iron atoms contain four times that amount, or 28.088 x 10 23 iron atoms. (To brush up on your mole math, see our module, The Mole and Atomic Mass ).

Note that when we were balancing the equation, we were thinking about the numbers of individual atoms on each side, attending to the law of conservation of matter that we can’t create or destroy atoms. When we’re thinking about proportions, however, we’re thinking about the coefficients in front of the particles , which represent the number of moles of each type of particle consumed or produced. These coefficients tell us how many moles of product can be produced with the number of moles of reactant present at the beginning of the reaction .

A chemical equation is an ingeniously compact way of communicating a lot of information in a short sequence of parts. Modern chemical equations reflect our understanding of matter being composed of atoms and of chemical reactions as a process of breaking bonds and rearranging atoms into new compounds . Mass is conserved in a chemical reaction , and the number of particles on each side of the equation must reflect this. A balanced equation also communicates the proportions of products and reactants involved in that reaction.

Table of Contents

Activate glossary term highlighting to easily identify key terms within the module. Once highlighted, you can click on these terms to view their definitions.

Activate NGSS annotations to easily identify NGSS standards within the module. Once highlighted, you can click on them to view these standards.

4.1 Writing and Balancing Chemical Equations

Learning objectives.

By the end of this section, you will be able to:

• Derive chemical equations from narrative descriptions of chemical reactions.
• Write and balance chemical equations in molecular, total ionic, and net ionic formats.

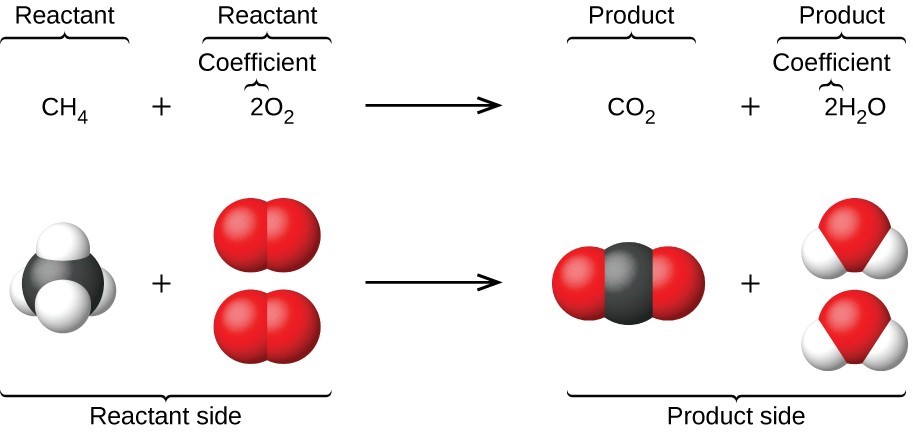
An earlier chapter of this text introduced the use of element symbols to represent individual atoms. When atoms gain or lose electrons to yield ions, or combine with other atoms to form molecules, their symbols are modified or combined to generate chemical formulas that appropriately represent these species. Extending this symbolism to represent both the identities and the relative quantities of substances undergoing a chemical (or physical) change involves writing and balancing a chemical equation . Consider as an example the reaction between one methane molecule (CH 4 ) and two diatomic oxygen molecules (O 2 ) to produce one carbon dioxide molecule (CO 2 ) and two water molecules (H 2 O). The chemical equation representing this process is provided in the upper half of Figure 4.2 , with space-filling molecular models shown in the lower half of the figure.

This example illustrates the fundamental aspects of any chemical equation:

• The substances undergoing reaction are called reactants , and their formulas are placed on the left side of the equation.
• The substances generated by the reaction are called products , and their formulas are placed on the right side of the equation.
• Plus signs (+) separate individual reactant and product formulas, and an arrow (⟶) (⟶) separates the reactant and product (left and right) sides of the equation.
• The relative numbers of reactant and product species are represented by coefficients (numbers placed immediately to the left of each formula). A coefficient of 1 is typically omitted.

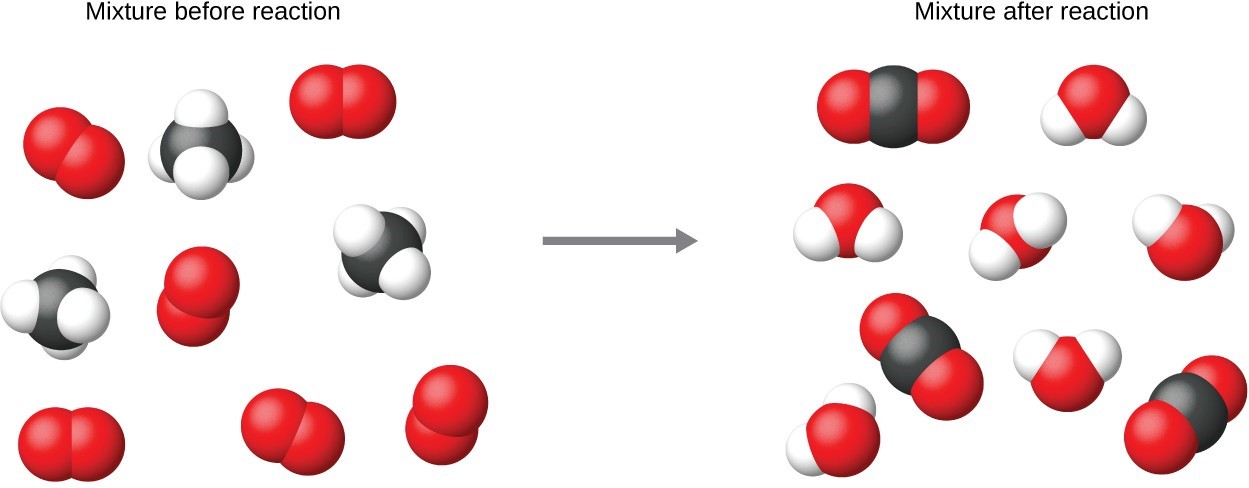
It is common practice to use the smallest possible whole-number coefficients in a chemical equation, as is done in this example. Realize, however, that these coefficients represent the relative numbers of reactants and products, and, therefore, they may be correctly interpreted as ratios. Methane and oxygen react to yield carbon dioxide and water in a 1:2:1:2 ratio. This ratio is satisfied if the numbers of these molecules are, respectively, 1-2-1-2, or 2-4-2-4, or 3-6-3-6, and so on ( Figure 4.3 ). Likewise, these coefficients may be interpreted with regard to any amount (number) unit, and so this equation may be correctly read in many ways, including:

• One methane molecule and two oxygen molecules react to yield one carbon dioxide molecule and two water molecules.
• One dozen methane molecules and two dozen oxygen molecules react to yield one dozen carbon dioxide molecules and two dozen water molecules.
• One mole of methane molecules and 2 moles of oxygen molecules react to yield 1 mole of carbon dioxide molecules and 2 moles of water molecules.

Balancing Equations

The chemical equation described in section 4.1 is balanced , meaning that equal numbers of atoms for each element involved in the reaction are represented on the reactant and product sides. This is a requirement the equation must satisfy to be consistent with the law of conservation of matter. It may be confirmed by simply summing the numbers of atoms on either side of the arrow and comparing these sums to ensure they are equal. Note that the number of atoms for a given element is calculated by multiplying the coefficient of any formula containing that element by the element’s subscript in the formula. If an element appears in more than one formula on a given side of the equation, the number of atoms represented in each must be computed and then added together. For example, both product species in the example reaction, CO 2 and H 2 O, contain the element oxygen, and so the number of oxygen atoms on the product side of the equation is

The equation for the reaction between methane and oxygen to yield carbon dioxide and water is confirmed to be balanced per this approach, as shown here:

A balanced chemical equation often may be derived from a qualitative description of some chemical reaction by a fairly simple approach known as balancing by inspection. Consider as an example the decomposition of water to yield molecular hydrogen and oxygen. This process is represented qualitatively by an unbalanced chemical equation:

Comparing the number of H and O atoms on either side of this equation confirms its imbalance:

The numbers of H atoms on the reactant and product sides of the equation are equal, but the numbers of O atoms are not. To achieve balance, the coefficients of the equation may be changed as needed. Keep in mind, of course, that the formula subscripts define, in part, the identity of the substance, and so these cannot be changed without altering the qualitative meaning of the equation. For example, changing the reactant formula from H 2 O to H 2 O 2 would yield balance in the number of atoms, but doing so also changes the reactant’s identity (it’s now hydrogen peroxide and not water). The O atom balance may be achieved by changing the coefficient for H 2 O to 2.

The H atom balance was upset by this change, but it is easily reestablished by changing the coefficient for the H 2 product to 2.

These coefficients yield equal numbers of both H and O atoms on the reactant and product sides, and the balanced equation is, therefore:

Example 4.1

Balancing chemical equations.

Next, count the number of each type of atom present in the unbalanced equation.

Though nitrogen is balanced, changes in coefficients are needed to balance the number of oxygen atoms. To balance the number of oxygen atoms, a reasonable first attempt would be to change the coefficients for the O 2 and N 2 O 5 to integers that will yield 10 O atoms (the least common multiple for the O atom subscripts in these two formulas).

The N atom balance has been upset by this change; it is restored by changing the coefficient for the reactant N 2 to 2.

The numbers of N and O atoms on either side of the equation are now equal, and so the equation is balanced.

Check Your Learning

It is sometimes convenient to use fractions instead of integers as intermediate coefficients in the process of balancing a chemical equation. When balance is achieved, all the equation’s coefficients may then be multiplied by a whole number to convert the fractional coefficients to integers without upsetting the atom balance. For example, consider the reaction of ethane (C 2 H 6 ) with oxygen to yield H 2 O and CO 2 , represented by the unbalanced equation:

Following the usual inspection approach, one might first balance C and H atoms by changing the coefficients for the two product species, as shown:

This results in seven O atoms on the product side of the equation, an odd number—no integer coefficient can be used with the O 2 reactant to yield an odd number, so a fractional coefficient, 7 2 , 7 2 , is used instead to yield a provisional balanced equation:

A conventional balanced equation with integer-only coefficients is derived by multiplying each coefficient by 2:

Finally with regard to balanced equations, recall that convention dictates use of the smallest whole-number coefficients . Although the equation for the reaction between molecular nitrogen and molecular hydrogen to produce ammonia is, indeed, balanced,

the coefficients are not the smallest possible integers representing the relative numbers of reactant and product molecules. Dividing each coefficient by the greatest common factor, 3, gives the preferred equation:

Link to Learning

Use this interactive tutorial for additional practice balancing equations.

Additional Information in Chemical Equations

The physical states of reactants and products in chemical equations very often are indicated with a parenthetical abbreviation following the formulas. Common abbreviations include s for solids, l for liquids, g for gases, and aq for substances dissolved in water ( aqueous solutions , as introduced in the preceding chapter). These notations are illustrated in the example equation here:

This equation represents the reaction that takes place when sodium metal is placed in water. The solid sodium reacts with liquid water to produce molecular hydrogen gas and the ionic compound sodium hydroxide (a solid in pure form, but readily dissolved in water).

Special conditions necessary for a reaction are sometimes designated by writing a word or symbol above or below the equation’s arrow. For example, a reaction carried out by heating may be indicated by the uppercase Greek letter delta (Δ) over the arrow.

Other examples of these special conditions will be encountered in more depth in later chapters.

Equations for Ionic Reactions

Given the abundance of water on earth, it stands to reason that a great many chemical reactions take place in aqueous media. When ions are involved in these reactions, the chemical equations may be written with various levels of detail appropriate to their intended use. To illustrate this, consider a reaction between ionic compounds taking place in an aqueous solution. When aqueous solutions of CaCl 2 and AgNO 3 are mixed, a reaction takes place producing aqueous Ca(NO 3 ) 2 and solid AgCl:

This balanced equation, derived in the usual fashion, is called a molecular equation because it doesn’t explicitly represent the ionic species that are present in solution. When ionic compounds dissolve in water, they may dissociate into their constituent ions, which are subsequently dispersed homogenously throughout the resulting solution (a thorough discussion of this important process is provided in the chapter on solutions). Ionic compounds dissolved in water are, therefore, more realistically represented as dissociated ions, in this case:

Unlike these three ionic compounds, AgCl does not dissolve in water to a significant extent, as signified by its physical state notation, s .

Explicitly representing all dissolved ions results in a complete ionic equation . In this particular case, the formulas for the dissolved ionic compounds are replaced by formulas for their dissociated ions:

Examining this equation shows that two chemical species are present in identical form on both sides of the arrow, Ca 2+ ( aq ) and NO 3 − ( a q ) . NO 3 − ( a q ) . These spectator ions —ions whose presence is required to maintain charge neutrality—are neither chemically nor physically changed by the process, and so they may be eliminated from the equation to yield a more succinct representation called a net ionic equation :

Following the convention of using the smallest possible integers as coefficients, this equation is then written:

This net ionic equation indicates that solid silver chloride may be produced from dissolved chloride and silver(I) ions, regardless of the source of these ions. These molecular and complete ionic equations provide additional information, namely, the ionic compounds used as sources of Cl − and Ag + .

Example 4.2

Ionic and molecular equations.

Balance is achieved easily in this case by changing the coefficient for NaOH to 2, resulting in the molecular equation for this reaction:

The two dissolved ionic compounds, NaOH and Na 2 CO 3 , can be represented as dissociated ions to yield the complete ionic equation:

Finally, identify the spectator ion(s), in this case Na + ( aq ), and remove it from each side of the equation to generate the net ionic equation:

Write balanced molecular, complete ionic, and net ionic equations for this process.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.

Access for free at https://openstax.org/books/chemistry-2e/pages/1-introduction

• Authors: Paul Flowers, Klaus Theopold, Richard Langley, William R. Robinson, PhD
• Publisher/website: OpenStax
• Book title: Chemistry 2e
• Publication date: Feb 14, 2019
• Location: Houston, Texas
• Book URL: https://openstax.org/books/chemistry-2e/pages/1-introduction
• Section URL: https://openstax.org/books/chemistry-2e/pages/4-1-writing-and-balancing-chemical-equations

© Jun 3, 2024 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

55 Writing and Balancing Chemical Equations

Learning objectives.

• Derive chemical equations from narrative descriptions of chemical reactions.
• Write and balance chemical equations

An earlier chapter of this text introduced the use of element symbols to represent individual atoms. When atoms gain or lose electrons to yield ions, or combine with other atoms to form molecules, their symbols are modified or combined to generate chemical formulas that appropriately represent these species. Extending this symbolism to represent both the identities and the relative quantities of substances undergoing a chemical (or physical) change involves writing and balancing a chemical equation . Consider as an example the reaction between one methane molecule ([latex]\text{CH}_4[/latex]) and two diatomic oxygen molecules ([latex]\text{O}_2[/latex]) to produce one carbon dioxide molecule ([latex]\text{CO}_2[/latex]) and two water molecules ([latex]\text{H}_2\text{O}[/latex]). The chemical equation representing this process is provided in the upper half of the following figure, with space-filling molecular models shown in the lower half of the figure.

This example illustrates the fundamental aspects of any chemical equation:

• The substances undergoing reaction are called reactants , and their formulas are placed on the left side of the equation.
• The substances generated by the reaction are called products , and their formulas are placed on the right side of the equation.
• Plus signs (+) separate individual reactant and product formulas, and an arrow [latex]( \rightarrow )[/latex] separates the reactant and product (left and right) sides of the equation.
• The relative numbers of reactant and product species are represented by coefficients  (numbers placed immediately to the left of each formula). A coefficient of 1 is typically omitted.

It is common practice to use the smallest possible whole-number coefficients in a chemical equation, as is done in this example. Realize, however, that these coefficients represent the relative numbers of reactants and products, and, therefore, they may be correctly interpreted as ratios. Methane and oxygen react to yield carbon dioxide and water in a 1:2:1:2 ratio. This ratio is satisfied if the numbers of these molecules are, respectively, 1-2-1-2, or 2-4-2-4, or 3-6-3-6, and so on. Likewise, these coefficients may be interpreted with regard to any amount (number) unit, and so this equation may be correctly read in many ways, including:

• One methane molecule and two oxygen molecules react to yield one carbon dioxide molecule and two water molecules.
• One dozen methane molecules and two dozen oxygen molecules react to yield one dozen carbon dioxide molecules and two dozen water molecules.

Balancing Equations

The chemical equation described in section 4.1 is balanced , meaning that equal numbers of atoms for each element involved in the reaction are represented on the reactant and product sides. This is a requirement the equation must satisfy to be consistent with the law of conservation of matter. It may be confirmed by simply summing the numbers of atoms on either side of the arrow and comparing these sums to ensure they are equal. Note that the number of atoms for a given element is calculated by multiplying the coefficient of any formula containing that element by the element’s subscript in the formula. If an element appears in more than one formula on a given side of the equation, the number of atoms represented in each must be computed and then added together. For example, both product species in the example reaction, [latex]\text{CO}_2[/latex] and [latex]\text{H}_2\text{O}[/latex], contain the element oxygen, and so the number of oxygen atoms on the product side of the equation is

[latex]\left( \text{1 CO}_2 \text{ molecule} \times \frac{ \text{2 O atoms} }{ \text{CO}_2 \text{ molecule} } \right) + \left( \text{2 H}_2\text{O molecules} \times \frac{ \text{1 O atom} }{ \text{H}_2\text{O molecule} } \right) = \text{4 O atoms}[/latex]

The equation for the reaction between methane and oxygen to yield carbon dioxide and water is confirmed to be balanced per this approach, as shown here:

[latex]\text{CH}_4 + \text{2O}_2 \longrightarrow \text{CO}_2 + \text{2H}_2\text{O}[/latex]

A balanced chemical equation often may be derived from a qualitative description of some chemical reaction by a fairly simple approach known as balancing by inspection. Consider as an example the decomposition of water to yield molecular hydrogen and oxygen. This process is represented qualitatively by an unbalanced chemical equation:

[latex]\text{H}_2\text{O} \longrightarrow \text{H}_2 + \text{O}_2 \ \ \ \ \text{(unbalanced)}[/latex]

Comparing the number of H and O atoms on either side of this equation confirms its imbalance:

The numbers of H atoms on the reactant and product sides of the equation are equal, but the numbers of O atoms are not. To achieve balance, the coefficients of the equation may be changed as needed. Keep in mind, of course, that the formula subscripts define, in part, the identity of the substance, and so these cannot be changed without altering the qualitative meaning of the equation. For example, changing the reactant formula from [latex]\text{H}_2\text{O}[/latex] to [latex]\text{H}_2\text{O}_2[/latex] would yield balance in the number of atoms, but doing so also changes the reactant’s identity (it’s now hydrogen peroxide and not water). The O atom balance may be achieved by changing the coefficient for [latex]\text{H}_2\text{O}[/latex] to 2.

[latex]\text{2H}_2\text{O} \longrightarrow \text{H}_2 + \text{O}_2 \ \ \ \ \text{(unbalanced)}[/latex]

The H atom balance was upset by this change, but it is easily reestablished by changing the coefficient for the [latex]\text{H}_2[/latex] product to 2.

[latex]\text{2H}_2\text{O} \longrightarrow \text{2H}_2 + \text{O}_2 \ \ \ \ \text{(balanced)}[/latex]

These coefficients yield equal numbers of both H and O atoms on the reactant and product sides, and the balanced equation is, therefore:

[latex]\text{2H}_2\text{O} \longrightarrow \text{2H}_2 + \text{O}_2[/latex]

Balancing Chemical Equations Write a balanced equation for the reaction of molecular nitrogen ([latex]\text{N}_2[/latex]) and oxygen ([latex]\text{O}_2[/latex]) to form dinitrogen pentoxide. Solution First, write the unbalanced equation.

[latex]\text{N}_2 + \text{O}_2 \longrightarrow \text{N}_2\text{O}_5 \ \ \ \ \text{(unbalanced)}[/latex]

Next, count the number of each type of atom present in the unbalanced equation.

Though nitrogen is balanced, changes in coefficients are needed to balance the number of oxygen atoms. To balance the number of oxygen atoms, a reasonable first attempt would be to change the coefficients for the [latex]\text{O}_2[/latex] and [latex]\text{N}_2\text{O}_5[/latex] to integers that will yield 10 O atoms (the least common multiple for the O atom subscripts in these two formulas).

[latex]\text{N}_2 + \text{5O}_2 \longrightarrow \text{2N}_2\text{O}_5 \ \ \ \ \text{(unbalanced)}[/latex]

The N atom balance has been upset by this change; it is restored by changing the coefficient for the reactant [latex]\text{N}_2[/latex] to 2.

[latex]\text{2N}_2 + \text{5O}_2 \longrightarrow \text{2N}_2\text{O}_5[/latex]

The numbers of N and O atoms on either side of the equation are now equal, and so the equation is balanced.

Check Your Learning Write a balanced equation for the decomposition of ammonium nitrate to form molecular nitrogen, molecular oxygen, and water. (Hint: Balance oxygen last, since it is present in more than one molecule on the right side of the equation.)

It is sometimes convenient to use fractions instead of integers as intermediate coefficients in the process of balancing a chemical equation. When balance is achieved, all the equation’s coefficients may then be multiplied by a whole number to convert the fractional coefficients to integers without upsetting the atom balance. For example, consider the reaction of ethane ([latex]\text{C}_2\text{H}_6[/latex]) with oxygen to yield [latex]\text{H}_2\text{O}[/latex] and [latex]\text{CO}_2[/latex], represented by the unbalanced equation:

[latex]\text{C}_2\text{H}_6 + \text{O}_2 \longrightarrow \text{H}_2\text{O} + \text{CO}_2 \ \ \ \ \text{(unbalanced)}[/latex]

Following the usual inspection approach, one might first balance C and H atoms by changing the coefficients for the two product species, as shown:

[latex]\text{C}_2\text{H}_6 + \text{O}_2 \longrightarrow \text{3H}_2\text{O} + 2\text{CO}_2 \ \ \ \ \text{(unbalanced)}[/latex]

This results in seven O atoms on the product side of the equation, an odd number—no integer coefficient can be used with the [latex]\text{O}_2[/latex] reactant to yield an odd number, so a fractional coefficient, [latex]\frac{7}{2}[/latex], is used instead to yield a provisional balanced equation:

[latex]\text{C}_2\text{H}_6 + \frac{7}{2}\text{O}_2 \longrightarrow \text{3H}_2\text{O} + \text{2CO}_2[/latex]

A conventional balanced equation with integer-only coefficients is derived by multiplying each coefficient by 2:

[latex]\text{2C}_2\text{H}_6 + \text{7O}_2 \longrightarrow \text{6H}_2\text{O} + 4\text{CO}_2[/latex]

Finally with regard to balanced equations, recall that convention dictates use of the smallest whole-number coefficients . Although the equation for the reaction between molecular nitrogen and molecular hydrogen to produce ammonia is, indeed, balanced,

[latex]\text{3N}_2 + \text{9H}_2 \longrightarrow \text{6NH}_3[/latex]

the coefficients are not the smallest possible integers representing the relative numbers of reactant and product molecules. Dividing each coefficient by the greatest common factor, 3, gives the preferred equation:

[latex]\text{N}_2 + \text{3H}_2 \longrightarrow \text{2NH}_3[/latex]

Use this interactive tutorial for additional practice balancing equations.

Additional Information in Chemical Equations

The physical states of reactants and products in chemical equations very often are indicated with a parenthetical abbreviation following the formulas. Common abbreviations include s for solids, l for liquids, g for gases, and aq for substances dissolved in water ( aqueous solutions , as introduced in the preceding chapter). These notations are illustrated in the example equation here:

[latex]\text{2Na} (s) + \text{2H}_2\text{O} (l) \longrightarrow \text{2NaOH} (aq) + \text{H}_2 (g)[/latex]

This equation represents the reaction that takes place when sodium metal is placed in water. The solid sodium reacts with liquid water to produce molecular hydrogen gas and the ionic compound sodium hydroxide (a solid in pure form, but readily dissolved in water).

Special conditions necessary for a reaction are sometimes designated by writing a word or symbol above or below the equation’s arrow. For example, a reaction carried out by heating may be indicated by the uppercase Greek letter delta ( Δ ) over the arrow.

[latex]\text{CaCO}_3 (s) \xrightarrow{\Delta} \text{CaO} (s) + \text{CO}_2 (g)[/latex]

Other examples of these special conditions will be encountered in more depth in later chapters.

KEY TAKEAWAYS

Chemical equations are symbolic representations of chemical and physical changes. Formulas for the substances undergoing the change (reactants) and substances generated by the change (products) are separated by an arrow and preceded by integer coefficients indicating their relative numbers. Balanced equations are those whose coefficients result in equal numbers of atoms for each element in the reactants and products.

Chemistry End of Chapter Exercises

• What does it mean to say an equation is balanced? Why is it important for an equation to be balanced? An equation is balanced when the same number of each element is represented on the reactant and product sides. Equations must be balanced to accurately reflect the law of conservation of matter.

(a) [latex]\text{PCl}_5 (s) + \text{H}_2\text{O} (l) \rightarrow \text{POCl}_3 (l) \text{ + 2HCl} (aq)[/latex]; (b) [latex]\text{3Cu} (s) \text{ + 8HNO}_3 (aq) \rightarrow \text{3Cu(NO}_3)_2 (aq) \text{ + 4H}_2\text{O} (l) \text{ + 2NO} (g)[/latex];

(c) [latex]\text{H}_2 (g) \text{ + I}_2 (s) \rightarrow \text{2HI} (s)[/latex];

(d) [latex]\text{4Fe} (s) \text{ + 3O}_2 (g) \rightarrow \text{2Fe}_2\text{O}_3 (s)[/latex];

(e) [latex]\text{2Na} (s) + \text{2H}_2\text{O} (l) \rightarrow \text{2NaOH} (aq) \text{ + H}_2 (g)[/latex];

(f) [latex]\text{(NH}_4)_2\text{Cr}_2\text{O}_7 (s) \rightarrow \text{Cr}_2\text{O}_3 (s) \text{ + N}_2 (g) \text{ + 4H}_2\text{O} (g)[/latex];

(g) [latex]\text{P}_4 (s) \text{ + 6Cl}_2 (g) \rightarrow \text{4PCl}_3 (l)[/latex];

(h) [latex]\text{PtCl}_4 (s) \rightarrow \text{Pt} (s) \text{ + 2Cl}_2 (g)[/latex]

• Balance the following equations: (a) [latex]\text{Ag} (s) \text{ + H}_2\text{S} (g) \text{ + O}_2 (g) \rightarrow \text{Ag}_2\text{S} (s) \text{ + H}_2\text{O} (l)[/latex] (b) [latex]\text{P}_4 (s) \text{ + O}_2 (g) \rightarrow \text{P}_4\text{O}_{10} (s)[/latex] (c) [latex]\text{Pb} (s) \text{+ H}_2\text{O} (l) \text{ + O}_2 (g) \rightarrow \text{Pb(OH)}_2 (s)[/latex] (d) [latex]\text{Fe} (s) \text{ + H}_2\text{O} (l) \rightarrow \text{Fe}_3\text{O}_4 (s) \text{ + H}_2 (g)[/latex] (e) [latex]\text{Sc}_2\text{O}_3 (s) \text{ + SO}_3 (l) \rightarrow \text{Sc}_2\text{(SO}_4)_3 (s)[/latex] (f) [latex]\text{Ca}_3\text{(PO}_4)_2 (aq) \text{ + H}_3\text{PO}_4 (aq) \rightarrow \text{Ca(H}_2\text{PO}_4)_2 (aq)[/latex] (g) [latex]\text{Al} (s) \text{ + H}_2\text{SO}_4 (aq) \rightarrow \text{Al}_2\text{(SO}_4)_3 (s) \text{ + H}_2 (g)[/latex] (h) [latex]\text{TiCl}_4 (s) \text{ + H}_2\text{O} (g) \rightarrow \text{TiO}_2 (s) \text{ + HCl} (g)[/latex]

(a) [latex]\text{CaCO}_3 (s) \rightarrow \text{CaO} (s) \text{ + CO}_2 (g)[/latex]; (b) [latex]\text{2C}_4\text{H}_{10} (g) \text{ + 13O}_2 (g) \rightarrow \text{8CO}_2 (g) \text{ + 10H}_2\text{O} (g)[/latex];

(c) [latex]\text{MgCl}_2 (aq) \text{ + 2NaOH} (aq) \rightarrow \text{Mg(OH)}_2 (s) \text{ + 2NaCl} (aq)[/latex];

(d) [latex]\text{2H}_2\text{O} (g) \text{ + 2Na} (s) \rightarrow \text{2NaOH} (s) \text{ + H}_2 (g)[/latex]

• Write a balanced equation describing each of the following chemical reactions.  (a) Solid potassium chlorate, [latex]\text{KClO}_3[/latex], decomposes to form solid potassium chloride and diatomic oxygen gas.     (b) Solid aluminum metal reacts with solid diatomic iodine to form solid [latex]\text{Al}_2\text{I}_6[/latex].     (c) When solid sodium chloride is added to aqueous sulfuric acid, hydrogen chloride gas and aqueous sodium sulfate are produced.     (d) Aqueous solutions of phosphoric acid and potassium hydroxide react to produce aqueous potassium dihydrogen phosphate and liquid water.

(a) [latex]\text{Ba(NO}_3)_2, \text{KClO}_3[/latex]; (b) [latex]\text{2KClO}_3 (s) \rightarrow \text{2KCl} (s) \text{ + 3O}_2 (g)[/latex];

(c) [latex]\text{2Ba(NO}_3)_2 (s) \rightarrow \text{2BaO} (s) \text{ + 2N}_2 (g) \text{ + 5O}_2 (g)[/latex];

(d)  [latex]\text{2Mg} (s) \text{ + O}_2 (g) \rightarrow \text{2MgO} (s)[/latex]; [latex]\text{4Al} (s) \text{ + 3O}_2 (g) \rightarrow \text{2Al}_2\text{O}_3 (s)[/latex]; [latex]\text{4Fe} (s) \text{ + 3O}_2 (g) \rightarrow \text{2Fe}_2\text{O}_3 (s)[/latex]

• Aqueous hydrogen fluoride (hydrofluoric acid) is used to etch glass and to analyze minerals for their silicon content. Hydrogen fluoride will also react with sand (silicon dioxide).  (a) Write an equation for the reaction of solid silicon dioxide with hydrofluoric acid to yield gaseous silicon tetrafluoride and liquid water.     (b) The mineral fluorite (calcium fluoride) occurs extensively in Illinois. Solid calcium fluoride can also be prepared by the reaction of aqueous solutions of calcium chloride and sodium fluoride, yielding aqueous sodium chloride as the other product. Write complete equations for this reaction [latex]\text{4HF} (aq) \text{ + SiO}_2(s) \rightarrow \text{SiF}_4(g) \text{ + 2H}_2\text{O}(l)[/latex];
• A novel process for obtaining magnesium from sea water involves several reactions. Write a balanced chemical equation for each step of the process.  (a) The first step is the decomposition of solid calcium carbonate from seashells to form solid calcium oxide and gaseous carbon dioxide.     (b) The second step is the formation of solid calcium hydroxide as the only product from the reaction of the solid calcium oxide with liquid water.     (c) Solid calcium hydroxide is then added to the seawater, reacting with dissolved magnesium chloride to yield solid magnesium hydroxide and aqueous calcium chloride.     (d) The solid magnesium hydroxide is added to a hydrochloric acid solution, producing dissolved magnesium chloride and liquid water.     (e) Finally, the magnesium chloride is melted and electrolyzed to yield liquid magnesium metal and diatomic chlorine gas.

This chapter is an adaptation of the chapter “ Writing and Balancing Chemical Equations ” in Chemistry: Atoms First 2e by OpenStax and is licensed under a CC BY 4.0 license.

Access for free at https://openstax.org/books/chemistry-atoms-first-2e/pages/1-introduction

symbolic representation of a chemical reaction

substance undergoing a chemical or physical change; shown on the left side of the arrow in a chemical equation

substance formed by a chemical or physical change; shown on the right side of the arrow in a chemical equation

number placed in front of symbols or formulas in a chemical equation to indicate their relative amount

chemical equation with equal numbers of atoms for each element in the reactant and product

one of the three positions in a trigonal bipyramidal geometry with 120° angles between them; the axial positions are located at a 90° angle

property of a molecule that describes the separation of charge determined by the sum of the individual bond moments based on the molecular structure

separation of charge in a bond that depends on the difference in electronegativity and the bond distance represented by partial charges or a vector

(also, bond length) distance between the nuclei of two bonded atoms

angle between any two covalent bonds that share a common atom

location in a trigonal bipyramidal geometry in which there is another atom at a 180° angle and the equatorial positions are at a 90° angle

force of attraction between nucleons that holds a nucleus together

Introductory Chemistry Copyright © by OpenStax is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License , except where otherwise noted.

Share This Book

Unit 3: The Mole – Chemical Formulas, Stoichiometry, Limiting Reactant, Percent Yield

Writing and balancing chemical equations, learning objectives.

By the end of this section, you will be able to:

• Derive chemical equations from narrative descriptions of chemical reactions.
• Write and balance chemical equations in molecular formats.

The preceding chapter introduced the use of element symbols to represent individual atoms. When atoms gain or lose electrons to yield ions, or combine with other atoms to form molecules, their symbols are modified or combined to generate chemical formulas that appropriately represent these species. Extending this symbolism to represent both the identities and the relative quantities of substances undergoing a chemical (or physical) change involves writing and balancing a chemical equation . Consider as an example the reaction between one methane molecule (CH 4 ) and two diatomic oxygen molecules (O 2 ) to produce one carbon dioxide molecule (CO 2 ) and two water molecules (H 2 O). The chemical equation representing this process is provided in the upper half of Figure 1, with space-filling molecular models shown in the lower half of the figure.

Figure 1. The reaction between methane and oxygen to yield carbon dioxide in water (shown at bottom) may be represented by a chemical equation using formulas (top).

This example illustrates the fundamental aspects of any chemical equation:

• The substances undergoing reaction are called reactants , and their formulas are placed on the left side of the equation.
• The substances generated by the reaction are called products , and their formulas are placed on the right sight of the equation.
• Plus signs (+) separate individual reactant and product formulas, and an arrow ([latex]\rightarrow[/latex]) separates the reactant and product (left and right) sides of the equation.
• The relative numbers of reactant and product species are represented by coefficients (numbers placed immediately to the left of each formula). A coefficient of 1 is typically omitted.

It is common practice to use the smallest possible whole-number coefficients in a chemical equation, as is done in this example. Realize, however, that these coefficients represent the relative numbers of reactants and products, and, therefore, they may be correctly interpreted as ratios. Methane and oxygen react to yield carbon dioxide and water in a 1:2:1:2 ratio. This ratio is satisfied if the numbers of these molecules are, respectively, 1-2-1-2, or 2-4-2-4, or 3-6-3-6, and so on (Figure 2). Likewise, these coefficients may be interpreted with regard to any amount (number) unit, and so this equation may be correctly read in many ways, including:

• One methane molecule and two oxygen molecules react to yield one carbon dioxide molecule and two water molecules.
• One dozen methane molecules and two dozen oxygen molecules react to yield one dozen carbon dioxide molecules and two dozen water molecules.
• One mole of methane molecules and 2 moles of oxygen molecules react to yield 1 mole of carbon dioxide molecules and 2 moles of water molecules.

Figure 2. Regardless of the absolute number of molecules involved, the ratios between numbers of molecules are the same as that given in the chemical equation.

Balancing Equations

A  balanced chemical is equation  has equal numbers of atoms for each element involved in the reaction are represented on the reactant and product sides. This is a requirement the equation must satisfy to be consistent with the law of conservation of matter. It may be confirmed by simply summing the numbers of atoms on either side of the arrow and comparing these sums to ensure they are equal. Note that the number of atoms for a given element is calculated by multiplying the coefficient of any formula containing that element by the element’s subscript in the formula. If an element appears in more than one formula on a given side of the equation, the number of atoms represented in each must be computed and then added together. For example, both product species in the example reaction, CO 2 and H 2 O, contain the element oxygen, and so the number of oxygen atoms on the product side of the equation is

[latex]\left(1{\text{CO}}_{2}\text{ molecule }\times \frac{\text{2 O atoms}}{{\text{CO}}_{2}\text{ molecule }}\right)+\left(2{\text{H}}_{2}\text{O molecule }\times \frac{\text{1 O atom}}{{\text{H}}_{2}\text{O molecule }}\right)=\text{4 O atoms}[/latex]

The equation for the reaction between methane and oxygen to yield carbon dioxide and water is confirmed to be balanced per this approach, as shown here:

[latex]{\text{CH}}_{4}+2{\text{O}}_{2}\rightarrow{\text{CO}}_{2}+2{\text{H}}_{2}\text{O}[/latex]

A balanced chemical equation often may be derived from a qualitative description of some chemical reaction by a fairly simple approach known as balancing by inspection. Consider as an example the decomposition of water to yield molecular hydrogen and oxygen. This process is represented qualitatively by an unbalanced chemical equation:

[latex]{\text{H}}_{2}\text{O}\rightarrow{\text{H}}_{2}+{\text{O}}_{2}\text{(unbalanced)}[/latex]

Comparing the number of H and O atoms on either side of this equation confirms its imbalance:

The numbers of H atoms on the reactant and product sides of the equation are equal, but the numbers of O atoms are not. To achieve balance, the coefficients of the equation may be changed as needed. Keep in mind, of course, that the formula subscripts define, in part, the identity of the substance, and so these cannot be changed without altering the qualitative meaning of the equation. For example, changing the reactant formula from H 2 O to H 2 O 2 would yield balance in the number of atoms, but doing so also changes the reactant’s identity (it’s now hydrogen peroxide and not water). The O atom balance may be achieved by changing the coefficient for H 2 O to 2.

[latex]\mathbf{2}\text{H}_{2}\text{O}\rightarrow{\text{H}}_{2}+{\text{O}}_{2}\text{(unbalanced)}[/latex]

The H atom balance was upset by this change, but it is easily reestablished by changing the coefficient for the H 2 product to 2.

[latex]2{\text{H}}_{2}\text{O}\rightarrow\mathbf{2}{\text{H}}_{2}+{\text{O}}_{2}\text{(balanced)}[/latex]

These coefficients yield equal numbers of both H and O atoms on the reactant and product sides, and the balanced equation is, therefore:

[latex]2{\text{H}}_{2}\text{O}\rightarrow 2{\text{H}}_{2}+{\text{O}}_{2}[/latex]

Example 1:  Balancing Chemical Equations

Write a balanced equation for the reaction of molecular nitrogen (N 2 ) and oxygen (O 2 ) to form dinitrogen pentoxide.

First, write the unbalanced equation:

[latex]{\text{N}}_{2}+{\text{O}}_{2}\rightarrow{\text{N}}_{2}{\text{O}}_{5}\text{(unbalanced)}[/latex]

Next, count the number of each type of atom present in the unbalanced equation.

Though nitrogen is balanced, changes in coefficients are needed to balance the number of oxygen atoms. To balance the number of oxygen atoms, a reasonable first attempt would be to change the coefficients for the O 2 and N 2 O 5 to integers that will yield 10 O atoms (the least common multiple for the O atom subscripts in these two formulas).

[latex]{\text{N}}_{2}+\mathbf{5}{\text{O}}_{2}\rightarrow\mathbf{2}{\text{N}}_{2}{\text{O}}_{5}\text{(unbalanced)}[/latex]

The N atom balance has been upset by this change; it is restored by changing the coefficient for the reactant N 2 to 2.

[latex]2{\text{N}}_{2}+5{\text{O}}_{2}\rightarrow 2{\text{N}}_{2}{\text{O}}_{5}[/latex]

The numbers of N and O atoms on either side of the equation are now equal, and so the equation is balanced.

Check Your Learning

Write a balanced equation for the decomposition of ammonium nitrate to form molecular nitrogen, molecular oxygen, and water. (Hint: Balance oxygen last, since it is present in more than one molecule on the right side of the equation.)

It is sometimes convenient to use fractions instead of integers as intermediate coefficients in the process of balancing a chemical equation. When balance is achieved, all the equation’s coefficients may then be multiplied by a whole number to convert the fractional coefficients to integers without upsetting the atom balance. For example, consider the reaction of ethane (C 2 H 6 ) with oxygen to yield H 2 O and CO 2 , represented by the unbalanced equation:

[latex]{\text{C}}_{2}{\text{H}}_{6}+{\text{O}}_{2}\rightarrow{\text{H}}_{2}\text{O}+{\text{CO}}_{2}\text{(unbalanced)}[/latex]

Following the usual inspection approach, one might first balance C and H atoms by changing the coefficients for the two product species, as shown:

[latex]{\text{C}}_{2}{\text{H}}_{6}+{\text{O}}_{2}\rightarrow 3{\text{H}}_{2}\text{O}+2{\text{CO}}_{2}\text{(unbalanced)}[/latex]

This results in seven O atoms on the product side of the equation, an odd number—no integer coefficient can be used with the O 2 reactant to yield an odd number, so a fractional coefficient, [latex]\displaystyle\frac{7}{2}[/latex] , is used instead to yield a provisional balanced equation:

[latex]{\text{C}}_{2}{\text{H}}_{6}+\frac{7}{2}{\text{O}}_{2}\rightarrow 3{\text{H}}_{2}\text{O}+2{\text{CO}}_{2}[/latex]

A conventional balanced equation with integer-only coefficients is derived by multiplying each coefficient by 2:

[latex]2{\text{C}}_{2}{\text{H}}_{6}+7{\text{O}}_{2}\rightarrow 6{\text{H}}_{2}\text{O}+4{\text{CO}}_{2}[/latex]

Finally with regard to balanced equations, recall that convention dictates use of the smallest whole-number coefficients . Although the equation for the reaction between molecular nitrogen and molecular hydrogen to produce ammonia is, indeed, balanced,

[latex]3{\text{N}}_{2}+9{\text{H}}_{2}\rightarrow 6{\text{NH}}_{3}[/latex]

the coefficients are not the smallest possible integers representing the relative numbers of reactant and product molecules. Dividing each coefficient by the greatest common factor, 3, gives the preferred equation:

[latex]{\text{N}}_{2}+3{\text{H}}_{2}\rightarrow 2{\text{NH}}_{3}[/latex]

Balance the following equations:

• [latex]{\text{PCl}}_{5}\text{(}s\text{)}+{\text{H}}_{2}\text{O(}l\text{)}\rightarrow{\text{POCl}}_{3}\text{(}l\text{)}+\text{HCl(}aq\text{)}[/latex]
• [latex]\text{Ag}\text{(}s\text{)}+{\text{H}}_{2}\text{S}\text{(}g\text{)}+{\text{O}}_{2}\text{(}g\text{)}\rightarrow{\text{Ag}}_{2}\text{S}\text{(}s\text{)}+{\text{H}}_{2}\text{O}\text{(}l\text{)}[/latex]
• [latex]\text{Cu(}s\text{)}+{\text{HNO}}_{3}\text{(}aq\text{)}\rightarrow\text{Cu}{\text{(}{\text{NO}}_{3}\text{)}}_{2}\text{(}aq\text{)}+{\text{H}}_{2}\text{O(}l\text{)}+\text{NO(}g\text{)}[/latex]
• [latex]{\text{P}}_{4}\text{(}s\text{)}+{\text{O}}_{2}\text{(}g\text{)}\rightarrow{\text{P}}_{4}{\text{O}}_{10}\text{(}s\text{)}[/latex]
• [latex]{\text{H}}_{2}\text{(}g\text{)}+{\text{I}}_{2}\text{(}s\text{)}\rightarrow\text{HI(}s\text{)}[/latex]
• [latex]\text{Pb(}s\text{)}+{\text{H}}_{2}\text{O(}l\text{)}+{\text{O}}_{2}\text{(}g\text{)}\rightarrow{\text{Pb(OH)}}_{2}\text{(}s\text{)}[/latex]
• [latex]\text{Fe(}s\text{)}+{\text{O}}_{2}\text{(}g\text{)}\rightarrow{\text{Fe}}_{2}{\text{O}}_{3}\text{(}s\text{)}[/latex]
• [latex]\text{Fe(}s\text{)}+{\text{H}}_{2}\text{O(}l\text{)}\rightarrow{\text{Fe}}_{3}{\text{O}}_{4}\text{(}s\text{)}+{\text{H}}_{2}\text{(}g\text{)}[/latex]
• [latex]\text{Na(}s\text{)}+{\text{H}}_{2}\text{O(}l\text{)}\rightarrow\text{NaOH}\text{(}aq\text{)}+{\text{H}}_{2}\text{(}g\text{)}[/latex]
• [latex]{\text{Sc}}_{2}{\text{O}}_{3}\text{(}s\text{)}+{\text{SO}}_{3}\text{(}l\text{)}\rightarrow{\text{Sc}}_{2}{\text{(}{\text{SO}}_{4}\text{)}}_{3}\text{(}s\text{)}[/latex]
• [latex]{\text{(}{\text{NH}}_{4}\text{)}}_{2}{\text{Cr}}_{2}{\text{O}}_{7}\text{(}s\text{)}\rightarrow{\text{Cr}}_{2}{\text{O}}_{3}\text{(}s\text{)}+{\text{N}}_{2}\text{(}g\text{)}+{\text{H}}_{2}\text{O(}g\text{)}[/latex]
• [latex]{\text{Ca}}_{3}{\text{(}{\text{PO}}_{4}\text{)}}_{2}\text{(}aq\text{)}+{\text{H}}_{3}{\text{PO}}_{4}\text{(}aq\text{)}\rightarrow\text{Ca}{\text{(}{\text{H}}_{2}{\text{PO}}_{4}\text{)}}_{2}\text{(}aq\text{)}[/latex]
• [latex]{\text{P}}_{4}\text{(}s\text{)}+{\text{Cl}}_{2}\text{(}g\text{)}\rightarrow{\text{PCl}}_{3}\text{(}l\text{)}[/latex]
• [latex]\text{Al(}s\text{)}+{\text{H}}_{2}{\text{SO}}_{4}\text{(}aq\text{)}\rightarrow{\text{Al}}_{2}{\text{(}{\text{SO}}_{4}\text{)}}_{3}\text{(}aq\text{)}+{\text{H}}_{2}\text{(}g\text{)}[/latex]
• [latex]{\text{PtCl}}_{4}\text{(}s\text{)}\rightarrow\text{Pt}\text{(}s\text{)}+{\text{Cl}}_{2}\text{(}g\text{)}[/latex]
• [latex]{\text{TiCl}}_{4}\text{(}s\text{)}+{\text{H}}_{2}\text{O(}g\text{)}\rightarrow{\text{TiO}}_{2}\text{(}s\text{)}+\text{HCl(}g\text{)}[/latex]

The balanced equations are as follows:

1. [latex]{\text{PCl}}_{5}\text{(}s\text{)}+{\text{H}}_{2}\text{O(}l\text{)}\rightarrow{\text{POCl}}_{3}\text{(}l\text{)}+2\text{HCl(}aq\text{);}[/latex]

3. [latex]3\text{Cu}\text{(}s\text{)}+8{\text{HNO}}_{3}\text{(}aq\text{)}\rightarrow 3\text{Cu}{\text{(}{\text{NO}}_{3}\text{)}}_{2}\text{(}aq\text{)}+4{\text{H}}_{2}\text{O(}l\text{)}+2\text{NO(}g\text{);}[/latex]

5. [latex]{\text{H}}_{2}\text{(}g\text{)}+{\text{I}}_{2}\text{(}s\text{)}\rightarrow 2\text{HI(}s\text{);}[/latex]

7. [latex]4\text{Fe(}s\text{)}+3{\text{O}}_{2}\text{(}g\text{)}\rightarrow 2{\text{Fe}}_{2}{\text{O}}_{3}\text{(}s\text{);}[/latex]

9. [latex]2\text{Na(}s\text{)}+2{\text{H}}_{2}\text{O(}l\text{)}\rightarrow 2\text{NaOH(}aq\text{)}+{\text{H}}_{2}\text{(}g\text{);}[/latex]

11. [latex]{\text{(}{\text{NH}}_{4}\text{)}}_{2}+{\text{Cr}}_{5}{\text{O}}_{7}\text{(}s\text{)}\rightarrow{\text{Cr}}_{2}{\text{O}}_{3}\text{(}s\text{)}+{\text{N}}_{2}\text{(}g\text{)}+4{\text{H}}_{2}\text{O(}g\text{);}[/latex]

13. [latex]{\text{P}}_{4}\text{(}s\text{)}+6{\text{Cl}}_{2}\text{(}g\text{)}\rightarrow 4{\text{PCl}}_{3}\text{(}l\text{);}[/latex]

15. [latex]{\text{PtCl}}_{4}\text{(}s\text{)}\rightarrow\text{Pt(}s\text{)}+2{\text{Cl}}_{2}\text{(}g\text{)}[/latex]

balanced equation:  chemical equation with equal numbers of atoms for each element in the reactant and product

chemical equation:  symbolic representation of a chemical reaction

coefficient:  number placed in front of symbols or formulas in a chemical equation to indicate their relative amount

product:  substance formed by a chemical or physical change; shown on the right side of the arrow in a chemical equation

reactant:  substance undergoing a chemical or physical change; shown on the left side of the arrow in a chemical equation

• Chemistry. Provided by : OpenStax College. Located at : http://openstaxcollege.org . License : CC BY: Attribution . License Terms : Download for free at https://openstaxcollege.org/textbooks/chemistry/get

Balancing Chemical Equations: Explanation, Review, and Examples

• The Albert Team
• Last Updated On: March 14, 2023

Of all the skills to know about in chemistry, balancing chemical equations is perhaps the most important to master. So many parts of chemistry depend on this vital skill, including stoichiometry, reaction analysis, and lab work. This comprehensive guide will show you the steps to balance even the most challenging reactions and will walk you through a series of examples, from simple to complex.

The Key to Balancing Chemical Equations

The ultimate goal for balancing chemical equations is to make both sides of the reaction, the reactants and the products, equal in the number of atoms per element. This stems from the universal law of the conservation of mass, which states that matter can neither be created nor destroyed. So, if we start with ten atoms of oxygen before a reaction, we need to end up with ten atoms of oxygen after a reaction. This means that chemical reactions do not change the actual building blocks of matter; rather, they just change the arrangement of the blocks. An easy way to understand this is to picture a house made of blocks. We can break the house apart and build an airplane, but the color and shape of the actual blocks do not change.

But how do we go about balancing these equations? We know that the number of atoms of each element needs to be the same on both sides of the equation, so it is just a matter of finding the correct coefficients (numbers in front of each molecule) to make that happen. It is best to start with the atom that shows up the least number of times on one side, and balance that first. Then, move on to the atom that shows up the second least number of times, and so on. In the end, make sure to count the number of atoms of each element on each side again, just to be sure.

Example of Balancing a Chemical Equation

Let’s illustrate this with an example by balancing this chemical equation:

P 4 O 10 + H 2 O → H 3 PO 4

First, let’s look at the element that appears least often. Notice that oxygen occurs twice on the left-hand side, so that is not a good element to start out with. We could either start with phosphorus or hydrogen, so let’s start with phosphorus. There are four atoms of phosphorus on the left-hand side, but only one on the right-hand side. So, we can put the coefficient of 4 on the molecule that has phosphorous on the right-hand side to balance them out.

P 4 O 10 + H 2 O → 4 H 3 PO 4

Now we can check hydrogen. We still want to avoid balancing oxygen, because it occurs in more than one molecule on the left-hand side. It is easiest to start with molecules that only appear once on each side. So, there are two molecules of hydrogen on the left-hand side and twelve on the right-hand side (notice that there are three per molecule of H 3 PO 4 , and we have four molecules). So, to balance those out, we have to put a six in front of H 2 O on the left.

P 4 O 10 + 6 H 2 O → 4 H 3 PO 4

At this point, we can check the oxygens to see if they balance. On the left, we have ten atoms of oxygen from P 4 O 10 and six from H 2 O for a total of 16. On the right, we have 16 as well (four per molecule, with four molecules). So, oxygen is already balanced. This gives us the final balanced equation of

Balancing Chemical Equations Practice Problems

Try to balance these ten equations on your own, then check the answers below. They range in difficulty level, so don’t get discouraged if some of them seem too hard. Just remember to start with the element that shows up the least, and proceed from there. The best way to approach these problems is slowly and systematically. Looking at everything at once can easily get overwhelming. Good luck!

• CO 2 + H 2 O → C 6 H 12 O 6 + O 2
• SiCl 4 + H 2 O → H 4 SiO 4 + HCl
• Al + HCl → AlCl 3 + H 2
• Na 2 CO 3 + HCl → NaCl + H 2 O + CO 2
• C 7 H 6 O 2 + O 2 → CO 2 + H 2 O
• Fe 2 (SO 4 ) 3 + KOH → K 2 SO 4 + Fe(OH) 3
• Ca 3 (PO 4 ) 2 + SiO 2 → P 4 O 10 + CaSiO 3
• KClO 3 → KClO 4 + KCl
• Al 2 (SO 4 ) 3 + Ca(OH) 2 → Al(OH) 3 + CaSO 4
• H 2 SO 4 + HI → H 2 S + I 2 + H 2 O

Complete Solutions:

1. co 2 + h 2 o → c 6 h 12 o 6 + o 2.

The first step to balancing chemical equations is to focus on elements that only appear once on each side of the equation. Here, both carbon and hydrogen fit this requirement. So, we will start with carbon. There is only one atom of carbon on the left-hand side, but six on the right-hand side. So, we add a coefficient of six to the carbon-containing molecule on the left.

6CO 2 + H 2 O → C 6 H 12 O 6 + O 2

Next, let’s look at hydrogen. There are two hydrogen atoms on the left and twelve on the right. So, we will add a coefficient of six on the hydrogen-containing molecule on the left.

6CO 2 + 6H 2 O → C 6 H 12 O 6 + O 2

Now, it is time to check the oxygen. There are a total of 18 oxygen molecules on the left (6×2 + 6×1). On the right, there are eight oxygen molecules. Now, we have two options to even out the right-hand side: We can either multiply C 6 H 12 O 6 or O 2 by a coefficient. However, if we change C 6 H 12 O 6 , the coefficients for everything else on the left-hand side will also have to change, because we will be changing the number of carbon and hydrogen atoms. To prevent this, it usually helps to only change the molecule containing the fewest elements; in this case, the O 2 . So, we can add a coefficient of six to the O 2 on the right. Our final answer will be:

6CO 2 + 6H 2 O → C 6 H 12 O 6 + 6O 2

2. SiCl 4 + H 2 O → H 4 SiO 4 + HCl

The only element that occurs more than once on the same side of the equation here is hydrogen, so we can start with any other element. Let’s start by looking at silicon. Notice that there is only one atom of silicon on either side, so we do not need to add any coefficients yet. Next, let’s look at chlorine. There are four chlorine atoms on the left side and only one on the right. So, we will add a coefficient of four on the right.

SiCl 4 + H 2 O → H 4 SiO 4 + 4HCl

Next, let’s look at oxygen. Remember that we first want to analyze all the elements that only occur once on one side of the equation. There is only one oxygen atom on the left, but four on the right. So, we will add a coefficient of four on the left-hand side of the equation.

SiCl 4 + 4H 2 O → H 4 SiO 4 + 4HCl

We are almost done! Now, we just have to check the number of hydrogen atoms on each side. The left has eight and the right also has eight, so we are done. Our final answer is

As always, make sure to double-check that the number of atoms of each element balances on each side before continuing.

3. Al + HCl → AlCl 3 + H 2

This problem is a bit tricky, so be careful. Whenever a single atom is alone on either side of the equation, it is easiest to start with that element. So, we will start by counting the aluminum atoms on both sides. There is one on the left and one on the right, so we do not need to add any coefficients yet. Next, let’s look at hydrogen. There is also one on the left, but two on the right. So, we will add a coefficient of two on the left.

Al + 2HCl → AlCl 3 + H 2

Next, we will look at chlorine. There are now two on the left, but three on the right. Now, this is not as straightforward as just adding a coefficient to one side. We need the number of chlorine atoms to be equal on both sides, so we need to get two and three to be equal. We can accomplish this by finding the lowest common multiple. In this case, we can multiply two by three and three by two to get the lowest common multiple of six. So, we will multiply 2HCl by three and AlCl 3 by two:

Al + 6HCl → 2AlCl 3 + H 2

We have looked at all the elements, so it is easy to say that we are done. However, always make sure to double-check. In this case, because we added a coefficient to the aluminum-containing molecule on the right-hand side, aluminum is no longer balanced. There is one on the left but two on the right. So, we will add one more coefficient.

2Al + 6HCl → 2AlCl 3 + H 2

We are not quite done yet. Looking over the equation one final time, we see that hydrogen has also been unbalanced. There are six on the left but two on the right. So, with one final adjustment, we get our final answer:

2Al + 6HCl → 2AlCl 3 + 3H 2

4. Na 2 CO 3 + HCl → NaCl + H 2 O + CO 2

Hopefully, by this point, balancing equations is becoming easier and you are getting the hang of it. Looking at sodium, we see that it occurs twice on the left, but once on the right. So, we can add our first coefficient to the NaCl on the right.

Na 2 CO 3 + HCl → 2NaCl + H 2 O + CO 2

Next, let’s look at carbon. There is one on the left and one on the right, so there are no coefficients to add. Since oxygen occurs in more than one place on the left, we will save it for last. Instead, look at hydrogen. There is one on the left and two on the right, so we will add a coefficient to the left.

Na 2 CO 3 + 2HCl → 2NaCl + H 2 O + CO 2

Then, looking at chlorine, we see that it is already balanced with two on each side. Now we can go back to look at oxygen. There are three on the left and three on the right, so our final answer is

5. C 7 H 6 O 2 + O 2 → CO 2 + H 2 O

We can start balancing this equation by looking at either carbon or hydrogen. Looking at carbon, we see that there are seven atoms on the left and only one on the right. So, we can add a coefficient of seven on the right.

C 7 H 6 O 2 + O 2 → 7CO 2 + H 2 O

Then, for hydrogen, there are six atoms on the left and two on the right. So, we will add a coefficient of three on the right.

C 7 H 6 O 2 + O 2 → 7CO 2 + 3H 2 O

Now, for oxygen, things will get a little tricky. Oxygen occurs in every molecule in the equation, so we have to be very careful when balancing it. There are four atoms of oxygen on the left and 17 on the right. There is no obvious way to balance these numbers, so we must use a little trick: fractions. Now, when balancing chemical equations, we cannot include fractions as it is not proper form, but it sometimes helps to use them to solve the problem. Also, try to avoid over-manipulating organic molecules. You can easily identify organic molecules, otherwise known as CHO molecules, because they are made up of only carbon, hydrogen, and oxygen. We don’t like to work with these molecules, because they are rather complex. Also, larger molecules tend to be more stable than smaller molecules, and less likely to react in large quantities.

So, to balance out the four and seventeen, we can multiply the O 2 on the left by 7.5. That will give us

C 7 H 6 O 2 + 7.5O 2 → 7CO 2 + 3H 2 O

Remember, fractions (and decimals) are not allowed in formal balanced equations, so multiply everything by two to get integer values. Our final answer is now

2C 7 H 6 O 2 + 15O 2 → 14CO 2 + 6H 2 O

6. Fe 2 (SO 4 ) 3 + KOH → K 2 SO 4 + Fe(OH) 3­-

We can start by balancing the iron on both sides. The left has two while the right only has one. So, we will add a coefficient of two to the right.

Fe 2 (SO 4 ) 3 + KOH → K 2 SO 4 + 2Fe(OH) 3­-

Then, we can look at sulfur. There are three on the left, but only one on the right. So, we will add a coefficient of three to the right-hand side.

Fe 2 (SO 4 ) 3 + KOH → 3K 2 SO 4 + 2Fe(OH) 3­-

We are almost done. All that is left is to balance the potassium. There is one atom on the left and six on the right, so we can balance these by adding a coefficient of six. Our final answer, then, is

Fe 2 (SO 4 ) 3 + 6KOH → 3K 2 SO 4 + 2Fe(OH) 3­-

7. Ca 3 (PO 4 ) 2 + SiO 2 → P 4 O 10 + CaSiO 3

Looking at calcium, we see that there are three on the left and one on the right, so we can add a coefficient of three on the right to balance them out.

Ca 3 (PO 4 ) 2 + SiO 2 → P 4 O 10 + 3CaSiO 3

Then, for phosphorus, we see that there are two on the left and four on the right. To balance these, add a coefficient of two on the left.

2Ca 3 (PO 4 ) 2 + SiO 2 → P 4 O 10 + 3CaSiO 3

Notice that by doing so, we changed the number of calcium atoms on the left. Every time you add a coefficient, double check to see if the step affects any elements you have already balanced. In this case, the number of calcium atoms on the left has increased to six while it is still three on the right, so we can change the coefficient on the right to reflect this change.

2Ca 3 (PO 4 ) 2 + SiO 2 → P 4 O 10 + 6CaSiO 3

Since oxygen occurs in every molecule in the equation, we will skip it for now. Focusing on silicon, we see that there is one on the left, but six on the right, so we can add a coefficient to the left.

2Ca 3 (PO 4 ) 2 + 6SiO 2 → P 4 O 10 + 6CaSiO 3

Now, we will check the number of oxygen atoms on each side. The left has 28 atoms and the right also has 28. So, after checking that all the other atoms are the same on both sides as well, we get a final answer of

8. KClO 3 → KClO 4 + KCl

This problem is particularly tricky because every atom, except oxygen, occurs in every molecule in the equation. So, since oxygen appears the least number of times, we will start there. There are three on the left and four on the right. To balance these, we find the lowest common multiple; in this case, 12. By adding a coefficient of four on the left and three on the right, we can balance the oxygens.

4KClO 3 → 3KClO 4 + KCl

Now, we can check potassium and chlorine. There are four potassium molecules on the left and four on the right, so they are balanced. Chlorine is also balanced, with four on each side, so we are finished, with a final answer of

9. Al 2 (SO 4 ) 3 + Ca(OH) 2 → Al(OH) 3 + CaSO 4

We can start here by balancing the aluminum atoms on both sides. The left has two molecules while the right only has one, so we will add a coefficient of two on the right.

Al 2 (SO 4 ) 3 + Ca(OH) 2 → 2Al(OH) 3 + CaSO 4

Now, we can check sulfur. There are three on the left and only one on the right, so adding a coefficient of three will balance these.

Al 2 (SO 4 ) 3 + Ca(OH) 2 → 2Al(OH) 3 + 3CaSO 4

Moving right along to calcium, there is only one on the left but three on the right, so we should add a coefficient of three.

Al 2 (SO 4 ) 3 + 3Ca(OH) 2 → 2Al(OH) 3 + 3CaSO 4

Double-checking all the atoms, we see that all the elements are balanced, so our final equation is

10. H 2 SO 4 + HI → H 2 S + I 2 + H 2 O

Since hydrogen occurs more than once on the left, we will temporarily skip it and move to sulfur. There is one atom on the left and one on the right, so there is nothing to balance yet. Looking at oxygen, there are four on the left and one on the right, so we can add a coefficient of four to balance them.

H 2 SO 4 + HI → H 2 S + I 2 + 4H 2 O

There is only one iodine on the left and two on the right, so a simple coefficient change can balance those.

H 2 SO 4 + 2HI → H 2 S + I 2 + 4H 2 O

Now, we can look at the most challenging element: hydrogen. On the left, there are four and on the right, there are ten. So, we know we have to change the coefficient of either H 2 SO 4 or HI. We want to change something that will require the least amount of tweaking afterwards, so we will change the coefficient of HI. To get the left-hand side to have ten atoms of hydrogen, we need HI to have eight atoms of hydrogen, since H 2 SO 4 already has two. So, we will change the coefficient from 2 to 8.

H 2 SO 4 + 8HI → H 2 S + I 2 + 4H 2 O

However, this also changes the balance for iodine. There are now eight on the left, but only two on the right. To fix this, we will add a coefficient of 4 on the right. After checking that everything else balances out as well, we get a final answer of

H 2 SO 4 + 8HI → H 2 S + 4I 2 + 4H 2 O

As with most skills, practice makes perfect when balancing chemical equations. Keep working hard and try to do as many problems as you can to help you hone your balancing skills.

Interested in a school license?​

Popular posts.

AP® Score Calculators

Simulate how different MCQ and FRQ scores translate into AP® scores

AP® Review Guides

The ultimate review guides for AP® subjects to help you plan and structure your prep.

Core Subject Review Guides

Review the most important topics in Physics and Algebra 1 .

SAT® Score Calculator

See how scores on each section impacts your overall SAT® score

ACT® Score Calculator

See how scores on each section impacts your overall ACT® score

Grammar Review Hub

Comprehensive review of grammar skills

AP® Posters

Download updated posters summarizing the main topics and structure for each AP® exam.