mathematical programming problem solving

About Project Euler

What is Project Euler?

Project Euler is a series of challenging mathematical/computer programming problems that will require more than just mathematical insights to solve. Although mathematics will help you arrive at elegant and efficient methods, the use of a computer and programming skills will be required to solve most problems. The motivation for starting Project Euler, and its continuation, is to provide a platform for the inquiring mind to delve into unfamiliar areas and learn new concepts in a fun and recreational context.

Who are the problems aimed at?

The intended audience include students for whom the basic curriculum is not feeding their hunger to learn, adults whose background was not primarily mathematics but had an interest in things mathematical, and professionals who want to keep their problem solving and mathematics on the cutting edge.

Currently we have 1288771 registered members who have solved at least one problem, representing 220 locations throughout the world, and collectively using 112 different programming languages to solve the problems.

Can anyone solve the problems?

The problems range in difficulty and for many the experience is inductive chain learning. That is, by solving one problem it will expose you to a new concept that allows you to undertake a previously inaccessible problem. So the determined participant will slowly but surely work his/her way through every problem.

In order to track your progress it is necessary to setup an account and have Cookies enabled.

If you already have an account, then Sign In . Otherwise, please Register – it's completely free!

However, as the problems are challenging, then you may wish to view the Problems before registering.

"Project Euler exists to encourage, challenge, and develop the skills and enjoyment of anyone with an interest in the fascinating world of mathematics."

The page has been left unattended for too long and that link/button is no longer active. Please refresh the page.

Browse Course Material

Course info.

• Prof. Dimitris Bertsimas

Departments

• Electrical Engineering and Computer Science
• Sloan School of Management

As Taught In

• Algorithms and Data Structures
• Software Design and Engineering
• Systems Engineering
• Applied Mathematics
• Discrete Mathematics

Learning Resource Types

Introduction to mathematical programming, course description.

You are leaving MIT OpenCourseWare

• Chapter 1: Mathematical Programming

Mathematical programming is a powerful tool with broad applicability across various sectors. In this series, we will delve into the origins, relevance, and practical applications of mathematical programming, with a particular emphasis on Linear Programming (LP) and Mixed Integer Linear Programming (MIP) models.

History of Mathematical Programming

Mathematical programming, also known as mathematical optimization, originated with the invention of linear programming by George Dantzig in 1947. Since then, it has become an indispensable tool for decision-making and resource allocation in a wide range of industries, including finance, logistics, manufacturing, and transportation.

The Key Components of Mathematical Programming

The field of mathematical programming encompasses a three-step process.

• Create your mathematical model . You start by translating your real-world problems mathematically, defining the questions you’re asking (decision variables), your limitations (constraints), and the goals you need to achieve (objectives).
• Develop algorithms . Develop algorithms that solve these mathematical programming models. Thankfully, there are many mathematical programming “solver” solutions available, including Gurobi, that include the algorithms you’ll need.
• Run the algorithms . Finally, you run your model through the solver to find the answer to your problem (i.e., answers to your questions, based on your unique objectives and constraints).

The Difference Between Mathematical Programming and Computer Programming

Mathematical programming is a problem-solving approach that uses mathematical models and algorithms to optimize decision-making processes. Computer programming, on the other hand, is about writing code to create software or systems that computers can execute. While they both involve the word “programming,” they have different focuses and objectives.

Exploring Linear Programming

Linear Programming (LP) is a widely used mathematical programming technique that involves optimizing (minimizing or maximizing) a linear objective function (your defined goals) subject to a set of linear constraints (your defined limitations). LP is particularly useful in situations where resources need to be allocated efficiently or where decisions need to be made to maximize or minimize a certain outcome.

To illustrate the concepts of LP, we will introduce a typical case study known as the “Furniture Problem.” Throughout this series, we will use the Furniture Problem to demonstrate the step-by-step process of formulating and solving LP models. By applying LP techniques to this practical scenario, you will gain a comprehensive understanding of how mathematical programming can be applied in real-world situations.

In addition to the case study, we will provide a general formulation for LP and MIP problems. Understanding the basic structure and components of LP models will enable you to tackle a wide range of optimization problems effectively.

Download the complete  Linear Programming Tutorial Series slide deck .

View the entire series:

• Welcome: Linear Programming Tutorial
• Chapter 2: Introduction to Linear Programming
• Chapter 3: Mixed Integer Linear Programming Problems
• Chapter 4: Furniture Factory Problem
• Chapter 5: Simplex Method
• Chapter 6: Modeling and Solving Linear Programming Problems
• Chapter 7: Sensitivity Analysis of Linear Programming Problems
• Chapter 8: Multiple Optimal Solutions
• Chapter 9: Unbounded Linear Programming Problems
• Chapter 10: Infeasible Linear Programming Problems
• Chapter 11: Linear Programming Overview – Further Considerations
• Chapter 12: Duality in Linear Programming
• Chapter 13: Optimality Conditions
• Chapter 14: Dual Simplex Method

Guidance for Your Journey

30 day free trial for commercial users, always free for academics.

GUROBI NEWSLETTER

Latest news and releases

• Chapter-1: Why Mixed-Integer Programming (MIP)
• Recommended Books, Blogs, and More

Try Gurobi for Free

Choose the evaluation license that fits you best, and start working with our Expert Team for technical guidance and support.

Evaluation License

Academic license, cloud trial.

Request free trial hours, so you can see how quickly and easily a model can be solved on the cloud.

Looking for documentation?

Jupyter Models

Case studies, privacy overview.

Or search by topic

Number and algebra

• The Number System and Place Value
• Calculations and Numerical Methods
• Fractions, Decimals, Percentages, Ratio and Proportion
• Properties of Numbers
• Patterns, Sequences and Structure
• Algebraic expressions, equations and formulae
• Coordinates, Functions and Graphs

Geometry and measure

• Angles, Polygons, and Geometrical Proof
• 3D Geometry, Shape and Space
• Measuring and calculating with units
• Transformations and constructions
• Pythagoras and Trigonometry
• Vectors and Matrices

Probability and statistics

• Handling, Processing and Representing Data
• Probability

Working mathematically

• Thinking mathematically
• Mathematical mindsets
• Cross-curricular contexts
• Physical and digital manipulatives

For younger learners

• Early Years Foundation Stage

Advanced mathematics

• Decision Mathematics and Combinatorics
• Advanced Probability and Statistics

Mathematical Programming Tasks

www.springer.com The European Mathematical Society

• StatProb Collection
• Recent changes
• Current events
• Random page
• Project talk
• Request account
• What links here
• Related changes
• Special pages
• Printable version
• Permanent link
• Page information
• View source

Mathematical programming

2020 Mathematics Subject Classification: Primary: 90Cxx [ MSN ][ ZBL ]

The branch of mathematics concerned with the theory and methods for solving problems on finding the extrema of functions on sets defined by linear and non-linear constraints (equalities and inequalities) in a finite-dimensional vector space . Mathematical programming is a branch of operations research , which comprises a wide class of control problems the mathematical models of which are finite-dimensional extremum problems. The problems of mathematical programming find applications in various areas of human activity where it is necessary to choose one of the possible ways of action, e.g. in solving numerous problems of control and planning of production processes as well as in problems of design and long-term planning. The term "mathematical programming" is connected with the fact that the goal of solving various problems is choosing programs of action.

The mathematical formulation of the problem of mathematical programming is: To minimize a scalar function $\phi(x)$ of a vector argument on the set \begin{equation} X=\left\{x\colon q_i(x)\geq 0,\; i=1,\ldots,k;\quad h_j(x)=0,\; j=1,\ldots,m \right\}, \end{equation} where $q_i(x)$ and $h_j(x)$ are scalar functions. The function $\phi(x)$ is called the objective function, and also the quality criterion, the set $X$ is called the feasible set, or the set of plans, a solution $x^*$ of the mathematical programming problem is an optimum point (or vector), a point of global minimum and also an optimal plan.

In mathematical programming one customarily distinguishes the following branches.

• Linear programming : The objective function $\phi(x)$ and the constraints $q_i(x)$ and $h_j(x)$ are linear.
• Quadratic programming : The objective function is quadratic and convex, while the feasible set is defined by linear equalities and inequalities.
• Convex programming : The objective function and the constraints are convex.
• Discrete programming / Integer programming : The solution is sought only at discrete, say integer, points of $X$.
• Stochastic programming : In contrast to deterministic problems, here the data contain an element of indeterminacy. For example, in stochastic problems of minimization of a linear function $\sum_{j=1}^{n}c_j x_j$ under linear constraints $\sum_{j=1}^{n}a_{ij} x_j\geq b_i$, $i=1,2,\ldots$, the parameters $c_j$, $a_{ij}$, $b_i$, or only some of them, are random.

The problems of linear, quadratic and convex programming have a common property: Local optimality implies global optimality. The so-called multi-extremum problems , for which the indicated property does not hold, are both considerably more difficult and less investigated.

At the basis of the theory of convex, and, in particular, linear and quadratic, programming lie the Karush-Kuhn-Tucker conditions , which gives necessary and sufficient conditions for the existence of an optimum point $x^*$: In order that $x^*$ be an optimum point, i.e. \begin{equation} \phi(x^*)=\min_{x\in X}\phi(x), \end{equation} \begin{equation} X=\left\{x\colon f_i(x)\geq 0,\; i=1,\ldots,k\right\}, \end{equation} it is necessary and sufficient that there exist a point $y^*=(y_1^*,\ldots,y_k^*)$ such that the pair $x^*$, $y^*$ be a saddle point of the Lagrange function \begin{equation} L(x,y)=\phi(x)+\sum_{i=1}^{k}y_i f_i(x) . \end{equation} The latter means that \begin{equation} L(x^*,y)\leq L(x^*,y^*)\leq L(x,y^*), \end{equation} for all $x$ and all $y\geq 0$. If the constraints $f_i(x)$ are non-linear, the theorem is valid under some additional assumptions on the feasible set, for example, the existence of a point $x\in X$ such that $f_i(x)>0$, $i=1,\ldots,k$ (Slater's regularity condition).

If $\phi(x)$ and $f_i(x)$ are differentiable functions , then the following relations characterize a saddle point:

Thus, the problem of convex programming reduces to the solution of a system of equations and inequalities. \begin{equation} \begin{aligned} \sum_{j=1}^{n}\frac{\partial L}{\partial x_j}x_j = 0;&\qquad \frac{\partial L}{\partial x_j} \geq 0,& j=1,\ldots,n;\\ \sum_{i=1}^{k}\frac{\partial L}{\partial y_i}y_i = 0;&\qquad \frac{\partial L}{\partial y_i} \leq 0,\quad y_i\geq 0,& i=1,\ldots,k. \end{aligned} \end{equation} On the basis of the Karush-Kuhn-Tucker conditions various iterative minimization methods were developed, which amount to searching for a saddle point of Lagrange's function.

In mathematical programming one of the main directions concerns computational methods for solving extremum problems. One of the widest used among these methods is the method of feasible directions. In this method a sequence $\{x_m\}$ of points of the set $X$ is constructed by the formula $x_{p+1}=x_p + \alpha_p s_p$. At each iteration, to calculate the point $x_{p+1}$ one has to choose a direction (a vector) $s_p$ and a step length (a number) $\alpha_p$. For $s_p$ one selects from among the feasible directions (i.e. directions at the point $x_p$, a small displacement along which does not lead out of the set $X$) the one that makes an acute angle with the direction $g(x_p)$ of steepest descent of the objective function (with the vector $g(x_p)=-\left.\frac{d \phi(x)}{dx}\right|_{x=x_p}$ if $\phi(x)$ is differentiable). Therefore, along the direction $s_p$ the function $\psi_p(\alpha)=\phi(x_p + \alpha s_p)$ is decreasing. The number $\alpha_p$ is determined from the conditions that $x_{p+1}\in X$ and $\phi(x_{p+1})<\phi(x_p)$. To calculate $s_p$ at $x_p$ one defines the cone of feasible directions, given by a system of inequalities, and one formulates the problem (of linear programming) of finding the possible direction along which the objective function decreases most quickly. This problem is readily solved using, say, the standard simplex method . The step length $\alpha_p$ is determined by solving the minimization problem for the function $\psi_p(\alpha)$. Under rather general assumptions it has been shown that the distance from $x_p$ to the set of stationary points of the original problem (i.e. the set of points at which the conditions necessary for a local minimum of $\phi(x)$ on $X$ are satisfied) tends to zero as $p\rightarrow\infty$. In the case when the original problem is a problem in convex programming, then, as $p\rightarrow\infty$, $x_p$ approaches the set of solutions (optimum points) of the original problem. The method of feasible directions admits an approximate solution of the indicated problems of determination of $s_p$ and $\alpha_p$, and in this sense it is stable with respect to computational errors.

For feasible sets of special structure (from the point of view of the simplicity of choosing $s_p$) one can apply minimization methods different from the method of feasible directions. Thus, in a gradient-projection method, as the descent direction at the point $x_p$ one takes $s_p=y_p - x_p$, where $y_p$ is the projection of $v_p=x_p+g(x_p)$, $g(x_p)=-\left.\frac{d \phi(x)}{dx}\right|_{x=x_p}$, on the set $X$.

If $X$ is given by linear constraints, one has the rather promising method of the conditional gradient: One linearizes the objective function at $x_p$ by constructing the function $l(x)=\phi(x)+\langle g(x_p),x_p - x\rangle$, and then, minimizing $l(x)$ on the set $X$, one finds a minimum point $y_p$ of it and one finally sets $s_p=y_p - x_p$.

Minimization methods for non-smooth functions were successfully elaborated. One of the representatives of this class is the method of the generalized gradient. By definition, a generalized gradient at $x_p$ is any vector $\tilde{g}(x_p)$ such that the inequality $\phi(y)-\phi(x_p)\geq\langle\tilde{g}(x_p),y-x_p\rangle$ holds for all $y\in X$. This method differs from the projection-gradient method in that for the point that is projected one takes $v_p=x_p-\tilde{g}(x_p)$.

Stochastic methods of minimization are also widely used. In the simplest variant of the method of random descent one takes for $s_p$ a random point on the $n$-dimensional unit sphere with center at the coordinate origin, and if $s_p$ is a feasible direction and if, in addition, $\phi(x)$ decreases along this direction, then a step is effected, i.e. one shifts to the point $x_{p+1}$. In the opposite case, the procedure for selecting $s_p$ is carried out anew.

A characteristic feature of the computational aspect of the methods for solving the problems in mathematical programming is that the application of these methods is invariably connected with the utilization of electronic computers. The main reason for this is that the problems in mathematical programming that formalize situations of control of real systems involve a large amount of work which cannot be performed by manual computation.

One of the widespread methods for investigating problems in mathematical programming is the method of penalty functions . This method essentially replaces the given mathematical programming problem by a sequence of parametric problems on unconditional minimization, such that when the parameter tends to infinity (in other cases, to zero) the solutions of these auxiliary problems converge to the solution of the original problem. Note that in an unconditional minimization problem every direction is feasible, and consequently the search for $s_p$ requires less effort in comparison with the solution of the same problem by the method of feasible directions. (For example, in the method of steepest descent one takes $s_p=-\left.\frac{d \phi(x)}{dx}\right|_{x=x_p}$.) The same is true concerning the search for $\alpha_p$.

An important direction of investigation in mathematical programming is the problem of stability. Here essential importance is attached to the study of the class of stable problems, that is, problems for which small perturbations (errors) in the data result in perturbations of the solutions that are also small. In the case of unstable problems an important role is reserved for a procedure of approximating the unstable problem by a sequence of stable problems — this is known as the regularization process.

Along with finite-dimensional problems, problems of mathematical programming in infinite-dimensional spaces are considered as well. Among the latter there are various extremum problems in mathematical economics, technology, problems of optimization of physical characteristics of nuclear reactors, and others. In the terminology of mathematical programming one formulates the problems in the corresponding function space of variational calculus and optimal control .

Mathematical programming has crystallized as a science in the 1950-s until 1970-s. This is first of all connected with the development of electronic computers and, hence, the mathematical processing of large amounts of data. On this basis one solves problems of control and planning, in which the application of mathematical methods is connected mainly with the construction of mathematical models and related extremal problems, among them problems of mathematical programming.

• Mathematics in science and technology
• Operations research, mathematical programming
• This page was last edited on 9 June 2016, at 09:14.
• Privacy policy
• About Encyclopedia of Mathematics
• Disclaimers
• Impressum-Legal

Learn by doing

Guided interactive problem solving that’s effective and fun. master concepts in 15 minutes a day., data analysis, computer science, programming & ai, science & engineering, join over 10 million people learning on brilliant, over 50,000 5-star reviews on ios app store and google play.

Master concepts in 15 minutes a day

Whether you’re a complete beginner or ready to dive into machine learning and beyond, Brilliant makes it easy to level up fast with fun, bite-sized lessons.

Effective, hands-on learning

Visual, interactive lessons make concepts feel intuitive — so even complex ideas just click. Our real-time feedback and simple explanations make learning efficient.

Learn at your level

Students and professionals alike can hone dormant skills or learn new ones. Progress through lessons and challenges tailored to your level. Designed for ages 13 to 113.

Guided bite-sized lessons

We make it easy to stay on track, see your progress, and build your problem solving skills one concept at a time.

Stay motivated

Form a real learning habit with fun content that’s always well-paced, game-like progress tracking, and friendly reminders.

Guided courses for every journey

All of our courses are crafted by award-winning teachers, researchers, and professionals from MIT, Caltech, Duke, Microsoft, Google, and more.

• Foundational Math
• Software Development
• Foundational Logic
• Data Science
• High School Math
• Engineering
• Statistics and Finance

Courses in Foundational Math

• Solving Equations
• Measurement
• Mathematical Fundamentals
• Reasoning with Algebra
• Functions and Quadratics

10k+ Ratings

60k+ Ratings

We use cookies to improve your experience on Brilliant. Learn more about our cookie policy and settings .

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

14. Solving Linear Programming Problems

• Last updated
• Save as PDF
• Page ID 26458

The following topics are included in this series of two videos.

• Solving the linear programming problem in video 1 in Chapter 13.
• Solving the linear programming problem in video 2 in Chapter 13.

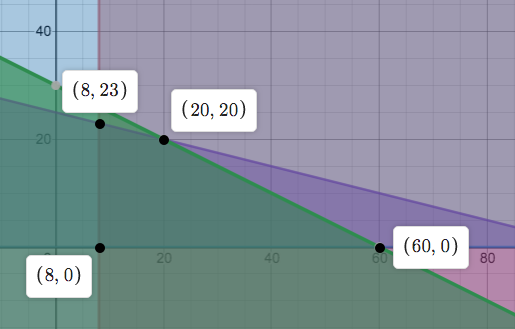
• A florist makes 2 special bouquets. Both types consist of Japanese irises and tulips. Type I consists of 1 dozen tulips and 1 dozen Japanese irises. Type II consists of 2 dozen tulips and 4 dozen Japanese irises. The profit on each Type I bouquet is $8 and the profit on each Type II bouquet is $18. The florist knows that they sell at least 8 Type I bouquets each day, so they always make at least 8 of these each day. There are only 60 dozen tulips and 100 dozen irises available each day. How many of each type of bouquet should the shop make each day to maximize profit? 

Google form

Main Navigation

• Accept offer and enrol
• Current Students

Personalise your experience

Did you mean..., diploma of arts and social sciences, art/science collaboration wins waterhouse natural science art prize, unit of study math3003 computational analysis (2025).

Future students: T: 1800 626 481 E: Email your enquiry here

Current students: Contact: Faculty of Science and Engineering

Students studying at an education collaboration: Please contact your relevant institution

updated - DO NOT REMOVE THIS LINE 6:08 AM on Tue, 9 April

Show me unit information for year

Unit snapshot.

UG Coursework Unit

Credit points

Faculty & college.

Faculty of Science and Engineering

Pre-requisites

MATH2003 - Calculus and Linear Algebra I

Unit description

Introduces students to the application of computational and numerical methods for simulation, optimisation, linear and non-linear equations, differentiation and integration. Develops skills in applying numerical methods for solving application problems, utilising software such as Microsoft Excel and Visual Basic for Applications programming.

Unit content

Module 1:  Mathematical programming

Availabilities

2025 unit offering information will be available in November 2024

Learning outcomes

Unit Learning Outcomes express learning achievement in terms of what a student should know, understand and be able to do on completion of a unit. These outcomes are aligned with the graduate attributes . The unit learning outcomes and graduate attributes are also the basis of evaluating prior learning.

On completion of this unit, students should be able to:

utilise Excel and Visual Basic for Applications to implement computational and numerical methods for solving problems

formulate and solve mathematical programming problems

implement numerical algorithms for computing solutions of problems such as non-linear and linear equations, numerical differentiation and numerical integration

demonstrate proficiency in the application of simulations, such as Monte Carlo simulations.

Fee information

Commonwealth Supported courses For information regarding Student Contribution Amounts please visit the Student Contribution Amounts .

Fee paying courses For postgraduate or undergraduate full-fee paying courses please check Domestic Postgraduate Fees OR Domestic Undergraduate Fees .

International

Please check the international course and fee list to determine the relevant fees.

Courses that offer this unit

Bachelor of education (2024), bachelor of education (2025), bachelor of science (2024), bachelor of science (2025), bachelor of engineering systems (honours), bachelor of business and enterprise (2024), bachelor of engineering systems (honours) (2025), bachelor of engineering systems (honours) (2024), bachelor of engineering systems (honours), bachelor of business (2025), any questions we'd love to help.

Handbook of Formal Optimization pp 1–26 Cite as

Solving Cropping Pattern Optimization Problems Using Robust Positive Mathematical Programming

• Mostafa Mardani Najafabadi 3 &
• Somayeh Shirzadi Laskookalayeh 4  
• Living reference work entry
• First Online: 06 February 2024

22 Accesses

Agricultural activities occur in an environment that is constantly changing. In each cropping season, farmers must make management decisions based on numerous factors, some of which are beyond their control and others which are not. The use of mathematical programming models in determining optimal decisions for farmers, predicting the outcomes of policy effects, and the occurrence of uncontrollable factors in the agriculture sector is beneficial. It can provide planners and farmers with appropriate awareness and understanding of the effects of each decision related to resource allocation and cropping patterns before implementing that decision. One of the problems with some cropping pattern models is the consideration of resource amounts as fixed and certain, neglecting the issue of uncertainty. This results in a significant difference between the estimated model and the behavior of the farmers. In this context, the formulation of a mathematical programming model aligned with the real world and considering its uncertainties is highly important. This chapter aims to present an appropriate mathematical programming model for decision-making in determining cropping patterns and optimal resource allocation. This model should be able to model the uncertainties of the real world in the agriculture sector in the best possible way and provide more desirable and practical results. Therefore, while discussing the generalities related to the features and application of mathematical programming models and their types, the chapter elaborates on the basic and extended models of policy analysis using Positive Mathematical Programming (PMP) and the Robust Optimization (RO) approach. Subsequently, the method and a practical example of the combined model of Robust Positive Mathematical Programming (RPMP) in solving cropping pattern optimization problems is explained.

This is a preview of subscription content, log in via an institution .

Afzali R, GharehBeygi M, Yazdanpanah Dero Q (2020) Climate changes and food policies: economic pathology. Clim Risk Manag 30:100249

Article   Google Scholar  

Aghapour Sabbaghi M, Nazari M, Araghinejad S, Soufizadeh S (2020) Economic impacts of climate change on water resources and agriculture in Zayandehroud river basin in Iran. Agric Water Manag 241:106323

Agudo-Domínguez A, Pérez-Blanco CD, Gil-García L, Ortega JA, Dasgupta S (2022) Climate-sensitive hydrological drought insurance for irrigated agriculture under deep uncertainty. Insightful results from the Cega River Basin in Spain. Agric Water Manag 274:107938

Akbari M, Najafi Alamdarlo H, Mosavi SH (2020) The effects of climate change and groundwater salinity on farmers’ income risk. Ecol Indic 110:105893

Aldaya MM, Gutiérrez-Martín C, Espinosa-Tasón J, Ederra I, Sánchez M (2023) The impact of the territorial gradient and the irrigation water price on agricultural production along the first phase of the Navarra Canal in Spain. Agric Water Manag 281:108245

Anonymous (2016) Agricultural statistics of Mazandaran Province. In: Technology, D.o.S.a.I. (ed) Agriculture Jihad organization

Google Scholar  

Arfini F (2001) Mathematical programming models employed in the analysis of the common agriculture policy. National Institute of Agricultural Economics, Italy, INEA, Osservatorio Sulle Politiche Agricole dell'UE, Working Papers

Ben-Tal A, Nemirovski A (1999) Robust solutions of uncertain linear programs. Oper Res Lett 25(1):1–13

Article   MathSciNet   Google Scholar  

Ben-Tal A, Nemirovski A (2000) Robust solutions of linear programming problems contaminated with uncertain data. Math Program 88(3):411–424

Bertsimas D, Sim M (2004) The price of robustness. Oper Res 52(1):35–53

Buysse J, Van Huylenbroeck G, Lauwers L (2007) Normative, positive and econometric mathematical programming as tools for incorporation of multifunctionality in agricultural policy modelling. Agric Ecosyst Environ 120(1):70–81

Cao Z, Zhu T, Cai X (2023) Hydro-agro-economic optimization for irrigated farming in an arid region: The Hetao Irrigation District, Inner Mongolia. Agric Water Manag 277:108095

Drud A (2010) CONOPT user guide. ARKI consulting and development A/S., Bagsvaerd, Denmark. Last Accessed 14th August 2013

El Ghaoui L, Lebret H (2000) Robust solutions to least-squares problems with uncertain data. SIAM J Matrix Anal Appl 18(4):1035–1064

El Ghaoui L, Oustry F, Lebret H (1998) Robust solutions to uncertain semidefinite programs. SIAM J Optim 9(1):33–52

Fernández FJ, Vásquez-Lavín F, Ponce RD, Garreaud R, Hernández F, Link O, Zambrano F, Hanemann M (2023) The economics impacts of long-run droughts: challenges, gaps, and way forward. J Environ Manag 344:118726

Fragoso R, Marques C, Lucas MR, Martins MB, Jorge R (2011) The economic effects of common agricultural policy on Mediterranean montado/dehesa ecosystem. J Policy Model 33(2):311–327

Frahan B, Buysse J, Polome P, Fernagut B, Harmignie O, Lauwers L, Van Huylenbroeck G, Van Meensel J (2007) Positive mathematical programming for agricultural and environmental policy analysis: review and practice, pp 129–154

Funk B, Amer SA, Ward FA (2023) Sustainable aquifer management for food security. Agric Water Manag 281:108073

Ghaffari A, Nasseri M, Pasebani Someeh A (2022) Assessing the economic effects of drought using Positive Mathematical Planning model under climate change scenarios. Heliyon 8(12):e11941

Gharye-Mirzaei M, Gholami S, Rahmani D (2023) A mathematical model for the optimization of agricultural supply chain under uncertain environmental and financial conditions: the case study of fresh date fruit. Environ Dev Sustain 3(3):519–541

Gohar AA, Ward FA (2010) Gains from expanded irrigation water trading in Egypt: an integrated basin approach. Ecol Econ 69(12):2535–2548

Gohar AA, Ward FA, Amer SA (2013) Economic performance of water storage capacity expansion for food security. J Hydrol 484:16–25

Gohar AA, Amer SA, Ward FA (2015) Irrigation infrastructure and water appropriation rules for food security. J Hydrol 520:85–100

Gorissen BL, Yanıkoğlu İ, den Hertog D (2015) A practical guide to robust optimization. Omega 53:124–137

Graveline N (2020) Combining flexible regulatory and economic instruments for agriculture water demand control under climate change in Beauce. Water Resour Econ 29:100143

Hassani Y, Hashemy Shahdany SM, Maestre JM, Zahraie B, Ghorbani M, Henneberry SR, Kulshreshtha SN (2019) An economic-operational framework for optimum agricultural water distribution in irrigation districts without water marketing. Agric Water Manag 221:348–361

He L, Horbulyk T, Ali MK, Le Roy DG, Klein KK (2012) Proportional water sharing vs. seniority-based allocation in the Bow River basin of Southern Alberta. Agric Water Manag 104:21–31

Housh M, Ostfeld A, Shamir U (2011) optimal multi-year management of a water supply system under uncertainty: robust counterpart approach. Water Resour Res

Howitt RE (1995) A calibration method for agricultural economic production models. J Agric Econ 46(2):147–159

Howitt RE (2005) PMP Based Production Models-Development and Integration. European Association of Agricultural Economists, Copenhagen

Howitt RE, Medellín-Azuara J, MacEwan D, Lund JR (2012) Calibrating disaggregate economic models of agricultural production and water management. Environ Model Softw 38:244–258

Ide J, Schöbel A (2016) Robustness for uncertain multi-objective optimization: a survey and analysis of different concepts. OR Spectr 38(1):235–271

Ji Y, Du J, Wu X, Wu Z, Qu D, Yang D (2021) Robust optimization approach to two-echelon agricultural cold chain logistics considering carbon emission and stochastic demand. Environ Dev Sustain 23(9):13731–13754

José Alem D, Morabito R (2012) Production planning in furniture settings via robust optimization. Comput Oper Res 39(2):139–150

Kalbali E, Ziaee S, Mardani Najafabadi M, Zakerinia M (2021) Approaches to adapting to impacts of climate change in northern Iran: the application of a hydrogy-economics model. J Clean Prod 280:124067

Layani G, Mehrjou S, Farajzadeh Z (2023) Effects of government policies reform on environmental sustainability: an integrated approach of PMP and system dynamics simulation model. J Clean Prod 426:138985

Lee K, Singh VP (2020) Analysis of uncertainty and non-stationarity in probable maximum precipitation in Brazos River basin. J Hydrol 590:125526

Maneta MP, Cobourn K, Kimball JS, He M, Silverman NL, Chaffin BC, Ewing S, Ji X, Maxwell B (2020) A satellite-driven hydro-economic model to support agricultural water resources management. Environ Model Softw 134:104836

Mardani Najafabadi M, Ashktorab N (2022) Mathematical programming approaches for modeling a sustainable cropping pattern under uncertainty: a case study in Southern Iran. Environ Dev Sustain 25:9731–9755

Martínez-Dalmau J, Gutiérrez-Martín C, Kahil T, Berbel J (2023) Impact of alternative water policies for drought adaptation in the Guadalquivir Mediterranean river basin, southern Spain. J Hydrol: Regional Stud 47:101444

Medellín-Azuara J, Harou JJ, Howitt RE (2010) Estimating economic value of agricultural water under changing conditions and the effects of spatial aggregation. Sci Total Environ 408(23):5639–5648

Medellín-Azuara J, Howitt RE, Harou JJ (2012) Predicting farmer responses to water pricing, rationing and subsidies assuming profit maximizing investment in irrigation technology. Agric Water Manag 108:73–82

Mills G (1984) Optimization in economic analysis. HarperCollins Publishers Ltd, London

Mulvey J, Vanderbei R, Zenios S (1995) Robust optimization of large-scale systems. Oper Res 43:264–281

Nahmias S (2005) Production and operations analysis. McGraw-Hill/Irwin, Singapore

Nevo A, Amir I (1991) CROPLOT – an expert system for determining the suitability of crops to plots. Agric Syst 37(3):225–241

Nevo A, Oad R, Podmore TH (1994) An integrated expert system for optimal crop planning. Agric Syst 45(1):73–92

Norton R, Hazell P (1986) Mathematical programming for economic analysis in agriculture

Paris Q (2010) Economic foundations of symmetric programming

Paris Q, Howitt RE (1998) An analysis of ill-posed production problems using maximum entropy: reply. Am J Agric Econ 84

Randall M, Montgomery J, Lewis A (2022) Robust temporal optimisation for a crop planning problem under climate change uncertainty. Operations Res Perspect 9:100219

Rodríguez-Flores JM, Gupta RS, Zeff HB, Reed PM, Medellín-Azuara J (2023) Identifying robust adaptive irrigation operating policies to balance deeply uncertain economic food production and groundwater sustainability trade-offs. J Environ Manag 345:118901

Röhm O, Dabbert S (2003) Integrating agri-environmental programs into regional production models: an extension of positive mathematical programming. Am J Agric Econ 85(1):254–265

Sabouhi M, Mardani M (2017) Linear robust data envelopment analysis: CCR model with uncertain data. Int J Productivity Qual Manage 22(2):262–280

Sahinidis NV (2004) Optimization under uncertainty: state-of-the-art and opportunities. Comput Chem Eng 28(6):971–983

Sapino F, Pérez-Blanco CD, Gutiérrez-Martín C, Frontuto V (2020) An ensemble experiment of mathematical programming models to assess socio-economic effects of agricultural water pricing reform in the Piedmont Region, Italy. J Environ Manag 267:110645

Sapino F, Pérez-Blanco CD, Gutiérrez-Martín C, García-Prats A, Pulido-Velazquez M (2022) Influence of crop-water production functions on the expected performance of water pricing policies in irrigated agriculture. Agric Water Manag 259:107248

Sheffi Y (2005) The resilient enterprise: overcoming vulnerability for competitive advantage. MIT Press, Cambridge, MA

Shirzadi Laskookalayeh S, Mardani Najafabadi M, Shahnazari A (2022) Investigating the effects of management of irrigation water distribution on farmers' gross profit under uncertainty: A new positive mathematical programming model. J Clean Prod 351:131277

Simchi-Levi D, Kaminsky P, Simchi-Levi E (2004) Managing the supply chain: the definitive guide for the business professional. McGraw-Hill, New York

Soyster AL (1973) Convex programming with set-inclusive constraints and applications to inexact linear programming. Oper Res 21(5):1154–1157

Thiele A (2004) A robust optimization approach to supply chains and revenue management. Department of Electrical Engineering and Computer Science. Massachusetts Institute of Technology, Cambridge, p 176

Wang S, Tan Q, Yang P, Zhang T, Zhang T (2023) Development of an inexact simulation-evaluation model for the joint analysis of water pricing and groundwater allocation policies. J Environ Manag 329

Zamani O, Grundmann P, Libra JA, Nikouei A (2019) Limiting and timing water supply for agricultural production – the case of the Zayandeh-Rud River Basin, Iran. Agric Water Manag 222:322–335

Zhu J, Wang X, Zhang L, Cheng H, Yang Z (2015) System dynamics modeling of the influence of the TN/TP concentrations in socioeconomic water on NDVI in shallow lakes. Ecol Eng 76:27–35

Download references

Author information

Authors and affiliations.

Department of Agricultural Economics, Faculty of Agricultural Engineering and Rural Development, Agricultural Sciences and Natural Resources University of Khuzestan, Mollasani, Iran

Mostafa Mardani Najafabadi

Department of Agricultural Economics, Faculty of Agricultural Engineering, Sari Agricultural Sciences and Natural Resources University, Sari, Iran

Somayeh Shirzadi Laskookalayeh

You can also search for this author in PubMed   Google Scholar

Corresponding author

Correspondence to Mostafa Mardani Najafabadi .

Editor information

Editors and affiliations.

Institute of Artificial Intelligence, MIT World Peace University, Pune, Pune, Maharashtra, India

Anand J. Kulkarni

Faculty of Engineering and IT, University of Technology Sydney, Ultimo, NSW, Australia

Amir H. Gandomi

Section Editor information

Institute of Artificial Intelligence, Dr Vishwanath Karad MIT World Peace University, Pune, India

Rights and permissions

Reprints and permissions

Copyright information

© 2024 Springer Nature Singapore Pte Ltd.

About this entry

Cite this entry.

Mardani Najafabadi, M., Shirzadi Laskookalayeh, S. (2024). Solving Cropping Pattern Optimization Problems Using Robust Positive Mathematical Programming. In: Kulkarni, A.J., Gandomi, A.H. (eds) Handbook of Formal Optimization. Springer, Singapore. https://doi.org/10.1007/978-981-19-8851-6_52-1

Download citation

DOI : https://doi.org/10.1007/978-981-19-8851-6_52-1

Received : 18 November 2023

Accepted : 25 November 2023

Published : 06 February 2024

Publisher Name : Springer, Singapore

Print ISBN : 978-981-19-8851-6

Online ISBN : 978-981-19-8851-6

eBook Packages : Springer Reference Intelligent Technologies and Robotics Reference Module Computer Science and Engineering

• Publish with us

Policies and ethics

• Find a journal
• Track your research