problem solving in inverse variation

Inverse Variation: Practice Problems

If $$ y $$ varies inversely as $$ x $$ and $$ y = 14 $$ when $$ x = 20 $$ . What is the value of $$ y $$ when $$ x $$ is 5?

Write down the variation equation.

$$ y = \frac k x $$

Use $$ \red{y = 14} $$ and $$ \blue{x = 20} $$ to find the value of $$ k $$. Then write down the updated variation equation.

$$ \begin{align*} \red{14} & = \frac k {\blue{20}}\\[6pt] \red{14}(\blue{20}) & = \frac k {\blue{20}}\cdot \blue {20}\\[6pt] 280 & = \frac k {\cancelred{20}}\cdot \cancelred{20}\\[6pt] k & = 280 \end{align*} $$

The updated variation equation is $$ y = \frac{280} x $$

Determine the value of $$ y $$ when $$ \blue{x = 5} $$ .

$$ \begin{align*} y & = \frac{280}{\blue x}\\[6pt] y & = \frac{280}{\blue 5} = 56 \end{align*} $$

$$ y = 56 $$ when $$ x = 5 $$ .

Suppose $$ s $$ varies indirectly as $$ t $$, and $$ s(1.5)=25 $$ . Determine the value of $$ s(2.25) $$ .

$$ s = \frac k t $$

Use $$ \red{s = 25} $$ and $$ \blue{t = 1.5} $$ to determine the value of $$ k $$. Then write down the updated variation equation.

$$ \begin{align*} \red{25} & = \frac k {\blue{1.5}}\\[6pt] \red{25}(\blue{1.5}) & = \frac k {\blue{1.5}}\cdot \blue{1.5}\\[6pt] 27.5 & = \frac k {\cancelred{1.5}}\cdot \cancelred{1.5}\\[6pt] k & = 37.5 \end{align*} $$

The updated variation equation is $$ s = \frac{37.5} t $$

Determine the value of $$ s $$ when $$ \blue{t = 2.25} $$ .

$$ \begin{align*} s & = \frac{37.5}{\blue t}\\[6pt] s & = \frac{37.5}{\blue{2.25}} = \frac{3750}{225} = \frac{50} 3 = 16\,\frac 2 3 \approx 16.667 \end{align*} $$

$$ s = \frac{50} 3 $$ when $$ t = 2.25 $$ .

Suppose $$ y $$ varies inversely as $$ x $$, and $$ y = 0.025 $$ when $$ x = 2 $$ . What is the value of $$ x $$ when $$ y = 0.4 $$ ?

Use $$ \red{y = 0.025} $$ and $$ \blue{x = 2} $$ to find the value of $$ k $$. Then write down the updated variation equation.

$$ \begin{align*} \red{0.025} & = \frac k {\blue 2}\\[6pt] \red{(0.025)}\blue 2 & = \frac k {\blue 2} \cdot \blue 2\\[6pt] 0.05 & = \frac k {\cancelred 2} \cdot \cancelred 2\\[6pt] k & = 0.05 = \frac 1 {20} \end{align*} $$

The updated variation equation is $$ y = \frac{0.05} x = \frac{1/20} x = \frac 1 {20x} $$

Determine the value of $$ x $$ when $$ \red{y = 0.4} $$ .

$$ \begin{align*} \red{0.4} & = \frac 1 {20x}\\[6pt] \red{0.4} \cdot (20x) & = 1\\[6pt] 8x & = 1\\[6pt] x & = \frac 1 8 = 0.125 \end{align*} $$

$$ x = 0.125 $$ when $$ y = 0.4 $$ .

Suppose $$ I $$ is inversely proportional to $$ R $$ and when $$ R = 200 $$ , $$ I = 35 $$ . Determine the value of $$ R $$ when $$ I = 100 $$ .

$$ I = \frac k R $$

Use $$ \red{I = 35} $$ and $$ \blue{R = 200} $$ to find the value of $$ k $$. Then write down the updated variation equation.

$$ \begin{align*} \red{35} & = \frac k {\blue{200}}\\[6pt] \red{35}(\blue{200}) & = \frac k {\blue{200}}\cdot \blue{200}\\[6pt] 7000 & = \frac k {\cancelred{200}}\cdot \cancelred{200}\\[6pt] k & = 7000 \end{align*} $$

The updated variation equation is $$ I = \frac{7000} R $$ .

Determine the value of $$ R $$ when $$ \red{I = 100} $$ .

$$ \begin{align*} \red{100} & = \frac{7000} R\\[6pt] 100R & = 7000\\[6pt] R & = \frac{7000}{100} = 70 \end{align*} $$

$$ R = 70 $$ when $$ I = 100 $$ .

Suppose $$ y $$ varies inversely as the square-root of $$ x $$. If $$ y = 8 $$ when $$ x = 49 $$ , determine the value of $$ y $$ when $$ x = 121 $$

$$ y = \frac k {\sqrt x} $$

Use $$ \red{y = 8} $$ and $$ \blue{x = 49} $$ to determine the value of $$ k $$. Then write down the updated variation equation.

$$ \begin{align*} \red 8 & = \frac k {\sqrt{\blue{49}}}\\[6pt] \red 8 & = \frac k 7\\[6pt] \red 8 (7) & = \frac k 7\cdot 7\\[6pt] 56 & = \frac k {\cancelred 7}\cdot \cancelred 7\\[6pt] k & = 56 \end{align*} $$

The updated variation equation is $$ y = \frac{56}{\sqrt x} $$

Determine the value of $$ y $$ when $$ \blue{x = 100} $$ .

$$ \begin{align*} y & = \frac{56}{\sqrt{\blue{100}}}\\[6pt] & = \frac{56}{10}\\[6pt] & = 5.6 \end{align*} $$

$$ y = 5.6 $$ when $$ x = 100 $$ .

Suppose $$ p $$ varies inversely as the cube of $$ q $$, and $$ p = 2 $$ when $$ q = 4 $$ . Determine the value of $$ q $$ when $$ p = 8 $$ .

$$ p = \frac k {q^3} $$

Use $$ \red{p = 2} $$ and $$ \blue{q = 4} $$ to determine the value of $$ k $$. Then write down the updated variation equation.

$$ \begin{align*} \red 2 & = \frac k {\blue 4^3}\\[6pt] \red 2 & = \frac k {64}\\[6pt] \red 2 (64) & = \frac k {\cancelred{64}} \cdot \cancelred{64}\\[6pt] k & = 128 \end{align*} $$

The updated variation equation is $$ p = \frac{128}{q^3} $$ .

Determine the value of $$ q $$ when $$ \red{p = 8} $$ .

$$ \begin{align*} \red 8 & = \frac{128}{q^3}\\[6pt] 8q^3 & = 128\\[6pt] q^3 & = \frac{128} 8\\[6pt] & = 16\\[6pt] q & = \sqrt[3]{16} = 2\sqrt[3] 2 \end{align*} $$

$$ q = 2\sqrt[3] 2 $$ when $$ p = 8 $$ .

Word Problems

Speed and travel time are inversely related (the faster you go, the shorter the travel time). Suppose the daily trip to school normally takes 20 minutes when your speed is 30 miles per hour. How long should the trip take if you drive 45 miles per hour instead (and don't get pulled over for speeding)?

Define variables to describe travel time and speed, and state the equation relating them.

Let's use $$ t $$ for time (in minutes).

Let's use $$ s $$ for speed (in miles per hour).

The equation we need then is $$ s = \frac k t $$ .

Use $$ \red{s = 30} $$ and $$ \blue{t = 20} $$ to determine the value of $$ k $$. Then write down the updated variation equation.

$$ \begin{align*} \red{30} & = \frac k {\blue{20}}\\[6pt] \red{30}(\blue{20}) & = \frac k {\blue{20}}\cdot\blue{20}\\[6pt] 600 & = \frac k {\cancelred{20}}\cdot\cancelred{20}\\[6pt] k & = 600 \end{align*} $$

The updated variation equation is $$ s = \frac{600} t $$ .

Use the equation to determine the travel time for the trip when speed is 45 miles per hour.

$$ \begin{align*} \red{45} & = \frac{600} t\\[6pt] \red{45}t & = 600\\[6pt] t & = \frac{600}{\red{45}}\\[6pt] & = \frac{40} 3\\[6pt] & = 13\frac 1 3 \end{align*} $$

The trip will take $$ 13\frac 1 3 $$ minutes (or 13 minutes and 20 seconds) if you drive at 45 miles per hour.

The Ideal Gas Law from chemistry can be written as $$ P = \frac k V $$ , where $$ P $$ is the pressure (in pascals) and $$ V $$ is the volume of the container (in cubic meters).

Suppose that when a particular gas is stored in a 0.25 cubic meter container, and exerts 40 pascals of pressure. How much pressure will the gas exert if it were transferred to a container that only holds a volume of $$ 0.1 $$ cubic meters.

Use $$ \red{P = 40} $$ and $$ \blue{V = 0.25} $$ to determine the value of $$ k $$. Then write down the updated variation equation.

$$ \begin{align*} \red{P} & = \frac k {\blue{V}}\\[6pt] \red{40} & = \frac k {\blue{0.25}}\\[6pt] \red{40}(\blue{0.25}) & = \frac k {\blue{0.25}}\cdot\blue{0.25}\\[6pt] 10 & = \frac k {\cancelred{0.25}}\cdot\cancelred{0.25}\\[6pt] k & = 10 \end{align*} $$

So for this particular gas, $$ P = \frac{10} V $$

Use the equation to determine the pressure when $$ \blue{V = 0.1} $$ .

$$ P = \frac{10}{\blue{0.1}} = 100 $$

The gas exerts a pressure of 100 pascals in a 0.1 cubic meter container.

The time it takes a block of ice to melt varies indirectly with temperature. If a block of ice that is 1/8 cubic meters in volume requires 6 hours to melt when it is $$72 ^\circ F $$ , at what temperature will the block melt in only 2 hours?

Define variables to represent temperature and time and write down the inverse variation equation.

Let $$ t = $$ time (in hours)

Let $$ T = $$ temperature (in degrees Fahrenheit)

The inverse variation equation will be

$$ t = \frac k T $$

Use $$ \red{t = 6} $$ and $$ \blue{T = 72} $$ to find the value of $$ k $$, then write down the updated version of the inverse variation equation.

$$ \begin{align*} \red t & = \frac k {\blue T}\\[6pt] \red 6 & = \frac k {\blue{72}}\\[6pt] \red 6(\blue{72}) & = \frac k {\blue{72}}\cdot\blue{72}\\[6pt] 432 & = \frac k {\cancelred{72}}\cdot\cancelred{72}\\[6pt] k & = 432 \end{align*} $$

The inverse variation equation is now $$ t = \frac{432} T $$ .

Determine the temperature required to have the block of ice melt in only $$ \blue{t = 2} $$ hours.

$$ \begin{align*} \blue 2 & = \frac{432} T\\[6pt] \blue 2T & = 432\\[6pt] T & = \frac{432}{\blue 2}\\[6pt] & = 216 \end{align*} $$

The 1/8 cubic meter block of ice will melt in only 2 hours if the temperature is $$ 216 ^\circ F $$ .

Suppose 4 adults can build a shed in 16 hours. How much quicker would it be to have 5 adults building the shed?

Confirm this is an inverse variation problem.

We note that (in an ideal world) having more adults working on a particular project will mean the task takes less time.

Since the time decreases as the number of workers increase, we can model this as an inverse variation.

Define variables to represent the quantities involved, and write down the inverse variation equation.

Let $$ w = $$ the number of workers building the shed.

Let $$ t = $$ the number of hours it takes to complete the shed.

The inverse variation equation is

$$ t = \frac k w $$

Use $$ \red{t = 16} $$ and $$ \blue{w = 4} $$ to determine the value of $$ k $$. Then write down the updated variation equation.

$$ \begin{align*} \red t & = \frac k {\red w}\\[6pt] \red{16} & = \frac k {\blue 4}\\[6pt] \red{16}(\blue 4) & = \frac k {\blue 4}\cdot \blue 4\\[6pt] 64 & = \frac k {\cancelred 4}\cdot \cancelred 4\\[6pt] k & = 64 \end{align*} $$

The updated variation equation is $$ t = \frac{64} w $$ .

Determine the length of time required for $$\blue{w = 5}$$ people to build the shed.

$$ t = \frac{64}{\blue 5} = 12\frac 4 5 = 12.8 $$

Determine the savings in time when 5 adults work on the shed versus only 4.

Note that the question didn't ask us, "How long does it take..." , but rather "How much quicker.." . This means we are interested in the difference between having 4 and 5 workers

$$ \mbox{Time saved} = (\mbox{time for 4 workers}) - (\mbox{time for 5 workers}) = 16 - 12.8 = 3.2 $$

Having 5 adults on the project instead of 4 will result in the shed be completed 3.2 hours more quickly (or 3 hours, 12 minutes more quickly).

The gravitational force (in newtons) between two objects is inversely proportional to square of the distance (in meters) between the centers of the objects.

Suppose the gravitational force between two particular objects is $$ 1.95\times 10^4 $$ newtons when they are separated by $$ 8.94\times 10^{12} $$ meters. If the gravitational force increases to $$ 4.1\times 10^6 $$ newtons, what has happened to the distance between the objects?

Define variables to represent the two quantities under investigation. Then write down the variation equation.

Let $$ F_g $$ represent the force due to gravity, measured in newtons.

Let $$ r $$ represent the distance between the centers of the objects, measured in meters.

The variation equation is $$ F_g = \frac k {r^2} $$ .

Use $$ \red{F_g = 1.95\times 10^4} $$ and $$ \blue{r = 8.94\times 10^{12}} $$ to determine the value of $$ k $$, then write down the updated variation equation.

$$ \begin{align*} \red{F_g} & = \frac k {\blue r^2}\\[6pt] \red{1.95\times 10^4} & = \frac k {(\blue{8.94\times 10^{12}})^2}\\[6pt] \red{1.95\times 10^4} & = \frac k {\blue{79.9236\times 10^{24}}}\\[6pt] \red{1.95\times 10^4}(\blue{79.9236\times 10^{24}}) & = \frac k {\blue{79.9236\times 10^{24}}}\cdot\blue{79.9236\times 10^{24}}\\[6pt] 1.5585102 \times 10^{30} & = \frac k {\cancelred{79.9236\times 10^{24}}}\cdot\cancelred{79.9236\times 10^{24}}\\[6pt] k & = 1.5585102 \times 10^{30}\\[6pt] & \approx 1.56 \times 10^{30} \end{align*} $$

The updated variation equation is $$ \displaystyle F_g = \frac{1.56\times 10^{30}}{r^2} $$ .

Determine the distance between the two objects if the force of gravity is $$ \red{F_g = 4.1\times 10^6} $$ newtons.

$$ \begin{align*} \red{4.1\times 10^6} & = \frac{1.56\times 10^{30}}{r^2}\\[6pt] (\red{4.1\times 10^6})r^2 & = 1.56\times 10^{30}\\[6pt] r^2 & = \frac{1.56\times 10^{30}}{\red{4.1\times 10^6}}\\[6pt] r^2 & = \frac{1.56}{4.1}\times \frac{10^{30}}{10^6}\\[6pt] & = 0.3805\times 10^{24}\\[6pt] r & = \pm\sqrt{0.3805\times 10^{24}}\\[6pt] & = 0.6169\times 10^{12}\\[6pt] & = 6.169 \times 10^{12} \end{align*} $$

The distance decreases to $$ 6.169\times 10^{12} $$ meters.

In the study of electricity, Ohm's Law says the electrical current (measured in amps) across a conductor is inversely proportional to electrical resistance (measured in ohms).

Suppose a particular circuit has a variable resistor that is currently set to 360 ohm, and this results in 1/3 amps of current. If the resistance were decreased to 80 ohms, what would the resulting change in current be?

Define variables to represent the quantities we are investigating, and then write down the appropriate variation equation.

Let $$ I = $$ electrical current, measured in amps.

Let $$ R = $$ electrical resistance, measured in volts.

The equation of variation is $$ I = \frac k R $$ .

Note: This is Ohm's Law, and the constant of proportionality represents the voltage on the circuit.

Use $$ \red{I = \frac 1 3} $$ and $$ \blue{R = 360} $$ to determine the value of $$ k $$. Then rewrite the variation equation.

$$ \begin{align*} \red I & = \frac k {\blue R}\\[6pt] \red{\frac 1 3} & = \frac k {\blue{360}}\\[6pt] \red{\frac 1 3}(\blue{360}) & = \frac k {\blue{360}}\cdot \blue{360}\\[6pt] 120 & = \frac k {\cancelred{360}}\cdot \cancelred{360}\\[6pt] k & = 120 \end{align*} $$

The variation equation is now $$ I = \frac{120} R $$ .

Use the equation to determine the current running through the circuit when the resistance drops to only $$ \blue{R = 80} $$ ohms.

$$ I = \frac{120}{\blue{80}} = \frac 3 2 $$

When the resistance decreases to 80 ohms, the current increases to 1.5 amps.

In economics, the basic Law of Demand tells us that as the price for a particular good (or service) increases, the demand for that good (or service) will decrease. This is an inverse variation relationship.

Suppose a new app is released for cell phones, and at a price of $$ \$4.99 $$ there are 3.2 million downloads each month. Later, the company that produced the app puts it on sale for $$ \$0.99 $$

(a) What will the accompanying change in the number of downloads per month be?

(b) If the wanted to phase out the app (for a newer, better one in development), and wanted to decrease the number of downloads per month to only $$ 500{,}000 $$ , what price should they charge for the app?

Define variables for the quantities we are investigating, then write down the appropriate variation equation.

Let $$ p = $$ the price, in dollars, for which the app is being sold.

Let $$ d = $$ the number of downloads per month, measured in millions of downloads per month.

So, $$ d = 1 $$ represents 1 million downloads per month.

The variation equation is $$ d = \frac k p $$ .

Use $$ \red{d = 3.2} $$ and $$ \blue{4.99} $$ to determine the value of $$ k $$, then write down the updated variation equation.

$$ \begin{align*} \red d & = \frac k {\blue p}\\[6pt] \red{3.2} & = \frac k {\blue{4.99}}\\[6pt] \red{3.2}(\blue{4.99}) & = \frac k {\blue{4.99}}\cdot \blue{4.99}\\[6pt] 15.968 & = \frac k {\cancelred{4.99}}\cdot \cancelred{4.99}\\[6pt] k & = 15.968 \end{align*} $$

The variation equation becomes $$ d = \frac{15.968} p $$ .

Use the variation equation to determine the number of downloads per month the company can expect from putting the app on sale for $$ \blue{p = \$0.99} $$ .

$$ d = \frac{15.968}{\blue{0.99}} = \frac{1596.8}{99} \approx 16.13 $$

The downloads should increase to approximately 16.13 million per month.

Use the variation equation to determine the price which will cause the number of downloads per month to decrease to only 5 hundred thousand ( $$ \red{d = 1/2} $$ ).

$$ \begin{align*} \red{\frac 1 2} & = \frac{15.968} p\\[6pt] \frac p 2 & = 15.968\\[6pt] p & = 31.936 \end{align*} $$

The price would need to be about $$ \$31.94 $$ to drive down the demand to only half a million.

(a) Demand will increase to about 16.13 million downloads per month.

(b) Increasing the price to about $$ \$31.94 $$ will drive down demand to $$ 500{,}000 $$ downloads per month.

When working with electrical circuits, it turns out that the electrical resistance is inversely proportional to the square of the current.

Suppose a particular circuit has a current measured at $$ 0.05 $$ amps with a resistance of 90 ohms.

(a) What will happen to the resistance if the current drops to only 0.01 amps?

(b) Suppose someone swaps out the 90-ohm resistor for one that is rated at only 60 ohms. What happens to the current?

Define variables for the quantities, then write down the variation equation.

Let $$ R = $$ the electrical resistance measured in ohms.

Let $$ I = $$ the electrical current measured in amps.

The variation equation is $$ R = \frac k {I^2} $$

Note: In a previous question about electrical circuits we mentioned the constant of proportionality was in fact the voltage on the circuit. This time, the constant of proportionality represents the electrical power (in watts).

Use $$ \red{R = 90} $$ and $$ \blue{I = 0.05} $$ to determine the value of $$ k $$, then write down the updated variation equation.

$$ \begin{align*} \red R & = \frac k {\blue I^2}\\[6pt] \red{90} & = \frac k {(\blue{0.05})^2}\\[6pt] \red{90}\cdot(\blue{0.0025}) & = \frac k {\blue{0.0025}}\cdot (\blue{0.0025})\\[6pt] 0.225 & = \frac k {\cancelred{0.0025}}\cdot (\cancelred{0.0025})\\[6pt] k & = 0.225 \end{align*} $$

The variation equation is now $$ \displaystyle R = \frac{0.225}{I^2} = \frac 9 {40I^2} $$

Determine what happens to the current if the resistance is changed to $$ \red{R = 60} $$ ohms.

$$ \begin{align*} \red{60} & = \frac 9 {40I^2}\\[6pt] \red{60}I^2 & = \frac 9 {40}\\[6pt] I^2 & = \frac 9 {2400}\\[6pt] I & = \sqrt{\frac 9 {2400}}\\[6pt] & = \frac 3 {20\sqrt 6}\\[6pt] & \approx 0.0612 \end{align*} $$

The current increases to $$ \frac 3 {20\sqrt 6} $$ or approximately 0.0612 amps.

Suppose an object is falling toward the earth, and it's speed is inversely proportional to the square root of the distance from the earth's surface.

Also, suppose the object's speed is 60 meters/second when it is 900 meters above the earth's surface. How close will the object be when it's velocity reaches 100 meters/second?

Define variables for the quantities we are interested in, then write down the variation equation.

$$ v = $$ velocity, in meters/second

$$ d = $$ distance from the earth's surface, in meters.

The variation equation is $$ \displaystyle v = \frac k {\sqrt d} $$ .

Use $$ \red{v = 60} $$ and $$ \blue{d =900} $$ to determine the value of $$ k $$, then write down the updated variation equation.

$$ \begin{align*} \red v & = \frac k {\sqrt{\blue d}}\\[6pt] \red{60} & = \frac k {\sqrt{\blue{900}}}\\[6pt] \red{60}(\blue{30}) & = \frac k {\blue{30}}\cdot\blue{30}\\[6pt] 1800 & = \frac k {\cancelred{30}}\cdot\cancelred{30}\\[6pt] k & = 1800 \end{align*} $$

The variation equation is now $$ v = \frac{1800}{\sqrt d} $$

Use the equation to determine the distance of the object from the earth's surface when it's velocity reaches $$ \red{v = 100} $$ meters per second.

$$ \begin{align*} \red{100} & = \frac{1800}{\sqrt d}\\[6pt] \sqrt d & = \frac{1800}{\red{100}} = 18\\[6pt] d & = 18^2 = 324 \end{align*} $$

The object is only 324 meters above the earth's surface when it's velocity reaches 100 meters per second.

Ultimate Math Solver (Free) Free Algebra Solver ... type anything in there!

Popular pages @ mathwarehouse.com.

8.9 Use Direct and Inverse Variation

Learning objectives.

By the end of this section, you will be able to:

• Solve direct variation problems
• Solve inverse variation problems

Be Prepared 8.9

Before you get started, take this readiness quiz.

If you miss a problem, go back to the section listed and review the material.

• Find the multiplicative inverse of −8 −8 . If you missed this problem, review Example 1.126 .
• Solve for n n : 45 = 20 n 45 = 20 n . If you missed this problem, review Example 2.13 .
• Evaluate 5 x 2 5 x 2 when x = 10 x = 10 . If you missed this problem, review Example 1.20 .

When two quantities are related by a proportion, we say they are proportional to each other. Another way to express this relation is to talk about the variation of the two quantities. We will discuss direct variation and inverse variation in this section.

Solve Direct Variation Problems

Lindsay gets paid $15 per hour at her job. If we let s be her salary and h be the number of hours she has worked, we could model this situation with the equation

Lindsay’s salary is the product of a constant, 15, and the number of hours she works. We say that Lindsay’s salary varies directly with the number of hours she works. Two variables vary directly if one is the product of a constant and the other.

Direct Variation

For any two variables x and y , y varies directly with x if

The constant k is called the constant of variation.

In applications using direct variation, generally we will know values of one pair of the variables and will be asked to find the equation that relates x and y . Then we can use that equation to find values of y for other values of x .

Example 8.86

How to solve direct variation problems.

If y varies directly with x and y = 20 y = 20 when x = 8 x = 8 , find the equation that relates x and y .

Try It 8.171

If y y varies directly as x x and y = 3 , when x = 10 . y = 3 , when x = 10 . find the equation that relates x and y .

Try It 8.172

If y y varies directly as x x and y = 12 when x = 4 y = 12 when x = 4 find the equation that relates x and y .

We’ll list the steps below.

Solve direct variation problems.

• Step 1. Write the formula for direct variation.
• Step 2. Substitute the given values for the variables.
• Step 3. Solve for the constant of variation.
• Step 4. Write the equation that relates x and y.

Now we’ll solve a few applications of direct variation.

Example 8.87

When Raoul runs on the treadmill at the gym, the number of calories, c , he burns varies directly with the number of minutes, m , he uses the treadmill. He burned 315 calories when he used the treadmill for 18 minutes.

• ⓐ Write the equation that relates c and m .
• ⓑ How many calories would he burn if he ran on the treadmill for 25 minutes?

Try It 8.173

The number of calories, c , burned varies directly with the amount of time, t, spent exercising. Arnold burned 312 calories in 65 minutes exercising.

• ⓐ Write the equation that relates c and t .
• ⓑ How many calories would he burn if he exercises for 90 minutes?

Try It 8.174

The distance a moving body travels, d , varies directly with time, t , it moves. A train travels 100 miles in 2 hours

ⓐ Write the equation that relates d and t . ⓑ How many miles would it travel in 5 hours?

In the previous example, the variables c and m were named in the problem. Usually that is not the case. We will have to name the variables in the next example as part of the solution, just like we do in most applied problems.

Example 8.88

The number of gallons of gas Eunice’s car uses varies directly with the number of miles she drives. Last week she drove 469.8 miles and used 14.5 gallons of gas.

• ⓐ Write the equation that relates the number of gallons of gas used to the number of miles driven.
• ⓑ How many gallons of gas would Eunice’s car use if she drove 1000 miles?

ⓑ Find g when m = 1000 . Write the equation that relates g and m . g = 0.031 m Substitute the given value for m . g = 0.031 ( 1000 ) Simplify. g = 31 Eunice’s car would use 31 gallons of gas if she drove it 1,000 miles. Find g when m = 1000 . Write the equation that relates g and m . g = 0.031 m Substitute the given value for m . g = 0.031 ( 1000 ) Simplify. g = 31 Eunice’s car would use 31 gallons of gas if she drove it 1,000 miles.

Notice that in this example, the units on the constant of variation are gallons/mile. In everyday life, we usually talk about miles/gallon.

Try It 8.175

The distance that Brad travels varies directly with the time spent traveling. Brad travelled 660 miles in 12 hours,

• ⓐ Write the equation that relates the number of miles travelled to the time.
• ⓑ How many miles could Brad travel in 4 hours?

Try It 8.176

The weight of a liquid varies directly as its volume. A liquid that weighs 24 pounds has a volume of 4 gallons.

• ⓐ Write the equation that relates the weight to the volume.
• ⓑ If a liquid has volume 13 gallons, what is its weight?

In some situations, one variable varies directly with the square of the other variable. When that happens, the equation of direct variation is y = k x 2 y = k x 2 . We solve these applications just as we did the previous ones, by substituting the given values into the equation to solve for k .

Example 8.89

The maximum load a beam will support varies directly with the square of the diagonal of the beam’s cross-section. A beam with diagonal 4” will support a maximum load of 75 pounds.

• ⓐ Write the equation that relates the maximum load to the cross-section.
• ⓑ What is the maximum load that can be supported by a beam with diagonal 8”?

ⓑ Find L when c = 8 . Write the equation that relates L and c . L = 4.6875 c 2 Substitute the given value for c . L = 4.6875 ( 8 ) 2 Simplify. L = 300 A beam with diagonal 8” could support a maximum load of 300 pounds. Find L when c = 8 . Write the equation that relates L and c . L = 4.6875 c 2 Substitute the given value for c . L = 4.6875 ( 8 ) 2 Simplify. L = 300 A beam with diagonal 8” could support a maximum load of 300 pounds.

Try It 8.177

The distance an object falls is directly proportional to the square of the time it falls. A ball falls 144 feet in 3 seconds.

• ⓐ Write the equation that relates the distance to the time.
• ⓑ How far will an object fall in 4 seconds?

Try It 8.178

The area of a circle varies directly as the square of the radius. A circular pizza with a radius of 6 inches has an area of 113.04 square inches.

• ⓐ Write the equation that relates the area to the radius.
• ⓑ What is the area of a pizza with a radius of 9 inches?

Solve Inverse Variation Problems

Many applications involve two variable that vary inversely . As one variable increases, the other decreases. The equation that relates them is y = k x y = k x .

Inverse Variation

For any two variables x and y , y varies inversely with x if

The word ‘inverse’ in inverse variation refers to the multiplicative inverse. The multiplicative inverse of x is 1 x 1 x .

We solve inverse variation problems in the same way we solved direct variation problems. Only the general form of the equation has changed. We will copy the procedure box here and just change ‘direct’ to ‘inverse’.

Solve inverse variation problems.

• Step 1. Write the formula for inverse variation.

Example 8.90

If y varies inversely with x x and y = 20 y = 20 when x = 8 x = 8 , find the equation that relates x and y .

Try It 8.179

If p p varies inversely with q q and p = 30 p = 30 when q = 12 q = 12 find the equation that relates p p and q . q .

Try It 8.180

If y y varies inversely with x x and y = 8 y = 8 when x = 2 x = 2 find the equation that relates x x and y y .

Example 8.91

The fuel consumption (mpg) of a car varies inversely with its weight. A car that weighs 3100 pounds gets 26 mpg on the highway.

• ⓐ Write the equation of variation.
• ⓑ What would be the fuel consumption of a car that weighs 4030 pounds?

ⓑ Find f when w = 4030 . Write the equation that relates f and w . f = 80,600 w Substitute the given value for w . f = 80,600 4030 Simplify. f = 20 A car that weighs 4030 pounds would have fuel consumption of 20 mpg. Find f when w = 4030 . Write the equation that relates f and w . f = 80,600 w Substitute the given value for w . f = 80,600 4030 Simplify. f = 20 A car that weighs 4030 pounds would have fuel consumption of 20 mpg.

Try It 8.181

A car’s value varies inversely with its age. Elena bought a two-year-old car for $20,000.

ⓐ Write the equation of variation. ⓑ What will be the value of Elena’s car when it is 5 years old?

Try It 8.182

The time required to empty a pool varies inversely as the rate of pumping. It took Lucy 2.5 hours to empty her pool using a pump that was rated at 400 gpm (gallons per minute).

• ⓑ How long will it take her to empty the pool using a pump rated at 500 gpm?

Example 8.92

The frequency of a guitar string varies inversely with its length. A 26” long string has a frequency of 440 vibrations per second.

• ⓑ How many vibrations per second will there be if the string’s length is reduced to 20” by putting a finger on a fret?

ⓑ Find f when L = 20 . Write the equation that relates f and L . f = 11,440 L Substitute the given value for L . f = 11,440 20 Simplify. f = 572 A 20” guitar string has frequency 572 vibrations per second. Find f when L = 20 . Write the equation that relates f and L . f = 11,440 L Substitute the given value for L . f = 11,440 20 Simplify. f = 572 A 20” guitar string has frequency 572 vibrations per second.

Try It 8.183

The number of hours it takes for ice to melt varies inversely with the air temperature. Suppose a block of ice melts in 2 hours when the temperature is 65 degrees.

• ⓑ How many hours would it take for the same block of ice to melt if the temperature was 78 degrees?

Try It 8.184

The force needed to break a board varies inversely with its length. Richard uses 24 pounds of pressure to break a 2-foot long board.

• ⓑ How many pounds of pressure is needed to break a 5-foot long board?

Section 8.9 Exercises

Practice makes perfect.

In the following exercises, solve.

If y y varies directly as x x and y = 14 , when x = 3 y = 14 , when x = 3 , find the equation that relates x and y x and y .

If p p varies directly as q q and p = 5 , when q = 2 p = 5 , when q = 2 , find the equation that relates p and q p and q .

If v v varies directly as w w and v = 24 , when w = 8 v = 24 , when w = 8 , find the equation that relates v and w . v and w .

If a a varies directly as b b and a = 16 , when b = 4 a = 16 , when b = 4 , find the equation that relates a and b . a and b .

If p p varies directly as q q and p = 9.6 , when q = 3 p = 9.6 , when q = 3 , find the equation that relates p and q . p and q .

If y y varies directly as x x and y = 12.4 , when x = 4 , y = 12.4 , when x = 4 , find the equation that relates x and y x and y

If a a varies directly as b b and a = 6 , when b = 1 3 a = 6 , when b = 1 3 , find the equation that relates a and b . a and b .

If v v varies directly as w w and v = 8 , when w = 1 2 v = 8 , when w = 1 2 , find the equation that relates v and w . v and w .

The amount of money Sally earns, P , varies directly with the number, n , of necklaces she sells. When Sally sells 15 necklaces she earns $150.

• ⓐ Write the equation that relates P and n .
• ⓑ How much money would she earn if she sold 4 necklaces?

The price, P , that Eric pays for gas varies directly with the number of gallons, g , he buys. It costs him $50 to buy 20 gallons of gas.

• ⓐ Write the equation that relates P and g .
• ⓑ How much would 33 gallons cost Eric?

Terri needs to make some pies for a fundraiser. The number of apples, a , varies directly with number of pies, p . It takes nine apples to make two pies.

• ⓐ Write the equation that relates a and p .
• ⓑ How many apples would Terri need for six pies?

Joseph is traveling on a road trip. The distance, d , he travels before stopping for lunch varies directly with the speed, v , he travels. He can travel 120 miles at a speed of 60 mph.

• ⓐ Write the equation that relates d and v .
• ⓑ How far would he travel before stopping for lunch at a rate of 65 mph?

The price of gas that Jesse purchased varies directly to how many gallons he purchased. He purchased 10 gallons of gas for $39.80.

• ⓐ Write the equation that relates the price to the number of gallons.
• ⓑ How much will it cost Jesse for 15 gallons of gas?

The distance that Sarah travels varies directly to how long she drives. She travels 440 miles in 8 hours.

• ⓐ Write the equation that relates the distance to the number of hours.
• ⓑ How far can Sally travel in 6 hours?

The mass of a liquid varies directly with its volume. A liquid with mass 16 kilograms has a volume of 2 liters.

• ⓐ Write the equation that relates the mass to the volume.
• ⓑ What is the volume of this liquid if its mass is 128 kilograms?

The length that a spring stretches varies directly with a weight placed at the end of the spring. When Sarah placed a 10 pound watermelon on a hanging scale, the spring stretched 5 inches.

• ⓐ Write the equation that relates the length of the spring to the weight.
• ⓑ What weight of watermelon would stretch the spring 6 inches?

The distance an object falls varies directly to the square of the time it falls. A ball falls 45 feet in 3 seconds.

• ⓑ How far will the ball fall in 7 seconds?

The maximum load a beam will support varies directly with the square of the diagonal of the beam’s cross-section. A beam with diagonal 6 inch will support a maximum load of 108 pounds.

• ⓐ Write the equation that relates the load to the diagonal of the cross-section.
• ⓑ What load will a beam with a 10 inch diagonal support?
• ⓑ What is the area of a personal pizza with a radius 4 inches?

The distance an object falls varies directly to the square of the time it falls. A ball falls 72 feet in 3 seconds,

• ⓑ How far will the ball have fallen in 8 seconds?

If y y varies inversely with x x and y = 5 y = 5 when x = 4 x = 4 find the equation that relates x x and y . y .

If p p varies inversely with q q and p = 2 p = 2 when q = 1 q = 1 find the equation that relates p p and q . q .

If v v varies inversely with w w and v = 6 v = 6 when w = 1 2 w = 1 2 find the equation that relates v v and w . w .

If a a varies inversely with b b and a = 12 a = 12 when b = 1 3 b = 1 3 find the equation that relates a a and b . b .

Write an inverse variation equation to solve the following problems.

The fuel consumption (mpg) of a car varies inversely with its weight. A Toyota Corolla weighs 2800 pounds and gets 33 mpg on the highway.

• ⓐ Write the equation that relates the mpg to the car’s weight.
• ⓑ What would the fuel consumption be for a Toyota Sequoia that weighs 5500 pounds?

A car’s value varies inversely with its age. Jackie bought a 10 year old car for $2,400.

• ⓐ Write the equation that relates the car’s value to its age.
• ⓑ What will be the value of Jackie’s car when it is 15 years old ?

The time required to empty a tank varies inversely as the rate of pumping. It took Janet 5 hours to pump her flooded basement using a pump that was rated at 200 gpm (gallons per minute),

• ⓐ Write the equation that relates the number of hours to the pump rate.
• ⓑ How long would it take Janet to pump her basement if she used a pump rated at 400 gpm?

The volume of a gas in a container varies inversely as pressure on the gas. A container of helium has a volume of 370 cubic inches under a pressure of 15 psi.

• ⓐ Write the equation that relates the volume to the pressure.
• ⓑ What would be the volume of this gas if the pressure was increased to 20 psi?

On a string instrument, the length of a string varies inversely as the frequency of its vibrations. An 11-inch string on a violin has a frequency of 400 cycles per second.

• ⓐ Write the equation that relates the string length to its frequency.
• ⓑ What is the frequency of a 10-inch string?

Paul, a dentist, determined that the number of cavities that develops in his patient’s mouth each year varies inversely to the number of minutes spent brushing each night. His patient, Lori, had 4 cavities when brushing her teeth 30 seconds (0.5 minutes) each night.

• ⓐ Write the equation that relates the number of cavities to the time spent brushing.
• ⓑ How many cavities would Paul expect Lori to have if she had brushed her teeth for 2 minutes each night?

The number of tickets for a sports fundraiser varies inversely to the price of each ticket. Brianna can buy 25 tickets at $5each.

• ⓐ Write the equation that relates the number of tickets to the price of each ticket.
• ⓑ How many tickets could Brianna buy if the price of each ticket was $2.50?

Boyle’s Law states that if the temperature of a gas stays constant, then the pressure varies inversely to the volume of the gas. Braydon, a scuba diver, has a tank that holds 6 liters of air under a pressure of 220 psi.

• ⓐ Write the equation that relates pressure to volume.
• ⓑ If the pressure increases to 330 psi, how much air can Braydon’s tank hold?

Mixed Practice

If y y varies directly as x x and y = 5 , when x = 3 . y = 5 , when x = 3 . , find the equation that relates x and y x and y .

If v v varies directly as w w and v = 21 , when w = 8 . v = 21 , when w = 8 . find the equation that relates v and w . v and w .

If p p varies inversely with q q and p = 5 p = 5 when q = 6 q = 6 , find the equation that relates p p and q . q .

If y y varies inversely with x x and y = 11 y = 11 when x = 3 x = 3 find the equation that relates x x and y . y .

If p p varies directly as q q and p = 10 , when q = 2 . p = 10 , when q = 2 . find the equation that relates p and q p and q .

If v v varies inversely with w w and v = 18 v = 18 when w = 1 3 w = 1 3 find the equation that relates v v and w . w .

The force needed to break a board varies inversely with its length. If Tom uses 20 pounds of pressure to break a 1.5-foot long board, how many pounds of pressure would he need to use to break a 6 foot long board?

The number of hours it takes for ice to melt varies inversely with the air temperature. A block of ice melts in 2.5 hours when the temperature is 54 degrees. How long would it take for the same block of ice to melt if the temperature was 45 degrees?

The length a spring stretches varies directly with a weight placed at the end of the spring. When Meredith placed a 6-pound cantaloupe on a hanging scale, the spring stretched 2 inches. How far would the spring stretch if the cantaloupe weighed 9 pounds?

The amount that June gets paid varies directly the number of hours she works. When she worked 15 hours, she got paid $111. How much will she be paid for working 18 hours?

The fuel consumption (mpg) of a car varies inversely with its weight. A Ford Focus weighs 3000 pounds and gets 28.7 mpg on the highway. What would the fuel consumption be for a Ford Expedition that weighs 5,500 pounds? Round to the nearest tenth.

The volume of a gas in a container varies inversely as the pressure on the gas. If a container of argon has a volume of 336 cubic inches under a pressure of 2,500 psi, what will be its volume if the pressure is decreased to 2,000 psi?

The distance an object falls varies directly to the square of the time it falls. If an object falls 52.8 feet in 4 seconds, how far will it fall in 9 seconds?

The area of the face of a Ferris wheel varies directly with the square of its radius. If the area of one face of a Ferris wheel with diameter 150 feet is 70,650 square feet, what is the area of one face of a Ferris wheel with diameter of 16 feet?

Everyday Math

Ride Service It costs $35 for a ride from the city center to the airport, 14 miles away.

• ⓐ Write the equation that relates the cost, c , with the number of miles, m .
• ⓑ What would it cost to travel 22 miles with this service?

Road Trip The number of hours it takes Jack to drive from Boston to Bangor is inversely proportional to his average driving speed. When he drives at an average speed of 40 miles per hour, it takes him 6 hours for the trip.

• ⓐ Write the equation that relates the number of hours, h , with the speed, s.
• ⓑ How long would the trip take if his average speed was 75 miles per hour?

Writing Exercises

In your own words, explain the difference between direct variation and inverse variation.

Make up an example from your life experience of inverse variation.

ⓐ After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.

ⓑ After looking at the checklist, do you think you are well-prepared for the next chapter? Why or why not?

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.

Access for free at https://openstax.org/books/elementary-algebra/pages/1-introduction

• Authors: Lynn Marecek, MaryAnne Anthony-Smith
• Publisher/website: OpenStax
• Book title: Elementary Algebra
• Publication date: Feb 22, 2017
• Location: Houston, Texas
• Book URL: https://openstax.org/books/elementary-algebra/pages/1-introduction
• Section URL: https://openstax.org/books/elementary-algebra/pages/8-9-use-direct-and-inverse-variation

© Feb 9, 2022 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

Inverse Variation Word Problems

Related Pages: Direct Variation Proportions Proportion Word Problems Joint And Combined Variation More Algebra Lessons

In these lessons, we will learn about inverse variation and how to solve applications that involve inverse variation.

The following diagrams show the differences between Direct Variation and Indirect Variation. Scroll down the page for examples and solutions.

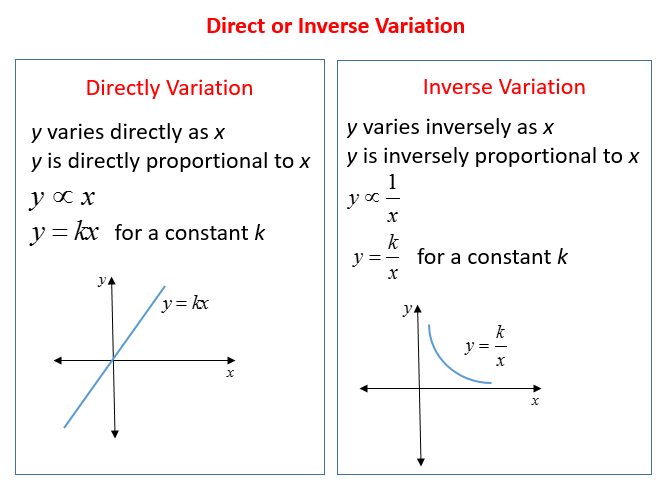
What Is Inverse Variation?

There are many situations in our daily lives that involve inverse variation (indirect variation).

For example, the number of days required to build a bridge varies inversely to the number of workers. As the number of workers increases, the number of days required to build would decrease and as the number of workers decreases, the number of days increases.

Another example would be that speed varies inversely to time. As speed increases, the time taken to cover the same distance decreases and as speed decreases, the time taken increases.

In general, when two variables x and y are such that xy = k where k is a non-zero constant, we say that y varies inversely with x.

Example: Suppose that y varies inversely as x and that y = 8 when x = 3. a) Form an equation connecting x and y. b) Calculate the value of y when x = 10.

a) Substitute x = 3 and y = 8 into the equation to obtain k 3 × 8 = k ⇒ k = 24 The equation is xy = 24

a) Find the equation connecting x and y. b) Find the value of y when x = 3.

How to define inverse variation and how to solve inverse variation problems?

• y varies inversely as x. y = 4 when x = 2. Determine the inverse variation equation. Then determine y when x = 16.
• The time, t, required to empty a tank varies inversely as the rate, r, of pumping. If a pump can empty a tank in 2.5 hours at a rate of 400 gallons per minute, how long will it take to empty a tank at 500 gallons per minute?
• The force, F, needed to break a board varies inversely with the length, L, of the board. If it takes 24 pounds of pressure to break a board 2 feet long, how many pounds of pressure would it take to break a board that is 5 feet long?
• y varies inversely as the square root of x. y = 6 when x = 16. Determine the inverse variation equation. Then determine y when x = 4.

How to solve a basic inverse variation problem?

Example: y varies inversely as x. y = 3 when x = 10. Determine the inverse variation equation. Then determine y when x = 6.

How to solve an inverse variation problem with a change of variables?

Example: Given m varies inversely as t, and m = 9 when t = 6, find the variation constant and the inverse variation equation. Then determine m when t = 27.

How to solve a inverse variation problem when k is a fraction?

Example: y varies inversely as x. y = 1/2 when x = 2/3. Find the variation constant and the inverse variation equation. Then determine y when x = 2/15.

What is the difference between direct and inverse variation?

In general, if two quantities vary directly, if one goes up so does the other. If one goes down so does the other. The following statements are equivalent

• y varies directly as x.
• y is directly proportional to x.
• y = kx for some constant k.

In general, if two quantities vary indirectly, if one goes up and the other goes down. The following statements are equivalent

• y varies indirectly as x.
• y is inversely proportional to x.
• y = k/x for some constant k.

How to tell if two variables vary inversely or directly?

Recognizing Direct and Inverse Variation

How to solve direct variation and indirect/inverse variation word problems?

Example: On a string instrument, the length of a string varies inversely as the frequency of its vibrations. An 11-inch string has a frequency of 400 cycles per second. Find the constant of proportionality and the frequency of a 10-inch string.

Inverse Variation Equations and Ordered Pairs

This video looks at inverse variation: identifying inverse variations from ordered pairs, writing inverse variation equations, graphing inverse variations, and finding missing values.

Example: Let x 1 = 4, y 1 = 12 and x 2 = 3. Let y vary inversely as x. Find y 2 .

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.

Inverse Variation Lesson

• Demonstrate an understanding of direct variation
• Learn how to solve an inverse variation problem
• Learn how to solve an inverse variation as a power problem
• Learn how to solve an inverse variation word problem

How to Solve an Inverse Variation Problem

Solving an inverse variation problem.

• Write the variation equation: y = k/x or k = xy
• Substitute in for the given values and find the value of k
• Rewrite the variation equation: y = k/x with the known value of k
• Substitute the remaining values and find the unknown

Inverse Variation as a Power

Inverse variation word problems, skills check:.

Solve each inverse variation problem.

y varies inversely with x and y = 3 when x = 8. Find y when x = 6.

Please choose the best answer.

Jacobs Medical Devices produces medical sponges. The cost of producing a medical sponge varies inversely with the number produced. When 10,000 medical sponges are produced, the cost is $2 per medical sponge. What is the cost per medical sponge for Jacobs Medical Devices to produce 25,000 medical sponges?

The current in a simple electrical circuit varies inversely with the resistance. If the current is 20 amps when the resistance is 5 ohms, find the current when the resistance is 8 ohms.

Congrats, Your Score is 100 %

Better Luck Next Time, Your Score is %

Ready for more? Watch the Step by Step Video Lesson   |   Take the Practice Test

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

3.9: Modeling Using Variation

• Last updated
• Save as PDF
• Page ID 1351

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Learning Objectives

• Solve direct variation problems.
• Solve inverse variation problems.
• Solve problems involving joint variation.

A used-car company has just offered their best candidate, Nicole, a position in sales. The position offers 16% commission on her sales. Her earnings depend on the amount of her sales. For instance, if she sells a vehicle for $4,600, she will earn $736. She wants to evaluate the offer, but she is not sure how. In this section, we will look at relationships, such as this one, between earnings, sales, and commission rate.

Solving Direct Variation Problems

In the example above, Nicole’s earnings can be found by multiplying her sales by her commission. The formula \(e=0.16s\) tells us her earnings, \(e\), come from the product of 0.16, her commission, and the sale price of the vehicle. If we create a table, we observe that as the sales price increases, the earnings increase as well, which should be intuitive. See Table 5.8.1 .

Table 5.8.1

Notice that earnings are a multiple of sales. As sales increase, earnings increase in a predictable way. Double the sales of the vehicle from $4,600 to $9,200, and we double the earnings from $736 to $1,472. As the input increases, the output increases as a multiple of the input. A relationship in which one quantity is a constant multiplied by another quantity is called direct variation . Each variable in this type of relationship varies directly with the other.

Figure 5.8.1 represents the data for Nicole’s potential earnings. We say that earnings vary directly with the sales price of the car. The formula \(y=kx^n\) is used for direct variation. The value \(k\) is a nonzero constant greater than zero and is called the constant of variation . In this case, \(k=0.16\) and \(n=1\). We saw functions like this one when we discussed power functions.

Figure has invalid source: image visible until saved.... src="/@api/deki/pages/=Bookshelves%252FPrecalculus%252FBook%25253A_Precalculus_(OpenStax)%252F03%25253A_Polynomial_and_Rational_Functions%252F3.9%25253A_Modeling_Using_Variation/files/CNX_Precalc_Figure_03_09_001.jpg

A General Note: DIRECT VARIATION

If \(x\) and \(y\) are related by an equation of the form

then we say that the relationship is direct variation and \(y\) varies directly with, or is proportional to, the \(n\)th power of \(x\). In direct variation relationships, there is a nonzero constant ratio \(k=\dfrac{y}{x^n}\), where \(k\) is called the constant of variation , which help defines the relationship between the variables.

Given a description of a direct variation problem, solve for an unknown.

• Identify the input, \(x\),and the output, \(y\).
• Determine the constant of variation. You may need to divide \(y\) by the specified power of \(x\) to determine the constant of variation.
• Use the constant of variation to write an equation for the relationship.
• Substitute known values into the equation to find the unknown.

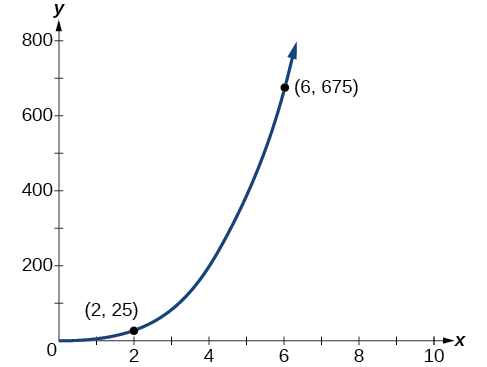
Solving a Direct Variation Problem

The quantity \(y\) varies directly with the cube of \(x\). If \(y=25\) when \(x=2\), find \(y\) when \(x\) is \(6\).

The general formula for direct variation with a cube is \(y=kx^3\). The constant can be found by dividing \(y\) by the cube of \(x\).

\(k=\dfrac{y}{x^3}\)

\(=\dfrac{25}{2^3}\)

\(=\dfrac{25}{8}\)

Now use the constant to write an equation that represents this relationship.

\(y=\dfrac{25}{8}x^3\)

Substitute \(x=6\) and solve for \(y\).

\(y=\dfrac{25}{8}{(6)}^3\)

The graph of this equation is a simple cubic, as shown in Figure 5.8.2 .

Do the graphs of all direct variation equations look like Example ?

No. Direct variation equations are power functions—they may be linear, quadratic, cubic, quartic, radical, etc. But all of the graphs pass through \((0,0)\).

The quantity \(y\) varies directly with the square of \(x\). If \(y=24\) when \(x=3\), find \(y\) when \(x\) is 4.

\(\frac{128}{3}\)

Solving Inverse Variation Problems

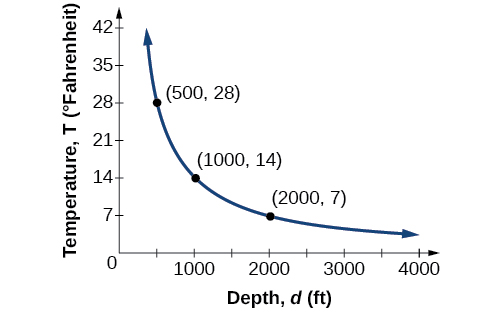
Water temperature in an ocean varies inversely to the water’s depth. The formula \(T=\frac{14,000}{d}\) gives us the temperature in degrees Fahrenheit at a depth in feet below Earth’s surface. Consider the Atlantic Ocean, which covers 22% of Earth’s surface. At a certain location, at the depth of 500 feet, the temperature may be 28°F.

If we create Table 5.8.2 , we observe that, as the depth increases, the water temperature decreases.

Table 5.8.2

We notice in the relationship between these variables that, as one quantity increases, the other decreases. The two quantities are said to be inversely proportional and each term varies inversely with the other. Inversely proportional relationships are also called inverse variations .

For our example, Figure 5.8.3 depicts the inverse variation. We say the water temperature varies inversely with the depth of the water because, as the depth increases, the temperature decreases. The formula \(y=\frac{k}{x}\) for inverse variation in this case uses \(k=14,000\).

A General Note: INVERSE VARIATION

\(y=\frac{k}{x^n}\)

where \(k\) is a nonzero constant, then we say that \(y\) varies inversely with the \(n\)th power of \(x\). In inversely proportional relationships, or inverse variations , there is a constant multiple \(k=x^ny\).

Writing a Formula for an Inversely Proportional Relationship

A tourist plans to drive 100 miles. Find a formula for the time the trip will take as a function of the speed the tourist drives.

Recall that multiplying speed by time gives distance. If we let \(t\) represent the drive time in hours, and \(v\) represent the velocity (speed or rate) at which the tourist drives, then \(vt=\)distance. Because the distance is fixed at 100 miles, \(vt=100\) so \(t=\frac{100}{v}\). Because time is a function of velocity, we can write \(t(v)\).

\(t(v)=\frac{100}{v}\)

\(=100v^{−1}\)

We can see that the constant of variation is 100 and, although we can write the relationship using the negative exponent, it is more common to see it written as a fraction. We say that time varies inversely with velocity.

Given a description of an indirect variation problem, solve for an unknown.

• Identify the input, \(x\), and the output, \(y\).
• Determine the constant of variation. You may need to multiply \(y\) by the specified power of \(x\) to determine the constant of variation.

Solving an Inverse Variation Problem

A quantity \(y\) varies inversely with the cube of \(x\). If \(y=25\) when \(x=2\), find \(y\) when \(x\) is \(6\).

The general formula for inverse variation with a cube is \(y=\frac{k}{x^3}\). The constant can be found by multiplying \(y\) by the cube of \(x\).

\(=2^3⋅25\)

Now we use the constant to write an equation that represents this relationship.

\(y=\dfrac{k}{x^3}\), \( k=200\)

\(y=\dfrac{200}{x^3}\)

\(y=\dfrac{200}{6^3}\)

\(=\dfrac{25}{27}\)

The graph of this equation is a rational function, as shown in Figure 5.8.4 .

A quantity \(y\) varies inversely with the square of \(x\). If \(y=8\) when \(x=3\), find \(y\) when \(x\) is \(4\).

\(\frac{9}{2}\)

Solving Problems Involving Joint Variation

Many situations are more complicated than a basic direct variation or inverse variation model. One variable often depends on multiple other variables. When a variable is dependent on the product or quotient of two or more variables, this is called joint variation . For example, the cost of busing students for each school trip varies with the number of students attending and the distance from the school. The variable \(c\),cost, varies jointly with the number of students, \(n\),and the distance, \(d\).

A General Note: JOINT VARIATION

Joint variation occurs when a variable varies directly or inversely with multiple variables.

For instance, if \(x\) varies directly with both \(y\) and \(z\), we have \(x=kyz\). If \(x\) varies directly with \(y\) and inversely with \(z\),we have \(x=\frac{ky}{z}\). Notice that we only use one constant in a joint variation equation.

A quantity \(x\) varies directly with the square of \(y\) and inversely with the cube root of \(z\). If \(x=6\) when \(y=2\) and \(z=8\), find \(x\) when \(y=1\) and \(z=27\).

Begin by writing an equation to show the relationship between the variables.

\(x=\dfrac{ky^2}{\sqrt[3]{z}}\)

Substitute \(x=6\), \(y=2\), and \(z=8\) to find the value of the constant \(k\).

\(6=\dfrac{k2^2}{\sqrt[3]{8}}\)

\(6=\dfrac{4k}{2}\)

Now we can substitute the value of the constant into the equation for the relationship.

\(x=\dfrac{3y^2}{\sqrt[3]{z}}\)

To find \(x\) when \(y=1\) and \(z=27\), we will substitute values for \(y\) and \(z\) into our equation.

\(x=\dfrac{3{(1)}^2}{\sqrt[3]{27}}\)

A quantity \(x\) varies directly with the square of \(y\) and inversely with \(z\). If \(x=40\) when \(y=4\) and \(z=2\), find \(x\) when \(y=10\) and \(z=25\).

Access these online resources for additional instruction and practice with direct and inverse variation.

• Direct Variation
• Inverse Variation
• Direct and Inverse Variation

Visit this website for additional practice questions from Learningpod.

Key Equations

Key concepts.

• A relationship where one quantity is a constant multiplied by another quantity is called direct variation. See Example .
• Two variables that are directly proportional to one another will have a constant ratio.
• A relationship where one quantity is a constant divided by another quantity is called inverse variation. See Example .
• Two variables that are inversely proportional to one another will have a constant multiple. See Example .
• In many problems, a variable varies directly or inversely with multiple variables. We call this type of relationship joint variation. See Example .

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.

Chapter 2: Linear Equations

2.7 Variation Word Problems

Direct variation problems.

There are many mathematical relations that occur in life. For instance, a flat commission salaried salesperson earns a percentage of their sales, where the more they sell equates to the wage they earn. An example of this would be an employee whose wage is 5% of the sales they make. This is a direct or a linear variation, which, in an equation, would look like:

[latex]\text{Wage }(x)=5\%\text{ Commission }(k)\text{ of Sales Completed }(y)[/latex]

[latex]x=ky[/latex]

A historical example of direct variation can be found in the changing measurement of pi, which has been symbolized using the Greek letter π since the mid 18th century. Variations of historical π calculations are Babylonian [latex]\left(\dfrac{25}{8}\right),[/latex] Egyptian [latex]\left(\dfrac{16}{9}\right)^2,[/latex] and Indian [latex]\left(\dfrac{339}{108}\text{ and }10^{\frac{1}{2}}\right).[/latex] In the 5th century, Chinese mathematician Zu Chongzhi calculated the value of π to seven decimal places (3.1415926), representing the most accurate value of π for over 1000 years.

Pi is found by taking any circle and dividing the circumference of the circle by the diameter, which will always give the same value: 3.14159265358979323846264338327950288419716… (42 decimal places). Using an infinite-series exact equation has allowed computers to calculate π to 10 13 decimals.

[latex]\begin{array}{c} \text{Circumference }(c)=\pi \text{ times the diameter }(d) \\ \\ \text{or} \\ \\ c=\pi d \end{array}[/latex]

All direct variation relationships are verbalized in written problems as a direct variation or as directly proportional and take the form of straight line relationships. Examples of direct variation or directly proportional equations are:

• [latex]x[/latex] varies directly as [latex]y[/latex]
• [latex]x[/latex] varies as [latex]y[/latex]
• [latex]x[/latex] varies directly proportional to [latex]y[/latex]
• [latex]x[/latex] is proportional to [latex]y[/latex]
• [latex]x[/latex] varies directly as the square of [latex]y[/latex]
• [latex]x[/latex] varies as [latex]y[/latex] squared
• [latex]x[/latex] is proportional to the square of [latex]y[/latex]
• [latex]x[/latex] varies directly as the cube of [latex]y[/latex]
• [latex]x[/latex] varies as [latex]y[/latex] cubed
• [latex]x[/latex] is proportional to the cube of [latex]y[/latex]
• [latex]x[/latex] varies directly as the square root of [latex]y[/latex]
• [latex]x[/latex] varies as the root of [latex]y[/latex]
• [latex]x[/latex] is proportional to the square root of [latex]y[/latex]

Example 2.7.1

Find the variation equation described as follows:

The surface area of a square surface [latex](A)[/latex] is directly proportional to the square of either side [latex](x).[/latex]

[latex]\begin{array}{c} \text{Area }(A) =\text{ constant }(k)\text{ times side}^2\text{ } (x^2) \\ \\ \text{or} \\ \\ A=kx^2 \end{array}[/latex]

Example 2.7.2

When looking at two buildings at the same time, the length of the buildings’ shadows [latex](s)[/latex] varies directly as their height [latex](h).[/latex] If a 5-story building has a 20 m long shadow, how many stories high would a building that has a 32 m long shadow be?

The equation that describes this variation is:

[latex]h=kx[/latex]

Breaking the data up into the first and second parts gives:

[latex]\begin{array}{ll} \begin{array}{rrl} \\ &&\textbf{1st Data} \\ s&=&20\text{ m} \\ h&=&5\text{ stories} \\ k&=&\text{find 1st} \\ \\ &&\text{Find }k\text{:} \\ h&=&kx \\ 5\text{ stories}&=&k\text{ (20 m)} \\ k&=&5\text{ stories/20 m}\\ k&=&0.25\text{ story/m} \end{array} & \hspace{0.5in} \begin{array}{rrl} &&\textbf{2nd Data} \\ s&=&\text{32 m} \\ h&=&\text{find 2nd} \\ k&=&0.25\text{ story/m} \\ \\ &&\text{Find }h\text{:} \\ h&=&kx \\ h&=&(0.25\text{ story/m})(32\text{ m}) \\ h&=&8\text{ stories} \end{array} \end{array}[/latex]

Inverse Variation Problems

Inverse variation problems are reciprocal relationships. In these types of problems, the product of two or more variables is equal to a constant. An example of this comes from the relationship of the pressure [latex](P)[/latex] and the volume [latex](V)[/latex] of a gas, called Boyle’s Law (1662). This law is written as:

[latex]\begin{array}{c} \text{Pressure }(P)\text{ times Volume }(V)=\text{ constant} \\ \\ \text{ or } \\ \\ PV=k \end{array}[/latex]

Written as an inverse variation problem, it can be said that the pressure of an ideal gas varies as the inverse of the volume or varies inversely as the volume. Expressed this way, the equation can be written as:

[latex]P=\dfrac{k}{V}[/latex]

Another example is the historically famous inverse square laws. Examples of this are the force of gravity [latex](F_{\text{g}}),[/latex] electrostatic force [latex](F_{\text{el}}),[/latex] and the intensity of light [latex](I).[/latex] In all of these measures of force and light intensity, as you move away from the source, the intensity or strength decreases as the square of the distance.

In equation form, these look like:

[latex]F_{\text{g}}=\dfrac{k}{d^2}\hspace{0.25in} F_{\text{el}}=\dfrac{k}{d^2}\hspace{0.25in} I=\dfrac{k}{d^2}[/latex]

These equations would be verbalized as:

• The force of gravity [latex](F_{\text{g}})[/latex] varies inversely as the square of the distance.
• Electrostatic force [latex](F_{\text{el}})[/latex] varies inversely as the square of the distance.
• The intensity of a light source [latex](I)[/latex] varies inversely as the square of the distance.

All inverse variation relationship are verbalized in written problems as inverse variations or as inversely proportional. Examples of inverse variation or inversely proportional equations are:

• [latex]x[/latex] varies inversely as [latex]y[/latex]
• [latex]x[/latex] varies as the inverse of [latex]y[/latex]
• [latex]x[/latex] varies inversely proportional to [latex]y[/latex]
• [latex]x[/latex] is inversely proportional to [latex]y[/latex]
• [latex]x[/latex] varies inversely as the square of [latex]y[/latex]
• [latex]x[/latex] varies inversely as [latex]y[/latex] squared
• [latex]x[/latex] is inversely proportional to the square of [latex]y[/latex]
• [latex]x[/latex] varies inversely as the cube of [latex]y[/latex]
• [latex]x[/latex] varies inversely as [latex]y[/latex] cubed
• [latex]x[/latex] is inversely proportional to the cube of [latex]y[/latex]
• [latex]x[/latex] varies inversely as the square root of [latex]y[/latex]
• [latex]x[/latex] varies as the inverse root of [latex]y[/latex]
• [latex]x[/latex] is inversely proportional to the square root of [latex]y[/latex]

Example 2.7.3

The force experienced by a magnetic field [latex](F_{\text{b}})[/latex] is inversely proportional to the square of the distance from the source [latex](d_{\text{s}}).[/latex]

[latex]F_{\text{b}} = \dfrac{k}{{d_{\text{s}}}^2}[/latex]

Example 2.7.4

The time [latex](t)[/latex] it takes to travel from North Vancouver to Hope varies inversely as the speed [latex](v)[/latex] at which one travels. If it takes 1.5 hours to travel this distance at an average speed of 120 km/h, find the constant [latex]k[/latex] and the amount of time it would take to drive back if you were only able to travel at 60 km/h due to an engine problem.

[latex]t=\dfrac{k}{v}[/latex]

[latex]\begin{array}{ll} \begin{array}{rrl} &&\textbf{1st Data} \\ v&=&120\text{ km/h} \\ t&=&1.5\text{ h} \\ k&=&\text{find 1st} \\ \\ &&\text{Find }k\text{:} \\ k&=&tv \\ k&=&(1.5\text{ h})(120\text{ km/h}) \\ k&=&180\text{ km} \end{array} & \hspace{0.5in} \begin{array}{rrl} \\ \\ \\ &&\textbf{2nd Data} \\ v&=&60\text{ km/h} \\ t&=&\text{find 2nd} \\ k&=&180\text{ km} \\ \\ &&\text{Find }t\text{:} \\ t&=&\dfrac{k}{v} \\ \\ t&=&\dfrac{180\text{ km}}{60\text{ km/h}} \\ \\ t&=&3\text{ h} \end{array} \end{array}[/latex]

Joint or Combined Variation Problems

In real life, variation problems are not restricted to single variables. Instead, functions are generally a combination of multiple factors. For instance, the physics equation quantifying the gravitational force of attraction between two bodies is:

[latex]F_{\text{g}}=\dfrac{Gm_1m_2}{d^2}[/latex]

• [latex]F_{\text{g}}[/latex] stands for the gravitational force of attraction
• [latex]G[/latex] is Newton’s constant, which would be represented by [latex]k[/latex] in a standard variation problem
• [latex]m_1[/latex] and [latex]m_2[/latex] are the masses of the two bodies
• [latex]d^2[/latex] is the distance between the centres of both bodies

To write this out as a variation problem, first state that the force of gravitational attraction [latex](F_{\text{g}})[/latex] between two bodies is directly proportional to the product of the two masses [latex](m_1, m_2)[/latex] and inversely proportional to the square of the distance [latex](d)[/latex] separating the two masses. From this information, the necessary equation can be derived. All joint variation relationships are verbalized in written problems as a combination of direct and inverse variation relationships, and care must be taken to correctly identify which variables are related in what relationship.

Example 2.7.5

The force of electrical attraction [latex](F_{\text{el}})[/latex] between two statically charged bodies is directly proportional to the product of the charges on each of the two objects [latex](q_1, q_2)[/latex] and inversely proportional to the square of the distance [latex](d)[/latex] separating these two charged bodies.

[latex]F_{\text{el}}=\dfrac{kq_1q_2}{d^2}[/latex]

Solving these combined or joint variation problems is the same as solving simpler variation problems.

First, decide what equation the variation represents. Second, break up the data into the first data given—which is used to find [latex]k[/latex]—and then the second data, which is used to solve the problem given. Consider the following joint variation problem.

Example 2.7.6

[latex]y[/latex] varies jointly with [latex]m[/latex] and [latex]n[/latex] and inversely with the square of [latex]d[/latex]. If [latex]y = 12[/latex] when [latex]m = 3[/latex], [latex]n = 8[/latex], and [latex]d = 2,[/latex] find the constant [latex]k[/latex], then use [latex]k[/latex] to find [latex]y[/latex] when [latex]m=-3[/latex], [latex]n = 18[/latex], and [latex]d = 3[/latex].

[latex]y=\dfrac{kmn}{d^2}[/latex]

[latex]\begin{array}{ll} \begin{array}{rrl} \\ \\ \\ && \textbf{1st Data} \\ y&=&12 \\ m&=&3 \\ n&=&8 \\ d&=&2 \\ k&=&\text{find 1st} \\ \\ &&\text{Find }k\text{:} \\ y&=&\dfrac{kmn}{d^2} \\ \\ 12&=&\dfrac{k(3)(8)}{(2)^2} \\ \\ k&=&\dfrac{12(2)^2}{(3)(8)} \\ \\ k&=& 2 \end{array} & \hspace{0.5in} \begin{array}{rrl} &&\textbf{2nd Data} \\ y&=&\text{find 2nd} \\ m&=&-3 \\ n&=&18 \\ d&=&3 \\ k&=&2 \\ \\ &&\text{Find }y\text{:} \\ y&=&\dfrac{kmn}{d^2} \\ \\ y&=&\dfrac{(2)(-3)(18)}{(3)^2} \\ \\ y&=&12 \end{array} \end{array}[/latex]

For questions 1 to 12, write the formula defining the variation, including the constant of variation [latex](k).[/latex]

• [latex]x[/latex] is jointly proportional to [latex]y[/latex] and [latex]z[/latex]
• [latex]x[/latex] varies jointly as [latex]z[/latex] and [latex]y[/latex]
• [latex]x[/latex] is jointly proportional with the square of [latex]y[/latex] and the square root of [latex]z[/latex]
• [latex]x[/latex] is inversely proportional to [latex]y[/latex] to the sixth power
• [latex]x[/latex] is jointly proportional with the cube of [latex]y[/latex] and inversely to the square root of [latex]z[/latex]
• [latex]x[/latex] is inversely proportional with the square of [latex]y[/latex] and the square root of [latex]z[/latex]
• [latex]x[/latex] varies jointly as [latex]z[/latex] and [latex]y[/latex] and is inversely proportional to the cube of [latex]p[/latex]
• [latex]x[/latex] is inversely proportional to the cube of [latex]y[/latex] and square of [latex]z[/latex]

For questions 13 to 22, find the formula defining the variation and the constant of variation [latex](k).[/latex]

• If [latex]A[/latex] varies directly as [latex]B,[/latex] find [latex]k[/latex] when [latex]A=15[/latex] and [latex]B=5.[/latex]
• If [latex]P[/latex] is jointly proportional to [latex]Q[/latex] and [latex]R,[/latex] find [latex]k[/latex] when [latex]P=12, Q=8[/latex] and [latex]R=3.[/latex]
• If [latex]A[/latex] varies inversely as [latex]B,[/latex] find [latex]k[/latex] when [latex]A=7[/latex] and [latex]B=4.[/latex]
• If [latex]A[/latex] varies directly as the square of [latex]B,[/latex] find [latex]k[/latex] when [latex]A=6[/latex] and [latex]B=3.[/latex]
• If [latex]C[/latex] varies jointly as [latex]A[/latex] and [latex]B,[/latex] find [latex]k[/latex] when [latex]C=24, A=3,[/latex] and [latex]B=2.[/latex]
• If [latex]Y[/latex] is inversely proportional to the cube of [latex]X,[/latex] find [latex]k[/latex] when [latex]Y=54[/latex] and [latex]X=3.[/latex]
• If [latex]X[/latex] is directly proportional to [latex]Y,[/latex] find [latex]k[/latex] when [latex]X=12[/latex] and [latex]Y=8.[/latex]
• If [latex]A[/latex] is jointly proportional with the square of [latex]B[/latex] and the square root of [latex]C,[/latex] find [latex]k[/latex] when [latex]A=25, B=5[/latex] and [latex]C=9.[/latex]
• If [latex]y[/latex] varies jointly with [latex]m[/latex] and the square of [latex]n[/latex] and inversely with [latex]d,[/latex] find [latex]k[/latex] when [latex]y=10, m=4, n=5,[/latex] and [latex]d=6.[/latex]
• If [latex]P[/latex] varies directly as [latex]T[/latex] and inversely as [latex]V,[/latex] find [latex]k[/latex] when [latex]P=10, T=250,[/latex] and [latex]V=400.[/latex]

For questions 23 to 37, solve each variation word problem.

• The electrical current [latex]I[/latex] (in amperes, A) varies directly as the voltage [latex](V)[/latex] in a simple circuit. If the current is 5 A when the source voltage is 15 V, what is the current when the source voltage is 25 V?
• The current [latex]I[/latex] in an electrical conductor varies inversely as the resistance [latex]R[/latex] (in ohms, Ω) of the conductor. If the current is 12 A when the resistance is 240 Ω, what is the current when the resistance is 540 Ω?
• Hooke’s law states that the distance [latex](d_s)[/latex] that a spring is stretched supporting a suspended object varies directly as the mass of the object [latex](m).[/latex] If the distance stretched is 18 cm when the suspended mass is 3 kg, what is the distance when the suspended mass is 5 kg?
• The volume [latex](V)[/latex] of an ideal gas at a constant temperature varies inversely as the pressure [latex](P)[/latex] exerted on it. If the volume of a gas is 200 cm 3 under a pressure of 32 kg/cm 2 , what will be its volume under a pressure of 40 kg/cm 2 ?
• The number of aluminum cans [latex](c)[/latex] used each year varies directly as the number of people [latex](p)[/latex] using the cans. If 250 people use 60,000 cans in one year, how many cans are used each year in a city that has a population of 1,000,000?
• The time [latex](t)[/latex] required to do a masonry job varies inversely as the number of bricklayers [latex](b).[/latex] If it takes 5 hours for 7 bricklayers to build a park wall, how much time should it take 10 bricklayers to complete the same job?
• The wavelength of a radio signal (λ) varies inversely as its frequency [latex](f).[/latex] A wave with a frequency of 1200 kilohertz has a length of 250 metres. What is the wavelength of a radio signal having a frequency of 60 kilohertz?
• The number of kilograms of water [latex](w)[/latex] in a human body is proportional to the mass of the body [latex](m).[/latex] If a 96 kg person contains 64 kg of water, how many kilograms of water are in a 60 kg person?
• The time [latex](t)[/latex] required to drive a fixed distance [latex](d)[/latex] varies inversely as the speed [latex](v).[/latex] If it takes 5 hours at a speed of 80 km/h to drive a fixed distance, what speed is required to do the same trip in 4.2 hours?
• The volume [latex](V)[/latex] of a cone varies jointly as its height [latex](h)[/latex] and the square of its radius [latex](r).[/latex] If a cone with a height of 8 centimetres and a radius of 2 centimetres has a volume of 33.5 cm 3 , what is the volume of a cone with a height of 6 centimetres and a radius of 4 centimetres?
• The centripetal force [latex](F_{\text{c}})[/latex] acting on an object varies as the square of the speed [latex](v)[/latex] and inversely to the radius [latex](r)[/latex] of its path. If the centripetal force is 100 N when the object is travelling at 10 m/s in a path or radius of 0.5 m, what is the centripetal force when the object’s speed increases to 25 m/s and the path is now 1.0 m?
• The maximum load [latex](L_{\text{max}})[/latex] that a cylindrical column with a circular cross section can hold varies directly as the fourth power of the diameter [latex](d)[/latex] and inversely as the square of the height [latex](h).[/latex] If an 8.0 m column that is 2.0 m in diameter will support 64 tonnes, how many tonnes can be supported by a column 12.0 m high and 3.0 m in diameter?
• The volume [latex](V)[/latex] of gas varies directly as the temperature [latex](T)[/latex] and inversely as the pressure [latex](P).[/latex] If the volume is 225 cc when the temperature is 300 K and the pressure is 100 N/cm 2 , what is the volume when the temperature drops to 270 K and the pressure is 150 N/cm 2 ?
• The electrical resistance [latex](R)[/latex] of a wire varies directly as its length [latex](l)[/latex] and inversely as the square of its diameter [latex](d).[/latex] A wire with a length of 5.0 m and a diameter of 0.25 cm has a resistance of 20 Ω. Find the electrical resistance in a 10.0 m long wire having twice the diameter.
• The volume of wood in a tree [latex](V)[/latex] varies directly as the height [latex](h)[/latex] and the diameter [latex](d).[/latex] If the volume of a tree is 377 m 3 when the height is 30 m and the diameter is 2.0 m, what is the height of a tree having a volume of 225 m 3 and a diameter of 1.75 m?

Answer Key 2.7

Intermediate Algebra Copyright © 2020 by Terrance Berg is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License , except where otherwise noted.

Share This Book

Become a math whiz with AI Tutoring, Practice Questions & more.

Word Problems: Inverse Variation

While direct variation describes a linear relationship between two variables, inverse variation describes another kind of relationship. For two quantities with inverse variation, as one quantity increases, the other quantity decreases.

For example, when you travel to a particular location, as your speed increases, the time it takes to arrive at that location decreases. When you decrease your speed, the time it takes to arrive at that location increases. So, the quantities are inversely proportional.

An inverse variation can be expressed by the equation x y = k or y = k x .

That is, y varies inversely as x if there is some nonzero constant k such that, x y = k or y = k x where x ≠ 0 and y ≠ 0 .

Some word problems require the use of inverse variation. Here are the ways to solve inverse variation word problems.

• Understand the problem.
• Write the formula.
• Identify the known values and substitute in the formula.
• Solve for the unknown.

The volume V of a gas varies inversely as the pressure P on it. If the volume is 240     cm 3 under pressure of 30     kg / cm 2 , what pressure has to be applied to have a volume of 160     cm 3 ?

The volume V varies inversely as the pressure P means when the volume increases, the pressure decreases and when the volume decreases, the pressure increases.

Now write the formula for inverse variation.

Substitute 240 for V 30 for P in the formula and find the constant

( 240 ) ( 30 ) = k

Now write an equation and solve for the unknown.

We have to find the pressure when the volume is 160     cm 3 .

( 160 ) ( P ) = 7200 .

Solve for P .

P = 7200 160           = 45

Therefore, pressure 45     kg / cm 2 be applied to have a volume of 160     cm 3 .

The length of a violin string varies inversely as the frequency of its vibrations. A violin string 14 inches long vibrates at a frequency of 450 cycles per second. Find the frequency of a 12 -inch violin string.

The length( l ) varies inversely as the frequency( f ), when the length increases, the frequency decreases and when the length decreases, the frequency increases.

Substitute 450 for f 14 for l in the formula and find the constant.

( 450 ) ( 14 ) = k

We have to find the frequency of 12 -inch violin string.

( 12 ) ( f ) = 6300 .

Solve for f .

f = 6300 12             = 525

Therefore, 12 -inch violin string vibrates at a frequency of 525 cycles per second.

• Certified Ethical Hacker Test Prep
• Mandarin Chinese Courses & Classes
• AFSP - Annual Filing Season Program Courses & Classes
• CLEP Introduction to Educational Psychology Tutors
• CFA Test Prep
• PE Exam - Professional Licensed Engineer Principles and Practice of Engineering Exam Courses & Classes
• USMLE Test Prep
• SAT Reading Courses & Classes
• Honors Physics Tutors
• NNAT Test Prep
• ACT Test Prep
• Series 7 Test Prep
• MOS - Microsoft Office Specialist Test Prep
• CCENT - Cisco Certified Entry Networking Technician Courses & Classes
• Macedonian Tutors
• California Bar Exam Test Prep
• Honors Biology Tutors
• Series 99 Courses & Classes
• Energy Management Tutors
• New Hampshire Bar Exam Courses & Classes
• Omaha Tutoring
• Columbus Tutoring
• Orlando Tutoring
• Charlotte Tutoring
• Richmond Tutoring
• Portland Tutoring
• Virginia Beach Tutoring
• Boulder Tutoring
• Raleigh-Durham Tutoring
• Pittsburgh Tutoring
• SSAT Tutors in San Francisco-Bay Area
• Math Tutors in Chicago
• GRE Tutors in New York City
• French Tutors in Seattle
• Physics Tutors in Atlanta
• French Tutors in Denver
• SSAT Tutors in Miami
• Spanish Tutors in Phoenix
• SSAT Tutors in Dallas Fort Worth
• English Tutors in Chicago

• HW Guidelines
• Study Skills Quiz
• Find Local Tutors
• Demo MathHelp.com
• Join MathHelp.com

Select a Course Below

• ACCUPLACER Math
• Math Placement Test
• PRAXIS Math
• + more tests
• 5th Grade Math
• 6th Grade Math
• Pre-Algebra
• College Pre-Algebra
• Introductory Algebra
• Intermediate Algebra
• College Algebra

Variation Word Problems

Equations Word Problems More Prob's

It's one thing to be able to take the words for a variation equation (such as " y varies directly as the square of x and inversely as the cube root of z ") and turn this into an equation that you can solve or use. It's another thing to extract the words from a word problem. But, because the lingo for variation equations is so specific, it's not really that hard. Just look for the keywords, and you're nearly home and dry.

The only other keywords (or "key-phrases", really) you might need to know are "is proportional to" which, in the strictly-mathematical sense, means "varies directly as"; and "is inversely proportional to" which means "varies inversely with".

Content Continues Below

MathHelp.com

Suppose that y is inversely proportional to x , and that y  = 0.4 when x  = 2.5 . Find y when x  = 4 .

Translating the above from the English into algebra, I see the key-phrase "inversely proportional to", which means "varies indirectly as". In practical terms, it means that the variable part that does the varying is going to be in the denominator. So I get the formula:

Plugging in the data point they gave me, I can solve for the value of k :

0.4 = k /(2.5)

(0.4)(2.5) = k = 1

Now that I have found the value of the variation constant, I can plug in the x -value they gave me, and find the value of y when x  = 4 :

Then my answer is:

Most word problems, of course, are not nearly as simple as the above example (or the ones on the previous page). Instead, you have to figure out which values go where, what the equation is, and how to interpret it. Fortunately, the keywords and key-phrases should generally be fairly clear, telling you exactly what format to use.

According to Hooke's Law, the force needed to stretch a spring is proportional to the amount the spring is stretched. If fifty pounds of force stretches a spring five inches, how much will the spring be stretched by a force of 120 pounds?

"Is proportional to" means "varies directly with", so the formula for Hooke's Law is:

...where " F " is the force and " d " is the distance that the spring is stretched.

Note: In physics, "weight" is a force. These Hooke's Law word problems, among other types, are often stated in terms of weight, and the weight they list is the force they mean.

First I have to solve for the value of k . They've given me the data point ( d , F) = (5, 50) , so I'll plug this in to the formula:

Now I know that the formula for this particular spring is:

(Hooke's Law doesn't change, but each spring is different, so each spring will have its own " k ".)

Once I know the formula, I can answer their question: "How much will the spring be stretched by a force of 120 pounds?" I'll plug the value they've given me for the force into the equation I've found:

Note that they did not ask "What is the value of ' d '?". They asked me for a distance. I need to be sure to answer the question that they actually asked. That final answer is the distance that the spring is stretched, including the units (which are "inches", in this case):

Note: If you give the above answer as being only " 12 ", the grader will be perfectly correct to count your answer as being at least partly wrong. The answer is not a number, but is a number of units.

Kepler's third law of planetary motion states that the square of the time required for a planet to make one revolution about the sun varies directly as the cube of the average distance of the planet from the sun. If you assume that Mars is 1.5 times as far from the sun as is the earth, find the approximate length of a Martian year.

This one is a bit different from the previous exercise. Normally, I've given given a relation in terms of variation with a plain old variable, like y . In this case, though, the variation relationship is between the square of the time and the cube of the distance. This means that the left-hand side of my equation will have a squared variable!

Advertisement

My variation formula is:

t 2 = k d 3

If I take " d  = 1 " to mean "the distance is one AU", an AU being an "astronomical unit" (the distance of earth from the sun), then the distance for Mars is 1.5 AU. Also, I will take " t  = 1 " to stand for "one earth year". Then, in terms of the planet Earth, I get:

(1) 2 = k  (1) 3

Then the formula, in terms of Earth, is:

Now I'll plug in the information for Mars (in comparison to earth):

t 2 = (1.5) 3

This is one of those times when a calculator's decimal approximation is probably going to be a little more useful in answering the question. I'll show the exact answer in my working, but I'll use a sensible approximation in my final answer. The decimal expansion starts as:

In other words, the Martian year is approximately the length of:

1.837 earth years

By the way, you can make the above answer more intuitive by finding the number of (Earth) days, approximately, represented by that " 0.837 " part of the answer above. Since the average Earth year, technically, has about 365.25 days, then the 0.837 of an Earth year is:

0.837 × 365.25 = 305.71425

Letting the "average" month have 365.25 ÷ 12 = 30.4375 days, then the above number of (Earth) days is:

305.71425 ÷ 30.4375 = 10.044

In other words, the Martian year is almost exactly one Earth year and ten Earth months long.

If you were writing for an audience (like a fellow student, as you'll be required to do in some class projects or essay questions), this "one year and ten months" form would probably be the best way to go.

The weight of a body varies inversely as the square of its distance from the center of the earth. If the radius of the earth is 4000 miles, how much would a 200 -pound man weigh 1000 miles above the surface of the earth?

Remembering that "weight" is a force, I'll let the weight be designated by " F ". The distance of a body from the center of the earth is " d   ". Then my variation formula is the following:

(200)(16,000,000) = k

3,200,000,000 = k

(Hey; there's nothing that says that the value of the variation constant k has to be small!)

The distance is always measured from the center of the earth. If the guy is in orbit a thousand miles up (from the surface of the planet), then his distance (from the center of the planet) is the 4000 miles from the center to the surface plus the 1000 miles from the surface to his ship. That is, d = 5000 . I'll plug this in to my equation, and solve for the value of the force (which is here called "weight") F :

Remembering my units, my answer is that, up in his spacecraft, the guy weighs:

URL: https://www.purplemath.com/modules/variatn2.htm

Page 1 Page 2 Page 3

Standardized Test Prep

College math, homeschool math, share this page.

• Terms of Use
• About Purplemath
• About the Author
• Tutoring from PM
• Advertising
• Linking to PM
• Site licencing

Visit Our Profiles

• Math Formulas

Inverse Variation Formula

Inverse variation formula refers to the relationship of two variables in which a variable increases in its value, the other variable decreases and vice-versa. In other words, the inverse variation is the mathematical expression of the relationship between two variables whose product is a constant.

Formula for Inverse Variable

The Inverse Variation Formula is,

Here, K is the constant of proportionality.

Solved Example Question

Question 1: If y varies inversely with x and when y = 100, x = 30. What is the value of y when x = 10?

Given, y = 100 x = 30

The inverse variation formula is,

y = (k ⁄ x)

100 = (k ⁄ 30)

k = 100 × 30

Now, x = 10 k = 3000

y = (3000 ⁄ 10)

Question 2: Suppose that y varies inversely as x when x = 10 and y = 12/5. Find the value of x when y = 8. Solution: Given, x = 10, y = 12/5 The inverse variation formula is: y = k/x xy = k Therefore, k = (10) × (12/5) = 24 Now, substitute the values of y and k in the equation xy = k, Thus, x(8) = 24 x = 24/8 = 3 Hence, the value of x = 3.

Question 3: In a manufacturing company, 20 men can do the job in 15 days. How many days will it take if 45 men do the same job? Solution: Here, when the manpower increases, they will need less than 15 days to complete the same job. So, this is an inverse variation. Let x be the number of men workers and let y be the number of days to complete the work. So, x 1 = 20,  x 2 = 45 and y 1 = 15 . By the product rule of inverse variation, (20)(15) = (45)(y 2 ) 300 = 45y 2 y 2 = 300/45 = 20/3 Therefore, 45 men can do the same job in 20/3 days.

Leave a Comment Cancel reply

Your Mobile number and Email id will not be published. Required fields are marked *

Request OTP on Voice Call

Post My Comment

• Share Share

Solver Title

Generating PDF...

• Pre Algebra Order of Operations Factors & Primes Fractions Long Arithmetic Decimals Exponents & Radicals Ratios & Proportions Percent Modulo Number Line Expanded Form Mean, Median & Mode
• Algebra Equations Inequalities System of Equations System of Inequalities Basic Operations Algebraic Properties Partial Fractions Polynomials Rational Expressions Sequences Power Sums Interval Notation Pi (Product) Notation Induction Logical Sets Word Problems
• Pre Calculus Equations Inequalities Scientific Calculator Scientific Notation Arithmetics Complex Numbers Polar/Cartesian Simultaneous Equations System of Inequalities Polynomials Rationales Functions Arithmetic & Comp. Coordinate Geometry Plane Geometry Solid Geometry Conic Sections Trigonometry
• Calculus Derivatives Derivative Applications Limits Integrals Integral Applications Integral Approximation Series ODE Multivariable Calculus Laplace Transform Taylor/Maclaurin Series Fourier Series Fourier Transform
• Functions Line Equations Functions Arithmetic & Comp. Conic Sections Transformation
• Linear Algebra Matrices Vectors
• Trigonometry Identities Proving Identities Trig Equations Trig Inequalities Evaluate Functions Simplify
• Statistics Mean Geometric Mean Quadratic Mean Average Median Mode Order Minimum Maximum Probability Mid-Range Range Standard Deviation Variance Lower Quartile Upper Quartile Interquartile Range Midhinge Standard Normal Distribution
• Physics Mechanics
• Chemistry Chemical Reactions Chemical Properties
• Finance Simple Interest Compound Interest Present Value Future Value
• Economics Point of Diminishing Return
• Conversions Roman Numerals Radical to Exponent Exponent to Radical To Fraction To Decimal To Mixed Number To Improper Fraction Radians to Degrees Degrees to Radians Hexadecimal Scientific Notation Distance Weight Time Volume
• Pre Algebra
• Pre Calculus
• Linear Algebra
• Trigonometry
• Conversions

Most Used Actions

Number line.

• x^{2}-x-6=0
• -x+3\gt 2x+1
• line\:(1,\:2),\:(3,\:1)
• prove\:\tan^2(x)-\sin^2(x)=\tan^2(x)\sin^2(x)
• \frac{d}{dx}(\frac{3x+9}{2-x})
• (\sin^2(\theta))'
• \lim _{x\to 0}(x\ln (x))
• \int e^x\cos (x)dx
• \int_{0}^{\pi}\sin(x)dx
• \sum_{n=0}^{\infty}\frac{3}{2^n}

step-by-step

inverse variation

• Practice, practice, practice Math can be an intimidating subject. Each new topic we learn has symbols and problems we have never seen. The unknowing...

Please add a message.

Message received. Thanks for the feedback.

Module 10: Rational and Radical Functions

Inverse and joint variation, learning outcomes.

• Solve an Inverse variation problem.
• Write a formula for an inversely proportional relationship.

Water temperature in an ocean varies inversely to the water’s depth. Between the depths of 250 feet and 500 feet, the formula [latex]T=\frac{14,000}{d}[/latex] gives us the temperature in degrees Fahrenheit at a depth in feet below Earth’s surface. Consider the Atlantic Ocean, which covers 22% of Earth’s surface. At a certain location, at the depth of 500 feet, the temperature may be 28°F.

If we create a table we observe that, as the depth increases, the water temperature decreases.

We notice in the relationship between these variables that, as one quantity increases, the other decreases. The two quantities are said to be inversely proportional and each term varies inversely with the other. Inversely proportional relationships are also called inverse variations .

For our example, the graph depicts the inverse variation . We say the water temperature varies inversely with the depth of the water because, as the depth increases, the temperature decreases. The formula [latex]y=\dfrac{k}{x}[/latex] for inverse variation in this case uses [latex]k=14,000[/latex].

A General Note: Inverse Variation

If [latex]x[/latex] and [latex]y[/latex] are related by an equation of the form

[latex]y=\dfrac{k}{{x}^{n}}[/latex]

where [latex]k[/latex] is a nonzero constant, then we say that [latex]y[/latex]  varies inversely with the [latex]n[/latex]th power of [latex]x[/latex]. In inversely proportional relationships, or inverse variations , there is a constant multiple [latex]k={x}^{n}y[/latex].

Example: Writing a Formula for an Inversely Proportional Relationship

A tourist plans to drive 100 miles. Find a formula for the time the trip will take as a function of the speed the tourist drives.

Recall that multiplying speed by time gives distance. If we let [latex]t[/latex] represent the drive time in hours, and [latex]v[/latex] represent the velocity (speed or rate) at which the tourist drives, then [latex]vt=[/latex] distance. Because the distance is fixed at 100 miles, [latex]vt=100[/latex]. Solving this relationship for the time gives us our function.

[latex]\begin{align}t\left(v\right)&=\dfrac{100}{v} \\[1mm] &=100{v}^{-1} \end{align}[/latex]

We can see that the constant of variation is 100 and, although we can write the relationship using the negative exponent, it is more common to see it written as a fraction.

How To: Given a description of an indirect variation problem, solve for an unknown.

• Identify the input, [latex]x[/latex], and the output, [latex]y[/latex].
• Determine the constant of variation. You may need to multiply [latex]y[/latex] by the specified power of [latex]x[/latex] to determine the constant of variation.
• Use the constant of variation to write an equation for the relationship.
• Substitute known values into the equation to find the unknown.

Example: Solving an Inverse Variation Problem

A quantity [latex]y[/latex] varies inversely with the cube of [latex]x[/latex]. If [latex]y=25[/latex] when [latex]x=2[/latex], find [latex]y[/latex] when [latex]x[/latex] is 6.

The general formula for inverse variation with a cube is [latex]y=\dfrac{k}{{x}^{3}}[/latex]. The constant can be found by multiplying [latex]y[/latex] by the cube of [latex]x[/latex].

[latex]\begin{align}k&={x}^{3}y \\[1mm] &={2}^{3}\cdot 25 \\[1mm] &=200 \end{align}[/latex]

Now we use the constant to write an equation that represents this relationship.

[latex]\begin{align}y&=\dfrac{k}{{x}^{3}},\hspace{2mm}k=200 \\[1mm] y&=\dfrac{200}{{x}^{3}} \end{align}[/latex]

Substitute [latex]x=6[/latex] and solve for [latex]y[/latex].

[latex]\begin{align}y&=\dfrac{200}{{6}^{3}} \\[1mm] &=\dfrac{25}{27} \end{align}[/latex]

Analysis of the Solution

The graph of this equation is a rational function.

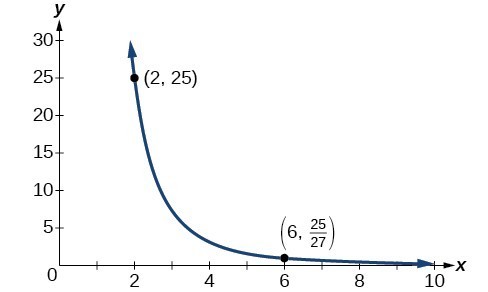
A quantity [latex]y[/latex] varies inversely with the square of [latex]x[/latex]. If [latex]y=8[/latex] when [latex]x=3[/latex], find [latex]y[/latex] when [latex]x[/latex] is 4.

[latex]\dfrac{9}{2}[/latex]

The following video presents a short lesson on inverse variation and includes more worked examples.

Joint Variation

Many situations are more complicated than a basic direct variation or inverse variation model. One variable often depends on multiple other variables. When a variable is dependent on the product or quotient of two or more variables, this is called joint variation . For example, the cost of busing students for each school trip varies with the number of students attending and the distance from the school. The variable [latex]c[/latex], cost, varies jointly with the number of students, [latex]n[/latex], and the distance, [latex]d[/latex].

A General Note: Joint Variation

Joint variation occurs when a variable varies directly or inversely with multiple variables.

For instance, if [latex]x[/latex] varies directly with both [latex]y[/latex] and [latex]z[/latex], we have [latex]x=kyz[/latex]. If [latex]x[/latex] varies directly with [latex]y[/latex] and inversely with [latex]z[/latex], we have [latex]x=\dfrac{ky}{z}[/latex]. Notice that we only use one constant in a joint variation equation.

Example: Solving Problems Involving Joint Variation

A quantity [latex]x[/latex] varies directly with the square of [latex]y[/latex] and inversely with the cube root of [latex]z[/latex]. If [latex]x=6[/latex] when [latex]y=2[/latex] and [latex]z=8[/latex], find [latex]x[/latex] when [latex]y=1[/latex] and [latex]z=27[/latex].

Begin by writing an equation to show the relationship between the variables.

[latex]x=\dfrac{k{y}^{2}}{\sqrt[3]{z}}[/latex]

Substitute [latex]x=6[/latex], [latex]y=2[/latex], and [latex]z=8[/latex] to find the value of the constant [latex]k[/latex].

[latex]\begin{align}6&=\dfrac{k{2}^{2}}{\sqrt[3]{8}} \\[1mm] 6&=\dfrac{4k}{2} \\[1mm] 3&=k \end{align}[/latex]

Now we can substitute the value of the constant into the equation for the relationship.

[latex]x=\dfrac{3{y}^{2}}{\sqrt[3]{z}}[/latex]

To find [latex]x[/latex] when [latex]y=1[/latex] and [latex]z=27[/latex], we will substitute values for [latex]y[/latex] and [latex]z[/latex] into our equation.

[latex]\begin{align}x&=\dfrac{3{\left(1\right)}^{2}}{\sqrt[3]{27}} \\[1mm] &=1 \end{align}[/latex]

[latex]x[/latex] varies directly with the square of [latex]y[/latex] and inversely with [latex]z[/latex]. If [latex]x=40[/latex] when [latex]y=4[/latex] and [latex]z=2[/latex], find [latex]x[/latex] when [latex]y=10[/latex] and [latex]z=25[/latex].

[latex]x=20[/latex]

The following video provides another worked example of a joint variation problem.

Contribute!

Improve this page Learn More

• Revision and Adaptation. Provided by : Lumen Learning. License : CC BY: Attribution
• Question ID 91393,91394. Authored by : Jenck,Michael (for Lumen Learning). License : CC BY: Attribution . License Terms : IMathAS Community License CC-BY + GPL
• College Algebra. Authored by : Abramson, Jay et al.. Provided by : OpenStax. Located at : http://cnx.org/contents/[email protected] . License : CC BY: Attribution . License Terms : Download for free at http://cnx.org/contents/[email protected]
• Inverse Variation. Authored by : James Sousa (Mathispower4u.com) for Lumen Learning. Located at : https://youtu.be/awp2vxqd-l4 . License : CC BY: Attribution
• Joint Variation: Determine the Variation Constant (Volume of a Cone). Authored by : James Sousa (Mathispower4u.com) for Lumen Learning. Provided by : Joint Variation: Determine the Variation Constant (Volume of a Cone). Located at : https://youtu.be/JREPATMScbM . License : CC BY: Attribution

Help | Advanced Search

Mathematics > Numerical Analysis

Title: non-intrusive optimal experimental design for large-scale nonlinear bayesian inverse problems using a bayesian approximation error approach.

Abstract: We consider optimal experimental design (OED) for nonlinear inverse problems within the Bayesian framework. Optimizing the data acquisition process for large-scale nonlinear Bayesian inverse problems is a computationally challenging task since the posterior is typically intractable and commonly-encountered optimality criteria depend on the observed data. Since these challenges are not present in OED for linear Bayesian inverse problems, we propose an approach based on first linearizing the associated forward problem and then optimizing the experimental design. Replacing an accurate but costly model with some linear surrogate, while justified for certain problems, can lead to incorrect posteriors and sub-optimal designs if model discrepancy is ignored. To avoid this, we use the Bayesian approximation error (BAE) approach to formulate an A-optimal design objective for sensor selection that is aware of the model error. In line with recent developments, we prove that this uncertainty-aware objective is independent of the exact choice of linearization. This key observation facilitates the formulation of an uncertainty-aware OED objective function using a completely trivial linear map, the zero map, as a surrogate to the forward dynamics. The base methodology is also extended to marginalized OED problems, accommodating uncertainties arising from both linear approximations and unknown auxiliary parameters. Our approach only requires parameter and data sample pairs, hence it is particularly well-suited for black box forward models. We demonstrate the effectiveness of our method for finding optimal designs in an idealized subsurface flow inverse problem and for tsunami detection.

Submission history

Access paper:.

• HTML (experimental)
• Other Formats

References & Citations

• Google Scholar
• Semantic Scholar

BibTeX formatted citation

Bibliographic and Citation Tools

Code, data and media associated with this article, recommenders and search tools.

• Institution

arXivLabs: experimental projects with community collaborators

arXivLabs is a framework that allows collaborators to develop and share new arXiv features directly on our website.

Both individuals and organizations that work with arXivLabs have embraced and accepted our values of openness, community, excellence, and user data privacy. arXiv is committed to these values and only works with partners that adhere to them.

Have an idea for a project that will add value for arXiv's community? Learn more about arXivLabs .

ChatGPT’s Next Magic Trick Is Singing and Solving Math Problems With Your Phone Camera

GPT-4o responds as fast as humans.

ChatGPT 4 may still be relatively new, but OpenAI is already iterating with an upgrade that can respond as quickly as humans do in normal conversation. The company showed off GPT-4o in a live demo , showing off its ability to use your phone’s camera to solve math equations and deliver a much more conversational voice assistant experience.

While we only have the event demo to go off of, GPT-4o looks impressive. It doesn’t even have to wait for you to finish your request and can roll with interruptions mid-prompt, bringing one step closer to living out Her in real life.

Even Faster Response Times

According to OpenAI, the GPT-4o model can respond as fast as 232 milliseconds to audio inputs. More realistically, it averages around 320 milliseconds to respond, which OpenAI said is similar to how fast humans respond in conversation.

On top of the speed, GPT-4o can handle interruptions and any adjustment requests. As seen in the bedtime story demo, GPT-4o immediately stopped talking when interrupted and quickly handled requests like adding more dramatic inflections, narrating in a robot voice, and even singing the entire prompt out loud. If that demo doesn’t convince you, two GPT-4o models improvising a song together should.

GPT-4o isn’t just more responsive to voice, it can also see better. The new vision features allow it to see through your device’s camera and understand things like handwritten math equations or messages . It’s eerie how genuinely touched GPT-4o sounds when it sees and understands a message that says “I Heart ChatGPT.” Even more impressive, GPT-4o can handle coding tasks and live translations between two people. This should feel way more natural than Google Translate when you’re trying to have a conversation in a foreign country.

Available for Free

OpenAI said the text and image capabilities for GPT-4o roll out today, but the voice feature will be coming to alpha within ChatGPT Plus in the coming weeks. Once it’s fully ready, the upgraded ChatGPT model will be available to all users, subscribers or otherwise. However, if you pay $20 per month for ChatGPT Plus , you’ll get five times the message limits of GPT-4o compared to the free version.

Anytime a large language model gets such an impressive update, we have to consider the potential for misuse . Considering how smoothly the live demo for solving the equation went, it looks like an even better way to help students get out of their math homework. However, OpenAI said that GPT-4o was built with new safety systems to offer guardrails on voice outputs. We’ll have to wait and see if these guardrails are enough.

Solving inverse nodal problem with frozen argument by using second Chebyshev wavelet method

• Published: 17 April 2024
• Volume 69 , pages 339–354, ( 2024 )

Cite this article

• Yu Ping Wang 1 ,
• Shahrbanoo Akbarpoor Kiasary 2 &
• Emrah Yılmaz 3  

We consider the inverse nodal problem for Sturm-Liouville (S-L) equation with frozen argument. Asymptotic behaviours of eigenfunctions, nodal parameters are represented in two cases and numerical algorithms are produced to solve the given problems. Subsequently, solution of inverse nodal problem is calculated by the second Chebyshev wavelet method (SCW), accuracy and effectiveness of the method are shown in some numerical examples.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Price excludes VAT (USA) Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Rent this article via DeepDyve

Institutional subscriptions

S. Akbarpoor, H. Koyunbakan, A. Dabbaghian : Solving inverse nodal problem with spectral parameter in boundary conditions. Inverse Probl. Sci. Eng. 27 (2019), 1790–1801.

Article   MathSciNet   Google Scholar  

S. Albeverio, R. O. Hryniv, L. P. Nizhnik : Inverse spectral problems for non-local Sturm-Liouville operators. Inverse Probl. 23 (2007), 523–535.

N. P. Bondarenko, S. A. Buterin, S. V. Vasiliev : An inverse spectral problem for Sturm-Liouville operators with frozen argument. J. Math. Anal. Appl. 472 (2019), 1028–1041.

N. P. Bondarenko, V. A. Yurko : An inverse problem for Sturm-Liouville differential operators with deviating argument. Appl. Math. Lett. 83 (2018), 140–144.

N. P. Bondarenko, V. A. Yurko : Partial inverse problems for the Sturm-Liouville equation with deviating argument. Math. Methods Appl. Sci. 41 (2018), 8350–8354.

G. Borg : Eine Umkehrung der Sturm-Liouvilleschen Eigenwertaufgabe: Bestimmung der Differentialgleichung durch die Eigenwerte. Acta Math. 78 (1946), 1–96. (In German.)

P. J. Browne, B. D. Sleeman : Inverse nodal problems for Sturm-Liouville equations with eigenparameter dependent boundary conditions. Inverse Probl. 12 (1996), 377–381.

S. A. Buterin, M. Kuznetsova : On the inverse problem for Sturm-Liouville-type operators with frozen argument: Rational case. Comput. Appl. Math. 39 (2020), Article ID 5, 15 pages.

S. A. Buterin, M. Pikula, V. A. Yurko : Sturm-Liouville differential operators with deviating argument. Tamkang J. Math. 48 (2017), 61–71.

MathSciNet   Google Scholar  

S. A. Buterin, C.-T. Shieh : Incomplete inverse spectral and nodal problems for differential pencils. Result. Math. 62 (2012), 167–179.

S. A. Buterin, S. V. Vasiliev : On recovering a Sturm-Liouville-type operator with the frozen argument rationally proportioned to the interval length. J. Inverse Ill-Posed Probl. 27 (2019), 429–438.

S. A. Buterin, V. A. Yurko : An inverse spectral problem for Sturm-Liouville operators with a large constant delay. Anal. Math. Phys. 9 (2019), 17–27.

X. Chen, Y. H. Cheng, C. K. Law : Reconstructing potentials from zeros of one eigenfunction. Trans. Am. Math. Soc. 363 (2011), 4831–4851.

Y.-H. Cheng, C. K. Law, J. Tsay : Remarks on a new inverse nodal problem. J. Math. Anal. Appl. 248 (2000), 145–155.

T. Gulsen, E. Yilmaz, S. Akbarpoor : Numerical investigation of the inverse nodal problem by Chebyshev interpolation method. Thermal Sci. 22 (2018), S123–S136.

Article   Google Scholar  

Y. Guo, G. Wei : Inverse problems: Dense nodal subset on an interior subinterval. J. Differ. Equations 255 (2013), 2002–2017.

O. H. Hald, J. R. McLaughlin : Solutions of inverse nodal problems. Inverse Probl. 5 (1989), 307–347.

Y.-T. Hu, N. P. Bondarenko, C.-F. Yang : Traces and inverse nodal problem for Sturm-Liouville operators with frozen argument. Appl. Math. Lett. 102 (2020), Article ID 106096, 7 pages.

A. M. Krall : The development of general differential and general differential-boundary systems. Rocky Mt. J. Math. 5 (1975), 493–542.

Y. V. Kuryshova : Inverse spectral problem for integro-differential operators. Math. Notes 81 (2007), 767–777.

C. K. Law, C.-L. Shen, C.-F. Yang : The inverse nodal problem on the smoothness of the potential function. Inverse Probl. 15 (1999), 253–263.

C. K. Law, C.-F. Yang : Reconstructing the potential function and its derivatives using nodal data. Inverse Probl. 14 (1998), 299–312.

J. R. McLaughlin : Inverse spectral theory using nodal points as data: A uniqueness result. J. Differ. Equations 73 (1988), 342–362.

A. Neamaty, S. Akbarpoor : Numerical solution of inverse nodal problem with an eigenvalue in the boundary condition. Inverse Probl. Sci. Eng. 25 (2017), 978–994.

L. Nizhnik : Inverse nonlocal Sturm-Liouville problem. Inverse Probl. 26 (2010), Article ID 125006, 9 pages.

M. Pikula : Determination of a differential operator of Sturm-Liouville type with retarded argument by two spectra. Mat. Vesn. 43 (1991), 159–171. (In Russian.)

Google Scholar  

J. Pöschel, E. Trubowitz : Inverse Spectral Theory. Pure and Applied Mathematics 130. Academic Press, Boston, 1987.

W. Rundell, P. E. Sacks : The reconstruction of Sturm-Liouville operators. Inverse Probl. 8 (1992), 457–482.

C.-T. Shieh, V. A. Yurko : Inverse nodal and inverse spectral problems for discontinuous boundary value problems. J. Math. Anal. Appl. 347 (2008), 266–272.

V. Vladičić, M. Pikula : An inverse problem for Sturm-Liouville-type differential equation with a constant delay. Sarajevo J. Math. 12 (2016), 83–88.

Y. P. Wang, K. Y. Lien, C.-T. Shieh : Inverse problems for the boundary value problem with the interior nodal subsets. Appl. Anal. 96 (2017), 1229–1239.

Y. P. Wang, C.-T. Shieh, H. Y. Miao : Reconstruction for Sturm-Liouville equations with a constant delay with twin-dense nodal subsets. Inverse Probl. Sci. Eng. 27 (2019), 608–617.

Y. P. Wang, V. A. Yurko : On the inverse nodal problems for discontinuous Sturm-Liouville operators. J. Differ. Equations 260 (2016), 4086–4109.

Y. P. Wang, M. Zhang, W. Zhao, X. Wei : Reconstruction for Sturm-Liouville operators with frozen argument for irrational cases. Appl. Math. Lett. 111 (2021), Article ID 106590, 6 pages.

Y. Wang, L. Zhu : SCW method for solving the fractional integro-differential equations with a weakly singular kernel. Appl. Math. Comput. 275 (2016), 72–80.

X. Wei, H. Miao, C. Ge, C. Zhao : An inverse problem for Sturm-Liouville operators with nodal data on arbitrarily-half intervals. Inverse Probl. Sci. Eng. 29 (2021), 305–317.

C.-F. Yang, X.-P. Yang : Inverse nodal problems for the Sturm-Liouville equation with polynomially dependent on the eigenparameter. Inverse Probl. Sci. Eng. 19 (2011), 951–961.

X.-F. Yang : A new inverse nodal problem. J. Differ. Equations 169 (2001), 633–653.

E. Yılmaz, H. Koyunbakan : Reconstruction of potential function and its derivatives for Sturm-Liouville problem with eigenvalues in boundary condition. Inverse Probl. Sci. Eng. 18 (2010), 935–944.

V. A. Yurko : An inverse spectral problem for integro-differential operators. Far East J. Math. Sci. (FJMS) 92 (2014), 247–261.

Download references

Author information

Authors and affiliations.

Department of Applied Mathematics, Nanjing Forestry University, No. 159 Longpan Rd., 210037, Nanjing, Jiangsu, P. R. China

Yu Ping Wang

Department of Mathematics, Jouybar Branch, Islamic Azad University, Jouybar, 4776186131, Iran

Shahrbanoo Akbarpoor Kiasary

Department of Mathematics, Firat University, 23119, Elazig, Turkey

Emrah Yılmaz

You can also search for this author in PubMed   Google Scholar

Corresponding author

Correspondence to Emrah Yılmaz .

Additional information

This work was supported by Nanjing Forestry University, Nanjing, People’s Republic of China, Islamic Azad University, Jouybar Branch, Jouybar, Iran and Firat University, Elazig, Türkiye.

Rights and permissions

Reprints and permissions

About this article

Wang, Y.P., Kiasary, S.A. & Yılmaz, E. Solving inverse nodal problem with frozen argument by using second Chebyshev wavelet method. Appl Math 69 , 339–354 (2024). https://doi.org/10.21136/AM.2024.0038-21

Download citation

Received : 18 February 2021

Published : 17 April 2024

Issue Date : June 2024

DOI : https://doi.org/10.21136/AM.2024.0038-21

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Sturm-Liouville equation
• inverse nodal problem
• Frozen argument
• nodal parameters
• Find a journal
• Publish with us
• Track your research