hypothesis space of

• Machine Learning Tutorial
• Data Analysis Tutorial
• Python - Data visualization tutorial
• Machine Learning Projects
• Machine Learning Interview Questions
• Machine Learning Mathematics
• Deep Learning Tutorial
• Deep Learning Project
• Deep Learning Interview Questions
• Computer Vision Tutorial
• Computer Vision Projects
• NLP Project
• NLP Interview Questions
• Statistics with Python
• 100 Days of Machine Learning

Hypothesis in Machine Learning

• Bayes Theorem in Machine learning
• How does Machine Learning Works?
• Understanding Hypothesis Testing
• An introduction to Machine Learning
• Types of Machine Learning
• How Machine Learning Will Change the World?
• Difference Between Machine Learning vs Statistics
• Difference between Statistical Model and Machine Learning
• Difference Between Machine Learning and Artificial Intelligence
• ML | Naive Bayes Scratch Implementation using Python
• Introduction to Machine Learning in R
• Introduction to Machine Learning in Julia
• Design a Learning System in Machine Learning
• Getting started with Machine Learning
• Machine Learning vs Artificial Intelligence
• Hypothesis Testing Formula
• Current Best Hypothesis Search
• What is the Role of Machine Learning in Data Science
• Removing stop words with NLTK in Python
• Decision Tree
• Linear Regression in Machine learning
• Agents in Artificial Intelligence
• Plotting Histogram in Python using Matplotlib
• One Hot Encoding in Machine Learning
• Best Python libraries for Machine Learning
• Introduction to Hill Climbing | Artificial Intelligence
• Clustering in Machine Learning
• Digital Image Processing Basics

The concept of a hypothesis is fundamental in Machine Learning and data science endeavours. In the realm of machine learning, a hypothesis serves as an initial assumption made by data scientists and ML professionals when attempting to address a problem. Machine learning involves conducting experiments based on past experiences, and these hypotheses are crucial in formulating potential solutions.

It’s important to note that in machine learning discussions, the terms “hypothesis” and “model” are sometimes used interchangeably. However, a hypothesis represents an assumption, while a model is a mathematical representation employed to test that hypothesis. This section on “Hypothesis in Machine Learning” explores key aspects related to hypotheses in machine learning and their significance.

Table of Content

How does a Hypothesis work?

Hypothesis space and representation in machine learning, hypothesis in statistics, faqs on hypothesis in machine learning.

A hypothesis in machine learning is the model’s presumption regarding the connection between the input features and the result. It is an illustration of the mapping function that the algorithm is attempting to discover using the training set. To minimize the discrepancy between the expected and actual outputs, the learning process involves modifying the weights that parameterize the hypothesis. The objective is to optimize the model’s parameters to achieve the best predictive performance on new, unseen data, and a cost function is used to assess the hypothesis’ accuracy.

In most supervised machine learning algorithms, our main goal is to find a possible hypothesis from the hypothesis space that could map out the inputs to the proper outputs. The following figure shows the common method to find out the possible hypothesis from the Hypothesis space:

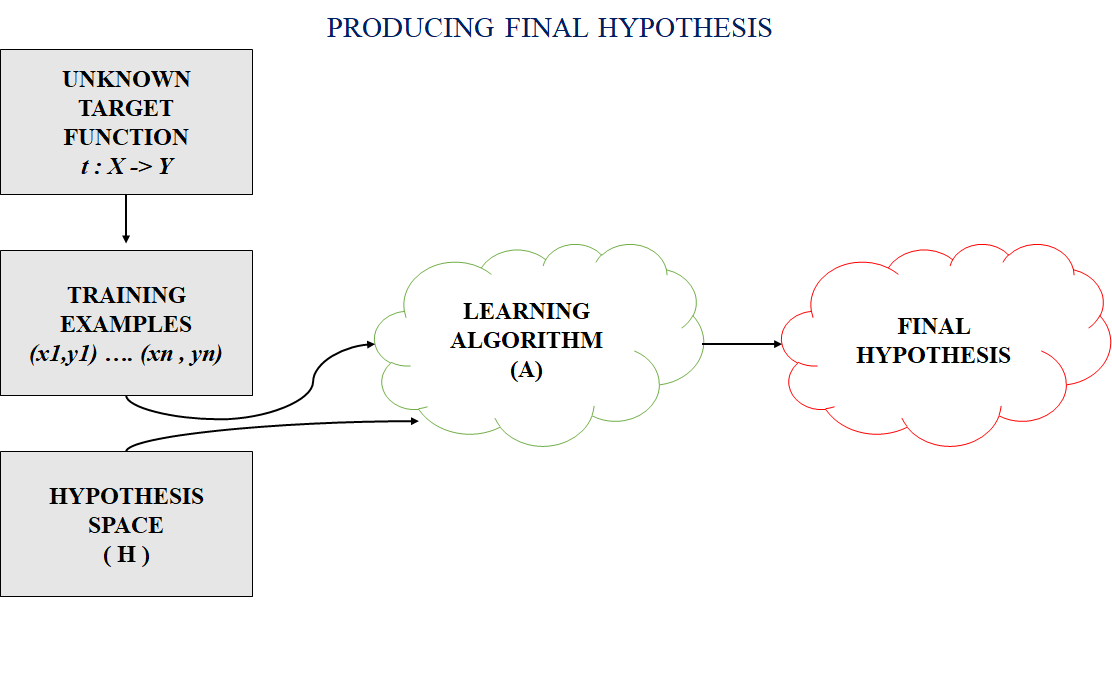
Hypothesis Space (H)

Hypothesis space is the set of all the possible legal hypothesis. This is the set from which the machine learning algorithm would determine the best possible (only one) which would best describe the target function or the outputs.

Hypothesis (h)

A hypothesis is a function that best describes the target in supervised machine learning. The hypothesis that an algorithm would come up depends upon the data and also depends upon the restrictions and bias that we have imposed on the data.

The Hypothesis can be calculated as:

[Tex]y = mx + b [/Tex]

• m = slope of the lines
• b = intercept

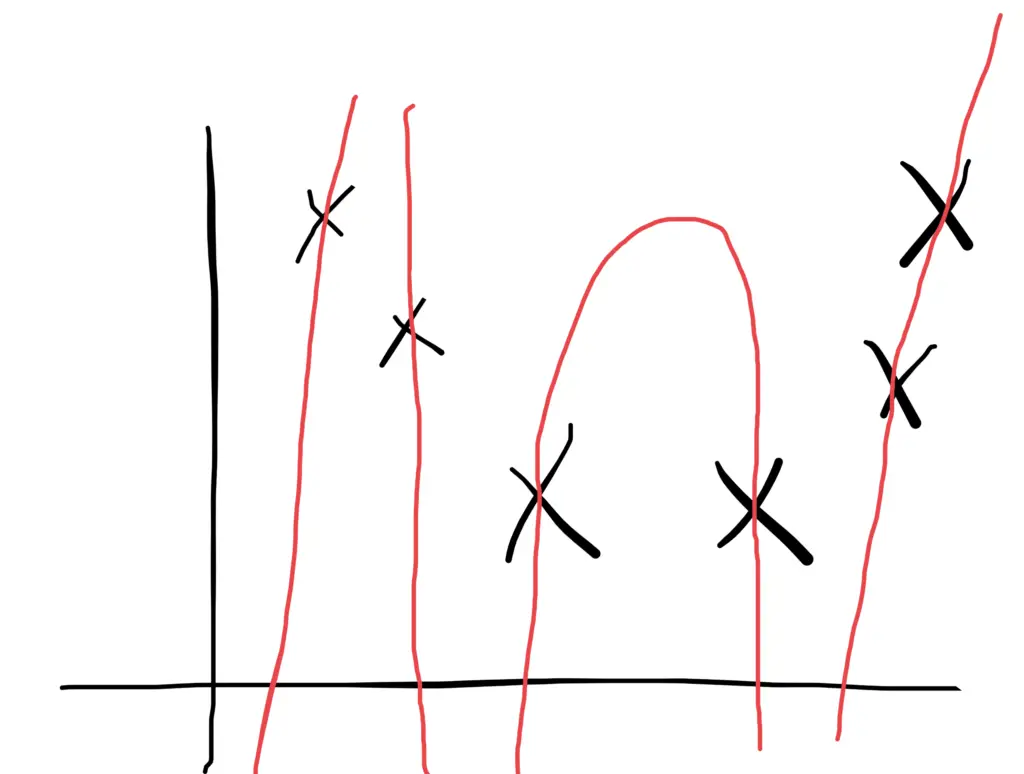
To better understand the Hypothesis Space and Hypothesis consider the following coordinate that shows the distribution of some data:

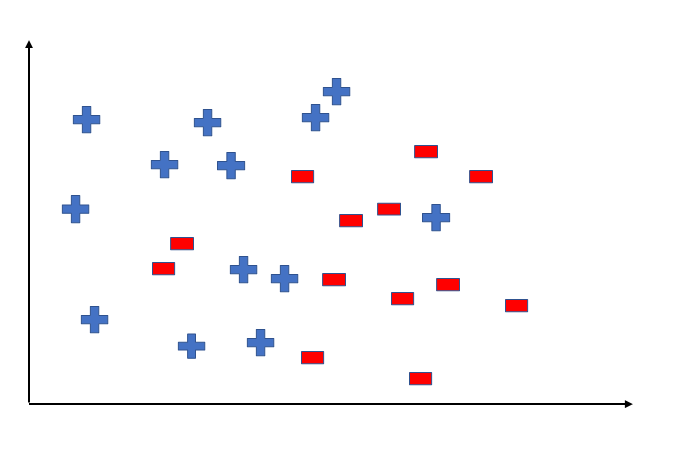
Say suppose we have test data for which we have to determine the outputs or results. The test data is as shown below:

We can predict the outcomes by dividing the coordinate as shown below:

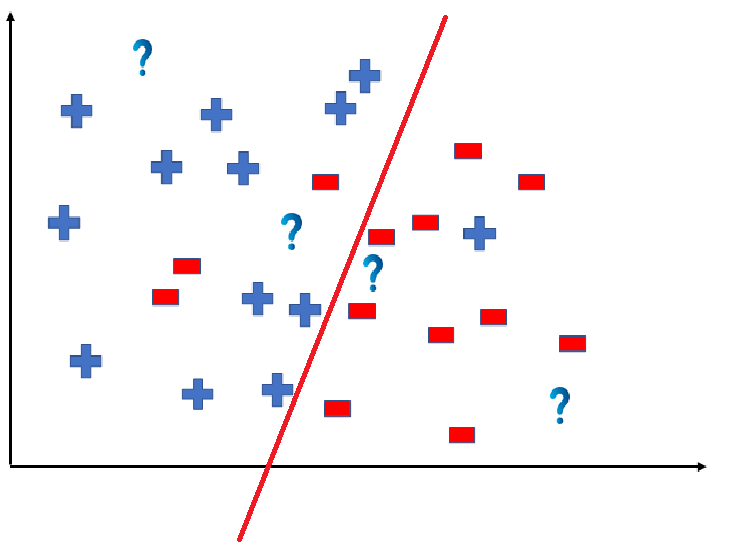
So the test data would yield the following result:

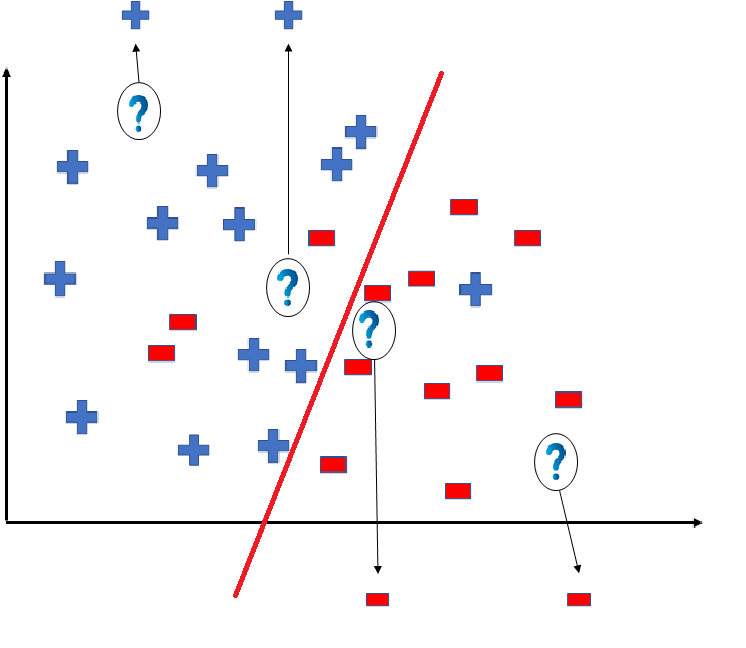
But note here that we could have divided the coordinate plane as:

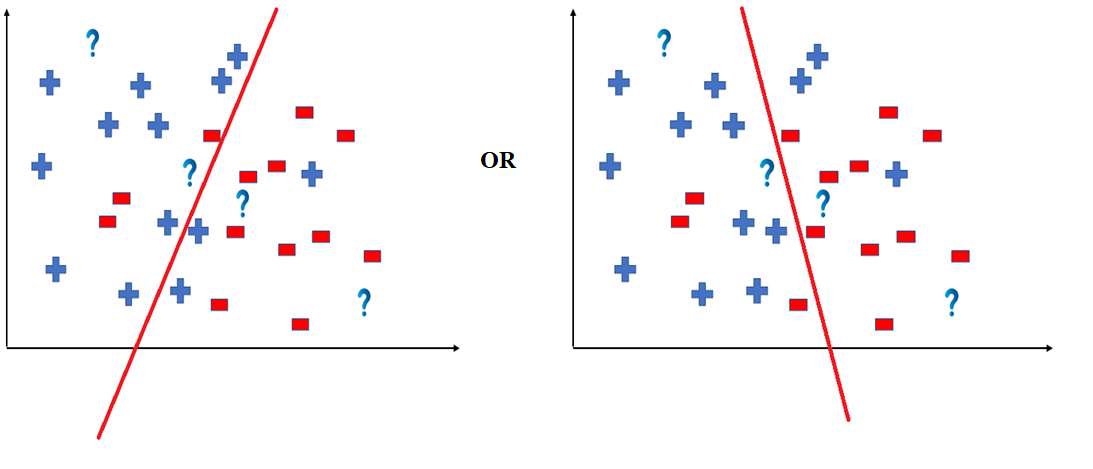
The way in which the coordinate would be divided depends on the data, algorithm and constraints.

• All these legal possible ways in which we can divide the coordinate plane to predict the outcome of the test data composes of the Hypothesis Space.
• Each individual possible way is known as the hypothesis.

Hence, in this example the hypothesis space would be like:

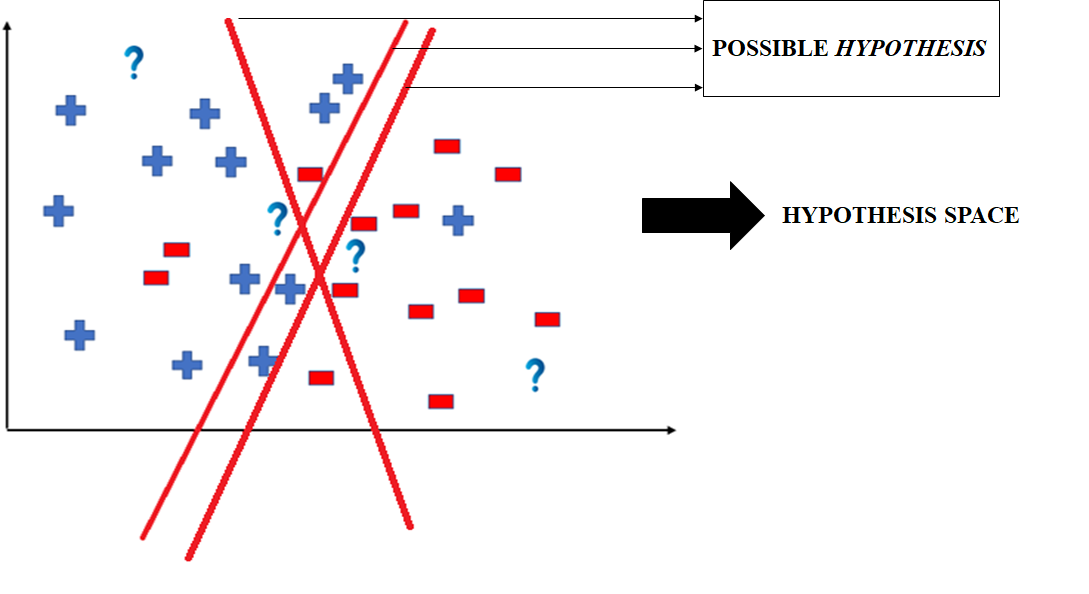
The hypothesis space comprises all possible legal hypotheses that a machine learning algorithm can consider. Hypotheses are formulated based on various algorithms and techniques, including linear regression, decision trees, and neural networks. These hypotheses capture the mapping function transforming input data into predictions.

Hypothesis Formulation and Representation in Machine Learning

Hypotheses in machine learning are formulated based on various algorithms and techniques, each with its representation. For example:

• Linear Regression : [Tex] h(X) = \theta_0 + \theta_1 X_1 + \theta_2 X_2 + … + \theta_n X_n[/Tex]
• Decision Trees : [Tex]h(X) = \text{Tree}(X)[/Tex]
• Neural Networks : [Tex]h(X) = \text{NN}(X)[/Tex]

In the case of complex models like neural networks, the hypothesis may involve multiple layers of interconnected nodes, each performing a specific computation.

Hypothesis Evaluation:

The process of machine learning involves not only formulating hypotheses but also evaluating their performance. This evaluation is typically done using a loss function or an evaluation metric that quantifies the disparity between predicted outputs and ground truth labels. Common evaluation metrics include mean squared error (MSE), accuracy, precision, recall, F1-score, and others. By comparing the predictions of the hypothesis with the actual outcomes on a validation or test dataset, one can assess the effectiveness of the model.

Hypothesis Testing and Generalization:

Once a hypothesis is formulated and evaluated, the next step is to test its generalization capabilities. Generalization refers to the ability of a model to make accurate predictions on unseen data. A hypothesis that performs well on the training dataset but fails to generalize to new instances is said to suffer from overfitting. Conversely, a hypothesis that generalizes well to unseen data is deemed robust and reliable.

The process of hypothesis formulation, evaluation, testing, and generalization is often iterative in nature. It involves refining the hypothesis based on insights gained from model performance, feature importance, and domain knowledge. Techniques such as hyperparameter tuning, feature engineering, and model selection play a crucial role in this iterative refinement process.

In statistics , a hypothesis refers to a statement or assumption about a population parameter. It is a proposition or educated guess that helps guide statistical analyses. There are two types of hypotheses: the null hypothesis (H0) and the alternative hypothesis (H1 or Ha).

• Null Hypothesis(H 0 ): This hypothesis suggests that there is no significant difference or effect, and any observed results are due to chance. It often represents the status quo or a baseline assumption.
• Aternative Hypothesis(H 1 or H a ): This hypothesis contradicts the null hypothesis, proposing that there is a significant difference or effect in the population. It is what researchers aim to support with evidence.

Q. How does the training process use the hypothesis?

The learning algorithm uses the hypothesis as a guide to minimise the discrepancy between expected and actual outputs by adjusting its parameters during training.

Q. How is the hypothesis’s accuracy assessed?

Usually, a cost function that calculates the difference between expected and actual values is used to assess accuracy. Optimising the model to reduce this expense is the aim.

Q. What is Hypothesis testing?

Hypothesis testing is a statistical method for determining whether or not a hypothesis is correct. The hypothesis can be about two variables in a dataset, about an association between two groups, or about a situation.

Q. What distinguishes the null hypothesis from the alternative hypothesis in machine learning experiments?

The null hypothesis (H0) assumes no significant effect, while the alternative hypothesis (H1 or Ha) contradicts H0, suggesting a meaningful impact. Statistical testing is employed to decide between these hypotheses.

Please Login to comment...

Similar reads.

• Machine Learning

Improve your Coding Skills with Practice

What kind of Experience do you want to share?

Programmathically

Introduction to the hypothesis space and the bias-variance tradeoff in machine learning.

In this post, we introduce the hypothesis space and discuss how machine learning models function as hypotheses. Furthermore, we discuss the challenges encountered when choosing an appropriate machine learning hypothesis and building a model, such as overfitting, underfitting, and the bias-variance tradeoff.

The hypothesis space in machine learning is a set of all possible models that can be used to explain a data distribution given the limitations of that space. A linear hypothesis space is limited to the set of all linear models. If the data distribution follows a non-linear distribution, the linear hypothesis space might not contain a model that is appropriate for our needs.

To understand the concept of a hypothesis space, we need to learn to think of machine learning models as hypotheses.

The Machine Learning Model as Hypothesis

Generally speaking, a hypothesis is a potential explanation for an outcome or a phenomenon. In scientific inquiry, we test hypotheses to figure out how well and if at all they explain an outcome. In supervised machine learning, we are concerned with finding a function that maps from inputs to outputs.

But machine learning is inherently probabilistic. It is the art and science of deriving useful hypotheses from limited or incomplete data. Our functions are not axioms that explain the data perfectly, and for most real-life problems, we will never have all the data that exists. Accordingly, we will not find the one true function that perfectly describes the data. Instead, we find a function through training a model to map from known training input to known training output. This way, the model gradually approximates the assumed true function that describes the distribution of the data. So we treat our model as a hypothesis that needs to be tested as to how well it explains the output from a given input. We do this using a test or validation data set.

The Hypothesis Space

During the training process, we select a model from a hypothesis space that is subject to our constraints. For example, a linear hypothesis space only provides linear models. We can approximate data that follows a quadratic distribution using a model from the linear hypothesis space.

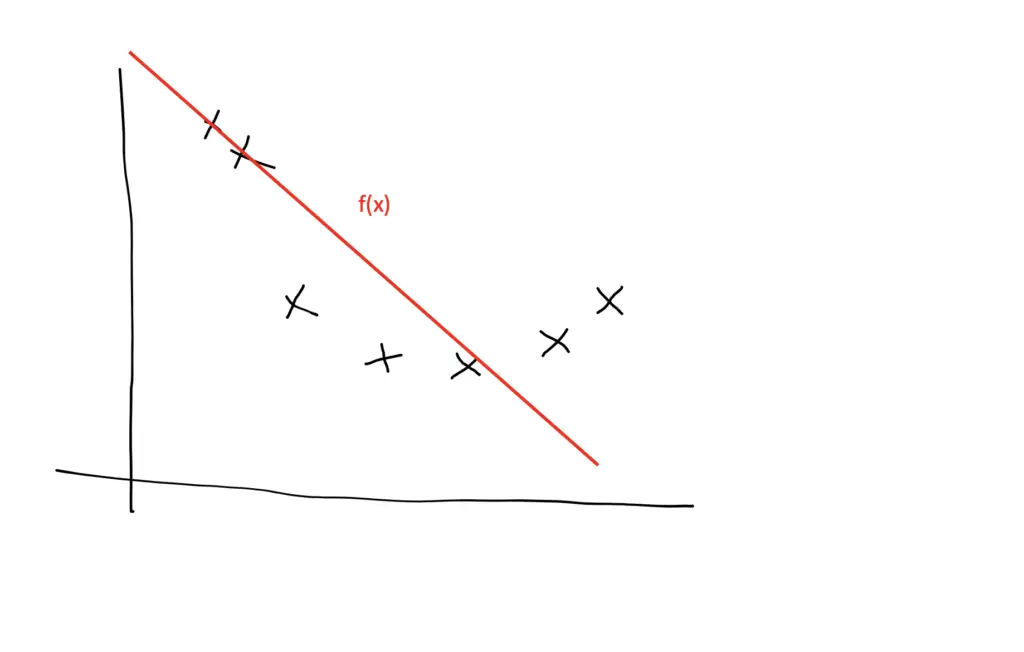
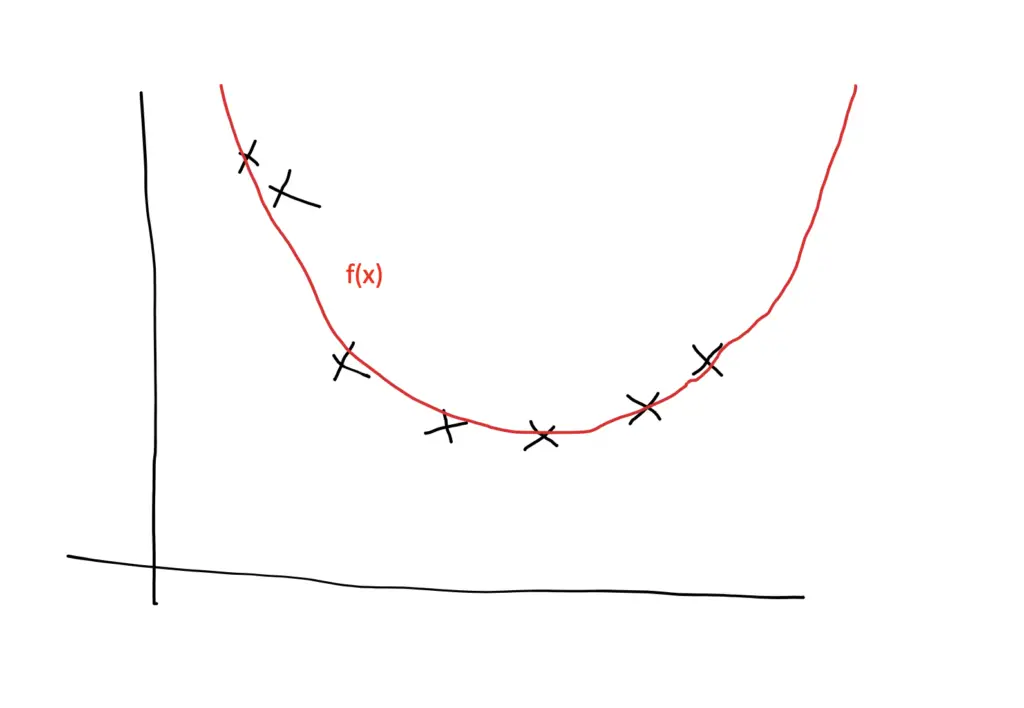
Of course, a linear model will never have the same predictive performance as a quadratic model, so we can adjust our hypothesis space to also include non-linear models or at least quadratic models.

The Data Generating Process

The data generating process describes a hypothetical process subject to some assumptions that make training a machine learning model possible. We need to assume that the data points are from the same distribution but are independent of each other. When these requirements are met, we say that the data is independent and identically distributed (i.i.d.).

Independent and Identically Distributed Data

How can we assume that a model trained on a training set will perform better than random guessing on new and previously unseen data? First of all, the training data needs to come from the same or at least a similar problem domain. If you want your model to predict stock prices, you need to train the model on stock price data or data that is similarly distributed. It wouldn’t make much sense to train it on whether data. Statistically, this means the data is identically distributed . But if data comes from the same problem, training data and test data might not be completely independent. To account for this, we need to make sure that the test data is not in any way influenced by the training data or vice versa. If you use a subset of the training data as your test set, the test data evidently is not independent of the training data. Statistically, we say the data must be independently distributed .

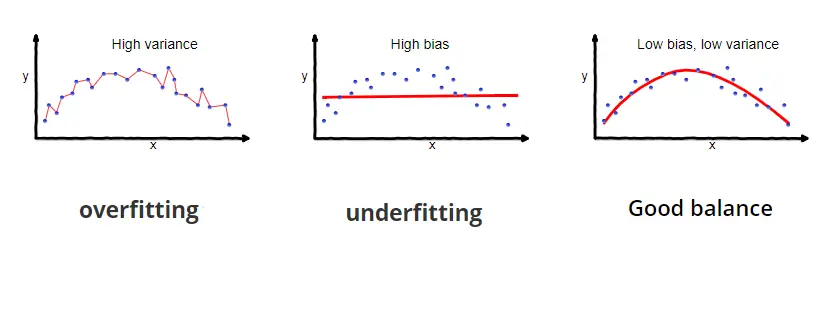
Overfitting and Underfitting

We want to select a model from the hypothesis space that explains the data sufficiently well. During training, we can make a model so complex that it perfectly fits every data point in the training dataset. But ultimately, the model should be able to predict outputs on previously unseen input data. The ability to do well when predicting outputs on previously unseen data is also known as generalization. There is an inherent conflict between those two requirements.

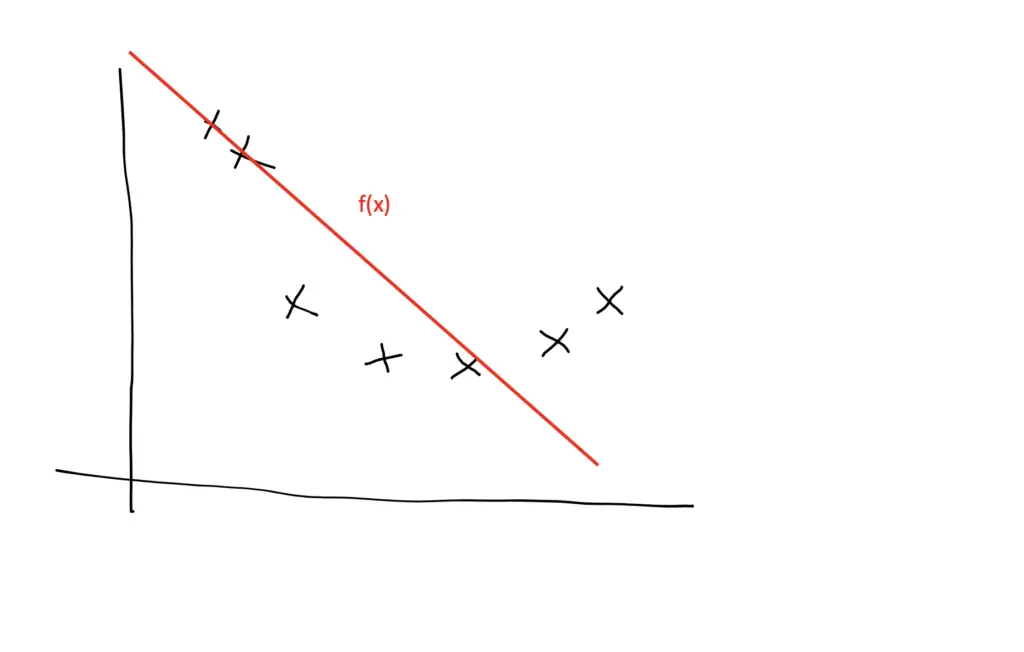
If we make the model so complex that it fits every point in the training data, it will pick up lots of noise and random variation specific to the training set, which might obscure the larger underlying patterns. As a result, it will be more sensitive to random fluctuations in new data and predict values that are far off. A model with this problem is said to overfit the training data and, as a result, to suffer from high variance .

To avoid the problem of overfitting, we can choose a simpler model or use regularization techniques to prevent the model from fitting the training data too closely. The model should then be less influenced by random fluctuations and instead, focus on the larger underlying patterns in the data. The patterns are expected to be found in any dataset that comes from the same distribution. As a consequence, the model should generalize better on previously unseen data.

But if we go too far, the model might become too simple or too constrained by regularization to accurately capture the patterns in the data. Then the model will neither generalize well nor fit the training data well. A model that exhibits this problem is said to underfit the data and to suffer from high bias . If the model is too simple to accurately capture the patterns in the data (for example, when using a linear model to fit non-linear data), its capacity is insufficient for the task at hand.

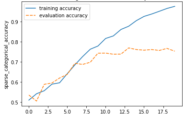
When training neural networks, for example, we go through multiple iterations of training in which the model learns to fit an increasingly complex function to the data. Typically, your training error will decrease during learning the more complex your model becomes and the better it learns to fit the data. In the beginning, the training error decreases rapidly. In later training iterations, it typically flattens out as it approaches the minimum possible error. Your test or generalization error should initially decrease as well, albeit likely at a slower pace than the training error. As long as the generalization error is decreasing, your model is underfitting because it doesn’t live up to its full capacity. After a number of training iterations, the generalization error will likely reach a trough and start to increase again. Once it starts to increase, your model is overfitting, and it is time to stop training.

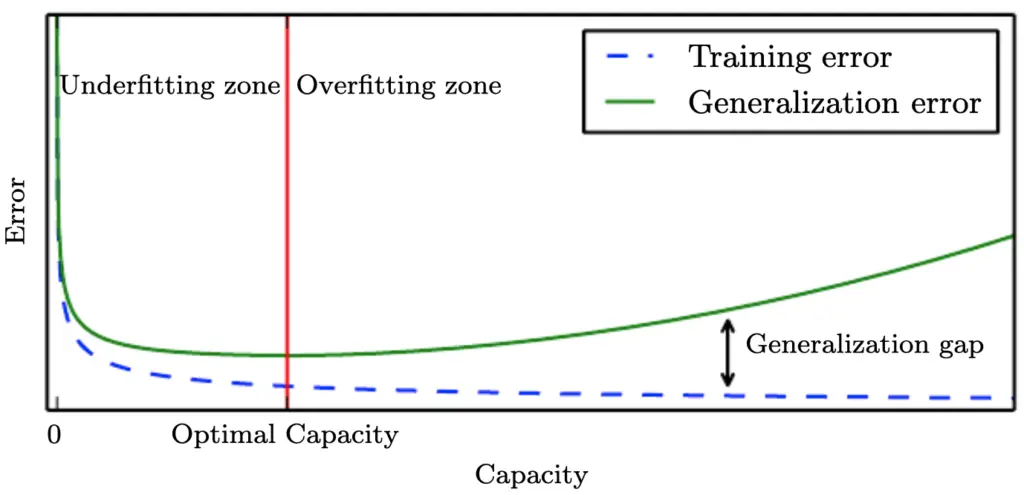
Ideally, you should stop training once your model reaches the lowest point of the generalization error. The gap between the minimum generalization error and no error at all is an irreducible error term known as the Bayes error that we won’t be able to completely get rid of in a probabilistic setting. But if the error term seems too large, you might be able to reduce it further by collecting more data, manipulating your model’s hyperparameters, or altogether picking a different model.

Bias Variance Tradeoff

We’ve talked about bias and variance in the previous section. Now it is time to clarify what we actually mean by these terms.

Understanding Bias and Variance

In a nutshell, bias measures if there is any systematic deviation from the correct value in a specific direction. If we could repeat the same process of constructing a model several times over, and the results predicted by our model always deviate in a certain direction, we would call the result biased.

Variance measures how much the results vary between model predictions. If you repeat the modeling process several times over and the results are scattered all across the board, the model exhibits high variance.

In their book “Noise” Daniel Kahnemann and his co-authors provide an intuitive example that helps understand the concept of bias and variance. Imagine you have four teams at the shooting range.

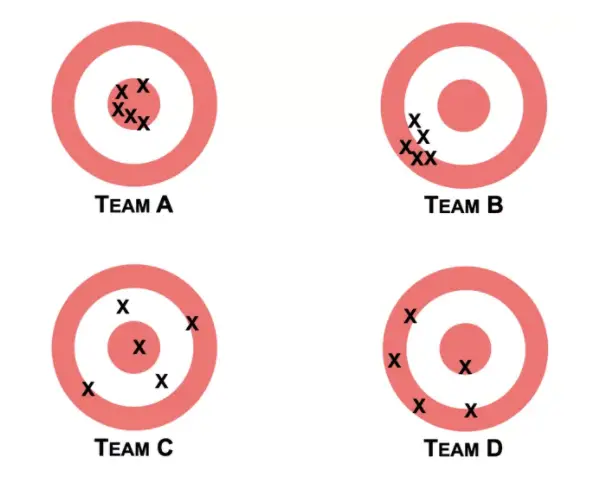
Team B is biased because the shots of its team members all deviate in a certain direction from the center. Team B also exhibits low variance because the shots of all the team members are relatively concentrated in one location. Team C has the opposite problem. The shots are scattered across the target with no discernible bias in a certain direction. Team D is both biased and has high variance. Team A would be the equivalent of a good model. The shots are in the center with little bias in one direction and little variance between the team members.

Generally speaking, linear models such as linear regression exhibit high bias and low variance. Nonlinear algorithms such as decision trees are more prone to overfitting the training data and thus exhibit high variance and low bias.

A linear model used with non-linear data would exhibit a bias to predict data points along a straight line instead of accomodating the curves. But they are not as susceptible to random fluctuations in the data. A nonlinear algorithm that is trained on noisy data with lots of deviations would be more capable of avoiding bias but more prone to incorporate the noise into its predictions. As a result, a small deviation in the test data might lead to very different predictions.

To get our model to learn the patterns in data, we need to reduce the training error while at the same time reducing the gap between the training and the testing error. In other words, we want to reduce both bias and variance. To a certain extent, we can reduce both by picking an appropriate model, collecting enough training data, selecting appropriate training features and hyperparameter values. At some point, we have to trade-off between minimizing bias and minimizing variance. How you balance this trade-off is up to you.

The Bias Variance Decomposition

Mathematically, the total error can be decomposed into the bias and the variance according to the following formula.

Remember that Bayes’ error is an error that cannot be eliminated.

Our machine learning model represents an estimating function \hat f(X) for the true data generating function f(X) where X represents the predictors and y the output values.

Now the mean squared error of our model is the expected value of the squared difference of the output produced by the estimating function \hat f(X) and the true output Y.

The bias is a systematic deviation from the true value. We can measure it as the squared difference between the expected value produced by the estimating function (the model) and the values produced by the true data-generating function.

Of course, we don’t know the true data generating function, but we do know the observed outputs Y, which correspond to the values generated by f(x) plus an error term.

The variance of the model is the squared difference between the expected value and the actual values of the model.

Now that we have the bias and the variance, we can add them up along with the irreducible error to get the total error.

A machine learning model represents an approximation to the hypothesized function that generated the data. The chosen model is a hypothesis since we hypothesize that this model represents the true data generating function.

We choose the hypothesis from a hypothesis space that may be subject to certain constraints. For example, we can constrain the hypothesis space to the set of linear models.

When choosing a model, we aim to reduce the bias and the variance to prevent our model from either overfitting or underfitting the data. In the real world, we cannot completely eliminate bias and variance, and we have to trade-off between them. The total error produced by a model can be decomposed into the bias, the variance, and irreducible (Bayes) error.

About Author

Related Posts

Hypothesis Spaces for Deep Learning

This paper introduces a hypothesis space for deep learning that employs deep neural networks (DNNs). By treating a DNN as a function of two variables, the physical variable and parameter variable, we consider the primitive set of the DNNs for the parameter variable located in a set of the weight matrices and biases determined by a prescribed depth and widths of the DNNs. We then complete the linear span of the primitive DNN set in a weak* topology to construct a Banach space of functions of the physical variable. We prove that the Banach space so constructed is a reproducing kernel Banach space (RKBS) and construct its reproducing kernel. We investigate two learning models, regularized learning and minimum interpolation problem in the resulting RKBS, by establishing representer theorems for solutions of the learning models. The representer theorems unfold that solutions of these learning models can be expressed as linear combination of a finite number of kernel sessions determined by given data and the reproducing kernel.

Key words : Reproducing kernel Banach space, deep learning, deep neural network, representer theorem for deep learning

1 Introduction

Deep learning has been a huge success in applications. Mathematically, its success is due to the use of deep neural networks (DNNs), neural networks of multiple layers, to describe decision functions. Various mathematical aspects of DNNs as an approximation tool were investigated recently in a number of studies [ 9 , 11 , 13 , 16 , 20 , 27 , 28 , 31 ] . As pointed out in [ 8 ] , learning processes do not take place in a vacuum. Classical learning methods took place in a reproducing kernel Hilbert space (RKHS) [ 1 ] , which leads to representation of learning solutions in terms of a combination of a finite number of kernel sessions [ 19 ] of a universal kernel [ 17 ] . Reproducing kernel Hilbert spaces as appropriate hypothesis spaces for classical learning methods provide a foundation for mathematical analysis of the learning methods. A natural and imperative question is what are appropriate hypothesis spaces for deep learning. Although hypothesis spaces for learning with shallow neural networks (networks of one hidden layer) were investigated recently in a number of studies, (e.g. [ 2 , 6 , 18 , 21 ] ), appropriate hypothesis spaces for deep learning are still absent. The goal of the present study is to understand this imperative theoretical issue.

The road-map of constructing the hypothesis space for deep learning may be described as follows. We treat a DNN as a function of two variables, one being the physical variable and the other being the parameter variable. We then consider the set of the DNNs as functions of the physical variable for the parameter variable taking all elements of the set of the weight matrices and biases determined by a prescribed depth and widths of the DNNs. Upon completing the linear span of the DNN set in a weak* topology, we construct a Banach space of functions of the physical variable. We establish that the resulting Banach space is a reproducing kernel Banach space (RKBS), on which point-evaluation functionals are continuous, and construct an asymmetric reproducing kernel, for the space, which is a function of the two variables, the physical variable and the parameter variable. We regard the constructed RKBS as the hypothesis space for deep learning. We remark that when deep neural networks reduce to shallow network (having only one hidden layer), our hypothesis space coincides the space for shallow learning studied in [ 2 ] .

Upon introducing the hypothesis space for deep learning, we investigate two learning models, the regularized learning and minimum interpolation problem in the resulting RKBS. We establish representer theorems for solutions of the learning models by employing theory of the reproducing kernel Banach space developed in [ 25 , 26 , 29 ] and representer theorems for solutions of learning in a general RKBS established in [ 4 , 23 , 24 ] . Like the representer theorems for the classical learning in RKHSs, the resulting representer theorems for the two deep learning models in the RKBS reveal that although the learning models are of infinite dimension, their solutions lay in finite dimensional manifolds. More specifically, they can be expressed as a linear combination of a finite number of kernel sessions, the reproducing kernel evaluated the parameter variable at points determined by given data. The representer theorems established in this paper is data-dependent. Even when deep neural networks reduce to a shallow network, the corresponding representer theorem is still new to our best acknowledge. The hypothesis space and the representer theorems for the two deep learning models in it provide us prosperous insights of deep learning and supply deep learning a sound mathematical foundation for further investigation.

We organize this paper in six sections. We describe in Section 2 an innate deep learning model with DNNs. Aiming at formulating reproducing kernel Banach spaces as hypothesis spaces for deep learning, in Section 3 we elucidate the notion of vector-valued reproducing kernel Banach spaces. Section 4 is entirely devoted to the development of the hypothesis space for deep learning. We specifically show that the completion of the linear span of the primitive DNN set, pertaining to the innate learning model, in a weak* topology is an RKBS, which constitutes the hypothesis space for deep learning. In Section 5, we study learning models in the RKBS, establishing representer theorems for solutions of two learning models (regularized learning and minimum norm interpolation) in the hypothesis space. We conclude this paper in Section 6 with remarks on advantages of learning in the proposed hypothesis space.

2 Learning with Deep Neural Networks

We describe in this section an innate learning model with DNNs, considered wildly in the machine learning community.

We first recall the notation of DNNs. Let s 𝑠 s italic_s and t 𝑡 t italic_t be positive integers. A DNN is a vector-valued function from ℝ s superscript ℝ 𝑠 \mathbb{R}^{s} blackboard_R start_POSTSUPERSCRIPT italic_s end_POSTSUPERSCRIPT to ℝ t superscript ℝ 𝑡 \mathbb{R}^{t} blackboard_R start_POSTSUPERSCRIPT italic_t end_POSTSUPERSCRIPT formed by compositions of functions, each of which is defined by an activation function applied to an affine map. Specifically, for a given univariate function σ : ℝ → ℝ : 𝜎 → ℝ ℝ \sigma:\mathbb{R}\to\mathbb{R} italic_σ : blackboard_R → blackboard_R , we define a vector-valued function by

𝑗 1 f_{j+1} italic_f start_POSTSUBSCRIPT italic_j + 1 end_POSTSUBSCRIPT , for j ∈ ℕ k − 1 𝑗 subscript ℕ 𝑘 1 j\in\mathbb{N}_{k-1} italic_j ∈ blackboard_N start_POSTSUBSCRIPT italic_k - 1 end_POSTSUBSCRIPT , we denote the consecutive composition of f j subscript 𝑓 𝑗 f_{j} italic_f start_POSTSUBSCRIPT italic_j end_POSTSUBSCRIPT , j ∈ ℕ k 𝑗 subscript ℕ 𝑘 j\in\mathbb{N}_{k} italic_j ∈ blackboard_N start_POSTSUBSCRIPT italic_k end_POSTSUBSCRIPT , by

whose domain is that of f 1 subscript 𝑓 1 f_{1} italic_f start_POSTSUBSCRIPT 1 end_POSTSUBSCRIPT . Suppose that D ∈ ℕ 𝐷 ℕ D\in\mathbb{N} italic_D ∈ blackboard_N is prescribed and fixed. Throughout this paper, we always let m 0 := s assign subscript 𝑚 0 𝑠 m_{0}:=s italic_m start_POSTSUBSCRIPT 0 end_POSTSUBSCRIPT := italic_s and m D := t assign subscript 𝑚 𝐷 𝑡 m_{D}:=t italic_m start_POSTSUBSCRIPT italic_D end_POSTSUBSCRIPT := italic_t . We specify positive integers m j subscript 𝑚 𝑗 m_{j} italic_m start_POSTSUBSCRIPT italic_j end_POSTSUBSCRIPT , j ∈ ℕ D − 1 𝑗 subscript ℕ 𝐷 1 j\in\mathbb{N}_{D-1} italic_j ∈ blackboard_N start_POSTSUBSCRIPT italic_D - 1 end_POSTSUBSCRIPT . For 𝐖 j ∈ ℝ m j × m j − 1 subscript 𝐖 𝑗 superscript ℝ subscript 𝑚 𝑗 subscript 𝑚 𝑗 1 \mathbf{W}_{j}\in\mathbb{R}^{m_{j}\times m_{j-1}} bold_W start_POSTSUBSCRIPT italic_j end_POSTSUBSCRIPT ∈ blackboard_R start_POSTSUPERSCRIPT italic_m start_POSTSUBSCRIPT italic_j end_POSTSUBSCRIPT × italic_m start_POSTSUBSCRIPT italic_j - 1 end_POSTSUBSCRIPT end_POSTSUPERSCRIPT and 𝐛 j ∈ ℝ m j subscript 𝐛 𝑗 superscript ℝ subscript 𝑚 𝑗 \mathbf{b}_{j}\in\mathbb{R}^{m_{j}} bold_b start_POSTSUBSCRIPT italic_j end_POSTSUBSCRIPT ∈ blackboard_R start_POSTSUPERSCRIPT italic_m start_POSTSUBSCRIPT italic_j end_POSTSUBSCRIPT end_POSTSUPERSCRIPT , j ∈ ℕ D 𝑗 subscript ℕ 𝐷 j\in\mathbb{N}_{D} italic_j ∈ blackboard_N start_POSTSUBSCRIPT italic_D end_POSTSUBSCRIPT , a DNN is a function defined by

Note that x 𝑥 x italic_x is the input vector and 𝒩 D superscript 𝒩 𝐷 \mathcal{N}^{D} caligraphic_N start_POSTSUPERSCRIPT italic_D end_POSTSUPERSCRIPT has D − 1 𝐷 1 D-1 italic_D - 1 hidden layers and an output layer, which is the D 𝐷 D italic_D -th layer.

A DNN may be represented in a recursive manner. From definition ( 1 ), a DNN can be defined recursively by

We write 𝒩 D superscript 𝒩 𝐷 \mathcal{N}^{D} caligraphic_N start_POSTSUPERSCRIPT italic_D end_POSTSUPERSCRIPT as 𝒩 D ⁢ ( ⋅ , { 𝐖 j , 𝐛 j } j = 1 D ) superscript 𝒩 𝐷 ⋅ superscript subscript subscript 𝐖 𝑗 subscript 𝐛 𝑗 𝑗 1 𝐷 \mathcal{N}^{D}(\cdot,\{\mathbf{W}_{j},\mathbf{b}_{j}\}_{j=1}^{D}) caligraphic_N start_POSTSUPERSCRIPT italic_D end_POSTSUPERSCRIPT ( ⋅ , { bold_W start_POSTSUBSCRIPT italic_j end_POSTSUBSCRIPT , bold_b start_POSTSUBSCRIPT italic_j end_POSTSUBSCRIPT } start_POSTSUBSCRIPT italic_j = 1 end_POSTSUBSCRIPT start_POSTSUPERSCRIPT italic_D end_POSTSUPERSCRIPT ) when it is necessary to indicate the dependence of DNNs on the parameters. In this paper, when we write the set { 𝐖 j , 𝐛 j } j = 1 D superscript subscript subscript 𝐖 𝑗 subscript 𝐛 𝑗 𝑗 1 𝐷 \{\mathbf{W}_{j},\mathbf{b}_{j}\}_{j=1}^{D} { bold_W start_POSTSUBSCRIPT italic_j end_POSTSUBSCRIPT , bold_b start_POSTSUBSCRIPT italic_j end_POSTSUBSCRIPT } start_POSTSUBSCRIPT italic_j = 1 end_POSTSUBSCRIPT start_POSTSUPERSCRIPT italic_D end_POSTSUPERSCRIPT associated with the neural network 𝒩 D superscript 𝒩 𝐷 \mathcal{N}^{D} caligraphic_N start_POSTSUPERSCRIPT italic_D end_POSTSUPERSCRIPT , we implicitly give it the order inherited from the definition of 𝒩 D superscript 𝒩 𝐷 \mathcal{N}^{D} caligraphic_N start_POSTSUPERSCRIPT italic_D end_POSTSUPERSCRIPT . Throughout this paper, we assume that the activation function σ 𝜎 \sigma italic_σ is continuous.

It is advantageous to consider the DNN 𝒩 D superscript 𝒩 𝐷 \mathcal{N}^{D} caligraphic_N start_POSTSUPERSCRIPT italic_D end_POSTSUPERSCRIPT defined above as a function of two variables, one being the physical variable x ∈ ℝ s 𝑥 superscript ℝ 𝑠 x\in\mathbb{R}^{s} italic_x ∈ blackboard_R start_POSTSUPERSCRIPT italic_s end_POSTSUPERSCRIPT and the other being the parameter variable θ := { 𝐖 j , 𝐛 j } j = 1 D assign 𝜃 superscript subscript subscript 𝐖 𝑗 subscript 𝐛 𝑗 𝑗 1 𝐷 \theta:=\{\mathbf{W}_{j},\mathbf{b}_{j}\}_{j=1}^{D} italic_θ := { bold_W start_POSTSUBSCRIPT italic_j end_POSTSUBSCRIPT , bold_b start_POSTSUBSCRIPT italic_j end_POSTSUBSCRIPT } start_POSTSUBSCRIPT italic_j = 1 end_POSTSUBSCRIPT start_POSTSUPERSCRIPT italic_D end_POSTSUPERSCRIPT . Given positive integers m j subscript 𝑚 𝑗 m_{j} italic_m start_POSTSUBSCRIPT italic_j end_POSTSUBSCRIPT , j ∈ ℕ D − 1 𝑗 subscript ℕ 𝐷 1 j\in\mathbb{N}_{D-1} italic_j ∈ blackboard_N start_POSTSUBSCRIPT italic_D - 1 end_POSTSUBSCRIPT , we let

denote the width set and define the primitive set of DNNs of D 𝐷 D italic_D layers by

Clearly, the set 𝒜 𝕎 subscript 𝒜 𝕎 \mathcal{A}_{\mathbb{W}} caligraphic_A start_POSTSUBSCRIPT blackboard_W end_POSTSUBSCRIPT defined by ( 3 ) depends not only on 𝕎 𝕎 \mathbb{W} blackboard_W but also on D 𝐷 D italic_D . For the sake of simplicity, we will not indicate the dependence on D 𝐷 D italic_D in our notation when ambiguity is not caused. For example, we will use 𝒩 𝒩 \mathcal{N} caligraphic_N for 𝒩 D superscript 𝒩 𝐷 \mathcal{N}^{D} caligraphic_N start_POSTSUPERSCRIPT italic_D end_POSTSUPERSCRIPT . Moreover, an element of 𝒜 𝕎 subscript 𝒜 𝕎 \mathcal{A}_{\mathbb{W}} caligraphic_A start_POSTSUBSCRIPT blackboard_W end_POSTSUBSCRIPT is a vector-valued function mapping from ℝ s superscript ℝ 𝑠 \mathbb{R}^{s} blackboard_R start_POSTSUPERSCRIPT italic_s end_POSTSUPERSCRIPT to ℝ t superscript ℝ 𝑡 \mathbb{R}^{t} blackboard_R start_POSTSUPERSCRIPT italic_t end_POSTSUPERSCRIPT . We shall understand the set 𝒜 𝕎 subscript 𝒜 𝕎 \mathcal{A}_{\mathbb{W}} caligraphic_A start_POSTSUBSCRIPT blackboard_W end_POSTSUBSCRIPT . To this end, we define the parameter space Θ Θ \Theta roman_Θ by letting

Note that Θ Θ \Theta roman_Θ is measurable. For x ∈ ℝ s 𝑥 superscript ℝ 𝑠 {x}\in\mathbb{R}^{s} italic_x ∈ blackboard_R start_POSTSUPERSCRIPT italic_s end_POSTSUPERSCRIPT and θ ∈ Θ 𝜃 Θ \theta\in\Theta italic_θ ∈ roman_Θ , we define

For x ∈ ℝ s 𝑥 superscript ℝ 𝑠 {x}\in\mathbb{R}^{s} italic_x ∈ blackboard_R start_POSTSUPERSCRIPT italic_s end_POSTSUPERSCRIPT and θ ∈ Θ 𝜃 Θ \theta\in\Theta italic_θ ∈ roman_Θ , there holds 𝒩 ⁢ ( x , θ ) ∈ ℝ t 𝒩 𝑥 𝜃 superscript ℝ 𝑡 \mathcal{N}({x},\theta)\in\mathbb{R}^{t} caligraphic_N ( italic_x , italic_θ ) ∈ blackboard_R start_POSTSUPERSCRIPT italic_t end_POSTSUPERSCRIPT . In this notation, set 𝒜 𝕎 subscript 𝒜 𝕎 \mathcal{A}_{\mathbb{W}} caligraphic_A start_POSTSUBSCRIPT blackboard_W end_POSTSUBSCRIPT may be written as

We now describe the innate learning model with DNNs. Suppose that a training dataset

is given and we would like to train a neural network from the dataset. We denote by ℒ ⁢ ( 𝒩 , 𝔻 m ) : Θ → ℝ : ℒ 𝒩 subscript 𝔻 𝑚 → Θ ℝ \mathcal{L}(\mathcal{N},\mathbb{D}_{m}):\Theta\to\mathbb{R} caligraphic_L ( caligraphic_N , blackboard_D start_POSTSUBSCRIPT italic_m end_POSTSUBSCRIPT ) : roman_Θ → blackboard_R a loss function determined by the dataset 𝔻 m subscript 𝔻 𝑚 \mathbb{D}_{m} blackboard_D start_POSTSUBSCRIPT italic_m end_POSTSUBSCRIPT . For example, a loss function may take the form

where ∥ ⋅ ∥ \|\cdot\| ∥ ⋅ ∥ is a norm of ℝ t superscript ℝ 𝑡 \mathbb{R}^{t} blackboard_R start_POSTSUPERSCRIPT italic_t end_POSTSUPERSCRIPT . Given a loss function, a typical deep learning model is to train the parameters θ ∈ Θ 𝕎 𝜃 subscript Θ 𝕎 \theta\in\Theta_{\mathbb{W}} italic_θ ∈ roman_Θ start_POSTSUBSCRIPT blackboard_W end_POSTSUBSCRIPT from the training dataset 𝔻 m subscript 𝔻 𝑚 \mathbb{D}_{m} blackboard_D start_POSTSUBSCRIPT italic_m end_POSTSUBSCRIPT by solving the optimization problem

where 𝒩 𝒩 \mathcal{N} caligraphic_N has the form in equation ( 5 ). Equivalently, optimization problem ( 7 ) may be written as

Model ( 8 ) is an innate learning model considered wildly in the machine learning community. Note that the set 𝒜 𝕎 subscript 𝒜 𝕎 \mathcal{A}_{\mathbb{W}} caligraphic_A start_POSTSUBSCRIPT blackboard_W end_POSTSUBSCRIPT lacks either algebraic or topological structures. It is difficult to conduct mathematical analysis for learning model ( 8 ). Even the existence of its solution is not guaranteed.

We introduce a vector space that contains 𝒜 𝕎 subscript 𝒜 𝕎 \mathcal{A}_{\mathbb{W}} caligraphic_A start_POSTSUBSCRIPT blackboard_W end_POSTSUBSCRIPT and consider learning in the vector space. For this purpose, given a set 𝕎 𝕎 \mathbb{W} blackboard_W of weight widths defined by ( 2 ), we define the set

In the next proposition, we present properties of ℬ 𝕎 subscript ℬ 𝕎 \mathcal{B}_{\mathbb{W}} caligraphic_B start_POSTSUBSCRIPT blackboard_W end_POSTSUBSCRIPT .

Proposition 1 .

If 𝕎 𝕎 \mathbb{W} blackboard_W is the width set defined by ( 2 ), then

(i) ℬ 𝕎 subscript ℬ 𝕎 \mathcal{B}_{\mathbb{W}} caligraphic_B start_POSTSUBSCRIPT blackboard_W end_POSTSUBSCRIPT defined by ( 9 ) is the smallest vector space on ℝ ℝ \mathbb{R} blackboard_R that contains the set 𝒜 𝕎 subscript 𝒜 𝕎 \mathcal{A}_{\mathbb{W}} caligraphic_A start_POSTSUBSCRIPT blackboard_W end_POSTSUBSCRIPT ,

(ii) ℬ 𝕎 subscript ℬ 𝕎 \mathcal{B}_{\mathbb{W}} caligraphic_B start_POSTSUBSCRIPT blackboard_W end_POSTSUBSCRIPT is of infinite dimension,

(iii) ℬ 𝕎 ⊂ ⋃ n ∈ ℕ 𝒜 n ⁢ 𝕎 subscript ℬ 𝕎 subscript 𝑛 ℕ subscript 𝒜 𝑛 𝕎 \mathcal{B}_{\mathbb{W}}\subset\bigcup_{n\in\mathbb{N}}\mathcal{A}_{n\mathbb{W}} caligraphic_B start_POSTSUBSCRIPT blackboard_W end_POSTSUBSCRIPT ⊂ ⋃ start_POSTSUBSCRIPT italic_n ∈ blackboard_N end_POSTSUBSCRIPT caligraphic_A start_POSTSUBSCRIPT italic_n blackboard_W end_POSTSUBSCRIPT .

It is clear that ℬ 𝕎 subscript ℬ 𝕎 \mathcal{B}_{\mathbb{W}} caligraphic_B start_POSTSUBSCRIPT blackboard_W end_POSTSUBSCRIPT may be identified as the linear span of 𝒜 𝕎 subscript 𝒜 𝕎 \mathcal{A}_{\mathbb{W}} caligraphic_A start_POSTSUBSCRIPT blackboard_W end_POSTSUBSCRIPT , that is,

Thus, ℬ 𝕎 subscript ℬ 𝕎 \mathcal{B}_{\mathbb{W}} caligraphic_B start_POSTSUBSCRIPT blackboard_W end_POSTSUBSCRIPT is the smallest vector space containing 𝒜 𝕎 subscript 𝒜 𝕎 \mathcal{A}_{\mathbb{W}} caligraphic_A start_POSTSUBSCRIPT blackboard_W end_POSTSUBSCRIPT . Item (ii) follows directly from the definition ( 9 ) of ℬ 𝕎 subscript ℬ 𝕎 \mathcal{B}_{\mathbb{W}} caligraphic_B start_POSTSUBSCRIPT blackboard_W end_POSTSUBSCRIPT .

It remains to prove Item (iii). To this end, we let f ∈ ℬ 𝕎 𝑓 subscript ℬ 𝕎 f\in\mathcal{B}_{\mathbb{W}} italic_f ∈ caligraphic_B start_POSTSUBSCRIPT blackboard_W end_POSTSUBSCRIPT . By the definition ( 9 ) of ℬ 𝕎 subscript ℬ 𝕎 \mathcal{B}_{\mathbb{W}} caligraphic_B start_POSTSUBSCRIPT blackboard_W end_POSTSUBSCRIPT , there exist n ′ ∈ ℕ superscript 𝑛 ′ ℕ n^{\prime}\in\mathbb{N} italic_n start_POSTSUPERSCRIPT ′ end_POSTSUPERSCRIPT ∈ blackboard_N , c l ∈ ℝ subscript 𝑐 𝑙 ℝ c_{l}\in\mathbb{R} italic_c start_POSTSUBSCRIPT italic_l end_POSTSUBSCRIPT ∈ blackboard_R , θ l ∈ Θ 𝕎 subscript 𝜃 𝑙 subscript Θ 𝕎 \theta_{l}\in\Theta_{\mathbb{W}} italic_θ start_POSTSUBSCRIPT italic_l end_POSTSUBSCRIPT ∈ roman_Θ start_POSTSUBSCRIPT blackboard_W end_POSTSUBSCRIPT , for l ∈ ℕ n ′ 𝑙 subscript ℕ superscript 𝑛 ′ l\in\mathbb{N}_{n^{\prime}} italic_l ∈ blackboard_N start_POSTSUBSCRIPT italic_n start_POSTSUPERSCRIPT ′ end_POSTSUPERSCRIPT end_POSTSUBSCRIPT such that

It suffices to show that f ∈ 𝒜 n ′ ⁢ 𝕎 𝑓 subscript 𝒜 superscript 𝑛 ′ 𝕎 f\in\mathcal{A}_{n^{\prime}\mathbb{W}} italic_f ∈ caligraphic_A start_POSTSUBSCRIPT italic_n start_POSTSUPERSCRIPT ′ end_POSTSUPERSCRIPT blackboard_W end_POSTSUBSCRIPT . Noting that θ l := { 𝐖 j l , 𝐛 j l } j = 1 D assign subscript 𝜃 𝑙 superscript subscript superscript subscript 𝐖 𝑗 𝑙 superscript subscript 𝐛 𝑗 𝑙 𝑗 1 𝐷 \theta_{l}:=\{\mathbf{W}_{j}^{l},\mathbf{b}_{j}^{l}\}_{j=1}^{D} italic_θ start_POSTSUBSCRIPT italic_l end_POSTSUBSCRIPT := { bold_W start_POSTSUBSCRIPT italic_j end_POSTSUBSCRIPT start_POSTSUPERSCRIPT italic_l end_POSTSUPERSCRIPT , bold_b start_POSTSUBSCRIPT italic_j end_POSTSUBSCRIPT start_POSTSUPERSCRIPT italic_l end_POSTSUPERSCRIPT } start_POSTSUBSCRIPT italic_j = 1 end_POSTSUBSCRIPT start_POSTSUPERSCRIPT italic_D end_POSTSUPERSCRIPT , for l ∈ ℕ n ′ 𝑙 subscript ℕ superscript 𝑛 ′ l\in\mathbb{N}_{n^{\prime}} italic_l ∈ blackboard_N start_POSTSUBSCRIPT italic_n start_POSTSUPERSCRIPT ′ end_POSTSUPERSCRIPT end_POSTSUBSCRIPT , we set

Clearly, we have that 𝐖 ~ 1 ∈ ℝ ( n ′ ⁢ m 1 ) × m 0 subscript ~ 𝐖 1 superscript ℝ superscript 𝑛 ′ subscript 𝑚 1 subscript 𝑚 0 \widetilde{\mathbf{W}}_{1}\in\mathbb{R}^{(n^{\prime}m_{1})\times{m_{0}}} over~ start_ARG bold_W end_ARG start_POSTSUBSCRIPT 1 end_POSTSUBSCRIPT ∈ blackboard_R start_POSTSUPERSCRIPT ( italic_n start_POSTSUPERSCRIPT ′ end_POSTSUPERSCRIPT italic_m start_POSTSUBSCRIPT 1 end_POSTSUBSCRIPT ) × italic_m start_POSTSUBSCRIPT 0 end_POSTSUBSCRIPT end_POSTSUPERSCRIPT , 𝐛 ~ j ∈ ℝ n ′ ⁢ m j subscript ~ 𝐛 𝑗 superscript ℝ superscript 𝑛 ′ subscript 𝑚 𝑗 \widetilde{\mathbf{b}}_{j}\in\mathbb{R}^{n^{\prime}m_{j}} over~ start_ARG bold_b end_ARG start_POSTSUBSCRIPT italic_j end_POSTSUBSCRIPT ∈ blackboard_R start_POSTSUPERSCRIPT italic_n start_POSTSUPERSCRIPT ′ end_POSTSUPERSCRIPT italic_m start_POSTSUBSCRIPT italic_j end_POSTSUBSCRIPT end_POSTSUPERSCRIPT , j ∈ ℕ D − 1 𝑗 subscript ℕ 𝐷 1 j\in\mathbb{N}_{D-1} italic_j ∈ blackboard_N start_POSTSUBSCRIPT italic_D - 1 end_POSTSUBSCRIPT , 𝐖 ~ j ∈ ℝ ( n ′ ⁢ m j ) × ( n ′ ⁢ m j − 1 ) subscript ~ 𝐖 𝑗 superscript ℝ superscript 𝑛 ′ subscript 𝑚 𝑗 superscript 𝑛 ′ subscript 𝑚 𝑗 1 \widetilde{\mathbf{W}}_{j}\in\mathbb{R}^{(n^{\prime}m_{j})\times(n^{\prime}m_{% j-1})} over~ start_ARG bold_W end_ARG start_POSTSUBSCRIPT italic_j end_POSTSUBSCRIPT ∈ blackboard_R start_POSTSUPERSCRIPT ( italic_n start_POSTSUPERSCRIPT ′ end_POSTSUPERSCRIPT italic_m start_POSTSUBSCRIPT italic_j end_POSTSUBSCRIPT ) × ( italic_n start_POSTSUPERSCRIPT ′ end_POSTSUPERSCRIPT italic_m start_POSTSUBSCRIPT italic_j - 1 end_POSTSUBSCRIPT ) end_POSTSUPERSCRIPT , j ∈ ℕ D − 1 \ { 1 } 𝑗 \ subscript ℕ 𝐷 1 1 j\in\mathbb{N}_{D-1}\backslash\{1\} italic_j ∈ blackboard_N start_POSTSUBSCRIPT italic_D - 1 end_POSTSUBSCRIPT \ { 1 } , 𝐖 ~ D ∈ ℝ m D × ( n ′ ⁢ m D − 1 ) subscript ~ 𝐖 𝐷 superscript ℝ subscript 𝑚 𝐷 superscript 𝑛 ′ subscript 𝑚 𝐷 1 \widetilde{\mathbf{W}}_{D}\in\mathbb{R}^{m_{D}\times(n^{\prime}m_{D-1})} over~ start_ARG bold_W end_ARG start_POSTSUBSCRIPT italic_D end_POSTSUBSCRIPT ∈ blackboard_R start_POSTSUPERSCRIPT italic_m start_POSTSUBSCRIPT italic_D end_POSTSUBSCRIPT × ( italic_n start_POSTSUPERSCRIPT ′ end_POSTSUPERSCRIPT italic_m start_POSTSUBSCRIPT italic_D - 1 end_POSTSUBSCRIPT ) end_POSTSUPERSCRIPT , and 𝐛 ~ D ∈ ℝ m D subscript ~ 𝐛 𝐷 superscript ℝ subscript 𝑚 𝐷 \widetilde{\mathbf{b}}_{D}\in\mathbb{R}^{m_{D}} over~ start_ARG bold_b end_ARG start_POSTSUBSCRIPT italic_D end_POSTSUBSCRIPT ∈ blackboard_R start_POSTSUPERSCRIPT italic_m start_POSTSUBSCRIPT italic_D end_POSTSUBSCRIPT end_POSTSUPERSCRIPT . Direct computation confirms that f ⁢ ( ⋅ ) = 𝒩 ⁢ ( ⋅ , θ ~ ) 𝑓 ⋅ 𝒩 ⋅ ~ 𝜃 f(\cdot)=\mathcal{N}(\cdot,\widetilde{\theta}) italic_f ( ⋅ ) = caligraphic_N ( ⋅ , over~ start_ARG italic_θ end_ARG ) with θ ~ := { 𝐖 ~ j , 𝐛 ~ j } j = 1 D assign ~ 𝜃 superscript subscript subscript ~ 𝐖 𝑗 subscript ~ 𝐛 𝑗 𝑗 1 𝐷 \widetilde{\theta}:=\{\widetilde{\mathbf{W}}_{j},\widetilde{\mathbf{b}}_{j}\}_% {j=1}^{D} over~ start_ARG italic_θ end_ARG := { over~ start_ARG bold_W end_ARG start_POSTSUBSCRIPT italic_j end_POSTSUBSCRIPT , over~ start_ARG bold_b end_ARG start_POSTSUBSCRIPT italic_j end_POSTSUBSCRIPT } start_POSTSUBSCRIPT italic_j = 1 end_POSTSUBSCRIPT start_POSTSUPERSCRIPT italic_D end_POSTSUPERSCRIPT . By definition ( 3 ), f ∈ 𝒜 n ′ ⁢ 𝕎 𝑓 subscript 𝒜 superscript 𝑛 ′ 𝕎 f\in\mathcal{A}_{n^{\prime}\mathbb{W}} italic_f ∈ caligraphic_A start_POSTSUBSCRIPT italic_n start_POSTSUPERSCRIPT ′ end_POSTSUPERSCRIPT blackboard_W end_POSTSUBSCRIPT . ∎

Proposition 1 reveals that ℬ 𝕎 subscript ℬ 𝕎 \mathcal{B}_{\mathbb{W}} caligraphic_B start_POSTSUBSCRIPT blackboard_W end_POSTSUBSCRIPT is the smallest vector space that contains 𝒜 𝕎 subscript 𝒜 𝕎 \mathcal{A}_{\mathbb{W}} caligraphic_A start_POSTSUBSCRIPT blackboard_W end_POSTSUBSCRIPT . Hence, it is a reasonable substitute of 𝒜 𝕎 subscript 𝒜 𝕎 \mathcal{A}_{\mathbb{W}} caligraphic_A start_POSTSUBSCRIPT blackboard_W end_POSTSUBSCRIPT . Motivated by Proposition 1 , we propose the following alternative learning model

For a given width set 𝕎 𝕎 \mathbb{W} blackboard_W , unlike learning model ( 8 ) which searches a minimizer in set 𝒜 𝕎 subscript 𝒜 𝕎 \mathcal{A}_{\mathbb{W}} caligraphic_A start_POSTSUBSCRIPT blackboard_W end_POSTSUBSCRIPT , learning model ( 10 ) seeks a minimizer in the vector space ℬ 𝕎 subscript ℬ 𝕎 \mathcal{B}_{\mathbb{W}} caligraphic_B start_POSTSUBSCRIPT blackboard_W end_POSTSUBSCRIPT , which contains 𝒜 𝕎 subscript 𝒜 𝕎 \mathcal{A}_{\mathbb{W}} caligraphic_A start_POSTSUBSCRIPT blackboard_W end_POSTSUBSCRIPT and is contained in 𝒜 := ⋃ n ∈ ℕ 𝒜 n ⁢ 𝕎 assign 𝒜 subscript 𝑛 ℕ subscript 𝒜 𝑛 𝕎 \mathcal{A}:=\bigcup_{n\in\mathbb{N}}\mathcal{A}_{n\mathbb{W}} caligraphic_A := ⋃ start_POSTSUBSCRIPT italic_n ∈ blackboard_N end_POSTSUBSCRIPT caligraphic_A start_POSTSUBSCRIPT italic_n blackboard_W end_POSTSUBSCRIPT . According to Proposition 1 , learning model ( 10 ) is “semi-equivalent” to learning model ( 8 ) in the sense that

where 𝒩 ℬ 𝕎 subscript 𝒩 subscript ℬ 𝕎 \mathcal{N}_{\mathcal{B}_{\mathbb{W}}} caligraphic_N start_POSTSUBSCRIPT caligraphic_B start_POSTSUBSCRIPT blackboard_W end_POSTSUBSCRIPT end_POSTSUBSCRIPT is a minimizer of model ( 10 ), 𝒩 𝒜 𝕎 subscript 𝒩 subscript 𝒜 𝕎 \mathcal{N}_{\mathcal{A}_{\mathbb{W}}} caligraphic_N start_POSTSUBSCRIPT caligraphic_A start_POSTSUBSCRIPT blackboard_W end_POSTSUBSCRIPT end_POSTSUBSCRIPT and 𝒩 𝒜 subscript 𝒩 𝒜 \mathcal{N}_{\mathcal{A}} caligraphic_N start_POSTSUBSCRIPT caligraphic_A end_POSTSUBSCRIPT are the minimizers of model ( 8 ) and model ( 8 ) with the set 𝒜 𝕎 subscript 𝒜 𝕎 \mathcal{A}_{\mathbb{W}} caligraphic_A start_POSTSUBSCRIPT blackboard_W end_POSTSUBSCRIPT replaced by 𝒜 𝒜 \mathcal{A} caligraphic_A , respectively. One might argue that since model ( 8 ) is a finite dimension optimization problem while model ( 10 ) is an infinite dimensional one, the alternative model ( 10 ) may add unnecessary complexity to the original model. Although model ( 10 ) is of infinite dimension, the algebraic structure of the vector space ℬ 𝕎 subscript ℬ 𝕎 \mathcal{B}_{\mathbb{W}} caligraphic_B start_POSTSUBSCRIPT blackboard_W end_POSTSUBSCRIPT and its topological structure that will be equipped later provide us with great advantages for mathematical analysis of learning on the space. As a matter of fact, the vector-valued RKBS to be obtained by completing the vector space ℬ 𝕎 subscript ℬ 𝕎 \mathcal{B}_{\mathbb{W}} caligraphic_B start_POSTSUBSCRIPT blackboard_W end_POSTSUBSCRIPT in a weak* topology will lead to the miraculous representer theorem, of the learned solution, which reduces the infinite dimensional optimization problem to a finite dimension one. This addresses the challenges caused by the infinite dimension of the space ℬ 𝕎 subscript ℬ 𝕎 \mathcal{B}_{\mathbb{W}} caligraphic_B start_POSTSUBSCRIPT blackboard_W end_POSTSUBSCRIPT .

3 Vector-Valued Reproducing Kernel Banach Space

It was proved in the last section that for a given width set 𝕎 𝕎 \mathbb{W} blackboard_W , the set ℬ 𝕎 subscript ℬ 𝕎 \mathcal{B}_{\mathbb{W}} caligraphic_B start_POSTSUBSCRIPT blackboard_W end_POSTSUBSCRIPT defined by ( 9 ) is the smallest vector space that contains the primitive set 𝒜 𝕎 subscript 𝒜 𝕎 \mathcal{A}_{\mathbb{W}} caligraphic_A start_POSTSUBSCRIPT blackboard_W end_POSTSUBSCRIPT . One of the aims of this paper is to establish that the vector space ℬ 𝕎 subscript ℬ 𝕎 \mathcal{B}_{\mathbb{W}} caligraphic_B start_POSTSUBSCRIPT blackboard_W end_POSTSUBSCRIPT is dense in a weak* topology in a vector-valued RKBS. For this purpose, in this section we describe the notion of vector-valued RKBSs.

A Banach space ℬ ℬ \mathcal{B} caligraphic_B with the norm ∥ ⋅ ∥ ℬ \|\cdot\|_{\mathcal{B}} ∥ ⋅ ∥ start_POSTSUBSCRIPT caligraphic_B end_POSTSUBSCRIPT is called a space of vector-valued functions on a prescribed set X 𝑋 X italic_X if ℬ ℬ \mathcal{B} caligraphic_B is composed of vector-valued functions defined on X 𝑋 X italic_X and for each f ∈ ℬ 𝑓 ℬ f\in\mathcal{B} italic_f ∈ caligraphic_B , ‖ f ‖ ℬ = 0 subscript norm 𝑓 ℬ 0 \|f\|_{\mathcal{B}}=0 ∥ italic_f ∥ start_POSTSUBSCRIPT caligraphic_B end_POSTSUBSCRIPT = 0 implies that f ⁢ ( x ) = 𝟎 𝑓 𝑥 0 f({x})=\mathbf{0} italic_f ( italic_x ) = bold_0 for all x ∈ X 𝑥 𝑋 {x}\in X italic_x ∈ italic_X . For each x ∈ X 𝑥 𝑋 {x}\in X italic_x ∈ italic_X , we define the point evaluation operator δ x : ℬ → ℝ n : subscript 𝛿 𝑥 → ℬ superscript ℝ 𝑛 \delta_{{x}}:\mathcal{B}\to\mathbb{R}^{n} italic_δ start_POSTSUBSCRIPT italic_x end_POSTSUBSCRIPT : caligraphic_B → blackboard_R start_POSTSUPERSCRIPT italic_n end_POSTSUPERSCRIPT as

We provide the definition of vector-valued RKBSs below.

Definition 2 .

A Banach space ℬ ℬ \mathcal{B} caligraphic_B of vector-valued functions from X 𝑋 X italic_X to ℝ n superscript ℝ 𝑛 \mathbb{R}^{n} blackboard_R start_POSTSUPERSCRIPT italic_n end_POSTSUPERSCRIPT is called a vector-valued RKBS if there exists a norm ∥ ⋅ ∥ \|\cdot\| ∥ ⋅ ∥ of ℝ n superscript ℝ 𝑛 \mathbb{R}^{n} blackboard_R start_POSTSUPERSCRIPT italic_n end_POSTSUPERSCRIPT such that for each x ∈ X 𝑥 𝑋 x\in X italic_x ∈ italic_X , the point evaluation operator δ x subscript 𝛿 𝑥 \delta_{x} italic_δ start_POSTSUBSCRIPT italic_x end_POSTSUBSCRIPT is continuous with respect to the norm ∥ ⋅ ∥ \|\cdot\| ∥ ⋅ ∥ of ℝ n superscript ℝ 𝑛 \mathbb{R}^{n} blackboard_R start_POSTSUPERSCRIPT italic_n end_POSTSUPERSCRIPT on ℬ ℬ \mathcal{B} caligraphic_B , that is, for each x ∈ X 𝑥 𝑋 x\in X italic_x ∈ italic_X , there exists a constant C x > 0 subscript 𝐶 𝑥 0 C_{x}>0 italic_C start_POSTSUBSCRIPT italic_x end_POSTSUBSCRIPT > 0 such that

Note that since all norms of ℝ n superscript ℝ 𝑛 \mathbb{R}^{n} blackboard_R start_POSTSUPERSCRIPT italic_n end_POSTSUPERSCRIPT are equivalent, if a Banach space ℬ ℬ \mathcal{B} caligraphic_B of vector-valued functions from X 𝑋 X italic_X to ℝ n superscript ℝ 𝑛 \mathbb{R}^{n} blackboard_R start_POSTSUPERSCRIPT italic_n end_POSTSUPERSCRIPT is a vector-valued RKBS with respect to a norm of ℝ n superscript ℝ 𝑛 \mathbb{R}^{n} blackboard_R start_POSTSUPERSCRIPT italic_n end_POSTSUPERSCRIPT , then it must be a vector-valued RKBS with respect to any other norm of ℝ n superscript ℝ 𝑛 \mathbb{R}^{n} blackboard_R start_POSTSUPERSCRIPT italic_n end_POSTSUPERSCRIPT . Thus, the property of point evaluation operators being continuous on space ℬ ℬ \mathcal{B} caligraphic_B is independent of the choice of the norm of the output space ℝ n superscript ℝ 𝑛 \mathbb{R}^{n} blackboard_R start_POSTSUPERSCRIPT italic_n end_POSTSUPERSCRIPT .

The notion of RKBSs was originally introduced in [ 29 ] , to guarantee the stability of sampling process and to serve as a hypothesis space for sparse machine learning. Vector-valued RKBSs were studied in [ 14 , 30 ] , in which the definition of the vector-valued RKBS involves an abstract Banach space, with a specific norm, as the output space of functions. In Definition 2 , we limit the output space to the Euclidean space ℝ n superscript ℝ 𝑛 \mathbb{R}^{n} blackboard_R start_POSTSUPERSCRIPT italic_n end_POSTSUPERSCRIPT without specifying a norm, due to the special property that norms on ℝ n superscript ℝ 𝑛 \mathbb{R}^{n} blackboard_R start_POSTSUPERSCRIPT italic_n end_POSTSUPERSCRIPT are all equivalent.

We reveal in the next proposition that point evaluation operators are continuous if and only if component-wise point evaluation functionals are continuous. To this end, for a vector-valued function f : X → ℝ n : 𝑓 → 𝑋 superscript ℝ 𝑛 f:X\to\mathbb{R}^{n} italic_f : italic_X → blackboard_R start_POSTSUPERSCRIPT italic_n end_POSTSUPERSCRIPT , for each j ∈ ℕ n 𝑗 subscript ℕ 𝑛 j\in\mathbb{N}_{n} italic_j ∈ blackboard_N start_POSTSUBSCRIPT italic_n end_POSTSUBSCRIPT , we denote by f j : X → ℝ : subscript 𝑓 𝑗 → 𝑋 ℝ f_{j}:X\to\mathbb{R} italic_f start_POSTSUBSCRIPT italic_j end_POSTSUBSCRIPT : italic_X → blackboard_R the j 𝑗 j italic_j -th component of f 𝑓 f italic_f , that is,

Proposition 3 .

We next identify a reproducing kernel for a vector-valued RKBS. We need the notion of the δ 𝛿 \delta italic_δ -dual space of a vector-valued RKBS. For a Banach space B 𝐵 B italic_B with a norm ∥ ⋅ ∥ B \|\cdot\|_{B} ∥ ⋅ ∥ start_POSTSUBSCRIPT italic_B end_POSTSUBSCRIPT , we denote by B * superscript 𝐵 B^{*} italic_B start_POSTSUPERSCRIPT * end_POSTSUPERSCRIPT the dual space of B 𝐵 B italic_B , which is composed of all continuous linear functionals on B 𝐵 B italic_B endowed with the norm

Suppose that ℬ ℬ \mathcal{B} caligraphic_B is a vector-valued RKBS of functions from X 𝑋 X italic_X to ℝ n superscript ℝ 𝑛 \mathbb{R}^{n} blackboard_R start_POSTSUPERSCRIPT italic_n end_POSTSUPERSCRIPT , with the dual space ℬ * superscript ℬ \mathcal{B}^{*} caligraphic_B start_POSTSUPERSCRIPT * end_POSTSUPERSCRIPT . We set

We identify in the next proposition a reproducing kernel for the vector-valued RKBS ℬ ℬ \mathcal{B} caligraphic_B under the assumption that the δ 𝛿 \delta italic_δ -dual space ℬ ′ superscript ℬ ′ \mathcal{B}^{\prime} caligraphic_B start_POSTSUPERSCRIPT ′ end_POSTSUPERSCRIPT is isometrically isomorphic to a Banach space of functions from a set X ′ superscript 𝑋 ′ X^{\prime} italic_X start_POSTSUPERSCRIPT ′ end_POSTSUPERSCRIPT to ℝ ℝ \mathbb{R} blackboard_R .

Proposition 4 .

Suppose that ℬ ℬ \mathcal{B} caligraphic_B is a vector-valued RKBS of functions from X 𝑋 X italic_X to ℝ n superscript ℝ 𝑛 \mathbb{R}^{n} blackboard_R start_POSTSUPERSCRIPT italic_n end_POSTSUPERSCRIPT and its δ 𝛿 \delta italic_δ -dual space ℬ ′ superscript ℬ normal-′ \mathcal{B}^{\prime} caligraphic_B start_POSTSUPERSCRIPT ′ end_POSTSUPERSCRIPT is isometrically isomorphic to a Banach space of functions from X ′ superscript 𝑋 normal-′ X^{\prime} italic_X start_POSTSUPERSCRIPT ′ end_POSTSUPERSCRIPT to ℝ ℝ \mathbb{R} blackboard_R , then there exists a unique vector-valued function K : X × X ′ → ℝ n normal-: 𝐾 normal-→ 𝑋 superscript 𝑋 normal-′ superscript ℝ 𝑛 K:X\times X^{\prime}\to\mathbb{R}^{n} italic_K : italic_X × italic_X start_POSTSUPERSCRIPT ′ end_POSTSUPERSCRIPT → blackboard_R start_POSTSUPERSCRIPT italic_n end_POSTSUPERSCRIPT such that K j ⁢ ( x , ⋅ ) ∈ ℬ ′ subscript 𝐾 𝑗 𝑥 normal-⋅ superscript ℬ normal-′ K_{j}(x,\cdot)\in\mathcal{B}^{\prime} italic_K start_POSTSUBSCRIPT italic_j end_POSTSUBSCRIPT ( italic_x , ⋅ ) ∈ caligraphic_B start_POSTSUPERSCRIPT ′ end_POSTSUPERSCRIPT for all x ∈ X 𝑥 𝑋 x\in X italic_x ∈ italic_X , j ∈ ℕ n 𝑗 subscript ℕ 𝑛 j\in\mathbb{N}_{n} italic_j ∈ blackboard_N start_POSTSUBSCRIPT italic_n end_POSTSUBSCRIPT , and

By defining the j 𝑗 j italic_j -th component of the vector-valued function K : X × X ′ → ℝ n : 𝐾 → 𝑋 superscript 𝑋 ′ superscript ℝ 𝑛 K:X\times X^{\prime}\to\mathbb{R}^{n} italic_K : italic_X × italic_X start_POSTSUPERSCRIPT ′ end_POSTSUPERSCRIPT → blackboard_R start_POSTSUPERSCRIPT italic_n end_POSTSUPERSCRIPT by

We call the vector-valued function K : X × X ′ → ℝ n : 𝐾 → 𝑋 superscript 𝑋 ′ superscript ℝ 𝑛 K:X\times X^{\prime}\rightarrow\mathbb{R}^{n} italic_K : italic_X × italic_X start_POSTSUPERSCRIPT ′ end_POSTSUPERSCRIPT → blackboard_R start_POSTSUPERSCRIPT italic_n end_POSTSUPERSCRIPT that satisfies K j ⁢ ( x , ⋅ ) ∈ ℬ ′ subscript 𝐾 𝑗 𝑥 ⋅ superscript ℬ ′ K_{j}(x,\cdot)\in\mathcal{B}^{\prime} italic_K start_POSTSUBSCRIPT italic_j end_POSTSUBSCRIPT ( italic_x , ⋅ ) ∈ caligraphic_B start_POSTSUPERSCRIPT ′ end_POSTSUPERSCRIPT for all x ∈ X 𝑥 𝑋 x\in X italic_x ∈ italic_X , j ∈ ℕ n 𝑗 subscript ℕ 𝑛 j\in\mathbb{N}_{n} italic_j ∈ blackboard_N start_POSTSUBSCRIPT italic_n end_POSTSUBSCRIPT and equation ( 14 ) the reproducing kernel for the vector-valued RKBS ℬ ℬ \mathcal{B} caligraphic_B . Moreover, equation ( 14 ) is called the reproducing property. Clearly, we have that K ⁢ ( x , ⋅ ) ∈ ( ℬ ′ ) n 𝐾 𝑥 ⋅ superscript superscript ℬ ′ 𝑛 K(x,\cdot)\in(\mathcal{B}^{\prime})^{n} italic_K ( italic_x , ⋅ ) ∈ ( caligraphic_B start_POSTSUPERSCRIPT ′ end_POSTSUPERSCRIPT ) start_POSTSUPERSCRIPT italic_n end_POSTSUPERSCRIPT for all x ∈ X 𝑥 𝑋 x\in X italic_x ∈ italic_X . The notion of the vector-valued RKBS and its reproducing kernel will serve as a basis for us to understand the hypothesis space for deep learning in the next section.

It is worth of pointing out that although ℬ ℬ \mathcal{B} caligraphic_B is a space of vector-valued functions, the δ 𝛿 \delta italic_δ -dual space ℬ ′ superscript ℬ ′ \mathcal{B}^{\prime} caligraphic_B start_POSTSUPERSCRIPT ′ end_POSTSUPERSCRIPT defined here is a space of scalar-valued functions. This is determined by the form of the point evaluation functionals in set Δ Δ \Delta roman_Δ defined by ( 13 ). The way of defining the δ 𝛿 \delta italic_δ -dual space of the vector-valued RKBS ℬ ℬ \mathcal{B} caligraphic_B is not unique. One can also define a δ 𝛿 \delta italic_δ -dual space of the vector-valued RKBS ℬ ℬ \mathcal{B} caligraphic_B as a space of vector-valued functions. In this paper, we adopt the current form of ℬ ′ superscript ℬ ′ \mathcal{B}^{\prime} caligraphic_B start_POSTSUPERSCRIPT ′ end_POSTSUPERSCRIPT since it is simple and sufficient to serve our purposes. Other forms of the δ 𝛿 \delta italic_δ -dual space will be investigated in a different occasion.

4 Hypothesis Space

In this section, we return to understanding the vector space ℬ 𝕎 subscript ℬ 𝕎 \mathcal{B}_{\mathbb{W}} caligraphic_B start_POSTSUBSCRIPT blackboard_W end_POSTSUBSCRIPT introduced in section 2 from the RKBS viewpoint. Specifically, our goal is to introduce a vector-valued RKBS in which the vector space ℬ 𝕎 subscript ℬ 𝕎 \mathcal{B}_{\mathbb{W}} caligraphic_B start_POSTSUBSCRIPT blackboard_W end_POSTSUBSCRIPT is weakly * {}^{*} start_FLOATSUPERSCRIPT * end_FLOATSUPERSCRIPT dense. The resulting vector-valued RKBS will serve as the hypothesis space for deep learning.

We first construct the vector-valued RKBS. Recalling the parameter space Θ Θ \Theta roman_Θ defined by equation ( 4 ), we use C 0 ⁢ ( Θ ) subscript 𝐶 0 Θ C_{0}(\Theta) italic_C start_POSTSUBSCRIPT 0 end_POSTSUBSCRIPT ( roman_Θ ) to denote the space of the continuous scalar-valued functions vanishing at infinity on Θ Θ \Theta roman_Θ . We equip the maximum norm on C 0 ⁢ ( Θ ) subscript 𝐶 0 Θ C_{0}(\Theta) italic_C start_POSTSUBSCRIPT 0 end_POSTSUBSCRIPT ( roman_Θ ) , namely, ‖ f ‖ ∞ := sup θ ∈ Θ | f ⁢ ( θ ) | assign subscript norm 𝑓 subscript supremum 𝜃 Θ 𝑓 𝜃 \|f\|_{\infty}:=\sup_{\theta\in\Theta}|f(\theta)| ∥ italic_f ∥ start_POSTSUBSCRIPT ∞ end_POSTSUBSCRIPT := roman_sup start_POSTSUBSCRIPT italic_θ ∈ roman_Θ end_POSTSUBSCRIPT | italic_f ( italic_θ ) | , for all f ∈ C 0 ⁢ ( Θ ) 𝑓 subscript 𝐶 0 Θ f\in C_{0}(\Theta) italic_f ∈ italic_C start_POSTSUBSCRIPT 0 end_POSTSUBSCRIPT ( roman_Θ ) . For the function 𝒩 ⁢ ( x , θ ) 𝒩 𝑥 𝜃 \mathcal{N}(x,\theta) caligraphic_N ( italic_x , italic_θ ) , x ∈ ℝ s 𝑥 superscript ℝ 𝑠 x\in\mathbb{R}^{s} italic_x ∈ blackboard_R start_POSTSUPERSCRIPT italic_s end_POSTSUPERSCRIPT , θ ∈ Θ 𝜃 Θ \theta\in\Theta italic_θ ∈ roman_Θ , defined by equation ( 5 ), we denote by 𝒩 k ⁢ ( x , θ ) subscript 𝒩 𝑘 𝑥 𝜃 \mathcal{N}_{k}({x},\theta) caligraphic_N start_POSTSUBSCRIPT italic_k end_POSTSUBSCRIPT ( italic_x , italic_θ ) the k 𝑘 k italic_k -th component of 𝒩 ⁢ ( x , θ ) 𝒩 𝑥 𝜃 \mathcal{N}({x},\theta) caligraphic_N ( italic_x , italic_θ ) , for k ∈ ℕ t 𝑘 subscript ℕ 𝑡 k\in\mathbb{N}_{t} italic_k ∈ blackboard_N start_POSTSUBSCRIPT italic_t end_POSTSUBSCRIPT . We require that all components 𝒩 k ⁢ ( x , ⋅ ) subscript 𝒩 𝑘 𝑥 ⋅ \mathcal{N}_{k}({x},\cdot) caligraphic_N start_POSTSUBSCRIPT italic_k end_POSTSUBSCRIPT ( italic_x , ⋅ ) with a weight belong to C 0 ⁢ ( Θ ) subscript 𝐶 0 Θ C_{0}(\Theta) italic_C start_POSTSUBSCRIPT 0 end_POSTSUBSCRIPT ( roman_Θ ) for all x ∈ ℝ s 𝑥 superscript ℝ 𝑠 x\in\mathbb{R}^{s} italic_x ∈ blackboard_R start_POSTSUPERSCRIPT italic_s end_POSTSUPERSCRIPT . Specifically, we assume that there exists a continuous weight function ρ : Θ → ℝ : 𝜌 → Θ ℝ \rho:\Theta\to\mathbb{R} italic_ρ : roman_Θ → blackboard_R such that the functions

An example of such a weight function is given by the rapidly decreasing function

We need a measure on the set Θ Θ \Theta roman_Θ . A Radon measure [ 10 ] on Θ Θ \Theta roman_Θ is a Borel measure on Θ Θ \Theta roman_Θ that is finite on all compact sets of Θ Θ \Theta roman_Θ , outer regular on all Borel sets of Θ Θ \Theta roman_Θ , and inner regular on all open sets of Θ Θ \Theta roman_Θ . Let ℳ ⁢ ( Θ ) ℳ Θ \mathcal{M}(\Theta) caligraphic_M ( roman_Θ ) denote the space of finite Radon measures μ : Θ → ℝ : 𝜇 → Θ ℝ \mu:\Theta\to\mathbb{R} italic_μ : roman_Θ → blackboard_R , equipped with the total variation norm

where E k subscript 𝐸 𝑘 E_{k} italic_E start_POSTSUBSCRIPT italic_k end_POSTSUBSCRIPT are required to be measurable. Note that ℳ ⁢ ( Θ ) ℳ Θ \mathcal{M}(\Theta) caligraphic_M ( roman_Θ ) is the dual space of C 0 ⁢ ( Θ ) subscript 𝐶 0 Θ C_{0}(\Theta) italic_C start_POSTSUBSCRIPT 0 end_POSTSUBSCRIPT ( roman_Θ ) (see, for example, [ 7 ] ). Moreover, the dual bilinear form on ℳ ⁢ ( Θ ) × C 0 ⁢ ( Θ ) ℳ Θ subscript 𝐶 0 Θ \mathcal{M}(\Theta)\times C_{0}(\Theta) caligraphic_M ( roman_Θ ) × italic_C start_POSTSUBSCRIPT 0 end_POSTSUBSCRIPT ( roman_Θ ) is given by

For μ ∈ ℳ ⁢ ( Θ ) 𝜇 ℳ Θ \mu\in\mathcal{M}(\Theta) italic_μ ∈ caligraphic_M ( roman_Θ ) , we let

We introduce the vector space

where f μ k superscript subscript 𝑓 𝜇 𝑘 f_{\mu}^{k} italic_f start_POSTSUBSCRIPT italic_μ end_POSTSUBSCRIPT start_POSTSUPERSCRIPT italic_k end_POSTSUPERSCRIPT , k ∈ ℕ t 𝑘 subscript ℕ 𝑡 k\in\mathbb{N}_{t} italic_k ∈ blackboard_N start_POSTSUBSCRIPT italic_t end_POSTSUBSCRIPT , are defined by equation ( 20 ) and ∥ ⋅ ∥ TV \|\cdot\|_{\mathrm{TV}} ∥ ⋅ ∥ start_POSTSUBSCRIPT roman_TV end_POSTSUBSCRIPT is defined as ( 18 ). Note that in definition ( 22 ) of the norm ‖ f μ ‖ ℬ 𝒩 subscript norm subscript 𝑓 𝜇 subscript ℬ 𝒩 \|f_{\mu}\|_{\mathcal{B}_{\mathcal{N}}} ∥ italic_f start_POSTSUBSCRIPT italic_μ end_POSTSUBSCRIPT ∥ start_POSTSUBSCRIPT caligraphic_B start_POSTSUBSCRIPT caligraphic_N end_POSTSUBSCRIPT end_POSTSUBSCRIPT , the infimum is taken over all the measures ν ∈ ℳ ⁢ ( Θ ) 𝜈 ℳ Θ \nu\in\mathcal{M}(\Theta) italic_ν ∈ caligraphic_M ( roman_Θ ) that satisfy t 𝑡 t italic_t equality constraints

In particular, in the case t = 1 𝑡 1 t=1 italic_t = 1 , where f μ subscript 𝑓 𝜇 f_{\mu} italic_f start_POSTSUBSCRIPT italic_μ end_POSTSUBSCRIPT reduces to a neural network of a scalar-valued output, the norm ‖ f μ ‖ ℬ 𝒩 subscript norm subscript 𝑓 𝜇 subscript ℬ 𝒩 \|f_{\mu}\|_{\mathcal{B}_{\mathcal{N}}} ∥ italic_f start_POSTSUBSCRIPT italic_μ end_POSTSUBSCRIPT ∥ start_POSTSUBSCRIPT caligraphic_B start_POSTSUBSCRIPT caligraphic_N end_POSTSUBSCRIPT end_POSTSUBSCRIPT is taken over the measures ν ∈ ℳ ⁢ ( Θ ) 𝜈 ℳ Θ \nu\in\mathcal{M}(\Theta) italic_ν ∈ caligraphic_M ( roman_Θ ) that satisfies only a single equality constraint. The bigger t 𝑡 t italic_t is, the larger the norm ‖ f μ ‖ ℬ 𝒩 subscript norm subscript 𝑓 𝜇 subscript ℬ 𝒩 \|f_{\mu}\|_{\mathcal{B}_{\mathcal{N}}} ∥ italic_f start_POSTSUBSCRIPT italic_μ end_POSTSUBSCRIPT ∥ start_POSTSUBSCRIPT caligraphic_B start_POSTSUBSCRIPT caligraphic_N end_POSTSUBSCRIPT end_POSTSUBSCRIPT will be. We remark that the special case of ℬ 𝒩 subscript ℬ 𝒩 \mathcal{B}_{\mathcal{N}} caligraphic_B start_POSTSUBSCRIPT caligraphic_N end_POSTSUBSCRIPT with 𝒩 𝒩 \mathcal{N} caligraphic_N being a scalar-valued neural network of a single hidden layer was recently studied in [ 2 ] .

𝑓 𝑀 𝑓 𝐵 B/M:=\{f+M:f\in B\} italic_B / italic_M := { italic_f + italic_M : italic_f ∈ italic_B } , with the quotient norm

It is known [ 15 ] that the quotient space B / M 𝐵 𝑀 B/M italic_B / italic_M is a Banach space. We say that a Banach space B 𝐵 B italic_B has a pre-dual space if there exists a Banach space B * subscript 𝐵 B_{*} italic_B start_POSTSUBSCRIPT * end_POSTSUBSCRIPT such that ( B * ) * = B superscript subscript 𝐵 𝐵 (B_{*})^{*}=B ( italic_B start_POSTSUBSCRIPT * end_POSTSUBSCRIPT ) start_POSTSUPERSCRIPT * end_POSTSUPERSCRIPT = italic_B and we call the space B * subscript 𝐵 B_{*} italic_B start_POSTSUBSCRIPT * end_POSTSUBSCRIPT a pre-dual space of B 𝐵 B italic_B . We also need the notion of annihilators. Let M 𝑀 M italic_M and M ′ superscript 𝑀 ′ M^{\prime} italic_M start_POSTSUPERSCRIPT ′ end_POSTSUPERSCRIPT be subsets of B 𝐵 B italic_B and B * superscript 𝐵 B^{*} italic_B start_POSTSUPERSCRIPT * end_POSTSUPERSCRIPT , respectively. The annihilator of M 𝑀 M italic_M in B * superscript 𝐵 B^{*} italic_B start_POSTSUPERSCRIPT * end_POSTSUPERSCRIPT is defined by

The annihilator of M ′ superscript 𝑀 ′ M^{\prime} italic_M start_POSTSUPERSCRIPT ′ end_POSTSUPERSCRIPT in B 𝐵 B italic_B is defined by

We review a result about the dual space of a closed subspace of a Banach space. Specifically, let M 𝑀 M italic_M be a closed subspace of a Banach space B 𝐵 B italic_B . For each ν ∈ B * 𝜈 superscript 𝐵 \nu\in B^{*} italic_ν ∈ italic_B start_POSTSUPERSCRIPT * end_POSTSUPERSCRIPT , we denote by ν | M evaluated-at 𝜈 𝑀 \nu|_{M} italic_ν | start_POSTSUBSCRIPT italic_M end_POSTSUBSCRIPT the restriction of ν 𝜈 \nu italic_ν to M 𝑀 M italic_M . It is clear that ν | M ∈ M * evaluated-at 𝜈 𝑀 superscript 𝑀 \nu|_{M}\in M^{*} italic_ν | start_POSTSUBSCRIPT italic_M end_POSTSUBSCRIPT ∈ italic_M start_POSTSUPERSCRIPT * end_POSTSUPERSCRIPT and ‖ ν | M ∥ M * ≤ ‖ ν ‖ B * evaluated-at subscript delimited-‖| 𝜈 𝑀 superscript 𝑀 subscript norm 𝜈 superscript 𝐵 \|\nu|_{M}\|_{M^{*}}\leq\|\nu\|_{B^{*}} ∥ italic_ν | start_POSTSUBSCRIPT italic_M end_POSTSUBSCRIPT ∥ start_POSTSUBSCRIPT italic_M start_POSTSUPERSCRIPT * end_POSTSUPERSCRIPT end_POSTSUBSCRIPT ≤ ∥ italic_ν ∥ start_POSTSUBSCRIPT italic_B start_POSTSUPERSCRIPT * end_POSTSUPERSCRIPT end_POSTSUBSCRIPT . The dual space M * superscript 𝑀 M^{*} italic_M start_POSTSUPERSCRIPT * end_POSTSUPERSCRIPT may be identified as B * / M ⟂ superscript 𝐵 superscript 𝑀 perpendicular-to B^{*}/M^{\perp} italic_B start_POSTSUPERSCRIPT * end_POSTSUPERSCRIPT / italic_M start_POSTSUPERSCRIPT ⟂ end_POSTSUPERSCRIPT . In fact, by Theorem 10.1 in Chapter III of [ 7 ] , the map τ : B * / M ⟂ → M * : 𝜏 → superscript 𝐵 superscript 𝑀 perpendicular-to superscript 𝑀 \tau:B^{*}/M^{\perp}\to M^{*} italic_τ : italic_B start_POSTSUPERSCRIPT * end_POSTSUPERSCRIPT / italic_M start_POSTSUPERSCRIPT ⟂ end_POSTSUPERSCRIPT → italic_M start_POSTSUPERSCRIPT * end_POSTSUPERSCRIPT defined by

is an isometric isomorphism between B * / M ⟂ superscript 𝐵 superscript 𝑀 perpendicular-to B^{*}/M^{\perp} italic_B start_POSTSUPERSCRIPT * end_POSTSUPERSCRIPT / italic_M start_POSTSUPERSCRIPT ⟂ end_POSTSUPERSCRIPT and M * superscript 𝑀 M^{*} italic_M start_POSTSUPERSCRIPT * end_POSTSUPERSCRIPT .

For the purpose of proving that ℬ 𝒩 subscript ℬ 𝒩 \mathcal{B}_{\mathcal{N}} caligraphic_B start_POSTSUBSCRIPT caligraphic_N end_POSTSUBSCRIPT is a Banach space, we identify the quotient space which is isometrically isomorphic to ℬ 𝒩 subscript ℬ 𝒩 \mathcal{B}_{\mathcal{N}} caligraphic_B start_POSTSUBSCRIPT caligraphic_N end_POSTSUBSCRIPT . To this end, we introduce a closed subspace of C 0 ⁢ ( Θ ) subscript 𝐶 0 Θ C_{0}(\Theta) italic_C start_POSTSUBSCRIPT 0 end_POSTSUBSCRIPT ( roman_Θ ) as

where the closure is taken in the maximum norm. From definition ( 23 ), it is clear that 𝒮 𝒮 \mathcal{S} caligraphic_S is a Banach space of functions defined on the parameter space Θ Θ \Theta roman_Θ .

Proposition 5 .

Let Θ normal-Θ \Theta roman_Θ be the parameter space defined by ( 4 ). If for each x ∈ ℝ s 𝑥 superscript ℝ 𝑠 x\in\mathbb{R}^{s} italic_x ∈ blackboard_R start_POSTSUPERSCRIPT italic_s end_POSTSUPERSCRIPT and k ∈ ℕ t 𝑘 subscript ℕ 𝑡 k\in\mathbb{N}_{t} italic_k ∈ blackboard_N start_POSTSUBSCRIPT italic_t end_POSTSUBSCRIPT , the function 𝒩 k ⁢ ( x , ⋅ ) ⁢ ρ ⁢ ( ⋅ ) ∈ C 0 ⁢ ( Θ ) subscript 𝒩 𝑘 𝑥 normal-⋅ 𝜌 normal-⋅ subscript 𝐶 0 normal-Θ \mathcal{N}_{k}({x},\cdot)\rho(\cdot)\in C_{0}(\Theta) caligraphic_N start_POSTSUBSCRIPT italic_k end_POSTSUBSCRIPT ( italic_x , ⋅ ) italic_ρ ( ⋅ ) ∈ italic_C start_POSTSUBSCRIPT 0 end_POSTSUBSCRIPT ( roman_Θ ) , then the space ℬ 𝒩 subscript ℬ 𝒩 \mathcal{B}_{\mathcal{N}} caligraphic_B start_POSTSUBSCRIPT caligraphic_N end_POSTSUBSCRIPT defined by ( 21 ) endowed with the norm ( 22 ) is a Banach space with a pre-dual space 𝒮 𝒮 \mathcal{S} caligraphic_S defined by ( 23 ).

We next let φ 𝜑 \varphi italic_φ be the map from ℬ 𝒩 subscript ℬ 𝒩 \mathcal{B}_{\mathcal{N}} caligraphic_B start_POSTSUBSCRIPT caligraphic_N end_POSTSUBSCRIPT to ℳ ⁢ ( Θ ) / 𝒮 ⟂ ℳ Θ superscript 𝒮 perpendicular-to \mathcal{M}(\Theta)/\mathcal{S}^{\perp} caligraphic_M ( roman_Θ ) / caligraphic_S start_POSTSUPERSCRIPT ⟂ end_POSTSUPERSCRIPT defined for f μ ∈ ℬ 𝒩 subscript 𝑓 𝜇 subscript ℬ 𝒩 f_{\mu}\in\mathcal{B}_{\mathcal{N}} italic_f start_POSTSUBSCRIPT italic_μ end_POSTSUBSCRIPT ∈ caligraphic_B start_POSTSUBSCRIPT caligraphic_N end_POSTSUBSCRIPT by

and show that φ 𝜑 \varphi italic_φ is an isometric isomorphism.

𝜇 superscript 𝜇 ′ \nu=\mu+\mu^{\prime} italic_ν = italic_μ + italic_μ start_POSTSUPERSCRIPT ′ end_POSTSUPERSCRIPT for some μ ′ ∈ 𝒮 ⟂ superscript 𝜇 ′ superscript 𝒮 perpendicular-to \mu^{\prime}\in\mathcal{S}^{\perp} italic_μ start_POSTSUPERSCRIPT ′ end_POSTSUPERSCRIPT ∈ caligraphic_S start_POSTSUPERSCRIPT ⟂ end_POSTSUPERSCRIPT . Hence, we get by definition ( 22 ) that

This together with the definition of the quotient norm yields that

which with ( 25 ) leads to ‖ φ ⁢ ( f μ ) ‖ ℳ ⁢ ( Θ ) / 𝒮 ⟂ = ‖ f μ ‖ ℬ 𝒩 subscript norm 𝜑 subscript 𝑓 𝜇 ℳ Θ superscript 𝒮 perpendicular-to subscript norm subscript 𝑓 𝜇 subscript ℬ 𝒩 \|\varphi(f_{\mu})\|_{\mathcal{M}(\Theta)/\mathcal{S}^{\perp}}=\|f_{\mu}\|_{% \mathcal{B}_{\mathcal{N}}} ∥ italic_φ ( italic_f start_POSTSUBSCRIPT italic_μ end_POSTSUBSCRIPT ) ∥ start_POSTSUBSCRIPT caligraphic_M ( roman_Θ ) / caligraphic_S start_POSTSUPERSCRIPT ⟂ end_POSTSUPERSCRIPT end_POSTSUBSCRIPT = ∥ italic_f start_POSTSUBSCRIPT italic_μ end_POSTSUBSCRIPT ∥ start_POSTSUBSCRIPT caligraphic_B start_POSTSUBSCRIPT caligraphic_N end_POSTSUBSCRIPT end_POSTSUBSCRIPT . In other words, φ 𝜑 \varphi italic_φ is an isometry. Due to its isometry property, φ 𝜑 \varphi italic_φ is injective. Clearly, φ 𝜑 \varphi italic_φ is surjective. Hence, it is bijective. Consequently, φ 𝜑 \varphi italic_φ is an isometric isomorphism from ℬ 𝒩 subscript ℬ 𝒩 \mathcal{B}_{\mathcal{N}} caligraphic_B start_POSTSUBSCRIPT caligraphic_N end_POSTSUBSCRIPT to the Banach space ℳ ⁢ ( Θ ) / 𝒮 ⟂ ℳ Θ superscript 𝒮 perpendicular-to \mathcal{M}(\Theta)/\mathcal{S}^{\perp} caligraphic_M ( roman_Θ ) / caligraphic_S start_POSTSUPERSCRIPT ⟂ end_POSTSUPERSCRIPT , and thus, ℬ 𝒩 subscript ℬ 𝒩 \mathcal{B}_{\mathcal{N}} caligraphic_B start_POSTSUBSCRIPT caligraphic_N end_POSTSUBSCRIPT is complete.

We now show that ℬ 𝒩 subscript ℬ 𝒩 \mathcal{B}_{\mathcal{N}} caligraphic_B start_POSTSUBSCRIPT caligraphic_N end_POSTSUBSCRIPT is isometrically isomorphic to the dual space of 𝒮 𝒮 \mathcal{S} caligraphic_S . Note that 𝒮 𝒮 \mathcal{S} caligraphic_S is a closed subspace of C 0 ⁢ ( Θ ) subscript 𝐶 0 Θ C_{0}(\Theta) italic_C start_POSTSUBSCRIPT 0 end_POSTSUBSCRIPT ( roman_Θ ) and ( C 0 ⁢ ( Θ ) ) * = ℳ ⁢ ( Θ ) superscript subscript 𝐶 0 Θ ℳ Θ (C_{0}(\Theta))^{*}=\mathcal{M}(\Theta) ( italic_C start_POSTSUBSCRIPT 0 end_POSTSUBSCRIPT ( roman_Θ ) ) start_POSTSUPERSCRIPT * end_POSTSUPERSCRIPT = caligraphic_M ( roman_Θ ) . By Theorem 10.1 in [ 7 ] with B := C 0 ⁢ ( Θ ) assign 𝐵 subscript 𝐶 0 Θ B:=C_{0}(\Theta) italic_B := italic_C start_POSTSUBSCRIPT 0 end_POSTSUBSCRIPT ( roman_Θ ) and M := 𝒮 assign 𝑀 𝒮 M:=\mathcal{S} italic_M := caligraphic_S , we have that the map τ : ℳ ⁢ ( Θ ) / 𝒮 ⟂ → 𝒮 * : 𝜏 → ℳ Θ superscript 𝒮 perpendicular-to superscript 𝒮 \tau:\mathcal{M}(\Theta)/\mathcal{S}^{\perp}\to\mathcal{S}^{*} italic_τ : caligraphic_M ( roman_Θ ) / caligraphic_S start_POSTSUPERSCRIPT ⟂ end_POSTSUPERSCRIPT → caligraphic_S start_POSTSUPERSCRIPT * end_POSTSUPERSCRIPT defined by

is an isometric isomorphism. As has been shown earlier, the map φ 𝜑 \varphi italic_φ defined by ( 25 ) is an isometric isomorphism from ℬ 𝒩 subscript ℬ 𝒩 \mathcal{B}_{\mathcal{N}} caligraphic_B start_POSTSUBSCRIPT caligraphic_N end_POSTSUBSCRIPT to ℳ ⁢ ( Θ ) / 𝒮 ⟂ ℳ Θ superscript 𝒮 perpendicular-to \mathcal{M}(\Theta)/\mathcal{S}^{\perp} caligraphic_M ( roman_Θ ) / caligraphic_S start_POSTSUPERSCRIPT ⟂ end_POSTSUPERSCRIPT . As a result, τ ∘ φ 𝜏 𝜑 \tau\circ\varphi italic_τ ∘ italic_φ provides an isometric isomorphism from ℬ 𝒩 subscript ℬ 𝒩 \mathcal{B}_{\mathcal{N}} caligraphic_B start_POSTSUBSCRIPT caligraphic_N end_POSTSUBSCRIPT to 𝒮 * superscript 𝒮 \mathcal{S}^{*} caligraphic_S start_POSTSUPERSCRIPT * end_POSTSUPERSCRIPT . ∎

Proposition 5 and the theorems that follow require that for each x ∈ ℝ s 𝑥 superscript ℝ 𝑠 x\in\mathbb{R}^{s} italic_x ∈ blackboard_R start_POSTSUPERSCRIPT italic_s end_POSTSUPERSCRIPT and k ∈ ℕ t 𝑘 subscript ℕ 𝑡 k\in\mathbb{N}_{t} italic_k ∈ blackboard_N start_POSTSUBSCRIPT italic_t end_POSTSUBSCRIPT , the function 𝒩 k ⁢ ( x , ⋅ ) ⁢ ρ ⁢ ( ⋅ ) subscript 𝒩 𝑘 𝑥 ⋅ 𝜌 ⋅ \mathcal{N}_{k}({x},\cdot)\rho(\cdot) caligraphic_N start_POSTSUBSCRIPT italic_k end_POSTSUBSCRIPT ( italic_x , ⋅ ) italic_ρ ( ⋅ ) belongs to C 0 ⁢ ( Θ ) subscript 𝐶 0 Θ C_{0}(\Theta) italic_C start_POSTSUBSCRIPT 0 end_POSTSUBSCRIPT ( roman_Θ ) . This requirement in fact imposes a hypothesis to the activation function σ 𝜎 \sigma italic_σ : (i) σ 𝜎 \sigma italic_σ is continuous and (ii) when the weight function ρ 𝜌 \rho italic_ρ is chosen as ( 17 ), we need to select the activation function σ 𝜎 \sigma italic_σ having a growth rate no greater than polynomials. We remark that many commonly used activation functions satisfy this requirement. They include the ReLU function

and the sigmoid function

Now that the space ℬ 𝒩 subscript ℬ 𝒩 \mathcal{B}_{\mathcal{N}} caligraphic_B start_POSTSUBSCRIPT caligraphic_N end_POSTSUBSCRIPT with the norm ∥ ⋅ ∥ ℬ 𝒩 \|\cdot\|_{\mathcal{B}_{\mathcal{N}}} ∥ ⋅ ∥ start_POSTSUBSCRIPT caligraphic_B start_POSTSUBSCRIPT caligraphic_N end_POSTSUBSCRIPT end_POSTSUBSCRIPT , guaranteed by Proposition 5 , is a Banach space, we denote by ℬ 𝒩 * superscript subscript ℬ 𝒩 \mathcal{B}_{\mathcal{N}}^{*} caligraphic_B start_POSTSUBSCRIPT caligraphic_N end_POSTSUBSCRIPT start_POSTSUPERSCRIPT * end_POSTSUPERSCRIPT the dual space of ℬ 𝒩 subscript ℬ 𝒩 \mathcal{B}_{\mathcal{N}} caligraphic_B start_POSTSUBSCRIPT caligraphic_N end_POSTSUBSCRIPT endowed with the norm

The dual space ℬ 𝒩 * superscript subscript ℬ 𝒩 \mathcal{B}_{\mathcal{N}}^{*} caligraphic_B start_POSTSUBSCRIPT caligraphic_N end_POSTSUBSCRIPT start_POSTSUPERSCRIPT * end_POSTSUPERSCRIPT is again a Banach space. Moreover, it follows from Proposition 5 that the space 𝒮 𝒮 \mathcal{S} caligraphic_S is a pre-dual space of ℬ 𝒩 subscript ℬ 𝒩 \mathcal{B}_{\mathcal{N}} caligraphic_B start_POSTSUBSCRIPT caligraphic_N end_POSTSUBSCRIPT , that is, ( ℬ 𝒩 ) * = 𝒮 . subscript subscript ℬ 𝒩 𝒮 (\mathcal{B}_{\mathcal{N}})_{*}=\mathcal{S}. ( caligraphic_B start_POSTSUBSCRIPT caligraphic_N end_POSTSUBSCRIPT ) start_POSTSUBSCRIPT * end_POSTSUBSCRIPT = caligraphic_S . We remark that the dual bilinear form on ℬ 𝒩 × 𝒮 subscript ℬ 𝒩 𝒮 \mathcal{B}_{\mathcal{N}}\times\mathcal{S} caligraphic_B start_POSTSUBSCRIPT caligraphic_N end_POSTSUBSCRIPT × caligraphic_S is given by

According to Proposition 5 , the space 𝒮 𝒮 \mathcal{S} caligraphic_S is the pre-dual space of ℬ 𝒩 subscript ℬ 𝒩 \mathcal{B}_{\mathcal{N}} caligraphic_B start_POSTSUBSCRIPT caligraphic_N end_POSTSUBSCRIPT , that is, 𝒮 * = ℬ 𝒩 superscript 𝒮 subscript ℬ 𝒩 \mathcal{S}^{*}=\mathcal{B}_{\mathcal{N}} caligraphic_S start_POSTSUPERSCRIPT * end_POSTSUPERSCRIPT = caligraphic_B start_POSTSUBSCRIPT caligraphic_N end_POSTSUBSCRIPT . Thus, we obtain that 𝒮 * * = ℬ 𝒩 * superscript 𝒮 absent superscript subscript ℬ 𝒩 \mathcal{S}^{**}=\mathcal{B}_{\mathcal{N}}^{*} caligraphic_S start_POSTSUPERSCRIPT * * end_POSTSUPERSCRIPT = caligraphic_B start_POSTSUBSCRIPT caligraphic_N end_POSTSUBSCRIPT start_POSTSUPERSCRIPT * end_POSTSUPERSCRIPT . It is well-known (for example, see [ 7 ] ) that 𝒮 ⊆ 𝒮 * * 𝒮 superscript 𝒮 absent \mathcal{S}\subseteq\mathcal{S}^{**} caligraphic_S ⊆ caligraphic_S start_POSTSUPERSCRIPT * * end_POSTSUPERSCRIPT in the sense of isometric embedding. Hence, 𝒮 ⊆ ℬ 𝒩 * 𝒮 superscript subscript ℬ 𝒩 \mathcal{S}\subseteq\mathcal{B}_{\mathcal{N}}^{*} caligraphic_S ⊆ caligraphic_B start_POSTSUBSCRIPT caligraphic_N end_POSTSUBSCRIPT start_POSTSUPERSCRIPT * end_POSTSUPERSCRIPT and there holds

We now turn to establishing that ℬ 𝒩 subscript ℬ 𝒩 \mathcal{B}_{\mathcal{N}} caligraphic_B start_POSTSUBSCRIPT caligraphic_N end_POSTSUBSCRIPT is a vector-valued RKBS on ℝ s superscript ℝ 𝑠 \mathbb{R}^{s} blackboard_R start_POSTSUPERSCRIPT italic_s end_POSTSUPERSCRIPT .

Theorem 6 .

Let Θ normal-Θ \Theta roman_Θ be the parameter space defined by ( 4 ). If for each x ∈ ℝ s 𝑥 superscript ℝ 𝑠 x\in\mathbb{R}^{s} italic_x ∈ blackboard_R start_POSTSUPERSCRIPT italic_s end_POSTSUPERSCRIPT and k ∈ ℕ t 𝑘 subscript ℕ 𝑡 k\in\mathbb{N}_{t} italic_k ∈ blackboard_N start_POSTSUBSCRIPT italic_t end_POSTSUBSCRIPT , the function 𝒩 k ⁢ ( x , ⋅ ) ⁢ ρ ⁢ ( ⋅ ) subscript 𝒩 𝑘 𝑥 normal-⋅ 𝜌 normal-⋅ \mathcal{N}_{k}({x},\cdot)\rho(\cdot) caligraphic_N start_POSTSUBSCRIPT italic_k end_POSTSUBSCRIPT ( italic_x , ⋅ ) italic_ρ ( ⋅ ) belongs to C 0 ⁢ ( Θ ) subscript 𝐶 0 normal-Θ C_{0}(\Theta) italic_C start_POSTSUBSCRIPT 0 end_POSTSUBSCRIPT ( roman_Θ ) , then the Banach space ℬ 𝒩 subscript ℬ 𝒩 \mathcal{B}_{\mathcal{N}} caligraphic_B start_POSTSUBSCRIPT caligraphic_N end_POSTSUBSCRIPT defined by ( 21 ) endowed with the norm ( 22 ) is a vector-valued RKBS on ℝ s superscript ℝ 𝑠 \mathbb{R}^{s} blackboard_R start_POSTSUPERSCRIPT italic_s end_POSTSUPERSCRIPT .

To this end, for any f μ ∈ ℬ 𝒩 subscript 𝑓 𝜇 subscript ℬ 𝒩 f_{\mu}\in\mathcal{B}_{\mathcal{N}} italic_f start_POSTSUBSCRIPT italic_μ end_POSTSUBSCRIPT ∈ caligraphic_B start_POSTSUBSCRIPT caligraphic_N end_POSTSUBSCRIPT , we obtain from definition ( 20 ) of f μ k superscript subscript 𝑓 𝜇 𝑘 f_{\mu}^{k} italic_f start_POSTSUBSCRIPT italic_μ end_POSTSUBSCRIPT start_POSTSUPERSCRIPT italic_k end_POSTSUPERSCRIPT that

for any ν ∈ ℳ ⁢ ( Θ ) 𝜈 ℳ Θ \nu\in\mathcal{M}(\Theta) italic_ν ∈ caligraphic_M ( roman_Θ ) satisfying f ν = f μ subscript 𝑓 𝜈 subscript 𝑓 𝜇 f_{\nu}=f_{\mu} italic_f start_POSTSUBSCRIPT italic_ν end_POSTSUBSCRIPT = italic_f start_POSTSUBSCRIPT italic_μ end_POSTSUBSCRIPT . By taking infimum of both sides of inequality ( 30 ) over ν ∈ ℳ ⁢ ( Θ ) 𝜈 ℳ Θ \nu\in\mathcal{M}(\Theta) italic_ν ∈ caligraphic_M ( roman_Θ ) satisfying f ν = f μ subscript 𝑓 𝜈 subscript 𝑓 𝜇 f_{\nu}=f_{\mu} italic_f start_POSTSUBSCRIPT italic_ν end_POSTSUBSCRIPT = italic_f start_POSTSUBSCRIPT italic_μ end_POSTSUBSCRIPT and employing definition ( 22 ), we obtain that

Next, we identify the reproducing kernel of the vector-valued RKBS ℬ 𝒩 subscript ℬ 𝒩 \mathcal{B}_{\mathcal{N}} caligraphic_B start_POSTSUBSCRIPT caligraphic_N end_POSTSUBSCRIPT . According to Proposition 4 , the existence of the reproducing kernel requires to characterize the δ 𝛿 \delta italic_δ -dual space of ℬ 𝒩 subscript ℬ 𝒩 \mathcal{B}_{\mathcal{N}} caligraphic_B start_POSTSUBSCRIPT caligraphic_N end_POSTSUBSCRIPT . We note that the δ 𝛿 \delta italic_δ -dual space ℬ 𝒩 ′ subscript superscript ℬ ′ 𝒩 \mathcal{B}^{\prime}_{\mathcal{N}} caligraphic_B start_POSTSUPERSCRIPT ′ end_POSTSUPERSCRIPT start_POSTSUBSCRIPT caligraphic_N end_POSTSUBSCRIPT is the closure of

in the norm topology ( 26 ) of ℬ 𝒩 * superscript subscript ℬ 𝒩 \mathcal{B}_{\mathcal{N}}^{*} caligraphic_B start_POSTSUBSCRIPT caligraphic_N end_POSTSUBSCRIPT start_POSTSUPERSCRIPT * end_POSTSUPERSCRIPT . We will show that Δ Δ \Delta roman_Δ is isometrically isomorphic to

a subspace of 𝒮 𝒮 \mathcal{S} caligraphic_S . To this end, we introduce a mapping Ψ : Δ → 𝕊 : Ψ → Δ 𝕊 \Psi:\Delta\to\mathbb{S} roman_Ψ : roman_Δ → blackboard_S by

for all m ∈ ℕ 𝑚 ℕ m\in\mathbb{N} italic_m ∈ blackboard_N , α j ∈ ℝ subscript 𝛼 𝑗 ℝ \alpha_{j}\in\mathbb{R} italic_α start_POSTSUBSCRIPT italic_j end_POSTSUBSCRIPT ∈ blackboard_R , x j ∈ ℝ s subscript 𝑥 𝑗 superscript ℝ 𝑠 {x}_{j}\in\mathbb{R}^{s} italic_x start_POSTSUBSCRIPT italic_j end_POSTSUBSCRIPT ∈ blackboard_R start_POSTSUPERSCRIPT italic_s end_POSTSUPERSCRIPT , k j ∈ ℕ t subscript 𝑘 𝑗 subscript ℕ 𝑡 k_{j}\in\mathbb{N}_{t} italic_k start_POSTSUBSCRIPT italic_j end_POSTSUBSCRIPT ∈ blackboard_N start_POSTSUBSCRIPT italic_t end_POSTSUBSCRIPT , and j ∈ ℕ m 𝑗 subscript ℕ 𝑚 j\in\mathbb{N}_{m} italic_j ∈ blackboard_N start_POSTSUBSCRIPT italic_m end_POSTSUBSCRIPT .

The map Ψ normal-Ψ \Psi roman_Ψ defined by ( 31 ) is an isometric isomorphism between Δ normal-Δ \Delta roman_Δ and 𝕊 𝕊 \mathbb{S} blackboard_S .

We next compute ‖ Ψ ⁢ ( ℓ ) ‖ ∞ subscript norm Ψ ℓ \|\Psi(\ell)\|_{\infty} ∥ roman_Ψ ( roman_ℓ ) ∥ start_POSTSUBSCRIPT ∞ end_POSTSUBSCRIPT . By noting that Ψ ⁢ ( ℓ ) ∈ 𝒮 Ψ ℓ 𝒮 \Psi(\ell)\in\mathcal{S} roman_Ψ ( roman_ℓ ) ∈ caligraphic_S and 𝒮 * = ℬ 𝒩 superscript 𝒮 subscript ℬ 𝒩 \mathcal{S}^{*}=\mathcal{B}_{\mathcal{N}} caligraphic_S start_POSTSUPERSCRIPT * end_POSTSUPERSCRIPT = caligraphic_B start_POSTSUBSCRIPT caligraphic_N end_POSTSUBSCRIPT , we have that

Substituting equation ( 27 ) with g := Ψ ⁢ ( ℓ ) assign 𝑔 Ψ ℓ g:=\Psi(\ell) italic_g := roman_Ψ ( roman_ℓ ) into the right hand side of the above equation, we get that

According to definition ( 31 ) of Ψ Ψ \Psi roman_Ψ , there holds for any f μ ∈ ℬ 𝒩 subscript 𝑓 𝜇 subscript ℬ 𝒩 f_{\mu}\in\mathcal{B}_{\mathcal{N}} italic_f start_POSTSUBSCRIPT italic_μ end_POSTSUBSCRIPT ∈ caligraphic_B start_POSTSUBSCRIPT caligraphic_N end_POSTSUBSCRIPT that

Comparing ( 32 ) and ( 34 ), we obtain that ‖ ℓ ‖ ℬ 𝒩 * = ‖ Ψ ⁢ ( ℓ ) ‖ ∞ subscript norm ℓ superscript subscript ℬ 𝒩 subscript norm Ψ ℓ \|\ell\|_{\mathcal{B}_{\mathcal{N}}^{*}}=\|\Psi(\ell)\|_{\infty} ∥ roman_ℓ ∥ start_POSTSUBSCRIPT caligraphic_B start_POSTSUBSCRIPT caligraphic_N end_POSTSUBSCRIPT start_POSTSUPERSCRIPT * end_POSTSUPERSCRIPT end_POSTSUBSCRIPT = ∥ roman_Ψ ( roman_ℓ ) ∥ start_POSTSUBSCRIPT ∞ end_POSTSUBSCRIPT and hence, Ψ Ψ \Psi roman_Ψ is an isometry between Δ Δ \Delta roman_Δ and 𝕊 𝕊 \mathbb{S} blackboard_S . The isometry of Ψ Ψ \Psi roman_Ψ further implies its injectivity. Moreover, Ψ Ψ \Psi roman_Ψ is linear and surjective. Thus, Ψ Ψ \Psi roman_Ψ is bijective. Therefore, Ψ Ψ \Psi roman_Ψ is an isometric isomorphism between Δ Δ \Delta roman_Δ and 𝕊 𝕊 \mathbb{S} blackboard_S . ∎

The isometrically isomorphic relation between Δ Δ \Delta roman_Δ and 𝕊 𝕊 \mathbb{S} blackboard_S is preserved after completing them. We state this result in the following lemma without proof.

Suppose that A 𝐴 A italic_A and B 𝐵 B italic_B are Banach spaces with norms ∥ ⋅ ∥ A \|\cdot\|_{A} ∥ ⋅ ∥ start_POSTSUBSCRIPT italic_A end_POSTSUBSCRIPT and ∥ ⋅ ∥ B \|\cdot\|_{B} ∥ ⋅ ∥ start_POSTSUBSCRIPT italic_B end_POSTSUBSCRIPT , respectively. Let A 0 subscript 𝐴 0 A_{0} italic_A start_POSTSUBSCRIPT 0 end_POSTSUBSCRIPT and B 0 subscript 𝐵 0 B_{0} italic_B start_POSTSUBSCRIPT 0 end_POSTSUBSCRIPT be dense subsets of A 𝐴 A italic_A and B 𝐵 B italic_B , respectively. If A 0 subscript 𝐴 0 A_{0} italic_A start_POSTSUBSCRIPT 0 end_POSTSUBSCRIPT is isometrically isomorphic to B 0 subscript 𝐵 0 B_{0} italic_B start_POSTSUBSCRIPT 0 end_POSTSUBSCRIPT , then A 𝐴 A italic_A is isometrically isomorphic to B 𝐵 B italic_B .

Lemma 8 may be obtained by applying Theorem 1.6-2 in [ 12 ] . With the help of Lemmas 7 and 8 , we identify in the following theorem the reproducing kernel for the RKBS ℬ 𝒩 subscript ℬ 𝒩 \mathcal{B}_{\mathcal{N}} caligraphic_B start_POSTSUBSCRIPT caligraphic_N end_POSTSUBSCRIPT .

Theorem 9 .

Let Θ normal-Θ \Theta roman_Θ be the parameter space defined by ( 4 ). Suppose that for each x ∈ ℝ s 𝑥 superscript ℝ 𝑠 x\in\mathbb{R}^{s} italic_x ∈ blackboard_R start_POSTSUPERSCRIPT italic_s end_POSTSUPERSCRIPT and k ∈ ℕ t 𝑘 subscript ℕ 𝑡 k\in\mathbb{N}_{t} italic_k ∈ blackboard_N start_POSTSUBSCRIPT italic_t end_POSTSUBSCRIPT , the function 𝒩 k ⁢ ( x , ⋅ ) ⁢ ρ ⁢ ( ⋅ ) subscript 𝒩 𝑘 𝑥 normal-⋅ 𝜌 normal-⋅ \mathcal{N}_{k}({x},\cdot)\rho(\cdot) caligraphic_N start_POSTSUBSCRIPT italic_k end_POSTSUBSCRIPT ( italic_x , ⋅ ) italic_ρ ( ⋅ ) belongs to C 0 ⁢ ( Θ ) subscript 𝐶 0 normal-Θ C_{0}(\Theta) italic_C start_POSTSUBSCRIPT 0 end_POSTSUBSCRIPT ( roman_Θ ) . If the vector-valued RKBS ℬ 𝒩 subscript ℬ 𝒩 \mathcal{B}_{\mathcal{N}} caligraphic_B start_POSTSUBSCRIPT caligraphic_N end_POSTSUBSCRIPT is defined by ( 21 ) with the norm ( 22 ), then the vector-valued function

is the reproducing kernel for space ℬ 𝒩 subscript ℬ 𝒩 \mathcal{B}_{\mathcal{N}} caligraphic_B start_POSTSUBSCRIPT caligraphic_N end_POSTSUBSCRIPT .

We employ Proposition 4 with X := ℝ s assign 𝑋 superscript ℝ 𝑠 X:=\mathbb{R}^{s} italic_X := blackboard_R start_POSTSUPERSCRIPT italic_s end_POSTSUPERSCRIPT and X ′ := Θ assign superscript 𝑋 ′ Θ X^{\prime}:=\Theta italic_X start_POSTSUPERSCRIPT ′ end_POSTSUPERSCRIPT := roman_Θ to establish that the function 𝒦 𝒦 \mathcal{K} caligraphic_K defined by ( 35 ) is the reproducing kernel of space ℬ 𝒩 subscript ℬ 𝒩 \mathcal{B}_{\mathcal{N}} caligraphic_B start_POSTSUBSCRIPT caligraphic_N end_POSTSUBSCRIPT . According to Lemma 7 , Δ Δ \Delta roman_Δ is isometrically isomorphic to 𝕊 𝕊 \mathbb{S} blackboard_S . Since ℬ 𝒩 ′ superscript subscript ℬ 𝒩 ′ \mathcal{B}_{\mathcal{N}}^{\prime} caligraphic_B start_POSTSUBSCRIPT caligraphic_N end_POSTSUBSCRIPT start_POSTSUPERSCRIPT ′ end_POSTSUPERSCRIPT and 𝒮 𝒮 \mathcal{S} caligraphic_S are the completion of Δ Δ \Delta roman_Δ and 𝕊 𝕊 \mathbb{S} blackboard_S , respectively, by Lemma 8 , we conclude that the δ 𝛿 \delta italic_δ -dual space ℬ 𝒩 ′ subscript superscript ℬ ′ 𝒩 \mathcal{B}^{\prime}_{\mathcal{N}} caligraphic_B start_POSTSUPERSCRIPT ′ end_POSTSUPERSCRIPT start_POSTSUBSCRIPT caligraphic_N end_POSTSUBSCRIPT of ℬ 𝒩 subscript ℬ 𝒩 \mathcal{B}_{\mathcal{N}} caligraphic_B start_POSTSUBSCRIPT caligraphic_N end_POSTSUBSCRIPT is isometrically isomorphic to 𝒮 𝒮 \mathcal{S} caligraphic_S , which is a Banach space of functions from Θ Θ \Theta roman_Θ to ℝ ℝ \mathbb{R} blackboard_R . Hence, Proposition 4 ensures that there exists a unique reproducing kernel for ℬ 𝒩 subscript ℬ 𝒩 \mathcal{B}_{\mathcal{N}} caligraphic_B start_POSTSUBSCRIPT caligraphic_N end_POSTSUBSCRIPT .

We next verify that the vector-valued function 𝒦 𝒦 \mathcal{K} caligraphic_K defined by ( 35 ) is the reproducing kernel for ℬ 𝒩 subscript ℬ 𝒩 \mathcal{B}_{\mathcal{N}} caligraphic_B start_POSTSUBSCRIPT caligraphic_N end_POSTSUBSCRIPT . By noting that the δ 𝛿 \delta italic_δ -dual space ℬ 𝒩 ′ subscript superscript ℬ ′ 𝒩 \mathcal{B}^{\prime}_{\mathcal{N}} caligraphic_B start_POSTSUPERSCRIPT ′ end_POSTSUPERSCRIPT start_POSTSUBSCRIPT caligraphic_N end_POSTSUBSCRIPT is isometrically isomorphic to 𝒮 𝒮 \mathcal{S} caligraphic_S , we have for each x ∈ ℝ s 𝑥 superscript ℝ 𝑠 x\in\mathbb{R}^{s} italic_x ∈ blackboard_R start_POSTSUPERSCRIPT italic_s end_POSTSUPERSCRIPT and each k ∈ ℕ t 𝑘 subscript ℕ 𝑡 k\in\mathbb{N}_{t} italic_k ∈ blackboard_N start_POSTSUBSCRIPT italic_t end_POSTSUBSCRIPT that 𝒦 k ⁢ ( x , ⋅ ) := 𝒩 k ⁢ ( x , ⋅ ) ⁢ ρ ⁢ ( ⋅ ) ∈ ℬ 𝒩 ′ assign subscript 𝒦 𝑘 𝑥 ⋅ subscript 𝒩 𝑘 𝑥 ⋅ 𝜌 ⋅ superscript subscript ℬ 𝒩 ′ \mathcal{K}_{k}(x,\cdot):=\mathcal{N}_{k}(x,\cdot)\rho(\cdot)\in\mathcal{B}_{% \mathcal{N}}^{\prime} caligraphic_K start_POSTSUBSCRIPT italic_k end_POSTSUBSCRIPT ( italic_x , ⋅ ) := caligraphic_N start_POSTSUBSCRIPT italic_k end_POSTSUBSCRIPT ( italic_x , ⋅ ) italic_ρ ( ⋅ ) ∈ caligraphic_B start_POSTSUBSCRIPT caligraphic_N end_POSTSUBSCRIPT start_POSTSUPERSCRIPT ′ end_POSTSUPERSCRIPT . The space 𝒮 𝒮 \mathcal{S} caligraphic_S , guaranteed by Proposition 5 , is a pre-dual space of ℬ 𝒩 subscript ℬ 𝒩 \mathcal{B}_{\mathcal{N}} caligraphic_B start_POSTSUBSCRIPT caligraphic_N end_POSTSUBSCRIPT . Hence, by equation ( 28 ) with g := 𝒦 k ⁢ ( x , ⋅ ) assign 𝑔 subscript 𝒦 𝑘 𝑥 ⋅ g:=\mathcal{K}_{k}(x,\cdot) italic_g := caligraphic_K start_POSTSUBSCRIPT italic_k end_POSTSUBSCRIPT ( italic_x , ⋅ ) , we obtain for each x ∈ ℝ s 𝑥 superscript ℝ 𝑠 x\in\mathbb{R}^{s} italic_x ∈ blackboard_R start_POSTSUPERSCRIPT italic_s end_POSTSUPERSCRIPT , k ∈ ℕ t 𝑘 subscript ℕ 𝑡 k\in\mathbb{N}_{t} italic_k ∈ blackboard_N start_POSTSUBSCRIPT italic_t end_POSTSUBSCRIPT that

Substituting equation ( 27 ) with g := 𝒦 k ⁢ ( x , ⋅ ) assign 𝑔 subscript 𝒦 𝑘 𝑥 ⋅ g:=\mathcal{K}_{k}(x,\cdot) italic_g := caligraphic_K start_POSTSUBSCRIPT italic_k end_POSTSUBSCRIPT ( italic_x , ⋅ ) into the right-hand side of the above equation leads to

This together with definitions ( 19 ), ( 35 ) and ( 20 ) implies the reproducing property

Consequently, 𝒦 𝒦 \mathcal{K} caligraphic_K is the reproducing kernel of ℬ 𝒩 subscript ℬ 𝒩 \mathcal{B}_{\mathcal{N}} caligraphic_B start_POSTSUBSCRIPT caligraphic_N end_POSTSUBSCRIPT . ∎

The reproducing kernel defined by ( 35 ) in Theorem 9 is an asymmetric kernel, unlike a reproducing kernel in a reproducing kernel Hilbert space, which is always symmetric. It is the asymmetry of the “kernel” that allows us to encode one variable of the kernel function as the physical variable and one as the parameter variable. Theorem 9 restricted to the shallow network is still new to our best acknowledge. We will show in the next section a solution of a deep learning model may be expressed as a combination of a finite number of kernel sessions, a kernel with the parameter variable evaluated at a point of the parameter space determined by given data.

Theorem 10 .

Let Θ normal-Θ \Theta roman_Θ be the parameter space defined by ( 4 ) and 𝕎 𝕎 \mathbb{W} blackboard_W the width set defined by ( 2 ). If for each x ∈ ℝ s 𝑥 superscript ℝ 𝑠 x\in\mathbb{R}^{s} italic_x ∈ blackboard_R start_POSTSUPERSCRIPT italic_s end_POSTSUPERSCRIPT and k ∈ ℕ t 𝑘 subscript ℕ 𝑡 k\in\mathbb{N}_{t} italic_k ∈ blackboard_N start_POSTSUBSCRIPT italic_t end_POSTSUBSCRIPT , the function 𝒩 k ⁢ ( x , ⋅ ) ⁢ ρ ⁢ ( ⋅ ) subscript 𝒩 𝑘 𝑥 normal-⋅ 𝜌 normal-⋅ \mathcal{N}_{k}({x},\cdot)\rho(\cdot) caligraphic_N start_POSTSUBSCRIPT italic_k end_POSTSUBSCRIPT ( italic_x , ⋅ ) italic_ρ ( ⋅ ) belongs to C 0 ⁢ ( Θ ) subscript 𝐶 0 normal-Θ C_{0}(\Theta) italic_C start_POSTSUBSCRIPT 0 end_POSTSUBSCRIPT ( roman_Θ ) , then ℬ 𝕎 subscript ℬ 𝕎 \mathcal{B}_{\mathbb{W}} caligraphic_B start_POSTSUBSCRIPT blackboard_W end_POSTSUBSCRIPT is a subspace of ℬ 𝒩 subscript ℬ 𝒩 \mathcal{B}_{\mathcal{N}} caligraphic_B start_POSTSUBSCRIPT caligraphic_N end_POSTSUBSCRIPT and

It has been shown in Proposition 1 that ℬ 𝕎 subscript ℬ 𝕎 \mathcal{B}_{\mathbb{W}} caligraphic_B start_POSTSUBSCRIPT blackboard_W end_POSTSUBSCRIPT is a vector space. We now show that ℬ 𝕎 subscript ℬ 𝕎 \mathcal{B}_{\mathbb{W}} caligraphic_B start_POSTSUBSCRIPT blackboard_W end_POSTSUBSCRIPT is a subspace of ℬ 𝒩 subscript ℬ 𝒩 \mathcal{B}_{\mathcal{N}} caligraphic_B start_POSTSUBSCRIPT caligraphic_N end_POSTSUBSCRIPT . For any f ∈ ℬ 𝕎 𝑓 subscript ℬ 𝕎 f\in{{{\mathcal{B}_{\mathbb{W}}}}} italic_f ∈ caligraphic_B start_POSTSUBSCRIPT blackboard_W end_POSTSUBSCRIPT , there exist n ∈ ℕ 𝑛 ℕ n\in\mathbb{N} italic_n ∈ blackboard_N , c l ∈ ℝ subscript 𝑐 𝑙 ℝ c_{l}\in\mathbb{R} italic_c start_POSTSUBSCRIPT italic_l end_POSTSUBSCRIPT ∈ blackboard_R , θ l ∈ Θ subscript 𝜃 𝑙 Θ \theta_{l}\in\Theta italic_θ start_POSTSUBSCRIPT italic_l end_POSTSUBSCRIPT ∈ roman_Θ , l ∈ ℕ n 𝑙 subscript ℕ 𝑛 l\in\mathbb{N}_{n} italic_l ∈ blackboard_N start_POSTSUBSCRIPT italic_n end_POSTSUBSCRIPT such that f = ∑ l = 1 n c l ⁢ 𝒩 ⁢ ( ⋅ , θ l ) ⁢ ρ ⁢ ( θ l ) 𝑓 superscript subscript 𝑙 1 𝑛 subscript 𝑐 𝑙 𝒩 ⋅ subscript 𝜃 𝑙 𝜌 subscript 𝜃 𝑙 f=\sum_{l=1}^{n}c_{l}\mathcal{N}(\cdot,\theta_{l})\rho(\theta_{l}) italic_f = ∑ start_POSTSUBSCRIPT italic_l = 1 end_POSTSUBSCRIPT start_POSTSUPERSCRIPT italic_n end_POSTSUPERSCRIPT italic_c start_POSTSUBSCRIPT italic_l end_POSTSUBSCRIPT caligraphic_N ( ⋅ , italic_θ start_POSTSUBSCRIPT italic_l end_POSTSUBSCRIPT ) italic_ρ ( italic_θ start_POSTSUBSCRIPT italic_l end_POSTSUBSCRIPT ) . By choosing μ := ∑ l = 1 n c l ⁢ δ θ l assign 𝜇 superscript subscript 𝑙 1 𝑛 subscript 𝑐 𝑙 subscript 𝛿 subscript 𝜃 𝑙 \mu:=\sum_{l=1}^{n}c_{l}\delta_{\theta_{l}} italic_μ := ∑ start_POSTSUBSCRIPT italic_l = 1 end_POSTSUBSCRIPT start_POSTSUPERSCRIPT italic_n end_POSTSUPERSCRIPT italic_c start_POSTSUBSCRIPT italic_l end_POSTSUBSCRIPT italic_δ start_POSTSUBSCRIPT italic_θ start_POSTSUBSCRIPT italic_l end_POSTSUBSCRIPT end_POSTSUBSCRIPT , we have that μ ∈ ℳ ⁢ ( Θ ) 𝜇 ℳ Θ \mu\in\mathcal{M}(\Theta) italic_μ ∈ caligraphic_M ( roman_Θ ) . We then obtain from definition ( 20 ) that

This together with the representation of f 𝑓 f italic_f yields that f = f μ 𝑓 subscript 𝑓 𝜇 f=f_{\mu} italic_f = italic_f start_POSTSUBSCRIPT italic_μ end_POSTSUBSCRIPT and thus, f ∈ ℬ 𝒩 𝑓 subscript ℬ 𝒩 f\in\mathcal{B}_{\mathcal{N}} italic_f ∈ caligraphic_B start_POSTSUBSCRIPT caligraphic_N end_POSTSUBSCRIPT . Consequently, we have that ℬ 𝕎 ⊆ ℬ 𝒩 subscript ℬ 𝕎 subscript ℬ 𝒩 \mathcal{B}_{\mathbb{W}}\subseteq\mathcal{B}_{\mathcal{N}} caligraphic_B start_POSTSUBSCRIPT blackboard_W end_POSTSUBSCRIPT ⊆ caligraphic_B start_POSTSUBSCRIPT caligraphic_N end_POSTSUBSCRIPT .

It remains to prove equation ( 37 ). Proposition 5 ensures that 𝒮 * = ℬ 𝒩 superscript 𝒮 subscript ℬ 𝒩 \mathcal{S}^{*}=\mathcal{B}_{\mathcal{N}} caligraphic_S start_POSTSUPERSCRIPT * end_POSTSUPERSCRIPT = caligraphic_B start_POSTSUBSCRIPT caligraphic_N end_POSTSUBSCRIPT , in the sense of being isometrically isomorphic. Hence, ℬ 𝕎 subscript ℬ 𝕎 \mathcal{B}_{\mathbb{W}} caligraphic_B start_POSTSUBSCRIPT blackboard_W end_POSTSUBSCRIPT is a subspace of the dual space of 𝒮 𝒮 \mathcal{S} caligraphic_S . It follows from Proposition 2.6.6 of [ 15 ] that ( ⟂ ℬ 𝕎 ) ⟂ = ℬ 𝕎 ¯ w * (^{\perp}\mathcal{B}_{\mathbb{W}})^{\perp}=\overline{\mathcal{B}_{\mathbb{W}}}% ^{w^{*}} ( start_POSTSUPERSCRIPT ⟂ end_POSTSUPERSCRIPT caligraphic_B start_POSTSUBSCRIPT blackboard_W end_POSTSUBSCRIPT ) start_POSTSUPERSCRIPT ⟂ end_POSTSUPERSCRIPT = over¯ start_ARG caligraphic_B start_POSTSUBSCRIPT blackboard_W end_POSTSUBSCRIPT end_ARG start_POSTSUPERSCRIPT italic_w start_POSTSUPERSCRIPT * end_POSTSUPERSCRIPT end_POSTSUPERSCRIPT . It suffices to verify that ( ⟂ ℬ 𝕎 ) ⟂ = ℬ 𝒩 (^{\perp}\mathcal{B}_{\mathbb{W}})^{\perp}=\mathcal{B}_{\mathcal{N}} ( start_POSTSUPERSCRIPT ⟂ end_POSTSUPERSCRIPT caligraphic_B start_POSTSUBSCRIPT blackboard_W end_POSTSUBSCRIPT ) start_POSTSUPERSCRIPT ⟂ end_POSTSUPERSCRIPT = caligraphic_B start_POSTSUBSCRIPT caligraphic_N end_POSTSUBSCRIPT . Due to definition ( 9 ) of ℬ 𝕎 subscript ℬ 𝕎 \mathcal{B}_{\mathbb{W}} caligraphic_B start_POSTSUBSCRIPT blackboard_W end_POSTSUBSCRIPT , g ∈ ⟂ ℬ 𝕎 superscript perpendicular-to 𝑔 subscript ℬ 𝕎 g\in^{\perp}\mathcal{B}_{\mathbb{W}} italic_g ∈ start_POSTSUPERSCRIPT ⟂ end_POSTSUPERSCRIPT caligraphic_B start_POSTSUBSCRIPT blackboard_W end_POSTSUBSCRIPT if and only if

To close this section, we summarize the properties of the space ℬ 𝒩 subscript ℬ 𝒩 \mathcal{B}_{\mathcal{N}} caligraphic_B start_POSTSUBSCRIPT caligraphic_N end_POSTSUBSCRIPT established in Theorems 6 , 9 and 10 as follows:

(i) The space ℬ 𝒩 subscript ℬ 𝒩 \mathcal{B}_{\mathcal{N}} caligraphic_B start_POSTSUBSCRIPT caligraphic_N end_POSTSUBSCRIPT is a vector-valued RKBS.

(ii) The vector-valued function 𝒦 𝒦 \mathcal{K} caligraphic_K defined by ( 35 ) is the reproducing kernel for space ℬ 𝒩 subscript ℬ 𝒩 \mathcal{B}_{\mathcal{N}} caligraphic_B start_POSTSUBSCRIPT caligraphic_N end_POSTSUBSCRIPT .

(iii) The space ℬ 𝒩 subscript ℬ 𝒩 \mathcal{B}_{\mathcal{N}} caligraphic_B start_POSTSUBSCRIPT caligraphic_N end_POSTSUBSCRIPT is the weak* completion of the vector space ℬ 𝕎 subscript ℬ 𝕎 \mathcal{B}_{\mathbb{W}} caligraphic_B start_POSTSUBSCRIPT blackboard_W end_POSTSUBSCRIPT .

These favorable properties of the space ℬ 𝒩 subscript ℬ 𝒩 \mathcal{B}_{\mathcal{N}} caligraphic_B start_POSTSUBSCRIPT caligraphic_N end_POSTSUBSCRIPT motivate us to take it as the hypothesis space for deep learning. Thus, we consider the following learning model

If we denote by 𝒩 ℬ 𝒩 subscript 𝒩 subscript ℬ 𝒩 \mathcal{N}_{\mathcal{B}_{\mathcal{N}}} caligraphic_N start_POSTSUBSCRIPT caligraphic_B start_POSTSUBSCRIPT caligraphic_N end_POSTSUBSCRIPT end_POSTSUBSCRIPT the neural network learned from the model ( 39 ), then, according to ( 11 ), we have that

Even though learning model ( 39 ) is like model ( 10 ), which is of infinite dimension (unlike model ( 8 ), which is of finite dimension), we will show in the next section that a solution of learning model ( 39 ) lays in a finite dimensional manifold determined by the kernel 𝒦 𝒦 \mathcal{K} caligraphic_K and a given data set.

5 Representer Theorems for Learning Solutions

In this section, we consider learning a target function in ℬ 𝒩 subscript ℬ 𝒩 \mathcal{B}_{\mathcal{N}} caligraphic_B start_POSTSUBSCRIPT caligraphic_N end_POSTSUBSCRIPT from the sampled dataset 𝔻 m subscript 𝔻 𝑚 \mathbb{D}_{m} blackboard_D start_POSTSUBSCRIPT italic_m end_POSTSUBSCRIPT defined by ( 6 ). Learning such a function is an ill-posed problem, whose solutions often suffer from overfitting. For this reason, instead of solving the learning model ( 39 ) directly, we consider a related regularization problem and MNI problem in the RKBS ℬ 𝒩 subscript ℬ 𝒩 \mathcal{B}_{\mathcal{N}} caligraphic_B start_POSTSUBSCRIPT caligraphic_N end_POSTSUBSCRIPT . The goal of this section is to establish representer theorems for solutions of these two learning models.

We start with describing the regularized learning problem in the vector-valued RKBS ℬ 𝒩 subscript ℬ 𝒩 \mathcal{B}_{\mathcal{N}} caligraphic_B start_POSTSUBSCRIPT caligraphic_N end_POSTSUBSCRIPT . For the dataset 𝔻 m subscript 𝔻 𝑚 \mathbb{D}_{m} blackboard_D start_POSTSUBSCRIPT italic_m end_POSTSUBSCRIPT defined by ( 6 ), we define the set 𝒳 := { x j : j ∈ ℕ m } assign 𝒳 conditional-set subscript 𝑥 𝑗 𝑗 subscript ℕ 𝑚 \mathcal{X}:=\{x_{j}:j\in\mathbb{N}_{m}\} caligraphic_X := { italic_x start_POSTSUBSCRIPT italic_j end_POSTSUBSCRIPT : italic_j ∈ blackboard_N start_POSTSUBSCRIPT italic_m end_POSTSUBSCRIPT } and the matrix 𝐘 := [ y j k : k ∈ ℕ t , j ∈ ℕ m ] ∈ ℝ t × m \mathbf{Y}:=[y_{j}^{k}:k\in\mathbb{N}_{t},j\in\mathbb{N}_{m}]\in\mathbb{R}^{t% \times m} bold_Y := [ italic_y start_POSTSUBSCRIPT italic_j end_POSTSUBSCRIPT start_POSTSUPERSCRIPT italic_k end_POSTSUPERSCRIPT : italic_k ∈ blackboard_N start_POSTSUBSCRIPT italic_t end_POSTSUBSCRIPT , italic_j ∈ blackboard_N start_POSTSUBSCRIPT italic_m end_POSTSUBSCRIPT ] ∈ blackboard_R start_POSTSUPERSCRIPT italic_t × italic_m end_POSTSUPERSCRIPT , where for each j ∈ ℕ m 𝑗 subscript ℕ 𝑚 j\in\mathbb{N}_{m} italic_j ∈ blackboard_N start_POSTSUBSCRIPT italic_m end_POSTSUBSCRIPT , y j k superscript subscript 𝑦 𝑗 𝑘 y_{j}^{k} italic_y start_POSTSUBSCRIPT italic_j end_POSTSUBSCRIPT start_POSTSUPERSCRIPT italic_k end_POSTSUPERSCRIPT , k ∈ ℕ t 𝑘 subscript ℕ 𝑡 k\in\mathbb{N}_{t} italic_k ∈ blackboard_N start_POSTSUBSCRIPT italic_t end_POSTSUBSCRIPT , are the components of vector y j subscript 𝑦 𝑗 y_{j} italic_y start_POSTSUBSCRIPT italic_j end_POSTSUBSCRIPT . We introduce an operator 𝐈 𝒳 : ℬ 𝒩 → ℝ t × m : subscript 𝐈 𝒳 → subscript ℬ 𝒩 superscript ℝ 𝑡 𝑚 \mathbf{I}_{\mathcal{X}}:{\mathcal{B}_{\mathcal{N}}}\rightarrow\mathbb{R}^{t% \times m} bold_I start_POSTSUBSCRIPT caligraphic_X end_POSTSUBSCRIPT : caligraphic_B start_POSTSUBSCRIPT caligraphic_N end_POSTSUBSCRIPT → blackboard_R start_POSTSUPERSCRIPT italic_t × italic_m end_POSTSUPERSCRIPT by

\mathcal{Q}:\mathbb{R}^{t\times m}\rightarrow\mathbb{R}_{+}:=[0,+\infty) caligraphic_Q : blackboard_R start_POSTSUPERSCRIPT italic_t × italic_m end_POSTSUPERSCRIPT → blackboard_R start_POSTSUBSCRIPT + end_POSTSUBSCRIPT := [ 0 , + ∞ ) and define

Examples of loss functions 𝒬 ⁢ ( 𝐌 ) 𝒬 𝐌 \mathcal{Q}({\mathbf{M}}) caligraphic_Q ( bold_M ) may be chosen as a norm of the matrix 𝐌 𝐌 \mathbf{M} bold_M . The proposed regularization problem is formed by adding a regularization term λ ⁢ ‖ f μ ‖ ℬ 𝒩 𝜆 subscript norm subscript 𝑓 𝜇 subscript ℬ 𝒩 \lambda\|f_{\mu}\|_{{\mathcal{B}_{\mathcal{N}}}} italic_λ ∥ italic_f start_POSTSUBSCRIPT italic_μ end_POSTSUBSCRIPT ∥ start_POSTSUBSCRIPT caligraphic_B start_POSTSUBSCRIPT caligraphic_N end_POSTSUBSCRIPT end_POSTSUBSCRIPT to the data fidelity term 𝒬 ⁢ ( 𝐈 𝒳 ⁢ ( f μ ) − 𝐘 ) 𝒬 subscript 𝐈 𝒳 subscript 𝑓 𝜇 𝐘 \mathcal{Q}(\mathbf{I}_{\mathcal{X}}(f_{\mu})-\mathbf{Y}) caligraphic_Q ( bold_I start_POSTSUBSCRIPT caligraphic_X end_POSTSUBSCRIPT ( italic_f start_POSTSUBSCRIPT italic_μ end_POSTSUBSCRIPT ) - bold_Y ) . That is,

where λ 𝜆 \lambda italic_λ is a positive regularization parameter. The learning model ( 42 ) allows us to learn a function f μ subscript 𝑓 𝜇 f_{\mu} italic_f start_POSTSUBSCRIPT italic_μ end_POSTSUBSCRIPT in the space ℬ 𝒩 subscript ℬ 𝒩 \mathcal{B}_{\mathcal{N}} caligraphic_B start_POSTSUBSCRIPT caligraphic_N end_POSTSUBSCRIPT by solving the optimization problem ( 42 ).

We first comment on the existence of a solution to the regularization problem ( 42 ). The next proposition follows directly from Proposition 40 of [ 23 ] .

Proposition 11 .

Suppose that m 𝑚 m italic_m distinct points x j ∈ ℝ s subscript 𝑥 𝑗 superscript ℝ 𝑠 x_{j}\in\mathbb{R}^{s} italic_x start_POSTSUBSCRIPT italic_j end_POSTSUBSCRIPT ∈ blackboard_R start_POSTSUPERSCRIPT italic_s end_POSTSUPERSCRIPT , j ∈ ℕ m 𝑗 subscript ℕ 𝑚 j\in\mathbb{N}_{m} italic_j ∈ blackboard_N start_POSTSUBSCRIPT italic_m end_POSTSUBSCRIPT , and 𝐘 ∈ ℝ t × m 𝐘 superscript ℝ 𝑡 𝑚 \mathbf{Y}\in\mathbb{R}^{t\times m} bold_Y ∈ blackboard_R start_POSTSUPERSCRIPT italic_t × italic_m end_POSTSUPERSCRIPT are given. If λ > 0 𝜆 0 \lambda>0 italic_λ > 0 and the loss function 𝒬 𝒬 \mathcal{Q} caligraphic_Q is lower semi-continuous on ℝ t × m superscript ℝ 𝑡 𝑚 \mathbb{R}^{t\times m} blackboard_R start_POSTSUPERSCRIPT italic_t × italic_m end_POSTSUPERSCRIPT , then the regularization problem ( 42 ) has at least one solution.

x\in\mathbb{R}_{+} italic_x ∈ blackboard_R start_POSTSUBSCRIPT + end_POSTSUBSCRIPT , which is lower semi-continuous, increasing and coercive. Since the loss function 𝒬 𝒬 \mathcal{Q} caligraphic_Q is lower semi-continuous on ℝ t × m superscript ℝ 𝑡 𝑚 \mathbb{R}^{t\times m} blackboard_R start_POSTSUPERSCRIPT italic_t × italic_m end_POSTSUPERSCRIPT , the assumptions in Proposition 40 of [ 23 ] are all satisfied. Thus, we conclude from Proposition 40 of [ 23 ] that the regularization problem ( 42 ) has at least one solution. ∎

It is known that regularization problems are closely related to MNI problems (see, for example, [ 23 ] ). The MNI problem aims at finding a vector-valued function f μ subscript 𝑓 𝜇 f_{\mu} italic_f start_POSTSUBSCRIPT italic_μ end_POSTSUBSCRIPT in ℬ 𝒩 subscript ℬ 𝒩 \mathcal{B}_{\mathcal{N}} caligraphic_B start_POSTSUBSCRIPT caligraphic_N end_POSTSUBSCRIPT , having the smallest norm and satisfying the interpolation condition f μ ⁢ ( x j ) = y j subscript 𝑓 𝜇 subscript 𝑥 𝑗 subscript 𝑦 𝑗 f_{\mu}(x_{j})=y_{j} italic_f start_POSTSUBSCRIPT italic_μ end_POSTSUBSCRIPT ( italic_x start_POSTSUBSCRIPT italic_j end_POSTSUBSCRIPT ) = italic_y start_POSTSUBSCRIPT italic_j end_POSTSUBSCRIPT , j ∈ ℕ m 𝑗 subscript ℕ 𝑚 j\in\mathbb{N}_{m} italic_j ∈ blackboard_N start_POSTSUBSCRIPT italic_m end_POSTSUBSCRIPT . In other words, the MNI problem has the form

We then reformulate the MNI problem ( 43 ) in an equivalent form as

Recall that the vector-valued function 𝒦 𝒦 \mathcal{K} caligraphic_K defined by ( 35 ) is the reproducing kernel for ℬ 𝒩 subscript ℬ 𝒩 \mathcal{B}_{\mathcal{N}} caligraphic_B start_POSTSUBSCRIPT caligraphic_N end_POSTSUBSCRIPT . By using the reproducing property ( 36 ), we represent the operator 𝐈 𝒳 subscript 𝐈 𝒳 \mathbf{I}_{\mathcal{X}} bold_I start_POSTSUBSCRIPT caligraphic_X end_POSTSUBSCRIPT defined by ( 40 ) as

Clearly, the MNI problem ( 45 ) includes t ⁢ m 𝑡 𝑚 tm italic_t italic_m interpolation conditions which are produced by the linear functionals in the set

A solution of the regularization problem ( 42 ) may be identified as a solution of an MNI problem in the form of ( 45 ) with different data. In fact, according to [ 23 ] , every solution f ^ μ ∈ ℬ 𝒩 subscript ^ 𝑓 𝜇 subscript ℬ 𝒩 \hat{f}_{\mu}\in\mathcal{B}_{\mathcal{N}} over^ start_ARG italic_f end_ARG start_POSTSUBSCRIPT italic_μ end_POSTSUBSCRIPT ∈ caligraphic_B start_POSTSUBSCRIPT caligraphic_N end_POSTSUBSCRIPT of the regularization problem ( 42 ) is also a solution of the MNI problem ( 45 ) with 𝐘 := 𝐈 𝒳 ⁢ ( f ^ μ ) assign 𝐘 subscript 𝐈 𝒳 subscript ^ 𝑓 𝜇 \mathbf{Y}:=\mathbf{I}_{\mathcal{X}}(\hat{f}_{\mu}) bold_Y := bold_I start_POSTSUBSCRIPT caligraphic_X end_POSTSUBSCRIPT ( over^ start_ARG italic_f end_ARG start_POSTSUBSCRIPT italic_μ end_POSTSUBSCRIPT ) . In addition, if f ^ μ ∈ ℬ 𝒩 subscript ^ 𝑓 𝜇 subscript ℬ 𝒩 \hat{f}_{\mu}\in\mathcal{B}_{\mathcal{N}} over^ start_ARG italic_f end_ARG start_POSTSUBSCRIPT italic_μ end_POSTSUBSCRIPT ∈ caligraphic_B start_POSTSUBSCRIPT caligraphic_N end_POSTSUBSCRIPT is a solution of the MNI problem ( 45 ), then f ^ μ subscript ^ 𝑓 𝜇 \hat{f}_{\mu} over^ start_ARG italic_f end_ARG start_POSTSUBSCRIPT italic_μ end_POSTSUBSCRIPT is a solution of the regularization problem

and there holds the relation

𝑡 𝑥 1 𝑡 𝑦 𝑧 tx+(1-t)y=z italic_t italic_x + ( 1 - italic_t ) italic_y = italic_z for some t ∈ ( 0 , 1 ) 𝑡 0 1 t\in(0,1) italic_t ∈ ( 0 , 1 ) implies that x = y = z 𝑥 𝑦 𝑧 x=y=z italic_x = italic_y = italic_z . By ext ⁢ ( A ) ext 𝐴 \mathrm{ext}(A) roman_ext ( italic_A ) we denote the set of extreme points of A 𝐴 A italic_A . The celebrated Krein-Milman theorem [ 15 ] states that if A 𝐴 A italic_A is a nonempty compact convex subset of 𝕏 𝕏 \mathbb{X} blackboard_X , then A 𝐴 A italic_A is the closed convex hull of its set of extreme points, that is, A = co ¯ ⁢ ( ext ⁢ ( A ) ) 𝐴 ¯ co ext 𝐴 A=\overline{\mathrm{co}}\left(\mathrm{ext}(A)\right) italic_A = over¯ start_ARG roman_co end_ARG ( roman_ext ( italic_A ) ) . Let B 𝐵 B italic_B be a Banach space endowed with norm ∥ ⋅ ∥ B \|\cdot\|_{B} ∥ ⋅ ∥ start_POSTSUBSCRIPT italic_B end_POSTSUBSCRIPT . Clearly, the norm ∥ ⋅ ∥ B \|\cdot\|_{B} ∥ ⋅ ∥ start_POSTSUBSCRIPT italic_B end_POSTSUBSCRIPT is a convex function on B 𝐵 B italic_B . The subdifferential of the norm function ∥ ⋅ ∥ B \|\cdot\|_{B} ∥ ⋅ ∥ start_POSTSUBSCRIPT italic_B end_POSTSUBSCRIPT at each f ∈ B \ { 0 } 𝑓 \ 𝐵 0 f\in B\backslash\{0\} italic_f ∈ italic_B \ { 0 } is defined by

Notice that the dual space B * superscript 𝐵 B^{*} italic_B start_POSTSUPERSCRIPT * end_POSTSUPERSCRIPT of B 𝐵 B italic_B equipped with the weak * {}^{*} start_FLOATSUPERSCRIPT * end_FLOATSUPERSCRIPT topology is a Hausdorff locally convex topological vector space. Moreover, for any f ∈ B \ { 0 } 𝑓 \ 𝐵 0 f\in B\backslash\{0\} italic_f ∈ italic_B \ { 0 } , the subdifferential set ∂ ∥ ⋅ ∥ B ( f ) \partial\|\cdot\|_{B}(f) ∂ ∥ ⋅ ∥ start_POSTSUBSCRIPT italic_B end_POSTSUBSCRIPT ( italic_f ) is a convex and weakly * {}^{*} start_FLOATSUPERSCRIPT * end_FLOATSUPERSCRIPT compact subset of B * superscript 𝐵 B^{*} italic_B start_POSTSUPERSCRIPT * end_POSTSUPERSCRIPT . Hence, the Krein-Milman theorem ensures that for any f ∈ B \ { 0 } 𝑓 \ 𝐵 0 f\in B\backslash\{0\} italic_f ∈ italic_B \ { 0 } ,

where the closed convex hull is taken under the weak * {}^{*} start_FLOATSUPERSCRIPT * end_FLOATSUPERSCRIPT topology of B * superscript 𝐵 B^{*} italic_B start_POSTSUPERSCRIPT * end_POSTSUPERSCRIPT .

We now review the representer theorem for the MNI problem in a general Banach space having a pre-dual space established in [ 24 ] . Suppose that B 𝐵 B italic_B is a Banach space having a pre-dual space B * subscript 𝐵 B_{*} italic_B start_POSTSUBSCRIPT * end_POSTSUBSCRIPT . Let ν j subscript 𝜈 𝑗 \nu_{j} italic_ν start_POSTSUBSCRIPT italic_j end_POSTSUBSCRIPT , j ∈ ℕ n 𝑗 subscript ℕ 𝑛 j\in\mathbb{N}_{n} italic_j ∈ blackboard_N start_POSTSUBSCRIPT italic_n end_POSTSUBSCRIPT , be linearly independent elements in B * subscript 𝐵 B_{*} italic_B start_POSTSUBSCRIPT * end_POSTSUBSCRIPT and 𝐳 := [ z j : j ∈ ℕ n ] ∈ ℝ n \mathbf{z}:=[z_{j}:j\in\mathbb{N}_{n}]\in\mathbb{R}^{n} bold_z := [ italic_z start_POSTSUBSCRIPT italic_j end_POSTSUBSCRIPT : italic_j ∈ blackboard_N start_POSTSUBSCRIPT italic_n end_POSTSUBSCRIPT ] ∈ blackboard_R start_POSTSUPERSCRIPT italic_n end_POSTSUPERSCRIPT be a given vector. Set 𝒱 := span ⁢ { ν j : j ∈ ℕ n } assign 𝒱 span conditional-set subscript 𝜈 𝑗 𝑗 subscript ℕ 𝑛 \mathcal{V}:=\mathrm{span}\{\nu_{j}:j\in\mathbb{N}_{n}\} caligraphic_V := roman_span { italic_ν start_POSTSUBSCRIPT italic_j end_POSTSUBSCRIPT : italic_j ∈ blackboard_N start_POSTSUBSCRIPT italic_n end_POSTSUBSCRIPT } . We define an operator ℒ : B → ℝ n : ℒ → 𝐵 superscript ℝ 𝑛 \mathcal{L}:B\rightarrow\mathbb{R}^{n} caligraphic_L : italic_B → blackboard_R start_POSTSUPERSCRIPT italic_n end_POSTSUPERSCRIPT by ℒ ( f ) := [ ⟨ ν j , f ⟩ B : j ∈ ℕ n ] ,  for all  f ∈ B , \mathcal{L}(f):=\left[\left\langle\nu_{j},f\right\rangle_{B}:j\in\mathbb{N}_{n% }\right],\text{ for all }f\in B, caligraphic_L ( italic_f ) := [ ⟨ italic_ν start_POSTSUBSCRIPT italic_j end_POSTSUBSCRIPT , italic_f ⟩ start_POSTSUBSCRIPT italic_B end_POSTSUBSCRIPT : italic_j ∈ blackboard_N start_POSTSUBSCRIPT italic_n end_POSTSUBSCRIPT ] , for all italic_f ∈ italic_B , and introduce a subset of B 𝐵 B italic_B as M 𝐳 := { f ∈ B : ℒ ⁢ ( f ) = 𝐳 } assign subscript 𝑀 𝐳 conditional-set 𝑓 𝐵 ℒ 𝑓 𝐳 {M_{\mathbf{z}}}:=\{f\in B:\mathcal{L}(f)=\mathbf{z}\} italic_M start_POSTSUBSCRIPT bold_z end_POSTSUBSCRIPT := { italic_f ∈ italic_B : caligraphic_L ( italic_f ) = bold_z } . The MNI problem with the given data { ( ν j , y j ) : j ∈ ℕ n } conditional-set subscript 𝜈 𝑗 subscript 𝑦 𝑗 𝑗 subscript ℕ 𝑛 \{(\nu_{j},y_{j}):j\in\mathbb{N}_{n}\} { ( italic_ν start_POSTSUBSCRIPT italic_j end_POSTSUBSCRIPT , italic_y start_POSTSUBSCRIPT italic_j end_POSTSUBSCRIPT ) : italic_j ∈ blackboard_N start_POSTSUBSCRIPT italic_n end_POSTSUBSCRIPT } considered in [ 24 ] has the form

The representer theorem established in Proposition 7 of [ 24 ] provides a representation of any extreme point of the solution set of the MNI problem ( 46 ) with 𝐳 ∈ ℝ n 𝐳 superscript ℝ 𝑛 \mathbf{z}\in\mathbb{R}^{n} bold_z ∈ blackboard_R start_POSTSUPERSCRIPT italic_n end_POSTSUPERSCRIPT . We describe this result in the next lemma.

Suppose that B 𝐵 B italic_B is a Banach space having a pre-dual space B * subscript 𝐵 B_{*} italic_B start_POSTSUBSCRIPT * end_POSTSUBSCRIPT . Let ν j ∈ B * subscript 𝜈 𝑗 subscript 𝐵 \nu_{j}\in B_{*} italic_ν start_POSTSUBSCRIPT italic_j end_POSTSUBSCRIPT ∈ italic_B start_POSTSUBSCRIPT * end_POSTSUBSCRIPT , j ∈ ℕ n 𝑗 subscript ℕ 𝑛 j\in\mathbb{N}_{n} italic_j ∈ blackboard_N start_POSTSUBSCRIPT italic_n end_POSTSUBSCRIPT , be linearly independent and 𝐳 ∈ ℝ n \ { 𝟎 } 𝐳 normal-\ superscript ℝ 𝑛 0 \mathbf{z}\in\mathbb{R}^{n}\backslash\{\mathbf{0}\} bold_z ∈ blackboard_R start_POSTSUPERSCRIPT italic_n end_POSTSUPERSCRIPT \ { bold_0 } . If 𝒱 𝒱 \mathcal{V} caligraphic_V and M 𝐳 subscript 𝑀 𝐳 {M_{\mathbf{z}}} italic_M start_POSTSUBSCRIPT bold_z end_POSTSUBSCRIPT are defined as above and ν ^ ∈ 𝒱 normal-^ 𝜈 𝒱 \hat{\nu}\in\mathcal{V} over^ start_ARG italic_ν end_ARG ∈ caligraphic_V satisfies

then for any extreme point f ^ normal-^ 𝑓 \hat{f} over^ start_ARG italic_f end_ARG of the solution set of the MNI problem ( 46 ), there exist γ j ∈ ℝ subscript 𝛾 𝑗 ℝ \gamma_{j}\in\mathbb{R} italic_γ start_POSTSUBSCRIPT italic_j end_POSTSUBSCRIPT ∈ blackboard_R , j ∈ ℕ n 𝑗 subscript ℕ 𝑛 j\in\mathbb{N}_{n} italic_j ∈ blackboard_N start_POSTSUBSCRIPT italic_n end_POSTSUBSCRIPT , with ∑ j ∈ ℕ n γ j = ‖ ν ^ ‖ B * subscript 𝑗 subscript ℕ 𝑛 subscript 𝛾 𝑗 subscript norm normal-^ 𝜈 subscript 𝐵 \sum_{j\in\mathbb{N}_{n}}\gamma_{j}=\|\hat{\nu}\|_{B_{*}} ∑ start_POSTSUBSCRIPT italic_j ∈ blackboard_N start_POSTSUBSCRIPT italic_n end_POSTSUBSCRIPT end_POSTSUBSCRIPT italic_γ start_POSTSUBSCRIPT italic_j end_POSTSUBSCRIPT = ∥ over^ start_ARG italic_ν end_ARG ∥ start_POSTSUBSCRIPT italic_B start_POSTSUBSCRIPT * end_POSTSUBSCRIPT end_POSTSUBSCRIPT and u j ∈ ext ( ∂ ∥ ⋅ ∥ B * ( ν ^ ) ) u_{j}\in\mathrm{ext}\left(\partial\|\cdot\|_{B_{*}}(\hat{\nu})\right) italic_u start_POSTSUBSCRIPT italic_j end_POSTSUBSCRIPT ∈ roman_ext ( ∂ ∥ ⋅ ∥ start_POSTSUBSCRIPT italic_B start_POSTSUBSCRIPT * end_POSTSUBSCRIPT end_POSTSUBSCRIPT ( over^ start_ARG italic_ν end_ARG ) ) , j ∈ ℕ n 𝑗 subscript ℕ 𝑛 j\in\mathbb{N}_{n} italic_j ∈ blackboard_N start_POSTSUBSCRIPT italic_n end_POSTSUBSCRIPT , such that

It was pointed out in [ 24 ] that the element ν ^ ^ 𝜈 \hat{\nu} over^ start_ARG italic_ν end_ARG satisfying ( 47 ) can be obtained through solving a dual problem of ( 46 ). Moreover, we remark that the solution set is a nonempty, convex and weakly * {}^{*} start_FLOATSUPERSCRIPT * end_FLOATSUPERSCRIPT compact subset of B 𝐵 B italic_B . Hence, by the Krein-Milman theorem, the set of extreme points of the solution set is nonempty and moreover, any solution of problem ( 46 ) can be expressed as the weak * {}^{*} start_FLOATSUPERSCRIPT * end_FLOATSUPERSCRIPT limit of a sequence in the convex hull of the set of extreme points.

We now present a representer theorem for a solution of the MNI problem ( 45 ), which is a direct consequence of Lemma 12 . We introduce a subspace of 𝒮 𝒮 \mathcal{S} caligraphic_S , which is defined by ( 23 ) and has been proved to be a pre-dual space of ℬ 𝒩 subscript ℬ 𝒩 \mathcal{B}_{\mathcal{N}} caligraphic_B start_POSTSUBSCRIPT caligraphic_N end_POSTSUBSCRIPT , by

We prepare applying Lemma 12 to the MNI problem ( 45 ). To this end, we introduce the dual problem of problem ( 45 ) as

Note that the dual problem is a finite dimensional optimization problem which has the same optimal value, denoted by C * superscript 𝐶 {C^{*}} italic_C start_POSTSUPERSCRIPT * end_POSTSUPERSCRIPT , as the MNI problem ( 45 ). It has been proved in [ 5 ] that there exists at least one solution for the dual problem of the MNI problem in ℓ 1 ⁢ ( ℕ ) subscript ℓ 1 ℕ \ell_{1}(\mathbb{N}) roman_ℓ start_POSTSUBSCRIPT 1 end_POSTSUBSCRIPT ( blackboard_N ) . By a similar argument, we can show the existence of a solution of the dual problem ( 49 ). Suppose that 𝐜 ^ := [ c ^ k ⁢ j : k ∈ ℕ t , j ∈ ℕ m ] ∈ ℝ t × m \hat{\mathbf{c}}:=[\hat{c}_{kj}:k\in\mathbb{N}_{t},j\in\mathbb{N}_{m}]\in% \mathbb{R}^{t\times m} over^ start_ARG bold_c end_ARG := [ over^ start_ARG italic_c end_ARG start_POSTSUBSCRIPT italic_k italic_j end_POSTSUBSCRIPT : italic_k ∈ blackboard_N start_POSTSUBSCRIPT italic_t end_POSTSUBSCRIPT , italic_j ∈ blackboard_N start_POSTSUBSCRIPT italic_m end_POSTSUBSCRIPT ] ∈ blackboard_R start_POSTSUPERSCRIPT italic_t × italic_m end_POSTSUPERSCRIPT is a solution of the dual problem ( 49 ). We let

Theorem 13 .

Proposition 5 ensures that the vector-valued RKBS ℬ 𝒩 subscript ℬ 𝒩 \mathcal{B}_{\mathcal{N}} caligraphic_B start_POSTSUBSCRIPT caligraphic_N end_POSTSUBSCRIPT has the pre-dual space 𝒮 𝒮 \mathcal{S} caligraphic_S . Note that the functionals in 𝕂 𝒳 subscript 𝕂 𝒳 \mathbb{K}_{\mathcal{X}} blackboard_K start_POSTSUBSCRIPT caligraphic_X end_POSTSUBSCRIPT belong to the pre-dual space 𝒮 𝒮 \mathcal{S} caligraphic_S and are linearly independent. Moreover, since g ^ ^ 𝑔 \hat{g} over^ start_ARG italic_g end_ARG is the function defined by ( 50 ), we have that g ^ ∈ 𝒱 𝒩 ^ 𝑔 subscript 𝒱 𝒩 \hat{g}\in\mathcal{V}_{\mathcal{N}} over^ start_ARG italic_g end_ARG ∈ caligraphic_V start_POSTSUBSCRIPT caligraphic_N end_POSTSUBSCRIPT , and according to Proposition 37 of [ 24 ] , g ^ ^ 𝑔 \hat{g} over^ start_ARG italic_g end_ARG satisfies the condition

Theorem 13 provides for each extreme point of the solution set of problem ( 45 ) an explicit and data-dependent representation by using the elements in ext ( ∂ ∥ ⋅ ∥ ∞ ( g ^ ) ) \mathrm{ext}(\partial\|\cdot\|_{\infty}(\hat{g})) roman_ext ( ∂ ∥ ⋅ ∥ start_POSTSUBSCRIPT ∞ end_POSTSUBSCRIPT ( over^ start_ARG italic_g end_ARG ) ) . Even more significantly, the essence of Theorem 13 is that although the MNI problem ( 45 ) is of infinite dimension, every extreme point of its solution set lays in a finite dimensional manifold spanned by t ⁢ m 𝑡 𝑚 tm italic_t italic_m elements h ℓ ∈ ext ( ∂ ∥ ⋅ ∥ ∞ ( g ^ ) ) h_{\ell}\in\mathrm{ext}(\partial\|\cdot\|_{\infty}(\hat{g})) italic_h start_POSTSUBSCRIPT roman_ℓ end_POSTSUBSCRIPT ∈ roman_ext ( ∂ ∥ ⋅ ∥ start_POSTSUBSCRIPT ∞ end_POSTSUBSCRIPT ( over^ start_ARG italic_g end_ARG ) ) .

As we have demonstrated earlier, the element g ^ ^ 𝑔 \hat{g} over^ start_ARG italic_g end_ARG satisfying ( 52 ) can be obtained by solving the dual problem ( 49 ) of ( 45 ). Since g ^ ^ 𝑔 \hat{g} over^ start_ARG italic_g end_ARG is an element in 𝒮 𝒮 \mathcal{S} caligraphic_S , the subdifferential ∂ ∥ ⋅ ∥ ∞ ( g ^ ) \partial\|\cdot\|_{\infty}(\hat{g}) ∂ ∥ ⋅ ∥ start_POSTSUBSCRIPT ∞ end_POSTSUBSCRIPT ( over^ start_ARG italic_g end_ARG ) is a subset of the space ℬ 𝒩 subscript ℬ 𝒩 \mathcal{B}_{\mathcal{N}} caligraphic_B start_POSTSUBSCRIPT caligraphic_N end_POSTSUBSCRIPT , which is the dual space of 𝒮 𝒮 \mathcal{S} caligraphic_S . Notice that the subdifferential set ∂ ∥ ⋅ ∥ ∞ ( g ^ ) \partial\|\cdot\|_{\infty}(\hat{g}) ∂ ∥ ⋅ ∥ start_POSTSUBSCRIPT ∞ end_POSTSUBSCRIPT ( over^ start_ARG italic_g end_ARG ) may not be included in space ℬ 𝕎 subscript ℬ 𝕎 \mathcal{B}_{\mathbb{W}} caligraphic_B start_POSTSUBSCRIPT blackboard_W end_POSTSUBSCRIPT defined by ( 9 ) which is spanned by the kernel sessions 𝒦 ⁢ ( ⋅ , θ ) 𝒦 ⋅ 𝜃 \mathcal{K}(\cdot,\theta) caligraphic_K ( ⋅ , italic_θ ) , θ ∈ Θ 𝜃 Θ \theta\in\Theta italic_θ ∈ roman_Θ . However, a learning solution in the vector-valued RKBS ℬ 𝒩 subscript ℬ 𝒩 \mathcal{B}_{\mathcal{N}} caligraphic_B start_POSTSUBSCRIPT caligraphic_N end_POSTSUBSCRIPT is expected to be represented by the kernel sessions 𝒦 ⁢ ( ⋅ , θ ) 𝒦 ⋅ 𝜃 \mathcal{K}(\cdot,\theta) caligraphic_K ( ⋅ , italic_θ ) , θ ∈ Θ 𝜃 Θ \theta\in\Theta italic_θ ∈ roman_Θ . For the purpose of obtaining a kernel representation for a solution of problem ( 45 ), alternatively to problem ( 45 ), we consider a closely related MNI problem in the measure space ℳ ⁢ ( Θ ) ℳ Θ \mathcal{M}(\Theta) caligraphic_M ( roman_Θ ) and apply the representer theorem established in [ 24 ] to it. We then translate the resulting representer theorem for the MNI problem in ℳ ⁢ ( Θ ) ℳ Θ \mathcal{M}(\Theta) caligraphic_M ( roman_Θ ) to that for problem ( 45 ), by using the relation between the solutions of these two problems.

We now introduce the MNI problem in the measure space ℳ ⁢ ( Θ ) ℳ Θ \mathcal{M}(\Theta) caligraphic_M ( roman_Θ ) with respect to the the sampled dataset 𝔻 m subscript 𝔻 𝑚 \mathbb{D}_{m} blackboard_D start_POSTSUBSCRIPT italic_m end_POSTSUBSCRIPT and show the relation between its solution and a solution of problem ( 45 ). By defining an operator 𝐈 ~ 𝒳 : ℳ ⁢ ( Θ ) → ℝ t × m : subscript ~ 𝐈 𝒳 → ℳ Θ superscript ℝ 𝑡 𝑚 \widetilde{\mathbf{I}}_{\mathcal{X}}:\mathcal{M}(\Theta)\rightarrow\mathbb{R}^% {t\times m} over~ start_ARG bold_I end_ARG start_POSTSUBSCRIPT caligraphic_X end_POSTSUBSCRIPT : caligraphic_M ( roman_Θ ) → blackboard_R start_POSTSUPERSCRIPT italic_t × italic_m end_POSTSUPERSCRIPT by

we formulate the MNI problem in ℳ ⁢ ( Θ ) ℳ Θ \mathcal{M}(\Theta) caligraphic_M ( roman_Θ ) as

The next proposition reveals the relation between the solutions of the MNI problems ( 45 ) and ( 54 ).

Proposition 14 .

Suppose that m 𝑚 m italic_m distinct points x j ∈ ℝ s subscript 𝑥 𝑗 superscript ℝ 𝑠 x_{j}\in\mathbb{R}^{s} italic_x start_POSTSUBSCRIPT italic_j end_POSTSUBSCRIPT ∈ blackboard_R start_POSTSUPERSCRIPT italic_s end_POSTSUPERSCRIPT , j ∈ ℕ m 𝑗 subscript ℕ 𝑚 j\in\mathbb{N}_{m} italic_j ∈ blackboard_N start_POSTSUBSCRIPT italic_m end_POSTSUBSCRIPT , and 𝐘 ∈ ℝ t × m \ { 𝟎 } 𝐘 normal-\ superscript ℝ 𝑡 𝑚 0 \mathbf{Y}\in\mathbb{R}^{t\times m}\backslash\{\mathbf{0}\} bold_Y ∈ blackboard_R start_POSTSUPERSCRIPT italic_t × italic_m end_POSTSUPERSCRIPT \ { bold_0 } are given, and the functionals in 𝕂 𝒳 subscript 𝕂 𝒳 \mathbb{K}_{\mathcal{X}} blackboard_K start_POSTSUBSCRIPT caligraphic_X end_POSTSUBSCRIPT are linearly independent. If μ ^ normal-^ 𝜇 {\hat{\mu}} over^ start_ARG italic_μ end_ARG is a solution of the MNI problem ( 54 ), then f μ ^ ( x ) := [ f μ ^ k ( x ) : k ∈ ℕ t ] ⊤ f_{\hat{\mu}}(x):=\left[f_{\hat{\mu}}^{k}(x):k\in\mathbb{N}_{t}\right]^{\top} italic_f start_POSTSUBSCRIPT over^ start_ARG italic_μ end_ARG end_POSTSUBSCRIPT ( italic_x ) := [ italic_f start_POSTSUBSCRIPT over^ start_ARG italic_μ end_ARG end_POSTSUBSCRIPT start_POSTSUPERSCRIPT italic_k end_POSTSUPERSCRIPT ( italic_x ) : italic_k ∈ blackboard_N start_POSTSUBSCRIPT italic_t end_POSTSUBSCRIPT ] start_POSTSUPERSCRIPT ⊤ end_POSTSUPERSCRIPT , x ∈ ℝ s 𝑥 superscript ℝ 𝑠 x\in\mathbb{R}^{s} italic_x ∈ blackboard_R start_POSTSUPERSCRIPT italic_s end_POSTSUPERSCRIPT , with f μ ^ k superscript subscript 𝑓 normal-^ 𝜇 𝑘 f_{\hat{\mu}}^{k} italic_f start_POSTSUBSCRIPT over^ start_ARG italic_μ end_ARG end_POSTSUBSCRIPT start_POSTSUPERSCRIPT italic_k end_POSTSUPERSCRIPT , k ∈ ℕ t 𝑘 subscript ℕ 𝑡 k\in\mathbb{N}_{t} italic_k ∈ blackboard_N start_POSTSUBSCRIPT italic_t end_POSTSUBSCRIPT , defined as in ( 20 ) with μ 𝜇 \mu italic_μ replaced by μ ^ normal-^ 𝜇 \hat{\mu} over^ start_ARG italic_μ end_ARG , is a solution of the MNI problem ( 45 ) and ‖ f μ ^ ‖ ℬ 𝒩 = ‖ μ ^ ‖ TV subscript norm subscript 𝑓 normal-^ 𝜇 subscript ℬ 𝒩 subscript norm normal-^ 𝜇 normal-TV \|f_{{\hat{\mu}}}\|_{\mathcal{B}_{\mathcal{N}}}=\|{\hat{\mu}}\|_{\mathrm{TV}} ∥ italic_f start_POSTSUBSCRIPT over^ start_ARG italic_μ end_ARG end_POSTSUBSCRIPT ∥ start_POSTSUBSCRIPT caligraphic_B start_POSTSUBSCRIPT caligraphic_N end_POSTSUBSCRIPT end_POSTSUBSCRIPT = ∥ over^ start_ARG italic_μ end_ARG ∥ start_POSTSUBSCRIPT roman_TV end_POSTSUBSCRIPT .

By equations ( 27 ) and ( 28 ) with g := 𝒦 k ⁢ ( x j , ⋅ ) assign 𝑔 subscript 𝒦 𝑘 subscript 𝑥 𝑗 ⋅ g:=\mathcal{K}_{k}(x_{j},\cdot) italic_g := caligraphic_K start_POSTSUBSCRIPT italic_k end_POSTSUBSCRIPT ( italic_x start_POSTSUBSCRIPT italic_j end_POSTSUBSCRIPT , ⋅ ) , we have for each k ∈ ℕ t 𝑘 subscript ℕ 𝑡 k\in\mathbb{N}_{t} italic_k ∈ blackboard_N start_POSTSUBSCRIPT italic_t end_POSTSUBSCRIPT and each j ∈ ℕ m 𝑗 subscript ℕ 𝑚 j\in\mathbb{N}_{m} italic_j ∈ blackboard_N start_POSTSUBSCRIPT italic_m end_POSTSUBSCRIPT that

Note that 𝒦 k ⁢ ( x j , ⋅ ) ∈ C 0 ⁢ ( Θ ) subscript 𝒦 𝑘 subscript 𝑥 𝑗 ⋅ subscript 𝐶 0 Θ \mathcal{K}_{k}(x_{j},\cdot)\in C_{0}(\Theta) caligraphic_K start_POSTSUBSCRIPT italic_k end_POSTSUBSCRIPT ( italic_x start_POSTSUBSCRIPT italic_j end_POSTSUBSCRIPT , ⋅ ) ∈ italic_C start_POSTSUBSCRIPT 0 end_POSTSUBSCRIPT ( roman_Θ ) can be viewed as a bounded linear functional on ℳ ⁢ ( Θ ) ℳ Θ \mathcal{M}(\Theta) caligraphic_M ( roman_Θ ) and

Substituting the above equation into the right hand of equation ( 56 ) leads to

By taking infimum of both sides of the inequality ( 57 ) over ν ∈ ℳ ⁢ ( Θ ) 𝜈 ℳ Θ \nu\in\mathcal{M}(\Theta) italic_ν ∈ caligraphic_M ( roman_Θ ) satisfying f μ = f ν subscript 𝑓 𝜇 subscript 𝑓 𝜈 f_{\mu}=f_{\nu} italic_f start_POSTSUBSCRIPT italic_μ end_POSTSUBSCRIPT = italic_f start_POSTSUBSCRIPT italic_ν end_POSTSUBSCRIPT and noting the definition ( 22 ) of the norm ‖ f μ ‖ ℬ 𝒩 subscript norm subscript 𝑓 𝜇 subscript ℬ 𝒩 \|f_{\mu}\|_{\mathcal{B}_{\mathcal{N}}} ∥ italic_f start_POSTSUBSCRIPT italic_μ end_POSTSUBSCRIPT ∥ start_POSTSUBSCRIPT caligraphic_B start_POSTSUBSCRIPT caligraphic_N end_POSTSUBSCRIPT end_POSTSUBSCRIPT , we get that

Again by the definition ( 22 ) of the norm ‖ f μ ‖ ℬ 𝒩 subscript norm subscript 𝑓 𝜇 subscript ℬ 𝒩 \|f_{\mu}\|_{\mathcal{B}_{\mathcal{N}}} ∥ italic_f start_POSTSUBSCRIPT italic_μ end_POSTSUBSCRIPT ∥ start_POSTSUBSCRIPT caligraphic_B start_POSTSUBSCRIPT caligraphic_N end_POSTSUBSCRIPT end_POSTSUBSCRIPT , we obtain that

Combining inequalities ( 58 ) with ( 59 ), we conclude that ‖ f μ ^ ‖ ℬ 𝒩 ≤ ‖ f μ ‖ ℬ 𝒩 subscript norm subscript 𝑓 ^ 𝜇 subscript ℬ 𝒩 subscript norm subscript 𝑓 𝜇 subscript ℬ 𝒩 \|f_{{\hat{\mu}}}\|_{\mathcal{B}_{\mathcal{N}}}\leq\|f_{\mu}\|_{\mathcal{B}_{% \mathcal{N}}} ∥ italic_f start_POSTSUBSCRIPT over^ start_ARG italic_μ end_ARG end_POSTSUBSCRIPT ∥ start_POSTSUBSCRIPT caligraphic_B start_POSTSUBSCRIPT caligraphic_N end_POSTSUBSCRIPT end_POSTSUBSCRIPT ≤ ∥ italic_f start_POSTSUBSCRIPT italic_μ end_POSTSUBSCRIPT ∥ start_POSTSUBSCRIPT caligraphic_B start_POSTSUBSCRIPT caligraphic_N end_POSTSUBSCRIPT end_POSTSUBSCRIPT . Therefore, f μ ^ subscript 𝑓 ^ 𝜇 f_{{\hat{\mu}}} italic_f start_POSTSUBSCRIPT over^ start_ARG italic_μ end_ARG end_POSTSUBSCRIPT is a solution of the MNI problem ( 45 ). Moreover, by taking μ = μ ^ 𝜇 ^ 𝜇 \mu={\hat{\mu}} italic_μ = over^ start_ARG italic_μ end_ARG in ( 58 ), we get that ‖ μ ^ ‖ TV ≤ ‖ f μ ^ ‖ ℬ 𝒩 subscript norm ^ 𝜇 TV subscript norm subscript 𝑓 ^ 𝜇 subscript ℬ 𝒩 \|{\hat{\mu}}\|_{\mathrm{TV}}\leq\|f_{{\hat{\mu}}}\|_{\mathcal{B}_{\mathcal{N}}} ∥ over^ start_ARG italic_μ end_ARG ∥ start_POSTSUBSCRIPT roman_TV end_POSTSUBSCRIPT ≤ ∥ italic_f start_POSTSUBSCRIPT over^ start_ARG italic_μ end_ARG end_POSTSUBSCRIPT ∥ start_POSTSUBSCRIPT caligraphic_B start_POSTSUBSCRIPT caligraphic_N end_POSTSUBSCRIPT end_POSTSUBSCRIPT . This together with inequality ( 59 ) leads to ‖ f μ ^ ‖ ℬ 𝒩 = ‖ μ ^ ‖ TV subscript norm subscript 𝑓 ^ 𝜇 subscript ℬ 𝒩 subscript norm ^ 𝜇 TV \|f_{{\hat{\mu}}}\|_{\mathcal{B}_{\mathcal{N}}}=\|{\hat{\mu}}\|_{\mathrm{TV}} ∥ italic_f start_POSTSUBSCRIPT over^ start_ARG italic_μ end_ARG end_POSTSUBSCRIPT ∥ start_POSTSUBSCRIPT caligraphic_B start_POSTSUBSCRIPT caligraphic_N end_POSTSUBSCRIPT end_POSTSUBSCRIPT = ∥ over^ start_ARG italic_μ end_ARG ∥ start_POSTSUBSCRIPT roman_TV end_POSTSUBSCRIPT . ∎

We next derive a representer theorem for a solution of problem ( 54 ) by employing Lemma 12 . Applying Lemma 12 to problem ( 54 ) requires the representation of the extreme points of the subdifferential set ∂ ∥ ⋅ ∥ ∞ ( g ) \partial\|\cdot\|_{\infty}(g) ∂ ∥ ⋅ ∥ start_POSTSUBSCRIPT ∞ end_POSTSUBSCRIPT ( italic_g ) for any nonzero g ∈ C 0 ⁢ ( Θ ) 𝑔 subscript 𝐶 0 Θ g\in C_{0}(\Theta) italic_g ∈ italic_C start_POSTSUBSCRIPT 0 end_POSTSUBSCRIPT ( roman_Θ ) . Here, the subdifferential set ∂ ∥ ⋅ ∥ ∞ ( g ) \partial\|\cdot\|_{\infty}(g) ∂ ∥ ⋅ ∥ start_POSTSUBSCRIPT ∞ end_POSTSUBSCRIPT ( italic_g ) is a subset of the measure space ℳ ⁢ ( Θ ) ℳ Θ \mathcal{M}(\Theta) caligraphic_M ( roman_Θ ) . For each g ∈ C 0 ⁢ ( Θ ) 𝑔 subscript 𝐶 0 Θ g\in C_{0}(\Theta) italic_g ∈ italic_C start_POSTSUBSCRIPT 0 end_POSTSUBSCRIPT ( roman_Θ ) , let Θ ⁢ ( g ) Θ 𝑔 \Theta(g) roman_Θ ( italic_g ) denote the subset of Θ Θ \Theta roman_Θ where the function g 𝑔 g italic_g attains its maximum norm ‖ g ‖ ∞ subscript norm 𝑔 \|g\|_{\infty} ∥ italic_g ∥ start_POSTSUBSCRIPT ∞ end_POSTSUBSCRIPT , that is,

For each g ∈ C 0 ⁢ ( Θ ) 𝑔 subscript 𝐶 0 Θ g\in C_{0}(\Theta) italic_g ∈ italic_C start_POSTSUBSCRIPT 0 end_POSTSUBSCRIPT ( roman_Θ ) , we introduce a subset of ℳ ⁢ ( Θ ) ℳ Θ \mathcal{M}(\Theta) caligraphic_M ( roman_Θ ) by

Lemma 26 26 26 26 in [ 24 ] essentially states that if g ∈ C 0 ⁢ ( Θ ) \ { 0 } 𝑔 \ subscript 𝐶 0 Θ 0 g\in C_{0}(\Theta)\backslash\{0\} italic_g ∈ italic_C start_POSTSUBSCRIPT 0 end_POSTSUBSCRIPT ( roman_Θ ) \ { 0 } , then

Proposition 15 .

Note that the measure space ℳ ⁢ ( Θ ) ℳ Θ \mathcal{M}(\Theta) caligraphic_M ( roman_Θ ) has the pre-dual space C 0 ⁢ ( Θ ) subscript 𝐶 0 Θ C_{0}(\Theta) italic_C start_POSTSUBSCRIPT 0 end_POSTSUBSCRIPT ( roman_Θ ) and the functionals 𝒦 k ⁢ ( x j , ⋅ ) subscript 𝒦 𝑘 subscript 𝑥 𝑗 ⋅ \mathcal{K}_{k}(x_{j},\cdot) caligraphic_K start_POSTSUBSCRIPT italic_k end_POSTSUBSCRIPT ( italic_x start_POSTSUBSCRIPT italic_j end_POSTSUBSCRIPT , ⋅ ) , k ∈ ℕ t 𝑘 subscript ℕ 𝑡 k\in\mathbb{N}_{t} italic_k ∈ blackboard_N start_POSTSUBSCRIPT italic_t end_POSTSUBSCRIPT , j ∈ ℕ m 𝑗 subscript ℕ 𝑚 j\in\mathbb{N}_{m} italic_j ∈ blackboard_N start_POSTSUBSCRIPT italic_m end_POSTSUBSCRIPT , which belong to the pre-dual space C 0 ⁢ ( Θ ) subscript 𝐶 0 Θ C_{0}(\Theta) italic_C start_POSTSUBSCRIPT 0 end_POSTSUBSCRIPT ( roman_Θ ) , are linearly independent. By Proposition 37 in [ 24 ] , the function g ^ ^ 𝑔 \hat{g} over^ start_ARG italic_g end_ARG defined by ( 50 ) satisfies g ^ ∈ 𝒱 𝒩 ^ 𝑔 subscript 𝒱 𝒩 \hat{g}\in\mathcal{V}_{\mathcal{N}} over^ start_ARG italic_g end_ARG ∈ caligraphic_V start_POSTSUBSCRIPT caligraphic_N end_POSTSUBSCRIPT and

It follows from equation ( 61 ) that for each ℓ ∈ ℕ t ⁢ m ℓ subscript ℕ 𝑡 𝑚 \ell\in\mathbb{N}_{tm} roman_ℓ ∈ blackboard_N start_POSTSUBSCRIPT italic_t italic_m end_POSTSUBSCRIPT , we have that u ℓ ∈ Ω ⁢ ( g ^ ) subscript 𝑢 ℓ Ω ^ 𝑔 u_{\ell}\in\Omega(\hat{g}) italic_u start_POSTSUBSCRIPT roman_ℓ end_POSTSUBSCRIPT ∈ roman_Ω ( over^ start_ARG italic_g end_ARG ) . By definition ( 60 ) of the set Ω ⁢ ( g ^ ) Ω ^ 𝑔 \Omega(\hat{g}) roman_Ω ( over^ start_ARG italic_g end_ARG ) , for each ℓ ∈ ℕ t ⁢ m ℓ subscript ℕ 𝑡 𝑚 \ell\in\mathbb{N}_{tm} roman_ℓ ∈ blackboard_N start_POSTSUBSCRIPT italic_t italic_m end_POSTSUBSCRIPT , there exists θ ℓ ∈ Θ ⁢ ( g ^ ) subscript 𝜃 ℓ Θ ^ 𝑔 \theta_{\ell}\in\Theta(\hat{g}) italic_θ start_POSTSUBSCRIPT roman_ℓ end_POSTSUBSCRIPT ∈ roman_Θ ( over^ start_ARG italic_g end_ARG ) such that u ℓ = sign ⁢ ( g ^ ⁢ ( θ ℓ ) ) ⁢ δ θ ℓ subscript 𝑢 ℓ sign ^ 𝑔 subscript 𝜃 ℓ subscript 𝛿 subscript 𝜃 ℓ u_{\ell}=\mathrm{sign}(\hat{g}(\theta_{\ell}))\delta_{\theta_{\ell}} italic_u start_POSTSUBSCRIPT roman_ℓ end_POSTSUBSCRIPT = roman_sign ( over^ start_ARG italic_g end_ARG ( italic_θ start_POSTSUBSCRIPT roman_ℓ end_POSTSUBSCRIPT ) ) italic_δ start_POSTSUBSCRIPT italic_θ start_POSTSUBSCRIPT roman_ℓ end_POSTSUBSCRIPT end_POSTSUBSCRIPT . Therefore, we may rewrite the representation ( 63 ) of μ ^ ^ 𝜇 \hat{\mu} over^ start_ARG italic_μ end_ARG as ( 62 ). ∎

Proposition 15 provides a representation for an extreme point of the solution set of the MNI problem ( 54 ). This solution can be converted via Proposition 14 to a solution of the MNI problem ( 45 ). We present this result in the next theorem.

Theorem 16 .

for some γ ℓ ∈ ℝ subscript 𝛾 normal-ℓ ℝ \gamma_{\ell}\in\mathbb{R} italic_γ start_POSTSUBSCRIPT roman_ℓ end_POSTSUBSCRIPT ∈ blackboard_R , ℓ ∈ ℕ t ⁢ m normal-ℓ subscript ℕ 𝑡 𝑚 \ell\in\mathbb{N}_{tm} roman_ℓ ∈ blackboard_N start_POSTSUBSCRIPT italic_t italic_m end_POSTSUBSCRIPT , with ∑ ℓ ∈ ℕ t ⁢ m γ ℓ = ‖ g ^ ‖ ∞ subscript normal-ℓ subscript ℕ 𝑡 𝑚 subscript 𝛾 normal-ℓ subscript norm normal-^ 𝑔 \sum_{\ell\in\mathbb{N}_{tm}}\gamma_{\ell}=\|\hat{g}\|_{\infty} ∑ start_POSTSUBSCRIPT roman_ℓ ∈ blackboard_N start_POSTSUBSCRIPT italic_t italic_m end_POSTSUBSCRIPT end_POSTSUBSCRIPT italic_γ start_POSTSUBSCRIPT roman_ℓ end_POSTSUBSCRIPT = ∥ over^ start_ARG italic_g end_ARG ∥ start_POSTSUBSCRIPT ∞ end_POSTSUBSCRIPT and θ ℓ ∈ Θ ⁢ ( g ^ ) subscript 𝜃 normal-ℓ normal-Θ normal-^ 𝑔 \theta_{\ell}\in\Theta(\hat{g}) italic_θ start_POSTSUBSCRIPT roman_ℓ end_POSTSUBSCRIPT ∈ roman_Θ ( over^ start_ARG italic_g end_ARG ) , ℓ ∈ ℕ t ⁢ m normal-ℓ subscript ℕ 𝑡 𝑚 \ell\in\mathbb{N}_{tm} roman_ℓ ∈ blackboard_N start_POSTSUBSCRIPT italic_t italic_m end_POSTSUBSCRIPT .

Substituting representation ( 62 ) of μ ^ ^ 𝜇 \hat{\mu} over^ start_ARG italic_μ end_ARG into the right-hand side of equation ( 65 ) yields that

Hypothesis Space

• Reference work entry
• Cite this reference work entry

• Eyke Hüllermeier 5 ,
• Thomas Fober 5 &
• Marco Mernberger 5  

125 Accesses

In machine learning, the goal of a supervised learning algorithm is to perform induction, i.e., to generalize a (finite) set of observations (the training data) into a general model of the domain. In this regard, the hypothesis space is defined as the set of candidate models considered by the algorithm.

More specifically, consider the problem of learning a mapping (model) \( f \in F = Y^X \) from an input space X to an output space Y , given a set of training data \( D = \left\{ {\left( {{x_1},{y_1}} \right),...,\left( {{x_n},{y_n}} \right)} \right\} \subset X \times Y \) . A learning algorithm A takes D as an input and produces a function (model, hypothesis) f ∈ H ⊂ F as an output, where H is the hypothesis space. This subset is determined by the formalism used to represent models (e.g., as logical formulas, linear functions, or non-linear functions implemented as artificial neural networks or decision trees ). Thus, the choice of the hypothesis space produces a representation...

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

• Available as PDF
• Read on any device
• Instant download
• Own it forever
• Available as EPUB and PDF
• Durable hardcover edition
• Dispatched in 3 to 5 business days
• Free shipping worldwide - see info

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Author information

Authors and affiliations.

Philipps-Universität Marburg, Hans-Meerwein-Straße, Marburg, Germany

Eyke Hüllermeier, Thomas Fober & Marco Mernberger

You can also search for this author in PubMed   Google Scholar

Corresponding author

Correspondence to Eyke Hüllermeier .

Editor information

Editors and affiliations.

Biomedical Sciences Research Institute, University of Ulster, Coleraine, UK

Werner Dubitzky

Department of Computer Science, University of Rostock, Rostock, Germany

Olaf Wolkenhauer

Department of Bio and Brain Engineering, Korea Advanced Institute of Science and Technology (KAIST), Daejeon, Republic of Korea

Kwang-Hyun Cho

Department of Biomedical Engineering, Rensselaer Polytechnic Institute, Troy, NY, USA

Hiroki Yokota

Rights and permissions

Reprints and permissions

Copyright information

© 2013 Springer Science+Business Media, LLC

About this entry

Cite this entry.

Hüllermeier, E., Fober, T., Mernberger, M. (2013). Hypothesis Space. In: Dubitzky, W., Wolkenhauer, O., Cho, KH., Yokota, H. (eds) Encyclopedia of Systems Biology. Springer, New York, NY. https://doi.org/10.1007/978-1-4419-9863-7_926

Download citation

DOI : https://doi.org/10.1007/978-1-4419-9863-7_926

Publisher Name : Springer, New York, NY

Print ISBN : 978-1-4419-9862-0

Online ISBN : 978-1-4419-9863-7

eBook Packages : Biomedical and Life Sciences Reference Module Biomedical and Life Sciences

Share this entry

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Publish with us

Policies and ethics

• Find a journal
• Track your research

Machine Learning

Artificial Intelligence

Control System

Supervised Learning

Classification, miscellaneous, related tutorials.

Interview Questions

• Send your Feedback to [email protected]

Help Others, Please Share

Learn Latest Tutorials

Transact-SQL

Reinforcement Learning

R Programming

React Native

Python Design Patterns

Python Pillow

Python Turtle

Preparation

Verbal Ability

Company Questions

Trending Technologies

Cloud Computing

Data Science

B.Tech / MCA

Data Structures

Operating System

Computer Network

Compiler Design

Computer Organization

Discrete Mathematics

Ethical Hacking

Computer Graphics

Software Engineering

Web Technology

Cyber Security

C Programming

Data Mining

Data Warehouse

ID3 Algorithm and Hypothesis space in Decision Tree Learning

The collection of potential decision trees is the hypothesis space searched by ID3. ID3 searches this hypothesis space in a hill-climbing fashion, starting with the empty tree and moving on to increasingly detailed hypotheses in pursuit of a decision tree that properly classifies the training data.

In this blog, we’ll have a look at the Hypothesis space in Decision Trees and the ID3 Algorithm. 

ID3 Algorithm: 

The ID3 algorithm (Iterative Dichotomiser 3) is a classification technique that uses a greedy approach to create a decision tree by picking the optimal attribute that delivers the most Information Gain (IG) or the lowest Entropy (H).

What is Information Gain and Entropy?  

Information gain: .

The assessment of changes in entropy after segmenting a dataset based on a characteristic is known as information gain.

It establishes how much information a feature provides about a class.

We divided the node and built the decision tree based on the value of information gained.

The greatest information gain node/attribute is split first in a decision tree method, which always strives to maximize the value of information gain. 

The formula for Information Gain: 

Entropy is a metric for determining the degree of impurity in a particular property. It denotes the unpredictability of data. The following formula may be used to compute entropy:

S stands for “total number of samples.”

P(yes) denotes the likelihood of a yes answer.

P(no) denotes the likelihood of a negative outcome.

• Calculate the dataset’s entropy.
• For each feature/attribute.

Determine the entropy for each of the category values.

Calculate the feature’s information gain.

• Find the feature that provides the most information.
• Repeat it till we get the tree we want.

Characteristics of ID3: 

• ID3 takes a greedy approach, which means it might become caught in local optimums and hence cannot guarantee an optimal result.
• ID3 has the potential to overfit the training data (to avoid overfitting, smaller decision trees should be preferred over larger ones).
• This method creates tiny trees most of the time, however, it does not always yield the shortest tree feasible.
• On continuous data, ID3 is not easy to use (if the values of any given attribute are continuous, then there are many more places to split the data on this attribute, and searching for the best value to split by takes a lot of time).

Over Fitting:  

Good generalization is the desired property in our decision trees (and, indeed, in all classification problems), as we noted before. 

This implies we want the model fit on the labeled training data to generate predictions that are as accurate as they are on new, unseen observations.

Capabilities and Limitations of ID3:

• In relation to the given characteristics, ID3’s hypothesis space for all decision trees is a full set of finite discrete-valued functions.
• As it searches across the space of decision trees, ID3 keeps just one current hypothesis. This differs from the prior version space candidate Elimination approach, which keeps the set of all hypotheses compatible with the training instances provided.
• ID3 loses the capabilities that come with explicitly describing all consistent hypotheses by identifying only one hypothesis. It is unable to establish how many different decision trees are compatible with the supplied training data.
• One benefit of incorporating all of the instances’ statistical features (e.g., information gain) is that the final search is less vulnerable to faults in individual training examples.
• By altering its termination criterion to allow hypotheses that inadequately match the training data, ID3 may simply be modified to handle noisy training data.
• In its purest form, ID3 does not go backward in its search. It never goes back to evaluate a choice after it has chosen an attribute to test at a specific level in the tree. As a result, it is vulnerable to the standard dangers of hill-climbing search without backtracking, resulting in local optimum but not globally optimal solutions.
• At each stage of the search, ID3 uses all training instances to make statistically based judgments on how to refine its current hypothesis. This is in contrast to approaches that make incremental judgments based on individual training instances (e.g., FIND-S or CANDIDATE-ELIMINATION ).

Hypothesis Space Search by ID3: 

• ID3 climbs the hill of knowledge acquisition by searching the space of feasible decision trees.
• It looks for all finite discrete-valued functions in the whole space. Every function is represented by at least one tree.
• It only holds one theory (unlike Candidate-Elimination). It is unable to inform us how many more feasible options exist.
• It’s possible to get stranded in local optima.
• At each phase, all training examples are used. Errors have a lower impact on the outcome.

• Share full article

Advertisement

Supported by

Guest Essay

I Thought the Bragg Case Against Trump Was a Legal Embarrassment. Now I Think It’s a Historic Mistake.

By Jed Handelsman Shugerman

Mr. Shugerman is a law professor at Boston University.

About a year ago, when Alvin Bragg, the Manhattan district attorney, indicted former President Donald Trump, I was critical of the case and called it an embarrassment. I thought an array of legal problems would and should lead to long delays in federal courts.

After listening to Monday’s opening statement by prosecutors, I still think the district attorney has made a historic mistake. Their vague allegation about “a criminal scheme to corrupt the 2016 presidential election” has me more concerned than ever about their unprecedented use of state law and their persistent avoidance of specifying an election crime or a valid theory of fraud.

To recap: Mr. Trump is accused in the case of falsifying business records. Those are misdemeanor charges. To elevate it to a criminal case, Mr. Bragg and his team have pointed to potential violations of federal election law and state tax fraud. They also cite state election law, but state statutory definitions of “public office” seem to limit those statutes to state and local races.

Both the misdemeanor and felony charges require that the defendant made the false record with “intent to defraud.” A year ago, I wondered how entirely internal business records (the daily ledger, pay stubs and invoices) could be the basis of any fraud if they are not shared with anyone outside the business. I suggested that the real fraud was Mr. Trump’s filing an (allegedly) false report to the Federal Election Commission, and that only federal prosecutors had jurisdiction over that filing.

A recent conversation with Jeffrey Cohen, a friend, Boston College law professor and former prosecutor, made me think that the case could turn out to be more legitimate than I had originally thought. The reason has to do with those allegedly falsified business records: Most of them were entered in early 2017, generally before Mr. Trump filed his Federal Election Commission report that summer. Mr. Trump may have foreseen an investigation into his campaign, leading to its financial records. He may have falsely recorded these internal records before the F.E.C. filing as consciously part of the same fraud: to create a consistent paper trail and to hide intent to violate federal election laws, or defraud the F.E.C.

In short: It’s not the crime; it’s the cover-up.

Looking at the case in this way might address concerns about state jurisdiction. In this scenario, Mr. Trump arguably intended to deceive state investigators, too. State investigators could find these inconsistencies and alert federal agencies. Prosecutors could argue that New York State agencies have an interest in detecting conspiracies to defraud federal entities; they might also have a plausible answer to significant questions about whether New York State has jurisdiction or whether this stretch of a state business filing law is pre-empted by federal law.

However, this explanation is a novel interpretation with many significant legal problems. And none of the Manhattan district attorney’s filings or today’s opening statement even hint at this approach.

Instead of a theory of defrauding state regulators, Mr. Bragg has adopted a weak theory of “election interference,” and Justice Juan Merchan described the case , in his summary of it during jury selection, as an allegation of falsifying business records “to conceal an agreement with others to unlawfully influence the 2016 election.”

As a reality check: It is legal for a candidate to pay for a nondisclosure agreement. Hush money is unseemly, but it is legal. The election law scholar Richard Hasen rightly observed , “Calling it election interference actually cheapens the term and undermines the deadly serious charges in the real election interference cases.”

In Monday’s opening argument, the prosecutor Matthew Colangelo still evaded specifics about what was illegal about influencing an election, but then he claimed , “It was election fraud, pure and simple.” None of the relevant state or federal statutes refer to filing violations as fraud. Calling it “election fraud” is a legal and strategic mistake, exaggerating the case and setting up the jury with high expectations that the prosecutors cannot meet.

The most accurate description of this criminal case is a federal campaign finance filing violation. Without a federal violation (which the state election statute is tethered to), Mr. Bragg cannot upgrade the misdemeanor counts into felonies. Moreover, it is unclear how this case would even fulfill the misdemeanor requirement of “intent to defraud” without the federal crime.

In stretching jurisdiction and trying a federal crime in state court, the Manhattan district attorney is now pushing untested legal interpretations and applications. I see three red flags raising concerns about selective prosecution upon appeal.

First, I could find no previous case of any state prosecutor relying on the Federal Election Campaign Act either as a direct crime or a predicate crime. Whether state prosecutors have avoided doing so as a matter of law, norms or lack of expertise, this novel attempt is a sign of overreach.

Second, Mr. Trump’s lawyers argued that the New York statute requires that the predicate (underlying) crime must also be a New York crime, not a crime in another jurisdiction. The district attorney responded with judicial precedents only about other criminal statutes, not the statute in this case. In the end, the prosecutors could not cite a single judicial interpretation of this particular statute supporting their use of the statute (a plea deal and a single jury instruction do not count).

Third, no New York precedent has allowed an interpretation of defrauding the general public. Legal experts have noted that such a broad “election interference” theory is unprecedented, and a conviction based on it may not survive a state appeal.

Mr. Trump’s legal team also undercut itself for its decisions in the past year: His lawyers essentially put all of their eggs in the meritless basket of seeking to move the trial to federal court, instead of seeking a federal injunction to stop the trial entirely. If they had raised the issues of selective or vindictive prosecution and a mix of jurisdictional, pre-emption and constitutional claims, they could have delayed the trial past Election Day, even if they lost at each federal stage.

Another reason a federal crime has wound up in state court is that President Biden’s Justice Department bent over backward not to reopen this valid case or appoint a special counsel. Mr. Trump has tried to blame Mr. Biden for this prosecution as the real “election interference.” The Biden administration’s extra restraint belies this allegation and deserves more credit.

Eight years after the alleged crime itself, it is reasonable to ask if this is more about Manhattan politics than New York law. This case should serve as a cautionary tale about broader prosecutorial abuses in America — and promote bipartisan reforms of our partisan prosecutorial system.

Nevertheless, prosecutors should have some latitude to develop their case during trial, and maybe they will be more careful and precise about the underlying crime, fraud and the jurisdictional questions. Mr. Trump has received sufficient notice of the charges, and he can raise his arguments on appeal. One important principle of “ our Federalism ,” in the Supreme Court’s terms, is abstention , that federal courts should generally allow state trials to proceed first and wait to hear challenges later.

This case is still an embarrassment, in terms of prosecutorial ethics and apparent selectivity. Nevertheless, each side should have its day in court. If convicted, Mr. Trump can fight many other days — and perhaps win — in appellate courts. But if Monday’s opening is a preview of exaggerated allegations, imprecise legal theories and persistently unaddressed problems, the prosecutors might not win a conviction at all.

Jed Handelsman Shugerman (@jedshug) is a law professor at Boston University.

The Times is committed to publishing a diversity of letters to the editor. We’d like to hear what you think about this or any of our articles. Here are some tips . And here’s our email: [email protected] .

Follow the New York Times Opinion section on Facebook , Instagram , TikTok , WhatsApp , X and Threads .

Did Life on Earth Come From Space? A New Study Gives the Theory a Boost

The building blocks of life might form more easily in outer space.

The origin of life on Earth is still enigmatic, but we are slowly unraveling the steps involved and the necessary ingredients. Scientists believe life arose in a primordial soup of organic chemicals and biomolecules on the early Earth, eventually leading to actual organisms.

It’s long been suspected that some of these ingredients may have been delivered from space. Now, a new study published in Science Advances shows that a special group of molecules, known as peptides, can form more easily under the conditions of space than those found on Earth. That means they could have been delivered to the early Earth by meteorites or comets – and that life may be able to form elsewhere, too.

The functions of life are upheld in our cells (and those of all living beings) by large, complex carbon-based (organic) molecules called proteins. How to make the large variety of proteins we need to stay alive is encoded in our DNA, which is itself a large and complex organic molecule.

However, these complex molecules are assembled from a variety of small and simple molecules such as amino acids – the so-called building blocks of life.

To explain the origin of life, we need to understand how and where these building blocks form and under what conditions they spontaneously assemble themselves into more complex structures. Finally we need to understand the step that enables them to become a confined, self-replicating system — a living organism.

This latest study sheds light on how some of these building blocks might have formed and assembled and how they ended up on Earth.

Steps to life

DNA is made up of about 20 different amino acids.

DNA is made up of about 20 different amino acids . Like letters of the alphabet, these are arranged in DNA’s double helix structure in different combinations to encrypt our genetic code.

Peptides are also an assemblage of amino acids in a chain-like structure. Peptides can be made up of as little as two amino acids, but also range to hundreds of amino acids.

The assemblage of amino acids into peptides is an important step because peptides provide functions such as “catalyzing” or enhancing reactions that are important to maintaining life. They are also candidate molecules that could have been further assembled into early versions of membranes, confining functional molecules in cell-like structures.

However, despite their potentially important role in the origin of life, it was not so straightforward for peptides to form spontaneously under the environmental conditions on the early Earth. In fact, the scientists behind the current study had previously shown that the cold conditions of space are actually more favorable to the formation of peptides.

In the very low density of clouds of molecules and dust particles in a part of space called the interstellar medium (see above), single atoms of carbon can stick to the surface of dust grains together with carbon monoxide and ammonia molecules. They then react to form amino acid-like molecules. When such a cloud becomes denser, and dust particles also start to stick together, these molecules can assemble into peptides.

In their new study, the scientists look at the dense environment of dusty disks, from which a new solar system with a star and planets emerges eventually. Such disks form when clouds suddenly collapse under the force of gravity. In this environment, water molecules are much more prevalent – forming ice on the surface of any growing agglomerates of particles that could inhibit the reactions that form peptides.

By emulating the reactions likely to occur in the interstellar medium in the laboratory, the study shows that, although the formation of peptides is slightly diminished, it is not prevented. Instead, as rocks and dust combine to form larger bodies such as asteroids and comets, these bodies heat up and allow for liquids to form. This boosts peptide formation in these liquids, and there’s a natural selection of further reactions resulting in even more complex organic molecules. These processes would have occurred during the formation of our own Solar System.

Many of the building blocks of life, such as amino acids, lipids, and sugars, can form in the space environment. Many have been detected in meteorites.

Because peptide formation is more efficient in space than on Earth, and because they can accumulate in comets, their impacts on the early Earth might have delivered loads that boosted the steps towards the origin of life on Earth.

So what does all this mean for our chances of finding alien life? Well, the building blocks for life are available throughout the universe. How specific the conditions need to be to enable them to self-assemble into living organisms is still an open question. Once we know that, we’ll have a good idea of how widespread or not life might be.

This article was originally published on The Conversation by Christian Schroeder at the University of Stirling. Read the origThe inal article here .

• Space Science

MTG nodded to her infamous 'Jewish space laser' theory in an amendment meant to mess up sending aid to Israel

• Rep. Marjorie Taylor Greene revisited tricky territory in an amendment to an Israel funding bill.
• Greene's amendment would divert cash from Israel to developing space lasers for the US border.
• A 2018 post suggesting that lasers in space caused a California wildfire has long haunted Greene.

Rep. Marjorie Taylor Greene made clear her opposition to sending extra money to Israel in a weirdly self-referential way.

The Georgia Republican filed an amendment to a $26.38 billion Israel aid bill that would divert some of that funding toward "the development of space laser technology on the southwest border" of the United States.

It was a not-so-subtle reference to a lowlight of her political past, when she suggested in a 2018 Facebook post that a Jewish-financed laser beam ignited one of the worst wildfires in California's history.

"I've previously voted to fund space lasers for Israel's defense," said Greene. "America needs to take our national security seriously and deserves the same type of defense for our border that Israel has and proudly uses."

The bill includes $1.2 billion for Israel's experimental Iron Beam system.

Israel has some of the best unmanned defense systems in the world. I’ve previously voted to fund space lasers for Israel’s defense. America needs to take our national security seriously and deserves the same type of defense for our border that Israel has and proudly uses. pic.twitter.com/oDeDqTXvQQ — Rep. Marjorie Taylor Greene🇺🇸 (@RepMTG) April 18, 2024

Greene's old conspiratorial social media rants were uncovered by outlets like CNN and Media Matters after she first took office in 2021.

Related stories

In the case of the "Jewish space lasers," she connected the wildfire to the Rothschild family of Jewish financiers, a favorite target of antisemitic conspiracy theories.

The "Jewish space laser" theory has become a staple piece of mockery for those attacking Greene, and is often brought up by reporters.

A video from early March shows Greene being less than thrilled to talk about the theory, telling British reporter Emily Maitlis to "fuck off" after she asked about it.

It might seem strange, then, for Greene to voluntarily go back to space-laser territory, given that it's often earned her mockery. But it's also in keeping with her MAGA Republican style, embracing the most eye-catching possible methods to signal her positions — in this case, her die-hard opposition to sending aid to other countries.

The suggestion isn't realistic and isn't meant to be — it was among a raft of amendments offered by Greene and allies like Rep. Paul Gosar of Arizona to make it harder to pass the bills.

Greene's office has not yet responded to a request for comment sent outside regular business hours.

The House is set to vote this weekend on a package of bills to send aid to Ukraine, Israel, and Taiwan — but in contrast to a $95.3 billion bill passed by the Senate two months ago, House members will take individual votes on each component.

President Joe Biden on Wednesday said that he supports the measures , and urged the House and Senate to quickly pass them so he could sign them into law.

Greene has voted against Israel aid in the past, and she's long been one of the most outspoken opponents of Ukraine aid . She also introduced seven amendments to the Ukraine aid bill, including provisions that would divert money to US disaster zones or force any members of Congress who support the bill to enlist in the Ukrainian military.

Watch: The House floor showdown between Lauren Boebert and Marjorie Taylor Greene is just the tip of the iceberg

• Main content

'I don't believe in space:' Texas Tech DB Tyler Owens makes bold statement at NFL combine

Earth to Tyler Owens.

The Texas Tech defensive back dropped a meteor at the NFL combine this week and he hasn't even run the 40-yard dash yet.

Owens told media members on Thursday that he doesn't believe in space. No, not that he isn't a fan of the Taylor Swift song . But that he actually doesn't think planets and stars and galaxies exist.

"I don't believe in space," Owens said in a video posted on X by Bleacher Report's Brent Sobleski . "I'm real religious, so I think we're alone right now. I don't think there's other planets and other stuff like that."

The NFL hopeful said going down the black hole of theories from the likes of NBA All-Star Kyrie Irving and multiplatinum rapper B.o.B that the earth is flat had him rethink what he'd been taught. The celebrities deny the theory that the earth revolves around the sun, which was proposed by ancient Greek astronomers and further established by Renaissance scientist Nicolaus Copernicus. Italian philosopher Galileo Galilei essentially confirmed the theory with his use of telescopes and stood trial before the Roman Catholic Church for his beliefs, which are now considered scientific fact.

NFL DRAFT HUB: Latest NFL Draft mock drafts, news, live picks, grades and analysis.

"I thought I used to believe in the heliocentric thing where we used to revolve around the sun and stuff," Owens continued with a smile on his face. "But then I started seeing flat earth stuff and I was like, this is kind of interesting. They started bringing up valid points, so I mean I don't know, could be real, couldn't be."

After three seasons at Texas, Owens felt the gravitational pull to Texas Tech, where he played two seasons. He was considered a super senior last year for utilizing an extra season due to the 2020 pandemic. Last year, he had 37 tackles, including 10 against Houston.

In making their decision to draft him, NFL teams will have to let his talent eclipse his unconventional beliefs.