homework 4 trigonometric ratios & finding missing sides

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

5.4: Right Triangle Trigonometry

• Last updated
• Save as PDF
• Page ID 1363

Learning Objectives

• Use right triangles to evaluate trigonometric functions.
• Find function values for 30°(\(\dfrac{\pi}{6}\)),45°(\(\dfrac{\pi}{4}\)),and 60°(\(\dfrac{\pi}{3}\)).
• Use equal cofunctions of complementary angles.
• Use the definitions of trigonometric functions of any angle.
• Use right-triangle trigonometry to solve applied problems.

Mt. Everest, which straddles the border between China and Nepal, is the tallest mountain in the world. Measuring its height is no easy task and, in fact, the actual measurement has been a source of controversy for hundreds of years. The measurement process involves the use of triangles and a branch of mathematics known as trigonometry. In this section, we will define a new group of functions known as trigonometric functions, and find out how they can be used to measure heights, such as those of the tallest mountains.

We have previously defined the sine and cosine of an angle in terms of the coordinates of a point on the unit circle intersected by the terminal side of the angle:

\[ \begin{align*} \cos t &= x \\ \sin t &=y \end{align*} \]

In this section, we will see another way to define trigonometric functions using properties of right triangles .

Using Right Triangles to Evaluate Trigonometric Functions

In earlier sections, we used a unit circle to define the trigonometric functions . In this section, we will extend those definitions so that we can apply them to right triangles. The value of the sine or cosine function of \(t\) is its value at \(t\) radians. First, we need to create our right triangle. Figure \(\PageIndex{1}\) shows a point on a unit circle of radius 1. If we drop a vertical line segment from the point \((x,y)\) to the x -axis, we have a right triangle whose vertical side has length \(y\) and whose horizontal side has length \(x\). We can use this right triangle to redefine sine, cosine, and the other trigonometric functions as ratios of the sides of a right triangle.

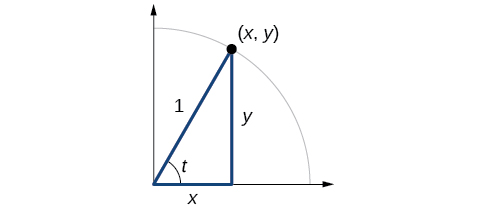
\[ \cos t= \frac{x}{1}=x \]

Likewise, we know

\[ \sin t= \frac{y}{1}=y \]

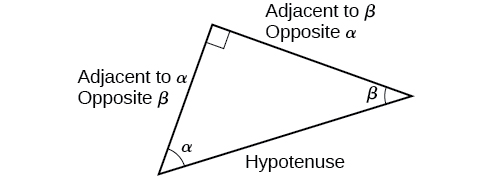
These ratios still apply to the sides of a right triangle when no unit circle is involved and when the triangle is not in standard position and is not being graphed using \((x,y)\) coordinates. To be able to use these ratios freely, we will give the sides more general names: Instead of \(x\),we will call the side between the given angle and the right angle the adjacent side to angle \(t\). (Adjacent means “next to.”) Instead of \(y\),we will call the side most distant from the given angle the opposite side from angle \(t\). And instead of \(1\),we will call the side of a right triangle opposite the right angle the hypotenuse . These sides are labeled in Figure \(\PageIndex{2}\).

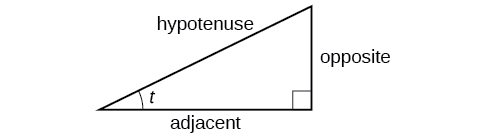
Understanding Right Triangle Relationships

Given a right triangle with an acute angle of \(t\),

\[\begin{align} \sin (t) &= \dfrac{\text{opposite}}{\text{hypotenuse}} \label{sindef}\\ \cos (t) &= \dfrac{\text{adjacent}}{\text{hypotenuse}} \label{cosdef}\\ \tan (t) &= \dfrac{\text{opposite}}{\text{adjacent}} \label{tandef}\end{align}\]

A common mnemonic for remembering these relationships is SohCahToa, formed from the first letters of “ S ine is o pposite over h ypotenuse, C osine is a djacent over h ypotenuse, T angent is o pposite over a djacent.”

how to: Given the side lengths of a right triangle and one of the acute angles, find the sine, cosine, and tangent of that angle

• Find the sine as the ratio of the opposite side to the hypotenuse.
• Find the cosine as the ratio of the adjacent side to the hypotenuse.
• Find the tangent is the ratio of the opposite side to the adjacent side.

Example \(\PageIndex{1}\): Evaluating a Trigonometric Function of a Right Triangle

Given the triangle shown in Figure \(\PageIndex{3}\), find the value of \(\cos α\).

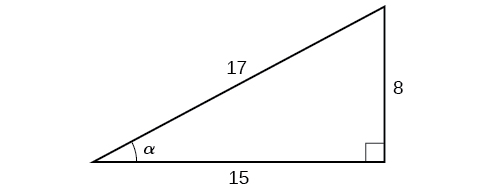
The side adjacent to the angle is 15, and the hypotenuse of the triangle is 17, so via Equation \ref{cosdef}:

\[\begin{align*} \cos (α) &= \dfrac{\text{adjacent}}{\text{hypotenuse}} \\[4pt] &= \dfrac{15}{17} \end{align*}\]

Exercise \(\PageIndex{1}\)

Given the triangle shown in Figure \(\PageIndex{4}\), find the value of \(\sin t\).

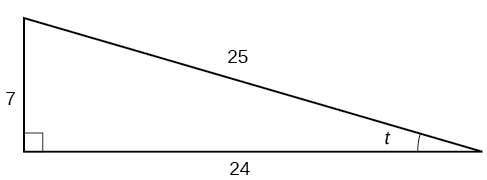
\(\frac{7}{25}\)

Relating Angles and Their Functions

When working with right triangles, the same rules apply regardless of the orientation of the triangle. In fact, we can evaluate the six trigonometric functions of either of the two acute angles in the triangle in Figure \(\PageIndex{5}\). The side opposite one acute angle is the side adjacent to the other acute angle, and vice versa.

We will be asked to find all six trigonometric functions for a given angle in a triangle. Our strategy is to find the sine, cosine, and tangent of the angles first. Then, we can find the other trigonometric functions easily because we know that the reciprocal of sine is cosecant, the reciprocal of cosine is secant, and the reciprocal of tangent is cotangent.

how to: Given the side lengths of a right triangle, evaluate the six trigonometric functions of one of the acute angles

• If needed, draw the right triangle and label the angle provided.
• Identify the angle, the adjacent side, the side opposite the angle, and the hypotenuse of the right triangle.
• sine as the ratio of the opposite side to the hypotenuse
• cosine as the ratio of the adjacent side to the hypotenuse
• tangent as the ratio of the opposite side to the adjacent side
• secant as the ratio of the hypotenuse to the adjacent side
• cosecant as the ratio of the hypotenuse to the opposite side
• cotangent as the ratio of the adjacent side to the opposite side

Example \(\PageIndex{2}\): Evaluating Trigonometric Functions of Angles Not in Standard Position

Using the triangle shown in Figure \(\PageIndex{6}\), evaluate \( \sin α, \cos α, \tan α, \sec α, \csc α,\) and \( \cot α\).

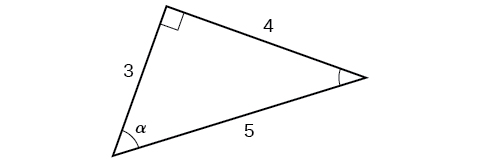
\[ \begin{align*} \sin α &= \dfrac{\text{opposite } α}{\text{hypotenuse}} = \dfrac{4}{5} \\ \cos α &= \dfrac{\text{adjacent to }α}{\text{hypotenuse}}=\dfrac{3}{5} \\ \tan α &= \dfrac{\text{opposite }α}{\text{adjacent to }α}=\dfrac{4}{3} \\ \sec α &= \dfrac{\text{hypotenuse}}{\text{adjacent to }α}= \dfrac{5}{3} \\ \csc α &= \dfrac{\text{hypotenuse}}{\text{opposite }α}=\dfrac{5}{4} \\ \cot α &= \dfrac{\text{adjacent to }α}{\text{opposite }α}=\dfrac{3}{4} \end{align*}\]

Exercise \(\PageIndex{2}\)

Using the triangle shown in Figure \(\PageIndex{7}\), evaluate \( \sin t, \cos t,\tan t, \sec t, \csc t,\) and \(\cot t\).

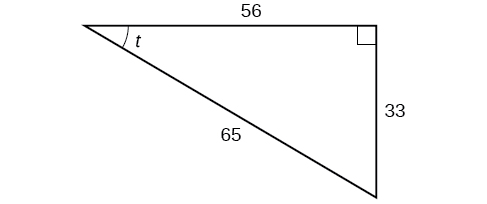
\[\begin{align*} \sin t &= \frac{33}{65}, \cos t= \frac{56}{65},\tan t= \frac{33}{56}, \\ \\ \sec t &= \frac{65}{56},\csc t= \frac{65}{33},\cot t= \frac{56}{33} \end{align*}\]

Finding Trigonometric Functions of Special Angles Using Side Lengths

We have already discussed the trigonometric functions as they relate to the special angles on the unit circle. Now, we can use those relationships to evaluate triangles that contain those special angles. We do this because when we evaluate the special angles in trigonometric functions, they have relatively friendly values, values that contain either no or just one square root in the ratio. Therefore, these are the angles often used in math and science problems. We will use multiples of \(30°, 60°,\) and \(45°\), however, remember that when dealing with right triangles, we are limited to angles between \(0° \text{ and } 90°\).

Suppose we have a \(30°,60°,90°\) triangle, which can also be described as a \(\frac{π}{6}, \frac{π}{3},\frac{π}{2}\) triangle. The sides have lengths in the relation \(s,\sqrt{3}s,2s.\) The sides of a \(45°,45°,90° \)triangle, which can also be described as a \(\frac{π}{4},\frac{π}{4},\frac{π}{2}\) triangle, have lengths in the relation \(s,s,\sqrt{2}s.\) These relations are shown in Figure \(\PageIndex{8}\).

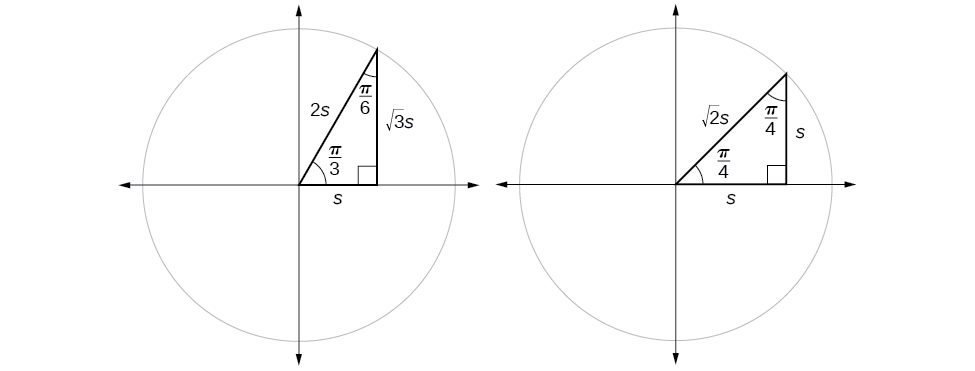
We can then use the ratios of the side lengths to evaluate trigonometric functions of special angles.

Given trigonometric functions of a special angle, evaluate using side lengths.

• Use the side lengths shown in Figure \(\PageIndex{8}\) for the special angle you wish to evaluate.
• Use the ratio of side lengths appropriate to the function you wish to evaluate.

Example \(\PageIndex{3}\): Evaluating Trigonometric Functions of Special Angles Using Side Lengths

Find the exact value of the trigonometric functions of \(\frac{π}{3}\), using side lengths.

\[\begin{align*} \sin (\dfrac{π}{3}) &= \dfrac{\text{opp}}{\text{hyp}}=\dfrac{\sqrt{3}s}{2s}=\dfrac{\sqrt{3}}{2} \\ \cos (\dfrac{π}{3}) &= \dfrac{\text{adj}}{\text{hyp}}=\dfrac{s}{2s}=\dfrac{1}{2} \\ \tan (\dfrac{π}{3}) &= \dfrac{\text{opp}}{\text{adj}} =\dfrac{\sqrt{3}s}{s}=\sqrt{3} \\ \sec (\dfrac{π}{3}) &= \dfrac{\text{hyp}}{\text{adj}} = \dfrac{2s}{s}=2 \\ \csc (\dfrac{π}{3}) &= \dfrac{\text{hyp}}{\text{opp}} =\dfrac{2s}{\sqrt{3}s}=\dfrac{2}{\sqrt{3}}=\dfrac{2\sqrt{3}}{3} \\ \cot (\dfrac{π}{3}) &= \dfrac{\text{adj}}{\text{opp}}=\dfrac{s}{\sqrt{3}s}=\dfrac{1}{\sqrt{3}}=\dfrac{\sqrt{3}}{3} \end{align*}\]

Exercise \(\PageIndex{3}\)

Find the exact value of the trigonometric functions of \(\frac{π}{4}\) using side lengths.

\( \sin (\frac{π}{4})=\frac{\sqrt{2}}{2}, \cos (\frac{π}{4})=\frac{\sqrt{2}}{2}, \tan (\frac{π}{4})=1,\)

\( \sec (\frac{π}{4})=\sqrt{2}, \csc (\frac{π}{4})=\sqrt{2}, \cot (\frac{π}{4}) =1 \)

Using Equal Cofunction of Complements

If we look more closely at the relationship between the sine and cosine of the special angles relative to the unit circle, we will notice a pattern. In a right triangle with angles of \(\frac{π}{6}\) and \(\frac{π}{3}\), we see that the sine of \(\frac{π}{3}\), namely \(\frac{\sqrt{3}}{2}\), is also the cosine of \(\frac{π}{6}\), while the sine of \(\frac{π}{6}\), namely \(\frac{1}{2},\) is also the cosine of \(\frac{π}{3}\) (Figure \(\PageIndex{9}\)).

\[\begin{align*} \sin \frac{π}{3} &= \cos \frac{π}{6}=\frac{\sqrt{3}s}{2s}=\frac{\sqrt{3}}{2} \\ \sin \frac{π}{6} &= \cos \frac{π}{3}=\frac{s}{2s}=\frac{1}{2} \end{align*}\]

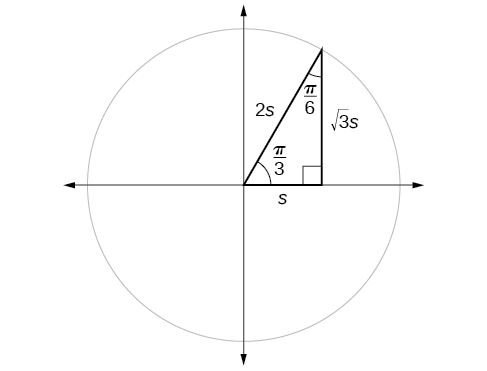
This result should not be surprising because, as we see from Figure \(\PageIndex{9}\), the side opposite the angle of \(\frac{π}{3}\) is also the side adjacent to \(\frac{π}{6}\), so \(\sin (\frac{π}{3})\) and \(\cos (\frac{π}{6})\) are exactly the same ratio of the same two sides, \(\sqrt{3} s\) and \(2s.\) Similarly, \( \cos (\frac{π}{3})\) and \( \sin (\frac{π}{6})\) are also the same ratio using the same two sides, \(s\) and \(2s\).

The interrelationship between the sines and cosines of \(\frac{π}{6}\) and \(\frac{π}{3}\) also holds for the two acute angles in any right triangle, since in every case, the ratio of the same two sides would constitute the sine of one angle and the cosine of the other. Since the three angles of a triangle add to π, and the right angle is \(\frac{π}{2}\), the remaining two angles must also add up to \(\frac{π}{2}\). That means that a right triangle can be formed with any two angles that add to \(\frac{π}{2}\)—in other words, any two complementary angles. So we may state a cofunction identity : If any two angles are complementary, the sine of one is the cosine of the other, and vice versa. This identity is illustrated in Figure \(\PageIndex{10}\).

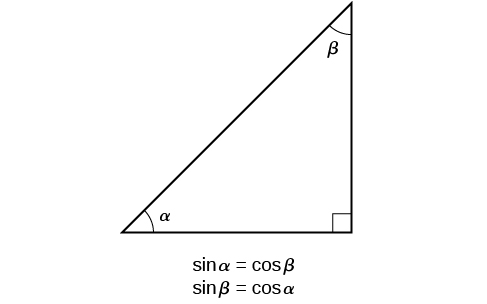
Using this identity, we can state without calculating, for instance, that the sine of \(\frac{π}{12}\) equals the cosine of \(\frac{5π}{12}\), and that the sine of \(\frac{5π}{12}\) equals the cosine of \(\frac{π}{12}\). We can also state that if, for a certain angle \(t, \cos t= \frac{5}{13},\) then \( \sin (\frac{π}{2}−t)=\frac{5}{13}\) as well.

COFUNCTION IDENTITIES

The cofunction identities in radians are listed in Table \(\PageIndex{1}\).

how to: Given the sine and cosine of an angle, find the sine or cosine of its complement.

• To find the sine of the complementary angle, find the cosine of the original angle.
• To find the cosine of the complementary angle, find the sine of the original angle.

Example \(\PageIndex{4}\): Using Cofunction Identities

If \( \sin t = \frac{5}{12},\) find \(( \cos \frac{π}{2}−t)\).

According to the cofunction identities for sine and cosine,

\[ \sin t= \cos (\dfrac{π}{2}−t). \nonumber\]

\[ \cos (\dfrac{π}{2}−t)= \dfrac{5}{12}. \nonumber\]

Exercise \(\PageIndex{4}\)

If \(\csc (\frac{π}{6})=2,\) find \( \sec (\frac{π}{3}).\)

Using Trigonometric Functions

In previous examples, we evaluated the sine and cosine in triangles where we knew all three sides. But the real power of right-triangle trigonometry emerges when we look at triangles in which we know an angle but do not know all the sides.

how to: Given a right triangle, the length of one side, and the measure of one acute angle, find the remaining sides

• For each side, select the trigonometric function that has the unknown side as either the numerator or the denominator. The known side will in turn be the denominator or the numerator.
• Write an equation setting the function value of the known angle equal to the ratio of the corresponding sides.
• Using the value of the trigonometric function and the known side length, solve for the missing side length.

Example \(\PageIndex{5}\): Finding Missing Side Lengths Using Trigonometric Ratios

Find the unknown sides of the triangle in Figure \(\PageIndex{11}\).

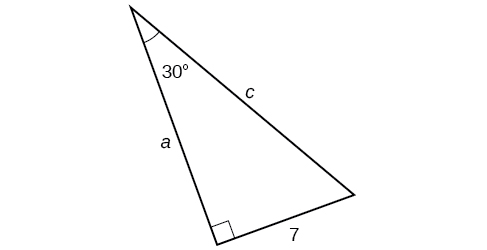
We know the angle and the opposite side, so we can use the tangent to find the adjacent side.

\[ \tan (30°)= \dfrac{7}{a} \nonumber\]

We rearrange to solve for \(a\).

\[\begin{align} a &=\dfrac{7}{ \tan (30°)} \\ & =12.1 \end{align} \nonumber\]

We can use the sine to find the hypotenuse.

\[ \sin (30°)= \dfrac{7}{c} \nonumber\]

Again, we rearrange to solve for \(c\).

\[\begin{align*} c &= \dfrac{7}{\sin (30°)} =14 \end{align*}\]

Exercise \(\PageIndex{5}\):

A right triangle has one angle of \(\frac{π}{3}\) and a hypotenuse of 20. Find the unknown sides and angle of the triangle.

\(\mathrm{adjacent=10; opposite=10 \sqrt{3}; }\) missing angle is \(\frac{π}{6}\)

Using Right Triangle Trigonometry to Solve Applied Problems

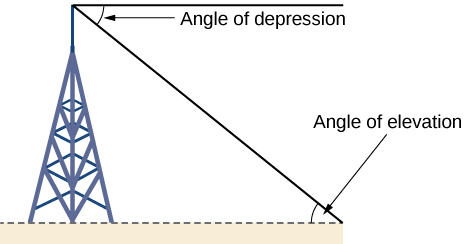
Right-triangle trigonometry has many practical applications. For example, the ability to compute the lengths of sides of a triangle makes it possible to find the height of a tall object without climbing to the top or having to extend a tape measure along its height. We do so by measuring a distance from the base of the object to a point on the ground some distance away, where we can look up to the top of the tall object at an angle. The angle of elevation of an object above an observer relative to the observer is the angle between the horizontal and the line from the object to the observer's eye. The right triangle this position creates has sides that represent the unknown height, the measured distance from the base, and the angled line of sight from the ground to the top of the object. Knowing the measured distance to the base of the object and the angle of the line of sight, we can use trigonometric functions to calculate the unknown height. Similarly, we can form a triangle from the top of a tall object by looking downward. The angle of depression of an object below an observer relative to the observer is the angle between the horizontal and the line from the object to the observer's eye. See Figure \(\PageIndex{12}\).

how to: Given a tall object, measure its height indirectly

• Make a sketch of the problem situation to keep track of known and unknown information.
• Lay out a measured distance from the base of the object to a point where the top of the object is clearly visible.
• At the other end of the measured distance, look up to the top of the object. Measure the angle the line of sight makes with the horizontal.
• Write an equation relating the unknown height, the measured distance, and the tangent of the angle of the line of sight.
• Solve the equation for the unknown height.

Example \(\PageIndex{6}\): Measuring a Distance Indirectly

To find the height of a tree, a person walks to a point 30 feet from the base of the tree. She measures an angle of 57° 57° between a line of sight to the top of the tree and the ground, as shown in Figure \(\PageIndex{13}\). Find the height of the tree.

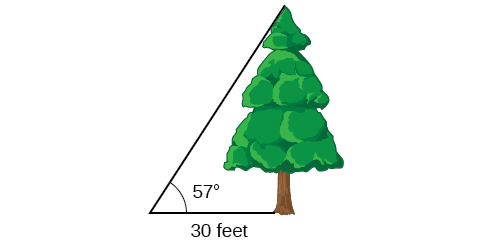
We know that the angle of elevation is \(57°\) and the adjacent side is 30 ft long. The opposite side is the unknown height.

The trigonometric function relating the side opposite to an angle and the side adjacent to the angle is the tangent. So we will state our information in terms of the tangent of \(57°\), letting \(h\) be the unknown height.

\[\begin{array}{cl} \tan θ = \dfrac{\text{opposite}}{\text{adjacent}} & \text{} \\ \tan (57°) = \dfrac{h}{30} & \text{Solve for }h. \\ h=30 \tan (57°) & \text{Multiply.} \\ h≈46.2 & \text{Use a calculator.} \end{array} \]

The tree is approximately 46 feet tall.

Exercise \(\PageIndex{6}\):

How long a ladder is needed to reach a windowsill 50 feet above the ground if the ladder rests against the building making an angle of \(\frac{5π}{12}\) with the ground? Round to the nearest foot.

About 52 ft

Access these online resources for additional instruction and practice with right triangle trigonometry.

• Finding Trig Functions on Calculator
• Finding Trig Functions Using a Right Triangle
• Relate Trig Functions to Sides of a Right Triangle
• Determine Six Trig Functions from a Triangle
• Determine Length of Right Triangle Side

Visit this website for additional practice questions from Learningpod.

Key Equations

Cofunction Identities

\[\begin{align*} \cos t &= \sin ( \frac{π}{2}−t) \\ \sin t &= \cos (\frac{π}{2}−t) \\ \tan t &= \cot (\frac{π}{2}−t) \\ \cot t &= \tan (\frac{π}{2}−t) \\ \sec t &= \csc (\frac{π}{2}−t) \\ \csc t &= \sec (\frac{π}{2}−t) \end{align*}\]

Key Concepts

• We can define trigonometric functions as ratios of the side lengths of a right triangle. See Example .
• The same side lengths can be used to evaluate the trigonometric functions of either acute angle in a right triangle. See Example .
• We can evaluate the trigonometric functions of special angles, knowing the side lengths of the triangles in which they occur. See Example .
• Any two complementary angles could be the two acute angles of a right triangle.
• If two angles are complementary, the cofunction identities state that the sine of one equals the cosine of the other and vice versa. See Example .
• We can use trigonometric functions of an angle to find unknown side lengths.
• Select the trigonometric function representing the ratio of the unknown side to the known side. See Example .
• Right-triangle trigonometry permits the measurement of inaccessible heights and distances.
• The unknown height or distance can be found by creating a right triangle in which the unknown height or distance is one of the sides, and another side and angle are known. See Example .

Trig Triangle Calculator

Right triangle trigonometry, using two sides for right triangle trigonometry calculation, using one angle and one side for right triangle trigonometry calculation, using area and one side for right triangle trig calculation, other trigonometry and triangle calculators.

If you're dealing with trigonometry and right triangles, this trig calculator for right triangles is here for you. This tool uses trigonometry to calculate these triangles, as long as you know:

• Two of its sides;
• One angle and one side; or
• The area and one side.

To learn more, keep reading this article that briefly discusses the trigonometry behind right triangles.

This trig triangle calculator uses the following widely-known trigonometric ratios, which relate the sides of a right triangle to its angles:

🙋 To know how to calculate or evaluate the sine, cosine, and tangent functions, visit our trig calculator .

Additionally, we can use the inverse trigonometric functions to solve for the angles if we know the length of the sides:

🙋 To know how to calculate or evaluate these inverse functions, visit our inverse sine , inverse cosine , and inverse tangent calculators .

Let's use the following triangle to explain how this calculator solves for the different sides and angles according to the information known.

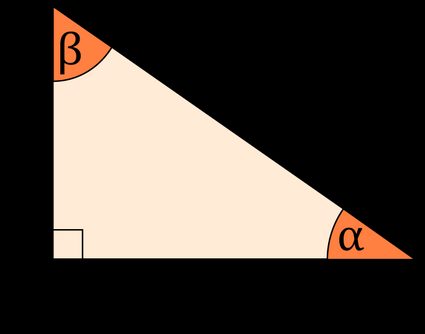
Finding the third side

If you know two sides, the easiest way to find the third side is by using the Pythagorean theorem ( what is the Pythagorean theorem ).

• Given a and b: c = a 2 + b 2 c = \sqrt{a^2 + b^2} c = a 2 + b 2 ​ ;
• Given a and c: b = c 2 − a 2 b = \sqrt{c^2 - a^2} b = c 2 − a 2 ​ ; and
• Given b and c: a = c 2 − b 2 a = \sqrt{c^2 - b^2} a = c 2 − b 2 ​ .

Finding the angles

Then, we can find α \alpha α or β \beta β by taking any of the inverse trigonometric functions mentioned previously:

Finding the angle

The sum of the internal angles of a triangle will always be 360 ° 360\degree 360° . In a right triangle , there's a right angle ( 90 ° 90\degree 90° ) and, therefore, the sum of the other two angles ( α \alpha α and β \beta β ) will be 90 ° 90\degree 90° . Therefore:

• Given β \beta β : α = 90 ° − β \alpha = 90\degree - \beta α = 90° − β ; or
• Given α \alpha α : β = 90 ° − α \beta = 90\degree - \alpha β = 90° − α

Finding the two missing sides

To find the two unknown sides, you can use the angle α \alpha α and the trigonometric ratios:

Given a : c = a / sin ⁡ α c = a/{\sin{\alpha}} c = a / sin α and b = a / tan ⁡ α b = a/{\tan{\alpha}} b = a / tan α ;

Given b : c = b / cos ⁡ α c = b/{\cos{\alpha}} c = b / cos α and a = b × tan ⁡ α a = b \times {\tan{\alpha}} a = b × tan α ; and

Given c : a = c × sin ⁡ α a = c \times \sin{\alpha} a = c × sin α and b = c × cos ⁡ α b = c \times {\cos{\alpha}} b = c × cos α ;

If you know a a a or b b b , use the right triangle area formula that relates the base ( b b b ) to the height ( a a a ) and solve for the unknown side:

• Given a: b = 2 × Area / a b = 2 \times \text{Area}/a b = 2 × Area / a ; and
• Given b: a = 2 × Area / b a = 2 \times \text{Area}/b a = 2 × Area / b .

Once you know at least two sides, use the second section method to obtain the angles.

• Trigonometry calculator ;
• Cosine triangle calculator ;
• Sine triangle calculator ;
• Right triangle trigonometry calculator ;
• Sine cosine tangent calculator ;
• Tangent ratio calculator ; and
• Tangent angle calculator .

What's the leg measurement of a 45-45-90 triangle of 18 cm hypotenuse?

If the hypotenuse of a 45-45-90 triangle measures 18 cm, the length of any of its two legs is 9√2 cm or 12.728 cm . To get to this answer:

Take the sin of any of the 45° angles, which equals any of the legs ( a ) divided by the hypotenuse ( c ):

sin(45°) = a / c

Solve for the leg ( a ): a = c × sin(45°)

Remember that sin(45°) = 1/√2 and input the hypotenuse c = 18 cm : a = 18 cm × (1/√2) : = 9/√2 cm = 12.728 cm

What's the leg measurement of a 45-45-90 triangle of 10√5 inches hypotenuse?

If the hypotenuse of a 45-45-90 triangle measures 10√5 inches, the length of any of its two legs is 5√10 inches or 15.81 inches . To get to this answer:

You can use the formula that relates the hypotenuse ( c ) to any of the legs ( a ) of a 45-45-90 triangle: c = a × √2

And solve for the leg a :

a = c /√2 = (10√5 in)/√2 = 5√10 in = 15.81 in.

Meat footprint

Radius of a circle, simplify ratio, steps to calories.

• Biology (99)
• Chemistry (98)
• Construction (144)
• Conversion (292)
• Ecology (30)
• Everyday life (261)
• Finance (569)
• Health (440)
• Physics (508)
• Sports (104)
• Statistics (182)
• Other (181)
• Discover Omni (40)

FIND THE MISSIND SIDE USING TRIGONOMETRIC RATIOS

Consider a right-angled triangle, right-angled at B.

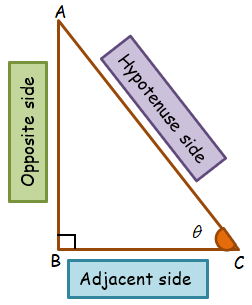
The trigonometry ratios for a specific angle θ. There are six trigonometric ratios.  

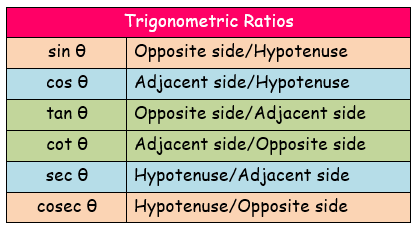
Find the value of x, giving your answer correct to 2 decimal places :

Example 1 :

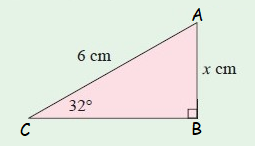
In the figure,

Opposite side (AB)  =  x cm

Hypotenuse (AC)  =  6 cm

Here θ  =  32˚

The sides opposite and hypotenuse are involving in the trigonometric ratio sin θ

sin θ  =  Opposite side/Hypotenuse  =  AB/AC

sin 32˚  =  x/6

By using the calculator, we get

0.529  =  x/6

(0.53 × 6)  =  x

x  =  3.18

So, the value of x is 3.18 cm

Example 2 :

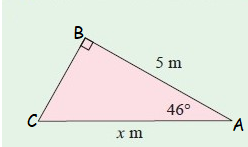
Hypotenuse side AC  =  x cm

Adjacent side AB  =  5 cm

Here θ  =  46˚

The sides hypotenuse and adjacent are involving in the trigonometric ratio sec θ

sec 46˚  =  Hypotenuse/Adjacent side  =  AC/AB

sec 46˚  =  x/5

1.44  =  x/5

(1.44 × 5)  =  x

x  =  7.2

So, the value of x is 7.20 cm

Example 3 :

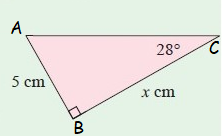
Opposite side AB  =  5 cm

Adjacent side BC  =  x cm

Here θ  =  28˚

The sides opposite and adjacent are involving in the trigonometric ratio tan θ

tan 28˚  =  Opposite side/Adjacent side  =  AB/BC

tan 28˚  =  5/x

0.532  =  5/x

x  =  5/0.532

x  =  9.4

So, the value of x is 9.40 cm

Find, to 2 significant figures, the value of θ :

Example 4 :

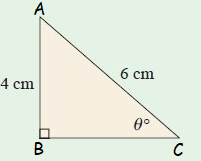
Solution  :

Opposite side AB  =  4 cm

Hypotenuse side AC  =  6 cm

Here θ  =  θ˚

sin θ  =  Opposite side/Hypotenuse side  =  AB/AC

sin θ˚  =  4/6

sin θ˚  =  2/3

 θ˚  =  sin -1 (2/3)

θ  =  42˚

So, the value of θ is 42˚

Example 5  :

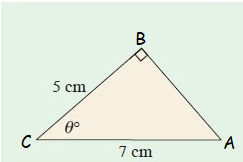
Hypotenuse side AC  =  7 cm

Adjacent side BC  =  5 cm

sec θ˚  =  Hypotenuse/Adjacent side  =  AC/BC

sec θ˚  =  7/5

θ˚  =  sec -1 (7/5)

θ  =  44˚

So, the value of θ is 44˚

Example 6 :

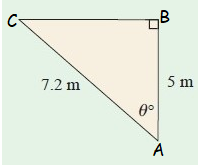
Hypotenuse side AC  =  7.2 cm

sec θ˚  =  Hypotenuse/Adjacent side  =  AC/AB

sec θ˚  =  7.2/5

θ˚  =  sec -1 (7.2/5)

θ  =  46˚

So, the value of θ is 46˚

Apart from the stuff given above,  i f  you need any other stuff in math, please use our google custom search here.

Kindly mail your feedback to   [email protected]

We always appreciate your feedback.

© All rights reserved. onlinemath4all.com

• Sat Math Practice
• SAT Math Worksheets
• PEMDAS Rule
• BODMAS rule
• GEMDAS Order of Operations
• Math Calculators
• Transformations of Functions
• Order of rotational symmetry
• Lines of symmetry
• Compound Angles
• Quantitative Aptitude Tricks
• Trigonometric ratio table
• Word Problems
• Times Table Shortcuts
• 10th CBSE solution
• PSAT Math Preparation
• Privacy Policy
• Laws of Exponents

Recent Articles

Algebraic and Numeric Expressions

Apr 06, 24 04:11 AM

Properties of Parallelograms Worksheet

Apr 06, 24 02:28 AM

Parallelogram Worksheet

Apr 06, 24 02:26 AM

• Precalculus
• Signup / Login

Using Trig Ratios to Solve for Missing Sides (Lesson 7.4)

Unit 1: reasoning in geometry, day 1: creating definitions, day 2: inductive reasoning, day 3: conditional statements, day 4: quiz 1.1 to 1.3, day 5: what is deductive reasoning, day 6: using deductive reasoning, day 7: visual reasoning, day 8: unit 1 review, day 9: unit 1 test, unit 2: building blocks of geometry, day 1: points, lines, segments, and rays, day 2: coordinate connection: midpoint, day 3: naming and classifying angles, day 4: vertical angles and linear pairs, day 5: quiz 2.1 to 2.4, day 6: angles on parallel lines, day 7: coordinate connection: parallel vs. perpendicular, day 8: coordinate connection: parallel vs. perpendicular, day 9: quiz 2.5 to 2.6, day 10: unit 2 review, day 11: unit 2 test, unit 3: congruence transformations, day 1: introduction to transformations, day 2: translations, day 3: reflections, day 4: rotations, day 5: quiz 3.1 to 3.4, day 6: compositions of transformations, day 7: compositions of transformations, day 8: definition of congruence, day 9: coordinate connection: transformations of equations, day 10: quiz 3.5 to 3.7, day 11: unit 3 review, day 12: unit 3 test, unit 4: triangles and proof, day 1: what makes a triangle, day 2: triangle properties, day 3: proving the exterior angle conjecture, day 4: angle side relationships in triangles, day 5: right triangles & pythagorean theorem, day 6: coordinate connection: distance, day 7: review 4.1-4.6, day 8: quiz 4.1to 4.6, day 9: establishing congruent parts in triangles, day 10: triangle congruence shortcuts, day 11: more triangle congruence shortcuts, day 12: more triangle congruence shortcuts, day 13: triangle congruence proofs, day 14: triangle congruence proofs, day 15: quiz 4.7 to 4.10, day 16: unit 4 review, day 17: unit 4 test, unit 5: quadrilaterals and other polygons, day 1: quadrilateral hierarchy, day 2: proving parallelogram properties, day 3: properties of special parallelograms, day 4: coordinate connection: quadrilaterals on the plane, day 5: review 5.1-5.4, day 6: quiz 5.1 to 5.4, day 7: areas of quadrilaterals, day 8: polygon interior and exterior angle sums, day 9: regular polygons and their areas, day 10: quiz 5.5 to 5.7, day 11: unit 5 review, day 12: unit 5 test, unit 6: similarity, day 1: dilations, scale factor, and similarity, day 2: coordinate connection: dilations on the plane, day 3: proving similar figures, day 4: quiz 6.1 to 6.3, day 5: triangle similarity shortcuts, day 6: proportional segments between parallel lines, day 7: area and perimeter of similar figures, day 8: quiz 6.4 to 6.6, day 9: unit 6 review, day 10: unit 6 test, unit 7: special right triangles & trigonometry, day 1: 45˚, 45˚, 90˚ triangles, day 2: 30˚, 60˚, 90˚ triangles, day 3: trigonometric ratios, day 4: using trig ratios to solve for missing sides, day 5: review 7.1-7.4, day 6: quiz 7.1 to 7.4, day 7: inverse trig ratios, day 8: applications of trigonometry, day 9: quiz 7.5 to 7.6, day 10: unit 7 review, day 11: unit 7 test, unit 8: circles, day 1: coordinate connection: equation of a circle, day 2: circle vocabulary, day 3: tangents to circles, day 4: chords and arcs, day 5: perpendicular bisectors of chords, day 6: inscribed angles and quadrilaterals, day 7: review 8.1-8.6, day 8: quiz 8.1 to 8.6, day 9: area and circumference of a circle, day 10: area of a sector, day 11: arc length, day 12: quiz 8.7 to 8.9, day 13: unit 8 review, day 14: unit 8 test, unit 9: surface area and volume, day 1: introducing volume with prisms and cylinders, day 2: surface area and volume of prisms and cylinders, day 3: volume of pyramids and cones, day 4: surface area of pyramids and cones, day 5: review 9.1-9.4, day 6: quiz 9.1 to 9.4, day 7: volume of spheres, day 8: surface area of spheres, day 9: problem solving with volume, day 10: volume of similar solids, day 11: quiz 9.5 to 9.8, day 12: unit 9 review, day 13: unit 9 test, unit 10: statistics and probability, day 1: categorical data and displays, day 2: measures of center for quantitative data, day 3: measures of spread for quantitative data, day 4: quiz review (10.1 to 10.3), day 5: quiz 10.1 to 10.3, day 6: scatterplots and line of best fit, day 7: predictions and residuals, day 8: models for nonlinear data, day 9: quiz review (10.4 to 10.6), day 10: quiz 10.4 to 10.6, day 11: probability models and rules, day 12: probability using two-way tables, day 13: probability using tree diagrams, day 14: quiz review (10.7 to 10.9), day 15: quiz 10.7 to 10.9, day 16: random sampling, day 17: margin of error, day 18: observational studies and experiments, day 19: random sample and random assignment, day 20: quiz review (10.10 to 10.13), day 21: quiz 10.10 to 10.13, learning targets.

Use a calculator to find sine, cosine, and tangent ratios for a given right triangle and interpret these ratios.

Given an angle and side in a right triangle, choose a trig ratio and use proportional reasoning to solve for a missing side.

Activity: Unlocking the Triangle

Lesson handouts, media locked.

Our Teaching Philosophy:

Experience first, formalize later (effl), experience first.

Today we make more explicit the connection between similar triangles and right triangle trigonometry by solving for a side in two different ways. First, students are given a similar triangle, much like they were in Unit 6. The ratio of sides is consistent in both triangles, so reasoning proportionally can help determine the missing side. While students may use the idea of scale factor to set up the ratio, we want to encourage them to consider the ratio of sides within a triangle. We purposefully chose the numbers to make this easy. Students should note that the hypotenuse is three times the length of the given leg, and use this to determine that the hypotenuse is 30 on triangle ABC. In question 3, students recognize that this ratio of ⅓ is given by the sine of the corresponding angle.

In question 4, we provide only information about the sine. Students should be able to tell that the given side is ⅖ of the hypotenuse and then use the Pythagorean theorem to solve for the other leg. Part b asks them to think about the angle in this triangle compared to when the sine ratio was ⅓. If the angle determines the ratio, then having different ratios means the angle must have been different! This is a sneak preview of lesson 7.4 when students study inverse trig. Question 5 is the big idea of today’s lesson. Knowing the value of a trig ratio is equivalent to being given a similar triangle, just in a shorthand form! So the trig ratio is the key to unlocking the triangle!

Finally in question 6 we break their tools and then provide the necessary information in the debrief. Remember that students don’t know how to use their calculator yet to determine the trig ratio. So when given a 40˚, 50˚, 90˚ triangle, they have no way to determine the ratios because they don’t have a similar triangle to refer back to nor is this one of the special right triangles they studied in Lesson 7.1. Their answer to the question should be “no.”

In the debrief, ask questions to get them to say that they need a ratio or relationship between the sides in this particular type of triangle. Ask them which ratio in particular they want (any of the three would work!). Then point out how they can “look up” that ratio using the calculator. Then send them back to their groups one last time to find the missing side, now that they know the ratio.

Guiding Questions

• (Question 4) Is this triangle similar to the previous one? How do you know?
• (Question 6) What information would you like to have to be able to figure out the rest of the triangle?

Formalize Later

Today’s lesson is fundamental to understanding the need for trig ratios! Instead of needing a similar triangle to refer back to, the sine, cosine, and tangent ratios are the key to unlocking any right triangle because they embed the same information as the similar triangle does, but in shorthand form. Note that when students were given a similar triangle in Unit 6 that acted as their reference triangle, the actual side lengths were not important, only the ratios of side lengths and angle measures were important, and this information is encoded in the sine, cosine and tangent ratios. The sine, cosine, and tangent ratios represent the entire set of similar triangles!

In the first Check Your Understanding (CYU) question, students tie together everything they know about trig ratios, similar triangles, and right triangles. Students should notice that since the adjacent to hypotenuse ratio in both triangles is ⅘, the triangles must be similar. The easiest way to make the second triangle is to make it a scale factor of the first, though some students might look for other numbers that are in a ratio of 4:5 instead of thinking of multiples of 4 and 5.

In questions 2 and 3, students solve more traditional right triangle trigonometry problems but the emphasis should be on first finding a ratio and then reasoning proportionally, instead of algebraically solving an equation. While students may set up a proportion, and actually isolate x, this is not the only valid method for solving.

Math Medic Help