uniformly accelerated motion problem solving

Physics Problems with Solutions

Electric Circuits
Electrostatic
Calculators
Practice Tests
Simulations
Uniform Acceleration Motion: Problems with Solutions

Problems on velocity and uniform acceleration are presented along with detailed solutions and tutorials can also be found in this website.

From rest, a car accelerated at 8 m/s 2 for 10 seconds. a) What is the position of the car at the end of the 10 seconds? b) What is the velocity of the car at the end of the 10 seconds? Solution to Problem 1

With an initial velocity of 20 km/h, a car accelerated at 8 m/s 2 for 10 seconds. a) What is the position of the car at the end of the 10 seconds? b) What is the velocity of the car at the end of the 10 seconds? Solution to Problem 2

A car accelerates uniformly from 0 to 72 km/h in 11.5 seconds. a) What is the acceleration of the car in m/s 2 ? b) What is the position of the car by the time it reaches the velocity of 72 km/h? Solution to Problem 3

An object is thrown straight down from the top of a building at a speed of 20 m/s. It hits the ground with a speed of 40 m/s. a) How high is the building? b) How long was the object in the air? Solution to Problem 4

A train brakes from 40 m/s to a stop over a distance of 100 m. a) What is the acceleration of the train? b) How much time does it take the train to stop? Solution to Problem 5

A boy on a bicycle increases his velocity from 5 m/s to 20 m/s in 10 seconds. a) What is the acceleration of the bicycle? b) What distance was covered by the bicycle during the 10 seconds? Solution to Problem 6

a) How long does it take an airplane to take off if it needs to reach a speed on the ground of 350 km/h over a distance of 600 meters (assume the plane starts from rest)? b) What is the acceleration of the airplane over the 600 meters? Solution to Problem 7

Starting from a distance of 20 meters to the left of the origin and at a velocity of 10 m/s, an object accelerates to the right of the origin for 5 seconds at 4 m/s 2 . What is the position of the object at the end of the 5 seconds of acceleration? Solution to Problem 8

What is the smallest distance, in meters, needed for an airplane touching the runway with a velocity of 360 km/h and an acceleration of -10 m/s 2 to come to rest? Solution to Problem 9

Problem 10:

To approximate the height of a water well, Martha and John drop a heavy rock into the well. 8 seconds after the rock is dropped, they hear a splash caused by the impact of the rock on the water. What is the height of the well. (Speed of sound in air is 340 m/s). Solution to Problem 10

Problem 11:

A rock is thrown straight up and reaches a height of 10 m. a) How long was the rock in the air? b) What is the initial velocity of the rock? Solution to Problem 11

Problem 12:

A car accelerates from rest at 1.0 m/s 2 for 20.0 seconds along a straight road . It then moves at a constant speed for half an hour. It then decelerates uniformly to a stop in 30.0 s. Find the total distance covered by the car. Solution to Problem 12

POPULAR PAGES

JEE-IIT-NCERT Physics & Math

Widget atas posting, uniform acceleration motion problems and solutions.

Problem #1

uniformly accelerated motion problem solving

Check Your Understanding

Answer: d = 1720 m

Answer: a = 8.10 m/s/s

Answers: d = 33.1 m and v f = 25.5 m/s

Answers: a = 11.2 m/s/s and d = 79.8 m

Answer: t = 1.29 s

Answers: a = 243 m/s/s

Answer: a = 0.712 m/s/s

Answer: d = 704 m

Answer: d = 28.6 m

Answer: v i = 7.17 m/s

Answer: v i = 5.03 m/s and hang time = 1.03 s (except for in sports commericals)

Answer: a = 1.62*10 5 m/s/s

Answer: d = 48.0 m

Answer: t = 8.69 s

Answer: a = -1.08*10^6 m/s/s

Answer: d = -57.0 m (57.0 meters deep)

Answer: v i = 47.6 m/s

Answer: a = 2.86 m/s/s and t = 30. 8 s

Answer: a = 15.8 m/s/s

Answer: v i = 94.4 mi/hr

Solutions to Above Problems

d = (0 m/s)*(32.8 s)+ 0.5*(3.20 m/s 2 )*(32.8 s) 2

Return to Problem 1

110 m = (0 m/s)*(5.21 s)+ 0.5*(a)*(5.21 s) 2

110 m = (13.57 s 2 )*a

a = (110 m)/(13.57 s 2 )

a = 8.10 m/ s 2

Return to Problem 2

d = (0 m/s)*(2.60 s)+ 0.5*(-9.8 m/s 2 )*(2.60 s) 2

d = -33.1 m (- indicates direction)

v f = v i + a*t

v f = 0 + (-9.8 m/s 2 )*(2.60 s)

v f = -25.5 m/s (- indicates direction)

Return to Problem 3

a = (46.1 m/s - 18.5 m/s)/(2.47 s)

a = 11.2 m/s 2

d = v i *t + 0.5*a*t 2

d = (18.5 m/s)*(2.47 s)+ 0.5*(11.2 m/s 2 )*(2.47 s) 2

d = 45.7 m + 34.1 m

(Note: the d can also be calculated using the equation v f 2 = v i 2 + 2*a*d)

Return to Problem 4

-1.40 m = (0 m/s)*(t)+ 0.5*(-1.67 m/s 2 )*(t) 2

-1.40 m = 0+ (-0.835 m/s 2 )*(t) 2

(-1.40 m)/(-0.835 m/s 2 ) = t 2

1.68 s 2 = t 2

Return to Problem 5

a = (444 m/s - 0 m/s)/(1.83 s)

a = 243 m/s 2

d = (0 m/s)*(1.83 s)+ 0.5*(243 m/s 2 )*(1.83 s) 2

d = 0 m + 406 m

Return to Problem 6

(7.10 m/s) 2 = (0 m/s) 2 + 2*(a)*(35.4 m)

50.4 m 2 /s 2 = (0 m/s) 2 + (70.8 m)*a

(50.4 m 2 /s 2 )/(70.8 m) = a

a = 0.712 m/s 2

Return to Problem 7

(65 m/s) 2 = (0 m/s) 2 + 2*(3 m/s 2 )*d

4225 m 2 /s 2 = (0 m/s) 2 + (6 m/s 2 )*d

(4225 m 2 /s 2 )/(6 m/s 2 ) = d

Return to Problem 8

d = (22.4 m/s + 0 m/s)/2 *2.55 s

d = (11.2 m/s)*2.55 s

Return to Problem 9

(0 m/s) 2 = v i 2 + 2*(-9.8 m/s 2 )*(2.62 m)

0 m 2 /s 2 = v i 2 - 51.35 m 2 /s 2

51.35 m 2 /s 2 = v i 2

v i = 7.17 m/s

Return to Problem 10

(0 m/s) 2 = v i 2 + 2*(-9.8 m/s 2 )*(1.29 m)

0 m 2 /s 2 = v i 2 - 25.28 m 2 /s 2

25.28 m 2 /s 2 = v i 2

v i = 5.03 m/s

To find hang time, find the time to the peak and then double it.

0 m/s = 5.03 m/s + (-9.8 m/s 2 )*t up

-5.03 m/s = (-9.8 m/s 2 )*t up

(-5.03 m/s)/(-9.8 m/s 2 ) = t up

t up = 0.513 s

hang time = 1.03 s

Return to Problem 11

(521 m/s) 2 = (0 m/s) 2 + 2*(a)*(0.840 m)

271441 m 2 /s 2 = (0 m/s) 2 + (1.68 m)*a

(271441 m 2 /s 2 )/(1.68 m) = a

a = 1.62*10 5 m /s 2

Return to Problem 12

(NOTE: the time required to move to the peak of the trajectory is one-half the total hang time - 3.125 s.)

First use: v f = v i + a*t

0 m/s = v i + (-9.8 m/s 2 )*(3.13 s)

0 m/s = v i - 30.7 m/s

v i = 30.7 m/s (30.674 m/s)

Now use: v f 2 = v i 2 + 2*a*d

(0 m/s) 2 = (30.7 m/s) 2 + 2*(-9.8 m/s 2 )*(d)

0 m 2 /s 2 = (940 m 2 /s 2 ) + (-19.6 m/s 2 )*d

-940 m 2 /s 2 = (-19.6 m/s 2 )*d

(-940 m 2 /s 2 )/(-19.6 m/s 2 ) = d

Return to Problem 13

-370 m = (0 m/s)*(t)+ 0.5*(-9.8 m/s 2 )*(t) 2

-370 m = 0+ (-4.9 m/s 2 )*(t) 2

(-370 m)/(-4.9 m/s 2 ) = t 2

75.5 s 2 = t 2

Return to Problem 14

(0 m/s) 2 = (367 m/s) 2 + 2*(a)*(0.0621 m)

0 m 2 /s 2 = (134689 m 2 /s 2 ) + (0.1242 m)*a

-134689 m 2 /s 2 = (0.1242 m)*a

(-134689 m 2 /s 2 )/(0.1242 m) = a

a = -1.08*10 6 m /s 2

(The - sign indicates that the bullet slowed down.)

Return to Problem 15

d = (0 m/s)*(3.41 s)+ 0.5*(-9.8 m/s 2 )*(3.41 s) 2

d = 0 m+ 0.5*(-9.8 m/s 2 )*(11.63 s 2 )

d = -57.0 m

(NOTE: the - sign indicates direction)

Return to Problem 16

(0 m/s) 2 = v i 2 + 2*(- 3.90 m/s 2 )*(290 m)

0 m 2 /s 2 = v i 2 - 2262 m 2 /s 2

2262 m 2 /s 2 = v i 2

v i = 47.6 m /s

Return to Problem 17

( 88.3 m/s) 2 = (0 m/s) 2 + 2*(a)*(1365 m)

7797 m 2 /s 2 = (0 m 2 /s 2 ) + (2730 m)*a

7797 m 2 /s 2 = (2730 m)*a

(7797 m 2 /s 2 )/(2730 m) = a

a = 2.86 m/s 2

88.3 m/s = 0 m/s + (2.86 m/s 2 )*t

(88.3 m/s)/(2.86 m/s 2 ) = t

t = 30. 8 s

Return to Problem 18

( 112 m/s) 2 = (0 m/s) 2 + 2*(a)*(398 m)

12544 m 2 /s 2 = 0 m 2 /s 2 + (796 m)*a

12544 m 2 /s 2 = (796 m)*a

(12544 m 2 /s 2 )/(796 m) = a

a = 15.8 m/s 2

Return to Problem 19

v f 2 = v i 2 + 2*a*d

(0 m/s) 2 = v i 2 + 2*(-9.8 m/s 2 )*(91.5 m)

0 m 2 /s 2 = v i 2 - 1793 m 2 /s 2

1793 m 2 /s 2 = v i 2

v i = 42.3 m/s

Now convert from m/s to mi/hr:

v i = 42.3 m/s * (2.23 mi/hr)/(1 m/s)

v i = 94.4 mi/hr

Return to Problem 20

school Campus Bookshelves
menu_book Bookshelves
perm_media Learning Objects
login Login
how_to_reg Request Instructor Account
hub Instructor Commons
Download Page (PDF)
Download Full Book (PDF)
Periodic Table
Physics Constants
Scientific Calculator
Reference & Cite
Tools expand_more
Readability

selected template will load here

This action is not available.

6.2: Uniformly Accelerated Motion

Last updated
Save as PDF
Page ID 6961

Jeremy Tatum
University of Victoria

Before studying motion in a resisting medium, a brief review of uniformly accelerating motion might be in order. That is, motion in which the resistance is zero. Any formulas that we develop for motion in a resisting medium must go to the formulas for uniformly accelerated motion as the resistance approaches zero.

One may imagine a situation in which a body starts with speed $ v_{0}$ and then accelerates at a rate $ a$. One may ask three questions:

How fast is it moving after time $ t$ ? How far has it moved in time $ t$ ? How fast is it moving after it has covered a distance $ x$ ?

The answers to these questions are well known to any student of physics:

\[ \ v= v_{0} +at, \tag{6.2.1}\label{eq:6.2.1} \]

\[ \ v= v_{0}t +\frac{1}{2}at^2, \tag{6.2.2}\label{eq:6.2.2} \]

\[ \ v^2= v_{0}^2 +2ax. \tag{6.2.3}\label{eq:6.2.3} \]

Since the acceleration is uniform, there is no need to use calculus to derive these. The first follows immediately from the meaning of acceleration. Distance travelled is the area under a speed : time graph. Figure VI.1 shows a speed : time graph for constant acceleration, and Equation $ \ref{eq:6.2.2}$ is obvious from a glance at the graph. Equation $ \ref{eq:6.2.3}$ can be obtained by elimination of $ t$ between Equations $ \ref{eq:6.2.1}$ and $ \ref{eq:6.2.2}$. (It can also be deduced from energy considerations, though that is rather putting the cart before the horse.)

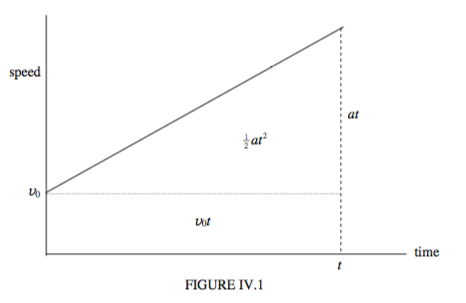
Nevertheless, although calculus is not necessary, it is instructive to see how calculus can be used to analyse uniformly accelerated motion, since calculus will be necessary in less simple situations. We shall be using calculus to answer the three questions posed earlier in the section.

For uniformly accelerated motion, the Equation of motion is

\[ \ \ddot{x}=a. \tag{6.2.4}\label{eq:6.2.4} \]

To answer the first question, we write $ \ddot{x}$ as $ \frac{dv}{dt}$, and then the integral (with initial condition $ x=0$ when $ t=0$) is

\[ \ v = v_{0} + at. \tag{6.2.5}\label{eq:6.2.5} \]

This is the first time integral. Next, we write $ v$ as $ \frac{dv}{dt}$ and integrate again with respect to time, to get

\[ \ x = v_{0}t + \frac{1}{2}at^2. \tag{6.2.6}\label{eq:6.2.6} \]

This is the second time integral. To obtain the answer to the third question, which will be called the space integral , we must remember to write $ \ddot{x} $ as $ v \frac{dv}{dt}$. Thus the Equation of motion (Equation $ \ref{eq:6.2.4}$) is

\[ \ v\frac{dv}{dx}= a. \tag{6.2.7}\label{eq:6.2.7} \]

When this is integrated with respect to $ x$ (with initial condition $ v=v_{0}$ when $ x=0$) we obtain

\[ \ v^{2} = v^2_{0} +2ax. \tag{6.2.8}\label{eq:6.2.8} \]

This is the space integral.

Here are a few quick examples of problems in uniformly accelerated motion. It is probably a good idea to work in algebra and obtain algebraic solutions to each problem. That is, even if you are told that the initial speed is 15 ms -1 , call it $v_{0}$, or, if you are told that the height is 900 feet, call it $ h$. You will probably find it helpful to sketch graphs either of distance versus time or speed versus time in most of the problems. One last little hint: Remember that the two solutions of a quadratic Equation are equal if $ b^{2}=4ac$.

Example $\PageIndex{1}$

A body is dropped from rest. The last third of the distance before it hits the ground is covered in time T. Show that the time taken for the entire fall to the ground is 5.45T.

Example $\PageIndex{2}$

The Lady is 8 metres from the bus stop, when the Bus, starting from rest at the bus stop, starts to move off with an acceleration of 0.4 m s -2 . What is the least speed at which the Lady must run in order to catch the Bus?

Answer: 2.53ms -1 .

Example $\PageIndex{3}$

A parachutist is descending at a constant speed of 10 feet per second. When she is at a height of 900 feet, her friend, directly below her, throws an apple up to her. What is the least speed at which he must throw the apple in order for it to reach her? How long does it take to reach her, what height is she at then, and what is the relative speed of parachutist and apple? Assume $ g$ = 32 ft s -2 . Neglect air resistance for the apple (but not for the parachutist!)

Answer:230fts -1 , 7.5s, 825 ft, 0fts -1 .

Example $\PageIndex{4}$

A lunar explorer performs the following experiment on the Moon in order to determine the gravitational acceleration $ g$ there. He tosses a lunar rock upwards at an initial speed of 15 m s -1 . Eight seconds later he tosses another rock upwards at an initial speed of 10 m s -1 . He observes that the rocks collide 16.32 seconds after the launch of the first rock. Calculate g and also the height of the collision.

Answer: 1.64ms -2 , 26.4m

Example $\PageIndex{5}$

Mr A and Mr B are discussing the merits of their cars. Mr A can go from 0 to 50 mph in ten seconds, and Mr B can go from 0 to 60 mph in 20 seconds. Mr B gives Mr A a start of one second. Assuming that each driver first accelerates uniformly to his maximum speed and thereafter travels at each uniform speed, how long does it take Mr B to catch Mr A, and how far have the cars travelled by then?

Answer: 41 s, half a mile.

I make the answers as follows. Let me know ( [email protected] ) if you think I have got any of them wrong.

Uniform Acceleration

September 13, 2023
Kinematics , Mechanics

Uniform acceleration is a specific type of motion in which an object’s velocity changes at a constant rate over time. It serves as a foundational concept in physics, particularly in the study of mechanics. The purpose of this article is to give readers a thorough understanding of uniform acceleration by looking into its definition, characteristics, kinematic equations, graphical representations, and real-world examples.

Table of Contents

Definition of Uniform Acceleration

If the velocity of a body changes by an equal amount in an equal interval of time, however, small the interval may be then its acceleration is said to be uniform.

Uniform acceleration ($ a $) can also be defined as the rate of change of velocity per unit time, where this rate of change remains constant. In mathematical terms, uniform acceleration is defined by the equation:

\[ a = \frac{{\Delta v}}{{\Delta t}} \]

Here, $ \Delta v $ represents the change in velocity, and $ \Delta t $ denotes the change in time.

Characteristics of Uniform Acceleration

Understanding the nuances of uniform acceleration becomes easier when we delve into its core characteristics. Here is a detailed breakdown:

Constant Rate of Change in Velocity

In uniform acceleration, the velocity of an object changes at a consistent rate.

Applicability of Kinematic Equations

Uniformly accelerated motion can be described using three fundamental kinematic equations: 1. $ v = u + at $ 2. $ s = ut + \frac{1}{2}at^2 $ 3. $ v^2 = u^2 + 2as $

Linear Velocity-Time Graph

A velocity-time graph for uniform acceleration is a straight line, and its slope equals the value of the constant acceleration.

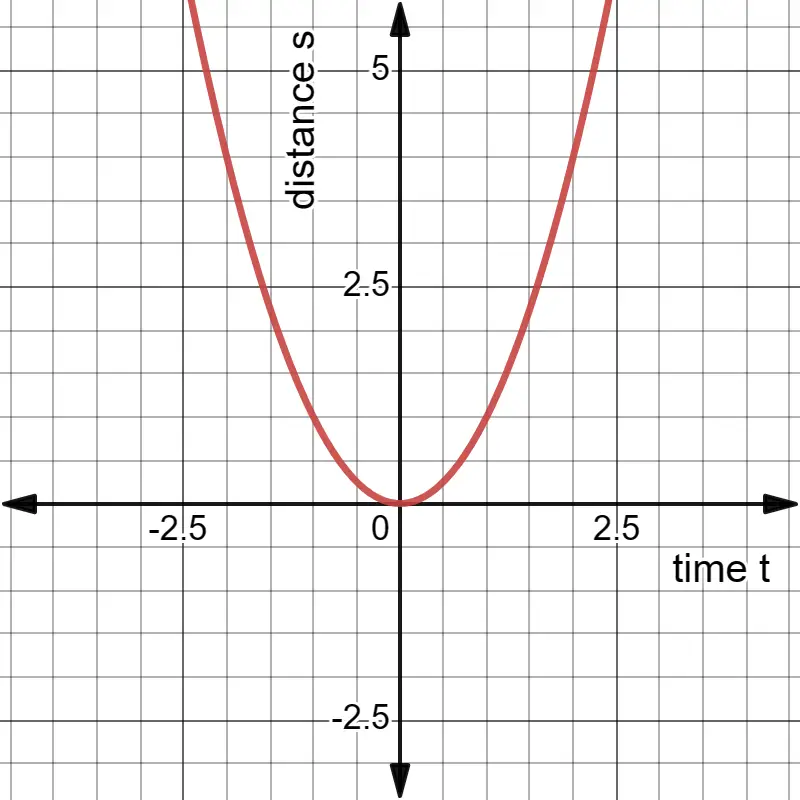
Parabolic Displacement-Time Graph

The displacement-time graph for such motion is a parabola, arising from the quadratic relationship $(\frac{1}{2}at^2)$ between displacement and time in the second equation of motion.

The figure given below shows the distance-time graph of an object moving with a uniform accelerated motion where acceleration $a=2m/s^2$.

Importance of Initial Conditions

Initial velocity ($ u $) and initial position ($ s_0 $) are essential parameters for problem-solving in uniformly accelerated motion. These conditions act as the starting point for any calculations involving kinematic equations.

Idealized Conditions

It is often an idealized model but serves as a practical approximation for real-world applications like free-falling objects in a vacuum or a car accelerating on a straight road.

Directional Aspects

Both the velocity and acceleration vectors can be in the same or opposite directions, determining whether the object speeds up or slows down.

Kinematic Equations for Uniformly Accelerated Motion

Uniformly accelerated motion can be modeled using the following kinematic equations:

1. First Equation of Motion \[ v = u + at \]

2. Second Equation of Motion: \[ s = ut + \frac{1}{2} a t^2 \]

3. Third Equation of Motion: \[ v^2 = u^2 + 2as \]

These equations allow us to relate position, velocity, and acceleration to time, making them invaluable tools for problem-solving.

Graphical Interpretation

In uniformly accelerated motion, different graphs can portray the relationship between parameters:

Velocity-Time Graph: A straight line indicates uniform acceleration, and its slope is equal to the value of the constant acceleration.
Displacement-Time Graph: This graph is a parabola, highlighting the quadratic nature of the relationship between displacement and time.

Examples of Uniform Acceleration

Understanding uniform acceleration conceptually often benefits from specific examples. Below are points illustrating scenarios where uniform acceleration is observed or can be a reasonable approximation.

Falling Objects in a Vacuum

Context: An object falling freely near the Earth’s surface in the absence of air resistance.
Acceleration: The gravitational acceleration $ g = 9.81 \, \text{m/s}^2 $ is constant.
Example Calculation: If an object starts from rest, its velocity after 2 seconds would be $ v = gt = 9.81 \times 2 = 19.62 \, \text{m/s} $.

Cars Accelerating from Rest

Context: A car accelerates from rest to reach a certain speed on a straight road.
Acceleration: Constant force from the engine results in constant acceleration.
Example Calculation: With $ a = 2 \, \text{m/s}^2 $ and starting from rest ($ u = 0 $), the car’s velocity after 3 seconds would be $ v = at = 2 \times 3 = 6 \, \text{m/s} $.

Inclined Plane without Friction

Context: An object sliding down an inclined plane without friction.
Acceleration: The component of the gravitational force along the incline provides a constant acceleration.
Example Calculation: If the incline is at $ 30^\circ $ and neglecting friction, the acceleration $ a = g \sin(30^\circ) = 4.905 \, \text{m/s}^2 $.

Spacecraft Thrust

Context: A spacecraft in outer space applying constant thrust.
Acceleration: Due to the constant thrust and lack of air resistance in space, the acceleration remains constant.
Example Calculation: With $ a = 0.5 \, \text{m/s}^2 $, the spacecraft’s velocity after 10 seconds from rest would be $ v = at = 0.5 \times 10 = 5 \, \text{m/s} $.

Elevator Moving Upward

Context: An elevator starts from rest and moves upward with constant acceleration. Acceleration: The motor provides a constant force, and thus, the acceleration is constant. Example Calculation: If $ a = 1 \, \text{m/s}^2 $, the elevator’s velocity after 4 seconds from rest would be $ v = at = 1 \times 4 = 4 \, \text{m/s} $.

Each of these examples can be analyzed using the kinematic equations for uniformly accelerated motion. They serve as practical applications of the concept, aiding in your understanding and problem-solving skills.

Questions and Answers

Is gravitational acceleration a form of uniform acceleration.

Yes, in a vacuum, gravitational acceleration is approximately constant near the Earth’s surface.

How can time $ t $ be calculated using the first equation of motion

Time can be determined by rearranging the first equation: $ t = \frac{v-u}{a} $.

Is uniform acceleration applicable in circular motion?

No, because the direction of acceleration changes continuously in circular motion.

By understanding its definitions, characteristics, and associated equations, you lay the groundwork for solving a wide range of problems in physics. Whether you’re observing a car accelerating on a straight road or an object free-falling in a vacuum, the concept of uniform acceleration frequently applies, making it essential for any student or practitioner of physics.

3.5: Solve Uniform Motion Applications

Last updated
Save as PDF
Page ID 49887

Learning Objectives

By the end of this section, you will be able to:

Solve uniform motion applications

Before you get started, take this readiness quiz.

Find the distance traveled by a car going 70 miles per hour for 3 hours. If you missed this problem, review Exercise 2.6.1 .
Solve $x+1.2(x−10)=98$. If you missed this problem, review Exercise 2.4.7 .
Convert 90 minutes to hours. If you missed this problem, review Exercise 1.11.1 .

Solve Uniform Motion Applications

When planning a road trip, it often helps to know how long it will take to reach the destination or how far to travel each day. We would use the distance, rate, and time formula, D=rt, which we have already seen.

In this section, we will use this formula in situations that require a little more algebra to solve than the ones we saw earlier. Generally, we will be looking at comparing two scenarios, such as two vehicles traveling at different rates or in opposite directions. When the speed of each vehicle is constant, we call applications like this uniform motion problems .

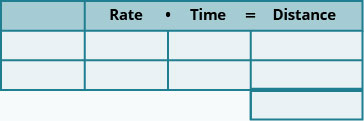
Our problem-solving strategies will still apply here, but we will add to the first step. The first step will include drawing a diagram that shows what is happening in the example. Drawing the diagram helps us understand what is happening so that we will write an appropriate equation. Then we will make a table to organize the information, like we did for the money applications.

The steps are listed here for easy reference:

USE A PROBLEM-SOLVING STRATEGY IN DISTANCE, RATE, AND TIME APPLICATIONS.

Draw a diagram to illustrate what it happening.

Create a table to organize the information.

Label the columns rate, time, distance.

List the two scenarios.

Write in the information you know.

$A table with three rows and four columns and an extra cell at the bottom of the fourth column. The first row is a header row and reads from left to right _____, Rate, Time, and Distance. The rest of the cells are blank.$

Identify what we are looking for.
Complete the chart.
Use variable expressions to represent that quantity in each row.

Multiply the rate times the time to get the distance.

Restate the problem in one sentence with all the important information.
Then, translate the sentence into an equation.
Solve the equation using good algebra techniques.
Check the answer in the problem and make sure it makes sense.
Answer the question with a complete sentence.

Example $\PageIndex{1}$

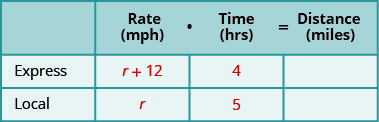
An express train and a local train leave Pittsburgh to travel to Washington, D.C. The express train can make the trip in 4 hours and the local train takes 5 hours for the trip. The speed of the express train is 12 miles per hour faster than the speed of the local train. Find the speed of both trains.

Step 1. Read the problem. Make sure all the words and ideas are understood.

$Pittsburgh and Washington, DC, are represented by two separate lines. There is a line marked Express Train from Pittsburgh to Washington that is 12 mph faster and 4 hours long. There is a line marked Local Train from Pittsburgh to Washington that take 5 hours. The space between Pittsburgh and Washington is marked distance.$

Create a table to organize the information. Label the columns “Rate,” “Time,” and “Distance.” List the two scenarios. Write in the information you know.

Step 2. Identify what we are looking for.

We are asked to find the speed of both trains. Notice that the distance formula uses the word “rate,” but it is more common to use “speed” when we talk about vehicles in everyday English.

Step 3. Name what we are looking for. Choose a variable to represent that quantity.

Complete the chart Use variable expressions to represent that quantity in each row. We are looking for the speed of the trains. Let’s let r represent the speed of the local train. Since the speed of the express train is 12 mph faster, we represent that as r+12.

\[\begin{aligned} r &=\text { speed of the local train } \\ r+12 &=\text { speed of the express train } \end{aligned}\]

Fill in the speeds into the chart.

$A table with three rows and four columns. The first row is a header row and reads from left to right _____, Rate (mph), Time (hrs), and Distance (miles). Below the blank header cell, we have Express and then Local. Below the Rate header cell, we have r plus 12 and then r. Below the Time header cell, we have 4 and then 5. The rest of the cells are blank.$

Step 4. Translate into an equation.

$The sentence, “The distance traveled by the express train equals the distance traveled by the local train,” can be translated to an equation. Translate “distance traveled by the express train” to 4 times the quantity r plus 12, and translate “distance traveled by the local train” to 5r. The full equation is 4 times the quantity r plus 12 equals 5r.$

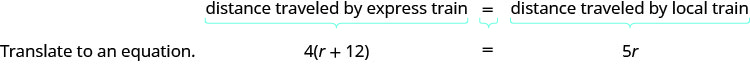
The equation to model this situation will come from the relation between the distances. Look at the diagram we drew above. How is the distance traveled by the express train related to the distance traveled by the local train?
Since both trains leave from Pittsburgh and travel to Washington, D.C. they travel the same distance. So we write:

Step 5. Solve the equation using good algebra techniques.

Step 7. Answer the question with a complete sentence.

Try It $\PageIndex{2}$

Wayne and Dennis like to ride the bike path from Riverside Park to the beach. Dennis’s speed is seven miles per hour faster than Wayne’s speed, so it takes Wayne 2 hours to ride to the beach while it takes Dennis 1.5 hours for the ride. Find the speed of both bikers.

Wayne 21 mph, Dennis 28 mph

Try It $\PageIndex{3}$

Jeromy can drive from his house in Cleveland to his college in Chicago in 4.5 hours. It takes his mother 6 hours to make the same drive. Jeromy drives 20 miles per hour faster than his mother. Find Jeromy’s speed and his mother’s speed.

Jeromy 80 mph, mother 60 mph

In Exercise $\PageIndex{4}$, the last example, we had two trains traveling the same distance. The diagram and the chart helped us write the equation we solved. Let’s see how this works in another case.

Example $\PageIndex{4}$

Christopher and his parents live 115 miles apart. They met at a restaurant between their homes to celebrate his mother’s birthday. Christopher drove 1.5 hours while his parents drove 1 hour to get to the restaurant. Christopher’s average speed was 10 miles per hour faster than his parents’ average speed. What were the average speeds of Christopher and of his parents as they drove to the restaurant?

$Christopher and Parents are represented by two separate lines. The distance between these two lines is marked 115 miles. Lunch is also located between Christopher and Parents. There is an arrow from Christopher that is marked 10 mph faster and 1.5 hours. There is an arrow from Parents marked 1 hour. These two arrows meet somewhere between Christopher and Parents.$

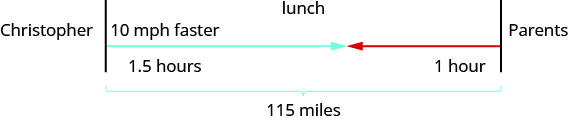
We are asked to find the average speeds of Christopher and his parents.

$A table with three rows and four columns and an extra cell at the bottom of the fourth column. The first row is a header row and reads from left to right blank, Rate (mph), Time (hrs), and Distance (miles). Below the blank header cell, we have Christopher and Parents. Below the rate header cell, we have r plus 10 and r. Below the time header cell, we have 1.5 and 1. Below the distance header cell, we have 1.5 times the quantity (r plus 10), r, and 115.$

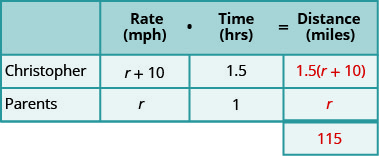
The distance Christopher travelled plus the distance his parents travel must add up to 115 miles. So we write:

$The sentence, “The distance traveled by Christopher plus the distance traveled by his parents equals 115 miles,” can be translated to an equation. Translate “distance traveled by Christopher” to 1.5 times the quantity r plus 10, and translate “distance traveled by his parents” to r. The full equation is 1.5 times the quantity r plus 10, plus r equals 115.$

$\begin{array} {cc} {} &{1.5(r + 10) + r = 115} \\ {} &{1.5r + 15 + r = 115} \\ {\text{Now solve this equation.}} &{2.5r + 15 = 115} \\{} &{2.5r = 100} \\{} &{r = 40} \\ {} &{\text{so the parents' speed was 40 mph.}} \\ {} &{r + 10} \\ {\text{Christopher's speed is r + 10}} &{40 + 10} \\ {} &{50} \\ {} &{\text{Christopher's speed was 50 mph.}} \\ {} &{} \end{array}$

Step 6. Check the answer in the problem and make sure it makes sense.

$\begin{array}{llll} {\text{Christopher drove}} &{50\text{ mph (1.5 hours)}} &{=} &{75\text{ miles}}\\ {\text{His parents drove}} &{40\text{ mph (1 hour)}} &{=} &{\underline{40 \text{ miles}}}\\ {} &{} &{} &{115\text{ miles}} \end{array}$

$\begin{array}{ll} {\textbf{Step 7. Answer}\text{ the question with a complete sentence.}} &{} \\{} &{\text{Christopher's speed was 50 mph.}}\\ {} &{\text{His parents' speed was 40 mph.}} \end{array}$

Try It $\PageIndex{5}$

Carina is driving from her home in Anaheim to Berkeley on the same day her brother is driving from Berkeley to Anaheim, so they decide to meet for lunch along the way in Buttonwillow. The distance from Anaheim to Berkeley is 410 miles. It takes Carina 3 hours to get to Buttonwillow, while her brother drives 4 hours to get there. The average speed Carina’s brother drove was 15 miles per hour faster than Carina’s average speed. Find Carina’s and her brother’s average speeds.

Carina 50 mph, brother 65 mph

Try It $\PageIndex{6}$

Ashley goes to college in Minneapolis, 234 miles from her home in Sioux Falls. She wants her parents to bring her more winter clothes, so they decide to meet at a restaurant on the road between Minneapolis and Sioux Falls. Ashley and her parents both drove 2 hours to the restaurant. Ashley’s average speed was seven miles per hour faster than her parents’ average speed. Find Ashley’s and her parents’ average speed.

parents 55 mph, Ashley 62 mph

As you read the next example, think about the relationship of the distances traveled. Which of the previous two examples is more similar to this situation?

Example $\PageIndex{7}$

Two truck drivers leave a rest area on the interstate at the same time. One truck travels east and the other one travels west. The truck traveling west travels at 70 mph and the truck traveling east has an average speed of 60 mph. How long will they travel before they are 325 miles apart?

$West and East are represented by two separate lines. The distance between these two lines is marked 325 miles. Rest stop is also located between West and East. There is an arrow from Rest stop heading toward West that is marked 70 mph. There is an arrow from Rest stop heading toward East that is marked 60 mph.$

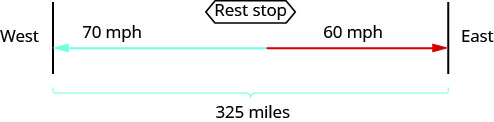
We are asked to find the amount of time the trucks will travel until they are 325 miles apart.

We are looking for the time traveled. Both trucks will travel the same amount of time. Let’s call the time t . Since their speeds are different, they will travel different distances. Complete the chart.

$A table with three rows and four columns and an extra cell at the bottom of the fourth column. The first row is a header row and reads from left to right blank, Rate (mph), Time (hrs), and Distance (miles). Below the blank header cell, we have West and East. Below the rate header cell, we have 70 and 60. Below the time head cell, we have t and t. Below the Distance header cell we have 70t, 60t, and 325.$

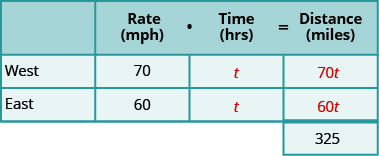
We need to find a relation between the distances in order to write an equation. Looking at the diagram, what is the relationship between the distance each of the trucks will travel? The distance traveled by the truck going west plus the distance traveled by the truck going east must add up to 325 miles. So we write:

$Distance traveled by westbound truck plus distance traveled by eastbound truck equals 325. The first part corresponds to 70t and the second part corresponds to 60.$

\[\begin{array} {lrll} {\text{Now solve this equation. }} & {70 t+60 t} &{=} &{325} \\ {} &{130 t} &{=} &{325} \\ {} &{t} &{=} &{2.5} \end{array}\]

$\begin{array}{llll} {\text{Truck going West}} &{70\text{ mph (2.5 hours)}} &{=} &{175\text{ miles}}\\ {\text{Truck going East}} &{60\text{ mph (2.5 hour)}} &{=} &{\underline{150 \text{ miles}}}\\ {} &{} &{} &{325\text{ miles}} \end{array}$

$\begin{array}{ll} \\{\textbf{Step 7. Answer}\text{ the question with a complete sentence.}} &{\text{It will take the truck 2.5 hours to be 325 miles apart.}} \end{array}$

Try It $\PageIndex{8}$

Pierre and Monique leave their home in Portland at the same time. Pierre drives north on the turnpike at a speed of 75 miles per hour while Monique drives south at a speed of 68 miles per hour. How long will it take them to be 429 miles apart?

Try It $\PageIndex{9}$

Thanh and Nhat leave their office in Sacramento at the same time. Thanh drives north on I-5 at a speed of 72 miles per hour. Nhat drives south on I-5 at a speed of 76 miles per hour. How long will it take them to be 330 miles apart?

MATCHING UNITS IN PROBLEMS

It is important to make sure the units match when we use the distance rate and time formula. For instance, if the rate is in miles per hour, then the time must be in hours.

Example $\PageIndex{10}$

When Katie Mae walks to school, it takes her 30 minutes. If she rides her bike, it takes her 15 minutes. Her speed is three miles per hour faster when she rides her bike than when she walks. What are her walking speed and her speed riding her bike?

First, we draw a diagram that represents the situation to help us see what is happening.

$A house and a school are represented by two separate lines. There is a line marked walking from the house to the school that takes 30 minutes. There is a line marked biking from the house to the school that take 15 minutes and is 3 mph faster. The space between the house and school is marked distance.$

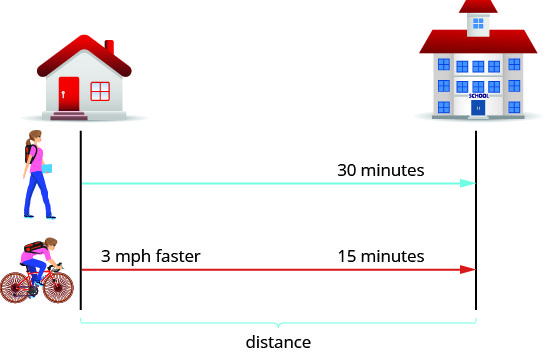
We are asked to find her speed walking and riding her bike. Let’s call her walking speed r . Since her biking speed is three miles per hour faster, we will call that speed r+3. We write the speeds in the chart.

The speed is in miles per hour, so we need to express the times in hours, too, in order for the units to be the same. Remember, one hour is 60 minutes. So:

\[\begin{array}{l}{30 \text { minutes is } \frac{30}{60} \text { or } \frac{1}{2} \text { hour }} \\ {15 \text { minutes is } \frac{15}{60} \text { or } \frac{1}{4} \text { hour }}\end{array}\]

Next, we multiply rate times time to fill in the distance column.

$A table with three rows and four columns. The first row is a header row and reads from left to right blank, Rate (mph), Time (hrs), and Distance (miles). Below the blank header cell, we have walk and bike. Below the rate header cell, we have r and r plus 3. Below the time header cell, we have 1/2 and 1/4. Below the distance cell we have 1/2 times r and 1/4 times the quantity (r plus 3).$

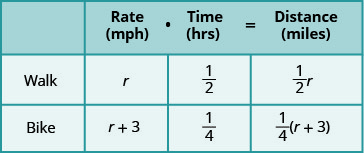
The equation will come from the fact that the distance from Katie Mae’s home to her school is the same whether she is walking or riding her bike.

Try It $\PageIndex{11}$

Suzy takes 50 minutes to hike uphill from the parking lot to the lookout tower. It takes her 30 minutes to hike back down to the parking lot. Her speed going downhill is 1.2 miles per hour faster than her speed going uphill. Find Suzy’s uphill and downhill speeds.

uphill 1.8 mph, downhill three mph

Try It $\PageIndex{12}$

Llewyn takes 45 minutes to drive his boat upstream from the dock to his favorite fishing spot. It takes him 30 minutes to drive the boat back downstream to the dock. The boat’s speed going downstream is four miles per hour faster than its speed going upstream. Find the boat’s upstream and downstream speeds.

upstream 8 mph, downstream 12 mph

In the distance, rate, and time formula, time represents the actual amount of elapsed time (in hours, minutes, etc.). If a problem gives us starting and ending times as clock times, we must find the elapsed time in order to use the formula.

Example $\PageIndex{13}$

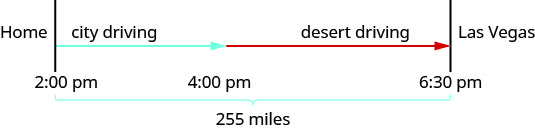
Hamilton loves to travel to Las Vegas, 255 miles from his home in Orange County. On his last trip, he left his house at 2:00 pm. The first part of his trip was on congested city freeways. At 4:00 pm, the traffic cleared and he was able to drive through the desert at a speed 1.75 times as fast as when he drove in the congested area. He arrived in Las Vegas at 6:30 pm. How fast was he driving during each part of his trip?

A diagram will help us model this trip.

$Home (2:00 pm) and Las Vegas (6:30 pm) are represented by two separate lines. The space between home and Las Vegas is marked 255 miles. There is an arrow marked city driving from Home/2:00 pm to 4:00 pm. Then there is an arrow marked desert driving from the tip of the previous one at 4:00 pm to Las Vegas/6:30 pm.$

Next, we create a table to organize the information.

We know the total distance is 255 miles. We are looking for the rate of speed for each part of the trip. The rate in the desert is 1.75 times the rate in the city. If we let r= the rate in the city, then the rate in the desert is 1.75r.

The times here are given as clock times. Hamilton started from home at 2:00 pm and entered the desert at 4:30 pm. So he spent two hours driving the congested freeways in the city. Then he drove faster from 4:00 pm until 6:30 pm in the desert. So he drove 2.5 hours in the desert.

Now, we multiply the rates by the times.

$A table with three rows and four columns and an extra cell at the bottom of the fourth column. The first row is a header row and reads from left to right blank, Rate (mph), Time (hrs), and Distance (miles). Below the blank header cell, we have city and desert. Below the rate header cell, we have r and 1.75r. Below the time head cell, we have 2 and 2.5. Below the Distance header cell we have 2r, 2.5 times 1.75r, and 255.$

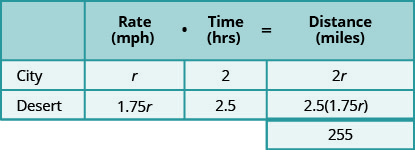
By looking at the diagram below, we can see that the sum of the distance driven in the city and the distance driven in the desert is 255 miles.

Try It $\PageIndex{14}$

Cruz is training to compete in a triathlon. He left his house at 6:00 and ran until 7:30. Then he rode his bike until 9:45. He covered a total distance of 51 miles. His speed when biking was 1.6 times his speed when running. Find Cruz’s biking and running speeds.

biking 16 mph, running 10 mph

Try It $\PageIndex{15}$

Phuong left home on his bicycle at 10:00. He rode on the flat street until 11:15, then rode uphill until 11:45. He rode a total of 31 miles. His speed riding uphill was 0.6 times his speed on the flat street. Find his speed biking uphill and on the flat street.

uphill 12 mph, flat street 20 mph

Key Concepts

D = rt where D = distance, r = rate, t = time
Read the problem. Make sure all the words and ideas are understood. Draw a diagram to illustrate what it happening. Create a table to organize the information: Label the columns rate, time, distance. List the two scenarios. Write in the information you know.
Name what we are looking for. Choose a variable to represent that quantity. Complete the chart. Use variable expressions to represent that quantity in each row. Multiply the rate times the time to get the distance.
Translate into an equation. Restate the problem in one sentence with all the important information. Then, translate the sentence into an equation.

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Mechanics (Essentials) - Class 11th

Course: mechanics (essentials) - class 11th > unit 4.

Using equations of motion (1 step numerical)

Using equations of motion (2 steps numerical)

Kinematic equations: numerical calculations
Calculating car's velocity using skid marks

Want to join the conversation?

Upvote Button navigates to signup page
Downvote Button navigates to signup page
Flag Button navigates to signup page

Video transcript

School Guide
Class 11 Syllabus
Class 11 Revision Notes
Maths Notes Class 11
Physics Notes Class 11
Chemistry Notes Class 11
Biology Notes Class 11
NCERT Solutions Class 11 Maths
RD Sharma Solutions Class 11
Math Formulas Class 11
CBSE Class 11 Physics Notes

Chapter 1: Physical World

What is Physics? Definition, History, Importance, Scope
How is Physics related to Other Sciences?
Fundamental Forces

Chapter 2: Units and Measurement

System of Units
Length Measurement
Measurement of Area, Volume and Density
Rounding Numbers
Dimensional Analysis
Significant Figures
Errors in Measurement

Chapter 3: Motion in a Straight Line

What is Motion?
Distance and Displacement
Speed and Velocity
Acceleration

Uniform Acceleration

Sample Problems on Equation of Motion
Solving Problems Based on Free Fall
Relative Motion
Relative Motion in One Dimension
Relative Motion in Two Dimension
Calculating Stopping Distance and Reaction Time

Chapter 4: Motion in a Plane

Scalar and Vector
Vector Operations
Product of Vectors
Scalar Product of Vectors
Dot and Cross Products on Vectors
Position and Displacement Vectors
Average Velocity
Motion in Two Dimension
Projectile Motion
Uniform Circular Motion
Centripetal Acceleration
Motion in Three Dimensions

Chapter 5: Laws of Motion

Contact and Non Contact Forces
Inertia Meaning
Law of Inertia
What is Impulse?
Solving Problems in Mechanics
Linear Momentum of a System of Particles
Newton's Second Law of Motion: Definition, Formula, Derivation, and Applications
Laws of Conservation of Momentum
What is Equilibrium? - Definition, Types, Laws, Effects
Law of Action and Reaction
Types of Friction - Definition, Static, Kinetic, Rolling and Fluid Friction
Increasing and Reducing Friction
Factors Affecting Friction
Motion Along a Rough Inclined Plane
Problems on Friction Formula
Centripetal and Centrifugal Force
Solved Examples on Dynamics of Circular Motion
Dynamics of Circular Motion
Motion in a Vertical Circle

Chapter 6: Work, Energy and Power

Work Energy Theorem
Practice Problems on Kinetic Energy
Work Done by a Variable Force
What is Potential Energy?
Potential Energy of a Spring
Practice Problems on Potential Energy
Law of Conservation of Energy
Difference Between Work and Energy
Types of Collisions
Collisions in One Dimension
Collisions in Two Dimensions

Chapter 7: Systems of Particles and Rotational Motion

Rigid Body - Definition, Rotation, Angular Velocity, Momentum
Motion of a Rigid Body
Centre of Mass
Center of Mass of Different Objects
Motion of Center of Mass
Torque and Angular Momentum
What are Couples? Definition, Moment of Couple, Applications
What is the Principle of Moments?
Centre of Gravity
Moment of Inertia
Kinematics of Rotational Motion
Dynamics of Rotational Motion
Angular Momentum in Case of Rotation About a Fixed Axis
Rolling Motion
Relation between Angular Velocity and Linear Velocity

Chapter 8: Gravitation

Kepler's Laws of Planetary Motion
Universal Law of Gravitation
Factors affecting Acceleration due to Gravity
Variation in Acceleration due to Gravity
Potential Energy
Escape Velocity
Binding Energy of Satellites
Weightlessness

Chapter 9: Mechanical Properties of Solids

Elastic Behavior of Materials
Elasticity and Plasticity
Stress and Strain
Hooke's Law
Stress-Strain Curve
Young's Modulus
Shear Modulus and Bulk Modulus
Poisson's Ratio
Elastic Potential Energy
Stress, Strain and Elastic Potential Energy

Chapter 10: Mechanical Properties of Fluids

Fluid Pressure
Pascal's Law
Variation of Pressure With Depth
How to calculate Atmospheric Pressure?
Hydraulic Machines
Streamline Flow
Bernoulli's Principle
Bernoulli's Equation
What is Viscosity?
Stoke's Law
Reynolds Number
Surface Tension

Chapter 11: Thermal Properties of Matter

Difference between Heat and Temperature
Temperature Scales
Ideal Gas Law
Thermal Expansion
Heat Capacity
Calorimetry
Change of State of Matter
Latent Heat
Thermal Conduction
Sample Problems on Heat Conduction
What is Radiation - Types, Scource, Ionizing and Non-Ionizing Radiation
Greenhouse Effect
Newton's Law of Cooling

Chapter 12: Thermodynamics

Thermodynamics
Zeroth Law of Thermodynamics
Heat, Internal Energy and Work
First Law of Thermodynamics
Specific Heat Capacity
Thermodynamic State Variables and Equation of State
Thermodynamic Processes
Second Law of Thermodynamics
Reversible and Irreversible Processes

Chapter 13: Kinetic Theory

Behavior of Gas Molecules - Kinetic Theory, Boyle's Law, Charles's Law
Molecular Nature of Matter - Definition, States, Types, Examples
Kinetic Theory of Gases
Mean Free Path - Definition, Formula, Derivation, Examples

Chapter 14: Oscillations

Oscillatory and Periodic Motion
Simple Harmonic Motion
Force Law for Simple Harmonic Motion
Displacement in Simple Harmonic Motion
Velocity and Acceleration in Simple Harmonic Motion
Energy in Simple Harmonic Motion
Some Systems executing Simple Harmonic Motion

Chapter 15: Waves

Introduction to Waves - Definition, Types, Properties
Speed of a Travelling Wave
Reflection of Waves
Properties of Waves
Principle of Superposition of Waves
Energy in Wave Motion
Doppler Effect - Definition, Formula, Examples

Uniformly Accelerated Motion or Uniform Acceleration in Physics is a motion in which the object is accelerated at constant acceleration. We have to keep in mind that uniform accelerated motion does not mean uniform velocity i.e. in uniform accelerated the velocity of the object increases linearly with time. An object drop from the top of the roof, a ball rolling downhill, a man jumping from an airplane, etc. are all instances of uniformly accelerated motion. It is crucial to note that due to the interference of gravity or friction, many instances of uniform application do not maintain absolute uniformity of acceleration .

In this article, we will learn about, uniform acceleration, uniform accelerated motion, uniform accelerated motion equations, and others in detail.

Table of Content

What is Uniform Acceleration?

Kinematic equations for uniformly accelerated motion, uniformly accelerated motion in a plane.

Practice Questions

If the rate of change of velocity remains constant then the object is said to be in state of Uniform Acceleration.

As we know acceleration is a vector quantity thus, the direction of motion remains the same in the case of constant acceleration.

Uniform Acceleration Examples

Some Examples of Uniformly accelerated motion are mentioned below:

Free-falling object under the force of gravity.
A ball rolling down a frictionless slope.
A bicycle rolling downhill when the brakes are applied.
Angular Acceleration

Uniform Accelerated Motion Formula

There are three formula that are explained by uniform accelerated motion. These formulas are used to explain the motion of an object. The three uniform accelerated motion formula are,

s = ut + 1/2at 2
v 2 = u 2 + 2as

Uniform Acceleration Graphs

The uniform acceleration graphs is a straight line graphs. The uniform acceleration graphs is added below,

Non-Uniform Acceleration Graphs

The non-uniform acceleration graph is the graph added below,

Kinematic Equations for Uniformly Accelerated Motion provide a relation between initial velocity, acceleration, final velocity, distance covered, and time taken by the object. Let’s take the initial velocity of an object as “u”, the constant acceleration applied to the object is “a”, and the final velocity achieved by the object under this acceleration is “v” velocity the time taken is “t” and the distance covered is “s”.

First Equation of Motion (Velocity Equation)

First Equation of Motion or Velocity Equation provides the relation between final and initial velocities, acceleration, and time, it is given by,

v = u + at where, v is the final velocity u is the initial velocity a is the acceleration t is the time taken by object

Second Equation of Motion (Distance Equation)

Second Equation of Motion or Distance Equation provides the relation between initial velocities, distance, acceleration, and time, it is given by,

s = ut + 1/2 at 2 where, s is the distance u is the initial velocity a is the acceleration t is the time taken by the object

Third Equation of Motion

Third Equation of Motion provides the relation between final and initial velocities, distance, and acceleration, it is given by,

v 2 = u 2 + 2as where, s is the distance v is the final velocity u is the initial velocity a is the acceleration

While using these equations sign convention must be followed. If one direction is taken to be positive then the other is taken as negative. A body in free fall can be considered to be in Uniform Accelerated Motion the body in free fall experiences the uniform acceleration of earth’s gravity. Generally, the upward motion of the object is considered to be positive whereas, the downward motion is considered to be negative.

Learn more about, Equation of Motion

Projectile motion is an example of Uniformly Accelerated Motion in a Plane. Projectile motion accelerates uniformly under the force of gravitation. As we know that gravity works only in a vertical direction i.e. in the y-direction the motion in the x-direction is of constant velocity. Thus, we see that projectile motion can be broken into two different motions, and the equation of motion is calculated separately in these two motions.

Uniformly Accelerated Motion is the motion of an object when the acceleration of the object remains constant. It can be in one dimension, two dimensions, or three dimensions.

V-T Graph for Uniform Accelerated Motion

In uniform accelerated motion the velocity of the object changes at constant speed. The graph for the same is added below,

Uniform and Non-Uniform Motion

Examples on Uniform Accelerated Motion

Example 1: If a body is moving at an acceleration of 2 m/s 2 . If the initial speed was 15m/s, what will be the speed in 5 seconds?

Solution:

Given, u = 15m/s a = 2 m/s 2 t = 5 For finding out the value of “v”, first equation of motion can be used. v = u + at Plugging the values in this equation, v = u + at = 15 + (2)(5) = 15 + 10 = 25 m/s

Example 2: If a body is moving at an acceleration of -5 m/s 2 . If the initial speed was 30m/s, what will be the distance co in 5 seconds?

Given, u = 40m/s a = -5 m/s 2 t = 5 For finding out the value of “v”, the first equation of motion can be used. v = u + at Plugging the values in this equation, v = u + at = 30 – (5)(5) = 30 – 25 = 5 m/s

Example 3: If a body is moving at an acceleration of -5 m/s 2 . If the initial speed was 40m/s, what will be the speed in 5 seconds?

Given, u = 40m/s a = -5 m/s 2 t = 5 For finding out the value of “s”, the first equation of motion can be used. s = ut + 1/2a(t) 2 Plugging the values in this equation, s = ut + 1/2a(t) 2 s = (40)(5) + 1/2(-5)(5) 2 s = 200 + (-125/2) s = 200 – 125/2 s = (400 – 125)/2 = 275/2

Example 4: If a body is moving at an acceleration of 10 m/s 2 . If the initial speed was 20m/s, what will be the speed in 2 seconds?

Given, u = 20 m/s a = 10 m/s 2 t = 2 For finding out the value of “s”, the first equation of motion can be used. s = ut + 1/2a(t) 2 Plugging the values in this equation, s = ut + 1/2a(t) 2 s = (20)(2) + 1/2(10)(2) 2 s = 40 + 20 = 60 m

Example 5: A racing car catches a speed of 20m/s in 2 seconds. Find the distance covered by the car in the process.

Solution:

Given, u = 0 m/s v = 20 m/s t = 2 For finding out the value of “a”, the first equation of motion can be used. v = u + at Plugging the values in this equation, v = u + at 20 = 0 + (a)(2) 20 = 2a a = 10 m/s 2 For finding out the distance, a third equation of motion will be used v 2 = u 2 + 2as 20 2 = 0 + 2(10)s 400 = 20s s = 20 m

Practice Questions on Uniform Acceleration

Q1: If the velocity of a car changes from 60 m/s to 70 m/s in 30 min and 70 m/s to 80 m/s in next 30 min. Verify if the car is in the Uniform Acceleration.

Q2: If a body starts moving at 10 m/s and its uniformly accelerates at 2m/s 2 . Find the distance covered by the body in 30 minutes

Q3: If the initial velocity of a bike is 45 m/s and its final velocity is 80 m/s accelerating uniformly for 10 minutes. Find the acceleration.

FAQs on Uniformly Accelerated Motion

1. define uniform acceleration.

Uniform acceleration is the acceleration that does not vary with time. In such cases, the rate of change of velocity remains constant.

2. What is Non-Uniform Motion?

An object moving with variable velocity is said to be non-uniform motion. In non uniform motion an object covers unequal distance in unequal time.

3. What is Uniformly Accelerated Motion?

Uniformly accelerated motion is defined by a motion in a straight line with a constant acceleration and zero difference.

4. What are Examples of Uniformly Accelerated Motion?

A ball rolling down a slope, a skydiver jumping out of a plane, a ball dropped from the top of a ladder, and a bicycle with its brakes engaged are all instances of uniformly accelerated motion.

5. Is Uniformly Accelerated Motion Uniform Motion?

No, uniform accelerated motion is not considered to uniform motion as in uniform motion velocity is constant whereas in uniform accelerated motion velocity is not constant.

6. What is Uniform Motion?

The motion of an object in which the object travels equal distance in equal interval of time is called the uniform motion. In uniform motion the velocity of object remains the constant.

7. When will you say a body is in Uniform Acceleration?

A body is said to be in uniform acceleration if its velocity changes at constant rate.

Please Login to comment...

Improve your Coding Skills with Practice

What kind of Experience do you want to share?

COMMENTS

Uniform Acceleration Motion: Problems with Solutions
It then decelerates uniformly to a stop in 30.0 s. Find the total distance covered by the car. Solution to Problem 12. More References and links. Velocity and Speed: Tutorials with Examples; Velocity and Speed: Problems with Solutions; Acceleration: Tutorials with Examples; Uniform Acceleration Motion: Problems with Solutions
Uniform acceleration motion Problems and Solutions
a = 15 m/s2. Problem #2. A car accelerates uniformly from 21,0 m/s to 35,0 m/s in 3,0 seconds. Determine the acceleration of the car and the distance traveled. Answer: Given: time t = 4,0 s, initial velocity vi = 21,0 m/s, and finale velocity vf = 35,0 m/s,
Kinematic Equations: Sample Problems and Solutions
Kinematic equations relate the variables of motion to one another. Each equation contains four variables. The variables include acceleration (a), time (t), displacement (d), final velocity (vf), and initial velocity (vi). If values of three variables are known, then the others can be calculated using the equations. This page demonstrates the process with 20 sample problems and accompanying ...
6.2: Uniformly Accelerated Motion
This is the first time integral. x = v0t + 1 2at2. (6.2.6) (6.2.6) x = v 0 t + 1 2 a t 2. This is the second time integral. To obtain the answer to the third question, which will be called the space integral, we must remember to write x¨ x ¨ as vdv dt v d v d t. Thus the Equation of motion (Equation 6.2.4 6.2.4) is.
PDF Solutions for Uniformly Accelerated Motion Problems WorksheetsCh6
1. a) a(t) = 1.2, v(t) = 1.2t, s(t) = 0.6 t2. Draw graphs indicating scale, important points and proper shape. b) Between 0 and 2 seconds, the object travels 2.4 meters and between 3 and 5 seconds it travels 9.6 meters. c) If the object went from 0 to 6 meters/second in 8 seconds, the acceleration is less and therefore the graph of v(t) is less ...
Uniformly Accelerated Motion
Directions: On this worksheet you will practice solving problems by using the five basic kinematics equations for uniformly accelerated motion. omit: Question 1 Scenario #1: A car accelerates uniformly from rest to a final speed of 24 m/sec in 10 seconds. How far does it travel during this period of acceleration?
Uniform Acceleration
Uniformly accelerated motion can be described using three fundamental kinematic equations: 1. $ v = u + at $ 2. $ s = ut + \frac{1}{2}at^2 $ ... are essential parameters for problem-solving in uniformly accelerated motion. These conditions act as the starting point for any calculations involving kinematic equations.
Uniformly-Accelerated Motion
Kinematic equations or uniformly accelerated equations are used to solve problems involving constant acceleration. The uniformly accelerated motion equations are the following: (1) v = v0 + at;
PDF Uniformly Accelerated Motion Super Problem
Uniformly Accelerated Motion Super Problem A ball is thrown upward at 25 m/s from the ground. 1. What is the initial velocity of the ball? 2. What is the acceleration of the ball? 3. What is the ball's velocity after 2 seconds? 4. What is the ball's velocity after 4 seconds? 5. What is the maximum height of the ball? 6.
PDF 1.6 Solving Uniform Acceleration Problems
t four of the five variables related to uniformly accelerated motion. An equation that involves the fifth variable, displacement, can be derived by determining the area under the (straight) line on a velocity-time graph, as shown on. page 43. This equation, d ( ) t , is then.
Using equations of motion (1 step numerical)
Transcript. In this video, we will solve 2 numerical on uniformly accelerated motion by using the three equations of motion (kinematic equations) v = u+at, s = ut + 1/2 at^2 and v^2 = u^2+2asWe will calculate the time taken in the first numerical and distance in another. Created by Mahesh Shenoy.
Uniformly Accelerated Motion (2/2): Problem-Solving Example
NOTE: The second-to-last equation from the bottom should read vf^2 = vi^2 + 2aΔx, not vf = ... In that equation, both of the velocities are squared. The vide...
How to solve uniform motion problems
The distance formula for uniform motion problems. In this lesson we'll look at how to compare and solve for different values in the ???\text{Distance}=\text{Rate} \cdot \text{Time}??? equation when you have related scenarios. Uniform motion explains the distance of an object when it travels at a constant speed, the rate, over a period of time.
3.5: Solve Uniform Motion Applications
Problem-Solving Strategy—Distance, Rate, and Time Applications. Read the problem. Make sure all the words and ideas are understood. Draw a diagram to illustrate what it happening. Create a table to organize the information: Label the columns rate, time, distance. List the two scenarios. Write in the information you know.
Solving Problems Using Kinematic Equations (Uniformly Accelerated Motion)
Learn how to solve motion problems in Physics using kinematic equations used in uniformly acceleration motion, i.e. acceleration is assumed constant.Watch ho...
PDF 0016 Lecture Notes
Uniformly Accelerated Motion (UAM) is motion of an object where the acceleration is constant. In other words, the acceleration remains uniform; the acceleration is equal to a number and that number does not change as a function of time. A ball rolling down an incline. A person falling from a plane. A bicycle on which you have applied the brakes.
Physics 71 Day 5 [Part 2/8]
In this video, we gave a guide and some strategies on how to solve problems involving kinematics of uniformly accelerated motion.
Using equations of motion (2 steps numerical)
- [Instructor] Let's solve two problems on accelerated motion, a little challenging one this time. Here's the first one. A tortoise accelerates uniformly from rest to 40 meters per second, covering a distance of 100 meters. Calculate the time taken to cover this distance. So let's think of what is to given to us and let's draw a diagram.
Uniform Accelerated Motion: Equations, Graphs, and Examples
Uniform Acceleration Examples. Some Examples of Uniformly accelerated motion are mentioned below: Free-falling object under the force of gravity. A ball rolling down a frictionless slope. A bicycle rolling downhill when the brakes are applied. Read More. Centripetal Acceleration. Angular Acceleration.
Uniformly Accelerated Motion: Exploring the Dynamics of Speed and
This equation gives us the average acceleration (a-bar) of an object during uniformly accelerated motion. It is the ratio of the change in velocity (delta v) to the change in time (delta t).. Derivation of the Formula of Instantaneous Acceleration. The formula for instantaneous acceleration can be derived from the equations of motion. By taking the derivative of the velocity equation with ...

Physics Problems with Solutions

Problem 10:

Problem 11:

Problem 12:

More References and links

POPULAR PAGES

JEE-IIT-NCERT Physics & Math

Post a Comment for "Uniform acceleration motion Problems and Solutions"

Check Your Understanding

Solutions to Above Problems

6.2: Uniformly Accelerated Motion

Example \(\PageIndex{1}\)

Example \(\PageIndex{2}\)

Example \(\PageIndex{3}\)

Example \(\PageIndex{4}\)

Example \(\PageIndex{5}\)

Uniform Acceleration

Definition of Uniform Acceleration

Characteristics of Uniform Acceleration

Constant Rate of Change in Velocity

Applicability of Kinematic Equations

Linear Velocity-Time Graph

Parabolic Displacement-Time Graph

Importance of Initial Conditions

Idealized Conditions

Directional Aspects

Kinematic Equations for Uniformly Accelerated Motion

Graphical Interpretation

Examples of Uniform Acceleration

Falling Objects in a Vacuum

Cars Accelerating from Rest

Inclined Plane without Friction

Spacecraft Thrust

Elevator Moving Upward

Questions and Answers

How can time \( t \) be calculated using the first equation of motion

Is uniform acceleration applicable in circular motion?

Further Reading

Related Posts:

Leave a Reply Cancel Reply

3.5: Solve Uniform Motion Applications

Learning Objectives

Solve Uniform Motion Applications

USE A PROBLEM-SOLVING STRATEGY IN DISTANCE, RATE, AND TIME APPLICATIONS.

Example \(\PageIndex{1}\)

Try It \(\PageIndex{2}\)

Try It \(\PageIndex{3}\)

Example \(\PageIndex{4}\)

Try It \(\PageIndex{5}\)

Try It \(\PageIndex{6}\)

Example \(\PageIndex{7}\)

Try It \(\PageIndex{8}\)

Try It \(\PageIndex{9}\)

MATCHING UNITS IN PROBLEMS

Example \(\PageIndex{10}\)

Try It \(\PageIndex{11}\)

Try It \(\PageIndex{12}\)

Example \(\PageIndex{13}\)

Try It \(\PageIndex{14}\)

Try It \(\PageIndex{15}\)

Key Concepts

Mechanics (Essentials) - Class 11th

Using equations of motion (2 steps numerical)

Want to join the conversation?

Video transcript

Chapter 1: Physical World

Chapter 2: Units and Measurement

Chapter 3: Motion in a Straight Line

Uniform Acceleration

Chapter 4: Motion in a Plane

Chapter 5: Laws of Motion

Chapter 6: Work, Energy and Power

Chapter 7: Systems of Particles and Rotational Motion

Chapter 8: Gravitation

Chapter 9: Mechanical Properties of Solids

Chapter 10: Mechanical Properties of Fluids

Chapter 11: Thermal Properties of Matter

Chapter 12: Thermodynamics

Chapter 13: Kinetic Theory

Chapter 14: Oscillations