chapter 2 data representation in computer systems

CHAPTER 2 Data Representation in Computer Systems

2.1 Introduction 37 2.2 Positional Numbering Systems 38 2.3 Decimal to Binary Conversions 38 2.3.1 Converting Unsigned Whole Numbers 39 2.3.2 Converting Fractions 41 2.3.3 Converting between Power-of-Two Radices 44 2.4 Signed Integer Representation 44 2.4.1 Signed Magnitude 44 2.4.2 Complement Systems 49 2.5 Floating-Point Representation 55 2.5.1 A Simple Model 56 2.5.2 Floating-Point Arithmetic 58 2.5.3 Floating-Point Errors 59 2.5.4 The IEEE-754 Floating-Point Standard 61 2.6 Character Codes 62 2.6.1 Binary-Coded Decimal 62 2.6.2 EBCDIC 63 2.6.3 ASCII 63 2.6.4 Unicode 65 2.7 Codes for Data Recording and Transmission 67 2.7.1 Non-Return-to-Zero Code 68 2.7.2 Non-Return-to-Zero-Invert Encoding 69 2.7.3 Phase Modulation (Manchester Coding) 70 2.7.4 Frequency Modulation 70 2.7.5 Run-Length-Limited Code 71 2.8 Error Detection and Correction 73 2.8.1 Cyclic Redundancy Check 73 2.8.2 Hamming Codes 77 2.8.3 Reed-Soloman 82 Chapter Summary 83

CMPS375 Class Notes Page 1/ 16 by Kuo-pao Yang

2.1 Introduction 37 • This chapter describes the various ways in which computers can store and manipulate numbers and characters. • Bit : The most basic unit of information in a digital computer is called a bit, which is a contraction of binary digit. • Byte : In 1964, the designers of the IBM System/360 main frame computer established a convention of using groups of 8 bits as the basic unit of addressable computer storage. They called this collection of 8 bits a byte. • Word: Computer words consist of two or more adjacent bytes that are sometimes addressed and almost always are manipulated collectively. Words can be 16 bits, 32 bits, 64 bits. • Nibbles : Eight-bit bytes can be divided into two 4-bit halves call nibbles.

2.2 Positional Numbering Systems 38 • Radix (or Base): The general idea behind positional numbering systems is that a numeric value is represented through increasing powers of a radix (or base).

System Radix Allowable Digits ------Decimal 10 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 Binary 2 0, 1 Octal 8 0, 1, 2, 3, 4, 5, 6, 7 Hexadecimal 16 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B , C , D , E , F

FIGURE 2.1 Some Number to Remember

EXAMPLE 2.1 Three numbers represented as powers of a radix. 2 1 0 -1 -2 243.5110 = 2 * 10 + 4 * 10 + 3 * 10 + 5 * 10 + 1 * 10 2 1 0 2123 = 2 * 3 + 1 * 3 + 2 * 3 = 2310 4 3 2 1 0 101102 = 1 * 2 + 0 * 2 + 1 * 2 + 1 * 2 + 0 * 2 = 2210

CMPS375 Class Notes Page 2/ 16 by Kuo-pao Yang

2.3 Decimal to Binary Conversions 38 • There are two important groups of number base conversions: 1. Conversion of decimal numbers to base- r numbers 2. Conversion of base-r numbers to decimal numbers

2.3.1 Converting Unsigned Whole Numbers 39 • EXAMPLE 2.3 Convert 10410 to base 3 using the division -remainder method. 10410 = 102123 • EXAMPLE 2.4 Convert 14710 to binary 14710 = 100100112 • A binary number with N bits can represent unsigned integer from 0 to 2n – 1. • Overflow: the result of an arithmetic operation is outside the range of allowable precision for the give number of bits.

2.3.2 Converting Fractions 41 • EXAMPLE 2.6 Convert 0.430410 to base 5. 0.430410 = 0.20345 • EXAMPLE 2.7 Convert 0.3437510 to binary with 4 bits to the right of the binary point. Reading from top to bottom, 0.3437510 = 0.01012 to four binary places. We simply discard (or truncate) our answer when the desired accuracy has been achieved. • EXAMPLE 2.8 Convert 31214 to base 3 First, convert to decimal 312144 = 21710 Then convert to base 3 We have 31214 = 220013

2.3.3 Converting between Power-of-Two Radices 44 • EXAMPLE 2.9 Convert 1100100111012 to octal and hexadecimal. 1100100111012 = 62358 Separate into groups of 3 for octal conversion 1100100111012 = C9D16 Separate into groups of 4 for octal conversion

CMPS375 Class Notes Page 3/ 16 by Kuo-pao Yang

2.4 Signed Integer Representation 44 • By convention, a “1” in the high-order bit indicate a negative number.

2.4.1 Signed Magnitude 44 • A signed-magnitude number has a sign as its left-most bit (also referred to as the high-order bit or the most significant bit) while the remaining bits represent the magnitude (or absolute value) of the numeric value. • N bits can represent –(2n-1 - 1) to 2n-1 -1 • EXAMPLE 2.10 Add 010011112 to 001000112 using signed-magnitude arithmetic. 010011112 (79) + 001000112 (35) = 011100102 (114) There is no overflow in this example • EXAMPLE 2.11 Add 010011112 to 011000112 using signed-magnitude arithmetic. An overflow condition and the carry is discarded, resulting in an incorrect sum. We obtain the erroneous result of 010011112 (79) + 011000112 (99) = 01100102 (50) • EXAMPLE 2.12 Subtract 010011112 from 011000112 using signed-magnitude arithmetic. We find 0110000112 (99) - 010011112 (79) = 000101002 (20) in signed- magnitude representation. • EXAMPLE 2.14 • EXAMPLE 2.15 • The signed magnitude has two representations for zero, 10000000 and 00000000 (and mathematically speaking, the simple shouldn’ t happen!).

2.4.2 Complement Systems 49 • One’ s Complement o This sort of bit-flipping is very simple to implement in computer hardware . o EXAMPLE 2.16 Express 2310 and -910 in 8-bit binary one’s complement form. 2310 = + (000101112) = 000101112 -910 = - (000010012) = 111101102 o EXAMPLE 2.17 o EXAMPLE 2.18 o The primary disadvantage of one’s complement is that we still have two representations for zero: 00000000 and 11111111 • Two’s Complement o Find the one’s complement and add 1. o EXAMPLE 2.19 Express 2310, -2310, and -910 in 8-bit binary two’s complement form. 2310 = + (000101112) = 000101112 -2310 = - (000101112) = 111010002 + 1 = 111010012 -910 = - (000010012) = 111101102 + 1 = 111101112 o EXAMPLE 2.20 o EXAMPLE 2.21 o A Simple Rule for Detecting an Overflow Condition: If the carry in the sign bit equals the carry out of the bit, no overflow has occurred. If the carry into the sign

CMPS375 Class Notes Page 4/ 16 by Kuo-pao Yang

bit is different from the carry out of the sign bit, over (and thus an error) has occurred. o EXAMPLE 2.22 Find the sum of 12610 and 810 in binary using two’s complement arithmetic. A one is carried into the leftmost bit, but a zero is carried out. Because these carries are not equal, an overflow has occurred. o N bits can represent –(2n-1) to 2n-1 -1. With signed-magnitude number, for example, 4 bits allow us to represent the value -7 through +7. However using two’s complement, we can represent the value -8 through +7. • Integer Multiplication and Division o For each digit in the multiplier, the multiplicand is “shifted” one bit to the left. When the multiplier is 1, the “shifted” multiplicand is added to a running sum of partial products. o EXAMPLE Find the product of 000001102 and 000010112. o When the divisor is much smaller than the dividend, we get a condition known as divide underflow, which the computer sees as the equivalent of division by zero. o Computer makes a distinction between integer division and floating-point division. ƒ With integer division, the answer comes in two parts: a quotient and a remainder. ƒ Floating-point division results in a number that is expressed as a binary fraction. ƒ Floating-point calculations are carried out in dedicated circuits call floating- point units, or FPU.

CMPS375 Class Notes Page 5/ 16 by Kuo-pao Yang

2.5 Floating-Point Representation 55 • In scientific notion, numbers are expressed in two parts: a fractional part call a mantissa, and an exponential part that indicates the power of ten to which the mantissa should be raised to obtain the value we need.

2.5.1 A Simple Model 56 • In digital computers, floating-point number consist of three parts: a sign bit, an exponent part (representing the exponent on a power of 2), and a fractional part called a significand (which is a fancy word for a mantissa).

1 bit 5 bits 8 bits

Sign bit Exponent Significand

FIGURE 2.2 Floating-Point Representation • Unbiased Exponent 5 0 00101 10001000 1710 = 0.100012 * 2 17 0 10001 10000000 6553610 = 0.12 * 2 • Biased Exponent: We select 16 because it is midway between 0 and 31 (our exponent has 5 bits, thus allowing for 25 or 32 values). Any number larger than 16 in the exponent field will represent a positive value. Value less than 16 will indicate negative values. 5 0 10101 10001000 1710 = 0.100012 * 2 The biased exponent is 16 + 5 = 21 -1 0 01111 10000000 0.2510 = 0.12 * 2 • EXAMPLE 2.23 • A normalized form is used for storing a floating-point number in memory. A normalized form is a floating-point representation where the leftmost bit of the significand will always be a 1. Example: Internal representation of (10.25)10

(10.25)10 = (1010.01) 2 (Un-normalized form) 0 = (1010.01) 2 x 2 . 1 = (101.001) 2 x 2 . : 4 = (.101001) 2 x 2 (Normalized form) 5 = (.0101001) 2 x 2 (Un-normalized form) 6 = (.00101001) 2 x 2 .

Internal representation of (10.25)10 is 0 10100 10100100

CMPS375 Class Notes Page 6/ 16 by Kuo-pao Yang

2.5.2 Floating-Point Arithmetic 58 • EXAMPLE 2.24: Renormalizing we retain the larger exponent and truncate the low- order bit. • EXAMPLE 2.25

2.5.3 Floating-Point Errors 59 • We intuitively understand that we are working in the system of real number. We know that this system is infinite. • Computers are finite systems, with finite storage. The more bits we use, the better the approximation. However, there is always some element of error, no matter how many bits we use.

2.5.4 The IEEE-754 Floating-Point Standard 61 • The IEEE-754 single precision floating point standard uses bias of 127 over its 8-bit exponent. An exponent of 255 indicates a special value. • The double precision standard has a bias of 1023 over its 11-bit exponent. The “special” exponent value for a double precision number is 2047, instead of the 255 used by the single precision standard.

Special bit patterns in IEEE-754

CMPS375 Class Notes Page 7/ 16 by Kuo-pao Yang

2.6 Character Codes 62 • Thus, human-understandable characters must be converted to computer- understandable bit patterns using some sort of character encoding scheme.

2.6.1 Binary-Coded Decimal 62 • Binary-coded Decimal (BCD) is a numeric coding system used primarily in IBM mainframe and midrange systems. • When stored in an 8-bit byte, the upper nibble is called the zone and the lower part is called the digit. • EXAMPLE 2.26 Represent -1265 in 3 bytes using packed BCD. The zoned-decimal coding for 1265 is: 1111 0001 1111 0010 1111 0110 1111 0101 After packing, this string becomes: 0001 0010 0110 0101 Adding the sign after the low-order digit and padding in high order bit should be 0000 for a result of: 0000 0001 0010 0110 0101 1101

FIGURE 2.5 Binary-Coded Decimal

2.6.2 EBCDIC 63 • EBCDIC (Extended Binary Coded Decimal Interchange Code) expand BCD from 6 bits to 8 bits. See Page 64 FIGURE 2.6.

CMPS375 Class Notes Page 8/ 16 by Kuo-pao Yang

2.6.3 ASCII 63 • ASCII: American Standard Code for Information Interchange • In 1967, a derivative of this alphabet became the official standard that we now call ASCII.

2.6.4 Unicode 65 • Both EBCDIC and ASCII were built around the Latin alphabet. • In 1991, a new international information exchange code called Unicode. • Unicode is a 16-bit alphabet that is downward compatible with ASCII and Latin-1 character set. • Because the base coding of Unicode is 16 bits, it has the capacity to encode the majority of characters used in every language of the world. • Unicode is currently the default character set of the Java programming language.

CMPS375 Class Notes Page 9/ 16 by Kuo-pao Yang

2.7 Codes for Data Recording and Transmission 67 2.7.1 Non-Return-to-Zero Code 68 • The simplest data recording and transmission code is the non-return-to-zero (NRZ) code. • NRZ encodes 1 as “high” and 0 as “low.” • The coding of OK (in ASCII) is shown below.

FIGURE 2.9 NRZ Encoding of OK

2.7.2 Non-Return-to-Zero-Invert Encoding 69 • The problem with NRZ code is that long strings of zeros and ones cause synchronization loss. • Non-return-to-zero-invert (NRZI) reduces this synchronization loss by providing a transition (either low-to-high or high-to-low) for each binary 1.

FIGURE 2.10 NRZI Encoding OK

2.7.3 Phase Modulation (Manchester Coding) 70 • Although it prevents loss of synchronization over long strings of binary ones, NRZI coding does nothing to prevent synchronization loss within long strings of zeros. • Manchester coding (also known as phase modulation) prevents this problem by encoding a binary one with an “up” transition and a binary zero with a “down” transition.

FIGURE 2.11 Phase Modulation (Manchester Coding) of the Word OK

CMPS375 Class Notes Page 10/ 16 by Kuo-pao Yang

2.7.4 Frequency Modulation 70 • For many years, Manchester code was the dominant transmission code for local area networks. • It is, however, wasteful of communications capacity because there is a transition on every bit cell. • A more efficient coding method is based upon the frequency modulation (FM) code. In FM, a transition is provided at each cell boundary. Cells containing binary ones have a mid-cell transition.

FIGURE 2.12 Frequency Modulation Coding of OK

• At first glance, FM is worse than Manchester code, because it requires a transition at each cell boundary. • If we can eliminate some of these transitions, we would have a more economical code. • Modified FM does just this. It provides a cell boundary transition only when adjacent cells contain zeros. • An MFM cell containing a binary one has a transition in the middle as in regular FM.

FIGURE 2.13 Modified Frequency Modulation Coding of OK

2.7.5 Run-Length-Limited Code 71 • The main challenge for data recording and trans-mission is how to retain synchronization without chewing up more resources than necessary. • Run-length-limited, RLL, is a code specifically designed to reduce the number of consecutive ones and zeros. • Some extra bits are inserted into the code. • But even with these extra bits RLL is remarkably efficient. • An RLL(d, k ) code dictates a minimum of d and a maximum of k consecutive zeros between any pair of consecutive ones. • RLL(2,7) has been the dominant disk storage coding method for many years. • An RLL(2,7) code contains more bit cells than its corresponding ASCII or EBCDIC character. • However, the coding method allows bit cells to be smaller, thus closer together, than in MFM or any other code.

CMPS375 Class Notes Page 11/ 16 by Kuo-pao Yang

• The RLL(2,7) coding for OK is shown below, compared to MFM. The RLL code (bottom) contains 25% fewer transitions than the MFM code (top).

FIGURE 2.16 MFM (top) and RLL(2, 7) Coding (bottom) for OK

• If the limiting factor in the design of a disk is the number of flux transitions per square millimeter, we can pack 50% more OKs in the same magnetic are using RLL than we could using MFM. • RLL is used almost exclusively in the manufacture of high-capacity disk drive.

CMPS375 Class Notes Page 12/ 16 by Kuo-pao Yang

2.8 Error Detection and Correction 73 • No communications channel or storage medium can be completely error-free.

2.8.1 Cyclic Redundancy Check 73 • Cyclic redundancy check (CRC) is a type of checksum used primarily in data communications that determines whether an error has occurred within a large block or stream of information bytes. • Arithmetic Modulo 2 The addition rules are as follows: 0 + 0 = 0 0 + 1 = 1 1 + 0 = 1 1 + 1 = 0 • EXAMPLE 2.27 Find the sum of 10112 and 1102 modulo 2. 10112 + 1102 = 11012 (mod 2) • EXAMPLE 2.28 Find the quotient and remainder when 10010112 is divided by 10112. Quotient 10102 and Remainder 1012. • Calculating and Using CRC o Suppose we want to transmit the information string: 10010112. o The receiver and sender decide to use the (arbitrary) polynomial pattern, 1011. o The information string is shifted left by one position less than the number of positions in the divisor. I = 10010110002 o The remainder is found through modulo 2 division (at right) and added to the information string: 10010110002 + 1002 = 10010110001002.

o If no bits are lost or corrupted, dividing the received information string by the agreed upon pattern will give a remainder of zero. o We see this is so in the calculation at the right. o Real applications use longer polynomials to cover larger information strings. • A remainder other than zero indicates that an error has occurred in the transmission. • This method work best when a large prime polynomial is used. • There are four standard polynomials used widely for this purpose: o CRC-CCITT (ITU-T): X16 + X12 + X5 + 1 o CRC-12: X12 + X11 + X3 + X2 + X + 1 o CRC-16 (ANSI): X16 + X15 + X2 + 1 o CRC-32: X32 + X26 + X23 + X22 + X16 + X12 + X11 + X10 + X8 + X7 + X6 + X4 + X + 1 • CRC-32 has been proven that CRCs using these polynomials can detect over 99.8% of all single-bit errors.

CMPS375 Class Notes Page 13/ 16 by Kuo-pao Yang

2.8.2 Hamming Codes 77 • Data communications channels are simultaneously more error-prone and more tolerant of errors than disk systems. • Hamming code use parity bits, also called check bits or redundant bits. • The final word, called a code word is an n-bit unit containing m data bits and r check bits. n = m + r • The Hamming distance between two code words is the number of bits in which two code words differ. 10001001 10110001 *** Hamming distance of these two code words is 3 • The minimum Hamming distance, D(min), for a code is the smallest Hamming distance between all pairs of words in the code. • Hamming codes can detect D(min) - 1 errors and correct [D(min) – 1 / 2] errors. • EXAMPLE 2.29 • EXAMPLE 2.30 00000 01011 10110 11101 D(min) = 3. Thus, this code can detect up to two errors and correct one single bit error.

• We are focused on single bit error. An error could occur in any of the n bits, so each code word can be associated with n erroneous words at a Hamming distance of 1. • Therefore, we have n + 1 bit patterns for each code word: one valid code word, and n erroneous words. With n-bit code words, we have 2n possible code words consisting of 2m data bits (where m = n + r). This gives us the inequality: (n + 1) * 2m < = 2n Because m = n + r, we can rewrite the inequality as: (m + r + 1) * 2m <= 2 m + r or (m + r + 1) <= 2r

CMPS375 Class Notes Page 14/ 16 by Kuo-pao Yang

• EXAMPLE 2.31 Using the Hamming code just described and even parity, encode the 8-bit ASCII character K. (The high-order bit will be zero.) Induce a single-bit error and then indicate how to locate the error. m = 8, we have (8 + r + 1) <= 2r then We choose r = 4 Parity bit at 1, 2, 4, 8 Char K 7510 = 010010112

1 = 1 5 = 1 + 4 9 = 1 + 8 2 = 2 6 = 2 + 4 10 = 2 + 8 3 = 1 + 2 7 = 1 + 2 + 4 11 = 1 + 2 + 8 4 = 4 8 = 8 12 = 4 + 8

We have the following code word as a result: 0 1 0 0 1 1 0 1 0 1 1 0 12 11 10 9 8 7 6 5 4 3 2 1

Parity b1 = b3 + b5 + b7 + b9 + b11 = 1 + 1 + 1 + 0 + 1 = 0 Parity b2 = b3 + b6 + b7 + b10 + b11 = 1 + 0 + 1 + 0 + 1 = 1 Parity b4 = b5 + b6 + b7 = 1 + 0 + 1 = 0 Parity b8 = b9 + b10 + b11 + b12 = 0 + 0 + 1 + 0 = 1

Let’s introduce an error in bit position b9, resulting in the code word: 0 1 0 1 1 1 0 1 0 1 1 0 12 11 10 9 8 7 6 5 4 3 2 1

Parity b1 = b3 + b5 + b7 + b9 + b11 = 1 + 1 + 1 + 1 + 1 = 1 (Error, should be 0) Parity b2 = b3 + b6 + b7 + b10 + b11 = 1 + 0 + 1 + 0 + 1 = 1 (OK) Parity b4 = b5 + b6 + b7 = 1 + 0 + 1 = 0 (OK) Parity b8 = b9 + b10 + b11 + b12 = 1 + 0 + 1 + 0 = 0 (Error, should be 1)

We found that parity bits 1 and 8 produced an error, and 1 + 8 = 9, which in exactly where the error occurred.

2.8.3 Reed-Soloman 82 • If we expect errors to occur in blocks, it stands to reason that we should use an error- correcting code that operates at a block level, as opposed to a Hamming code, which operates at the bit level. • A Reed-Soloman (RS) code can be thought of as a CRC that operates over entire characters instead of only a few bits. • RS codes, like CRCs, are systematic: The parity bytes are append to a block of information bytes. • RS (n, k) code are defined using the following parameters: o s = The number of bits in a character (or “ symbol ”). o k = The number of s-bit characters comprising the data block. o n = The number of bits in the code word. • RS (n, k) can correct (n-k)/2 errors in the k information bytes.

CMPS375 Class Notes Page 15/ 16 by Kuo-pao Yang

• Reed-Soloman error-correction algorithms lend themselves well to implementation in computer hardware. • They are implemented in high-performance disk drives for mainframe computers as well as compact disks used for music and data storage. These implementations will be described in Chapter 7.

Chapter Summary 83 • Computers store data in the form of bits, bytes, and words using the binary numbering system. • Hexadecimal numbers are formed using four-bit groups called nibbles (or nybbles). • Signed integers can be stored in one’s complement, two’s complement, or signed magnitude representation. • Floating-point numbers are usually coded using the IEEE 754 floating-point standard. • Character data is stored using ASCII, EBCDIC, or Unicode. • Data transmission and storage codes are devised to convey or store bytes reliably and economically. • Error detecting and correcting codes are necessary because we can expect no transmission or storage medium to be perfect. • CRC, Reed-Soloman, and Hamming codes are three important error control codes.

CMPS375 Class Notes Page 16/ 16 by Kuo-pao Yang

Chapter 2 Data Representation in Computer Systems

Related documents

Add this document to collection(s)

You can add this document to your study collection(s)

Add this document to saved

You can add this document to your saved list

Suggest us how to improve StudyLib

(For complaints, use another form )

Input it if you want to receive answer

Snapsolve any problem by taking a picture. Try it in the Numerade app?

The Essentials Of Computer Organization And Architecture

Linda null, julia lobur, data representation in computer systems - all with video answers.

Chapter Questions

Perform the following base conversions using subtraction or division-remainder: a) $458_{10}=$________ 3 b) $677_{10}=$________ 5 c) $1518_{10}=$_______ 7 d) $4401_{10}=$_______ 9

Perform the following base conversions using subtraction or division-remainder: a) $588_{10}=$_________ 3 b) $2254_{10}=$________ 5 c) $652_{10}=$________ 7 d) $3104_{10}=$________ 9

Convert the following decimal fractions to binary with a maximum of six places to the right of the binary point: a) 26.78125 b) 194.03125 c) 298.796875 d) 16.1240234375

Convert the following decimal fractions to binary with a maximum of six places to the right of the binary point: a) 25.84375 b) 57.55 c) 80.90625 d) 84.874023

Represent the following decimal numbers in binary using 8 -bit signed magnitude, one's complement, and two's complement: a) 77 b) -42 c) 119 d) -107

Using a "word" of 3 bits, list all of the possible signed binary numbers and their decimal equivalents that are representable in: a) Signed magnitude b) One's complement c) Two's complement

Using a "word" of 4 bits, list all of the possible signed binary numbers and their decimal equivalents that are representable in: a) Signed magnitude b) One's complement c) Two's complement

From the results of the previous two questions, generalize the range of values (in decimal) that can be represented in any given $x$ number of bits using: a) Signed magnitude b) One's complement c) Two's complement

Given a (very) tiny computer that has a word size of 6 bits, what are the smallest negative numbers and the largest positive numbers that this computer can represent in each of the following representations? a) One's complement b) Two's complement

You have stumbled on an unknown civilization while sailing around the world. The people, who call themselves Zebronians, do math using 40 separate characters (probably because there are 40 stripes on a zebra). They would very much like to use computers, but would need a computer to do Zebronian math, which would mean a computer that could represent all 40 characters. You are a computer designer and decide to help them. You decide the best thing is to use $\mathrm{BCZ}$, Binary-Coded Zebronian (which is like $\mathrm{BCD}$ except it codes Zebronian, not Decimal). How many bits will you need to represent each character if you want to use the minimum number of bits?

Perform the following binary multiplications: a) 1100 $\times 101$ b) 10101 $\times 111$ c) 11010 $\times 1100$

Perform the following binary multiplications: a) 1011 $\times 101$ b) 10011 $\times 1011$ c) 11010 $\times 101$

Perform the following binary divisions: a) $101101 \div 101$ b) $10000001 \div 101$ c) $1001010010 \div 1011$

Perform the following binary divisions: a) $11111101 \div 1011$ b) $110010101 \div 1001$ c) $1001111100 \div 1100$

Use the double-dabble method to convert $10212_{3}$ directly to decimal. (Hint: you have to change the multiplier.)

Using signed-magnitude representation, complete the following operations: \[ \begin{aligned} +0+(-0) &=\\ (-0)+0 &=\\ 0+0 &=\\ (-0)+(-0) &= \end{aligned} \]

Suppose a computer uses 4 -bit one's complement numbers. Ignoring overflows, what value will be stored in the variable $j$ after the following pseudocode routine terminates? \[ \begin{array}{ll} 0 \rightarrow j & \text { // Store } 0 \text { in } j \text { . } \\ -3 \rightarrow k & \text { // store }-3 \text { in } k \text { . } \end{array} \] while $k \neq 0$ \[ j=j+1 \] \[ k=k-1 \] end while

If the floating-point number storage on a certain system has a sign bit, a 3 -bit exponent, and a 4-bit significand: a) What is the largest positive and the smallest negative number that can be stored on this system if the storage is normalized? (Assume no bits are implied, there is no biasing, exponents use two's complement notation, and exponents of all zeros and all ones are allowed.) b) What bias should be used in the exponent if we prefer all exponents to be nonnegative? Why would you choose this bias?

Using the model in the previous question, including your chosen bias, add the following floating-point numbers and express your answer using the same notation as the addend and augend:

$$\begin{array}{|llllllll|} \hline 0 & 1 & 1 & 1 & 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 1 & 1 & 0 & 0 & 1 \\ \hline \end{array}$$ Calculate the relative error, if any, in your answer to the previous question.

Assume we are using the simple model for floating-point representation as given in this book (the representation uses a 14 -bit format, 5 bits for the exponent with a bias of $16, \text { a normalized mantissa of } 8 \text { bits, and a single sign bit for the number })$ a) Show how the computer would represent the numbers 100.0 and 0.25 using this floating-point format. b) Show how the computer would add the two floating-point numbers in part a by changing one of the numbers so they are both expressed using the same power of 2. c) Show how the computer would represent the sum in part b using the given floating-point representation. What decimal value for the sum is the computer actually storing? Explain.

What causes divide underflow and what can be done about it?

Why do we usually store floating-point numbers in normalized form? What is the advantage of using a bias as opposed to adding a sign bit to the exponent?

Let $a=1.0 \times 2^{9}, b=-1.0 \times 2^{9}$ and $c=1.0 \times 2^{1} .$ Using the floating-point model described in the text (the representation uses a 14 -bit format, 5 bits for the exponent with a bias of $16,$ a normalized mantissa of 8 bits, and a single sign bit for the number), perform the following calculations, paying close attention to the order of operations. What can you say about the algebraic properties of floating-point arithmetic in our finite model? Do you think this algebraic anomaly holds under multiplication as well as addition? $$\begin{array}{l} b+(a+c)= \\ (b+a)+c= \end{array}$$

a) Given that the ASCII code for A is 1000001 , what is the ASCII code for $\mathrm{J} ?$ b) Given that the EBCDIC code for A is 11000001 , what is the EBCDIC code for J?

Assume a 24 -bit word on a computer. In these 24 bits, we wish to represent the value 295 a) If our computer uses even parity, how would the computer represent the decimal value $295 ?$ b) If our computer uses 8 -bit ASCII and even parity, how would the computer represent the string $295 ?$ c) If our computer uses packed $\mathrm{BCD}$, how would the computer represent the number $+295 ?$

Decode the following ASCII message, assuming 7 -bit ASCII characters and no parity: 1001010100111110010001001110010000010001001000101

Why would a system designer wish to make Unicode the default character set for their new system? What reason(s) could you give for not using Unicode as a default?

Write the 7 -bit ASCII code for the character 4 using the following encoding: a) Non-return-to-zero b) Non-return-to-zero-invert c) Manchester code d) Frequency modulation e) Modified frequency modulation f) Run length limited (Assume 1 is "high," and 0 is "'low.")

Why is NRZ coding seldom used for recording data on magnetic media?

Assume we wish to create a code using 3 information bits, 1 parity bit (appended to the end of the information), and odd parity. List all legal code words in this code. What is the Hamming distance of your code?

Are the error-correcting Hamming codes systematic? Explain.

Compute the Hamming distance of the following code: 0011010010111100 0000011110001111 0010010110101101 0001011010011110

Compute the Hamming distance of the following code: 0000000101111111 0000001010111111 0000010011011111 0000100011101111 0001000011110111 0010000011111011 01000000111111101 1000000011111110

Suppose we want an error-correcting code that will allow all single-bit errors to be corrected for memory words of length 10. a) How many parity bits are necessary? b) Assuming we are using the Hamming algorithm presented in this chapter to design our error-correcting code, find the code word to represent the 10 -bit information word: 1001100110.

Suppose we are working with an error-correcting code that will allow all single-bit errors to be corrected for memory words of length $7 .$ We have already calculated that we need 4 check bits, and the length of all code words will be $11 .$ Code words are created according to the Hamming algorithm presented in the text. We now receive the following code word: 10101011110 Assuming even parity, is this a legal code word? If not, according to our error-correcting code, where is the error?

Repeat exercise 35 using the following code word: 01111010101

Name two ways in which Reed-Soloman coding differs from Hamming coding.

When would you choose a CRC code over a Hamming code? A Hamming code over a CRC?

Find the quotients and remainders for the following division problems modulo 2 a) $1010111_{2} \div 1101_{2}$ b) $1011111_{2} \div 11101_{2}$ c) $1011001101_{2} \div 10101_{2}$ d) $111010111_{2} \div 10111_{2}$

Find the quotients and remainders for the following division problems modulo 2 a) $1111010_{2} \div 1011_{2}$ b) $1010101_{2} \div 1100_{2}$ c) $1101101011_{2} \div 10101_{2}$ d) $1111101011_{2} \div 101101_{2}$

Using the CRC polynomial 1011 , compute the CRC code word for the information word, 1011001 . Check the division performed at the receiver.

Using the CRC polynomial 1101 , compute the CRC code word for the information word, $01001101 .$ Check the division performed at the receiver.

Pick an architecture (such as 80486 , Pentium, Pentium IV, SPARC, Alpha, or MIPS). Do research to find out how your architecture approaches the concepts introduced in this chapter. For example, what representation does it use for negative values? What character codes does it support?

Data Representation

Class 11 - computer science with python sumita arora, checkpoint 2.1.

What are the bases of decimal, octal, binary and hexadecimal systems ?

The bases are:

• Decimal — Base 10
• Octal — Base 8
• Binary — Base 2
• Hexadecimal — Base 16

What is the common property of decimal, octal, binary and hexadecimal number systems ?

Decimal, octal, binary and hexadecimal number systems are all positional-value system .

Complete the sequence of following binary numbers : 100, 101, 110, ............... , ............... , ............... .

100, 101, 110, 111 , 1000 , 1001 .

Complete the sequence of following octal numbers : 525, 526, 527, ............... , ............... , ............... .

525, 526, 527, 530 , 531 , 532 .

Complete the sequence of following hexadecimal numbers : 17, 18, 19, ............... , ............... , ............... .

17, 18, 19, 1A , 1B , 1C .

Convert the following binary numbers to decimal and hexadecimal:

(c) 101011111

(e) 10010101

(f) 11011100

Converting to decimal:

Equivalent decimal number = 8 + 2 = 10

Therefore, (1010) 2 = (10) 10

Converting to hexadecimal:

Grouping in bits of 4:

1010 undefined \underlinesegment{1010} 1010 ​

Therefore, (1010) 2 = (A) 16

Equivalent decimal number = 32 + 16 + 8 + 2 = 58

Therefore, (111010) 2 = (58) 10

0011 undefined 1010 undefined \underlinesegment{0011} \quad \underlinesegment{1010} 0011 ​ 1010 ​

Therefore, (111010) 2 = (3A) 16

Equivalent decimal number = 256 + 64 + 16 + 8 + 4 + 2 + 1 = 351

Therefore, (101011111) 2 = (351) 10

0001 undefined 0101 undefined 1111 undefined \underlinesegment{0001} \quad \underlinesegment{0101} \quad \underlinesegment{1111} 0001 ​ 0101 ​ 1111 ​

Therefore, (101011111) 2 = (15F) 16

Equivalent decimal number = 8 + 4 = 12

Therefore, (1100) 2 = (12) 10

1100 undefined \underlinesegment{1100} 1100 ​

Therefore, (1100) 2 = (C) 16

Equivalent decimal number = 1 + 4 + 16 + 128 = 149

Therefore, (10010101) 2 = (149) 10

1001 undefined 0101 undefined \underlinesegment{1001} \quad \underlinesegment{0101} 1001 ​ 0101 ​

Therefore, (101011111) 2 = (95) 16

Equivalent decimal number = 4 + 8 + 16 + 64 + 128 = 220

Therefore, (11011100) 2 = (220) 10

1101 undefined 1100 undefined \underlinesegment{1101} \quad \underlinesegment{1100} 1101 ​ 1100 ​

Therefore, (11011100) 2 = (DC) 16

Convert the following decimal numbers to binary and octal :

Converting to binary:

Therefore, (23) 10 = (10111) 2

Converting to octal:

Therefore, (23) 10 = (27) 8

Therefore, (100) 10 = (1100100) 2

Therefore, (100) 10 = (144) 8

Therefore, (145) 10 = (10010001) 2

Therefore, (145) 10 = (221) 8

Therefore, (19) 10 = (10011) 2

Therefore, (19) 10 = (23) 8

Therefore, (121) 10 = (1111001) 2

Therefore, (121) 10 = (171) 8

Therefore, (161) 10 = (10100001) 2

Therefore, (161) 10 = (241) 8

Convert the following hexadecimal numbers to binary :

(A6) 16 = (10100110) 2

(A07) 16 = (101000000111) 2

(7AB4) 16 = (111101010110100) 2

(BE) 16 = (10111110) 2

(BC9) 16 = (101111001001) 2

(9BC8) 16 = (1001101111001000) 2

Convert the following binary numbers to hexadecimal and octal :

(a) 10011011101

(b) 1111011101011011

(c) 11010111010111

(d) 1010110110111

(e) 10110111011011

(f) 1111101110101111

0100 undefined 1101 undefined 1101 undefined \underlinesegment{0100} \quad \underlinesegment{1101} \quad \underlinesegment{1101} 0100 ​ 1101 ​ 1101 ​

Therefore, (10011011101) 2 = (4DD) 16

Converting to Octal:

Grouping in bits of 3:

010 undefined 011 undefined 011 undefined 101 undefined \underlinesegment{010} \quad \underlinesegment{011} \quad \underlinesegment{011} \quad \underlinesegment{101} 010 ​ 011 ​ 011 ​ 101 ​

Therefore, (10011011101) 2 = (2335) 8

1111 undefined 0111 undefined 0101 undefined 1011 undefined \underlinesegment{1111} \quad \underlinesegment{0111} \quad \underlinesegment{0101} \quad \underlinesegment{1011} 1111 ​ 0111 ​ 0101 ​ 1011 ​

Therefore, (1111011101011011) 2 = (F75B) 16

001 undefined 111 undefined 011 undefined 101 undefined 011 undefined 011 undefined \underlinesegment{001} \quad \underlinesegment{111} \quad \underlinesegment{011} \quad \underlinesegment{101} \quad \underlinesegment{011} \quad \underlinesegment{011} 001 ​ 111 ​ 011 ​ 101 ​ 011 ​ 011 ​

Therefore, (1111011101011011) 2 = (173533) 8

0011 undefined 0101 undefined 1101 undefined 0111 undefined \underlinesegment{0011} \quad \underlinesegment{0101} \quad \underlinesegment{1101} \quad \underlinesegment{0111} 0011 ​ 0101 ​ 1101 ​ 0111 ​

Therefore, (11010111010111) 2 = (35D7) 16

011 undefined 010 undefined 111 undefined 010 undefined 111 undefined \underlinesegment{011} \quad \underlinesegment{010} \quad \underlinesegment{111} \quad \underlinesegment{010} \quad \underlinesegment{111} 011 ​ 010 ​ 111 ​ 010 ​ 111 ​

Therefore, (11010111010111) 2 = (32727) 8

0001 undefined 0101 undefined 1011 undefined 0111 undefined \underlinesegment{0001} \quad \underlinesegment{0101} \quad \underlinesegment{1011} \quad \underlinesegment{0111} 0001 ​ 0101 ​ 1011 ​ 0111 ​

Therefore, (1010110110111) 2 = (15B7) 16

001 undefined 010 undefined 110 undefined 110 undefined 111 undefined \underlinesegment{001} \quad \underlinesegment{010} \quad \underlinesegment{110} \quad \underlinesegment{110} \quad \underlinesegment{111} 001 ​ 010 ​ 110 ​ 110 ​ 111 ​

Therefore, (1010110110111) 2 = (12667) 8

0010 undefined 1101 undefined 1101 undefined 1011 undefined \underlinesegment{0010} \quad \underlinesegment{1101} \quad \underlinesegment{1101} \quad \underlinesegment{1011} 0010 ​ 1101 ​ 1101 ​ 1011 ​

Therefore, (10110111011011) 2 = (2DDB) 16

010 undefined 110 undefined 111 undefined 011 undefined 011 undefined \underlinesegment{010} \quad \underlinesegment{110} \quad \underlinesegment{111} \quad \underlinesegment{011} \quad \underlinesegment{011} 010 ​ 110 ​ 111 ​ 011 ​ 011 ​

Therefore, (10110111011011) 2 = (26733) 8

1111 undefined 1011 undefined 1010 undefined 1111 undefined \underlinesegment{1111} \quad \underlinesegment{1011} \quad \underlinesegment{1010} \quad \underlinesegment{1111} 1111 ​ 1011 ​ 1010 ​ 1111 ​

Therefore, (1111101110101111) 2 = (FBAF) 16

001 undefined 111 undefined 101 undefined 110 undefined 101 undefined 111 undefined \underlinesegment{001} \quad \underlinesegment{111} \quad \underlinesegment{101} \quad \underlinesegment{110} \quad \underlinesegment{101} \quad \underlinesegment{111} 001 ​ 111 ​ 101 ​ 110 ​ 101 ​ 111 ​

Therefore, (1111101110101111) 2 = (175657) 8

Checkpoint 2.2

Multiple choice questions.

The value of radix in binary number system is ..........

The value of radix in octal number system is ..........

The value of radix in decimal number system is ..........

The value of radix in hexadecimal number system is ..........

Which of the following are not valid symbols in octal number system ?

Which of the following are not valid symbols in hexadecimal number system ?

Which of the following are not valid symbols in decimal number system ?

The hexadecimal digits are 1 to 0 and A to ..........

The binary equivalent of the decimal number 10 is ..........

Question 10

ASCII code is a 7 bit code for ..........

• other symbol
• all of these ✓

Question 11

How many bytes are there in 1011 1001 0110 1110 numbers?

Question 12

The binary equivalent of the octal Numbers 13.54 is.....

• 1101.1110 ✓
• None of these

Question 13

The octal equivalent of 111 010 is.....

Question 14

The input hexadecimal representation of 1110 is ..........

Question 15

Which of the following is not a binary number ?

Question 16

Convert the hexadecimal number 2C to decimal:

Question 17

UTF8 is a type of .......... encoding.

• extended ASCII

Question 18

UTF32 is a type of .......... encoding.

Question 19

Which of the following is not a valid UTF8 representation?

• 2 octet (16 bits)
• 3 octet (24 bits)
• 4 octet (32 bits)
• 8 octet (64 bits) ✓

Question 20

Which of the following is not a valid encoding scheme for characters ?

Fill in the Blanks

The Decimal number system is composed of 10 unique symbols.

The Binary number system is composed of 2 unique symbols.

The Octal number system is composed of 8 unique symbols.

The Hexadecimal number system is composed of 16 unique symbols.

The illegal digits of octal number system are 8 and 9 .

Hexadecimal number system recognizes symbols 0 to 9 and A to F .

Each octal number is replaced with 3 bits in octal to binary conversion.

Each Hexadecimal number is replaced with 4 bits in Hex to binary conversion.

ASCII is a 7 bit code while extended ASCII is a 8 bit code.

The Unicode encoding scheme can represent all symbols/characters of most languages.

The ISCII encoding scheme represents Indian Languages' characters on computers.

UTF8 can take upto 4 bytes to represent a symbol.

UTF32 takes exactly 4 bytes to represent a symbol.

Unicode value of a symbol is called code point .

True/False Questions

A computer can work with Decimal number system. False

A computer can work with Binary number system. True

The number of unique symbols in Hexadecimal number system is 15. False

Number systems can also represent characters. False

ISCII is an encoding scheme created for Indian language characters. True

Unicode is able to represent nearly all languages' characters. True

UTF8 is a fixed-length encoding scheme. False

UTF32 is a fixed-length encoding scheme. True

UTF8 is a variable-length encoding scheme and can represent characters in 1 through 4 bytes. True

UTF8 and UTF32 are the only encoding schemes supported by Unicode. False

Type A: Short Answer Questions

What are some number systems used by computers ?

The most commonly used number systems are decimal, binary, octal and hexadecimal number systems.

What is the use of Hexadecimal number system on computers ?

The Hexadecimal number system is used in computers to specify memory addresses (which are 16-bit or 32-bit long). For example, a memory address 1101011010101111 is a big binary address but with hex it is D6AF which is easier to remember. The Hexadecimal number system is also used to represent colour codes. For example, FFFFFF represents White, FF0000 represents Red, etc.

What does radix or base signify ?

The radix or base of a number system signifies how many unique symbols or digits are used in the number system to represent numbers. For example, the decimal number system has a radix or base of 10 meaning it uses 10 digits from 0 to 9 to represent numbers.

What is the use of encoding schemes ?

Encoding schemes help Computers represent and recognize letters, numbers and symbols. It provides a predetermined set of codes for each recognized letter, number and symbol. Most popular encoding schemes are ASCI, Unicode, ISCII, etc.

Discuss UTF-8 encoding scheme.

UTF-8 is a variable width encoding that can represent every character in Unicode character set. The code unit of UTF-8 is 8 bits called an octet. It uses 1 to maximum 6 octets to represent code points depending on their size i.e. sometimes it uses 8 bits to store the character, other times 16 or 24 or more bits. It is a type of multi-byte encoding.

How is UTF-8 encoding scheme different from UTF-32 encoding scheme ?

UTF-8 is a variable length encoding scheme that uses different number of bytes to represent different characters whereas UTF-32 is a fixed length encoding scheme that uses exactly 4 bytes to represent all Unicode code points.

What is the most significant bit and the least significant bit in a binary code ?

In a binary code, the leftmost bit is called the most significant bit or MSB. It carries the largest weight. The rightmost bit is called the least significant bit or LSB. It carries the smallest weight. For example:

1 M S B 0 1 1 0 1 1 0 L S B \begin{matrix} \underset{\bold{MSB}}{1} & 0 & 1 & 1 & 0 & 1 & 1 & \underset{\bold{LSB}}{0} \end{matrix} MSB 1 ​ ​ 0 ​ 1 ​ 1 ​ 0 ​ 1 ​ 1 ​ LSB 0 ​ ​

What are ASCII and extended ASCII encoding schemes ?

ASCII encoding scheme uses a 7-bit code and it represents 128 characters. Its advantages are simplicity and efficiency. Extended ASCII encoding scheme uses a 8-bit code and it represents 256 characters.

What is the utility of ISCII encoding scheme ?

ISCII or Indian Standard Code for Information Interchange can be used to represent Indian languages on the computer. It supports Indian languages that follow both Devanagari script and other scripts like Tamil, Bengali, Oriya, Assamese, etc.

What is Unicode ? What is its significance ?

Unicode is a universal character encoding scheme that can represent different sets of characters belonging to different languages by assigning a number to each of the character. It has the following significance:

• It defines all the characters needed for writing the majority of known languages in use today across the world.
• It is a superset of all other character sets.
• It is used to represent characters across different platforms and programs.

What all encoding schemes does Unicode use to represent characters ?

Unicode uses UTF-8, UTF-16 and UTF-32 encoding schemes.

What are ASCII and ISCII ? Why are these used ?

ASCII stands for American Standard Code for Information Interchange. It uses a 7-bit code and it can represent 128 characters. ASCII code is mostly used to represent the characters of English language, standard keyboard characters as well as control characters like Carriage Return and Form Feed. ISCII stands for Indian Standard Code for Information Interchange. It uses a 8-bit code and it can represent 256 characters. It retains all ASCII characters and offers coding for Indian scripts also. Majority of the Indian languages can be represented using ISCII.

What are UTF-8 and UTF-32 encoding schemes. Which one is more popular encoding scheme ?

UTF-8 is a variable length encoding scheme that uses different number of bytes to represent different characters whereas UTF-32 is a fixed length encoding scheme that uses exactly 4 bytes to represent all Unicode code points. UTF-8 is the more popular encoding scheme.

What do you understand by code point ?

Code point refers to a code from a code space that represents a single character from the character set represented by an encoding scheme. For example, 0x41 is one code point of ASCII that represents character 'A'.

What is the difference between fixed length and variable length encoding schemes ?

Variable length encoding scheme uses different number of bytes or octets (set of 8 bits) to represent different characters whereas fixed length encoding scheme uses a fixed number of bytes to represent different characters.

Type B: Application Based Questions

Convert the following binary numbers to decimal:

Equivalent decimal number = 1 + 4 + 8 = 13

Therefore, (1101) 2 = (13) 10

Equivalent decimal number = 2 + 8 + 16 + 32 = 58

Equivalent decimal number = 1 + 2 + 4 + 8 + 16 + 64 + 256 = 351

Convert the following binary numbers to decimal :

Equivalent decimal number = 4 + 8 = 12

(b) 10010101

(c) 11011100

Convert the following decimal numbers to binary:

Therefore, (0.25) 10 = (0.01) 2

Therefore, (122) 10 = (1111010) 2

(We stop after 5 iterations if fractional part doesn't become 0)

Therefore, (0.675) 10 = (0.10101) 2

Convert the following decimal numbers to octal:

Therefore, (122) 10 = (172) 8

Therefore, (0.675) 10 = (0.53146) 8

Convert the following hexadecimal numbers to binary:

(23D) 16 = (1000111101) 2

Convert the following binary numbers to hexadecimal:

(a) 1010110110111

(b) 10110111011011

(c) 0110101100

0001 undefined 1010 undefined 1100 undefined \underlinesegment{0001} \quad \underlinesegment{1010} \quad \underlinesegment{1100} 0001 ​ 1010 ​ 1100 ​

Therefore, (0110101100) 2 = (1AC) 16

Convert the following octal numbers to decimal:

Equivalent decimal number = 7 + 40 + 128 = 175

Therefore, (257) 8 = (175) 10

Equivalent decimal number = 7 + 16 + 320 + 1536 = 1879

Therefore, (3527) 8 = (1879) 10

Equivalent decimal number = 3 + 16 + 64 = 83

Therefore, (123) 8 = (83) 10

Integral part

Fractional part.

Equivalent decimal number = 5 + 384 + 0.125 + 0.0312 = 389.1562

Therefore, (605.12) 8 = (389.1562) 10

Convert the following hexadecimal numbers to decimal:

Equivalent decimal number = 6 + 160 = 166

Therefore, (A6) 16 = (166) 10

Equivalent decimal number = 11 + 48 + 256 + 40960 = 41275

Therefore, (A13B) 16 = (41275) 10

Equivalent decimal number = 5 + 160 + 768 = 933

Therefore, (3A5) 16 = (933) 10

Equivalent decimal number = 9 + 224 = 233

Therefore, (E9) 16 = (233) 10

Equivalent decimal number = 3 + 160 + 3072 + 28672 = 31907

Therefore, (7CA3) 16 = (31907) 10

Convert the following decimal numbers to hexadecimal:

Therefore, (132) 10 = (84) 16

Therefore, (2352) 10 = (930) 16

Therefore, (122) 10 = (7A) 16

Therefore, (0.675) 10 = (0.ACCCC) 16

Therefore, (206) 10 = (CE) 16

Therefore, (3619) 10 = (E23) 16

Convert the following hexadecimal numbers to octal:

(38AC) 16 = (11100010101100) 2

011 undefined   100 undefined   010 undefined   101 undefined   100 undefined \underlinesegment{011}\medspace\underlinesegment{100}\medspace\underlinesegment{010}\medspace\underlinesegment{101}\medspace\underlinesegment{100} 011 ​ 100 ​ 010 ​ 101 ​ 100 ​

(38AC) 16 = (34254) 8

(7FD6) 16 = (111111111010110) 2

111 undefined   111 undefined   111 undefined   010 undefined   110 undefined \underlinesegment{111}\medspace\underlinesegment{111}\medspace\underlinesegment{111}\medspace\underlinesegment{010}\medspace\underlinesegment{110} 111 ​ 111 ​ 111 ​ 010 ​ 110 ​

(7FD6) 16 = (77726) 8

(ABCD) 16 = (1010101111001101) 2

001 undefined   010 undefined   101 undefined   111 undefined   001 undefined   101 undefined \underlinesegment{001}\medspace\underlinesegment{010}\medspace\underlinesegment{101}\medspace\underlinesegment{111}\medspace\underlinesegment{001}\medspace\underlinesegment{101} 001 ​ 010 ​ 101 ​ 111 ​ 001 ​ 101 ​

(ABCD) 16 = (125715) 8

Convert the following octal numbers to binary:

Therefore, (123) 8 = ( 001 undefined   010 undefined   011 undefined \bold{\underlinesegment{001}}\medspace\bold{\underlinesegment{010}}\medspace\bold{\underlinesegment{011}} 001 ​ 010 ​ 011 ​ ) 2

Therefore, (3527) 8 = ( 011 undefined   101 undefined   010 undefined   111 undefined \bold{\underlinesegment{011}}\medspace\bold{\underlinesegment{101}}\medspace\bold{\underlinesegment{010}}\medspace\bold{\underlinesegment{111}} 011 ​ 101 ​ 010 ​ 111 ​ ) 2

Therefore, (705) 8 = ( 111 undefined   000 undefined   101 undefined \bold{\underlinesegment{111}}\medspace\bold{\underlinesegment{000}}\medspace\bold{\underlinesegment{101}} 111 ​ 000 ​ 101 ​ ) 2

Therefore, (7642) 8 = ( 111 undefined   110 undefined   100 undefined   010 undefined \bold{\underlinesegment{111}}\medspace\bold{\underlinesegment{110}}\medspace\bold{\underlinesegment{100}}\medspace\bold{\underlinesegment{010}} 111 ​ 110 ​ 100 ​ 010 ​ ) 2

Therefore, (7015) 8 = ( 111 undefined   000 undefined   001 undefined   101 undefined \bold{\underlinesegment{111}}\medspace\bold{\underlinesegment{000}}\medspace\bold{\underlinesegment{001}}\medspace\bold{\underlinesegment{101}} 111 ​ 000 ​ 001 ​ 101 ​ ) 2

Therefore, (3576) 8 = ( 011 undefined   101 undefined   111 undefined   110 undefined \bold{\underlinesegment{011}}\medspace\bold{\underlinesegment{101}}\medspace\bold{\underlinesegment{111}}\medspace\bold{\underlinesegment{110}} 011 ​ 101 ​ 111 ​ 110 ​ ) 2

Convert the following binary numbers to octal

111 undefined 010 undefined \underlinesegment{111} \quad \underlinesegment{010} 111 ​ 010 ​

Therefore, (111010) 2 = (72) 8

(b) 110110101

110 undefined 110 undefined 101 undefined \underlinesegment{110} \quad \underlinesegment{110} \quad \underlinesegment{101} 110 ​ 110 ​ 101 ​

Therefore, (110110101) 2 = (665) 8

(c) 1101100001

001 undefined 101 undefined 100 undefined 001 undefined \underlinesegment{001} \quad \underlinesegment{101} \quad \underlinesegment{100} \quad \underlinesegment{001} 001 ​ 101 ​ 100 ​ 001 ​

Therefore, (1101100001) 2 = (1541) 8

011 undefined 001 undefined \underlinesegment{011} \quad \underlinesegment{001} 011 ​ 001 ​

Therefore, (11001) 2 = (31) 8

(b) 10101100

010 undefined 101 undefined 100 undefined \underlinesegment{010} \quad \underlinesegment{101} \quad \underlinesegment{100} 010 ​ 101 ​ 100 ​

Therefore, (10101100) 2 = (254) 8

(c) 111010111

111 undefined 010 undefined 111 undefined \underlinesegment{111} \quad \underlinesegment{010} \quad \underlinesegment{111} 111 ​ 010 ​ 111 ​

Therefore, (111010111) 2 = (727) 8

Add the following binary numbers:

(i) 10110111 and 1100101

1 1 0 1 1 1 0 1 1 1 1 1 1 + 1 1 0 0 1 0 1 1 0 0 0 1 1 1 0 0 \begin{matrix} & & \overset{1}{1} & \overset{1}{0} & 1 & 1 & \overset{1}{0} & \overset{1}{1} & \overset{1}{1} & 1 \\ + & & & 1 & 1 & 0 & 0 & 1 & 0 & 1 \\ \hline & \bold{1} & \bold{0} & \bold{0} & \bold{0} & \bold{1} & \bold{1} & \bold{1} & \bold{0} & \bold{0} \end{matrix} + ​ 1 ​ 1 1 0 ​ 0 1 1 0 ​ 1 1 0 ​ 1 0 1 ​ 0 1 0 1 ​ 1 1 1 1 ​ 1 1 0 0 ​ 1 1 0 ​ ​

Therefore, (10110111) 2 + (1100101) 2 = (100011100) 2

(ii) 110101 and 101111

1 1 1 1 0 1 1 1 0 1 1 + 1 0 1 1 1 1 1 1 0 0 1 0 0 \begin{matrix} & & \overset{1}{1} & \overset{1}{1} & \overset{1}{0} & \overset{1}{1} & \overset{1}{0} & 1 \\ + & & 1 & 0 & 1 & 1 & 1 & 1 \\ \hline & \bold{1} & \bold{1} & \bold{0} & \bold{0} & \bold{1} & \bold{0} & \bold{0} \end{matrix} + ​ 1 ​ 1 1 1 1 ​ 1 1 0 0 ​ 0 1 1 0 ​ 1 1 1 1 ​ 0 1 1 0 ​ 1 1 0 ​ ​

Therefore, (110101) 2 + (101111) 2 = (1100100) 2

(iii) 110111.110 and 11011101.010

0 1 0 1 1 1 1 1 0 1 1 1 1 1 1 1 . 1 1 1 0 + 1 1 0 1 1 1 0 1 . 0 1 0 1 0 0 0 1 0 1 0 1 . 0 0 0 \begin{matrix} & & \overset{1}{0} & \overset{1}{0} & \overset{1}{1} & \overset{1}{1} & \overset{1}{0} & \overset{1}{1} & \overset{1}{1} & \overset{1}{1} & . & \overset{1}{1} & 1 & 0 \\ + & & 1 & 1 & 0 & 1 & 1 & 1 & 0 & 1 & . & 0 & 1 & 0 \\ \hline & \bold{1} & \bold{0} & \bold{0} & \bold{0} & \bold{1} & \bold{0} & \bold{1} & \bold{0} & \bold{1} & \bold{.} & \bold{0} & \bold{0} & \bold{0} \end{matrix} + ​ 1 ​ 0 1 1 0 ​ 0 1 1 0 ​ 1 1 0 0 ​ 1 1 1 1 ​ 0 1 1 0 ​ 1 1 1 1 ​ 1 1 0 0 ​ 1 1 1 1 ​ . . . ​ 1 1 0 0 ​ 1 1 0 ​ 0 0 0 ​ ​

Therefore, (110111.110) 2 + (11011101.010) 2 = (100010101) 2

(iv) 1110.110 and 11010.011

0 1 1 1 1 1 1 0 1 . 1 1 1 0 + 1 1 0 1 0 . 0 1 1 1 0 1 0 0 1 . 0 0 1 \begin{matrix} & & \overset{1}{0} & \overset{1}{1} & \overset{1}{1} & 1 & \overset{1}{0} & . & \overset{1}{1} & 1 & 0 \\ + & & 1 & 1 & 0 & 1 & 0 & . & 0 & 1 & 1 \\ \hline & \bold{1} & \bold{0} & \bold{1} & \bold{0} & \bold{0} & \bold{1} & \bold{.} & \bold{0} & \bold{0} & \bold{1} \end{matrix} + ​ 1 ​ 0 1 1 0 ​ 1 1 1 1 ​ 1 1 0 0 ​ 1 1 0 ​ 0 1 0 1 ​ . . . ​ 1 1 0 0 ​ 1 1 0 ​ 0 1 1 ​ ​

Therefore, (1110.110) 2 + (11010.011) 2 = (101001.001) 2

Question 21

Given that A's code point in ASCII is 65, and a's code point is 97. What is the binary representation of 'A' in ASCII ? (and what's its hexadecimal representation). What is the binary representation of 'a' in ASCII ?

Binary representation of 'A' in ASCII will be binary representation of its code point 65.

Converting 65 to binary:

Therefore, binary representation of 'A' in ASCII is 1000001.

Converting 65 to Hexadecimal:

Therefore, hexadecimal representation of 'A' in ASCII is (41) 16 .

Similarly, converting 97 to binary:

Therefore, binary representation of 'a' in ASCII is 1100001.

Question 22

Convert the following binary numbers to decimal, octal and hexadecimal numbers.

(i) 100101.101

Decimal Conversion of integral part:

Decimal Conversion of fractional part:

Equivalent decimal number = 1 + 4 + 32 + 0.5 + 0.125 = 37.625

Therefore, (100101.101) 2 = (37.625) 10

Octal Conversion

100 undefined 101 undefined . 101 undefined \underlinesegment{100} \quad \underlinesegment{101} \quad \bold{.} \quad \underlinesegment{101} 100 ​ 101 ​ . 101 ​

Therefore, (100101.101) 2 = (45.5) 8

Hexadecimal Conversion

0010 undefined 0101 undefined   .   1010 undefined \underlinesegment{0010} \quad \underlinesegment{0101} \medspace . \medspace \underlinesegment{1010} 0010 ​ 0101 ​ . 1010 ​

Therefore, (100101.101) 2 = (25.A) 16

(ii) 10101100.01011

Equivalent decimal number = 4 + 8 + 32 + 128 + 0.25 + 0.0625 + 0.03125 = 172.34375

Therefore, (10101100.01011) 2 = (172.34375) 10

010 undefined 101 undefined 100 undefined . 010 undefined 110 undefined \underlinesegment{010} \quad \underlinesegment{101} \quad \underlinesegment{100} \quad \bold{.} \quad \underlinesegment{010} \quad \underlinesegment{110} 010 ​ 101 ​ 100 ​ . 010 ​ 110 ​

Therefore, (10101100.01011) 2 = (254.26) 8

1010 undefined 1100 undefined   .   0101 undefined   1000 undefined \underlinesegment{1010} \quad \underlinesegment{1100} \medspace . \medspace \underlinesegment{0101} \medspace \underlinesegment{1000} 1010 ​ 1100 ​ . 0101 ​ 1000 ​

Therefore, (10101100.01011) 2 = (AC.58) 16

Decimal Conversion:

Equivalent decimal number = 2 + 8 = 10

001 undefined 010 undefined \underlinesegment{001} \quad \underlinesegment{010} 001 ​ 010 ​

Therefore, (1010) 2 = (12) 8

(iv) 10101100.010111

Equivalent decimal number = 4 + 8 + 32 + 128 + 0.25 + 0.0625 + 0.03125 + 0.015625 = 172.359375

Therefore, (10101100.010111) 2 = (172.359375) 10

010 undefined 101 undefined 100 undefined . 010 undefined 111 undefined \underlinesegment{010} \quad \underlinesegment{101} \quad \underlinesegment{100} \quad \bold{.} \quad \underlinesegment{010} \quad \underlinesegment{111} 010 ​ 101 ​ 100 ​ . 010 ​ 111 ​

Therefore, (10101100.010111) 2 = (254.27) 8

1010 undefined 1100 undefined   .   0101 undefined   1100 undefined \underlinesegment{1010} \quad \underlinesegment{1100} \medspace . \medspace \underlinesegment{0101} \medspace \underlinesegment{1100} 1010 ​ 1100 ​ . 0101 ​ 1100 ​

Therefore, (10101100.010111) 2 = (AC.5C) 16

Data Representation in Computer: Number Systems, Characters, Audio, Image and Video

• Post author: Anuj Kumar
• Post published: 16 July 2021
• Post category: Computer Science
• Post comments: 0 Comments

Table of Contents

• 1 What is Data Representation in Computer?
• 2.1 Binary Number System
• 2.2 Octal Number System
• 2.3 Decimal Number System
• 2.4 Hexadecimal Number System
• 3.4 Unicode
• 4 Data Representation of Audio, Image and Video
• 5.1 What is number system with example?

What is Data Representation in Computer?

A computer uses a fixed number of bits to represent a piece of data which could be a number, a character, image, sound, video, etc. Data representation is the method used internally to represent data in a computer. Let us see how various types of data can be represented in computer memory.

Before discussing data representation of numbers, let us see what a number system is.

Number Systems

Number systems are the technique to represent numbers in the computer system architecture, every value that you are saving or getting into/from computer memory has a defined number system.

A number is a mathematical object used to count, label, and measure. A number system is a systematic way to represent numbers. The number system we use in our day-to-day life is the decimal number system that uses 10 symbols or digits.

The number 289 is pronounced as two hundred and eighty-nine and it consists of the symbols 2, 8, and 9. Similarly, there are other number systems. Each has its own symbols and method for constructing a number.

A number system has a unique base, which depends upon the number of symbols. The number of symbols used in a number system is called the base or radix of a number system.

Let us discuss some of the number systems. Computer architecture supports the following number of systems:

Binary Number System

Octal number system, decimal number system, hexadecimal number system.

A Binary number system has only two digits that are 0 and 1. Every number (value) represents 0 and 1 in this number system. The base of the binary number system is 2 because it has only two digits.

The octal number system has only eight (8) digits from 0 to 7. Every number (value) represents with 0,1,2,3,4,5,6 and 7 in this number system. The base of the octal number system is 8, because it has only 8 digits.

The decimal number system has only ten (10) digits from 0 to 9. Every number (value) represents with 0,1,2,3,4,5,6, 7,8 and 9 in this number system. The base of decimal number system is 10, because it has only 10 digits.

A Hexadecimal number system has sixteen (16) alphanumeric values from 0 to 9 and A to F. Every number (value) represents with 0,1,2,3,4,5,6, 7,8,9,A,B,C,D,E and F in this number system. The base of the hexadecimal number system is 16, because it has 16 alphanumeric values.

Here A is 10, B is 11, C is 12, D is 13, E is 14 and F is 15 .

Data Representation of Characters

There are different methods to represent characters . Some of them are discussed below:

The code called ASCII (pronounced ‘􀀏’.S-key”), which stands for American Standard Code for Information Interchange, uses 7 bits to represent each character in computer memory. The ASCII representation has been adopted as a standard by the U.S. government and is widely accepted.

A unique integer number is assigned to each character. This number called ASCII code of that character is converted into binary for storing in memory. For example, the ASCII code of A is 65, its binary equivalent in 7-bit is 1000001.

Since there are exactly 128 unique combinations of 7 bits, this 7-bit code can represent only128 characters. Another version is ASCII-8, also called extended ASCII, which uses 8 bits for each character, can represent 256 different characters.

For example, the letter A is represented by 01000001, B by 01000010 and so on. ASCII code is enough to represent all of the standard keyboard characters.

It stands for Extended Binary Coded Decimal Interchange Code. This is similar to ASCII and is an 8-bit code used in computers manufactured by International Business Machines (IBM). It is capable of encoding 256 characters.

If ASCII-coded data is to be used in a computer that uses EBCDIC representation, it is necessary to transform ASCII code to EBCDIC code. Similarly, if EBCDIC coded data is to be used in an ASCII computer, EBCDIC code has to be transformed to ASCII.

ISCII stands for Indian Standard Code for Information Interchange or Indian Script Code for Information Interchange. It is an encoding scheme for representing various writing systems of India. ISCII uses 8-bits for data representation.

It was evolved by a standardization committee under the Department of Electronics during 1986-88 and adopted by the Bureau of Indian Standards (BIS). Nowadays ISCII has been replaced by Unicode.

Using 8-bit ASCII we can represent only 256 characters. This cannot represent all characters of written languages of the world and other symbols. Unicode is developed to resolve this problem. It aims to provide a standard character encoding scheme, which is universal and efficient.

It provides a unique number for every character, no matter what the language and platform be. Unicode originally used 16 bits which can represent up to 65,536 characters. It is maintained by a non-profit organization called the Unicode Consortium.

The Consortium first published version 1.0.0 in 1991 and continues to develop standards based on that original work. Nowadays Unicode uses more than 16 bits and hence it can represent more characters. Unicode can represent characters in almost all written languages of the world.

Data Representation of Audio, Image and Video

In most cases, we may have to represent and process data other than numbers and characters. This may include audio data, images, and videos. We can see that like numbers and characters, the audio, image, and video data also carry information.

We will see different file formats for storing sound, image, and video .

Multimedia data such as audio, image, and video are stored in different types of files. The variety of file formats is due to the fact that there are quite a few approaches to compressing the data and a number of different ways of packaging the data.

For example, an image is most popularly stored in Joint Picture Experts Group (JPEG ) file format. An image file consists of two parts – header information and image data. Information such as the name of the file, size, modified data, file format, etc. is stored in the header part.

The intensity value of all pixels is stored in the data part of the file. The data can be stored uncompressed or compressed to reduce the file size. Normally, the image data is stored in compressed form. Let us understand what compression is.

Take a simple example of a pure black image of size 400X400 pixels. We can repeat the information black, black, …, black in all 16,0000 (400X400) pixels. This is the uncompressed form, while in the compressed form black is stored only once and information to repeat it 1,60,000 times is also stored.

Numerous such techniques are used to achieve compression. Depending on the application, images are stored in various file formats such as bitmap file format (BMP), Tagged Image File Format (TIFF), Graphics Interchange Format (GIF), Portable (Public) Network Graphic (PNG).

What we said about the header file information and compression is also applicable for audio and video files. Digital audio data can be stored in different file formats like WAV, MP3, MIDI, AIFF, etc. An audio file describes a format, sometimes referred to as the ‘container format’, for storing digital audio data.

For example, WAV file format typically contains uncompressed sound and MP3 files typically contain compressed audio data. The synthesized music data is stored in MIDI(Musical Instrument Digital Interface) files.

Similarly, video is also stored in different files such as AVI (Audio Video Interleave) – a file format designed to store both audio and video data in a standard package that allows synchronous audio with video playback, MP3, JPEG-2, WMV, etc.

FAQs About Data Representation in Computer

What is number system with example.

Let us discuss some of the number systems. Computer architecture supports the following number of systems: 1. Binary Number System 2. Octal Number System 3. Decimal Number System 4. Hexadecimal Number System

Related posts:

10 Types of Computers | History of Computers, Advantages

What is microprocessor evolution of microprocessor, types, features.

• What is operating system? Functions, Types, Types of User Interface

What is Cloud Computing? Classification, Characteristics, Principles, Types of Cloud Providers

What is debugging types of errors.

• What are Functions of Operating System? 6 Functions
• What is Flowchart in Programming? Symbols, Advantages, Preparation

Advantages and Disadvantages of Flowcharts

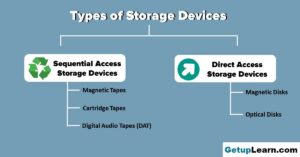
What is c++ programming language c++ character set, c++ tokens, what are c++ keywords set of 59 keywords in c ++, what are data types in c++ types, what are operators in c different types of operators in c, what are expressions in c types, what are decision making statements in c types, types of storage devices, advantages, examples, you might also like.

What is Big Data? Characteristics, Tools, Types, Internet of Things (IOT)

What is Computer System? Definition, Characteristics, Functional Units, Components

Types of Computer Software: Systems Software, Application Software

What is Artificial Intelligence? Functions, 6 Benefits, Applications of AI

10 Evolution of Computing Machine, History

What is Problem Solving Algorithm?, Steps, Representation

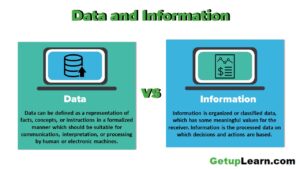
Data and Information: Definition, Characteristics, Types, Channels, Approaches

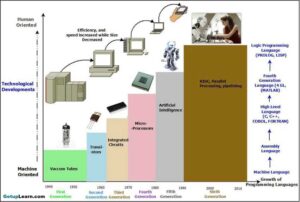
Generations of Computer First To Fifth, Classification, Characteristics, Features, Examples

• Entrepreneurship
• Organizational Behavior
• Financial Management
• Communication
• Human Resource Management
• Sales Management
• Marketing Management

The Essentials of Computer Organization and Architecture, 6th Edition by Linda Null

Get full access to The Essentials of Computer Organization and Architecture, 6th Edition and 60K+ other titles, with a free 10-day trial of O'Reilly.

There are also live events, courses curated by job role, and more.

© Paggi Eleanor/Shutterstock

CHAPTER 2 Data Representation in Computer Systems

There are 10 kinds of people in the world—those who understand binary and those who don’t. —Anonymous

Get The Essentials of Computer Organization and Architecture, 6th Edition now with the O’Reilly learning platform.

O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

Don’t leave empty-handed

Get Mark Richards’s Software Architecture Patterns ebook to better understand how to design components—and how they should interact.

It’s yours, free.

Check it out now on O’Reilly

Dive in for free with a 10-day trial of the O’Reilly learning platform—then explore all the other resources our members count on to build skills and solve problems every day.

• My presentations

Auth with social network:

Download presentation

We think you have liked this presentation. If you wish to download it, please recommend it to your friends in any social system. Share buttons are a little bit lower. Thank you!

Presentation is loading. Please wait.

Chapter 2 Data Representation in Computer Systems.

Published by Dwayne Barker Modified over 8 years ago

Similar presentations

Presentation on theme: "Chapter 2 Data Representation in Computer Systems."— Presentation transcript:

The Binary Numbering Systems

2-1 Chapter 2 - Data Representation Computer Architecture and Organization by M. Murdocca and V. Heuring © 2007 M. Murdocca and V. Heuring Computer Architecture.

Chapter 2: Data Representation

Principles of Computer Architecture Miles Murdocca and Vincent Heuring Chapter 2: Data Representation.

CHAPTER 2 Number Systems, Operations, and Codes

Data Representation in Computer Systems

Digital Fundamentals Floyd Chapter 2 Tenth Edition

Level ISA3: Information Representation

Assembly Language and Computer Architecture Using C++ and Java

Data Representation in Computer Systems Chapter 2.

CSC 221 Computer Organization and Assembly Language

© 2009 Pearson Education, Upper Saddle River, NJ All Rights ReservedFloyd, Digital Fundamentals, 10 th ed Digital Fundamentals Tenth Edition Floyd.

Lecture 6 Topics Character codes Error Detection and Correction

Information Representation (Level ISA3) Floating point numbers.

Computer Arithmetic Nizamettin AYDIN

About project

© 2024 SlidePlayer.com Inc. All rights reserved.

Page Statistics

Table of contents.

• Introduction to Functional Computer
• Fundamentals of Architectural Design

Data Representation

• Instruction Set Architecture : Instructions and Formats
• Instruction Set Architecture : Design Models
• Instruction Set Architecture : Addressing Modes
• Performance Measurements and Issues
• Computer Architecture Assessment 1
• Fixed Point Arithmetic : Addition and Subtraction
• Fixed Point Arithmetic : Multiplication
• Fixed Point Arithmetic : Division
• Floating Point Arithmetic
• Arithmetic Logic Unit Design
• CPU's Data Path
• CPU's Control Unit
• Control Unit Design
• Concepts of Pipelining
• Computer Architecture Assessment 2
• Pipeline Hazards
• Memory Characteristics and Organization
• Cache Memory
• Virtual Memory
• I/O Communication and I/O Controller
• Input/Output Data Transfer
• Direct Memory Access controller and I/O Processor
• CPU Interrupts and Interrupt Handling
• Computer Architecture Assessment 3

Course Computer Architecture

Digital computers store and process information in binary form as digital logic has only two values "1" and "0" or in other words "True or False" or also said as "ON or OFF". This system is called radix 2. We human generally deal with radix 10 i.e. decimal. As a matter of convenience there are many other representations like Octal (Radix 8), Hexadecimal (Radix 16), Binary coded decimal (BCD), Decimal etc.

Every computer's CPU has a width measured in terms of bits such as 8 bit CPU, 16 bit CPU, 32 bit CPU etc. Similarly, each memory location can store a fixed number of bits and is called memory width. Given the size of the CPU and Memory, it is for the programmer to handle his data representation. Most of the readers may be knowing that 4 bits form a Nibble, 8 bits form a byte. The word length is defined by the Instruction Set Architecture of the CPU. The word length may be equal to the width of the CPU.

The memory simply stores information as a binary pattern of 1's and 0's. It is to be interpreted as what the content of a memory location means. If the CPU is in the Fetch cycle, it interprets the fetched memory content to be instruction and decodes based on Instruction format. In the Execute cycle, the information from memory is considered as data. As a common man using a computer, we think computers handle English or other alphabets, special characters or numbers. A programmer considers memory content to be data types of the programming language he uses. Now recall figure 1.2 and 1.3 of chapter 1 to reinforce your thought that conversion happens from computer user interface to internal representation and storage.

• Data Representation in Computers

Information handled by a computer is classified as instruction and data. A broad overview of the internal representation of the information is illustrated in figure 3.1. No matter whether it is data in a numeric or non-numeric form or integer, everything is internally represented in Binary. It is up to the programmer to handle the interpretation of the binary pattern and this interpretation is called Data Representation . These data representation schemes are all standardized by international organizations.

Choice of Data representation to be used in a computer is decided by

• The number types to be represented (integer, real, signed, unsigned, etc.)
• Range of values likely to be represented (maximum and minimum to be represented)
• The Precision of the numbers i.e. maximum accuracy of representation (floating point single precision, double precision etc)
• If non-numeric i.e. character, character representation standard to be chosen. ASCII, EBCDIC, UTF are examples of character representation standards.
• The hardware support in terms of word width, instruction.

Before we go into the details, let us take an example of interpretation. Say a byte in Memory has value "0011 0001". Although there exists a possibility of so many interpretations as in figure 3.2, the program has only one interpretation as decided by the programmer and declared in the program.

• Fixed point Number Representation

Fixed point numbers are also known as whole numbers or Integers. The number of bits used in representing the integer also implies the maximum number that can be represented in the system hardware. However for the efficiency of storage and operations, one may choose to represent the integer with one Byte, two Bytes, Four bytes or more. This space allocation is translated from the definition used by the programmer while defining a variable as integer short or long and the Instruction Set Architecture.

In addition to the bit length definition for integers, we also have a choice to represent them as below:

• Unsigned Integer : A positive number including zero can be represented in this format. All the allotted bits are utilised in defining the number. So if one is using 8 bits to represent the unsigned integer, the range of values that can be represented is 28 i.e. "0" to "255". If 16 bits are used for representing then the range is 216 i.e. "0 to 65535".
• Signed Integer : In this format negative numbers, zero, and positive numbers can be represented. A sign bit indicates the magnitude direction as positive or negative. There are three possible representations for signed integer and these are Sign Magnitude format, 1's Compliment format and 2's Complement format .

Signed Integer – Sign Magnitude format: Most Significant Bit (MSB) is reserved for indicating the direction of the magnitude (value). A "0" on MSB means a positive number and a "1" on MSB means a negative number. If n bits are used for representation, n-1 bits indicate the absolute value of the number. Examples for n=8:

Examples for n=8:

0010 1111 = + 47 Decimal (Positive number)

1010 1111 = - 47 Decimal (Negative Number)

0111 1110 = +126 (Positive number)

1111 1110 = -126 (Negative Number)

0000 0000 = + 0 (Postive Number)

1000 0000 = - 0 (Negative Number)

Although this method is easy to understand, Sign Magnitude representation has several shortcomings like

• Zero can be represented in two ways causing redundancy and confusion.
• The total range for magnitude representation is limited to 2n-1, although n bits were accounted.
• The separate sign bit makes the addition and subtraction more complicated. Also, comparing two numbers is not straightforward.

Signed Integer – 1’s Complement format: In this format too, MSB is reserved as the sign bit. But the difference is in representing the Magnitude part of the value for negative numbers (magnitude) is inversed and hence called 1’s Complement form. The positive numbers are represented as it is in binary. Let us see some examples to better our understanding.

1101 0000 = - 47 Decimal (Negative Number)

1000 0001 = -126 (Negative Number)

1111 1111 = - 0 (Negative Number)

• Converting a given binary number to its 2's complement form

Step 1 . -x = x' + 1 where x' is the one's complement of x.

Step 2 Extend the data width of the number, fill up with sign extension i.e. MSB bit is used to fill the bits.

Example: -47 decimal over 8bit representation

As you can see zero is not getting represented with redundancy. There is only one way of representing zero. The other problem of the complexity of the arithmetic operation is also eliminated in 2’s complement representation. Subtraction is done as Addition.

More exercises on number conversion are left to the self-interest of readers.

• Floating Point Number system

The maximum number at best represented as a whole number is 2 n . In the Scientific world, we do come across numbers like Mass of an Electron is 9.10939 x 10-31 Kg. Velocity of light is 2.99792458 x 108 m/s. Imagine to write the number in a piece of paper without exponent and converting into binary for computer representation. Sure you are tired!!. It makes no sense to write a number in non- readable form or non- processible form. Hence we write such large or small numbers using exponent and mantissa. This is said to be Floating Point representation or real number representation. he real number system could have infinite values between 0 and 1.

Representation in computer

Unlike the two's complement representation for integer numbers, Floating Point number uses Sign and Magnitude representation for both mantissa and exponent . In the number 9.10939 x 1031, in decimal form, +31 is Exponent, 9.10939 is known as Fraction . Mantissa, Significand and fraction are synonymously used terms. In the computer, the representation is binary and the binary point is not fixed. For example, a number, say, 23.345 can be written as 2.3345 x 101 or 0.23345 x 102 or 2334.5 x 10-2. The representation 2.3345 x 101 is said to be in normalised form.

Floating-point numbers usually use multiple words in memory as we need to allot a sign bit, few bits for exponent and many bits for mantissa. There are standards for such allocation which we will see sooner.

• IEEE 754 Floating Point Representation

We have two standards known as Single Precision and Double Precision from IEEE. These standards enable portability among different computers. Figure 3.3 picturizes Single precision while figure 3.4 picturizes double precision. Single Precision uses 32bit format while double precision is 64 bits word length. As the name suggests double precision can represent fractions with larger accuracy. In both the cases, MSB is sign bit for the mantissa part, followed by Exponent and Mantissa. The exponent part has its sign bit.

It is to be noted that in Single Precision, we can represent an exponent in the range -127 to +127. It is possible as a result of arithmetic operations the resulting exponent may not fit in. This situation is called overflow in the case of positive exponent and underflow in the case of negative exponent. The Double Precision format has 11 bits for exponent meaning a number as large as -1023 to 1023 can be represented. The programmer has to make a choice between Single Precision and Double Precision declaration using his knowledge about the data being handled.

The Floating Point operations on the regular CPU is very very slow. Generally, a special purpose CPU known as Co-processor is used. This Co-processor works in tandem with the main CPU. The programmer should be using the float declaration only if his data is in real number form. Float declaration is not to be used generously.

• Decimal Numbers Representation

Decimal numbers (radix 10) are represented and processed in the system with the support of additional hardware. We deal with numbers in decimal format in everyday life. Some machines implement decimal arithmetic too, like floating-point arithmetic hardware. In such a case, the CPU uses decimal numbers in BCD (binary coded decimal) form and does BCD arithmetic operation. BCD operates on radix 10. This hardware operates without conversion to pure binary. It uses a nibble to represent a number in packed BCD form. BCD operations require not only special hardware but also decimal instruction set.

• Exceptions and Error Detection

All of us know that when we do arithmetic operations, we get answers which have more digits than the operands (Ex: 8 x 2= 16). This happens in computer arithmetic operations too. When the result size exceeds the allotted size of the variable or the register, it becomes an error and exception. The exception conditions associated with numbers and number operations are Overflow, Underflow, Truncation, Rounding and Multiple Precision . These are detected by the associated hardware in arithmetic Unit. These exceptions apply to both Fixed Point and Floating Point operations. Each of these exceptional conditions has a flag bit assigned in the Processor Status Word (PSW). We may discuss more in detail in the later chapters.

• Character Representation

Another data type is non-numeric and is largely character sets. We use a human-understandable character set to communicate with computer i.e. for both input and output. Standard character sets like EBCDIC and ASCII are chosen to represent alphabets, numbers and special characters. Nowadays Unicode standard is also in use for non-English language like Chinese, Hindi, Spanish, etc. These codes are accessible and available on the internet. Interested readers may access and learn more.

1. Track your progress [Earn 200 points]

Mark as complete

2. Provide your ratings to this chapter [Earn 100 points]