math problem solving model

Math Problem Solving Strategies

In these lessons, we will learn some math problem solving strategies for example, Verbal Model (or Logical Reasoning), Algebraic Model, Block Model (or Singapore Math), Guess & Check Model and Find a Pattern Model.

Related Pages Solving Word Problems Using Block Models Heuristic Approach to Problem-Solving Algebra Lessons

Problem Solving Strategies

The strategies used in solving word problems:

• What do you know?
• What do you need to know?
• Draw a diagram/picture

Solution Strategies Label Variables Verbal Model or Logical Reasoning Algebraic Model - Translate Verbal Model to Algebraic Model Solve and Check.

Solving Word Problems

Step 1: Identify (What is being asked?) Step 2: Strategize Step 3: Write the equation(s) Step 4: Answer the question Step 5: Check

Problem Solving Strategy: Guess And Check

Using the guess and check problem solving strategy to help solve math word problems.

Example: Jamie spent $40 for an outfit. She paid for the items using $10, $5 and $1 bills. If she gave the clerk 10 bills in all, how many of each bill did she use?

Problem Solving : Make A Table And Look For A Pattern

• Identify - What is the question?
• Plan - What strategy will I use to solve the problem?
• Solve - Carry out your plan.
• Verify - Does my answer make sense?

Example: Marcus ran a lemonade stand for 5 days. On the first day, he made $5. Every day after that he made $2 more than the previous day. How much money did Marcus made in all after 5 days?

Find A Pattern Model (Intermediate)

In this lesson, we will look at some intermediate examples of Find a Pattern method of problem-solving strategy.

Example: The figure shows a series of rectangles where each rectangle is bounded by 10 dots. a) How many dots are required for 7 rectangles? b) If the figure has 73 dots, how many rectangles would there be?

a) The number of dots required for 7 rectangles is 52.

b) If the figure has 73 dots, there would be 10 rectangles.

Example: Each triangle in the figure below has 3 dots. Study the pattern and find the number of dots for 7 layers of triangles.

The number of dots for 7 layers of triangles is 36.

Example: The table below shows numbers placed into groups I, II, III, IV, V and VI. In which groups would the following numbers belong? a) 25 b) 46 c) 269

Solution: The pattern is: The remainder when the number is divided by 6 determines the group. a) 25 ÷ 6 = 4 remainder 1 (Group I) b) 46 ÷ 6 = 7 remainder 4 (Group IV) c) 269 ÷ 6 = 44 remainder 5 (Group V)

Example: The following figures were formed using matchsticks.

a) Based on the above series of figures, complete the table below.

b) How many triangles are there if the figure in the series has 9 squares?

c) How many matchsticks would be used in the figure in the series with 11 squares?

b) The pattern is +2 for each additional square.   18 + 2 = 20   If the figure in the series has 9 squares, there would be 20 triangles.

c) The pattern is + 7 for each additional square   61 + (3 x 7) = 82   If the figure in the series has 11 squares, there would be 82 matchsticks.

Example: Seven ex-schoolmates had a gathering. Each one of them shook hands with all others once. How many handshakes were there?

Total = 6 + 5 + 4 + 3 + 2 + 1 = 21 handshakes.

The following video shows more examples of using problem solving strategies and models. Question 1: Approximate your average speed given some information Question 2: The table shows the number of seats in each of the first four rows in an auditorium. The remaining ten rows follow the same pattern. Find the number of seats in the last row. Question 3: You are hanging three pictures in the wall of your home that is 16 feet wide. The width of your pictures are 2, 3 and 4 feet. You want space between your pictures to be the same and the space to the left and right to be 6 inches more than between the pictures. How would you place the pictures?

The following are some other examples of problem solving strategies.

Explore it/Act it/Try it (EAT) Method (Basic) Explore it/Act it/Try it (EAT) Method (Intermediate) Explore it/Act it/Try it (EAT) Method (Advanced)

Finding A Pattern (Basic) Finding A Pattern (Intermediate) Finding A Pattern (Advanced)

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.

The Frayer Model for Math

ThoughtCo. / Deb Russell

• Math Tutorials
• Pre Algebra & Algebra
• Exponential Decay
• Worksheets By Grade

The Frayer Model is a graphic organizer that was traditionally used for language concepts, specifically to enhance the development of vocabulary. However, graphic organizers are great tools to support thinking through problems in math . When given a specific problem, we need to use the following process to guide our thinking which is usually a four-step process:

• What is being asked? Do I understand the question?
• What strategies might I use?
• How will I solve the problem?
• What is my answer? How do I know? Did I fully answer the question?

Learning to Use the Frayer Model in Math

These 4 steps are then applied to the Frayer model template ( print the PDF ) to guide the problem-solving process and develop an effective way of thinking. When the graphic organizer is used consistently and frequently, over time, there will be a definite improvement in the process of solving problems in math. Students who were afraid to take risks will develop confidence in approaching the solving of math problems.

Let's take a very basic problem to show what the thinking process would be for using the Frayer Model.

Sample Problem and Solution

A clown was carrying a bunch of balloons. The wind came along and blew away 7 of them and now he only has 9 balloons left. How many balloons did the clown begin with?

Using the Frayer Model to Solve the Problem:

• Understand :  I need to find out how many balloons the clown had before the wind blew them away.
• Plan:  I could draw a picture of how many balloons he has and how many balloons the wind blew away.
• Solve:  The drawing would show all of the balloons, the child may also come up with the number sentence as well.
• Check : Re-read the question and put the answer in written format.

Although this problem is a basic problem, the unknown is at the beginning of the problem which often stumps young learners. As learners become comfortable with using a graphic organizer like a  4 block method  or the Frayer Model which is modified for math, the ultimate result is improved problem-solving skills. The Frayer Model also follows the steps to solving problems in math.

• Graphic Organizers in Math
• Math Word Problems for Third Graders
• 2nd Grade Math Word Problems
• Examples of Problem Solving with 4 Block
• Problem Solving in Mathematics
• How to Use Math Journals in Class
• Algebra: Using Mathematical Symbols
• Sixth Grade Word Problems
• 7 Steps to Math Success
• The Horse Problem: A Math Challenge
• Quiz 8th-Graders With These Math Word Problems
• Math Stumper: Use Two Squares to Make Separate Pens for Nine Pigs
• Solving Problems Involving Distance, Rate, and Time
• Realistic Math Problems Help 6th-graders Solve Real-Life Questions
• Lesson Plan Step #8 - Assessment and Follow-Up
• Christmas Word Problem Worksheets

Critical & Creative Thinking - OER & More Resources: IDEAL problem solving

• Self evaluation
• Creating goals
• Creating personal mission statement
• Creative Thinking
• Problem Solving
• IDEAL problem solving
• CRITICAL THINKING
• Critical Thinking Tips
• Logic Terms
• Logic Traps
• Free OER Textbooks
• More Thinking: OER
• Ethics - OER Textbooks
• Evidence-Based Critical Thinking
• BELIEFS & BIAS
• Limits of Perception
• Reality & Assumptions
• Stereotypes & Race
• MAKING YOUR CASE
• Argument (OER)
• Inductive Arguments
• Information Literacy: Be Savvy about your Sources
• Persuasive Speaking (OER)
• Philosophy & Thinking
• WiPhi Philosophy Project
• Browse All Guides

VM: I had to inter-library loan this item to read the original content.  This is highly cited throughout literature, so I wanted to have a good grasp on what it covered.  Here are my notes and commentary:

•  Full text From TNtech.edu: "Ideal Problem Solver, 2 ed." (c) 1984, 1993 more... less... Thanks to Center for Assessment & Improvement of Learning - Reports & Publications"
• Full text from ERIC: The IDEAL Workplace: Strategies for Improving Learning, Problem Solving, and Creativity
• Show your support: The Ideal Problem Solver: A Guide to Improving Thinking, Learning, and Creativity Second Edition

The reason you should learn the IDEAL method is so you don't need to avoid problems.  The more know about and practice problem solving, the easier it gets.  It is learnable skill. It also prompts you to look for problems and solutions instead of just doing things the same old way.

Improvement of problem solving skills.  

Model for analyzing the processes that underlie effective problem solving.

IDEAL Model for improving problem solving (Verbatim copy of Fig 2.1; p.12)

I = Identifying the problem.

D = Define and represent the problem.

E = Explore possible strategies.

A = Act on the strategies.

L = Look back and evaluate the effects of your activities.

ELABORATION:

I = Identifying that there is a problem that, once described as a problem, may be solved or improved.

D = Define and represent the problem.  Draw it instead of trying to imagine it.

E = Explore possible strategies & alternative approaches or viewpoints. 

General strategies: Break problem down into small simple problems. Working a problem backwards. Build scale model Try simulation experiment, with smaller or simpler sets.

A = Act on the strategies. Try, then reflect or recall. Actively try learning strategy.

L = Look back and evaluate the effects of your activities. Look at results of learning strategy used: Does it work to allow full recall?

"Many students make the mistake of assuming that they have "learned" adequately if the information seems to make sense as they read it in a textbook or hear it in a lecture."    (p. 23" Must  use or practice, recall, or paraphrase - in order to evaluate effectiveness of learning.  

Math: Do example problems before looking at solution to practice concepts.  Look at solution to see where you went wrong (or not). 

Don't let the test be the first time you evaluate your understanding of material

Problem identification and definition.

Proof of concept - act/look/evaluate.

To find an answer to a problem, you can dig deeper, or dig somewhere else.  

Question assumptions about limits  The old - think outside the box- strategy.

When memorizing, know what you need to remember  Definitions?  Concepts? Graphs?  Dates?  each teacher has different priorities...ask them what to focus on

Ways to solve problem of learning new information.

Techniques for improving memory.

Short term meomory

Long term memory

Remembering people's names

Studying for an essay test.

Using cues to retrieve information.  For example, you can remember IDEAL first and that will help you reconstruct the idea of how to solve problems.

Some strategies for remembering information:

Make a story full of memorable images.  

Funny obnoxious "vivid images" or "mental pictures" are more memorabl e. (Ex: random words in a list, passwords, people's names. Banana vomit haunts me.)

Rehearse over and over - over learn.   (Ex: Memorizing a phone number 867-5309 )

Rehearse words in groups - chunking. (Ex: Memorizing a part in a play, poems, pledges, short stories.)

Organize words into conceptual categories - Look for unifying relationships. (Recall, order not important. Ex: Shopping list, points in an essay.)

Look for similarities and coincidences in the words themselves. (Ex: How many words have e's, or 2 syllables, or have pun-ishing homonyms)

The feet that use the manual transmission car pedals are, from left to right: ​ C ( L eft-foot) utch , the  B( R ight-foot) ake , and the  A ccelerato ( R ight-foot)

Does order mimic alphabetical order? The manual transmission car pedals are, from left to right, the C lutch, the B rake, and the A ccelerator )   

Use Acronyms I dentify D efine ​E xplore A ct ​L ook

Acronym- easily remembered word: FACE

Acrostic- easily remembered phrase:    E very G ood B oy D eserves F udge

• Modified image source: Commons.wikimedia.org

Don't waste time studying what you already know

Image - Name Strategy:

What is unique about the person?  What is unique about their name?

Find a relationship between the two.

Other Pairing Strategies:

method of loci: arranging words to be remembered in association with familiar location or path .

Peg-word method: arranging words to be remembered in association with number order or alphabet letter order .

Strategies to comprehend new information.

more difficult than

Strategies to memorize new information.

Learning with understanding - comprehending new information.

Knowledge of CORE CONCEPTS in a field SIMPLIFIES problem solving. 

Ways to approach a problem of learning information that seems to be arbitrary:

Over-learn:  rehearse the facts until they are mastered.  2+2=4

Find relationships between images or words that are memorable: story telling, silmilarieties, vivid images, pegging, etc.

When a concept seems unclear, learn more about it.

Memory- can be of seemingly arbitrary words or numbers: ROTE (Ex. Facts and relationships) appearance

Comprehension - is understanding significance or relationships or function

Novices often forced to memorize information until they learn enough (related concepts and context) to understand it.

The mere memorization of information rarely provides useful conceptual tools that enable one to solve new problems later on. (p. 61,69)

Taking notes will not necessarily lead to effective recall prompts. How do you know when you understand material? Self-test by trying to explain material to another person.That will expose gaps in understanding.

Recall answers or solve problems out of order to be sure you know which concepts to apply and why.

Look at mistakes made as soon as possible, and learn where you went wrong.

Uses of information require more or less precision in understanding, depending on context. (A pilot must know more about an airplane than a passenger.)

Evaluation basics: evaluate factual claims look for flaws in logic question assumptions that form the basis of the argument

Correlation does not necessarily prove cause and effect.

Importance of being able to criticize ideas and generate alternatives.

Strategies for effective criticism.

Strategies for formulating creative solutions.

Finding/understanding implicit assumptions that hamper brainstorming.

Strategies for making implicit assumptions explicit.

"The uncreative mind can spot wrong answers, but it takes a creative mnd to spot wrong questions ." Emphasis added. - Anthony Jay, (p.93)

Making implicit assumptions explicit: look for inconsistencies question assumptions make predictions analyze worst case get feedback & criticism from others

Increase generation of novel ideas: break down problem into smaller parts analyze properties on a simpler level use analogies use brainstorming give it a rest, sleep on it don't be in a hurry, let ideas incubate: ​talk to others, read, keep the problem in the back of your mind try to communicate your ideas as clearly as possible, preferably in writing. attempting to write or teach an idea can function as a discovery technique

Strategies for Effective Communication

What we are trying to accomplish (goal)

Evaluating communication fro effectiveness:

Identify and Define: Have you given audience basis to understand different points of view about a topic? Different problem definitions can lead to different solutions. Did you Explore pros and cons of different strategies? Did you take Action and then Look at consequences? Did you organize your content into main points that are easy to identify and remeber?

Did you use analogies and background information to put facts into context?

Did you make sure your facts were accurate and did you avoid making assumptions?Always check for logical fallacies and inconsistencies.  Did you include information that is novel and useful, instead of just regurgitating what everyone already knows?

After you communicate, get feedback and evaluate your strategies.  Look for effects, and learn from your mistakes.  (p. 117)

Identify and Define what (problem) you want to communicate, with respect to your audience and your goals. Explore strategies for communicating your ideas.Act - based on your strategies. Look at effects.

Summaries of Useful  Attitudes and Strategies: Anybody can use the IDEAL system to improve their problem solving skills.

Related Resources:

• Teaching The IDEAL Problem-Solving Method To Diverse Learners Written by: Amy Sippl
• << Previous: Problem Solving
• Next: CRITICAL THINKING >>
• Last Updated: Mar 13, 2024 3:04 PM
• URL: https://library.fvtc.edu/Thinking

About Us • Contact Us • FVTC Terms of Service • Sitemap FVTC Privacy Statement • FVTC Library Services Accessibility Statement DISCLAIMER: Any commercial mentions on our website are for instructional purposes only. Our guides are not a substitute for professional legal or medical advice. Fox Valley Technical College • Library Services • 1825 N. Bluemound Drive • Room G113 Appleton, WI 54912-2277 • United States • (920) 735-5653 © 2024 • Fox Valley Technical College • All Rights Reserved.

The https://library.fvtc.edu/ pages are hosted by SpringShare. Springshare Privacy Policy.

Powerful online learning at your pace

What IS Problem-Solving?

Ask teachers about problem-solving strategies, and you’re opening a can of worms! Opinions about the “best” way to teach problem-solving are all over the board. And teachers will usually argue for their process quite passionately.

When I first started teaching math over 25 years ago, it was very common to teach “keywords” to help students determine the operation to use when solving a word problem. For example, if you see the word “total” in the problem, you always add. Rather than help students become better problem solvers, the use of keywords actually resulted in students who don’t even feel the need to read and understand the problem–just look for the keywords, pick out the numbers, and do the operation indicated by the keyword.

This post contains affiliate links, which simply means that when you use my link and purchase a product, I receive a small commission. There is no additional cost to you, and I only link to books and products that I personally use and recommend.

Another common strategy for teaching problem-solving is the use of acrostics that students can easily remember to perform the “steps” in problem-solving. CUBES is an example. Just as with keywords, however, students often follow the steps with little understanding. As an example, a common step is to underline or highlight the question. But if you ask students why they are underlining or highlighting the question, they often can’t tell you. The question is , in fact, super important, but they’ve not been told why. They’ve been told to underline the question, so they do.

The problem with both keywords and the rote-step strategies is that both methods try to turn something that is inherently messy into an algorithm! It’s way past time that we leave both methods behind.

First, we need to broaden the definition of problem-solving. Somewhere along the line, problem-solving became synonymous with “word problems.” In reality, it’s so much more. Every one of us solves dozens or hundreds of problems every single day, and most of us haven’t solved a word problem in years. Problem-solving is often described as  figuring out what to do when you don’t  know what to do.  My power went out unexpectedly this morning, and I have work to do. That’s a problem that I had to solve. I had to think about what the problem was, what my options were, and formulate a plan to solve the problem. No keywords. No acrostics. I’m using my phone as a hotspot and hoping my laptop battery doesn’t run out. Problem solved. For now.

If you want to get back to what problem-solving really is, you should consult the work of George Polya. His book, How to Solve It , which was first published in 1945, outlined four principles for problem-solving. The four principles are: understand the problem, devise a plan, carry out the plan, and look back. This document from UC Berkeley’s Mathematics department is a great 4-page overview of Polya’s process. You can probably see that the keyword and rote-steps strategies were likely based on Polya’s method, but it really got out of hand. We need to help students think , not just follow steps.

I created both primary and intermediate posters based on Polya’s principles. Grab your copies for free here !

I would LOVE to hear your comments about problem-solving!

Similar Posts

The Hiding Assessment in Action

Fluency and flexibility with numbers are the hallmarks of mathematical thinking. For our students to excel in mathematics, they must understand how numbers can be composed and decomposed. That’s why…

FREE Number Sense Technology Tools

I love combining great math with technology. If that sounds good to you, too, you’ll want to check out these free number sense technology tools from DreamBox. You’ll find this…

So You Want to Be a Math Coach?

I get emails from time to time from readers who are new math coaches seeking advice. That’s in part, I think, because coaching positions are not often well-defined. Sometimes, to…

Concrete Learning for Subtraction with Regrouping

Earlier in the week, I wrote about the importance of following the concrete, representational, abstract (CRA) sequence for math instruction. One thing I failed to mention is that the types…

Telling Time to the Hour and Half Hour

The math standards are carefully aligned to gradually develop concepts over a period of time. A great example is telling time. In First Grade, students are required to tell time…

Technology-Based Model Drawing

It’s yet another great technology find!!  I was just in a training for model drawing, and I was reminded of a GREAT website for learning and teaching model drawing.  If…

Do you tutor teachers?

I do professional development for district and schools, and I have online courses.

You make a great point when you mentioned that teaching students to look for “keywords” is not teaching students to become better problem solvers. I was once guilty of using the CUBES strategy, but have since learned to provide students with opportunity to grapple with solving a problem and not providing them with specified steps to follow.

I think we’ve ALL been there! We learn and we do better. 🙂

Love this article and believe that we can do so much better as math teachers than just teaching key words! Do you have an editable version of this document? We are wanting to use something similar for our school, but would like to tweak it just a bit. Thank you!

I’m sorry, but because of the clip art and fonts I use, I am not able to provide an editable version.

Hi Donna! I am working on my dissertation that focuses on problem-solving. May I use your intermediate poster as a figure, giving credit to you in my citation with your permission, for my section on Polya’s Traditional Problem-Solving Steps? You laid out the process so succinctly with examples that my research could greatly benefit from this image. Thank you in advance!

Absolutely! Good luck with your dissertation!

Leave a Reply Cancel reply

Your email address will not be published. Required fields are marked *

Mobile Navigation

Improving mathematical reasoning with process supervision.

Illustration: Ruby Chen

We've trained a model to achieve a new state-of-the-art in mathematical problem solving by rewarding each correct step of reasoning (“process supervision”) instead of simply rewarding the correct final answer (“outcome supervision”). In addition to boosting performance relative to outcome supervision, process supervision also has an important alignment benefit: it directly trains the model to produce a chain-of-thought that is endorsed by humans.

More resources

Introduction.

In recent years, large language models have greatly improved in their ability to perform complex multi-step reasoning. However, even state-of-the-art models still produce logical mistakes, often called hallucinations . Mitigating hallucinations is a critical step towards building aligned AGI.

We can train reward models to detect hallucinations using either outcome supervision , which provides feedback based on a final result, or process supervision , which provides feedback for each individual step in a chain-of-thought. Building on previous work [^reference-1] , we conduct a detailed comparison of these two methods using the MATH dataset [^reference-2] as our testbed. We find that process supervision leads to significantly better performance, even when judged by outcomes. To encourage related research, we release our full dataset of process supervision.

Alignment impact

Process supervision has several alignment advantages over outcome supervision. It directly rewards the model for following an aligned chain-of-thought, since each step in the process receives precise supervision. Process supervision is also more likely to produce interpretable reasoning, since it encourages the model to follow a human-approved process. In contrast, outcome supervision may reward an unaligned process, and it is generally harder to scrutinize.

In some cases, safer methods for AI systems can lead to reduced performance [^reference-3] , a cost which is known as an alignment tax . In general, any alignment tax may hinder the adoption of alignment methods, due to pressure to deploy the most capable model. Our results below show that process supervision in fact incurs a negative alignment tax, at least in the math domain. This could increase the adoption of process supervision, which we believe would have positive alignment side-effects.

Solving MATH problems

We evaluate our process-supervised and outcome-supervised reward models using problems from the MATH test set. We generate many solutions for each problem and then pick the solution ranked the highest by each reward model. The graph shows the percentage of chosen solutions that reach the correct final answer, as a function of the number of solutions considered. Not only does the process-supervised reward model perform better across the board, but the performance gap widens as we consider more solutions per problem. This shows us that the process-supervised reward model is much more reliable.

We showcase 10 problems and solutions below, along with commentary about the reward model’s strengths and weaknesses.

Explore examples in 3 categories:

• True positives
• True negatives
• False positives

Model attempt

This challenging trigonometry problem requires applying several identities in a not-at-all obvious succession. Most solution attempts fail, because it is hard to choose which identities are actually helpful. Although GPT-4 usually can’t solve this problem (only . 1 % .1\% .1% of solution attempts reach the correct answer), the reward model correctly recognizes that this solution is valid.

It is unknown how broadly these results will generalize beyond the domain of math, and we consider it important for future work to explore the impact of process supervision in other domains. If these results generalize, we may find that process supervision gives us the best of both worlds – a method that is both more performant and more aligned than outcome supervision.

• Hunter Lightman
• Vineet Kosaraju
• Harri Edwards
• Ilya Sutskever

Acknowledgments

Contributors.

Bowen Baker, Teddy Lee, John Schulman, Greg Brockman, Kendra Rimbach, Hannah Wong, Thomas Degry

Math teaching support you can trust

resources downloaded

one-on-one tutoring sessions

schools supported

[FREE] Fun Math Games & Activities

Engage your students with our ready-to-go packs of no-prep games and activities for a range of abilities across Kindergarten to Grade 5!

The Ultimate Guide To The Bar Model: How To Teach It And Use It In Elementary School

Pete richardson.

Teaching the bar model in elementary school is essential if you want students to do well in their reasoning and problem solving skills. Here’s your step-by-step guide on how to teach the bar model using math mastery lessons from Pre-K and Kindergarten right up to 5th grade level questions.

First we will look at the four operations and a progression of bar model representations that can be applied across all grades in elementary school.

Then we will look at more complex bar model examples, including how to apply bar models to other concepts such as fraction and equations.

What is a bar model in math?

How to draw a bar model, bar models: pre-k to third grade, bar models: 3rd grade to 5th grade, bar models: middle school and beyond, fun math games and activities packs for kindergarten to 5th grade.

Individual packs for K-5 containing fun math games and activities to do with your students

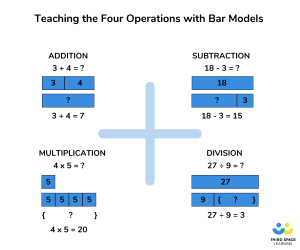
What is a bar model ? In math a bar model, also known as a strip diagram , is a pictorial representation of a problem or concept where bars or boxes are used to represent the known and unknown quantities. Bar models are most often used to solve number problems with the four operations – addition and subtraction , multiplication and division.

In word problems, bar models help children visualize the problem and decide which operations to use.

The bar model is the pictorial stage in the concrete pictorial abstract (CPA) approach to learning and is central to math mastery. Bar models will not, however, do the calculations for the students; they simply make it easier for learners to work out which equation must be done to solve the problem.

What is the bar model in math?

The bar model is used by drawing out a bar to represent the known and unknown quantities in a given problem. Encouraging a child to use the bar model in a problem can help them to understand conceptually what math operation is required from the problem, and how each part combines to make the whole.

An understanding of bar models is essential for teaching word problems , especially those using four operations (addition, subtraction, multiplication, division), fractions and algebra. Here the bar model shows us that if 2 rectangles out of 3 rectangles are green, then two thirds of 12 must be 8.

Why use the bar model method in math?

The bar model is used in Singapore and Asian Math textbooks and is an essential part of the mastery math approach used by schools at all stages.

By using the bar method to visualize problems, students are able to tackle any kind of number problem or complex word problem.

Because bar models only require pencils and paper, they are highly versatile and can be very useful for tests.

The use of bar models are also useful for learning at an early stage, from showing number bonds to ten or partitioning numbers as part of your place value work. 

Once a child is secure in their use of the bar model for the four operations and can conceptualize its versatility, they can start to use it to visualize many other math topics and problems, such as statistics and data handling .

The Singapore Bar Model Method

‘The Singapore Math Model’ is another name for the bar model method. Despite this name however the Singapore bar model (like most of the math mastery approach) is based heavily on the work of Bruner, Dienes and Bishop about the best way to help children learn: teaching for mastery. 

Bar models act as a ‘bridge’ between the concrete, pictorial and abstract (CPA in math); once children are secure with using pictorial versions of their concrete materials, they can progress to using bars as visual representations.  

Bars are a more abstract way of representing amounts, making the transition to using wholly abstract numbers significantly less difficult. 

The Part Whole Method

Also known as the ‘part part whole’ method or the comparison model, this kind of bar model uses rectangles to represent the known and unknown quantities as parts of a whole. This is an excellent method to help students represent the very common ‘missing number’ problems. 

This can be done in two ways:

• As discrete parts to a whole – each unit in the problem has its own individual box, similar to using Numicon cubes. 
• As continuous parts to a whole – units are grouped into one box for each amount in the problem e.g. in 26 + 52, 26 would have one long bar, not 26 smaller rectangles joined together.

When using the part-whole method, proportionality is key; all the bars must be roughly proportional to each other e.g. 6 should be about twice the length of 3. 

Part-whole models are generally used to visually represent the four operations, fractions, measurement, algebra and ratios, but can be applied to many more topics in the common core (as long as they’re relevant!).

Read more: What Is The Part Whole Model ?

There are a few steps involved in drawing a bar model and using it to solve a problem:

• Read the question carefully
• Circle the important information
• Determine the variables: who? what?
• Make a plan for solving the problem: what operation needs to be used?
• Draw the unit bars based on the information
• Re-read the problem to make sure that the bar models match the information given
• Complete the problem using the determined operation.

Bar model addition

Students in Pre-K and Kindergarten will routinely come across expressions such as 4+3.

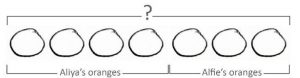
Often, these expressions will be presented as word problems: Aliya has 4 oranges. Alfie has 3 oranges. How many oranges are there altogether? To help children fully understand later stages of the bar model, it is crucial they begin with concrete representations.

There are 2 models that can be used to represent addition:

Once they are used to the format and able to represent word problems with models in this way themselves (assigning ‘labels’ verbally), the next stage is to replace the ‘real’ objects with objects that represent what is being discussed (in this case, we replace the ‘real’ oranges with button counters):

The next stage is to move away from the concrete to the pictorial. As with all the stages, when students are ready for the next stage is a judgment call that is best decided upon within your school.

A general rule of thumb would be that towards the end of kindergarten or start of first grade, students should be able to understand and represent simple addition and subtraction problems pictorially and assign written labels in a bar model.

The penultimate stage is to represent each object as part of a bar, in preparation for the final stage:

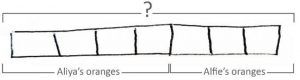
The final stage moves away from the 1:1 representation. Each quantity is represented approximately as a rectangular bar:

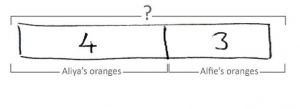
As mentioned before, it is a judgment call for your school to make, but if you want students to use the bar model to support them at the end of semester tests towards the later stage of their early years, they are going to need to have had a fair amount of experience in this final stage.

Bar model subtraction

The same concrete to pictorial stages can be applied to subtraction. However, whereas with addition it is really down to the student’s preference as to which of the 2 bar representations to use, with subtraction the teacher can nudge students to one or the other.

The reason? One represents a ‘part-part-whole’ model, the other a ‘find the difference’ model. Each will be more suited to different word problems and different learners. Let’s examine those at the final stage of the bar model:

Part-part-whole

Austin has 18 lego bricks. He used 15 pieces to build a small car. How many pieces does he have left?

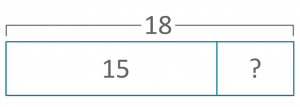
Equation: 18 – 15 =

Find the difference

Austin has 18 lego bricks. Lionel has 3 lego bricks. How many more lego bricks does Austin have than Lionel?

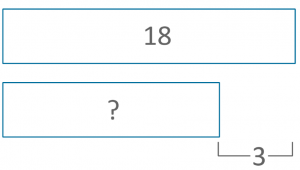
Equation: 18 – 3 =

Bar model multiplication

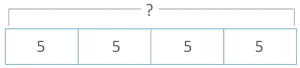
Bar model multiplication starts with the same ‘real’ and ‘representative counters’ stages as addition and subtraction. Then it moves to its final stage, drawing rectangular bars to represent each group:

Each box contains 5 cookies. Lionel buys 4 boxes. How many cookies does Lionel have?

Bar model division

Due to the complexity of division, it is recommended to keep grouping and sharing until the final stage of the bar model is understood. Then word problems such as the 2 below can be introduced:

Grace has 27 lollipops. She wants to share them amongst 9 friends by putting them in party bags. How many lollipops will go into each party bag?

Grace has 27 lollipops for her party friends. She wants each friend to have 3 lollipops. How many friends can she invite to her party?

Bar models in assessments

The key question at any grade level is, “what do we know?” By training students to ask this when presented with word problems themselves, they quickly become independent at drawing bar models.

For example, in the problem: Egg boxes can hold 6 eggs. We need to fill 7 boxes. How many eggs will we need?

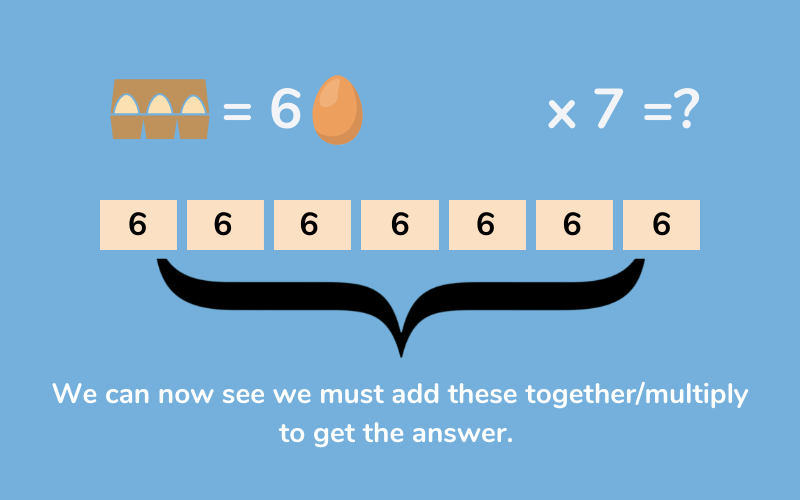
We know that there will be 7 egg boxes, so we know we can draw 7 rectangular bars. We know that each box holds 6 eggs, so we can write ‘6 eggs’ or ‘6’ in each of those 7 rectangular bars. We know we need to find the amount of eggs we have altogether. We can see we will need to use repeated addition or multiplication to solve the problem.

Bar model for the four operations word problems

Let’s ramp up the difficulty a little. In a sample assessment, students are asked:

A bag of 5 lemons costs $1. A bag of 4 oranges costs $1.80. How much more does one orange cost than one lemon?

Students could represent this problem in the below bar model, simply by asking and answering ‘what do we know?’

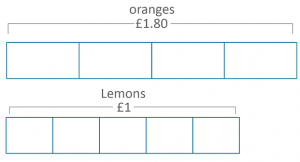
From here it should be straightforward for the students to ‘see’ or visualize their next step. Namely, dividing $1.80 by 4 and $1 by 5. Some students will not need the bar model to represent the next stage, but if they do, they would solve and then allocate the cost onto the model:

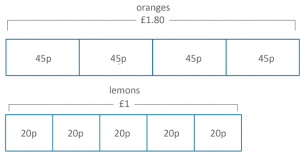
Then those students that needed this stage, should be able to see that to answer the question, they need to solve 45¢ – 20¢. With the answer of 25¢.

Bar model for word problems with fractions

Here’s another example from tests involving fractions and how it can be solved using a fraction bar model . 

On Saturday Lara read two fifths of her book. On Sunday, she read the other 90 pages to finish the book. How many pages are there in Lara’s book? If we create our bar model for what we know:

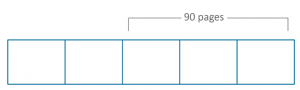
Students will then see that they can divide 90 by 3:

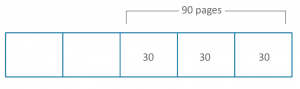
As fractions are ‘equal parts’ – a concept they should be familiar with from third grade – they know that the other 2 fifths (Saturday’s reading) will be 30 pages each:

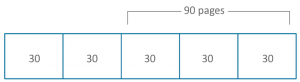
Then they can solve 30 x 5 = 150

Equations with the bar model

There are lots of other areas where bar models can assist student’s understanding such as ratio, percentages and equations. In this final example, we look at how an equation can be demystified using the comparison model:

2a + 7 = a + 11

Let’s draw what we know in a comparison model, as we know both sides of the equation will equal the same total:

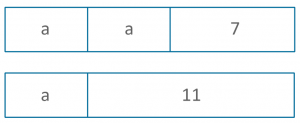
The bars showing 7 and 11 could have been a lot smaller or larger as we don’t know their relative value to ‘a’ at this stage. However, it is crucial that the ‘a’ appearing first in both bars is understood to be equal (even if it is only approximately equal when drawn freehand in the bar). This allows the student to ‘see’ that to work out the second ‘a’ in the top bar, they can solve 11-7.

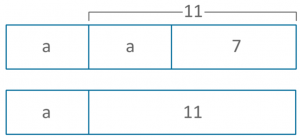
So if that ‘a’ is 4, then both the other ‘a’s will also be 4. So each side of the equation will total 15. The below model shows all sections completed. This is not necessary for the students to do, the representation is merely useful until they can see the steps necessary to solve whatever they are faced with:

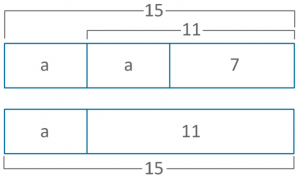
Where next?

Now you’re persuaded (we hope!) that the bar model in math is going to revolutionize problem solving across your school from early years onwards.

If you don’t believe me, use this problem to grab their attention:

Hussain wins first prize for his spectacular cake version of the Eiffel Tower. He generously gives three fifths of his winnings to his children and spends a third of what he had left. He has $80 left. How much money did he win?

With or without bar models? Which is easier? My guess is your staff will be hooked!

More on the bar model and math mastery techniques

• Third Space Sample Lessons on the Bar Model
• Benefits of following a mastery in math approach
• Bar model applied to improper fractions

Do you have students who need extra support in math? Give your students more opportunities to consolidate learning and practice skills through personalized math tutoring with their own dedicated online math tutor. Each student receives differentiated instruction designed to close their individual learning gaps, and scaffolded learning ensures every student learns at the right pace. Lessons are aligned with your state’s standards and assessments, plus you’ll receive regular reports every step of the way. Personalized one-on-one math tutoring programs are available for: – 2nd grade tutoring – 3rd grade tutoring – 4th grade tutoring – 5th grade tutoring – 6th grade tutoring – 7th grade tutoring – 8th grade tutoring Why not learn more about how it works ?

The content in this article was originally written by primary school deputy head teacher Pete Richardson and has since been revised and adapted for US schools by elementary math teacher Jaclyn Wassell.

Ultimate Guide to Metacognition [FREE]

Looking for a summary on metacognition in relation to math teaching and learning?

Check out this guide featuring practical examples, tips and strategies to successfully embed metacognition across your school to accelerate math growth.

Privacy Overview

• Enroll & Pay
• Prospective Students
• Current Students
• Degree Programs

Explicitly Model Mathematics Concepts/Skills & Problem Solving Strategies

What is the purpose of explicitly modeling mathematics concepts/skills and problem solving strategies.

The purpose of explicitly modeling mathematics concepts/skills and problem solving strategies is twofold. First, explicit modeling of a target mathematics concept/skill provides students a clear and accessible format for initially acquiring an understanding of the mathematics concept/skill. Explicit modeling by you provides students with a clear, accurate, multi-sensory model of the skill or concept. Students must first be able to access the attributes of a concept/skill before they can be expected to understand it and be able to use it in meaningful ways. Explicit teacher modeling does just that. Second, by explicitly modeling effective strategies for approaching particular problem solving situations, you provide students a process for becoming independent learners and problem solvers. While peers can sometimes be effective models for students, students with special needs require a well qualified teacher to provide such modeling, at least in the initial phases of instruction.

What is Explicit Modeling?

Explicit modeling involves well-prepared teachers employing a variety of instructional techniques to illuminate the key attributes of any given mathematics concept/skill. In a sense, you serve as a "bridge of learning" for your student, an accessible bridge between the student and the particular mathematics concept/skill they are learning:

The level of teacher support you provide your students depends on how much of a learning bridge they need. In particular, students with learning problems need a well-established learning bridge (teacher model). They learn most effectively when their teacher provides clear and multi-sensory models of a mathematics concept/skill during math instruction.

What are some important considerations when implementing Explicit Modeling?

The teacher purposefully sets the stage for understanding by identifying what students will learn (visually and auditorily), providing opportunities for students to link what they already know (e.g. prerequisite concepts/skills they have already mastered, prior real-life experiences they have had, areas of interest based on your students' age, culture, ethnicity, etc.), and discussing with students how what they are going to learn has relevance/meaning for their immediate lives.

• Teacher breaks math concept/skill into learnable parts/steps. Think about the concept/skill and break it down into 3-4 features or parts.
• Teacher clearly describes features of the math concept or steps in performing math skill using visual examples.
• Teacher describes/models using multi-sensory techniques. Use as many "input" pathways as possible for any given concept/skill including auditory, visual, tactile, and kinesthetic means. For example, when modeling how to compare values of different fractions to determine "greater than," you might verbalize each step of the process for comparing fractions while pointing to each step written on chart paper (auditory and visual), represent each fraction using fraction circle pieces, running your finger around the perimeter of each piece, laying one fraction piece over the other one and running your finger along the space not covered up by the fraction of lesser value/area; "thinking aloud" by saying your thoughts aloud as you examine each fraction piece (visual, kinesthetic, auditory), verbalizing your answer and why you determined why one fraction was greater than the other, and having students run their fingers along the same fraction pieces and uncovered space (auditory, visual, tactile, kinesthetic).
• Teacher provides both examples and non-examples of the mathematics concept/skill. For example, in the above example, you might compare two different fractions using same process but place the fraction of greater value/area on top of the fraction of lesser value/area. Then prompt student thinking of why this is not an example of "greater than."
• Explicitly cue students to essential attributes of the mathematics concept/skill you model. For example, when associating the written fraction to the fraction pieces and their respective values, color code the numerator and denominator in ways that represent the meaning of the fraction pieces they use. Cue students to the color-coding and what each color represents. Then demonstrate how each written fraction relates to the "whole' circle:

2/4 = 2 of four equal pieces

• Teacher engages students in learning through demonstrating enthusiasm, through maintaining a lively pace, through periodically questioning students, and through checking for student understanding. Explicit modeling is not meant to be a passive learning experience for students. On the contrary, it is critical to involve students as you model.
• After modeling several examples and non-examples, begin to have your students demonstrate a few steps of the process.
• As students demonstrate greater understanding, ask them to complete more and more of the process.
• When students demonstrate complete understanding, have various students "teach" you by modeling the entire process.
• Play a game where you and your students try to "catch" each other making a mistake or leaving out a step in the process.

How do I implement Explicit Modeling?

• Select the appropriate level of understanding to model the concept/skill or problem solving strategy (concrete, representational, abstract).
• Ensure that your students have the prerequisite skills to perform the skill or use the problem solving strategy.
• Break down the concept/skill or problem solving strategy into logical and learnable parts (Ask yourself, "What do I do and what do I think as I perform the skill?"). The strategies you can link to from this site are already broken down into steps.
• Provide a meaningful context for the concept/skill or problem solving strategy (e.g. word or story problem suited to the age and interests of your students. Invite parents/family members of your students or members of the community who work in an area that can be meaningfully applied to the concept/skill or strategy and ask them to show how they use the concept/skill/strategy in their work.
• Provide visual, auditory, kinesthetic (movement), and tactile means for illustrating important aspects of the concept/skill (e.g. visually display word problem and equation, orally cue students by varying vocal intonations, point, circle, highlight computation signs or important information in story problems).
• "Think aloud" as you illustrate each feature or step of the concept/skill/strategy (e.g. say aloud what you are thinking as you problem-solve so students can better "visualize" the metacognitive aspects of understanding or doing the concept/skill/strategy).
• Link each step of the problem solving process (e.g. restate what you did in the previous step, what you are going to do in the next step, and why the next step is important to the previous step).
• Periodically check student understanding with questions, remodeling steps when there is confusion.
• Maintain a lively pace while being conscious of student information processing difficulties (e.g. need additional time to process questions).
• Model a concept/skill at least three times.

How does Explicitly Modeling Mathematics Concepts/Skills and Problem Solving Strategies help students who have learning problems?

• Teacher as model makes the concept/skill clear and learnable.
• High level of teacher support and direction enables student to make meaningful cognitive connections.
• Provides students who have attention problems, processing problems, memory retrieval problems, and metacognitive difficulties an accessible "learning map" to the concept/skill/strategy.
• Links between parts/steps are directly made, making confusion and misunderstanding less likely.
• Multi-sensory cueing provides students multiple modes to process and thereby learn information.
• Teaching students effective problem solving strategies provides them a means for solving problems independently and assists them to develop their metacognitive awareness.

What Mathematics Problem Solving Strategies can I teach my students?

Mathematics problem solving strategies that have research support or that have been field tested with students can be accessed by clicking on the link below. These strategies are organized according to mathematics concept/skill area. Each strategy is described and an example of how each strategy can be used is also provided. 

What are additional resources I can use to help me implement Explicitly Modeling Mathematics Concepts/Skills and Problem Solving Strategies?

MathVIDS is an interactive CD-ROM/website for teachers who are teaching math to students who are having difficulty learning mathematics. The development of MathVIDS was sponsored through funding by the Virginia Department of Education.

Model Drawing for Math Problem Solving

Model Drawing is a highly effective method for solving Math questions that involve fractions and remainders. Drawing bar models allows your child to visualise the relationship between “Part” vs “Whole” clearly.

In this tutorial, we look at two questions taken from 2021 Prelim papers to help you learn how to use model drawing.

But before you read on, you might want to download this entire revision notes in PDF format to print it out for your child, or to read it later.

This will be delivered to your email inbox.

The first question is taken from the Tao Nan School Paper 2 and is worth 2 marks. This is a basic fraction question that can be solved using model drawing.

The key concept is that half of 3 units (3u) is $3. Since Alan used 7 units of his allowance on food, he had 3 units left.

He spent half of the remaining 3 units, and he had $3 left. This means the other half of the 3 units is $3. To visualize this, a model drawing is necessary.

Step 1: Visualisation – Model the provided information

The first part of the model drawing is a long bar to represent the number of units. Alan’s allowance at first was 10 units, meaning the bar must have 10 equal parts.

Then, indicate the number of units spent on food (F). In this example, that is 7 units.

Alan spent half of his remaining allowance on stationary items. In the model drawing above, his remaining allowance is 3 units. However, 3 units cannot be split into half directly.

So, we have to split the middle unit into 2 halves to indicate that he spent half of his allowance on stationary (S). The other half would then be $3.

Because one unit has been split into 2 halves, we have to split all the remaining units into 2 parts as well. This ensures that there are equal units throughout.

Step 2: Start solving the question

Since 3 units (3u) = $3, then 1 unit (1u) is $1. Because we’ve split every unit into 2 parts, Alan’s allowance will not be 10 units anymore. It will be 20 instead.

Make sure that your child or student uses the new total units when solving this type of question using model drawing.

Naturally, 20 units would be $20, and this is the final answer to this question.

This is a more complex question taken from the Catholic High School Paper 2, and it is worth 3 marks.

Since 3 4 of the fruits were removed, 1 4 of the fruits were left. That means 1 8 of the apples and 30 pears = 1 8 of the total number of fruits.

Step 1: Visualisation

Begin model drawing and split the bar into five equal groups.

Explanation : 5 was the original denominator, indicating the total number of fruits.

Out of 5 units, 4 were apples (A) and the rest were pears (P). Indicate that as shown in the worksheet below:

There were 4 units of apples. However, 1 8 of the apples were left. In this case, we can't indicate 1 8 right away. So, we have to split the 4 units into 2 groups.

To ensure that all units are the same, we also split the unit representing the pears. Now we have 10 units in total. Next, shade the unit that represents the number of apples left.

There were 30 pairs left, and we do not know how many units that represents. So, we shade a random part of the unit to indicate these remaining pears.

The two shaded portions represent 1 4 of the total, and the unshaded portion would naturally be 3 4 of the fruits that were removed.

Based on the shaded areas, 7 units (7u) of apples and 2 units (2u) minus 30 pears were removed.

This means that 7u and 2u - 30 is 3 4 of the total number of fruits. So, the shaded 1u of apples + 30 would be 1 4 of the total number of fruits. The equation forms of this information would be as follows:

To make a fair comparison during model drawing, ensure that the values on the right-hand side of both equations are the same. To convert 1 4 into 3 4 , multiply the entire equation by 3.

The above effectively means that 9u – 30 is actually the same as 3u + 90. So, write that in another equation.

This point gets a bit tricky because your child may not yet learn to change the sign from positive to negative or vice versa when changing sides.

So, draw another smaller model representing 9u – 30. When we remove 30 from 9u, we are left with the length shown below the smaller model:

The length indicated in the second bar is also the same as 3u + 90. That means the portion between the end of 3u and the rest of the bar makes up 6 units (6u).

Therefore, 6u is 90 + 30, which would give us 120. Once this visualisation is done, you can write it in an equation form.

From here, you can determine the value of 1 unit which is 20. However, the question asked for the number of fruits that were in the box at first.

At first, we used a denominator of 5. So, our model drawing had 5 parts. However, each unit was split into 2 parts, making the new total units 10. That gives us a total of 200 fruits, and that is the final answer to this question.

I hope this tutorial was easy for you to follow, especially the second question. We used the method of elimination in simultaneous equations to solve the second question, but we did so in a way where P6 students can understand.

You might want to download this entire revision notes in PDF format to print it out for your child, or to read it later.

If you have any questions or suggestions, please leave them in the comments below.

You can also watch the full Model Drawing video tutorial here:

To Your Child’s Success,

Ms Elaine Wee Math and Science Specialist Jimmy Maths and Grade Solution Learning Centre

Does your child need help in his or her studies?

1) Live Zoom Lessons at Grade Solution Learning Centre

At Grade Solution Learning Centre, we are a team of dedicated educators whose mission is to guide your child to academic success.  Here are the services we provide:

– Live Zoom lessons

– EdaptIQ™, a smart learning platform that tracks your child’s progress, strengths, and weaknesses through personalized digital worksheets.

– 24/7 Homework Helper Service

We provide all these services above at a very affordable monthly fee to allow as many students as possible to access such learning opportunities.

We specialize in English, Math, and Science subjects.

You can see our fees and schedules here >> https://gradesolution.com.sg/schedule/

2) Pre-recorded Online courses on Jimmymaths.com

If you are looking for something that fits your budget, or prefer your child learn at his or her own pace, you can join our pre-recorded online Math courses.

Your child can:

– Learn from recorded videos

– Get access to lots of common exam questions to ensure sufficient practice

– Get unlimited support and homework help

You can see the available courses here >>  https://jimmymaths.com/our-courses/

• PRIMARY SCHOOL
• SECONDARY SCHOOL
• LOGIN / REGISTER

1-800-852-2435

• Web Based Assessment
• View Proposal

Moving with Math Learning System

• The Learning System
• The Difference
• Problem Solving
• Response to Intervention
• Scientifically Based Research & Results
• Professional Development
• Assessment Technology
• Product Features
• Connections Pre-Kindergarten
• Connections (Pre-K – 2)
• Extensions 2nd Edition – Generic
• Extensions 2nd Edition CCSS
• Extensions 2nd Edition CCSS-CA
• Extensions 2nd Edition TEKS
• Extensions 2nd Edition – Spanish
• Foundations (1-4) Generic
• Foundations (1-4) CCSS
• Foundations (1-4) TX
• Foundations (1-4) Spanish
• Foundations Algebra (5-8+) Generic
• Foundations Algebra (5-8+) CCSS
• Foundations Algebra (5-8+) TX
• Moving With Algebra (7+)
• Math by Topic 2nd Edition (1-8+)
• Math By Topic (1 – 8+)
• Online Assessment
• Home-Based Education (Pre-K – 8+)
• Manipulatives (Pre-K – 9+)
• Pre-Kindergarten and Emersion
• Summer School
• Common Core
• Special Education and Title 1
• ELL/Dual Language
• Tutoring/Pull-Out/Resource Labs
• Double Dose/Replacement Units
• Correlated to State Standards
• Home-Based Education (Pre-K - 8+)

Problem Solving in Every Lesson

Using research-based strategies to teach problem solving, the hands-on difference in problem-solving.

Students using manipulatives are engaged in problem solving situations every day as they explore and discover the essential underpinnings of mathematical concepts.

Steps and Strategies for Problem-Solving

Students develop and apply a five-step problem solving model and discover that a variety of strategies may be used to solve the same problem.

5-Step Problem-Solving Model

1. Read and understand.

2. Find the question and needed facts.

3. Decide on process.

4. Estimate and compare.

5. Solve and check back.

Common Problem-Solving Strategies

1. Act it out.

2. Use a model.

3. Draw a picture.

4. Simplify

5. Make a table. Find a pattern.

Real-World Problem Solving

Real-world problems are used as the vehicle to introduce lessons. As students write word problems related to a computation, they develop understanding of the structure of a word problem. Understanding the relationship between elements in a word problem is essential to solving the problem.

Learning System

Market research confirms.

"In my 23 years doing market research I have never seen such outstanding numbers like those which Math Teachers Press received on the recent Best Customer Study. I have never had a client earn a perfect grade on a subject in which every single Best Customer gives a client an "A" grade."

What Educators Say

"To solve a problem is to find a way where no way is known offhand, to find a way out of difficulty, to find a way around an obstacle, to attain a desired end, that is not immediately attainable by appropriate means."

"Math Teachers Press has developed a teaching tool to help teachers change their practice."

"The activities you selected highlighted the importance of helping students move from the concrete to the abstract in stages. You also modeled differentiation as you tailored each session to meet the diverse needs of our participants."

"The workshops helped teachers reach students who are struggling in math ... Teacher evaluations were positive ... The teachers have reported student improvement."

Home   |   News   |   Exhibits   |   Employment   |   Workshops      Moving with Math - Makes Math Easy.

Math Teachers Press, Inc.

Personal Privacy Statement   |   On Line Privacy Statement   |   FERPA Statement   |   User End Agreement

© 2024 Math Teacher's Press, Inc

• For a new problem, you will need to begin a new live expert session.
• You can contact support with any questions regarding your current subscription.
• You will be able to enter math problems once our session is over.
• I am only able to help with one math problem per session. Which problem would you like to work on?
• Does that make sense?
• I am currently working on this problem.
• Are you still there?
• It appears we may have a connection issue. I will end the session - please reconnect if you still need assistance.
• Let me take a look...
• Can you please send an image of the problem you are seeing in your book or homework?
• If you click on "Tap to view steps..." you will see the steps are now numbered. Which step # do you have a question on?
• Please make sure you are in the correct subject. To change subjects, please exit out of this live expert session and select the appropriate subject from the menu located in the upper left corner of the Mathway screen.
• What are you trying to do with this input?
• While we cover a very wide range of problems, we are currently unable to assist with this specific problem. I spoke with my team and we will make note of this for future training. Is there a different problem you would like further assistance with?
• Mathway currently does not support this subject. We are more than happy to answer any math specific question you may have about this problem.
• Mathway currently does not support Ask an Expert Live in Chemistry. If this is what you were looking for, please contact support.
• Mathway currently only computes linear regressions.
• We are here to assist you with your math questions. You will need to get assistance from your school if you are having problems entering the answers into your online assignment.
• Have a great day!
• Hope that helps!
• You're welcome!
• Per our terms of use, Mathway's live experts will not knowingly provide solutions to students while they are taking a test or quiz.

Please ensure that your password is at least 8 characters and contains each of the following:

• a special character: @$#!%*?&

• Solve equations and inequalities
• Simplify expressions
• Factor polynomials
• Graph equations and inequalities
• Advanced solvers
• All solvers
• Arithmetics
• Determinant
• Percentages
• Scientific Notation
• Inequalities

What can QuickMath do?

QuickMath will automatically answer the most common problems in algebra, equations and calculus faced by high-school and college students.

• The algebra section allows you to expand, factor or simplify virtually any expression you choose. It also has commands for splitting fractions into partial fractions, combining several fractions into one and cancelling common factors within a fraction.
• The equations section lets you solve an equation or system of equations. You can usually find the exact answer or, if necessary, a numerical answer to almost any accuracy you require.
• The inequalities section lets you solve an inequality or a system of inequalities for a single variable. You can also plot inequalities in two variables.
• The calculus section will carry out differentiation as well as definite and indefinite integration.
• The matrices section contains commands for the arithmetic manipulation of matrices.
• The graphs section contains commands for plotting equations and inequalities.
• The numbers section has a percentages command for explaining the most common types of percentage problems and a section for dealing with scientific notation.

Math Topics

More solvers.

• Add Fractions
• Simplify Fractions

• Our Mission

Problem-Based Instruction in Middle and High School Math

PBI allows students to investigate real-world mathematical questions, increasing engagement with and understanding of course material.

Coach , facilitator , and guide on the side are phrases we have heard being used to describe the teacher’s role in PBI (problem-based instruction). Our idea of PBI is that students are exploring, inquiring, and crafting their own knowledge instead of being spoon-fed information by their teacher. In PBI the teacher moves from being the main disseminator of knowledge to a tool students use to help them guide their own exploration. The teacher must be well prepared and well versed in the content to be able to guide students to appropriate resources, answer questions, and ensure students remain on the correct trajectory with their inquiry. It is the role of the teacher as the content expert to come alongside the students to share resources, encourage, ask probing questions, and ensure students have a supportive environment in which to explore, inquire, and craft their understanding.

The preparations for a teacher in a PBI setting come largely before a PBI lesson is launched in the classroom. Teachers need to prepare resources, craft the driving question or problem scenario, and ensure all project aspects are planned and clear. If connections are being made to community entities or entities outside of the classroom, those arrangements must be secured by the teacher before initiating the PBI so that student experiences are well crafted and flow smoothly. While planning the PBI experience, teachers must also be intimately aware of their students’ learning needs.

Students learn at different rates and will seek different levels of content exploration. Scaffolding a lesson to accommodate student learning needs is a necessity in PBI. Teachers must know how to meet individual learning needs and what accommodations will have to be made, and then seek ways to provide support and structure within this framework. Teachers should also be familiar with the instructional learning goals targeted by the PBI lesson to ensure accuracy and adherence to these learning goals throughout the lesson.

Perhaps the most crucial trait of a teacher in a PBI lesson is flexibility. While teachers can plan, plan, and plan, it is almost guaranteed that something will not go as planned. Sometimes students stretch beyond the planned learning target and go deeper with their inquiry than expected. Other times students will hit a roadblock and will require extra support and encouragement. Sometimes schedules change, unexpected events occur, and the pacing for the lesson becomes offset. Teacher flexibility and fluidity will help encourage students to remain focused on their inquiry while knowing their knowledge journey is supported by their teacher.

PBI FROM THE STUDENT’S PERSPECTIVE

“When am I ever going to use this?” “Can you just tell me the steps needed to do this?” If you are or ever have been a math teacher, these are questions you have probably heard from students repeatedly and probably have become frustrated by. However, instead of getting frustrated, we should ask ourselves why these questions continue to permeate our mathematics classrooms. The answer? Students are not engaged in authentic mathematics while they are learning, but rather they are following prescribed steps in a rote memorized fashion to reach an answer. True learning is not regurgitating steps but rather seeing the connectedness of content and understanding the practical usability of different solution strategies.

In traditional mathematics classrooms, the teacher stands at the front of the room, demonstrates several step-by-step examples (typically devoid of real-world context) of a new skill, and then releases students to try it independently. As soon as students begin to struggle, the teacher walks them through the problem step-by-step. Students are exposed to word problems and applications at the end of the unit and then only minimally. As a result, students have developed a mathematical identity that defines their role in math class not as learners of mathematics and problem solvers but as performers whose only goal is to get questions right (Boaler, 2022). They disconnect from mathematics because they view it as rote procedures with no interesting or practical application.

PBI also allows students to learn and practice critical 21st-century skills needed to be successful no matter where their path in life and career takes them. Because PBI is collaborative in nature, students are learning to work together in team settings. They are learning to discuss their thoughts and share ideas so that others can understand and engage in dialogue around the shared comments and disseminate their findings/comments/ideas through various verbal, written, or multimedia platforms.

No matter how clearly or repeatedly a teacher explains a mathematical concept or skill, understanding can occur only when students connect new information with previously learned skills. Sure, using traditional methods may support students in memorizing enough steps to allow them to pass their unit assessment or even their end-of-course assessment, but is that truly learning? Rote regurgitation of memorized steps rarely results in long-term learning that translates to solving real-life problems or even to subsequent courses taken during their academic careers. To achieve this level of mathematical understanding, students must be able to engage in authentic mathematical tasks that allow them to collaborate, problem-solve, and problematize. In other words, mathematics is not something students learn by watching; it’s something they learn by doing. One of our students described PBI as a puzzle: “You look for pieces you need when you need them, and then all of a sudden, the whole picture comes together.”

In contrast to student experiences in traditional classrooms, students in a PBI environment feel immersed in their learning. They begin to believe that their voice matters and immediately see the applicability and practicality of what they are learning. Instead of “When am I ever going to use this?” and “Just tell me what the steps are,” students ask questions that prompt exploration, resulting in learning in context. Yes, students are working with manipulatives; yes, sometimes they complete practice worksheets; yes, students are working with their teacher(s) and peer(s), but each activity is carefully crafted toward its purpose relative to the problem/task to be solved/completed. In PBI lessons, there is no longer a feeling that students are learning content because it is in chapter 2 and they just finished chapter 1, so chapter 2 is what comes next . . . instead, the content is explored in context to give meaning and applicability.

Transitioning from a traditional classroom environment to one grounded in PBI can be challenging for students. PBI pushes students to think. PBI pushes students to go beyond what they think they know and to use what they know to “figure out” new concepts. PBI is different from how most students have been learning mathematics for years—it pushes them outside their comfort zone. As a result, students will push back. They will complain.

However, we can tell you from firsthand experience that if teachers remain consistent and support students through this struggle without compromising the foundations that PBI is built upon, students will not only accept this new way of learning mathematics but will thrive because of it. One of our students explained it this way: “This class is different. We don’t just cover content through lectures and you [the teacher] telling us what to do. We explore and discuss ideas, and suddenly I feel like I just know it. I feel like I have learned more in this math class than all of my other math classes combined.”

Reprinted by permission of the Publisher. From Sarah Ferguson and Denise L. Polojac-Chenoweth, Implementing Problem-Based Instruction in Secondary Mathematics Classrooms , New York: Teachers College Press. Copyright © 2024 by Teachers College, Columbia University. All rights reserved.

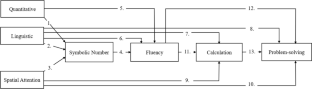
The cognitive foundations of different hierarchical levels of mathematical skills in primary school children: extending the mathematics pathways model

• Published: 25 March 2024

Cite this article

• Jie Xu 1 &
• Dan Cai   ORCID: orcid.org/0000-0002-3005-7724 2  

Although previous research has demonstrated that the acquisition of mathematical skills requires support from multiple cognitive abilities, the associations between cognitive precursors in different domains and mathematics at different hierarchical levels among primary school children are not well understood. This study explores the cognitive mechanisms underlying primary school children’s mathematics learning by extending the original pathways model. A total of 409 children participated v.in the study. A battery of cognitive, symbolic number processing, and mathematics measures were performed on the participants. The cognitive pathways supported children’s symbolic number skills, which in turn provided the foundation for formal mathematics. Different hierarchical mathematics skills were supported by different cognitive constellations. A hierarchical progressive development structure was found, from cognitive precursors, through symbolic number processing, to basic math fluency and complex numerical computation, and then, to problem-solving. The study also tried to divide children into two groups, grades 1–3 and 4–5. The exploratory results showed that there were commonalities and differences in the cognitive basis of mathematics learning in the two groups. These findings further explained the cognitive mechanisms underlying mathematical development in primary school children, with possible implications for the effective teaching and practice of mathematics knowledge and early identification and intervention of learning difficulties.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Price includes VAT (Russian Federation)

Instant access to the full article PDF.

Rent this article via DeepDyve

Institutional subscriptions

Data availability

The dataset generated and the material analyzed during the current study will be available from the corresponding author upon reasonable request.

Ackerman, P. L. (1988). Determinants of individual differences during skill acquisition: Cognitive abilities and information processing. Journal of Experimental Psychology: General, 117 , 288–318. https://doi.org/10.1037/0096-3445.117.3.288

Article   Google Scholar  

Allen, K., Higgins, S., & Adams, J. (2019). The relationship between visuospatial working memory and mathematical performance in school-aged children: A systematic review. Educational Psychology Review, 31 (3), 509–531. https://doi.org/10.1007/s10648-019-09470-8

Alloway, T. P., & Passolunghi, M. C. (2011). The relationship between working memory, IQ, and mathematical skills in children. Learning and Individual Differences, 21 (1), 133–137.

Ashkenazi, S., Rosenberg-Lee, M., Metcalfe, A. W. S., Swigart, A. G., & Menon, V. (2013). Visuo–spatial working memory is an important source of domain-general vulnerability in the development of arithmetic cognition. Neuropsychologia, 51 (11), 2305–2317. https://doi.org/10.1016/j.neuropsychologia.2013.06.031

Baron, R. M., & Kenny, D. A. (1986). The moderator–mediator variable distinction in social psychological research: Conceptual, strategic and statistical considerations. Journal of Personality and Social Psychology, 51 , 1173–1182.

Barsalou, L. W. (2008). Grounded cognition. Annual Review of Psychology, 59 (1), 617–645. https://doi.org/10.1146/annurev.psych.59.103006.093639

Braeuning, D., Hornung, C., Hoffmann, D., Lambert, K., Ugen, S., Fischbach, A., Schiltz, C., Hübner N., Nagengast, B., & Moeller, K. (2021). Long-term relevance and interrelation of symbolic and non-symbolic abilities in mathematical-numerical development: Evidence from large-scale assessment data. Cognitive Development , 58 , 101008. https://doi.org/10.1016/j.cogdev.2021.101008 .

Cai, D., Zhang, L., Li, Y., Wei, W., & Georgiou, G. K. (2018). The role of approximate number system in different mathematics skills across grades. Frontiers in Psychology, 9 , 1733. https://doi.org/10.3389/fpsyg.2018.01733

Carr, M., & Alexeev, N. (2011). Fluency, accuracy, and gender predict developmental trajectories of arithmetic strategies. Journal of Educational Psychology, 103 (3), 617–631. https://doi.org/10.1037/a0023864

Cheng, D., Xiao, Q., Chen, Q., Cui, J., & Zhou, X. (2018). Dyslexia and dyscalculia are characterized by common visual perception deficits. Developmental Neuropsychology, 43 (6), 497–507. https://doi.org/10.1080/87565641.2018.1481068

Cirino, P. T. (2011). The interrelationships of mathematical precursors in kindergarten. Journal of Experimental Child Psychology, 108 (4), 713–733. https://doi.org/10.1016/j.jecp.2010.11.004

Cirino, P. T., Tolar, T. D., Fuchs, L. S., & Huston-Warren, E. (2016). Cognitive and numerosity predictors of mathematical skills in middle school. Journal of Experimental Child Psychology, 145 , 95–119. https://doi.org/10.1016/j.jecp.2015.12.010

Cornoldi, C., Rigoni, F., Venneri, A., & Vecchi, T. (2000). Passive and active processes in visuo-spatial memory: Double dissociation in developmental learning disabilities. Brain and Cognition, 43 (1–3), 117–120.

Google Scholar  

Cowan, R., Donlan, C., Shepherd, D.-L., Cole-Fletcher, R., Saxton, M., & Hurry, J. (2011). Basic calculation proficiency and mathematics achievement in elementary school children. Journal of Educational Psychology, 103 (4), 786–803. https://doi.org/10.1037/a0024556

Das, J. P., & Misra, S. B. (2015). Cognitive planning and executive functions . New Delhi: Sage.

Dehaene, S., Piazza, M., Pinel, P., & Cohen, L. (2003). Three parietal circuits for number processing. Cognitive Neuropsychology, 20 (3), 487–506. https://doi.org/10.1080/02643290244000239

Dehaene, S. (2011). The number sense: How the mind creates mathematics, Rev. and updated ed . New York, NY: Oxford University Press.

Deng, M., Cai, D., Zhou, X., & Leung, A. W. S. (2022). Executive function and planning features of students with different types of learning difficulties in Chinese junior middle school. Learning Disability Quarterly , 45 (2), 134–143. https://doi.org/10.1177/0731948720929006

Fazio, L. K., Bailey, D. H., Thompson, C. A., & Siegler, R. S. (2014). Relations of different types of numerical magnitude representations to each other and to mathematics achievement. Journal of Experimental Child Psychology, 123 , 53–72. https://doi.org/10.1016/j.jecp.2014.01.013

Feigenson, L., Dehaene, S., & Spelke, E. (2004). Core systems of number. Trends in Cognitive Sciences, 8 (7), 307–314. https://doi.org/10.1016/j.tics.2004.05.002

Fias, W., & Bonato, M. (2018). Chapter 12 – Which space for numbers? In A. Henik & W. Fias (Eds.). Heterogeneity of function in numerical cognition (pp. 233–242). Academic Press. Retrieved from http://www.sciencedirect.com/science/article/pii/B9780128115299000121

Finke, S., Freudenthaler, H. H., & Landerl, K. (2020). Symbolic processing mediates the relation between nonsymbolic processing and later arithmetic performance. Frontiers in Psychology, 11 , 549. https://doi.org/10.3389/fpsyg.2020.00549

Friedman, N. P., Corley, R. P., Hewitt, J. K., & Wright, K. P., Jr. (2009). Individual differences in childhood sleep problems predict later cognitive executive control. Sleep, 32 (3), 323–333. https://doi.org/10.1093/sleep/32.3.323

Fuchs, L. S., Gilbert, J. K., Powell, S. R., Cirino, P. T., Fuchs, D., Hamlett, C. L., & Tolar, T. D. (2016). The role of cognitive processes, foundational math skill, and calculation accuracy and fluency in word-problem solving versus prealgebraic knowledge. Developmental Psychology, 52 (12), 2085–2098. https://doi.org/10.1037/dev0000227

Fuchs, L. S., Geary, D. C., Compton, D. L., Fuchs, D., Hamlett, C. L., Seethaler, P. M., Bryant, J. D., & Schatschneider, C. (2010). Do different types of school mathematics development depend on different constellations of numerical versus general cognitive abilities?. Developmental Psychology , 46 (6), 1731. https://doi.org/10.1037/a0020662

Georgiou, G. K., Wei, W., Inoue, T., Das, J. P., & Deng, C. (2020). Cultural influences on the relation between executive functions and academic achievement. Reading and Writing, 33 (4), 991–1013. https://doi.org/10.1007/s11145-019-09961-8

Gilmore, C. (2023). Understanding the complexities of mathematical cognition: A multi-level framework. Quarterly Journal of Experimental Psychology, 76 (9), 1953–1972. https://doi.org/10.1177/17470218231175325

Gimbert, F., Camos, V., Gentaz, E., & Mazens, K. (2019). What predicts mathematics achievement? Developmental change in 5- and 7-year-old children. Journal of Experimental Child Psychology, 178 , 104–120. https://doi.org/10.1016/j.jecp.2018.09.013

Gliksman, Y., Berebbi, S., & Henik, A. (2022). Math fluency during primary school. Brain Sciences, 12 (3), 371. https://doi.org/10.3390/brainsci12030371

Halberda, J., & Feigenson, L. (2008). Developmental change in the acuity of the “number sense”: The approximate number system in 3-, 4-, 5-, and 6-year-olds and adults. Developmental Psychology, 44 (5), 1457–1465. https://doi.org/10.1037/a0012682

Hawes, Z., Sokolowski, H. M., Ononye, C. B., & Ansari, D. (2019). Neural underpinnings of numerical and spatial cognition: An fMRI meta-analysis of brain regions associated with symbolic number, arithmetic, and mental rotation. Neuroscience and Biobehavioral Reviews, 103 , 316–336. https://doi.org/10.1016/j.neubiorev.2019.05.007

Hornung, C., Schiltz, C., Brunner, M., & Martin, R. (2014). Predicting first-grade mathematics achievement: The contributions of domain-general cognitive abilities, nonverbal number sense, and early number competence. Frontiers in Psychology, 5 , 272. https://doi.org/10.3389/fpsyg.2014.00272

Inglis, M., Attridge, N., Batchelor, S., & Gilmore, C. (2011). Non-verbal number acuity correlates with symbolic mathematics achievement: But only in children. Psychonomic Bulletin and Review, 18 (6), 1222–1229. https://doi.org/10.3758/s13423-011-0154-1

LeFevre, J. A., Fast, L., Skwarchuk, S. L., Smith-Chant, B. L., Bisanz, J., Kamawar, D., & Penner-Wilger, M. (2010). Pathways to mathematics: Longitudinal predictors of performance. Child Development, 81 (6), 1753–1767. https://doi.org/10.1111/j.1467-8624.2010.01508.x

Li, Y., & Geary, D. C. (2013). Developmental gains in visuospatial memory predict gains in mathematics achievement. PloS one, 8 (7), e70160. https://doi.org/10.1371/journal.pone.0070160

Lin, X., & Powell, S. R. (2021). The roles of initial mathematics, reading, and cognitive skills in subsequent mathematics performance: A meta-analytic structural equation modeling approach. Review of Educational Research, 92 (2), 288–325. https://doi.org/10.3102/00346543211054576

Locuniak, M. N., & Jordan, N. C. (2008). Using kindergarten number sense to predict calculation fluency in second grade. Journal of Learning Disabilities, 41 (5), 451–459. https://doi.org/10.1177/0022219408321126

Mix, K. S., Levine, S. C., Cheng, Y. L., Young, C., Hambrick, D. Z., Ping, R., & Konstantopoulos, S. (2016). Separate but correlated: The latent structure of space and mathematics across development. Journal of Experimental Psychology: General, 145 (9), 1206.

Mix, K. S., & Cheng, Y.–L. (2012). Chapter 6 – The relation between space and math: developmental and educational implications. In J. B. Benson (Ed.), Advances in child development and behavior (Vol. 42, pp. 197–243). Burlington, VT: Academic Press.

Mundy, E., & Gilmore, C. K. (2009). Children’s mapping between symbolic and nonsymbolic representations of number. Journal of Experimental Child Psychology, 103 (4), 490–502. https://doi.org/10.1016/j.jecp.2009.02.003

Naglieri, J. A., Das, J. P., & Goldstein, S. (2014). Cognitive assessment system -second edition (2nd ed.) . Austin, TX: Pro-Ed.

National Reading Panel. (Ed.). (2000). Teaching children to read: An evidence-based assessment of the scientific research literature on reading and its implications for reading instruction . Bethesda, MD: National Institute of Child Health and Development. Retrieved from http://www.nichd.nih.gov/publications/nrp/report.htm

Newcombe, N. S., & Shipley, T. F. (2012). Thinking about spatial thinking: New typology, new assessments. In J. S. Gero (Ed.), Studying visual and spatial reasoning in design creativity. New York, NY: Springer.

Peng, P., Yang, X., & Meng, X. (2017). The relation between approximate number system and early arithmetic: The mediation role of numerical knowledge. Journal of Experimental Child Psychology, 157 , 111–124. https://doi.org/10.1016/j.jecp.2016.12.011

Price, G., & Fuchs, L. (2016). The mediating relation between symbolic and nonsymbolic foundations of math competence. PLoS ONE, 11 , e0148981. https://doi.org/10.1371/journal.pone.0148981

Purpura, D. J., & Ganley, C. M. (2014). Working memory and language: Skill–specific or domain–general relations to mathematics? Journal of Experimental Child Psychology, 122 , 104–121. https://doi.org/10.1016/j.jecp.2013.12.009

Sasanguie, D., Defever, E., Maertens, B., & Reynvoet, B. (2014). The approximate number system is not predictive for symbolic number processing in kindergarteners. Quarterly Journal of Experimental Psychology, 67 (2), 271–280. https://doi.org/10.1080/17470218.2013.803581

Schneider, M., Beeres, K., Coban, L., Merz, S., Susan Schmidt, S., Stricker, J., & De Smedt, B. (2017). Associations of non-symbolic and symbolic numerical magnitude processing with mathematical competence: A meta-analysis. Developmental science, 20 (3), e12372. https://doi.org/10.1111/desc.12372

Simmons, F. R., Willis, C., & Adams, A. M. (2012). Different components of working memory have different relationships with different mathematical skills. Journal of Experimental Child Psychology, 111 (2), 139–155. https://doi.org/10.1016/j.jecp.2011.08.011

Sowinski, C., LeFevre, J.–A., Skwarchuk, S.–L., Kamawar, D., Bisanz, J., & Smith–Chant, B. (2015). Refining the quantitative pathway of the Pathways to Mathematics model. Journal of Experimental Child Psychology , 131 , 73–93. https://doi.org/10.1016/j.jecp.2014.11.004

Swanson, H. L., Jerman, O., & Zheng, X. (2008). Growth in working memory and mathematical problem solving in children at risk and not at risk for serious math difficulties. Journal of Educational Psychology, 100 (2), 343–379. https://doi.org/10.1037/0022-0663.100.2.343

Träff, U., Olsson, L., Skagerlund, K., & Östergren, R. (2018). Cognitive mechanisms underlying third graders’ arithmetic skills: Expanding the pathways to mathematics model. Journal of Experimental Child Psychology, 167 , 369–387. https://doi.org/10.1016/j.jecp.2017.11.010

Träff, U., Skagerlund, K., Östergren, R., & Skagenholt, M. (2023). The importance of domain-specific number abilities and domain-general cognitive abilities for early arithmetic achievement and development. British Journal of Educational Psychology, 93 (3), 825–841. https://doi.org/10.1111/bjep.12599

Umiltà, C., Priftis, K., & Zorzi, M. (2009). The spatial representation of numbers: Evidence from neglect and pseudoneglect. Experimental Brain Research, 192 (3), 561–569. https://doi.org/10.1007/s00221-008-1623-2

Ünal, Z. E., Greene, N. R., Lin, X., & Geary, D. C. (2023). What is the source of the correlation between reading and mathematics achievement? Two Meta-Analytic Studies. Educational Psychology Review, 35 (1), 4. https://doi.org/10.1007/s10648-023-09717-5

Uttal, D. H., & Cohen, C. A. (2012). Spatial thinking and STEM education: When, why and how. Psychology of Learning and Motivation, 57 , 147–181. https://doi.org/10.1016/B978-0-12-394293-7.00004-2

Vanbinst, K., Ceulemans, E., Peters, L., Ghesquière, P., & De Smedt, B. (2018). Developmental trajectories of children’s symbolic numerical magnitude processing skills and associated cognitive competencies. Journal of Experimental Child Psychology, 166 , 232–250. https://doi.org/10.1016/j.jecp.2017.08.008

Vogel, S., Haigh, T., Sommerauer, G., Spindler, M., Brunner, C., Lyons, I., & Grabner, R. (2017). Processing the order of symbolic numbers: A reliable and unique predictor of arithmetic fluency. Journal of Numerical Cognition, 3 , 288–308. https://doi.org/10.5964/jnc.v3i2.55

Wechsler, D. (2009). Wechsler individual achievement test . San Antonio, TX: Psychological Corparation.

Whitley, S. J. R. I. (2019). Oral reading fluency and MAZE selection for predicting 5th and 6th grade students’ reading and math achievement on a high stakes summative assessment. Reading Improvement, 56 (1), 24–35.

Woolley, G. (2011). Reading comprehension: Assisting children with learning difficulties . New York, NY: Springer.

Xu, C., Di Lonardo Burr, S., & LeFevre, J.-A. (2023). The hierarchical relations among mathematical competencies: From fundamental numeracy to complex mathematical skills. Canadian Journal of Experimental Psychology / Revue canadienne de psychologie expérimentale , 77 (4), 284–295. https://doi.org/10.1037/cep0000311

Zhang, X. (2016). Linking language, visual–spatial, and executive function skills to number competence in very young Chinese children. Early Childhood Research Quarterly, 36 , 178–189. https://doi.org/10.1016/j.ecresq.2015.12.010

Download references

This work was supported by the General Project of Education Science by Shanghai Philosophy and Social Sciences (grant number A2021002), the Program for Professor of Special Appointment (Eastern Scholar) at Shanghai Institutions of Higher Learning, and the Shanghai Shuguang Program by the Shanghai Education Development Foundation and the Shanghai Municipal Education Commission (grant number 20SG45, and the Research Base of Online Education for Shanghai Middle and Primary Schools.

Author information

Authors and affiliations.

School of Psychology, Shanghai Normal University, Shanghai, China

You can also search for this author in PubMed   Google Scholar

Corresponding author

Correspondence to Dan Cai .

Ethics declarations

Ethical approval.

Ethical approvals were obtained from the Research Ethics Committee of the corresponding author’s university. All procedures performed in studies involving human participants were in accordance with the ethical standards of the institutional and/or national research committee.

Informed consent

Informed consent was obtained from all individual participants included in the study.

Conflict of interest

The authors declare no competing interests.

Additional information

Publisher's note.

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Jie Xu . School of Psychology, Shanghai Normal University, Shanghai, China.

Dan Cai . School of Psychology, Shanghai Normal University, Shanghai, China. Email: [email protected].

Current themes of research:

The cognitive foundations of mathematical learning.

Most relevant publications in the field of Psychology Education

Cai, D*., Zhao, J., Chen, Z., & Liu, D. (2022). Executive functions training for 7-to 10-year-old students with mathematics difficulty: Instant effects and 6-month sustained effects.  Journal of Learning Disabilities , 00222194221117513. https://doi.org/10.1177/00222194221117513

Shi, X., Xu, J., Wang, F., & Cai, D*. (2022). Cognitive processing features of elementary school children with mathematical anxiety: Attentional control theory-based explanation.  Journal of Experimental Child Psychology, 224 , 105513. https://doi.org/10.1016/j.jecp.2022.105513

Deng, M., Cai, D*., Zhou, X., & Leung, A. W. (2022). Executive function and planning features of students with different types of learning difficulties in Chinese junior middle school.  Learning disability quarterly, 45 (2), 134-143. https://doi.org/10.1177/0731948720929006

Cai, D*., Viljaranta, J., & Georgiou, G. K. (2018). Direct and indirect effects of self-concept of ability on math skills.  Learning and individual differences, 61 , 51-58. https://doi.org/10.1016/j.lindif.2017.11.009

Cai, D., Zhang, L., Li, Y., Wei, W., & Georgiou, G. K. (2018). The role of approximate number system in different mathematics skills across grades. Frontiers in psychology, 9 , 1733. https://doi.org/10.3389/fpsyg.2018.01733

Zhu, M., Cai, D*., & Leung, A. W. (2017). Number line estimation predicts mathematical skills: Difference in grades 2 and 4.  Frontiers in psychology, 8 , 1576. https://doi.org/10.3389/fpsyg.2017.01576

Cai, D*., Li, Q. W., & Deng, C. P. (2013). Cognitive processing characteristics of 6th to 8th grade Chinese students with mathematics learning disability: Relationships among working memory, PASS processes, and processing speed.  Learning and individual differences, 27 , 120-127. https://doi.org/10.1016/j.lindif.2013.07.008

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Xu, J., Cai, D. The cognitive foundations of different hierarchical levels of mathematical skills in primary school children: extending the mathematics pathways model. Eur J Psychol Educ (2024). https://doi.org/10.1007/s10212-024-00823-8

Download citation

Received : 12 May 2023

Revised : 19 February 2024

Accepted : 26 February 2024

Published : 25 March 2024

DOI : https://doi.org/10.1007/s10212-024-00823-8

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Primary school children
• Mathematics learning
• Symbolic number processing
• Cognitive abilities
• Find a journal
• Publish with us
• Track your research

Help | Advanced Search

Computer Science > Computation and Language

Title: improving large language model fine-tuning for solving math problems.

Abstract: Despite their success in many natural language tasks, solving math problems remains a significant challenge for large language models (LLMs). A large gap exists between LLMs' pass-at-one and pass-at-N performance in solving math problems, suggesting LLMs might be close to finding correct solutions, motivating our exploration of fine-tuning methods to unlock LLMs' performance. Using the challenging MATH dataset, we investigate three fine-tuning strategies: (1) solution fine-tuning, where we fine-tune to generate a detailed solution for a given math problem; (2) solution-cluster re-ranking, where the LLM is fine-tuned as a solution verifier/evaluator to choose among generated candidate solution clusters; (3) multi-task sequential fine-tuning, which integrates both solution generation and evaluation tasks together efficiently to enhance the LLM performance. With these methods, we present a thorough empirical study on a series of PaLM 2 models and find: (1) The quality and style of the step-by-step solutions used for fine-tuning can make a significant impact on the model performance; (2) While solution re-ranking and majority voting are both effective for improving the model performance when used separately, they can also be used together for an even greater performance boost; (3) Multi-task fine-tuning that sequentially separates the solution generation and evaluation tasks can offer improved performance compared with the solution fine-tuning baseline. Guided by these insights, we design a fine-tuning recipe that yields approximately 58.8% accuracy on the MATH dataset with fine-tuned PaLM 2-L models, an 11.2% accuracy improvement over the few-shot performance of pre-trained PaLM 2-L model with majority voting.

Submission history

Access paper:.

• Other Formats

References & Citations

• Google Scholar
• Semantic Scholar

BibTeX formatted citation

Bibliographic and Citation Tools

Code, data and media associated with this article, recommenders and search tools.

• Institution

arXivLabs: experimental projects with community collaborators

arXivLabs is a framework that allows collaborators to develop and share new arXiv features directly on our website.

Both individuals and organizations that work with arXivLabs have embraced and accepted our values of openness, community, excellence, and user data privacy. arXiv is committed to these values and only works with partners that adhere to them.

Have an idea for a project that will add value for arXiv's community? Learn more about arXivLabs .