paytm 50 essay answers

• International
• Today’s Paper
• Expresso Live
• Premium Stories
• Express Shorts
• Health & Wellness
• Board Exam Results

RBI action against Paytm: probable causes, effects, and what happens to your money

Given the significant customer base of the paytm, once the poster boy of india’s fintech revolution, the rbi action could impact a large number of customers. we explain what the order means.

The Reserve Bank of India (RBI) on Wednesday (January 31) barred Paytm Payments Bank from offering all its core services — including accounts and wallets — from March, effectively crippling the company’s business.

The action is technically not a cancellation of the licence of Paytm Payments Bank, but it constricts the company’s operations to a very large extent.

However, the central bank has allowed the withdrawal or utilisation of balance amounts by customers “without any restrictions, up to their available balance”.

Paytm, which was once the poster boy of India’s fintech revolution, has a significant customer base. On its website, Paytm Payments Bank says it has more than 100 million know your customer (KYC) verified customers.

“We are also the largest issuer of FASTag with over 8 million FASTag units issued,” the website says.

Paytm founder and Chairman Vijay Shekhar Sharma is part-time chairman of the bank.

What does the RBI direction say?

Paytm Payments Bank has been barred from offering almost all of its key services — accepting deposits or top-ups in any customer account, prepaid instruments, wallets, FASTags, National Common Mobility Card (NCMC), etc., after February 29 in the wake of “persistent non-compliances and material supervisory concerns”.

“No other banking services…like fund transfers (irrespective of name and nature of services like AEPS, IMPS, etc.), BBPOU and UPI facility should be provided by the bank after February 29, 2024,” the RBI has said.

It has directed that the nodal accounts of the parent company One97 Communications and Paytm Payments Services should be terminated at the earliest, and not later than February 29.

The settlement of all pipeline transactions and nodal accounts — in respect of all transactions initiated on or before February 29 — should be completed by March 15, and no transactions shall be permitted thereafter, the central bank has said.

Can customers use or withdraw their stored balances in various Paytm instruments?

As per the RBI, withdrawal or utilisation of balances by customers from their Paytm accounts including savings bank accounts, current accounts, prepaid instruments, FASTags, NCMC, etc. are permitted without any restrictions, “up to their available balance”.

The RBI statement, however, does not mention a number of other services like loans, mutual funds, bill payments, digital gold, and credit cards.

What has Paytm said in response to the RBI action?

As Paytm shares fell 20 per cent on the exchanges on Thursday (February 1), One97 Communications Ltd said it was “taking immediate steps to comply with RBI directions”, including working with the regulator to address their concerns as quickly as possible.

Depending on the nature of the resolution, the company expects the RBI action to have a worst-case impact of Rs 300-500 crore on its annual EBITDA (earnings before interest, tax, depreciation and amortisation) going forward.

Also, going forward, One97 Communications will be working only with other banks, and not with Paytm Payments Bank, it said in an exchange filing.

“We offer acquiring services to merchants in partnership with several leading banks in the country and will continue to expand third-party bank partnerships. The Paytm Payment Gateway business (online merchants) will continue to offer payment solutions to its existing merchants,” it said.

OCL’s offline merchant payment network offerings like Paytm QR, Paytm Soundbox, Paytm Card Machine, will continue as usual, where it can onboard new offline merchants as well, Paytm said.

What led to the RBI’s action against Paytm?

The central bank gave no reasons for its action. However, Paytm Payments Bank has been facing scrutiny from RBI since 2018.

Sources said the RBI’s action could be due to concerns on KYC compliance and IT-related issues. The central bank is concerned about allowing any institution or banking entity to expose depositors’ money to such risks.

It is learnt that Paytm Payments Bank and its parent OCL also came under RBI scrutiny for purported lack of requisite information barriers within the group, and data access to China-based entities that were indirect shareholders in the payments bank through their stake in the parent company.

The failure to address these concerns at multiple levels over an extended period led to the latest action by the RBI, it is learnt.

Antfin, an affiliate of the Chinese conglomerate Alibaba, is a shareholder in One97 Communications — as of December 31, 2023, Antfin held 9.89% stake in the company, stock exchange data show. Given the frosty relationship between India and China over the past few years, Chinese investments in Indian companies have attracted intense scrutiny by Indian regulators.

What other actions has RBI taken against Paytm earlier?

In October 2023, the RBI had fined Paytm Payments Bank Rs 5.39 crore due to deficiencies in regulatory compliance. According to the regulator, the payments bank had failed to identify the beneficial owner in respect of entities onboarded by it for providing payout services; did not monitor payout transactions and failed to carry out risk profiling of entities availing payout services; had breached the regulatory ceiling of end-of-the-day balance in certain customer advance accounts; and had delayed reporting a cyber security incident.

In March 2022, the RBI directed Paytm Payments Bank to stop the onboarding of new customers with immediate effect. The Comprehensive System Audit report and subsequent compliance validation report of the external auditors revealed “persistent non-compliances and continued material supervisory concerns in the bank”, warranting further supervisory action, the RBI said on January 31.

Even before 2022, the central bank had made certain observations in 2018 about the processes the company followed to acquire new users, especially on KYC norms.

The RBI also had concerns over the close relationship between Paytm Payments Bank and its parent One97 Communications. Payments banks are required to maintain an arm’s length distance from promoter group entities. OCL held 49% stake in Paytm Payments Bank, while 51% was held by Paytm founder Vijay Shekhar Sharma.

There were also allegations that the payments bank had failed to meet the Rs 100-crore net worth criteria, and had exceeded the Rs 1-lakh deposit limit allowed per account for payments banks at the time.

Sukalp Sharma is a Senior Assistant Editor with The Indian Express and writes on a host of subjects and sectors, notably energy and aviation. He has over 13 years of experience in journalism with a body of work spanning areas like politics, development, equity markets, corporates, trade, and economic policy. Before joining The Indian Express, Sukalp had long and enriching stints at financial newswire Informist and the Express Group’s pink paper The Financial Express. He considers himself an above-average photographer, which goes well with his love for travel. ... Read More

• Express Explained

His brother Romit Antil told  The Indian Express  that Chirag had gone to Canada in September 2022 on a study visa and used to share an apartment with his friends. He was shot dead near the apartment on the intersection of East 55th Avenue and Main Street, Vancouver, around 11 pm.

More Explained

Best of Express

EXPRESS OPINION

Apr 15: Latest News

• 01 Lok Sabha polls 2024: Retaining Ramtek seat a challenge for Shinde-led Sena
• 02 Olympic qualification: With women’s 10m air pistol bronze, Palak Gulia makes it 16 out of 16 pistol/rifle quotas for Paris Games
• 03 Shinde calls Sena UBT ‘Uth Bas Sena’, takes a dig at Thackeray
• 04 Can country where 80 crore people survive on free ration become ‘vishwaguru’: Akhilesh
• 05 Man held in Chhattisgarh for using abusive language against PM Modi
• Elections 2024
• Political Pulse
• Entertainment
• Movie Review
• Newsletters
• Gold Rate Today
• Silver Rate Today
• Petrol Rate Today
• Diesel Rate Today
• Web Stories

Payment Banks in India – The PayTM Case – Explained Pointwise

PYQ Discussion 2024 Batch-1, An opportunity to revise 2011-2023 PYQ’s, Batch Starts 24th April 2024 Click Here   for more information

The recent case of RBI’s crackdown on Paytm has put the spotlight on the operations of Payment Banks In India. RBI has ordered Paytm Payments Bank Ltd (PPBL) to halt most of its business including taking further deposits, conducting credit transactions and carrying out top-ups on any customer accounts, prepaid instruments, wallets, and cards for paying road tolls after February 29, 2024.

Reasons for RBI Clampdown on Paytm payments Bank

What are Payment Banks? What are their features?

Historical Background- Payment Banks in India were established in 2014 based on the recommendations of the Nachiket Mor Committee . It was set up to operate on a smaller scale with minimal credit risk.

Objective- The main objective is to advance financial inclusion by offering banking and financial services to the unbanked and under-banked areas. It also caters to the needs of uncovered masses in the banking sector like the migrant labour force, low-income households and small entrepreneurs.

Legal Provisions- The legal provisions governing the payment banking operations in India are mentioned below- a. These banks have to register as a Public Limited Company under the Companies Act 2013 and obtain licence as per Banking Regulation Act 1949 . They are also regulated by the RBI Act 1934, Foreign Exchange Management Act 1999 and Payment and Settlement Systems Act, 2007. b. The minimum capital requirement is 100 crores . For the first five years, the stake of promoters should not be less than 40%. Foreign shareholdings will also be allowed as per FDI rules for private banks in India. c. The voting right of the shareholder is capped to 10% and which can be raised to 26% from the approval of Reserve Bank of India. The banks should be fully networked from the beginning.

Features- These Banks have several distinct features when compared to the conventional Banks. These are mentioned below-

Payment Banks operating in India- Currently only 6 banks are operating in the country- Airtel Payments Bank Limited, India Post Payments Bank Limited, Fino Payments Bank Limited, Paytm Payments Bank Limited, NSDL Payments Bank Limited and Jio Payments Bank Limited.

What is The Significance of these Banks for India?

1. Promotion of Financial inclusion- These banks have promoted financial inclusion by catering to financial services to the unbanked sections of the society like migrant workers, low-income households and small scale entrepreneurs.

2. Expanded Geographical reach- These banks have a wider geographical reach due to its technology oriented services,  unlike traditional banks whose geographical outreach is constrained by the requirements of physical infrastructure.

3. Zero balance accounts and No minimum balance accounts- These banks offer a zero balance account or a no minimum balance account without any extra or hidden charge, unlike a commercial bank who levy charges if the customer doesn’t hold a minimum balance in their account.

4. Complements the financial efforts of traditional banks- Payments banks complement the financial efforts of traditional banks by partnering to sell mutual funds , pension products , and insurance products through their platform. For ex- SBI Life Insurance product through Paytm.

5. Low Value, High Volume Transactions- They have provided effective infrastructure to deal with low value, high volume transactions. For Ex- Use of Paytm QR codes by the vegetable Vendors to grocery shop owners .

6. Higher rates of Interest- The rates of interest being offered by these banks is higher in comparison to the traditional banks . For Ex- ROI of Payment Bank is generally around 7% whereas as ROI of commercial bank ~3.5 and 6 per cent.

What are The Challenges with Payment Banks in India?

1. Low avenues of profitability- These banks are not allowed to lend money and earn interest income unlike traditional banks. Further, the stringent SLR requirements of 75% demand liabilities to be invested in G-secs have impinged on the avenues of profitability of these banks. For ex- The operational payments banks showed net losses of Rs 516.5crore for financial year 2018.

2. Low return on equity- The cap on the amount of demand deposits at Rs 2,00,000 and the 15% capital to Risk Weighted Assets ratio , has severely impacted the returns on equities of payment bank in India. Their return on equity is less than 5%.

3. Digital Divide and slow internet connectivity- These banks have no physical presence and their banking operations are solely reliant on internet connectivity. However, the rural-urban divide in internet connectivity has impacted their expansion and penetration .

4. Large number of dormant accounts- The large number of dormant zero balance accounts have impacted the operations of payment bank in India. They have also been used as conduits for personal loan scams and Money Laundering . For ex- Out of the 35 crore Paytm payment bank accounts, 31 cr remained dormant and were misused.

5. Cut-throat Competition- These banks are facing cut-throat competition from the payment wallets like Phone pe, Bharat Pe and conventional commercial banks payment bank services like SBI yono, ICICI i mobile pay.

6. Increasing number of Defunct Payment Bank- The over-regulated functioning and huge losses , have led to increase in the number of banks surrendering their licences and halting their operations. For ex- Cholamandalam Distribution Services , Sun Pharmaceuticals , Tech Mahindra and Aditya Birla Payment Bank have surrendered their licences.

Read More UPSC Topics-

What should be the way forward.

1. Open up more avenues of profit generation- RBI must increase deposit limits of payment bank. Also, a mechanism must be worked out to let these banks transfer the surplus money in the demand deposit accounts to the universal banks.

2. Facilitate Infrastructure sharing- RBI should take measure to facilitate infrastructure sharing among the traditional banks and Payment Bank. For ex- Payment bank desks in traditional bank branches.

3. Increased Internet connectivity- The internet connectivity in rural areas must be increased for the entry of new players in the payment bank market as payment bank sector is dominated by telecom giants like Airtel and Jio  which have their own network.

4. Increase the scope of operations- The payment bank should be allowed to offer their own mutual fund and insurance products to enhance their source of revenue generation and profitability.

5. Increase regulatory vigilance- The compliance of e-KYC and no frill accounts must be regularly undertaken by the RBI to prevent future crisis like the Paytm crisis . The recommendations of the Anand Sinha committee must be implemented to ring-fence the banking operations of the payment bank from the ownership structure.

Type your email…

Search Articles

Latest articles.

• 10 PM Daily UPSC Current Affairs 14th April – 2024 | Revision Test
• UPSC Prelims Marathon 14th April – Revision – 2024
• Download EPIC! March 2024 – The Monthly Current Affairs Magazine by ForumIAS
• 10 PM UPSC Current Affairs Quiz 13 April, 2024
• 9 PM UPSC Current Affairs Articles 13 April, 2024
• Potential impacts of AI: The future of work in the Al era
• Concerns related to India’s interest rates: Last-mile transmission a big hurdle to policy rate cut
• Current state of global coal power – problem with coal
• Solutions for job creation: India’s missing jobs
• Significance of making rules simple to boost export

Prelims 2024 Current Affairs

• Art and Culture
• Indian Economy
• Science and Technology
• Environment  & Ecology
• International Relations
• Polity &  Nation
• Important Bills and Acts
• International Organizations
• Index, Reports and Summits
• Government Schemes and Programs
• Miscellaneous
• Species in news

• Firstpost Defence Summit
• Entertainment
• Web Stories
• Health Supplement
• First Sports
• Fast and Factual
• Between The Lines
• Firstpost America

What is RBI’s order against Paytm? How will it affect customers?

The RBI has barred Paytm Payments Bank from offering its services including accounts and wallet after 29 February. This includes accepting deposits or top-ups in any account, prepaid instruments, wallets, and FASTags. What happens to your money if you are a Paytm user?

In India, digital payments have become a way of life and Paytm is among the most common payment gateway. However, in a big setback to Paytm Payments Bank, the Reserve Bank of India (RBI) has barred it from offering its core services from March. This includes accounts and payments.

The move will essentially restrict the fintech company’s operations and impact its huge customer base. While customers are allowed to withdraw and use the balance amount in wallets, the central bank has ordered Paytm Payments Bank to stop accepting fresh deposits in its accounts or wallets after 29 February.

“No further deposits or credit transactions or top ups shall be allowed in any customer accounts, prepaid instruments, wallets, FASTags, NCMC cards, etc. after February 29, 2024, other than any interest, cashbacks, or refunds which may be credited anytime,” Yogesh Dayal, a chief general manager with the central bank, said in a press statement on Wednesday.

We take a look at the RBI’s direction and what this means for Paytm users.

Why has RBI imposed restrictions on Paytm Payments Bank?

Paytm was the leader when India’s fintech revolution started. But Paytm Payments Bank ran into trouble soon after and has been under the RBI scanner since 2018.

The central bank has not specified reasons for its latest action against Paytm, but it could be because of RBI’s concerns on KYC compliance and IT-related issues, sources were quoted as saying by The Indian Express .

Paytm Payments Bank and its parent company One97 Communication have come under scrutiny for the “purported lack of requisite information barriers within the group and data access to China-based entities that were indirect shareholders in the payments back through their stake in the parent company”, the report says.

An alleged persistent “non-compliance” prompted the central bank to take the latest action against Paytm.

What does the RBI order say?

The central bank has barred the Paytm Payments Bank from offering all of its main services. It cannot accept deposits or top-ups in wallets in any customer account. It has imposed restrictions on prepaid instruments, FASTags (the electronic toll collection system), and the National Common Mobility Card (NCMC), after 29 February.

The RBI said that the Paytm Payments Bank should not offer any other services like fund transfers such as AEPS, IMPS, bill payments and UPI facilities.

The settlement of all pipeline transactions and nodal accounts, regarding transactions initiated on or before February 29, should be completed by 15 March. No transactions will be permitted after the said deadline.

How will the RBI direction affect customers?

Customers can only add funds to their Paytm Payments Bank until 29 February. After that, they cannot add any money to their savings bank account.

No debit or credit transactions including those through wallets will be allowed. Users will not be able to receive or send any money from their accounts. They will also not be able to make any money transfers or bill payments or carry out UP transactions. However, the RBI allows exceptions for interest, cashbacks, or refunds to be credited at any time.

The RBI directive affects Paytm’s banking operations but it does not mention if transactions made via external banks will be affected. This means you will be able to make UPI payments through Paytm if it is linked to an external bank, according to a report by India Today . However, since Paytm Wallet is powered by Paytm Payments Bank you may not be able to use the wallet.

“The RBI’s move primarily targets Paytm’s banking operations, allowing customers to still utilise Paytm for digital payments as long as their account remains connected to an external bank, even after February 29,” Gaurav Goel, founder-director, Fynocrat Technologies, was quoted as saying by India Today .

Can customers use or withdraw balances in Paytm instruments?

According to the RBI order, the withdrawal or utilisation of the balance money from their Paytm accounts including savings bank accounts, current accounts, prepaid instruments, FASTags, and NCMC are allowed without any restrictions, “up to their available balance”.

The RBI does not mention other services like loans, mutual funds, bill payments, digital gold, and credit cards.

How many customers are likely to be affected?

According to the Paytm Payments Bank website, it has over 100 million know-your-customer (KYC) verified customers. “We are also the largest issuer of FASTag with over 8 million FASTag units issued,” it says.

In December, 57 million transactions were reported through Paytm Fastags, among the highest in the industry.

What has Paytm Payments Bank said?

Paytm Payments Bank has said it is taking “immediate steps” to comply with RBI’s directions.

One 97 Communications Limited (OCL), as a payments company, works with various banks (not just Paytm Payments Bank), on various payments products, the fintech company said in a statement on Thursday.

Update: Paytm Payments Bank Limited, an associate of Paytm receives RBI directions. Paytm to expand its existing relationships with leading third-party banks to distribute payments and financial services products. Read more here: https://t.co/NsPCOxp6VJ pic.twitter.com/fQjozyR11m — Paytm (@Paytm) January 31, 2024

“We now will accelerate the plans and completely move to other bank partners. Going forward, OCL will be working only with other banks, and not with Paytm Payments Bank Limited. The next phase of OCL’s journey is to continue to expand its payments and financial services business, only in partnerships with other banks,” the statement read.

How will the RBI order affect Patym?

According to Paytm, it expects a “worst case impact” of Rs 300 crore to Rs 500 crore to its annual earnings from RBI’s order. However, the company said it expects to “continue on its trajectory” to improve its profitability, reports NDTV .

What are RBI’s earlier actions against Paytm?

In October last year, the RBI slapped a fine of Rs 5.39 crore on Paytm Payments Bank because of deficiencies in regulatory compliance.

In March 2022, it directed Paytm Payments Bank to stop onboarding new customers immediately. A Comprehensive System Audit report and subsequent compliance validation report of the external auditors revealed persistent non-compliance and continued material supervisory concerns in the bank, warranting further supervisory action, the RBI said, without disclosing details.

In 2018, the RBI made observations about the processes the company followed to get new users, especially on KYC notes. The central bank was also concerned over the close relations between Paytm Payments Bank and One97 Communications.

With inputs from agencies

Find us on YouTube

Related Stories

Finance Minister Sitharaman tells RBI, regulators to meet fintech startups every month following Paytm fiasco

Head-on | From West to India, reversing the brain drain

Vantage | Why Chinese firms are wrong about their scrutiny by India

Can Paytm survive the crisis facing Paytm Payments Bank?

What happened to Paytm Payments Bank? RBI's clampdown explained

• Medium Text

WHAT IS THE BANK? WHAT DOES IT DO?

Who owns paytm payments bank how is it related to paytm, what did the rbi do what prompted the action, what will paytm do, impact on paytm, can the bank meet outflows.

Get a look at the day ahead in U.S. and global markets with the Morning Bid U.S. newsletter. Sign up here.

Reporting by Ira Dugal in Mumbai and Indranil Sarkar in Bengaluru; Editing by William Mallard

Our Standards: The Thomson Reuters Trust Principles. New Tab , opens new tab

Business Chevron

South Korea finmin vows measures to stabilise market volatility if needed

South Korea's finance minister stepped up warnings on Monday that the government is ready to act to counter any renewed volatility in currency markets after the won has extended declines against the dollar to hit the lowest in a year and a half.

• Revolutionizing Digital Communication: The Power of Olly and AI
• AI-Powered Video Editing with Snapy.ai: The Future of Content Creation is Here
• Dawn of AI-Powered Video Editing: Transform Your Videos with Silence Remover Online
• The Dawn of Generative AI: Why and How to Adopt it for your Business
• Harnessing the Power of Generative AI for Business Innovation: An Exclusive Consultancy Approach

Original content with a single minded focus on value addition.

Case study: The Journey of Paytm

With this piece, we’ll try to understand the case study of Paytm, which will explain how the brand went from being a mere recharge app back in 2010, to hosting everything as of today. This case study also explains the current difficulties of Paytm given the increasing competition and the loss of interest of the investors.

Started by Vijay Shekhar Sharma, as a Recharge platform in 2010, Paytm (One 97 Communications Ltd) became the most successful mobile payment and money transfer app used in India a few years back. For a country which had 95% of monetary transactions made in cash prior to demonetization , it was difficult for Paytm to make customers believe in digital money. But, Paytm did the drill, they tapped the un-served/under-served lots of India and enabled them to do cashless transactions. And, by the means of cashbacks and offers, Paytm raced ahead of its then rivals – Freecharge, PayU, Mobikwik, etc.

However, the picture seems to be changing today. After the entry of players like Google Pay & PhonePe, the brand is starting to fall behind in the race . And given the poised release of WhatsApp Pay somewhere this month (June, 2020), things are only going to be tougher for the company. Let us understand the journey of Paytm to essentially understand their position today.

Business Aspects and Expansion:

Paytm has always focused on the customer-centric approach. This is evident from that fact that, even before Paytm started with wallet services, the company built a 24×7 customer care service. It understood that digital payments were still new in India and so, it had to ensure their customers get all the right support. This enabled people to get their queries solved and trust their money with Paytm. It has spent nearly Rs.14,500 crore to convince Indians to substitute cash with digital payments . One can clearly understand how Paytm must have pivotal role in our Hon. Prime Ministers’ Digital India dream.

In 2014, the company did one of their major launches – that is the Paytm Wallet. This enabled the users to directly pay without entering an OTP again and again. Which was again new for the customers, given they thought using OTP kept their money safe. Now, one might think this to be the wrong move. However, this was one of the features that gave Paytm the best results. When a user kept its money in the Paytm wallet, they were not charged. However, Paytm kept the money with Escrow accounts which fetched Paytm interests.

Demonetization – An opportunity for Paytm:

Anyway. Let’s continue, and understand when the future actually started to look fortunate for Paytm. We’d all remember Demonetization, don’t we? Ah, those long ATM hours, lots of money with not value. Those were the days.

While demonetization spelled doom for most of us, it was actually a fortune for Paytm, and we don’t need to tell you why. Or do we? Okay. So, our Hon. Prime Minister had a vision to turn the economy digital. Digital could help the Government track the money and essentially reduce the influx of black money in the economy.

Now, Paytm was the biggest digital payments app back then. And so, when the demonetization happened, it went through the roofs! It extended services to retail stores, Kiranas, Vegetable shops, Saloons, even Pan shops! It was everywhere! Paytm grabbed the biggest piece of all the online payments happening during that period.

Given the progress Paytm was making and the amount of Government support they were enjoying, it got into aggressive marketing which showcased the involvement of retail shop owners.

Anyway, that was a time to be remembered both for us and Paytm, alike.

The pain-points:

All the good stuff probably ended in the paragraph above, let us now try to understand the challenges the brand has faced in the recent past.

Paytm vs PayPal:

While Paytm was busy counting its profits after Demonetization, a US-based payments company PayPal filed a case against Paytm for using a logo similar to its own. They look pretty similar, PayPal was probably right. 

PayPal accused Paytm of using the similar logo which it had been using since 2007. This would create confusion in Indian customers about the platform. The case is still in court and if Paypal wins, Paytm would have to pay heavy charges for trademark infringement.

UPI (Unified Payments Interface):

With the launch of Unified Payments Interface, two major giants – Google Pay and PhonePe entered the market and people preferred UPI transactions over Paytm wallet transactions. To keep up the race, Paytm also launched BHIM UPI transaction mode but recorded lower transactions than its rivals.

Do you know why?

FMA. The first mover advantage. Paytm probably thought that their wallets will sustain them against these players, which was nice, in theory. We all would remember, right? Google Pay actually went rogue with the middle class of the country, do you remember your friends telling you to send some cash just to gain some extra bucks in the transaction?

Little did you understand that you were actually getting used to using Google Pay, smart. Use less money in marketing and instead give that away to the customers!

Current picture:

Paytm has been losing ground to its competitors with bigger pockets. To add salt to the injury, the Jio-Facebook deal is posing enormous threat to the company. Jio has already started on-boarding local shops on their platform. Who will then essentially host motivate these owners to use Facebook’s WhatsApp Pay, poised to launch in June, 2020.

Given that WhatsApp has around 400 million users in India, integrating payment here would make it convenient for the users to just send money. And, essentially, inconvenient for Paytm. This has raised concerns amongst investors about Paytm’s total valuation and business model. With the losses mounting up, it would be difficult for Paytm to keep its head above the water and continue the trust of its investors.

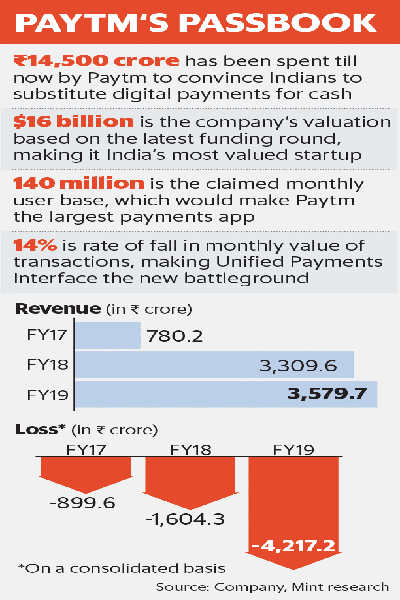
Classic example of why you must choose your niche. If you have ever used Paytm, you will realize that the company actually tried to expand into a lot of spaces. It tried to have movie bookings, travel, bill payments, shopping deals, banking and finance (Paytm banks) and what not! Maintaining so much requires equal amount of capital, and having concerned investors on board will not make that happen for you.

Anyway, that’s it for this piece. This brilliant piece was penned down by Geeta Belani , go drop her a thank. Share this piece with your best friend, and share your thoughts as to what Paytm can do to improve their stance as of right now?

Have a good one!

• Trump vs Twitter: The Content Moderation Game
• BCG Matrix with examples of 4 popular brands

You May Also Like

Case study: The Rise and Fall of WeWork

Case Study: The YES Bank Crisis

Maggi Case study: The 2015 Maggi crisis

8 thoughts on “ case study: the journey of paytm ”.

Pingback: COVID-19: Bane for the World, Boon for EdTech in India | CaseReads

Pingback: Concepts at ease: What are Neobanks? | www.casereads.com

Pingback: Neobanks In India: Understanding What Are Neobanks?

Pingback: Wirecard Scandal Explained: A Modern-day Hera Pheri

Pingback: The Resurgence Against The App Store Monopoly

Pingback: FinTech In India And The World: Evolution, Impact, And Uses

Pingback: Idea Cellular Case Study: From Idea To Vi

Pingback: The 101 Of Consumer Promotions With Examples

Comments are closed.

• Business News
• India Business News
• Paytm's wallet services curtailed by RBI: What happens now

Paytm's wallet services curtailed by RBI: What happens now

About the Author

The TOI Business Desk is a vigilant and dedicated team of journalists committed to delivering the latest and most relevant business news from around the world to readers of The Times of India. The primary focus of the TOI Business Desk is to keep a watchful eye on the global business landscape, covering a wide spectrum of industries, markets, economic trends, in-depth analysis, exclusive reports and breaking stories that impact businesses and economies. With a mission to provide valuable insights and updates, the desk ensures that TOI readers are well-informed about the ever-changing and dynamic world of commerce and can navigate the complexities of the business world. Read More

Visual Stories

PPF Calculator

This financial tool allows one to resolve their queries related to Public Provident Fund account.

FD Calculator

When investing in a fixed deposit, the amount you deposit earns interest as per the prevailing...

NPS Calculator

The National Pension System or NPS is a measure to introduce a degree of financial stability...

Mutual Fund Calculator

Mutual Funds are one of the most incredible investment strategies that offer better returns...

Other Times Group News Sites

Popular categories, hot on the web, trending topics, living and entertainment, latest news.

example cover letter for internship

Paytm - How Is It Transforming the World of Digital Transactions?

Himaya Presthitha , Manisha Mishra

In our daily lives, making bill payments and transactions used to rely solely on handling cash. Nonetheless, the shortcomings of cash-based techniques have been brought to light by the changing needs of the market and the move towards digital transactions.

Enter Paytm , an innovative digital payment app that has been available in India since 2010 and has completely changed the way that transactions and bill payments are made. Paytm, a smooth substitute, has been important in the transition to digital financial transactions , signifying a noteworthy turning point in India's payment history.

In this article, we will delve into the successful journey of Paytm, its founder, business model, funding, acquisitions, competitors, and more.

Paytm - Company Highlights

Paytm - About Paytm - Industry Paytm - Founder and Team Paytm - Startup Story Paytm - Mission and Vision Paytm - Name, Tagline, and Logo Paytm - Products and Services Paytm - Business Model Paytm - Revenue Model Paytm - ESOPs Paytm - Challenges Faced Paytm - Funding and Investors Paytm - Investments Paytm - Acquisitions Paytm - Growth Paytm - Sponsorship Paytm - IPO Paytm - Value Proposition Paytm - Awards and Achievements Paytm - Partnerships Paytm - Competitors Paytm - Future Plans

Paytm - About

Vijay Shekhar Sharma launched Paytm, a well-known provider of digital payments and financial services . Paytm was initially designed to make online money transfers easier for consumers and businesses alike, but it has gradually expanded its services. Later, it offers financial services, eCommerce capabilities, and cell and DTH recharging assistance. Indians have come to love this platform since it is so convenient and easy to use.

With the goal of assisting Indian app developers and entrepreneurs, Paytm has expanded its offerings over time to include stockbroking , the National Pension System (NPS) , Paytm First Games , Paytm Insurance , and a mini app store . Paytm's dedication to provide its users a wide range of easily accessible financial products is reflected in this expansion.

Paytm - Industry

According to a Statista study report, the fintech industry in India with the biggest growth potential is expected to be investment tech , which is expected to develop at a rate of 30% between 2022 and 2030 . The financial software as a service industry is projected to grow at a Compound Annual Growth Rate (CAGR) of 27% during the same time frame. Based on an informative analysis by Statista, the country's fintech business is expected to be valued at over $2 trillion USD in 2030 , indicating a dynamic and booming ecosystem.

Paytm - Founder and Team

Paytm was founded by Vijay Shekhar Sharma in 2010.

Vijay Shekhar Sharma

Vijay Shekhar Sharma, the founder and CEO of Paytm , made significant strides in the business world, earning recognition and accolades for his entrepreneurial prowess. In 2017, Forbes named him the youngest billionaire in India, putting his net worth at $1.3 billion. A notable winner of the Uttar Pradesh government's highest civilian award, the Yash Bharati, Sharma cemented his standing in the corporate world. He was listed as the 62nd richest person in India by Forbes in 2020.

Vijay Shekhar Sharma started his academic career at Delhi College of Engineering, where he studied electronics and communications for his B.E. His career path led him through roles such as Business Development at RiverRun Software Group and Tech Head at India Today Group Online. Eventually, he founded One97 Communications Limited, the parent company of Paytm, and further expanded his influence by founding Paytm Payments Bank.

Sharma's impressive career path highlights his business savvy and enduring influence on the financial technology scene in India.

The team at Paytm is 10,001+ strong, as per its LinkedIn profile.

Paytm - Startup Story

Vijay Shekhar Sharma's entrepreneurial journey commenced in Aligarh, where his middle-class upbringing instilled determination and resilience. Vijay was educated in Hindi, so he had to overcome a language barrier. Nevertheless, he performed well academically and was accepted to Delhi College of Engineering, where he eventually received a B.E. in Electronics and Communications Engineering.

Vijay's entrepreneurial journey began when he created indiasite.net while still a college student in 1997. His ambition persisted even after selling the website after two years. He established One97 Communications in 2000 and provides services for mobile content. This business endeavor served as an introduction to Paytm, which began operations in 2010 in Noida with a $2 million initial investment. Under Vijay's inspiring direction, Paytm quickly changed from a distributor of mobile entertainment to a pioneer in digital payments in India.

Vijay Shekhar Sharma's startup story not only encapsulates his personal journey of overcoming challenges but also mirrors the transformative growth and impact of Paytm on India's fintech landscape.

Paytm - Mission and Vision

Mission: The company mission on its website is "We will bring Half-a-Billion Indians to the Mainstream Economy."

Vision: The company vision is to become India's leading payments App .

Paytm - Name, Tagline, and Logo

Paytm is a venture under the umbrella of its parent company, One 97 Communications .

Paytm - Products and Services

Paytm Mall Launch (February 2017): Paytm introduced Paytm Mall in February 2017 as part of a calculated effort to break into the eCommerce space. Alibaba provided an initial $200 million capital infusion to Paytm Mall, which was then able to maintain steady backing from Ant Financial and Alibaba in order to strengthen the Paytm wallet.

Contactless In-Store Ordering Innovation (April 2020): Paytm introduced the concept of 'contactless in-store ordering' to promote minimal physical contact in the wake of the COVID-19 pandemic. This initiative aimed to redefine the retail experience and enhance safety measures.

Mini App Store Introduction (October 5, 2020): In an attempt to counter the Google Play Store's hegemony in the digital space, Paytm launched a micro app store to assist Indian app developers and entrepreneurs.

Card SoundBox Design Launch (July, 2023): Paytm unveiled the Card Soundbox, a revolutionary device empowering merchants to seamlessly accept mobile and card payments across various networks, including Visa, Mastercard, American Express, and RuPay. The device simplifies transactions with a convenient 'tap and pay' feature, showcasing Paytm's commitment to innovative payment solutions.

Paytm - Business Model

Pioneering India's QR and mobile payments revolution, Paytm's business model centers on advancing financial inclusion through a broad spectrum of payments and financial services. The key components of this model can be summarized as follows:

Comprehensive Payments Ecosystem: The core of Paytm's business model is to attract merchants and customers by offering a wide range of payment options. With UPI acting as a low-cost acquisition channel, the platform cross-sells high-margin banking and merchant services by utilizing insights.

Empowering Customers: In addition to Paytm Payment Instruments, Paytm offers a variety of third-party payment choices, such as cards and online banking, to empower its users. They make it easier to pay for things online, promoting convenience with the Paytm app and allowing QR code-based in-store and third-party app transactions.

Subscription-Led Ecosystem for Merchants: Paytm provides its partners with technology tools so they may take payments using a variety of methods. Reconciliations are made easier by subscription-based devices, and beginning merchants can accept payments using a free mobile QR code, mostly using Paytm Payment Instruments or UPI.

Merchant Growth Through Platform Engagement: When customers use the platform's payment options, it encourages merchants to sign up as well, which feeds back into itself and results in a high volume of repeat business. Significant consumer stickiness and retention are fueled by this combination.

Paytm - Revenue Model

Paytm generates revenue through a diversified set of streams, some of the prominent one are listed below:

Profitable UPI Use: Paytm makes money through the widely-used Unified Payments Interface (UPI).

Monetization avenues: Paytm makes money on its platform through selling of loans and payment devices, as well as from subscription revenue, payment processing fees, and marketing services it offers to other companies via its Commerce and Cloud business.

Co-Branded Credit Cards: Co-branded credit card partnerships with banks such as SBI and HDFC generate income from upfront distribution and lifetime usage fees.

Diverse Revenue Streams: Paytm's strong business strategy guarantees profits from non-UPI and UPI transactions, resulting in a steady and stable flow of income.

Paytm - ESOPs

As of August 15, 2021 , 166 former and current workers of Paytm who exercised their options under the ESOP Scheme 2008 and ESOP Scheme 2009 have received approximately 10,11,582 equity shares valued at Rs 189 crore . This action is a component of Paytm's continuous dedication to appreciating and thanking its employees. Employee incentives were further enhanced by the company's May 2022 grant of stock options valued estimates at Rs 222 crore under the ESOP plan.

Furthermore, Paytm revealed the granting of 17,06,829 stock options through the 'One 97 Employees Stock Option Scheme 2019' to eligible employees. By providing perks to qualified workers, this program seeks to increase their involvement in the expansion of the business.

Based on the stock prices of One97 Communications of July, 2023 , Fintrackr has estimated that the total value of the new ESOPs given by the company is around Rs 145 crore . Paytm's attempts to promote employee involvement and connect their interests with the company's long-term development are in line with this strategic allocation of equity shares.

Paytm - Challenges Faced

Paytm has encountered a series of challenges as it sought to reshape the cultural landscape of India, where both internet access and smartphones were once deemed unaffordable. The company has faced hurdles included critical issues such as transaction glitches, advertising missteps, and even a trademark infringement case against the Paytm brand.

In 2018, Paytm faced a significant challenge when its e-commerce arm, Paytm Mall, allegedly experienced a major data breach on August 30. Firefox Monitor reports state that the hacked data included sensitive information such phone numbers, email addresses, and dates of birth for approximately 3.4 million clients. However, according to reports dated July 28, 2022, Paytm denied these allegations and insisted that all users' data was secure.

On September 18, 2020, the Google Play Store abruptly removed the Paytm app, purportedly for breaking rules regarding unlicensed gambling apps.

As for 2022, on August 1, 2022, reports surfaced that three Paytm employees had burned PhonePe QR codes in bulk. This presented a new challenge. PhonePe responded by reporting the incident to the police.

When the Reserve Bank of India (RBI) ordered Paytm Payments Bank to stop accepting new clients owing to supervisory concerns, the bank faced a major obstacle in the regulatory environment of 2022.

Ultimately, Paytm made strategic steps to optimize costs in 2023 in response to financial concerns. On December 25, 2023, a news source stated that the corporation has started a workforce reduction program, with at least 1,000 employees being let go from a variety of divisions. This action showed the company's dedication to solving problems by maximizing staff expenses.

In the wake of the Reserve Bank of India's proceedings against Paytm Payments Bank, Paytm is facing regulatory issues. Because of continuous non-compliance and supervisory concerns, the RBI has prohibited fresh deposits from March 15, 2024, as per news report of February 18, 2024. This emphasizes how important it is for the fintech industry to follow regulations.

Paytm - Funding and Investors

The company has raised funding of around $3.54 billion over 15 rounds of funding.

Here are some of the most prominent funding rounds for Paytm:

Paytm - Investments

Paytm has invested in 19 companies to date. The Indian fintech unicorn further revealed on May 21, 2022, that it would be investing a total of Rs 950 crore in Paytm General Insurance Limited (PGIL) in multiple tranches over the next 10 years.

Here's a list of the prominent investments in Paytm:

The company has exited from four companies: Little, CreditMate, TapChief, and AbhiBus.

Paytm - Acquisitions

Here are the notable acquisitions made by Paytm:

Paytm - Growth

Since its establishment in August 2010, Paytm has firmly established itself as the most popular payments app in India, routinely ranking among the top UPI apps in the nation.

Furthermore, as per the company's records with the Registrar of Companies, Paytm has rebranded itself as "Pai Platforms" in a calculated move, according to news dated February 9, 2024. This development is consistent with the company's resolve to innovate and adjust to the changing Indian digital market environment.

Some of the prominent company's growth highlights are:

• Paytm monthly active users surpasses 10 crore as per the news report of January 23, 2024.
• As of January 2024, Paytm boasts over 300 million wallets and 30 million bank accounts , reflecting widespread adoption.
• Paytm revealed that merchants' Gross Merchandise Values (GMV) increased by an astounding 39% year over year to Rs 1.47 lakh crore as per news report of August 2023.
• Merchant subscriptions experienced substantial growth, reaching 82 lakh , with an addition of 41 lakh new subscriptions over the past year as per news report of August 2023.
• The number of monthly users on the platform increased significantly by 19%, to an astounding 9.3 cror e as per news report of August, 2023.
• The user base of Paytm exceeded 58 million account holders as of March 2022, highlighting its continuous growth and popularity in the digital payments landscape.
• Paytm became India's first payment app to cross 10 crore app download s in 2017, which was a major milestone.

According to the news report of January 19, 2024, the company's income from operations increased by 13.2% to Rs 2,850.5 crore in the third quarter of the fiscal year that ends in March 2024, from Rs 2,518.6 crore in Q2 FY24. When compared to Rs 2,062.2 crore in Q3 FY23, the operating revenue grew by 38.2%.

Comparing Q3 FY24 to Q2 FY24 , the company's overall expenses increased to Rs 3,216.3 crore from Rs 2,936.7 crore . Interestingly, Paytm's losses in Q3 FY24 dropped to Rs 221.7 crore from Rs 291.7 crore in Q2 FY24 , a 24% decrease.

Expenses Breakdown

Paytm - sponsorship.

• Paytm has emerged as the official sponsor of the 37th National Games, which took place at the Jawaharlal Nehru Stadium in Fatorda, South Goa, The competition was officially inaugurated by Prime Minister Narendra Modi.

“We are excited to be the official sponsor for the National Games in Goa. As pioneers of mobile payments in India, we have been working towards our mission to bring half a billion Indians into the mainstream economy. From our leadership in in-store payments, empowering merchants with digitalization of their business to enabling users with seamless and accessible payments, we are championing Digital India.” said Abhay Sharma, Chief Business Officer.

• BCCI awards Paytm the company its title sponsorship rights for BCCI International and Domestic seasons between 2019 and 2023. However, Paytm asked to pull out of the deal, and Mastercard replaced Paytm, as per the reports dated July 26, 2022.
• Paytm was the associate sponsor of the Sony TV network, which was awarded the telecast rights of IPL.

Paytm - IPO

One97 Communications, the parent company of Paytm, filed a draft red herring prospectus with the Securities and Exchange Board of India in July 2021, indicating its intention to begin an initial public offering (IPO), which was a big step toward becoming public.

Then, in November 2021, Paytm pulled off a successful IPO, raising a whopping Rs 18,300 crore (US $2.3 billion) and reaching a US $20 billion valuation. This accomplishment represented a turning point in the business's history, demonstrating the trust of investors and adding to the changing Indian financial market environment.

Paytm - Value Proposition

Paytm's primary service proposition was initially centered around recharging, which remains a prominent aspect of its business. Over time, the company diversified its services, introducing the Paytm Wallet , e-commerce vertical , Digital Gold , and more.

Paytm creates value for Merchants.

The company adds value to businesses by providing a variety of digital payment methods, encompassing traditional options like debit and credit cards and innovative solutions like QR codes, email links, text messages, and its digital wallet. Additionally, Paytm supplies the necessary hardware for in-store purchases and integrates payment services into its Smart Retail platform, offering retailers a comprehensive solution for managing payments, analytics, inventory, and customer engagement.

Paytm creates value for individuals.

Paytm garnered recognition for empowering customers to go cashless without the hassles of opening a bank account, generating value for consumers in a nation where cash payments have historically been the norm.

Paytm - Awards and Achievements

Paytm has won numerous accolades. Following is a list of a few of the well-known ones:

• 2012: Paytm received the ‘Most Innovative Startup of the Year’ Award from Franchise India.
• 2013: The company was recognized with the Knowledge Fabre Best Mobile Wallet Program Award.
• 2014: Paytm achieved ‘Gold Winner’ at the MMA Smarties in the Mobile App category and was the winner of the Indian Express IT Award.
• 2015: Paytm secured the Best Digital Wallet Award at IAMAI India Digital Award.
• 2016: Paytm was the winner of the FT Future of Fintech Award and also received the ET Brand Equity Most Trusted Brand of the Year.
• 2017: Paytm was honored with the Diamond SABRE Award in the Company of the Year category at SABRE Awards.

Paytm - Partnerships

• October 22, 2018: Paytm has collaborated with Softbank Group and Yahoo Japan to launch its e-wallet service in Japan called PayPay.
• Paytm was also announced as the official partner of the Mumbai Indians.
• June 22, 2020: Paytm partnered with Tata Starbucks on June 22, 2020, which is a pan-India partnership for a contactless dining solution.
• February 26, 2021: Paytm and Ola partnered with IndusInd Bank and applied to the RBI for the NUE license.
• April 19, 2021: Paytm saw a partnership with the Life Insurance Corporation of India to help facilitate digital payments.
• July 19, 2021: Paytm partnered with IndusInd Bank to enable payments from the fixed deposit accounts held by the users of the latter.
• August 23, 2021: Paytm partnered with HDFC Bank to provide solutions across payment gateways, POS machines, and other credit products.
• September 27, 2021: Paytm brings real-time international remittances into the Paytm mobile wallet by partnering with Ria Money Transfer.
• December 3, 2021: Paytm partnered with PMS Bazaar with a view to helping manage the portfolio of HNIs, who have a minimum investment of Rs 50 lakh.
• November 15, 2023 Paytm has partnered with Amadeus, and for the next three years, it will include the travel technology company's platform into search, booking, and payment processes.

Paytm - Competitors

Some of the top competitors for Paytm are:

Paytm - Future Plans

Paytm is strategically positioned for robust future growth, unveiling ambitious plans for international expansion and AI integration as per news report of December, 2023 . The company, known for its innovative financial services platform, is set to extend its footprint to the global market, signaling a significant leap in its reach and influence.

Notably, Paytm envisions not only broadening its geographical presence but also aspiring to become a leader in AI technology within the financial services sector.

Who is the current owner of Paytm?

Paytm is owned by the Indian company One97 Communications Ltd.

Is Paytm a Chinese company?

Paytm is an Indian company, but one of its major investors is Ant Financial, which is a major Chinese investor . Resilient Asset Management, wholly controlled by Vijay Shekhar Sharma, received a 10.3% shareholding in the Noida-based business from Ant Financial in 2023.

Why was Paytm banned?

Paytm was banned from the Play Store for allegedly violating its gambling policies.

Is Paytm for businesses free?

Yes, there are no charges for setting up your Paytm for Business account.

What is the Paytm CEO's name?

The name of the Paytm CEO is Vijay Shekhar Sharma , who has been the founder and CEO of the company since it was founded back in 2010.

How many employees work at Paytm?

There are more than 10,000 employees at Paytm.

Is Paytm an Indian company?

Paytm is an Indian fintech company that specializes in digital payments and ecommerce and comes with the facility of digital wallets.

Paytm operates in how many countries?

Paytm currently operates in India, where the Paytm payments bank was founded, and in two other countries, namely Canada and Japan, as of now.

Which country made or developed the Paytm app?

Paytm is developed in India, and the development of Paytm and its processes happens internally. Therefore, even the Paytm app and numerous other things associated with the brand and its functioning are developed internally by the brand itself.

Is Paytm profitable?

In FY23, the company reduced losses compared to FY22, with losses totaling Rs 1,776 crore, down from Rs 2,396 crore in the previous fiscal year, FY22.

What are the countries where Paytm is available?

Though Paytm is an Indian company, it supports international payments from over 200 countries with the help of all major international cards, even without any additional API integration.

Must have tools for startups - Recommended by StartupTalky

• Convert Visitors into Leads- SeizeLead
• Payment Gateway- Razorpay
• Spy on your Competitors- Adspyder
• Manage your business smoothly- Google Workspace

Plant-Based Protein Gaining Traction in India

Vegetarian and vegan alternatives have increased in Indian restaurants since the new year started. The recent introduction of vegan burger patties and nuggets by ITC demonstrates the growth of this sector. Various forms of food production may now give greater consideration to vegan options. As per the analysis by CNBC,

Lights, Camera, Action! Opportunities for Growth and Innovation in the Indian YouTube Ecosystem

India's love affair with YouTube is undeniable. With the world's second-largest internet user base, with just under half of its population (49.15%), India boasts a booming YouTube landscape. Oxford Economics’ findings have unveiled a remarkable impact of YouTube’s creative ecosystem on the Indian economy. The study reveals that

Can Patient Capital Change VC? Rainmatter Capital's Experiment in India

In the burgeoning Indian startup ecosystem, Rainmatter Capital stands out as a unique venture capital firm. Founded in 2016 by Zerodha, a leading online brokerage firm, Rainmatter takes a non-traditional approach to investing.  Beyond the Bottom Line: A Patient Capital Approach Focus Areas: Fintech, Health, and Storytelling Operational Insights: Collaboration

Tech & Tradition: How India's Tourism is Going Global

India, a land steeped in vibrant culture, ancient history, and breathtaking landscapes, is on a mission to become a global tourism hub. The travel and tourism sector in India is already a significant contributor to the economy, generating ₹15.7 lakh crore (US$230 billion) in 2022 as per the

PayTM Interview Questions

Before you step up to appear for the PayTM interview, make sure you are well-versed in what the interview is going to ask in varying rounds. This post by MindMajix outlines the latest PayTM interview questions with answers. Alongside this, you can also learn about the interview process, PayTM leadership skills, and more.

• Abstraction in Java
• Clojure Tutorial
• Control Statements in Java
• Core Java Interview Questions
• Data Types in java
• Top 9 Java EE Frameworks
• Java EE vs Spring Framework
• Java Frameworks List - Top 14 Java Frameworks
• Java Interview Questions
• Java Tutorial
• Java Web Dynpro Interview Questions
• JavaFX Interview Questions
• Method Overloading in Java
• Multithreading in Java
• List of Popular Open Source Java Build tools
• Operators in Java
• Program Logics in Java
• String Handling in Java
• Why You Should Learn Java Programming
• Data Structures Interview Questions
• Exception Handling in Java
• Multithreading Interview Questions
• Design Patterns Interview Questions and Answers
• C++ Interview Questions and Answers
• JSP Interview Questions
• EJB Interview Questions
• SOAP in Web Services
• JPA Interview Questions
• DXC Interview Questions and Answers
• Java Architect Interview Questions
• Java Concurrency Interview Questions
• What is Java Concurrency?
• What is JPA - Complete Tutorial Guide
• What is EJB?
• Java Collections Interview Questions
• Java Swing Tutorial
• Java Stream Tutorial
• Linked List Interview Questions
• Compiler Design Interview Questions
• Java Collection Tutorial
• Java Stream Interview Questions
• Thymeleaf vs JSP
• Thymeleaf Tutorial - What is Thymeleaf
• Socket Programming in Java - What is TCP
• Apache Tomcat Interview Questions
• Capgemini Interview Questions
• Zoho Interview Questions
• PwC Interview Questions
• Hexaware Interview Questions
• Intuit Interview Questions
• Tech Mahindra Interview Questions
• Qualcomm Interview Questions
• Arcesium Interview Questions
• DXC Technology Interview Questions
• Java Developer Job Description
• MAQ Software Interview Questions
• Amdocs Interview Questions
• TCS NQT Interview Questions
• Virtusa Interview Questions
• Siemens Interview Questions
• Tricky Java Interview Questions
• Explore real-time issues getting addressed by experts
• Test and Explore your knowledge

PayTM Recruitment Process

Paytm technical interview questions.

• Experienced

PayTM Coding Interview Questions

Paytm leadership principles, tips to crack paytm interview.

• FAQ for PayTM

Abbreviated for Pay Through Mobile, PayTM is an Indian technology company that has its headquarters in Noida. This brand focuses on financial services, e-commerce, and digital payment systems. Currently, the app is available in more than ten Indian languages. On this platform, you can easily avail a gamut of services, including mobile recharge, event bookings, utility bill payments, travel booking, and much more. Through the PayTM app, you also get an in-store payment option through a QR code. Considering the technicality behind managing the app and keeping its functionality up-to-date, there is a constant demand for skillful software engineers at PayTM. Employees at this firm get to work in a fast-paced environment and create valuable products, thus, experiencing the utmost exposure. So, if you’re ready to be a part of this company, MindMajix brings you a list of the latest PayTM interview questions with answers for you to read through and prepare for the interview. 

Top 10 Frequently Asked PayTM Interview Questions

• Briefly describe the singleton design pattern.
• What do you know about virtual memory?
• Can you explain namespaces in Python?
• Define Unix kernel.
• What is DHCP? State its advantages and disadvantages.
• What are the features of Hadoop?
• What do you know about a bug's life cycle?
• Write a C++ function to showcase all nodes in a circular linked list.
• Define macros in C/C++. Give an example.
• In an integer array, how can you get matching elements?

The interview process at PayTM begins with you applying for the job. And then, an interview will be scheduled with you if you turn out to be a suitable candidate for the vacancy. Once you’re shortlisted, you will have to undergo different processes and a series of interviews.

Online Coding Round

This online coding round ranges anywhere between easy to medium when it comes to complexity and critical analysis of your problem-solving competency. Usually, in this round, you will have to answer questions pertaining to data structures and algorithms on varying platforms, such as HackerEarth, Cocobues, Hackkerank, and more. This round can last anywhere between 60-70 minutes. You will have to use your problem-solving skills and understanding of data structures and algorithms to clear the round. Furthermore, if you have a competitive coding experience, it will be a plus point for you.

Technical Interview Round

This round comprises almost four to six in-person interviews. You will be asked to use a whiteboard or a HackerRank to solve the questions and challenges. Every interview may include 5-10 minutes of discussion about your past work experience. You may also have to answer behavioral and situational interview questions. And then, you will be asked a series of data structures and algorithms questions. To stand out in this round, make sure you are well-versed in the development of distributed systems, working with APIs, cloud-based technologies, and SQL queries. Apart from this, get ready with selected programming languages, object-oriented programming concepts, networking, operating systems, and database management systems.

HR Interview Round

This Human Resource round tries to comprehend whether you are a cultural match for the company. To ace this round, you must study the brand and its products thoroughly. You may have to answer puzzle-based questions that are meant to evaluate your intelligence level. The questions are also designed to check how well you can adapt to challenging and awkward situations.

After getting to know the PayTM interview process, the next step is to make you familiar with the types of interview questions asked here. Below-mentioned are the latest PayTM interview questions for freshers and experienced, along with coding questions. Let’s have a look further.

PayTM Technical Interview Questions for Freshers

If you’re a fresher and would like to get a job at PayTM, here is the list of interview questions that you cannot afford to ignore.

1. What do you know about web applications?

Also known as a web app, a web application is software that runs on a web server in contrast to the computer-based software app that runs on the Operating System (OS) of a device. To access a web app, you will need a web browser and an active network connection. The user (also called a client) gets to access services from an off-site server that a third party hosts in these apps. These servers are generally developed on a client and server architecture. 

2. Briefly describe the singleton design pattern. 

It is a software engineering design pattern that limits the instantiation of a class to one single instance. This is beneficial when just one object is required to coordinate system-wide actions. The singleton is regarded as one of the most important design patterns. Since creating a different database connection for every object is an expensive affair, we sometimes only need one instance of the class, like one database connection that is shared by different instances. In the same manner, instead of developing different managers, an app can have one error or configuration manager that can handle all the issues. 

3. What do you know about virtual memory?

Virtual memory is a memory type that is created on a storage device for some time period. When the RAM of a computer gets drained because of multiple processes running simultaneously, virtual memory is created. The OS makes a part of the storage disc available to be used as RAM. Significantly, virtual memory is slower as compared to primary memory as the processing power gets used by moving data and not by performing instructions. When a computer has to use virtual memory, latency increases. The OS uses swapping to move data between virtual memory and RAM. 

4. Can you explain namespaces in Python?

The namespace is a significant notion for structuring and organizing code that is specifically useful in bigger projects. To make this entire process simpler, a namespace is used that helps manage the names in a program with ease. Through this, you can make sure that names are diverse and not misunderstood.  

5. Define Unix kernel.

The Unix kernel is considered the heart of the OS. It helps connect to the memory, processor, and I/O management along with hardware devices. The kernel handles user requests through system calls that shift the process from a user to kernel space. Each time a user process makes any system call, like open(), exec(), read(), and more, a context switch takes place. A context switch is referred to a mechanism for changing the processes’ state. A process can be halted until the system call gets completed, or it can even continue.  

6. How can you define marshaling?

Marshaling is referred to the conversion of an object’s memory representation into a format that can be transferred or saved to other software apps. This process converts an object into a serialized form that lets faraway objects communicate with each other.  The object of marshaling is to have a similar object present in one operating program be available in another. 

7. Do you understand anything about system calls?

Through a system call, a computer program or a piece of software requests a service from the kernel of the OS where it is executing. This is a way for the program to interact with the OS. The Application Program Interface (API) is generally used to offer services from the OS to user programs. It further acts as a link between the OS and the process, thus, letting user-level programs request services from the OS. System calls, so far, are the only way that enables entry into the kernel system. 

8. In JavaScript, what is functional programming?

Functional programming is the programming paradigm that helps deal with mathematical functions. Here, the focal point is to write pure and sophisticated functions. Considering that JavaScript is a multi-paradigm language, you can integrate several paradigms in a single code piece. At the same time, you can use functional programming, procedural, and object-oriented paradigms with JavaScript. 

9. Mention a key difference between computer software and a computer program.

The key difference between computer software and a computer program is that the former is a collection of different programs used to complete different tasks. On the other hand, the latter is a set of instructions that are expressed in a programming language. A program can be software but not vice versa. 

10. Which is the best SDLC model?

Accordingly, Agile is the best SDLC model and also the one that is prevalently used in the IT industry. The reason behind it being the best is that it is a hybrid of iterative and incremental approaches and works accurately in a flexible environment.

Check Out: SDLC Interview Questions and Answers

PayTM Technical Interview Questions for Experienced 

If you are an experienced person and are looking for a job at PayTM, here is a list of interview questions to prepare. 

11. What is DHCP? State its advantages and disadvantages.

DHCP is Dynamic Host Configuration Protocol. It has a server and client architecture. 

Advantages of DHCP:

• It is easy to set up, and it assigns IP addresses automatically to request clients. This results in the decreased time needed to manually configure IP addresses.
• It prevents incorrect or twice assignment of IP addresses; thus, it doesn’t cause any dispute in IP addresses.
• It is advantageous for mobile users as the newer network sends the associated configuration parameters instantly.
• The deployment doesn’t result in extra expenditure.
• It can handle several things, including super scopes and multicast.
• It simplifies the entire network administration.

Disadvantages of DHCP:

• A relay agent is needed to make sure the DHCP server handles every communication for both network segments since DHCP packets cannot traverse routers. 
• Upon the assigning of new IP addresses, the machine name remains constant.
• The server of DHCP can get unauthorized access to the IP addresses through credential details submission because there is no secure method for client authentication.

12. What are the advantages and disadvantages of a star topology in a computer network?

In a computer network, the spoke hub distribution concept gets used in the star topology. Every host in the star network is linked to a central hub. In the simplest form, a single hub works as a message route. Star network is one of the most commonly used computer network topologies. 

Advantages of Star Topology

• It can be examined, set up, and changed with ease.
• Transferring, uninstalling, and adding devices is simple.
•  The nodes that have failed get affected. Others remain operational.
• High performance can be accomplished with little network traffic and a small number of nodes. 

Disadvantages of Star Topology

• If the concentrator or hub fails, the linked nodes get disabled.
• A lack of accurate termination or a damaged cable can bring the network offline.
• Setting up a star topology is expensive.
• The capacity of the hub comprehends the performance.
• There could be substantial delays in buses because of the heavy network load.

13. What are the features of Hadoop?

Some of the Hadoop features are as follows:

• OpenSource: Since it is open-source, Hadoop can be used free of cost. The source code is available online so that anybody can read and edit it according to their needs.
• Flexibility: Hadoop is developed in a way that it can effectively handle any dataset type, including structured, semi-structured, and unstructured. This means that it can evaluate any data type, irrespective of the form; thus, making it completely adaptable. It turns out to be extremely advantageous to organizations as it lets them process large sets of datasets instantly. As a result, businesses can use Hadoop to evaluate essential insights from data sources like email, social media, and other sources. The flexibility of Hadoop lets it be used for fraud detection, data warehousing, log processing, and more.
• Fault Tolerance: Hadoop is something that runs on commodity hardware that can crash at any time. In Hadoop, data is duplicated across several DataNodes in a Hadoop cluster, making sure data is available even if one of the systems fails. If a machine faces a technical issue, you can easily read the data from that specific machine. Since the data is replicated or copied by default, it can be read from other nodes available in a Hadoop cluster.
• High Availability: With fault tolerance, high availability can be ensured in a Hadoop cluster. If any of the DataNodes fails because of fault tolerance, the data can be recovered from other nodes where the same data is replicated. The Hadoop cluster that has the highest availability has two or multiple Name Nodes, such as Passive NameNode and Active NameNode. If one fails, the other will take over.
• Clusters with High Scalability: Hadoop is an extremely scalable model. A huge amount of data is split across varying low-cost devices in a cluster. It gets processed in parallel. As per the business needs, the number of nodes or computers can be decreased or increased.
• Cost-Effective: Contrary to traditional relational databases, which need expensive CPUs and high-end hardware to deal with big data, Hadoop leverages inexpensive commodity technology. It results in a pocket-friendly paradigm.

Check Out: Hadoop Interview Questions

14. What do you know about schedulers? How do they work in an OS? List down different scheduler types found in OS. 

Schedulers are special computer programs that regulate how processes get scheduled in different ways. Their major responsibility is to comprehend the jobs that should be entered into a system and which processes should be executed. 

Here are three types of schedulers in an OS:

• Long-Term Scheduler: Also known as a task scheduler, it comprehends which apps can be accepted for processing into a system. Before a process is executed, it is chosen from the ready queue and is loaded into memory. The process then gets loaded into memory for CPU scheduling. The primary goal of the job scheduler is to deliver a well-balanced mixture of operations, including CPU-bound workloads and input/output. 
• Medium-Term Scheduler: This is used to shift programs in the primary memory. It frees the RAM that processes consume. This results in multiprogramming reduced to a minimum. The medium-term scheduler manages the swapped-out processes. 
• Short-Term Scheduler: It is also called a CPU scheduler, and its objective is to enhance the system performance as per the set of predetermined criteria. It is the process of transition. The CPU scheduler chooses one of the ready-to-run processes and assigns CPU time to the same. 

15. How do you differentiate between local variables and global variables?

We can differentiate between global variables and local variables on the basis of their features. 

Global variables have the below-mentioned features:

• Variables that are defined outside of a specific function or in the global space are called global variables.
• Any function can modify and access the global variable’s value from anywhere in the program.
• In case a variable is given a new value, it is implicitly local, and we can designate it as ‘global.’ 

Local variables have the below-mentioned features:

• Any variable that is declared in a function is known as a local variable. It only exists in the local space and not in the global space. 
• Variables can only be accessed in the local body. 
•  If, anywhere in the function, a variable gets a new value, it is regarded as local.

16. What are storage classes in C? What are storage classes in C?

Storage classes can be used to define the properties of a function or a variable. During a program’s execution, the durability, visibility, and scope of a variable help track its presence. There are four different storage classes in the C programming language, such as:

• Auto: In this class, every variable that is supplied inside a block or a function gets stored here by default. Auto variables can be used only within the function or block wherein they were defined and not outside them. However, you can access them outside of the scope through pointers that point to a memory address where a variable is stored. Whenever declared, an auto gets a garbage value by default. 
• Extern: With the “extern” term, you can comprehend that the variable gets defined outside of a block wherein it is used. It gets a value in any other block, which can be updated or overwritten in another block. We can make an ordinary global variable an extern through the ‘extern’ keyword before its definition or declaration in any block or function. This simply means that instead of creating a new variable, we get to only access and use the global variable. With the extern keyword, we can make a function and variable more visible. 
• Register: This storage class is used to declare register variables, which are the same as auto variables as far as functionality is concerned. The primary difference here is that the compiler attempts to store the variable in the register of the CPU in case there is a free registration. Otherwise, the data gets stored only in memory. To define some variables that can be accessed often throughout the program, the register keyword is used. 
• Static: This type is used to define static variables, which are prevalently used in the C language. Static variables are used to preserve the value even once they are removed from the scope. Thus, it is safe to say that they are initialized only once and exist till the program comes to an end.

17. What do you know about a bug's life cycle?

Also known as the defect life cycle, the bug life cycle is a process used to advance the defect via several phases of its existence. This lifetime starts when a tester reports a problem and ends when that issue is fixed. In a defect workflow, the following fault states can take place:

• New: A defect gets this status when it is documented for the first time.
• Assigned: When a tester has filed the bug report, their lead approves and assigns the same to the programming team.
• Open: The developer begins evaluating and fixing the issue.
• Fixed: Once the required code patch is done, the developer gets to mark the issue as ‘fixed.
• Pending Retest: After resolving the issue, the developer offers the tester a unique code to retest. Since the software testing is pending from the tester’s end, it gets marked as ‘pending retest.
• Retest: At this stage, a tester gets to retest the code to ensure that the problem is resolved.
• Reopened: If the issue still persists, the status gets changed to ‘reopened’, and the entire life cycle gets repeated.
• Verified: Once the issue is fixed and the tester has retested the code, it gets verified.
• Closed: A ‘closed’ tag is used when the issue doesn’t exist any longer. 

18. What are the different layers in the OSI model?

Open Systems Interconnection (OSI) was founded in 1984 by the International Organization for Standardization (ISO). The OSI model has seven layers with different functions for every tier. However, these layers work together to transfer data across the world from one person to another. The layers are:

• Physical Layer: This one is the lowest layer and is responsible for establishing a physical link between different devices. The layer stores bits of information and sends individual bits from a node to the consecutive one. The physical layer gets data and turns the same into 0s and 1s before it sends the data to the next layer. 
• Data Link Layer: This layer is responsible for transporting the message from one node to the next. The primary function of this layer is to make sure the data transferred between nodes is error-free. There are sublayers to the data link layer, such as Control of Media Access (MAC) and Control of Logical Links ( LLC ).
• Network Layer: This one is liable for transferring data between hosts that are linked to varying networks. It also handles packet routing, which is a process of choosing the shortest path among various to send a packer. The network layer includes the IP addresses of the sender and the receiver in the header. 
• Transport Layer: This layer offers services to the application layer. Herein, the segments are regarded as data units. The transport layer is responsible for delivering the message from start to finish. This layer identifies successful data transmission. And, in case of a mistake, it re-transmits the data.
• Session Layer: This one is in charge of creating connections, guaranteeing security, maintaining sessions, and authenticating users.
• Presentation Layer: In this layer, the data is obtained from the application layer and processed so that it can be delivered across the entire network in the right format.
• Application Layer: This is at the top of the OSI model and is integrated by network applications. This layer generates the information to be transmitted through the network. It also works as a window through which app services can connect to the network, and the information is displayed to the user. 

19. What do you know about socket programming? List down its advantages and disadvantages in Java. 

Socket programming is referred to as a method that allows two network nodes to communicate with each other. One socket monitors the traffic on a certain port at an IP address while the other is connecting to it. 

Advantages of Java Sockets

• Sockets are plentiful and adaptable. For regular communications, socket-based programming is easy to develop.
• Sockets cause low network traffic. Unlike CGI scripts and HTML forms, Java applets can send updated data. 

Disadvantages of Java Sockets

• Security limitations could be difficult at times.
• Socket-based connections are limited to the transfer of raw data packets between different programs. 
• There are restrictions in the reusability as data formats and protocols are specific to the application. 

20. Can you explain the modularization concept?

Modularization comes up when the functionality of a program is broken down into different, independent modules. Each of these modules carries the information required to execute only a part of the intended capability. To put it simply, this practice helps divide the program into small modules so that you can deal with them separately. Through modularization, we can add smaller and independent modules to a program without being affected by the complications of the other functionalities of that program. 

For those who are into coding, these questions with answers will be useful in the interview. 

21. Write a C++ function to showcase all nodes in a circular linked list.

22. what are callback functions in javascript give an example..

A callback function is one such function that gets input from another function and is called from within the outer function to complete the operation or routine. Here is an example of the same:

23. Define macros in C/C++. Give an example.

Macros are preprocessor directives that can be replaced at the time of compiling. As a result, in a program, a macro is named a section of code. This name is substituted by the compiler with a real code piece. One disadvantage of macros is that they change the code instead of function calls. 

24. How can you reverse a string in Java?

In Java, to reverse a string, we will first have to declare the string. And then, take the length of that string and loop through the string’s characters. Next, we will have to add those characters in reverse order in a new string.

25. How will you determine if a string is a palindrome?

When the string stays just the same on reversing the character’s order in that string, it is a palindrome. It can easily be achieved by reversing the original string first and checking whether the reversed string is equal to the original. 

26. How will you find out if the given two strings are anagrams?

We can ensure that two strings are anagrams in case they comprise the same group of characters in several sequences. 

27. In an integer array, how can you get matching elements?

To get the matching elements, we will have to declare an array. Next, we will nest a few loops to compare the numbers with the ones present in the array. We will then print the matching elements. 

28. How to swap two numbers without the third variable?

For this, the first step is to declare two variables and then initialize those variables with values. Make ‘b’ the sum of these two numbers. Then, minus the ‘b’ (sum) from a; thus, a is swapped. Next, minus a from ‘b’ (sum); thus, b is swapped. 

29. How can you discover the factorial of an integer?

30. how to integrate the insertion sort algorithm.

To do so, we will assume that the first element in an array has to be sorted. The second element will be stored differently in a key. This will sort the first two elements. Then, we can take the third element and compare it with those on the left. This process will continue until we get to a point where the array can be sorted. 

Here are some leadership principles being followed at PayTM that you should be wary of:

• Push boundaries : People at this company think differently. They find new ways to innovate and leverage technology to streamline everything.
• Entrepreneurial spirit: They set objectives and create plans to achieve them. They eradicate barriers and let curiosity be the guiding force. 
• Do great things fast: They concentrate on executing flawlessly. They work together effectively as a team.
• We before me: The team at Paytm is committed to solving real problems. They learn from failures and celebrate successes together.
• Communicate: They bring the best ideas by communicating with like-minded people. They brainstorm, speak up, and bring out the best product.
• Sharing is growing: They don’t stop themselves from sharing a good idea. They encourage every idea that helps add value to a new feature or product. 
• Increase your speed: Test yourself to see how quickly you can solve coding problems and questions. This will help you enhance the overall reasoning frameworks and skills for problem-solving.
• Maintain a positive outlook: Mainting a welcoming and positive attitude is always advantageous. You must introduce yourself with utmost confidence. Also, make sure you begin the conversation on a favorable note.
• Demonstrate your experiences: You must share your experiences and stay ready to showcase leadership, academic, teamwork, and professional success along with problem-solving and communication abilities.
• Know yourself: You must be familiar with your weaknesses and strengths. Make sure you learn how to put your talents and experiences in a qualified way. Once in a while, during the interview, put forth an example that will help you stand out. 

PayTM Interview Frequently Asked Questions

1. is the paytm interview hard.

The questions asked in a PayTM interview range between moderate to difficult levels. 

2. How many rounds will be there in a PayTM interview?

There will be three rounds that you will have to go through to clear the PayTM interview. These rounds comprise an online coding round, a technical interview round, and the HR interview round. 

3. What is the full form of PayTM?

Pay Through Mobile is the full form of PayTM.

4. What are the advantages of working at PayTM?

There is plenty of benefits you can get when employed at PayTM, such as team outings, health insurance, job training, soft skill training, free transport, child care, education assistance, free food, and more. 

5. What is the basic salary at PayTM?

On average, you can earn anywhere between Rs. 2,50,581 to Rs. 11,00000 a year, depending on your position and experience. 

Preparing for a PayTM interview is not a difficult task, given that you are equipped with the right set of resources. Having said that, this post comprises all the latest PayTM interview questions and answers you can read through and prepare yourself well. Are you looking forward to becoming a Core Java Developer ? Check out the Core Java Training and get certified.

Stay updated with our newsletter, packed with Tutorials, Interview Questions, How-to's, Tips & Tricks, Latest Trends & Updates, and more ➤ Straight to your inbox!

Although from a small-town, Himanshika dreams big to accomplish varying goals. Working in the content writing industry for more than 5 years now, she has acquired enough experience while catering to several niches and domains. Currently working on her technical writing skills with Mindmajix, Himanshika is looking forward to explore the diversity of the IT industry. You can reach out to her on LinkedIn . 

Copyright © 2013 - 2024 MindMajix Technologies

Paytm Shares Have Surged Over 50% YTD, But Analyst Still Sees Over 20% Upside

Paytm ‘s share price has been on an impressive bull run since the start of the year and analysts at BofA Securities see the stock going further up.

The Paytm Analyst: The Sachin Salgaonkar -led analyst team at BofA Securities maintained the ‘buy’ rating on the stock with a price target of ₹1,020. The price indicates an over 20% upside from the stock’s current market price of around ₹835.

The Paytm Thesis: The firm noted that Vijay Shekar Sharma buying a 10.3% stake in Paytm from Antfin removes an overhang on the stock from the risk that Antfin in future may look to reduce its stake leading to

more supply.

The firm added that the reduction of a Chinese entity’s stake in the company would likely have a positive impact on its overall fundamentals. The firm highlighted that in November 2022, the Reserve Bank of India (RBI) rejected Paytm Payments Services Limited’s (PPSL) application to operate as a payment aggregator.

The RBI granted PPSL 120 days to reapply for the license and instructed the company, which is a wholly owned subsidiary of Paytm, not to onboard new online merchants until approval is obtained. This decision was reportedly made to allow PPSL time to comply with foreign direct investment (FDI) guidelines. Now the brokerage firm anticipates that such concerns are unlikely to persist moving forward.

Price Action: Paytm’s share price was down 1.38% to trade at ₹838.95 in early trade on Tuesday.

Read Next: Why Investors Are Punishing PB Fintech Shares Even After Stellar Results

This article Paytm Shares Have Surged Over 50% YTD, But Analyst Still Sees Over 20% Upside originally appeared on Benzinga.com

• I'M AN INSTRUCTOR
• I'M A STUDENT

Find what you need to succeed.

• Our Mission
• Our Leadership
• Learning Science
• Macmillan Learning AI
• Sustainability
• Diversity, Equity, and Inclusion
• Accessibility
• Astronomy Biochemistry Biology Chemistry College Success Communication Economics Electrical Engineering English Environmental Science Geography Geology History Mathematics Music & Theater Nutrition and Health Philosophy & Religion Physics Psychology Sociology Statistics Value
• Digital Offerings
• Inclusive Access
• Lab Solutions
• LMS Integration
• Curriculum Solutions
• Training and Demos
• First Day of Class
• Administrators
• Affordable Solutions
• Badging & Certification
• iClicker and Your Content
• Student Store
• News & Media
• Contact Us & FAQs
• Find Your Rep
• Booksellers
• Macmillan International Support
• International Translation Rights
• Request Permissions
• Report Piracy

Psychology in Everyday Life

A portable anthology seventh edition | ©2023 samuel cohen.

ISBN:9781319483616

Take notes, add highlights, and download our mobile-friendly e-books.

ISBN:9781319331658

Read and study old-school with our bound texts.

Portable, affordable, and highly teachable

50 Essays: A Portable Anthology is a bestselling value-priced reader because its virtues dont stop at the price. The book’s carefully chosen selections engage students and include both classic essays and high-interest, contemporary readings. The editorial apparatus is flexible and unobtrusive enough to support a variety of approaches to teaching composition. The seventh edition features new voices on culturally relevant topics as well as an enhanced documentation guide establishing the importance of conducting research and evaluating sources, and new pre-reading questions to guide students as they develop their skills as critical readers.

New to This Edition

Seventh Edition | ©2023

Samuel Cohen

Digital Options

Read online (or offline) with all the highlighting and notetaking tools you need to be successful in this course.

Learn About E-book

Seventh Edition | 2023

Table of Contents

Samuel Cohen (PhD, City University of New York) is Associate Professor of English at the University of Missouri. He is the author of After the End of History: American Fiction in the 1990s , co-editor (with James Peacock) of The Clash Takes on the World: Transnational Perspectives on The Only Band that Matters , co-editor (with Lee Konstantinou) of The Legacy of David Foster Wallace , Series Editor of The New American Canon: The Iowa Series in Contemporary Literature and Culture , and has published in such journals as Novel , Clio , Twentieth-Century Literature , The Journal of Basic Writing, and Dialogue: A Journal for Writing Specialists. For Bedford/St. Martins, he is author of 50 Essays: A Portable Anthology and coauthor of Literature: The Human Experience .

Seventh Edition | 2023

Instructor Resources

Need instructor resources for your course, download resources.

You need to sign in to unlock your resources.

50 Essays 7th edition Sample Syllabi

50 essays transition guide - 6th edition to 7th edition, instructor's resource manual for 50 essays.

You've selected:

Click the E-mail Download Link button and we'll send you an e-mail at with links to download your instructor resources. Please note there may be a delay in delivering your e-mail depending on the size of the files.

Your download request has been received and your download link will be sent to .

Please note you could wait up to 30 to 60 minutes to receive your download e-mail depending on the number and size of the files. We appreciate your patience while we process your request.

Check your inbox, trash, and spam folders for an e-mail from [email protected] .

If you do not receive your e-mail, please visit macmillanlearning.com/support .

Related Titles

Select a demo to view:

We are happy to offer free Achieve access in addition to the physical sample you have selected. Sample this version now as opposed to waiting for the physical edition.

The Economic Times daily newspaper is available online now.

Paytm stock: goldman sachs answers 5 most-asked questions by investors.

The foreign brokerage said investors it spoke to felt that Paytm’s third quarter results were encouraging in terms of topline performance.

ICICI Sec sees 62% jump in Paytm, initiates coverage with buy rating

Investor losses in Paytm, Nykaa, PB & Zomato mount to Rs 1.3L cr since Day 1

​Goldman Sachs upgrades Paytm with a target price of Rs 1,460

Read More News on

Download The Economic Times News App to get Daily Market Updates & Live Business News.

Subscribe to The Economic Times Prime and read the Economic Times ePaper Online.and Sensex Today .

Top Trending Stocks: SBI Share Price , Axis Bank Share Price , HDFC Bank Share Price , Infosys Share Price , Wipro Share Price , NTPC Share Price

• View More Stories

Find this comment offensive?

Choose your reason below and click on the Report button. This will alert our moderators to take action

Reason for reporting:

Your Reason has been Reported to the admin.

To post this comment you must

Log In/Connect with:

Fill in your details:

Will be displayed

Will not be displayed

Share this Comment:

Uh-oh this is an exclusive story available for selected readers only..

Worry not. You’re just a step away.

Prime Account Detected!

It seems like you're already an ETPrime member with

Login using your ET Prime credentials to enjoy all member benefits

Log out of your current logged-in account and log in again using your ET Prime credentials to enjoy all member benefits.

To read full story, subscribe to ET Prime

₹34 per week

Billed annually at ₹2499 ₹1749

Super Saver Sale - Flat 30% Off

On ET Prime Membership

Unlock this story and enjoy all members-only benefits.

Offer Exclusively For You

Save up to Rs. 700/-

ON ET PRIME MEMBERSHIP

Get 1 Year Free

With 1 and 2-Year ET prime membership

Get Flat 40% Off

Then ₹ 1749 for 1 year

ET Prime at ₹ 49 for 1 month

Stay Ahead in the New Financial Year

Get flat 20% off on ETPrime

90 Days Prime access worth Rs999 unlocked for you

Exclusive Economic Times Stories, Editorials & Expert opinion across 20+ sectors

Stock analysis. Market Research. Industry Trends on 4000+ Stocks

​Get 1 Year Complimentary Subscription of TOI+ worth Rs.799/-​

Stories you might be interested in

• Testimonial
• Web Stories

Learning Home

Not Now! Will rate later

• Sample Aptitude Questions of Paytm

• 320               
• 75                  
• 150               
• 180               
•  62                 
• 82                  
• 78                  
• 68                  
• Rs. 84,000 
• Rs. 77,000 
• Rs. 1,10,000                                     
•  Rs. 59,000
•  Rs. 68,000
• 135               
• 125               
• 140               
• 130               
• 76                
• 76.5            
• 85                
• 80                
• Careers in Paytm
• All About Paytm
• Test Pattern & Selection Procedure of Paytm
• Paytm Reasoning Questions
• Paytm Sample Verbal Questions
• Actual Paytm Interview Questions
• Technical Questions asked in Paytm
• Free Mock Paytm Placement Paper
• Paytm Job Vacancies
• Join free preparation course of Paytm
• Complete preparation course of Paytm
• 123           
• 115           
• 119           
• 108           
• 648             
• 1800          
• 2700          
• 2000          
• 10                                                    
• 6                                                      
• 5                                                      
• 4                                                      
• 18 years                                          
• 20 years                                          
• 22 years                                          
•  25 years
• 50                                                  
•  40                                                 
• 80                                                  
• 60                                                  

Most Popular Articles - PS

Placement Papers of all major companies

List of IT Companies

Aptitude Questions of all Major Companies

Test Pattern of all major companies

Technical Questions of all major companies

List of Core Companies

Interview Questions of all major companies

All About GATE Entrance Exam

How to prepare for Aptitude Tests?

GATE Previous Year Papers

Download our app.

• Learn on-the-go
• Unlimited Prep Resources
• Better Learning Experience
• Personalized Guidance

Get More Out of Your Exam Preparation - Try Our App!

• Testimonial
• Web Stories

Learning Home

Not Now! Will rate later

Paytm Interview Questions

Excerpts from interview #1:

• How will you balance a binary search tree?
• Write a program to implement two stack in an array.
• A number is given , find the next greatest palindrome.
• On a given database, design a SQL query.
• Tell me how Face book maintained the friend’s list.
• Write a code to create mirror image of tree.
• Questions based on binary and ternary search tree.
• Give an example of an O (n) algorithm and O (n*n) algorithm such that the algorithm is slower.
• Introduce yourself.
• Are you ready to handle a team under pressure?
• What challenges are you facing presently and how are you dealing with them?
• Basic puzzles questions
• What do you know about our competitors?

Excerpts from interview #2:

• Write a program of advanced Fibonacci series.
• Tell me the difference between process and thread.
• Puzzles based questions.
• On a clicking a node in a tree, all the adjacent edges are turned on. Calculate min of clicks such that all the edges are turned on.
• Where to store local variables?
• How will you store a series of mobile number in memory efficiently (less space)?
• Write a code of a general series where the next element is the sum of last k terms.
•  Write a code to find angle between clock’s two ends.
• Write a program to print all interleaving of given two strings.
• Rate yourself on a scale from 1 to 10? Justify the score?
• Which type of dance does you like the most?
• Tell me about your family background.
•  Why Paytm?
• How would your dream day at Paytm?
• Actual Paytm Interview Questions
• All About Paytm
• Sample Aptitude Questions of Paytm
• Free Mock Paytm Placement Paper
• Join free prep course for Paytm
• Test Pattern & Selection Procedure of Paytm
• Technical Questions asked in Paytm
• Paytm Sample Verbal Questions
• Paytm Reasoning Questions
• Complete preparation course of Paytm

Excerpts from interview #3:

• Write a program to segregate 0s and 1s in an array.
• Write a code to create a largest subarray with equal number of 0s and 1s.
• What is a “null pointer assignment” error? What are bus errors, memory faults, and core dumps?
• Can a file other than an .h file be included with #include?
• Coin change problem.
• Write a code to reverse linked list in a group of size 3.
• How can you determine the size of an allocated portion of memory?
• What is pragma?
• Tell me the difference between a free-standing and a hosted environment.
• How can you right justify a string?
• Tell me about yourself and your family background.
• What kind of person would you refuse to work with?
• What motivates you to do your best on the job?
• What is more important to you : money or work?
• What do you regard as the significant achievement in your life?
• What position do you prefer on a team working on a project?

Excerpts from interview #4:

• Write a program to find the minimum distance between two given characters of a string.
• Write a code on matrix multiplication.
• Write a code to find a sub array which has zero sums for a given array.
• Write a program to find the maximum area of rectangle for a given histogram.
• How would you use the functions fseek(),fread(), fwrite() , and ftell()?
• What is the most efficient way to store 1 million phone numbers memory-wise?
• Write a program to find the whether a number is anArmstrong.
• Can include files be nested? How many levels deep can include files be nested?
• What state are the doors in after the last pass? Which of the doors are opend now and which one are closed?
• What is the concatenation operator?
• How will you prove yourself as an innovative person at work?
• What have you done to improve your knowledge in the last year?
• In what sort of company do you like to work in? Why?
• Describe your work ethics.
• Who is the CEO of Paytm?

Excerpts from interview #5:

• Write a program to search a number in a row wise-column wise sorted matrix.
• Write a code to arrange the given array in the form of a<b>c<d>e<f>g…….
• Given a doubly linked list with one pointer of each node pointing to the next node just like in a singly linked list. The second pointer(orbit pointer) however can point to any node in the list and not just the previous node. Write a program in to create a copy of this list.
• Give m equations and n variables. How many solutions are possible in each case?
• (i) m<n,(ii) m=n (iii) m>n
• Write a program of prime number using recursion.
• Write SQL queries on Self Join and Inner Join.
• What is the difference between heap memory and stack memory?
• What are memory tables?
• Tell me about yourself.
• What are the challenges you facing in IT?
• What are your achievements in life?
• Do you work well under pressure?
• Where do you see yourself in 5 years ?

Excerpts from Interview #6:

• Is it better to use malloc () or calloc()?
• When should a far pointer be used?
• What will the preprocessor do for a program?
• What is the benefit of using enum to declare a constant?
• What is meant by data hiding?
• What do you by Function Overloading?
• Explain the key functions of data binding?
• State two uses of pointers in C?
• Explain the importance of method overloading?
• What do you mean Abstraction?
• Introduce Yourself?
• State your three strengths.
• Who is the present President of US?
• What has been your biggest regret and achievement up to date?
• What does success mean to you?
• Where do you see yourself after 10 years?
• Interview Preparation
• Group Discussion
• Question Bank
• Essay/E-mail Writing

Most Popular Articles - PS

Dell Interview Questions

Ericsson Interview Questions

Essar Interview Questions

EY Interview Questions

EXL Interview Questions

Expedia Interview Questions

Fidelity Interview Questions

Flextronics Interview Questions

John Deere Interview Questions

Download our app.

• Learn on-the-go
• Unlimited Prep Resources
• Better Learning Experience
• Personalized Guidance

Get More Out of Your Exam Preparation - Try Our App!