what is research gap and rationale

How to Write the Rationale for a Research Paper

• Research Process
• Peer Review

A research rationale answers the big SO WHAT? that every adviser, peer reviewer, and editor has in mind when they critique your work. A compelling research rationale increases the chances of your paper being published or your grant proposal being funded. In this article, we look at the purpose of a research rationale, its components and key characteristics, and how to create an effective research rationale.

Updated on September 19, 2022

The rationale for your research is the reason why you decided to conduct the study in the first place. The motivation for asking the question. The knowledge gap. This is often the most significant part of your publication. It justifies the study's purpose, novelty, and significance for science or society. It's a critical part of standard research articles as well as funding proposals.

Essentially, the research rationale answers the big SO WHAT? that every (good) adviser, peer reviewer, and editor has in mind when they critique your work.

A compelling research rationale increases the chances of your paper being published or your grant proposal being funded. In this article, we look at:

• the purpose of a research rationale
• its components and key characteristics
• how to create an effective research rationale

What is a research rationale?

Think of a research rationale as a set of reasons that explain why a study is necessary and important based on its background. It's also known as the justification of the study, rationale, or thesis statement.

Essentially, you want to convince your reader that you're not reciting what other people have already said and that your opinion hasn't appeared out of thin air. You've done the background reading and identified a knowledge gap that this rationale now explains.

A research rationale is usually written toward the end of the introduction. You'll see this section clearly in high-impact-factor international journals like Nature and Science. At the end of the introduction there's always a phrase that begins with something like, "here we show..." or "in this paper we show..." This text is part of a logical sequence of information, typically (but not necessarily) provided in this order:

Here's an example from a study by Cataldo et al. (2021) on the impact of social media on teenagers' lives.

Note how the research background, gap, rationale, and objectives logically blend into each other.

The authors chose to put the research aims before the rationale. This is not a problem though. They still achieve a logical sequence. This helps the reader follow their thinking and convinces them about their research's foundation.

Elements of a research rationale

We saw that the research rationale follows logically from the research background and literature review/observation and leads into your study's aims and objectives.

This might sound somewhat abstract. A helpful way to formulate a research rationale is to answer the question, “Why is this study necessary and important?”

Generally, that something has never been done before should not be your only motivation. Use it only If you can give the reader valid evidence why we should learn more about this specific phenomenon.

A well-written introduction covers three key elements:

• What's the background to the research?
• What has been done before (information relevant to this particular study, but NOT a literature review)?
• Research rationale

Now, let's see how you might answer the question.

1. This study complements scientific knowledge and understanding

Discuss the shortcomings of previous studies and explain how'll correct them. Your short review can identify:

• Methodological limitations . The methodology (research design, research approach or sampling) employed in previous works is somewhat flawed.

Example : Here , the authors claim that previous studies have failed to explore the role of apathy “as a predictor of functional decline in healthy older adults” (Burhan et al., 2021). At the same time, we know a lot about other age-related neuropsychiatric disorders, like depression.

Their study is necessary, then, “to increase our understanding of the cognitive, clinical, and neural correlates of apathy and deconstruct its underlying mechanisms.” (Burhan et al., 2021).

• Contextual limitations . External factors have changed and this has minimized or removed the relevance of previous research.

Example : You want to do an empirical study to evaluate the effects of the COVID-19 pandemic on the number of tourists visiting Sicily. Previous studies might have measured tourism determinants in Sicily, but they preceded COVID-19.

• Conceptual limitations . Previous studies are too bound to a specific ideology or a theoretical framework.

Example : The work of English novelist E. M. Forster has been extensively researched for its social, political, and aesthetic dimensions. After the 1990s, younger scholars wanted to read his novels as an example of gay fiction. They justified the need to do so based on previous studies' reliance on homophobic ideology.

This kind of rationale is most common in basic/theoretical research.

2. This study can help solve a specific problem

Here, you base your rationale on a process that has a problem or is not satisfactory.

For example, patients complain about low-quality hospital care on weekends (staff shortages, inadequate attention, etc.). No one has looked into this (there is a lack of data). So, you explore if the reported problems are true and what can be done to address them. This is a knowledge gap.

Or you set out to explore a specific practice. You might want to study the pros and cons of several entry strategies into the Japanese food market.

It's vital to explain the problem in detail and stress the practical benefits of its solution. In the first example, the practical implications are recommendations to improve healthcare provision.

In the second example, the impact of your research is to inform the decision-making of businesses wanting to enter the Japanese food market.

This kind of rationale is more common in applied/practical research.

3. You're the best person to conduct this study

It's a bonus if you can show that you're uniquely positioned to deliver this study, especially if you're writing a funding proposal .

For an anthropologist wanting to explore gender norms in Ethiopia, this could be that they speak Amharic (Ethiopia's official language) and have already lived in the country for a few years (ethnographic experience).

Or if you want to conduct an interdisciplinary research project, consider partnering up with collaborators whose expertise complements your own. Scientists from different fields might bring different skills and a fresh perspective or have access to the latest tech and equipment. Teaming up with reputable collaborators justifies the need for a study by increasing its credibility and likely impact.

When is the research rationale written?

You can write your research rationale before, or after, conducting the study.

In the first case, when you might have a new research idea, and you're applying for funding to implement it.

Or you're preparing a call for papers for a journal special issue or a conference. Here , for instance, the authors seek to collect studies on the impact of apathy on age-related neuropsychiatric disorders.

In the second case, you have completed the study and are writing a research paper for publication. Looking back, you explain why you did the study in question and how it worked out.

Although the research rationale is part of the introduction, it's best to write it at the end. Stand back from your study and look at it in the big picture. At this point, it's easier to convince your reader why your study was both necessary and important.

How long should a research rationale be?

The length of the research rationale is not fixed. Ideally, this will be determined by the guidelines (of your journal, sponsor etc.).

The prestigious journal Nature , for instance, calls for articles to be no more than 6 or 8 pages, depending on the content. The introduction should be around 200 words, and, as mentioned, two to three sentences serve as a brief account of the background and rationale of the study, and come at the end of the introduction.

If you're not provided guidelines, consider these factors:

• Research document : In a thesis or book-length study, the research rationale will be longer than in a journal article. For example, the background and rationale of this book exploring the collective memory of World War I cover more than ten pages.
• Research question : Research into a new sub-field may call for a longer or more detailed justification than a study that plugs a gap in literature.

Which verb tenses to use in the research rationale?

It's best to use the present tense. Though in a research proposal, the research rationale is likely written in the future tense, as you're describing the intended or expected outcomes of the research project (the gaps it will fill, the problems it will solve).

Example of a research rationale

Research question : What are the teachers' perceptions of how a sense of European identity is developed and what underlies such perceptions?

Braun, V., & Clarke, V. (2006). Using thematic analysis in psychology. Qualitative Research in Psychology , 3(2), 77-101.

Burhan, A.M., Yang, J., & Inagawa, T. (2021). Impact of apathy on aging and age-related neuropsychiatric disorders. Research Topic. Frontiers in Psychiatry

Cataldo, I., Lepri, B., Neoh, M. J. Y., & Esposito, G. (2021). Social media usage and development of psychiatric disorders in childhood and adolescence: A review. Frontiers in Psychiatry , 11.

CiCe Jean Monnet Network (2017). Guidelines for citizenship education in school: Identities and European citizenship children's identity and citizenship in Europe.

Cohen, l, Manion, L., & Morrison, K. (2018). Research methods in education . Eighth edition. London: Routledge.

de Prat, R. C. (2013). Euroscepticism, Europhobia and Eurocriticism: The radical parties of the right and left “vis-à-vis” the European Union P.I.E-Peter Lang S.A., Éditions Scientifiques Internationales.

European Commission. (2017). Eurydice Brief: Citizenship education at school in Europe.

Polyakova, A., & Fligstein, N. (2016). Is European integration causing Europe to become more nationalist? Evidence from the 2007–9 financial crisis. Journal of European Public Policy , 23(1), 60-83.

Winter, J. (2014). Sites of Memory, Sites of Mourning: The Great War in European Cultural History . Cambridge: Cambridge University Press.

The AJE Team

See our "Privacy Policy"

Ensure your structure and ideas are consistent and clearly communicated

Pair your Premium Editing with our add-on service Presubmission Review for an overall assessment of your manuscript.

• Privacy Policy

Buy Me a Coffee

Home » Research Gap – Types, Examples and How to Identify

Research Gap – Types, Examples and How to Identify

Table of Contents

Research Gap

Definition:

Research gap refers to an area or topic within a field of study that has not yet been extensively researched or is yet to be explored. It is a question, problem or issue that has not been addressed or resolved by previous research.

How to Identify Research Gap

Identifying a research gap is an essential step in conducting research that adds value and contributes to the existing body of knowledge. Research gap requires critical thinking, creativity, and a thorough understanding of the existing literature . It is an iterative process that may require revisiting and refining your research questions and ideas multiple times.

Here are some steps that can help you identify a research gap:

• Review existing literature: Conduct a thorough review of the existing literature in your research area. This will help you identify what has already been studied and what gaps still exist.
• Identify a research problem: Identify a specific research problem or question that you want to address.
• Analyze existing research: Analyze the existing research related to your research problem. This will help you identify areas that have not been studied, inconsistencies in the findings, or limitations of the previous research.
• Brainstorm potential research ideas : Based on your analysis, brainstorm potential research ideas that address the identified gaps.
• Consult with experts: Consult with experts in your research area to get their opinions on potential research ideas and to identify any additional gaps that you may have missed.
• Refine research questions: Refine your research questions and hypotheses based on the identified gaps and potential research ideas.
• Develop a research proposal: Develop a research proposal that outlines your research questions, objectives, and methods to address the identified research gap.

Types of Research Gap

There are different types of research gaps that can be identified, and each type is associated with a specific situation or problem. Here are the main types of research gaps and their explanations:

Theoretical Gap

This type of research gap refers to a lack of theoretical understanding or knowledge in a particular area. It can occur when there is a discrepancy between existing theories and empirical evidence or when there is no theory that can explain a particular phenomenon. Identifying theoretical gaps can lead to the development of new theories or the refinement of existing ones.

Empirical Gap

An empirical gap occurs when there is a lack of empirical evidence or data in a particular area. It can happen when there is a lack of research on a specific topic or when existing research is inadequate or inconclusive. Identifying empirical gaps can lead to the development of new research studies to collect data or the refinement of existing research methods to improve the quality of data collected.

Methodological Gap

This type of research gap refers to a lack of appropriate research methods or techniques to answer a research question. It can occur when existing methods are inadequate, outdated, or inappropriate for the research question. Identifying methodological gaps can lead to the development of new research methods or the modification of existing ones to better address the research question.

Practical Gap

A practical gap occurs when there is a lack of practical applications or implementation of research findings. It can occur when research findings are not implemented due to financial, political, or social constraints. Identifying practical gaps can lead to the development of strategies for the effective implementation of research findings in practice.

Knowledge Gap

This type of research gap occurs when there is a lack of knowledge or information on a particular topic. It can happen when a new area of research is emerging, or when research is conducted in a different context or population. Identifying knowledge gaps can lead to the development of new research studies or the extension of existing research to fill the gap.

Examples of Research Gap

Here are some examples of research gaps that researchers might identify:

• Theoretical Gap Example : In the field of psychology, there might be a theoretical gap related to the lack of understanding of the relationship between social media use and mental health. Although there is existing research on the topic, there might be a lack of consensus on the mechanisms that link social media use to mental health outcomes.
• Empirical Gap Example : In the field of environmental science, there might be an empirical gap related to the lack of data on the long-term effects of climate change on biodiversity in specific regions. Although there might be some studies on the topic, there might be a lack of data on the long-term effects of climate change on specific species or ecosystems.
• Methodological Gap Example : In the field of education, there might be a methodological gap related to the lack of appropriate research methods to assess the impact of online learning on student outcomes. Although there might be some studies on the topic, existing research methods might not be appropriate to assess the complex relationships between online learning and student outcomes.
• Practical Gap Example: In the field of healthcare, there might be a practical gap related to the lack of effective strategies to implement evidence-based practices in clinical settings. Although there might be existing research on the effectiveness of certain practices, they might not be implemented in practice due to various barriers, such as financial constraints or lack of resources.
• Knowledge Gap Example: In the field of anthropology, there might be a knowledge gap related to the lack of understanding of the cultural practices of indigenous communities in certain regions. Although there might be some research on the topic, there might be a lack of knowledge about specific cultural practices or beliefs that are unique to those communities.

Examples of Research Gap In Literature Review, Thesis, and Research Paper might be:

• Literature review : A literature review on the topic of machine learning and healthcare might identify a research gap in the lack of studies that investigate the use of machine learning for early detection of rare diseases.
• Thesis : A thesis on the topic of cybersecurity might identify a research gap in the lack of studies that investigate the effectiveness of artificial intelligence in detecting and preventing cyber attacks.
• Research paper : A research paper on the topic of natural language processing might identify a research gap in the lack of studies that investigate the use of natural language processing techniques for sentiment analysis in non-English languages.

How to Write Research Gap

By following these steps, you can effectively write about research gaps in your paper and clearly articulate the contribution that your study will make to the existing body of knowledge.

Here are some steps to follow when writing about research gaps in your paper:

• Identify the research question : Before writing about research gaps, you need to identify your research question or problem. This will help you to understand the scope of your research and identify areas where additional research is needed.
• Review the literature: Conduct a thorough review of the literature related to your research question. This will help you to identify the current state of knowledge in the field and the gaps that exist.
• Identify the research gap: Based on your review of the literature, identify the specific research gap that your study will address. This could be a theoretical, empirical, methodological, practical, or knowledge gap.
• Provide evidence: Provide evidence to support your claim that the research gap exists. This could include a summary of the existing literature, a discussion of the limitations of previous studies, or an analysis of the current state of knowledge in the field.
• Explain the importance: Explain why it is important to fill the research gap. This could include a discussion of the potential implications of filling the gap, the significance of the research for the field, or the potential benefits to society.
• State your research objectives: State your research objectives, which should be aligned with the research gap you have identified. This will help you to clearly articulate the purpose of your study and how it will address the research gap.

Importance of Research Gap

The importance of research gaps can be summarized as follows:

• Advancing knowledge: Identifying research gaps is crucial for advancing knowledge in a particular field. By identifying areas where additional research is needed, researchers can fill gaps in the existing body of knowledge and contribute to the development of new theories and practices.
• Guiding research: Research gaps can guide researchers in designing studies that fill those gaps. By identifying research gaps, researchers can develop research questions and objectives that are aligned with the needs of the field and contribute to the development of new knowledge.
• Enhancing research quality: By identifying research gaps, researchers can avoid duplicating previous research and instead focus on developing innovative research that fills gaps in the existing body of knowledge. This can lead to more impactful research and higher-quality research outputs.
• Informing policy and practice: Research gaps can inform policy and practice by highlighting areas where additional research is needed to inform decision-making. By filling research gaps, researchers can provide evidence-based recommendations that have the potential to improve policy and practice in a particular field.

Applications of Research Gap

Here are some potential applications of research gap:

• Informing research priorities: Research gaps can help guide research funding agencies and researchers to prioritize research areas that require more attention and resources.
• Identifying practical implications: Identifying gaps in knowledge can help identify practical applications of research that are still unexplored or underdeveloped.
• Stimulating innovation: Research gaps can encourage innovation and the development of new approaches or methodologies to address unexplored areas.
• Improving policy-making: Research gaps can inform policy-making decisions by highlighting areas where more research is needed to make informed policy decisions.
• Enhancing academic discourse: Research gaps can lead to new and constructive debates and discussions within academic communities, leading to more robust and comprehensive research.

Advantages of Research Gap

Here are some of the advantages of research gap:

• Identifies new research opportunities: Identifying research gaps can help researchers identify areas that require further exploration, which can lead to new research opportunities.
• Improves the quality of research: By identifying gaps in current research, researchers can focus their efforts on addressing unanswered questions, which can improve the overall quality of research.
• Enhances the relevance of research: Research that addresses existing gaps can have significant implications for the development of theories, policies, and practices, and can therefore increase the relevance and impact of research.
• Helps avoid duplication of effort: Identifying existing research can help researchers avoid duplicating efforts, saving time and resources.
• Helps to refine research questions: Research gaps can help researchers refine their research questions, making them more focused and relevant to the needs of the field.
• Promotes collaboration: By identifying areas of research that require further investigation, researchers can collaborate with others to conduct research that addresses these gaps, which can lead to more comprehensive and impactful research outcomes.

Disadvantages of Research Gap

While research gaps can be advantageous, there are also some potential disadvantages that should be considered:

• Difficulty in identifying gaps: Identifying gaps in existing research can be challenging, particularly in fields where there is a large volume of research or where research findings are scattered across different disciplines.
• Lack of funding: Addressing research gaps may require significant resources, and researchers may struggle to secure funding for their work if it is perceived as too risky or uncertain.
• Time-consuming: Conducting research to address gaps can be time-consuming, particularly if the research involves collecting new data or developing new methods.
• Risk of oversimplification: Addressing research gaps may require researchers to simplify complex problems, which can lead to oversimplification and a failure to capture the complexity of the issues.
• Bias : Identifying research gaps can be influenced by researchers’ personal biases or perspectives, which can lead to a skewed understanding of the field.
• Potential for disagreement: Identifying research gaps can be subjective, and different researchers may have different views on what constitutes a gap in the field, leading to disagreements and debate.

About the author

Muhammad Hassan

Researcher, Academic Writer, Web developer

You may also like

Research Paper Conclusion – Writing Guide and...

Appendices – Writing Guide, Types and Examples

Research Report – Example, Writing Guide and...

Delimitations in Research – Types, Examples and...

Scope of the Research – Writing Guide and...

Research Contribution – Thesis Guide

• Affiliate Program

• UNITED STATES
• 台灣 (TAIWAN)
• TÜRKIYE (TURKEY)
• Academic Editing Services
• - Research Paper
• - Journal Manuscript
• - Dissertation
• - College & University Assignments
• Admissions Editing Services
• - Application Essay
• - Personal Statement
• - Recommendation Letter
• - Cover Letter
• - CV/Resume
• Business Editing Services
• - Business Documents
• - Report & Brochure
• - Website & Blog
• Writer Editing Services
• - Script & Screenplay
• Our Editors
• Client Reviews
• Editing & Proofreading Prices
• Wordvice Points
• Partner Discount
• Plagiarism Checker
• APA Citation Generator
• MLA Citation Generator
• Chicago Citation Generator
• Vancouver Citation Generator
• - APA Style
• - MLA Style
• - Chicago Style
• - Vancouver Style
• Writing & Editing Guide
• Academic Resources
• Admissions Resources

How to Write the Rationale of the Study in Research (Examples)

What is the Rationale of the Study?

The rationale of the study is the justification for taking on a given study. It explains the reason the study was conducted or should be conducted. This means the study rationale should explain to the reader or examiner why the study is/was necessary. It is also sometimes called the “purpose” or “justification” of a study. While this is not difficult to grasp in itself, you might wonder how the rationale of the study is different from your research question or from the statement of the problem of your study, and how it fits into the rest of your thesis or research paper. 

The rationale of the study links the background of the study to your specific research question and justifies the need for the latter on the basis of the former. In brief, you first provide and discuss existing data on the topic, and then you tell the reader, based on the background evidence you just presented, where you identified gaps or issues and why you think it is important to address those. The problem statement, lastly, is the formulation of the specific research question you choose to investigate, following logically from your rationale, and the approach you are planning to use to do that.

Table of Contents:

How to write a rationale for a research paper , how do you justify the need for a research study.

• Study Rationale Example: Where Does It Go In Your Paper?

The basis for writing a research rationale is preliminary data or a clear description of an observation. If you are doing basic/theoretical research, then a literature review will help you identify gaps in current knowledge. In applied/practical research, you base your rationale on an existing issue with a certain process (e.g., vaccine proof registration) or practice (e.g., patient treatment) that is well documented and needs to be addressed. By presenting the reader with earlier evidence or observations, you can (and have to) convince them that you are not just repeating what other people have already done or said and that your ideas are not coming out of thin air. 

Once you have explained where you are coming from, you should justify the need for doing additional research–this is essentially the rationale of your study. Finally, when you have convinced the reader of the purpose of your work, you can end your introduction section with the statement of the problem of your research that contains clear aims and objectives and also briefly describes (and justifies) your methodological approach. 

When is the Rationale for Research Written?

The author can present the study rationale both before and after the research is conducted. 

• Before conducting research : The study rationale is a central component of the research proposal . It represents the plan of your work, constructed before the study is actually executed.
• Once research has been conducted : After the study is completed, the rationale is presented in a research article or  PhD dissertation  to explain why you focused on this specific research question. When writing the study rationale for this purpose, the author should link the rationale of the research to the aims and outcomes of the study.

What to Include in the Study Rationale

Although every study rationale is different and discusses different specific elements of a study’s method or approach, there are some elements that should be included to write a good rationale. Make sure to touch on the following:

• A summary of conclusions from your review of the relevant literature
• What is currently unknown (gaps in knowledge)
• Inconclusive or contested results  from previous studies on the same or similar topic
• The necessity to improve or build on previous research, such as to improve methodology or utilize newer techniques and/or technologies

There are different types of limitations that you can use to justify the need for your study. In applied/practical research, the justification for investigating something is always that an existing process/practice has a problem or is not satisfactory. Let’s say, for example, that people in a certain country/city/community commonly complain about hospital care on weekends (not enough staff, not enough attention, no decisions being made), but you looked into it and realized that nobody ever investigated whether these perceived problems are actually based on objective shortages/non-availabilities of care or whether the lower numbers of patients who are treated during weekends are commensurate with the provided services.

In this case, “lack of data” is your justification for digging deeper into the problem. Or, if it is obvious that there is a shortage of staff and provided services on weekends, you could decide to investigate which of the usual procedures are skipped during weekends as a result and what the negative consequences are. 

In basic/theoretical research, lack of knowledge is of course a common and accepted justification for additional research—but make sure that it is not your only motivation. “Nobody has ever done this” is only a convincing reason for a study if you explain to the reader why you think we should know more about this specific phenomenon. If there is earlier research but you think it has limitations, then those can usually be classified into “methodological”, “contextual”, and “conceptual” limitations. To identify such limitations, you can ask specific questions and let those questions guide you when you explain to the reader why your study was necessary:

Methodological limitations

• Did earlier studies try but failed to measure/identify a specific phenomenon?
• Was earlier research based on incorrect conceptualizations of variables?
• Were earlier studies based on questionable operationalizations of key concepts?
• Did earlier studies use questionable or inappropriate research designs?

Contextual limitations

• Have recent changes in the studied problem made previous studies irrelevant?
• Are you studying a new/particular context that previous findings do not apply to?

Conceptual limitations

• Do previous findings only make sense within a specific framework or ideology?

Study Rationale Examples

Let’s look at an example from one of our earlier articles on the statement of the problem to clarify how your rationale fits into your introduction section. This is a very short introduction for a practical research study on the challenges of online learning. Your introduction might be much longer (especially the context/background section), and this example does not contain any sources (which you will have to provide for all claims you make and all earlier studies you cite)—but please pay attention to how the background presentation , rationale, and problem statement blend into each other in a logical way so that the reader can follow and has no reason to question your motivation or the foundation of your research.

Background presentation

Since the beginning of the Covid pandemic, most educational institutions around the world have transitioned to a fully online study model, at least during peak times of infections and social distancing measures. This transition has not been easy and even two years into the pandemic, problems with online teaching and studying persist (reference needed) . 

While the increasing gap between those with access to technology and equipment and those without access has been determined to be one of the main challenges (reference needed) , others claim that online learning offers more opportunities for many students by breaking down barriers of location and distance (reference needed) .  

Rationale of the study

Since teachers and students cannot wait for circumstances to go back to normal, the measures that schools and universities have implemented during the last two years, their advantages and disadvantages, and the impact of those measures on students’ progress, satisfaction, and well-being need to be understood so that improvements can be made and demographics that have been left behind can receive the support they need as soon as possible.

Statement of the problem

To identify what changes in the learning environment were considered the most challenging and how those changes relate to a variety of student outcome measures, we conducted surveys and interviews among teachers and students at ten institutions of higher education in four different major cities, two in the US (New York and Chicago), one in South Korea (Seoul), and one in the UK (London). Responses were analyzed with a focus on different student demographics and how they might have been affected differently by the current situation.

How long is a study rationale?

In a research article bound for journal publication, your rationale should not be longer than a few sentences (no longer than one brief paragraph). A  dissertation or thesis  usually allows for a longer description; depending on the length and nature of your document, this could be up to a couple of paragraphs in length. A completely novel or unconventional approach might warrant a longer and more detailed justification than an approach that slightly deviates from well-established methods and approaches.

Consider Using Professional Academic Editing Services

Now that you know how to write the rationale of the study for a research proposal or paper, you should make use of our free AI grammar checker , Wordvice AI, or receive professional academic proofreading services from Wordvice, including research paper editing services and manuscript editing services to polish your submitted research documents.

You can also find many more articles, for example on writing the other parts of your research paper , on choosing a title , or on making sure you understand and adhere to the author instructions before you submit to a journal, on the Wordvice academic resources pages.

How To Find A Research Gap, Quickly

A step-by-step guide for new researchers

By: Derek Jansen (MBA) | Reviewer: Eunice Rautenbach (DTech) | April 2023

If you’ve got a dissertation, thesis or research project coming up, one of the first (and most important) things you’ll need to do is find a suitable research gap . In this post, we’ll share a straightforward process to help you uncover high-quality, original research gaps in a very time-efficient manner.

Overview: Finding Research Gaps

• What exactly is a research gap?
• Research gap vs research topic
• How to find potential research gaps
• How to evaluate research gaps (and topics)
• Key takeaways

What is a research gap?

As a starting point, it’s useful to first define what we mean by research gap, to ensure we’re all on the same page. The term “research gap” gets thrown around quite loosely by students and academics alike, so let’s clear that up.

Simply put, a research gap is any space where there’s a lack of solid, agreed-upon research regarding a specific topic, issue or phenomenon. In other words, there’s a lack of established knowledge and, consequently, a need for further research.

Let’s look at a hypothetical example to illustrate a research gap.

Within the existing research regarding factors affect job satisfaction , there may be a wealth of established and agreed-upon empirical work within a US and UK context , but very little research within Eastern nations such as Japan or Korea . Given that these nations have distinctly different national cultures and workforce compositions compared to the West, it’s plausible that the factors that contribute toward job satisfaction may also be different. Therefore, a research gap emerges for studies that explore this matter.

This example is purely hypothetical (and there’s probably plenty of research covering this already), but it illustrates the core point that a research gap reflects a lack of firmly established knowledge regarding a specific matter . Given this lack, an opportunity exists for researchers (like you) to go on and fill the gap.

So, it’s the same as a research topic?

Not quite – but they are connected. A research gap refers to an area where there’s a lack of settled research , whereas a research topic outlines the focus of a specific study . Despite being different things, these two are related because research gaps are the birthplace of research topics. In other words, by identifying a clear research gap, you have a foundation from which you can build a research topic for your specific study. Your study is unlikely to resolve the entire research gap on it’s own, but it will contribute towards it .

If you’d like to learn more, we’ve got a comprehensive post that covers research gaps (including the different types of research gaps), as well as an explainer video below.

How to find a research gap

Now that we’ve defined what a research gap is, it’s time to get down to the process of finding potential research gaps that you can use as a basis for potential research topics. Importantly, it’s worth noting that this is just one way (of many) to find a research gap (and consequently a topic). We’re not proposing that it’s the only way or best way, but it’s certainly a relatively quick way to identify opportunities.

Step 1: Identify your broad area of interest

The very first step to finding a research gap is to decide on your general area of interest . For example, if you were undertaking a dissertation as part of an MBA degree, you may decide that you’re interested in corporate reputation, HR strategy, or leadership styles. As you can see, these are broad categories – there’s no need to get super specific just yet. Of course, if there is something very specific that you’re interested in, that’s great – but don’t feel pressured to narrow it down too much right now.

Equally important is to make sure that this area of interest is allowed by your university or whichever institution you’ll be proposing your research to. This might sound dead obvious, but you’ll be surprised how many times we’ve seen students run down a path with great excitement, only to later learn that their university wants a very specific area of focus in terms of topic (and their area of interest doesn’t qualify).

Step 2: Do an initial literature scan

Once you’ve pinned down your broad area (or areas) of interest, the next step is to head over to Google Scholar to undertake an initial literature scan . If you’re not familiar with this tool, Google Scholar is a great starting point for finding academic literature on pretty much any topic, as it uses Google’s powerful search capabilities to hunt down relevant academic literature. It’s certainly not the be-all and end-all of literature search tools, but it’s a useful starting point .

Within Google Scholar, you’ll want to do a few searches using keywords that are relevant to your area of interest. Sticking with our earlier example, we could use the key phrase “job satisfaction”, or we may want to get a little more specific – perhaps “job satisfaction for millennials” or “job satisfaction in Japan”.

It’s always a good idea to play around with as many keywords/phrases as you can think up.  Take an iterative approach here and see which keywords yield the most relevant results for you. Keep each search open in a new tab, as this will help keep things organised for the next steps.

Once you’ve searched for a few different keywords/phrases, you’ll need to do some refining for each of the searches you undertook. Specifically, you’ll need to filter the results down to the most recent papers . You can do this by selecting the time period in the top left corner (see the example below).

Filtering to the current year is typically a good choice (especially for fast-moving research areas), but in some cases, you may need to filter to the last two years . If you’re undertaking this task in January or February, for example, you’ll likely need to select a two-year period.

Need a helping hand?

Step 3: Review and shortlist articles that interest you

Once you’ve run a few searches using different keywords and phrases, you’ll need to scan through the results to see what looks most relevant and interesting to you. At this stage, you can just look at the titles and abstracts (the description provided by Google Scholar) – don’t worry about reading the actual article just yet.

Next, select 5 – 10 articles that interest you and open them up. Here, we’re making the assumption that your university has provided you with access to a decent range of academic databases. In some cases, Google Scholar will link you directly to a PDF of the article, but in most cases, you’ll need paid access. If you don’t have this (for example, if you’re still applying to a university), you can look at two options:

Open-access articles – these are free articles which you can access without any journal subscription. A quick Google search (the regular Google) will help you find open-access journals in your area of interest, but you can also have a look at DOAJ and Elsevier Open Access.

DeepDyve – this is a monthly subscription service that allows you to get access to a broad range of journals. At the time of shooting this video, their monthly subscription is around $50 and they do offer a free trial, which may be sufficient for your project.

Step 4: Skim-read your article shortlist

Now, it’s time to dig into your article shortlist and do some reading. But don’t worry, you don’t need to read the articles from start to finish – you just need to focus on a few key sections.

Specifically, you’ll need to pay attention to the following:

• The abstract (which you’ve probably already read a portion of in Google Scholar)
• The introduction – this will give you a bit more detail about the context and background of the study, as well as what the researchers were trying to achieve (their research aims)
• The discussion or conclusion – this will tell you what the researchers found

By skimming through these three sections for each journal article on your shortlist, you’ll gain a reasonable idea of what each study was about, without having to dig into the painful details. Generally, these sections are usually quite short, so it shouldn’t take you too long.

Step 5: Go “FRIN hunting”

This is where the magic happens. Within each of the articles on your shortlist, you’ll want to search for a few very specific phrases , namely:

• Future research
• Further research
• Research opportunities
• Research directions

All of these terms are commonly found in what we call the “FRIN” section . FRIN stands for “further research is needed”. The FRIN is where the researchers explain what other researchers could do to build on their study, or just on the research area in general. In other words, the FRIN section is where you can find fresh opportunities for novel research . Most empirical studies will either have a dedicated FRIN section or paragraph, or they’ll allude to the FRIN toward the very end of the article. You’ll need to do a little scanning, but it’s usually pretty easy to spot.

It’s worth mentioning that naturally, the FRIN doesn’t hand you a list of research gaps on a platter. It’s not a silver bullet for finding research gaps – but it’s the closest thing to it. Realistically, the FRIN section helps you shortcut the gap-hunting process  by highlighting novel research avenues that are worth exploring.

This probably sounds a little conceptual, so let’s have a look at a few examples:

The impact of overeducation on job outcomes: Evidence from Saudi Arabia (Alzubaidi, 2020)

If you scroll down to the bottom of this article, you’ll see there’s a dedicated section called “Limitations and directions for future research”. Here they talk about the limitations of the study and provide suggestions about how future researchers could improve upon their work and overcome the limitations.

Perceived organizational support and job satisfaction: a moderated mediation model of proactive personality and psychological empowerment (Maan et al, 2020)

In this article, within the limitations section, they provide a wonderfully systematic structure where they discuss each limitation, followed by a proposal as to how future studies can overcome the respective limitation. In doing so, they are providing very specific research opportunities for other researchers.

Medical professionals’ job satisfaction and telemedicine readiness during the COVID-19 pandemic: solutions to improve medical practice in Egypt (El-Mazahy et al, 2023)

In this article, they don’t have a dedicated section discussing the FRIN, but we can deduct it based on the limitations section. For example, they state that an evaluation of the knowledge about telemedicine and technology-related skills would have enabled studying their independent effect on the perception of telemedicine.

Follow this FRIN-seeking process for the articles you shortlisted and map out any potentially interesting research gaps . You may find that you need to look at a larger number of articles to find something interesting, or you might find that your area of interest shifts as you engage in the reading – this is perfectly natural. Take as much time as you need to develop a shortlist of potential research gaps that interest you.

Importantly, once you’ve developed a shortlist of potential research gaps, you need to return to Google Scholar to double-check that there aren’t fresh studies that have already addressed the gap. Remember, if you’re looking at papers from two years ago in a fast-moving field, someone else may have jumped on it . Nevertheless, there could still very well be a unique angle you could take – perhaps a contextual gap (e.g. a specific country, industry, etc.).

Ultimately, the need for originality will depend on your specific university’s requirements and the level of study. For example, if you’re doing an undergraduate research project, the originality requirements likely won’t be as gruelling as say a Masters or PhD project. So, make sure you have a clear understanding of what your university’s expectations are. A good way to do this is to look at past dissertations and theses for your specific programme. You can usually find these in the university library or by asking the faculty.

How to evaluate potential research gaps

Once you’ve developed a shortlist of potential research gaps (and resultant potential research topics) that interest you, you’ll need to systematically evaluate  them  to choose a winner. There are many factors to consider here, but some important ones include the following:

• Originality and value – is the topic sufficiently novel and will addressing it create value?
• Data access – will you be able to get access to the sample of interest?
• Costs – will there be additional costs involved for data collection and/or analysis?
• Timeframes – will you be able to collect and analyse the data within the timeframe required by your university?
• Supervisor support – is there a suitable supervisor available to support your project from start to finish?

To help you evaluate your options systematically, we’ve got a topic evaluation worksheet that allows you to score each potential topic against a comprehensive set of criteria. You can access the worksheet completely free of charge here .

Recap: Key Takeaways

We’ve covered quite a lot of ground in this post. Here are the key takeaways:

• A research gap is any space where there’s a lack of solid, agreed-upon research regarding a specific topic/issue/phenomenon.
• Unique research topics emerge from research gaps , so it’s essential to first identify high-quality research gaps before you attempt to define a topic.
• To find potential research gaps, start by seeking out recent journal articles on Google Scholar and pay particular attention to the FRIN section to identify novel opportunities.
• Once you have a shortlist of prospective research gaps and resultant topic ideas, evaluate them systematically using a comprehensive set of criteria.

If you’d like to get hands-on help finding a research gap and research topic, be sure to check out our private coaching service , where we hold your hand through the research journey, step by step.

Psst… there’s more (for free)

This post is part of our dissertation mini-course, which covers everything you need to get started with your dissertation, thesis or research project. 

You Might Also Like:

Very useful for me, but i am still confusing review of literature review, how to find out topic related previous research.

Powerful notes! Thanks a lot.

This is helpful. Thanks a lot.

Thank you very much for this. It is really a great opportunity for me to learn the research journey.

Very Useful

It nice job

Submit a Comment Cancel reply

Your email address will not be published. Required fields are marked *

Save my name, email, and website in this browser for the next time I comment.

• Print Friendly

Community Blog

Keep up-to-date on postgraduate related issues with our quick reads written by students, postdocs, professors and industry leaders.

How do you Write the Rationale for Research?

• By DiscoverPhDs
• October 21, 2020

What is the Rationale of Research?

The term rationale of research means the reason for performing the research study in question. In writing your rational you should able to convey why there was a need for your study to be carried out. It’s an important part of your research paper that should explain how your research was novel and explain why it was significant; this helps the reader understand why your research question needed to be addressed in your research paper, term paper or other research report.

The rationale for research is also sometimes referred to as the justification for the study. When writing your rational, first begin by introducing and explaining what other researchers have published on within your research field.

Having explained the work of previous literature and prior research, include discussion about where the gaps in knowledge are in your field. Use these to define potential research questions that need answering and explain the importance of addressing these unanswered questions.

The rationale conveys to the reader of your publication exactly why your research topic was needed and why it was significant . Having defined your research rationale, you would then go on to define your hypothesis and your research objectives.

Final Comments

Defining the rationale research, is a key part of the research process and academic writing in any research project. You use this in your research paper to firstly explain the research problem within your dissertation topic. This gives you the research justification you need to define your research question and what the expected outcomes may be.

The purpose of research is to enhance society by advancing knowledge through developing scientific theories, concepts and ideas – find out more on what this involves.

Considering whether to do an MBA or a PhD? If so, find out what their differences are, and more importantly, which one is better suited for you.

The term rationale of research means the reason for performing the research study in question.

Join thousands of other students and stay up to date with the latest PhD programmes, funding opportunities and advice.

Browse PhDs Now

Learning how to effectively collaborate with others is an important skill for anyone in academia to develop.

This post gives you the best questions to ask at a PhD interview, to help you work out if your potential supervisor and lab is a good fit for you.

Akshay is in the final year of his PhD researching how well models can predict Indian monsoon low-pressure systems. The results of his research will help improve disaster preparedness and long-term planning.

Prof Raghupathi gained his PhD in Biochemistry and Molecular Biology from Virginia Commonwealth University in 1991. He is now a professor in the Department of Neurobiology & Anatomy at Drexel University College of Medicine.

Join Thousands of Students

We use cookies on this site to enhance your experience

By clicking any link on this page you are giving your consent for us to set cookies.

A link to reset your password has been sent to your email.

Back to login

We need additional information from you. Please complete your profile first before placing your order.

Thank you. payment completed., you will receive an email from us to confirm your registration, please click the link in the email to activate your account., there was error during payment, orcid profile found in public registry, download history, how to write the rationale for your research.

• Charlesworth Author Services
• 19 November, 2021

The rationale for one’s research is the justification for undertaking a given study. It states the reason(s) why a researcher chooses to focus on the topic in question, including what the significance is and what gaps the research intends to fill. In short, it is an explanation that rationalises the need for the study. The rationale is typically followed by a hypothesis/ research question (s) and the study objectives.

When is the rationale for research written?

The rationale of a study can be presented both before and after the research is conducted. 

• Before : The rationale is a crucial part of your research proposal , representing the plan of your work as formulated before you execute your study.
• After : Once the study is completed, the rationale is presented in a research paper or dissertation to explain why you focused on the particular question. In this instance, you would link the rationale of your research project to the study aims and outcomes.

Basis for writing the research rationale

The study rationale is predominantly based on preliminary data . A literature review will help you identify gaps in the current knowledge base and also ensure that you avoid duplicating what has already been done. You can then formulate the justification for your study from the existing literature on the subject and the perceived outcomes of the proposed study.

Length of the research rationale

In a research proposal or research article, the rationale would not take up more than a few sentences . A thesis or dissertation would allow for a longer description, which could even run into a couple of paragraphs . The length might even depend on the field of study or nature of the experiment. For instance, a completely novel or unconventional approach might warrant a longer and more detailed justification.

Basic elements of the research rationale

Every research rationale should include some mention or discussion of the following: 

• An overview of your conclusions from your literature review
• Gaps in current knowledge
• Inconclusive or controversial findings from previous studies
• The need to build on previous research (e.g. unanswered questions, the need to update concepts in light of new findings and/or new technical advancements). 

Example of a research rationale

Note: This uses a fictional study.

Abc xyz is a newly identified microalgal species isolated from fish tanks. While Abc xyz algal blooms have been seen as a threat to pisciculture, some studies have hinted at their unusually high carotenoid content and unique carotenoid profile. Carotenoid profiling has been carried out only in a handful of microalgal species from this genus, and the search for microalgae rich in bioactive carotenoids has not yielded promising candidates so far. This in-depth examination of the carotenoid profile of Abc xyz will help identify and quantify novel and potentially useful carotenoids from an untapped aquaculture resource .

In conclusion

It is important to describe the rationale of your research in order to put the significance and novelty of your specific research project into perspective. Once you have successfully articulated the reason(s) for your research, you will have convinced readers of the importance of your work!

Maximise your publication success with Charlesworth Author Services.

Charlesworth Author Services , a trusted brand supporting the world’s leading academic publishers, institutions and authors since 1928. 

To know more about our services, visit: Our Services

Share with your colleagues

Related articles.

How to identify Gaps in research and determine your original research topic

Charlesworth Author Services 14/09/2021 00:00:00

Tips for designing your Research Question

Charlesworth Author Services 01/08/2017 00:00:00

Why and How to do a literature search

Charlesworth Author Services 17/08/2020 00:00:00

Related webinars

Bitesize Webinar: How to write and structure your academic article for publication - Module 1: Know when are you ready to write

Charlesworth Author Services 04/03/2021 00:00:00

Bitesize Webinar: How to write and structure your academic article for publication- Module 3: Understand the structure of an academic paper

Bitesize Webinar: How to write and structure your academic article for publication: Module 4: Prepare to write your academic paper

Bitesize Webinar: How to write and structure your academic article for publication: Module 5: Conduct a Literature Review

Article sections.

How to write an Introduction to an academic article

Writing a strong Methods section

Charlesworth Author Services 12/03/2021 00:00:00

Strategies for writing the Results section in a scientific paper

Charlesworth Author Services 27/10/2021 00:00:00

How to Write a Rationale: A Guide for Research and Beyond

Ever found yourself scratching your head, wondering how to justify your choice of a research topic or project? You’re not alone! Writing a rationale, which essentially means explaining the ‘why’ behind your decisions, is crucial to any research process. It’s like the secret sauce that adds flavour to your research recipe. So, the only thing you need to know is how to write a rationale.

What is a Rationale?

A rationale in research is essentially the foundation of your study. It serves as the justification for undertaking a particular research project. At its core, the rationale explains why the research was conducted or needs to be conducted, thus addressing a specific knowledge gap or research question.

Here’s a breakdown of the key elements involved in crafting a rationale:

Linking Background to Research Question: 

The rationale should connect the background of the study to your specific research question. It involves presenting and discussing existing data on your topic, identifying gaps or issues in the current understanding, and explaining why addressing them is important​.

Objectives and Significance: 

Your rationale should clearly outline your research objectives – what you hope to discover or achieve through the study. It should also emphasize the subject’s significance in your field and explain why more or better research is needed​.

Methodological Approach: 

The rationale should briefly describe your proposed research method , whether qualitative (descriptive) or quantitative (experimental), and justify this choice​.

Justifying the Need for Research: 

The rationale isn’t just about what you’re doing and why it’s necessary. It can involve highlighting methodological, contextual, or conceptual limitations in previous studies and explaining how your research aims to overcome these limitations. Essentially, you’re making a case for why your research fills a crucial gap in existing knowledge​​.

Presenting Before and After Research: 

Interestingly, the rationale can be presented before and after the research. Before the research, it forms a central part of the research proposal, setting out the plan for the work. After the research, it’s presented in a research article or dissertation to explain the focus on a specific research question and link it to the study’s aims and outcomes​.

Elements to Include: 

A good rationale should include a summary of conclusions from your literature review, identify what is currently unknown, discuss inconclusive or contested results from previous studies, and emphasize the necessity to improve or build on previous research​.

Creating a rationale is a vital part of the research process, as it not only sets the stage for your study but also convinces readers of the value and necessity of your work.

How to Write a Rationale:

Writing a rationale for your research is crucial in conducting and presenting your study. It involves explaining why your research is necessary and important. Here’s a guide to help you craft a compelling rationale:

Identify the Problem or Knowledge Gap: 

Begin by clearly stating the issue or gap in knowledge that your research aims to address. Explain why this problem is important and merits investigation. It is the foundation of your rationale and sets the stage for the need for your research.​

Review the Literature: 

Conduct a thorough review of existing literature on your topic. It helps you understand what research has already been done and what gaps or open questions exist. Your rationale should build on this background by highlighting these gaps and emphasizing the importance of addressing them​​​​.

Define Your Research Questions/Hypotheses: 

Based on your understanding of the problem and literature review, clearly state the research questions or hypotheses that your study aims to explore. These should logically stem from the identified gaps or issues.

Explain Your Research Approach: 

Describe the methods you will use for your research, including data collection and analysis techniques. Justify why these methods are appropriate for addressing your research questions or hypotheses​​.

Discuss the Potential Impact of Your Research:  Explain the significance of your study. Consider both theoretical contributions and practical implications. For instance, how does your research advance existing knowledge? Does it have real-world applications? Is it relevant to a specific field or community?​

Consider Ethical Considerations: 

If your research involves human or animal subjects, discuss the ethical aspects and how you plan to conduct your study responsibly​.

Contextualise Your Study: 

Justify the relevance of your research by explaining how it fits into the broader context. Connect your study to current trends, societal needs, or academic discussions​​.

Support with Evidence: 

Provide evidence or examples that underscore the need for your research. It could include citing relevant studies, statistics, or scenarios that illustrate the problem or gap your research addresses​.

Methodological, Contextual, and Conceptual Limitations: 

Address any limitations of previous research and how your study aims to overcome them. It can include methodological flaws in previous studies, changes in external factors that make past research less relevant, or the need to study a phenomenon within a new conceptual framework​.

Placement in Your Paper: 

Typically, the rationale is written toward the end of the introduction section of your paper, providing a logical lead-in to your research questions and methodology​​.

By following these steps and considering your audience’s perspective, you can write a strong and compelling rationale that clearly communicates the significance and necessity of your research project.

Frequently Asked Questions:

What makes a good research rationale.

A good rationale clearly identifies a gap in existing knowledge, builds on previous research, and outlines why your study is necessary and significant.

How detailed should my literature review be in the rationale?

Your literature review should be comprehensive enough to highlight the gaps your research aims to fill, but it should not overshadow the rationale itself.

Conclusion: 

A well-crafted rationale is your ticket to making your research stand out. It’s about bridging gaps, challenging norms, and paving the way for new discoveries. So go ahead, make your rationale the cornerstone of your research narrative!

Award-Winning Results

Team of 11+ experts, 10,000+ page #1 rankings on google, dedicated to smbs, $175,000,000 in reported client revenue.

Up until working with Casey, we had only had poor to mediocre experiences outsourcing work to agencies. Casey & the team at CJ&CO are the exception to the rule.

Communication was beyond great, his understanding of our vision was phenomenal, and instead of needing babysitting like the other agencies we worked with, he was not only completely dependable but also gave us sound suggestions on how to get better results, at the risk of us not needing him for the initial job we requested (absolute gem).

This has truly been the first time we worked with someone outside of our business that quickly grasped our vision, and that I could completely forget about and would still deliver above expectations.

I honestly can't wait to work in many more projects together!

Related Articles

View All Post

Conversion Rate Optimization , Copywriting , Customer Experience

How to Tap Into What Your Customers Love & Hate

Casey Jones

Advertising , Copywriting

What does a Copywriter do at an Ad Agency: Things You Should Know if You’re a Copywriter

Copywriting

How to Write a Marketing Script: Take Your Marketing to the Next Level in 2023

*The information this blog provides is for general informational purposes only and is not intended as financial or professional advice. The information may not reflect current developments and may be changed or updated without notice. Any opinions expressed on this blog are the author’s own and do not necessarily reflect the views of the author’s employer or any other organization. You should not act or rely on any information contained in this blog without first seeking the advice of a professional. No representation or warranty, express or implied, is made as to the accuracy or completeness of the information contained in this blog. The author and affiliated parties assume no liability for any errors or omissions.

Identifying Research Gaps to Pursue Innovative Research

This article is an excerpt from a lecture given by my Ph.D. guide, a researcher in public health. She advised us on how to identify research gaps to pursue innovative research in our fields.

What is a Research Gap?

Today we are talking about the research gap: what is it, how to identify it, and how to make use of it so that you can pursue innovative research. Now, how many of you have ever felt you had discovered a new and exciting research question , only to find that it had already been written about? I have experienced this more times than I can count. Graduate studies come with pressure to add new knowledge to the field. We can contribute to the progress and knowledge of humanity. To do this, we need to first learn to identify research gaps in the existing literature.

A research gap is, simply, a topic or area for which missing or insufficient information limits the ability to reach a conclusion for a question. It should not be confused with a research question, however. For example, if we ask the research question of what the healthiest diet for humans is, we would find many studies and possible answers to this question. On the other hand, if we were to ask the research question of what are the effects of antidepressants on pregnant women, we would not find much-existing data. This is a research gap. When we identify a research gap, we identify a direction for potentially new and exciting research.

How to Identify Research Gap?

Considering the volume of existing research, identifying research gaps can seem overwhelming or even impossible. I don’t have time to read every paper published on public health. Similarly, you guys don’t have time to read every paper. So how can you identify a research gap?

There are different techniques in various disciplines, but we can reduce most of them down to a few steps, which are:

• Identify your key motivating issue/question
• Identify key terms associated with this issue
• Review the literature, searching for these key terms and identifying relevant publications
• Review the literature cited by the key publications which you located in the above step
• Identify issues not addressed by  the literature relating to your critical  motivating issue

It is the last step which we all find the most challenging. It can be difficult to figure out what an article is  not  saying. I like to keep a list of notes of biased or inconsistent information. You could also track what authors write as “directions for future research,” which often can point us towards the existing gaps.

Different Types of Research Gaps

Identifying research gaps is an essential step in conducting research, as it helps researchers to refine their research questions and to focus their research efforts on areas where there is a need for more knowledge or understanding.

1. Knowledge gaps

These are gaps in knowledge or understanding of a subject, where more research is needed to fill the gaps. For example, there may be a lack of understanding of the mechanisms behind a particular disease or how a specific technology works.

2. Conceptual gaps

These are gaps in the conceptual framework or theoretical understanding of a subject. For example, there may be a need for more research to understand the relationship between two concepts or to refine a theoretical framework.

3. Methodological gaps

These are gaps in the methods used to study a particular subject. For example, there may be a need for more research to develop new research methods or to refine existing methods to address specific research questions.

4. Data gaps

These are gaps in the data available on a particular subject. For example, there may be a need for more research to collect data on a specific population or to develop new measures to collect data on a particular construct.

5. Practical gaps

These are gaps in the application of research findings to practical situations. For example, there may be a need for more research to understand how to implement evidence-based practices in real-world settings or to identify barriers to implementing such practices.

Examples of Research Gap

Limited understanding of the underlying mechanisms of a disease:.

Despite significant research on a particular disease, there may be a lack of understanding of the underlying mechanisms of the disease. For example, although much research has been done on Alzheimer’s disease, the exact mechanisms that lead to the disease are not yet fully understood.

Inconsistencies in the findings of previous research:

When previous research on a particular topic has inconsistent findings, there may be a need for further research to clarify or resolve these inconsistencies. For example, previous research on the effectiveness of a particular treatment for a medical condition may have produced inconsistent findings, indicating a need for further research to determine the true effectiveness of the treatment.

Limited research on emerging technologies:

As new technologies emerge, there may be limited research on their applications, benefits, and potential drawbacks. For example, with the increasing use of artificial intelligence in various industries, there is a need for further research on the ethical, legal, and social implications of AI.

How to Deal with Literature Gap?

Once you have identified the literature gaps, it is critical to prioritize. You may find many questions which remain to be answered in the literature. Often one question must be answered before the next can be addressed. In prioritizing the gaps, you have identified, you should consider your funding agency or stakeholders, the needs of the field, and the relevance of your questions to what is currently being studied. Also, consider your own resources and ability to conduct the research you’re considering. Once you have done this, you can narrow your search down to an appropriate question.

Tools to Help Your Search

There are thousands of new articles published every day, and staying up to date on the literature can be overwhelming. You should take advantage of the technology that is available. Some services include  PubCrawler ,  Feedly ,  Google Scholar , and PubMed updates. Stay up to date on social media forums where scholars share new discoveries, such as Twitter. Reference managers such as  Mendeley  can help you keep your references well-organized. I personally have had success using Google Scholar and PubMed to stay current on new developments and track which gaps remain in my personal areas of interest.

The most important thing I want to impress upon you today is that you will struggle to  choose a research topic  that is innovative and exciting if you don’t know the existing literature well. This is why identifying research gaps starts with an extensive and thorough  literature review . But give yourself some boundaries.  You don’t need to read every paper that has ever been written on a topic. You may find yourself thinking you’re on the right track and then suddenly coming across a paper that you had intended to write! It happens to everyone- it happens to me quite often. Don’t give up- keep reading and you’ll find what you’re looking for.

Class dismissed!

How do you identify research gaps? Share your thoughts in the comments section below.

Frequently Asked Questions

A research gap can be identified by looking for a topic or area with missing or insufficient information that limits the ability to reach a conclusion for a question.

Identifying a research gap is important as it provides a direction for potentially new research or helps bridge the gap in existing literature.

Gap in research is a topic or area with missing or insufficient information. A research gap limits the ability to reach a conclusion for a question.

Thank u for your suggestion.

Very useful tips specially for a beginner

Thank you. This is helpful. I find that I’m overwhelmed with literatures. As I read on a particular topic, and in a particular direction I find that other conflicting issues, topic a and ideas keep popping up, making me more confused.

I am very grateful for your advice. It’s just on point.

The clearest, exhaustive, and brief explanation I have ever read.

Thanks for sharing

Thank you very much.The work is brief and understandable

Thank you it is very informative

Thanks for sharing this educative article

Thank you for such informative explanation.

Great job smart guy! Really outdid yourself!

Nice one! I thank you for this as it is just what I was looking for!😃🤟

Thank you so much for this. Much appreciated

Thank you so much.

Rate this article Cancel Reply

Your email address will not be published.

Enago Academy's Most Popular Articles

• Reporting Research

Choosing the Right Analytical Approach: Thematic analysis vs. content analysis for data interpretation

In research, choosing the right approach to understand data is crucial for deriving meaningful insights.…

Comparing Cross Sectional and Longitudinal Studies: 5 steps for choosing the right approach

The process of choosing the right research design can put ourselves at the crossroads of…

• Career Corner

Unlocking the Power of Networking in Academic Conferences

Embarking on your first academic conference experience? Fear not, we got you covered! Academic conferences…

Research Recommendations – Guiding policy-makers for evidence-based decision making

Research recommendations play a crucial role in guiding scholars and researchers toward fruitful avenues of…

• AI in Academia

Disclosing the Use of Generative AI: Best practices for authors in manuscript preparation

The rapid proliferation of generative and other AI-based tools in research writing has ignited an…

Intersectionality in Academia: Dealing with diverse perspectives

Meritocracy and Diversity in Science: Increasing inclusivity in STEM education

Avoiding the AI Trap: Pitfalls of relying on ChatGPT for PhD applications

Sign-up to read more

Subscribe for free to get unrestricted access to all our resources on research writing and academic publishing including:

• 2000+ blog articles
• 50+ Webinars
• 10+ Expert podcasts
• 50+ Infographics
• 10+ Checklists
• Research Guides

We hate spam too. We promise to protect your privacy and never spam you.

I am looking for Editing/ Proofreading services for my manuscript Tentative date of next journal submission:

When should AI tools be used in university labs?

•   [email protected]
• Shapiro Library
• SNHU Library Frequently Asked Questions

FAQ: What is a research gap and how do I find one?

• 7 Academic Integrity & Plagiarism
• 63 Academic Support, Writing Help, & Presentation Help
• 29 Access/Remote Access
• 7 Accessibility
• 9 Building/Facilities
• 8 Career/Job Information
• 26 Catalog/Print Books
• 28 Circulation
• 128 Citing Sources
• 14 Copyright
• 310 Databases
• 24 Directions/Location
• 18 Faculty Resources/Needs
• 7 Hours/Contacts
• 1 Innovation Lab & Makerspace/3D Printing
• 25 Interlibrary Loan
• 43 IT/Computer/Printing Support
• 3 Library Instruction
• 40 Library Technology Help
• 8 Multimedia
• 17 Online Programs
• 20 Periodicals
• 25 Policies
• 8 RefWorks/Citation Managers
• 5 Research Guides (LibGuides)
• 221 Research Help
• 23 University Services

Last Updated: Jun 27, 2023 Views: 455405

What is a research gap.

A research gap is a question or a problem that has not been answered by any of the existing studies or research within your field. Sometimes, a research gap exists when there is a concept or new idea that hasn't been studied at all. Sometimes you'll find a research gap if all the existing research is outdated and in need of new/updated research (studies on Internet use in 2001, for example). Or, perhaps a specific population has not been well studied (perhaps there are plenty of studies on teenagers and video games, but not enough studies on toddlers and video games, for example). These are just a few examples, but any research gap you find is an area where more studies and more research need to be conducted. Please view this video clip from our Sage Research Methods database for more helpful information: How Do You Identify Gaps in Literature?

How do I find one?

It will take a lot of research and reading.  You'll need to be very familiar with all the studies that have already been done, and what those studies contributed to the overall body of knowledge about that topic. Make a list of any questions you have about your topic and then do some research to see if those questions have already been answered satisfactorily. If they haven't, perhaps you've discovered a gap!  Here are some strategies you can use to make the most of your time:

• One useful trick is to look at the “suggestions for future research” or conclusion section of existing studies on your topic. Many times, the authors will identify areas where they think a research gap exists, and what studies they think need to be done in the future.
• As you are researching, you will most likely come across citations for seminal works in your research field. These are the research studies that you see mentioned again and again in the literature.  In addition to finding those and reading them, you can use a database like Web of Science to follow the research trail and discover all the other articles that have cited these. See the FAQ: I found the perfect article for my paper. How do I find other articles and books that have cited it? on how to do this. One way to quickly track down these seminal works is to use a database like SAGE Navigator, a social sciences literature review tool. It is one of the products available via our SAGE Knowledge database.
• In the PsycINFO and PsycARTICLES databases, you can select literature review, systematic review, and meta analysis under the Methodology section in the advanced search to quickly locate these. See the FAQ: Where can I find a qualitative or quantitative study? for more information on how to find the Methodology section in these two databases.
• In CINAHL , you can select Systematic review under the Publication Type field in the advanced search. 
• In Web of Science , check the box beside Review under the Document Type heading in the “Refine Results” sidebar to the right of the list of search hits.
• If the database you are searching does not offer a way to filter your results by document type, publication type, or methodology in the advanced search, you can include these phrases (“literature reviews,” meta-analyses, or “systematic reviews”) in your search string.  For example, “video games” AND “literature reviews” could be a possible search that you could try.

Please give these suggestions a try and contact a librarian for additional assistance.

Content authored by: GS

• Share on Facebook

Was this helpful? Yes 371 No 151

Frequently Asked Questions (FAQs) are a self-serve option for users to search and find answers to their questions. 

Use the search box above to type your question to search for an answer or browse existing FAQs by group, topic, etc.

Tell Me More

Link to Question Form

More assistance.

Submit a Question

Related FAQs

• Research Process

What is a Research Gap

• 3 minute read
• 278.8K views

Table of Contents

If you are a young researcher, or even still finishing your studies, you’ll probably notice that your academic environment revolves around certain research topics, probably linked to your department or to the interest of your mentor and direct colleagues. For example, if your department is currently doing research in nanotechnology applied to medicine, it is only natural that you feel compelled to follow this line of research. Hopefully, it’s something you feel familiar with and interested in – although you might take your own twists and turns along your career.

Many scientists end up continuing their academic legacy during their professional careers, writing about their own practical experiences in the field and adapting classic methodologies to a present context. However, each and every researcher dreams about being a pioneer in a subject one day, by discovering a topic that hasn’t been approached before by any other scientist. This is a research gap.

Research gaps are particularly useful for the advance of science, in general. Finding a research gap and having the means to develop a complete and sustained study on it can be very rewarding for the scientist (or team of scientists), not to mention how its new findings can positively impact our whole society.

How to Find a Gap in Research

How many times have you felt that you have finally formulated THAT new and exciting question, only to find out later that it had been addressed before? Probably more times than you can count.

There are some steps you can take to help identify research gaps, since it is impossible to go through all the information and research available nowadays:

• Select a topic or question that motivates you: Research can take a long time and surely a large amount of physical, intellectual and emotional effort, therefore choose a topic that can keep you motivated throughout the process.
• Find keywords and related terms to your selected topic: Besides synthesizing the topic to its essential core, this will help you in the next step.
• Use the identified keywords to search literature: From your findings in the above step, identify relevant publications and cited literature in those publications.
• Look for topics or issues that are missing or not addressed within (or related to) your main topic.
• Read systematic reviews: These documents plunge deeply into scholarly literature and identify trends and paradigm shifts in fields of study. Sometimes they reveal areas or topics that need more attention from researchers and scientists.

Keeping track of all the new literature being published every day is an impossible mission. Remember that there is technology to make your daily tasks easier, and reviewing literature can be one of them. Some online databases offer up-to-date publication lists with quite effective search features:

• Elsevier’s Scope
• Google Scholar

Of course, these tools may be more or less effective depending on knowledge fields. There might be even better ones for your specific topic of research; you can learn about them from more experienced colleagues or mentors.

Find out how FINER research framework can help you formulate your research question.

Literature Gap

The expression “literature gap” is used with the same intention as “research gap.” When there is a gap in the research itself, there will also naturally be a gap in the literature. Nevertheless, it is important to stress out the importance of language or text formulations that can help identify a research/literature gap or, on the other hand, making clear that a research gap is being addressed.

When looking for research gaps across publications you may have noticed sentences like:

…has/have not been… (studied/reported/elucidated) …is required/needed… …the key question is/remains… …it is important to address…

These expressions often indicate gaps; issues or topics related to the main question that still hasn’t been subject to a scientific study. Therefore, it is important to take notice of them: who knows if one of these sentences is hiding your way to fame.

Language Editing Services by Elsevier Author Services:

• Manuscript Review

Systematic Review VS Meta-Analysis

Literature Review in Research Writing

You may also like.

Descriptive Research Design and Its Myriad Uses

Five Common Mistakes to Avoid When Writing a Biomedical Research Paper

Making Technical Writing in Environmental Engineering Accessible

To Err is Not Human: The Dangers of AI-assisted Academic Writing

When Data Speak, Listen: Importance of Data Collection and Analysis Methods

Choosing the Right Research Methodology: A Guide for Researchers

Why is data validation important in research?

Writing a good review article

Input your search keywords and press Enter.

An official website of the United States government

The .gov means it's official. Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you're on a federal government site.

The site is secure. The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

• Publications
• Account settings
• Browse Titles

NCBI Bookshelf. A service of the National Library of Medicine, National Institutes of Health.

Framework for Determining Research Gaps During Systematic Review: Evaluation

Methods Research Reports

Investigators: Karen A Robinson , PhD, Oluwaseun Akinyede , MPH, Tania Dutta , MS, MPP, Veronica Ivey Sawin , BA, Tianjing Li , MD, PhD, Merianne Rose Spencer , BS, Charles M Turkelson , PhD, and Christine Weston , PhD.

Affiliations

• Copyright and Permissions

Structured Abstract

Background:.

Research gaps prevent systematic reviewers from making conclusions and, ultimately, limit our ability to make informed health care decisions. While there are well-defined methods for conducting a systematic review, there has been no explicit process for the identification of research gaps from systematic reviews. In a prior project we developed a framework to facilitate the systematic identification and characterization of research gaps from systematic reviews. This framework uses elements of PICOS (Population, Intervention, Comparison, Outcomes, Setting) to describe the gaps and categorizes the reasons for the gaps as (A) insufficient or imprecise information, (B) biased information, (C) inconsistent or unknown consistency results, and/or (D) not the right information.

To further develop and evaluate a framework for the identification and characterization of research gaps from systematic reviews.

We conducted two types of evaluation: (1) We applied the framework to existing systematic reviews, and (2) Evidence-based Practice Centers (EPCs) applied the framework either during a systematic review or during a future research needs project (FRN). EPCs provided feedback on the framework using an evaluation form.

Our application of the framework to 50 systematic reviews identified about 600 unique research gaps. Key issues emerging from this evaluation included the need to clarify instructions for dealing with multiple comparisons (lumping vs. splitting) and need for guidance on applying the framework retrospectively. We received evaluation forms from seven EPCs. EPCs applied the framework in 8 projects, five of which were FRNs. Challenges identified by the EPCs led to revisions in the instructions including guidance for teams to decide a priori whether to limit the use of the framework to questions for which strength of evidence has been assessed, and the level of detail needed for the characterization of the gaps.

Conclusions:

Our team evaluated a revised framework, and developed guidance for its application. A final version is provided that incorporates revisions based on use of the framework across existing systematic reviews and feedback from other EPCs on their use of the framework. Future research is needed to evaluate the relative costs and benefits of using the framework, for review authors and for users of the systematic reviews.

• Collapse All
• Acknowledgments
• Peer Reviewers
• Introduction
• Review and Revise Framework and Develop Detailed Instructions
• Test Framework and Instructions Through Application to Existing Systematic Reviews
• Evaluate Implementation of Framework
• Revise and Finalize Framework and Instructions
• Peer Review and Public Commentary
• Key Findings
• Limitations
• Future Research
• Implications for Practice
• Conclusions
• Appendix A JHU EPC Frameworks Project: Research Gaps Worksheet and Instructions (Original)
• Appendix B JHU EPC Framework Evaluation Form
• Appendix C JHU EPC Frameworks Project: Research Gaps Worksheet and Instructions
• Appendix D Listing of Reviews Included in Retrospective Application of Framework
• Appendix E Detailed Analysis of Evaluation of the Use of the Research Gaps Framework by Evidence-based Practice Centers (EPCs)
• Appendix F JHU EPC Frameworks Project: Research Gaps Worksheet and Instructions (Final)

Prepared for: Agency for Healthcare Research and Quality, U.S. Department of Health and Human Services 1 , Contract No. 290-2007-10061-I. Prepared by: Johns Hopkins University Evidence-based Practice Center, Baltimore, MD

Suggested citation:

Robinson KA, Akinyede O, Dutta T, Sawin VI, Li T, Spencer MR, Turkelson CM, Weston C. Framework for Determining Research Gaps During Systematic Review: Evaluation. Methods Research Report. (Prepared by Johns Hopkins University Evidence-based Practice Center under Contract No. 290-2007-10061-I.) AHRQ Publication No. 13-EHC019-EF. Rockville, MD: Agency for Health care Research and Quality. February 2013. www.effectivehealthcare.ahrq.gov/reports/final.cfm .

This report is based on research conducted by the Johns Hopkins University Evidence-based Practice Center (EPC) under contract to the Agency for Healthcare Research and Quality (AHRQ), Rockville, MD (Contract No. 290-2007-10061-I). The findings and conclusions in this document are those of the authors, who are responsible for its contents; the findings and conclusions do not necessarily represent the views of AHRQ. Therefore, no statement in this report should be construed as an official position of AHRQ or of the U.S. Department of Health and Human Services.

The information in this report is intended to help health care decisionmakers—patients and clinicians, health system leaders, and policymakers, among others—make well informed decisions and thereby improve the quality of health care services. This report is not intended to be a substitute for the application of clinical judgment. Anyone who makes decisions concerning the provision of clinical care should consider this report in the same way as any medical reference and in conjunction with all other pertinent information, i.e., in the context of available resources and circumstances presented by individual patients.

This report may be used, in whole or in part, as the basis for development of clinical practice guidelines and other quality enhancement tools, or as a basis for reimbursement and coverage policies. AHRQ or U.S. Department of Health and Human Services endorsement of such derivative products may not be stated or implied.

None of the investigators have any affiliations or financial involvement that conflicts with the material presented in this report.

540 Gaither Road, Rockville, MD 20850; www ​.ahrq.gov

• Cite this Page Robinson KA, Akinyede O, Dutta T, et al. Framework for Determining Research Gaps During Systematic Review: Evaluation [Internet]. Rockville (MD): Agency for Healthcare Research and Quality (US); 2013 Feb.
• PDF version of this title (425K)

Other titles in these collections

• AHRQ Methods for Effective Health Care
• Health Services/Technology Assessment Texts (HSTAT)

Related information

• NLM Catalog Related NLM Catalog Entries

Similar articles in PubMed

• Review Frameworks for Determining Research Gaps During Systematic Reviews [ 2011] Review Frameworks for Determining Research Gaps During Systematic Reviews Robinson KA, Saldanha IJ, Mckoy NA. 2011 Jun
• Review Development of a framework to identify research gaps from systematic reviews. [J Clin Epidemiol. 2011] Review Development of a framework to identify research gaps from systematic reviews. Robinson KA, Saldanha IJ, McKoy NA. J Clin Epidemiol. 2011 Dec; 64(12):1325-30. Epub 2011 Sep 19.
• Review Prioritization Criteria Methodology for Future Research Needs Proposals Within the Effective Health Care Program: PiCMe-Prioritization Criteria Methods [ 2013] Review Prioritization Criteria Methodology for Future Research Needs Proposals Within the Effective Health Care Program: PiCMe-Prioritization Criteria Methods Andrews J. 2013 Jan
• How has the impact of 'care pathway technologies' on service integration in stroke care been measured and what is the strength of the evidence to support their effectiveness in this respect? [Int J Evid Based Healthc. 2008] How has the impact of 'care pathway technologies' on service integration in stroke care been measured and what is the strength of the evidence to support their effectiveness in this respect? Allen D, Rixson L. Int J Evid Based Healthc. 2008 Mar; 6(1):78-110.
• Review Grading the Strength of a Body of Evidence When Assessing Health Care Interventions for the Effective Health Care Program of the Agency for Healthcare Research and Quality: An Update. [Methods Guide for Effectivenes...] Review Grading the Strength of a Body of Evidence When Assessing Health Care Interventions for the Effective Health Care Program of the Agency for Healthcare Research and Quality: An Update. Berkman ND, Lohr KN, Ansari M, McDonagh M, Balk E, Whitlock E, Reston J, Bass E, Butler M, Gartlehner G, et al. Methods Guide for Effectiveness and Comparative Effectiveness Reviews. 2008

Recent Activity

• Framework for Determining Research Gaps During Systematic Review: Evaluation Framework for Determining Research Gaps During Systematic Review: Evaluation

Your browsing activity is empty.

Activity recording is turned off.

Turn recording back on

Connect with NLM

National Library of Medicine 8600 Rockville Pike Bethesda, MD 20894

Web Policies FOIA HHS Vulnerability Disclosure

Help Accessibility Careers

Rationale for the Study

It is important for you to be able to explain the importance of the research you are conducting by providing valid arguments. Rationale for the study, also referred to as justification for the study, is reason why you have conducted your study in the first place. This part in your paper needs to explain uniqueness and importance of your research. Rationale for the study needs to be specific and ideally, it should relate to the following points:

1. The research needs to contribute to the elimination of a gap in the literature. Elimination of gap in the present literature is one of the compulsory requirements for your study. In other words, you don’t need to ‘re-invent the wheel’ and your research aims and objectives need to focus on new topics. For example, you can choose to conduct an empirical study to assess the implications of COVID-19 pandemic on the numbers of tourists visitors in your city. This might be previously undressed topic, taking into account that COVID-19 pandemic is a relatively recent phenomenon.

Alternatively, if you cannot find a new topic to research, you can attempt to offer fresh perspectives on existing management, business or economic issues. For example, while thousands of studies have been previously conducted to study various aspects of leadership, this topic as far from being exhausted as a research area. Specifically, new studies can be conducted in the area of leadership to analyze the impacts of new communication mediums such as TikTok, and other social networking sites on leadership practices.

You can also discuss the shortcomings of previous works devoted to your research area. Shortcomings in previous studies can be divided into three groups:

a) Methodological limitations . Methodology employed in previous study may be flawed in terms of research design, research approach or sampling.

b) Contextual limitations . Relevance of previous works may be non-existent for the present because external factors have changed.

c) Conceptual limitations . Previous studies may be unjustifiably bound up to a particular model or an ideology.

While discussing the shortcomings of previous studies you should explain how you are going to correct them. This principle is true to almost all areas in business studies i.e. gaps or shortcomings in the literature can be found in relation to almost all areas of business and economics.

2. The research can be conducted to solve a specific problem. It helps if you can explain why you are the right person and in the right position to solve the problem. You have to explain the essence of the problem in a detailed manner and highlight practical benefits associated with the solution of the problem. Suppose, your dissertation topic is “a study into advantages and disadvantages of various entry strategies into Chinese market”. In this case, you can say that practical implications of your research relates to assisting businesses aiming to enter Chinese market to do more informed decision making.

Alternatively, if your research is devoted to the analysis of impacts of CSR programs and initiatives on brand image, practical contributions of your study would relate to contributing to the level of effectiveness of CSR programs of businesses.

Additional examples of studies that can assist to address specific practical problems may include the following:

• A study into the reasons of high employee turnover at Hanson Brick
• A critical analysis of employee motivation problems at Esporta, Finchley Road, London
• A research into effective succession planning at Microsoft
• A study into major differences between private and public primary education in the USA and implications of these differences on the quality of education

However, it is important to note that it is not an obligatory for a dissertation   to be associated with the solution of a specific problem. Dissertations can be purely theory-based as well. Examples of such studies include the following:

• Born or bred: revising The Great Man theory of leadership in the 21 st century
• A critical analysis of the relevance of McClelland’s Achievement theory to the US information technology industry
• Neoliberalism as a major reason behind the emergence of the global financial and economic crisis of 2007-2009
• Analysis of Lewin’s Model of Change and its relevance to pharmaceutical sector of France

3. Your study has to contribute to the level of professional development of the researcher . That is you. You have to explain in a detailed manner in what ways your research contributes to the achievement of your long-term career aspirations.

For example, you have selected a research topic of “ A critical analysis of the relevance of McClelland’s Achievement theory in the US information technology industry ”.  You may state that you associate your career aspirations with becoming an IT executive in the US, and accordingly, in-depth knowledge of employee motivation in this industry is going to contribute your chances of success in your chosen career path.

Therefore, you are in a better position if you have already identified your career objectives, so that during the research process you can get detailed knowledge about various aspects of your chosen industry.

My e-book, The Ultimate Guide to Writing a Dissertation in Business Studies: a step by step assistance offers practical assistance to complete a dissertation with minimum or no stress. The e-book covers all stages of writing a dissertation starting from the selection to the research area to submitting the completed version of the work within the deadline.

John Dudovskiy

• 34.9k views
• Literature Search

Q: What are gaps in literature?

My paper is about: Teachers' perspectives on parents' involvement with their educationally exceptional children in completing their assignments.

Asked by Linda Waller on 19 Nov, 2019

I wasn’t entirely clear about your question, including the subject of your paper. So, I have edited it for greater clarity. I understand that you wish to know about literature gaps for your study and how to go about identifying these gaps. As for your subject, as that is a very specific topic, I will not be in a position to help you. However, I can provide some suggestions and tips that you can use to identify literature gaps for your subject.

A literature gap, or research gap, is an unexplored topic revealed during a literature search that has scope for research or further exploration. To identify literature gaps, you need to do a thorough review of existing literature in both the broad and specific areas of your topic. You could go through both the Introduction and Discussion sections of existing papers in the subject area to identify such gaps. Apart from a study of the existing literature, you may also be able to identify research gaps based on your own analysis of the problem and existing literature. Thus, for your present subject, you could try to find out more about questions such as educationally exceptional children and their special requirements and challenges; attitudes and behaviors of parents of such children; ways in which these parents help their children to maximize their potential (and how beneficial or detrimental this can be); and also opinions from child and adult psychologists, sociologists, and learning experts. Note that these are only examples to guide you and help you get started. Your own literature review will reveal specific potential directions for your study.

Finally, here are some resources to guide you further:

• Don't know where to start? 6 Tips on identifying research gaps
• How can I describe the gap in literature when no previous research has been done on the problem?

Answered by Editage Insights on 28 Nov, 2019

• Upvote this Answer

This content belongs to the Conducting Research Stage

Confirm that you would also like to sign up for free personalized email coaching for this stage.

Trending Searches

• Statement of the problem
• Background of study
• Scope of the study
• Types of qualitative research
• Rationale of the study
• Concept paper
• Literature review
• Introduction in research
• Under "Editor Evaluation"
• Ethics in research

Recent Searches

• Review paper
• Responding to reviewer comments
• Predatory publishers
• Scope and delimitations
• Open access
• Plagiarism in research
• Journal selection tips
• Editor assigned
• Types of articles
• "Reject and Resubmit" status
• Decision in process
• Conflict of interest

Home » Education » What is the Difference Between Research Gap and Research Problem

What is the Difference Between Research Gap and Research Problem

The main difference between research gap and research problem is that a research gap identifies a gap in knowledge about a subject, whereas a research problem identifies and articulates the need for research .

Research gap and research problem are two very similar elements of a research study. They are closely related and play a crucial role in research. In fact, a researcher cannot identify a research problem without a research gap, and it’s impossible to conduct a research study without both. A researcher first identifies a research gap (an area that has not been explored in previous literature on the subject) after conducting a thorough literature review . Then he/she formulates a clear research problem from this research gap.

Key Areas Covered

1.  What is a Research Gap       – Definition, Features, Function 2. What is a Research Problem      – Definition, Features, Function 3.  Difference Between Research Gap and Research Problem      – Comparison of Key Differences

Research Gap, Research Problem

What is a Research Gap

A research gap is a key element in any research study. It’s the center of a research project and determines the area that lacks crucial information. We can define a research gap as a question that has not been addressed or an area of interest that has not been explored in previous literature on the subject. For example, a researcher in the field of health or medicine can research the long-term effects of Covid-19 vaccines, which is a research gap in the existing literature on the subject. To identify the research gap, the researcher has to gather and study all relevant books, reports, and journal articles on the subject. Researchers can usually decide on their research gap once they have conducted their literature review.

A research gap can exist when there are no studies on a new concept or idea. Sometimes, researchers can also find a research gap if the existing research is not up to date and needs modification or updates. For example, research on internet use in 2002 is no longer valid today, and the data needs modification. A researcher can also choose a specific population that has not been studied well.

What is a Research Problem

A research problem is a question(s) the researcher wants to answer through his study. Research problems introduce the readers to the topic that is being discussed. It also places the problem in a particular context, defining the parameters of the investigation. Finally, it provides the framework for reporting the results of the research, reveals what is necessary to conduct the research, and explains how the information will be presented.

A research problem must cover the essential issues at hand and be specific. Moreover, the researcher must present it logically and clearly. The research problem must also ensure that the research is based on actual facts and evidence and not on beliefs and opinions.

There are four general types of research problems:

• Casuist Research Problem – involves the determination of right and wrong in questions of conduct or conscience
• Difference Research Problem – compares and contrasts two or more phenomena
• Descriptive Research Problem – describes the significance of a state, situation, phenomenon
• Relational Research Problem – indicates a relationship between two or more variables

Without a well-defined research problem, a researcher will be more likely to end up with an unfocused and unmanageable research study.

Difference Between Research Gap and Research Problem

A research gap is an area of interest that has not been explored in previous literature on the subject, while a research problem is a definite or clear statement about an area of concern that points to a need for meaningful understanding and deliberate investigation.

First, the researcher has to identify a research gap in the area of interest and then form his/her research problem.

A research gap identifies a gap in knowledge about a subject, whereas a research problem identifies and articulates the need for research.

A researcher identifies a research gap after conducting a thorough literature review. Then he/she formulates a clear research problem from this research gap. Therefore, the difference between research gap and research problem is the order of sequence. A research gap further justifies the research problem.

1. “ FAQ: What is a research gap and how do I find one? ” Shapiro Library. Southern New Hampshire University. 2. McCombes, Shona. “ How to Define a Research Problem | Ideas & Examples ” Scribber.

Image Courtesy:

1. “ Concept-man-papers-person-plan ” (CC0) via Pixabay

About the Author: Hasa

Hasanthi is a seasoned content writer and editor with over 8 years of experience. Armed with a BA degree in English and a knack for digital marketing, she explores her passions for literature, history, culture, and food through her engaging and informative writing.

​You May Also Like These

Leave a reply cancel reply.

PHILO-notes

Free Online Learning Materials

What is a Research Gap and How to Identify it?

This lecture will briefly discuss the meaning, nature, and dynamics of a research gap. In particular, it will address the following questions:

1) What is a research gap ?

2) What is the importance of identifying the research gap?

3) How to identify a research gap?

In addressing these three important questions, this lecture will give more weight on the third question. This is because many fledgling scholars and master’s and doctoral students struggled in identifying the gap in their research, thesis, or dissertation. Hence, it is the goal of this lecture to spare them the unnecessary burden of circling the mountain several times before getting to the top.

So, what is a research gap?

Understood more broadly, a research gap is the problem that researchers would want to see addressed in the research. As the name suggests, it is the gap that researchers fill with their proposed research project.

Hence, a research gap is “what is missing” or “what is not addressed” in the current state of knowledge. Put simply, a research gap is the question or problem that has not been answered in your area of specialization. For this reason, the research gap establishes “the need” or the “importance, urgency, and necessity” of your proposed research project, thesis, or dissertation.

This explains why all types of research always begin with a research gap. Indeed, no research activity is possible without the research gap.

Please note that this is what experienced reviewers or thesis/dissertation panel members are looking for during thesis or dissertation proposal defense. Thus, if your proposed thesis or dissertation does not have or does not clearly articulate the research gap, then chances are your thesis or dissertation proposal will be rejected and you have to do your research again from scratch.

This is the problem with many master’s and doctoral students when they write their thesis or dissertation. In most cases, because they are inexperienced researchers and, sometimes, they do not consult their thesis/dissertation adviser regularly, they simply start with a research aim and thought that it’s already the research gap. But the research gap is not the same with the research aim. And in some cases, master’s and doctoral students just copied or patterned their thesis or dissertation on previous researches.

Let us consider the example below.

Supposed the working title of the thesis/dissertation proposal is “Imposed Career Study among University Students in Hong Kong”. With this title, we can have the following research aim:

“The proposed research aims to determine the lived experiences of those students who were just forced to take a certain career course according to the wishes of their parents or significant others and how it affects the psycho-emotional and social wellbeing of these students.”

Again, many master’s and doctoral students thought that the aim is already the problem or the research gap of the proposed research project. But as already mentioned, it is not.

So, what could possibly be the research gap of the above proposed research project?

Based on the above research aim, we can have, for example, the idea:

“The researcher may have learned from experience or through literature review that there are university students in Hong Kong who were just forced to take certain career course according to the wishes of their parents or significant others and that these students were devastated and became rebellious in schools. For this reason, these students may become social delinquents in the future. Now, based on the researcher’s initial review of related literature, it was found out that no study has been conducted on the topic.”

As we can see, the problem is that there are university students in Hong Kong who were just forced to take a certain career course according to the wishes of their parents or significant others. As a result of being just forced to take a certain career course, these students have become devastated and rebellious, which in turn will make them as social delinquents in the future. Also, there has been no study conducted on this topic in Hong Kong. This is exactly what we meant by a “research gap”. This is “what is missing” or “what has not been addressed” in the current state of knowledge in this field. And with this research gap, we can now formulate the research aims, which reads:

If one may ask why the need for this study, then the researcher may add:

“The researcher argues that there is a need to determine the lived experiences of these students so that we can create a career decision-making program as an alternative in addressing the problem.”

As we can see, identifying the research gap and articulating it in the “background” or “rationale” of the study is important not only because it will spare the researcher the unnecessary toil of making major revision, but also because it will make the research publishable. For sure, if the researcher clearly identifies the research gap and articulates it in the background of the study, the reviewers or thesis defense panel members will be able to conclude right away that the proposed research project is unique and original because it is not a duplication of what have been done in the past. This will also send a message to the reviewers or thesis defense panel members that the researcher has deep knowledge of the topic under investigation. As is well known, finding original and innovative topics in the chosen field as well as identifying and articulating the research gap is never an easy feat.

Now that we have briefly discussed the nature and meaning of a research gap and its importance, the next question is how do we identify the research gap?

For experienced researchers, because they already have broad and deep knowledge on their chosen field of specialization, they can easily identify a research gap. However, for fledgling scholars as well as master’s and doctoral students, as already mentioned, identifying a research gap is never an easy feat. But the application of some proven techniques will somehow help ease the process. 

Let me briefly discuss the three important techniques in identifying a research gap. 

Of course, there are a number of techniques on how to identify a research gap, but the three points introduced below are the most effective ones. 

First, when thinking of a topic in your field of specialization, it would greatly help if you start with something that you are passionate about, something that would seem like second skin to you. 

For some obvious reason, being passionate at something makes you push yourself harder, and despite working long hours on it, you will still manage to smile. In fact, if you love what you are doing, then long and hard labor is turned into “play”. Hence, despite the hardships, you keep doing your research because you enjoyed it. 

Of course, starting with something that you are passionate about in relation to identifying a research gap involves “choosing a particular topic” in your discipline or field of specialization. For instance, if your discipline is “education”, then you might be passionate about doing research on “teachers’ burnout level”, “philosophy of education”, “critical pedagogy”, or “lived experiences of teachers handling subjects not in line with their field of specialization”.

If your discipline is psychology, then you might be passionate about doing research on “social cognition”, “social control”, “racism”, “verbal communication”, or even “attraction, romance, and love”.

Second, once you have chosen a topic that you are passionate about, the next step is to “determine the mega trends and recent debates” in your discipline or field of specialization. This is important because once you know the mega trends or recent debates in your discipline or field of specialization, you can easily identify what have and have not been done in your discipline.

Determining the mega trends and recent debates in your discipline is also important because it will ensure that your research is timely and necessary. You have to remember that you do not do research for the sake of doing research, of completing a master’s or doctoral degree. You do research because there is a problem that needs to be addressed. Hence, a particular research is timely if the topic is one of the mega trends and recent debates in the field and it is necessary if it attempts to address a serious problem that requires urgent consideration.

Of course, determining the mega trends and recent debates in your discipline implies doing a literature review. This leads us to the third and last point.

Needless to say, you need to review recent literature in your chosen discipline or field of specialization so you may know what scholars have done so far. In this way, you will be able to identify possible gaps that you can fill in. For example, if your discipline is anthropology and you are passionate about doing research on the indigenous peoples in Southeast Asia, then you need to review literature on indigenous peoples in Southeast Asia in the last, say, 3-5 years.

Now, suppose several famous scholars on indigenous peoples in Southeast Asia have published on “the marginalization” of the Dayak indigenous people in Borneo, then this is precisely one of the mega trends and recent debates in this field of specialization.

Suppose you are interested in joining the discussion or debate on this topic, then you need to identify what have not been done by those scholars. It could be a problem that remains unsolved or a new insight that may help shed light on the issue being debated upon.

How do you do this?

Suppose there are 5 famous scholars working on the topic “the marginalization” of the indigenous peoples in Southeast Asia, particularly the Dayak indigenous people in Borneo. What you need to do now is review these pieces of literature and identify their concepts and arguments. For instance, you may say:

Scholar 1 , in her work titled “Modernism and the Dayak People of Borneo”, says that the Dayak indigenous peoples in Borneo have been pushed further to the periphery by the forces of modernity, such as consumerism. 

Scholar 2 , in his work titled “Militarism in Borneo”, argues that one of the causes of the marginalization of the Dayak people in Borneo is the imposition of militarization in the island. 

Scholar 3 , in her work titled “The Resiliency of the Dayak People”, says that despite the constant presence of social forces that marginalized the Dayak people, the researcher found out that the Dayak people are very resilient. In fact, they have overcome every challenge that they faced and easily returned to their normal life. 

Scholar 4 , in his work titled “Different Faces of Marginalization in Borneo”, says that the Dayak people have been marginalized by different forces of globalization, such as the logging and mining companies. 

Lastly, scholar 5 , in her work titled “Rights, Recognition, and the Dayak People”, narrates not only how the Dayak people have been marginalized by the forces of globalization but also the basic and inalienable rights of the Dayak people.

Now, after reviewing these important pieces of literature about the marginalization of the Dayak people, you realized that no scholar on the Dayak people, so far as you know, has done research on “the way in which the Dayak people resisted any forms of marginalization”. 

As you can see, this issue is one of the important topics on the debate about the marginalization of the Dayak people in Borneo, yet no scholar has brought this issue on the table. Hence, this could be a possible “gap” in this area of specialization that you can fill in with your research on the way in which the Dayak people resisted any forms of marginalization. 

With this “research gap”, you may work, for example, on “the Dayak people’s struggle for recognition of their rights to ancestral domain”. Your working title may read:

“ Self-Determination and the Dayak People’s Struggle for Recognition ” 

And your research’s main goal reads: 

“ This proposed thesis aims to explore how the Dayak people in Borneo resisted the forces of globalization that marginalized them .” 

So, that’s what a research gap is and how to identify it.

Please note, however, that what I shared above are just some of the techniques on how to identify a research gap. There are other techniques that might help you in identifying a research gap or you may want to develop your own. What is important at this point is that through the discussion above you have now a basic understanding of what a research gap is and how to identify it. 

And lastly, please note that the principles that we applied in the above discussion on how to identify a research gap can be applied to all disciplines, be they social sciences, humanities, natural sciences, education, engineering, mathematics, or psychology.

Disclaimer: Early release articles are not considered as final versions. Any changes will be reflected in the online version in the month the article is officially released.

Volume 30, Number 4—April 2024

Ten Years of High-Consequence Pathogens—Research Gains, Readiness Gaps, and Future Goals

Suggested citation for this article

In 2014, high-consequence pathogens were described as those causing high mortality but having infrequent spillover from animals and rare human-to-human transmission ( 1 ). Since then, high-consequence pathogens such as ebolaviruses, monkeypox virus (MPXV), and henipaviruses have challenged that description. Unbeknownst to the authors of the 2014 article ( 1 ), Orthoebolavirus zairense (Zaire Ebola virus) was circulating at that time in Guinea, resulting in the world’s largest known Ebola virus disease (EVD) outbreak. The West Africa EVD outbreak redefined our understanding of high-consequence pathogens, demonstrating their substantial potential for communicable spread; in Guinea, Liberia, and Sierra Leone, > 28,600 persons were infected and > 11,300 patients died. EVD cases were exported to 7 other countries by infected travelers and healthcare workers; containment took 2 years, a coordinated multinational effort, thousands of volunteers, and billions of dollars ( 2 ). The outbreak also drove medical progress; clinical trials tested new Ebola virus vaccines ( 3 ), and epidemiologic investigations showed filoviruses can persist in semen and spread through sexual contact ( 4 ).

During 2014–2024, eleven additional Ebola virus outbreaks have been recognized; the second largest known outbreak infected 3,470 persons in North Kivu, Democratic Republic of the Congo (DRC), during 2018–2020 ( 5 ). Virus sequencing data suggested that > 3 outbreaks were most likely caused by a persistently infected survivor from a previous outbreak ( 5 ). Other viral hemorrhagic fevers (VHFs) also occurred. In 2019, Chapare virus caused illness in 9 patients in Bolivia, 4 of whom died; 3 healthcare workers were infected through probable nosocomial exposure, and Chapare virus was shown to persist for months in semen after acute infection ( 6 ). In 2022, Marburg virus was reported in Equatorial Guinea and Tanzania, infecting 24 laboratory-confirmed patients and killing 17 persons ( 7 ); Orthoebolavirus sudanense (Sudan virus) infected 164 and killed 55 persons in Uganda ( 5 ).

Despite achievements in Ebola virus vaccine development, similar success has lagged for medical countermeasures for other VHFs. Without vaccines or proven therapeutics, primary mitigation measures are rapid identification and isolation of case-patients, contact tracing, and strong infection control practices. Even with accessible vaccines, the response speed is key; delayed detection and response can result in larger outbreaks requiring more resources and time to control. During the 2018 DRC outbreak, regional insecurities impeded early detection and rapid response and likely contributed to the outbreak scale and complexity ( 8 ).

Despite successful variola virus eradication, orthopoxviruses remain high-consequence pathogens that create complex control challenges. During 2014–2024, reports of mpox caused by MPXV surged in regions where the virus is enzootic. During 2017–2022, increased reports of mpox in Nigeria initially raised little concern, even though mpox was diagnosed in occasional travelers from Nigeria who had no history of animal contact ( 9 ). In May 2022, MPXV clade II began circulating person-to-person globally, primarily through sexual contact among gay, bisexual, and other men who have sex with men ( 10 ). Thanks to smallpox preparedness work performed by the US Centers for Disease Control and Prevention and other partners, regulatory agency-approved diagnostics, the JYNNEOS vaccine ( https://www.jynneos.com ), and TPOXX therapeutic agent (SIGA Technologies, https://www.siga.com ) were available in some countries; however, limited early supplies of the JYNNEOS vaccine and lack of licensure in some countries meant the vaccine was not accessible to all persons at risk for MPXV exposure. Before the global mpox outbreak, no real-world efficacy data for TPOXX was available; clinical trials are ongoing. After the mpox outbreak peak in 2022, MPXV has continued to circulate at low levels through 2024; since 2022, >90,000 cases have been reported worldwide ( 11 ). Since 2023, similar surveillance signals have been seen in DRC with MPXV clade I ( 12 ), raising concerns for another global mpox outbreak caused by a more lethal virus clade.

Henipaviruses are high-consequence pathogens within the Paramyxoviridae family; >600 human infections caused by Nipah and Hendra virus have been reported in the published literature ( 13 ). During 2014–2024, seasonal outbreaks of Nipah virus have occurred regularly in Bangladesh and India, but the geographic range of the natural reservoir hosts, Pteropus spp. bats, includes Bhutan, Cambodia China, Indonesia, Madagascar, Malaysia, Maldives, Myanmar, Nepal, Pakistan, Philippines, Sri Lanka and Thailand ( 14 ). In Bangladesh and India, infection risk factors include date palm sap production or consumption ( 15 ), but person-to-person transmission has also been documented among families and close contacts; nosocomial transmission to healthcare workers remains a substantial risk factor ( 13 ). During a 2018 outbreak in India, Nipah virus infected 23 persons with a mortality rate >90%; of those cases, 19 were attributed to person-to-person spread among healthcare workers and patients in hospital settings ( 16 ). Nipah virus is considered to have substantial pandemic potential because it infects multiple mammal species, is endemic in densely human populated regions, and is an RNA virus that can have high mutation rates.

Despite a decade of ecologic studies, no definitive reservoir has been identified for Ebola virus or MPXV, making it challenging to provide clear messaging to prevent animal spillover events. Investments in early detection and response in disease-endemic countries can prevent virus spread after a spillover event. In Uganda, VHF detection rates dropped from an average of 2 weeks to only 2 days after targeted investments in diagnostic capacity were initiated ( 17 ). Furthermore, earlier detection translated into more rapid control measure use; the average numbers of cases per outbreak dropped from >100 before to 5 cases after those investments ( 17 ). However, investments are difficult to sustain and require continuous training, funding, and political will.

Since the description in 2014 ( 1 ), the past decade has redefined high-consequence pathogens as serious and deadly agents that pose a substantial threat to domestic and global security. Many of those pathogens are contagious, most spread from animals to humans, and some can be used as bioterrorism agents. The effects of a changing climate and increasing human–animal interactions associated with population growth and agriculture, global travel and trade, political instability, and human migration events ensure outbreaks of high-consequence pathogens will continue to pose public health threats. The 10 years since 2014 have shown how person-to-person transmission of high-consequence pathogens can fuel large, complex outbreaks, emphasizing the need for swift, effective detection and control at the earliest stages of emergence.

Recognizing the value of early detection and rapid response, a 7-1-7 framework has been proposed as a global metric for pandemic prevention ( 18 ): 7 days to detect emergence, 1 day to notify/mobilize a response, and 7 days to implement control measures. The framework is being piloted worldwide and has been adopted as a regional strategy in Africa. However, to meet this goal, improvements in local capacity, including specimen transport, laboratory diagnostics, trained healthcare and laboratory workers, defined reporting structures, and a robust public health workforce, are urgently needed worldwide where high-consequence pathogens continue to emerge. Investments in high-containment facilities, world-class subject matter experts, and cutting edge technologies are also critical to ensure robust public health testing capabilities at home and abroad and a more rapid resolution to outbreaks caused by high-consequence pathogens.

Dr. McQuiston is the principal deputy director of the Division of High-Consequence Pathogens and Pathology, National Center for Emerging and Zoonotic Infectious Diseases, Centers for Disease Control and Prevention, Atlanta, Georgia, USA. Her research interests focus on preparedness and response activities related to high-consequence pathogens.

• Belay  ED , Monroe  SS . Low-incidence, high-consequence pathogens. Emerg Infect Dis . 2014 ; 20 : 319 – 21 . DOI PubMed Google Scholar
• Centers for Disease Control and Prevention . Cost of the Ebola epidemic [ cited 2024 Jan 29 ]. https://www.cdc.gov/vhf/ebola/history/2014-2016-outbreak/cost-of-ebola.html
• Malenfant  JH , Joyce  A , Choi  MJ , Cossaboom  CM , Whitesell  AN , Harcourt  BH , et al. Use of Ebola vaccine: expansion of recommendations of the Advisory Committee on Immunization Practices to include two additional populations—United States, 2021. MMWR Morb Mortal Wkly Rep . 2022 ; 71 : 290 – 2 . DOI PubMed Google Scholar
• Mate  SE , Kugelman  JR , Nyenswah  TG , Ladner  JT , Wiley  MR , Cordier-Lassalle  T , et al. Molecular evidence of sexual transmission of Ebola virus. N Engl J Med . 2015 ; 373 : 2448 – 54 . DOI PubMed Google Scholar
• Centers for Disease Control and Prevention . History of Ebola disease outbreaks [ cited 2024 Jan 29 ]. https://www.cdc.gov/vhf/ebola/history/chronology.html
• Centers for Disease Control and Prevention . Marburg virus disease outbreaks [ cited 2024 Jan 29 ] https://www.cdc.gov/vhf/marburg/outbreaks/chronology.html
• Loayza Mafayle  R , Morales-Betoulle  ME , Romero  C , Cossaboom  CM , Whitmer  S , Alvarez Aguilera  CE , et al. Chapare hemorrhagic fever and virus detection in rodents in Bolivia in 2019. N Engl J Med . 2022 ; 386 : 2283 – 94 . DOI PubMed Google Scholar
• Aruna  A , Mbala  P , Minikulu  L , Mukadi  D , Bulemfu  D , Edidi  F , et al. ; CDC Ebola Response . Ebola Virus Disease Outbreak - Democratic Republic of the Congo, August 2018-November 2019. MMWR Morb Mortal Wkly Rep . 2019 ; 68 : 1162 – 5 . DOI PubMed Google Scholar
• Rao  AK , Schulte  J , Chen  TH , Hughes  CM , Davidson  W , Neff  JM , et al. ; July 2021 Monkeypox Response Team . Monkeypox in a traveler returning from Nigeria—Dallas, Texas, July 2021. MMWR Morb Mortal Wkly Rep . 2022 ; 71 : 509 – 16 . DOI PubMed Google Scholar
• McQuiston  JH , Braden  CR , Bowen  MD , McCollum  AM , McDonald  R , Carnes  N , et al. The CDC domestic mpox response—United States, 2022–2023. MMWR Morb Mortal Wkly Rep . 2023 ; 72 : 547 – 52 . DOI PubMed Google Scholar
• Centers for Disease Control and Prevention . 2022–2023 Mpox outbreak global map [ cited 2024 Jan 29 ]. https://www.cdc.gov/poxvirus/Mpox/response/2022/world-map.html
• Centers for Disease Control and Prevention Health Alert Network . Mpox caused by human-to-human transmission of monkeypox virus with geographic spread in the Democratic Republic of the Congo [ cited 2024 Jan 29 ]. https://emergency.cdc.gov/han/2023/han00501.asp
• Hegde  ST , Lee  KY , Styczynski  A , Jones  FK , Gomes  I , Das  P , et al. Potential for person-to-person transmission of henipaviruses: a systemic review of the literature. J Infect Dis. 2023 ;Oct 31:jiad467.
• Walsh  MG . Mapping the risk of Nipah virus spillover into human populations in South and Southeast Asia. Trans R Soc Trop Med Hyg . 2015 ; 109 : 563 – 71 . DOI PubMed Google Scholar
• Islam  A , McKee  C , Ghosh  PK , Abedin  J , Epstein  JH , Daszak  P , et al. Seasonality of date palm sap feeding behavior by bats in Bangladesh. EcoHealth . 2021 ; 18 : 359 – 71 . DOI PubMed Google Scholar
• Arunkumar  G , Chandni  R , Mourya  DT , Singh  SK , Sadanandan  R , Sudan  P , et al. ; Nipah Investigators People and Health Study Group . Outbreak investigation of Nipah virus disease in Kerala, India, 2018. J Infect Dis . 2019 ; 219 : 1867 – 78 . DOI PubMed Google Scholar
• Shoemaker  TR , Balinandi  S , Tumusiime  A , Nyakarahuka  L , Lutwama  J , Mbidde  E , et al. Impact of enhanced viral haemorrhagic fever surveillance on outbreak detection and response in Uganda. Lancet Infect Dis . 2018 ; 18 : 373 – 5 . DOI PubMed Google Scholar
• Frieden  TR , Lee  CT , Bochner  AF , Buissonnière  M , McClelland  A . 7-1-7: an organising principle, target, and accountability metric to make the world safer from pandemics. Lancet . 2021 ; 398 : 638 – 40 . DOI PubMed Google Scholar

Suggested citation for this article : McQuiston JH, Montgomery JM, Hutson CL. Ten years of high-consequence pathogens—research gains, readiness gaps, and future goals. Emerg Infect Dis. 2024 Apr [ date cited ]. https://doi.org/10.3201/eid3004.240160

DOI: 10.3201/eid3004.240160

Original Publication Date: March 11, 2024

Table of Contents – Volume 30, Number 4—April 2024

Please use the form below to submit correspondence to the authors or contact them at the following address:

Jennifer H. McQuiston, Centers for Disease Control and Prevention, 1600 Clifton Rd NE, Mailstop H24-12, Atlanta, GA 30329-4018, USA

Comment submitted successfully, thank you for your feedback.

There was an unexpected error. Message not sent.

Exit Notification / Disclaimer Policy

• The Centers for Disease Control and Prevention (CDC) cannot attest to the accuracy of a non-federal website.
• Linking to a non-federal website does not constitute an endorsement by CDC or any of its employees of the sponsors or the information and products presented on the website.
• You will be subject to the destination website's privacy policy when you follow the link.
• CDC is not responsible for Section 508 compliance (accessibility) on other federal or private website.

Metric Details

What is the altmetric attention score.

The Altmetric Attention Score for a research output provides an indicator of the amount of attention that it has received. The score is derived from an automated algorithm, and represents a weighted count of the amount of attention Altmetric picked up for a research output.

An official website of the United States government

Here’s how you know

Official websites use .gov A .gov website belongs to an official government organization in the United States.

Secure .gov websites use HTTPS A lock ( Lock A locked padlock ) or https:// means you’ve safely connected to the .gov website. Share sensitive information only on official, secure websites.

• Researchers
• Survey Respondents

“Excess Mortality” During COVID-19 Varied by Race, Ethnicity, Geography

• Census.gov /
• America Counts: Stories /
• “Excess Mortality" During COVID-19 Varied by Race, Ethnicity, Geography

Black-White Mortality Gaps Widened During Pandemic, Hispanic Mortality Advantage Disappeared

An additional 573,000 people died in the United States during the first year of the COVID-19 pandemic but “excess mortality” at the national level masks substantial variations by state, age, sex, and race and ethnicity, according to new U.S. Census Bureau research recently published in Demography .

“Excess mortality” refers to deaths from any cause above what is expected from recent mortality trends.

This research shows the pandemic widened the mortality gap between the nation’s Black and White populations and completely erased the mortality advantage of the Hispanic population in relation to the non-Hispanic White population.

• Excess mortality among non-Hispanic AIAN, Hispanic, and non-Hispanic Black individuals 65 and over far surpassed rates of their non-Hispanic White counterparts.

Overall, males ages 65 and older, non-Hispanic American Indian or Alaskan Native (AIAN), Hispanic and non-Hispanic Black individuals experienced higher rates of excess mortality than other groups, according to the research.

Excess mortality also varied over time and across states as the pandemic unfolded.

During the initial onset of the pandemic (April to June 2020), New York and neighboring states saw high excess mortality but by summer (July-September), the South had the highest excess mortality.

The longest and most deadly wave (from October 2020 to March 2021) in the pandemic’s first year resulted in substantial excess mortality in virtually all states but it was highest in Mississippi, Louisiana, New York, New Jersey and Washington, D.C.

How We Track Excess Mortality

Mortality data used in this research come from an anonymized version of the Social Security Administration’s Numerical Identification (Numident) database, which contains date of birth, date of death and sex information for all individuals ever assigned a Social Security Number (SSN) (Figure 1).

Self-reported race/ethnicity and last known state of residence are found by linking individuals in the Numident to their responses to the 2000 and 2010 decennial censuses, 2001 to 2019 responses to the American Community Survey (ACS) and other administrative records .

Those with or without an SSN who could not be linked to a decennial census or ACS response were excluded from the analysis.

Excess mortality is calculated as the difference between the actual mortality rate and the mortality rate we would expect to see in the hypothetical absence of, in this case, the COVID-19 pandemic.

We drew mortality data for the April 1, 2020 to March 31, 2021 period from Numident death information. We estimated expected mortality by modeling the actual rates from April 1, 2010 to March 31, 2020 and extrapolating this decade-long trend into the pandemic era.

If the COVID-19 pandemic had not occurred, we’d expect a national mortality rate of approximately 9.3 persons per 10,000 per month (Figure 2). The rate of persons per 10,000 per month is referred to as “person-months” or “PMs”.

But the mortality rate actually observed in the first year of the pandemic was 11.1 per 10,000 PMs, resulting in a national excess mortality rate of 1.8 per 10,000 PMs or 216 per 100,000 persons per year. (The full paper provides details on how and why these estimates differ from National Center for Health Statistics (NCHS) estimates.)

Excess Mortality by Age, Sex, Race/Ethnicity

By linking various population data sources, we can estimate excess mortality for detailed population subgroups.

Census Bureau data, which gathers self-reported race and ethnicity responses, is an improvement over the less reliable race and ethnicity assignments on death certificates made by coroners and next-of-kin. We use these responses to categorize individuals into one of seven race and ethnicity groups “alone” (not in combination with another race or ethnicity) or into a multiple race group.

Excess mortality was higher for men of all ages and race/ethnicities and for all those age 65 and older (Figure 3).

But differences by race/ethnicity were particularly striking:

• Similarly, while excess mortality among non-Hispanic White individuals was almost entirely confined to those 65 and older, we found evidence of substantial excess mortality among younger working-age (ages 25-64) Hispanic, non-Hispanic Black and non-Hispanic AIAN populations. For example, while the excess mortality rate for non-Hispanic White men ages 65-74 was 3.2 per 10,000 PMs, their younger non-Hispanic AIAN counterparts ages 45-54 experienced a comparable rate of 3.7 per 10,000.

With or without the pandemic, we would expect to see differences in mortality among racial and ethnic groups, which complicates comparisons. For example, the average non-Hispanic White person in the United States is older than the average Hispanic individual and, because mortality increases with age, mortality rates tend to be higher on average for non-Hispanic White populations than for Hispanic populations.

The methodology we used to control for these differences applies group-specific mortality rates to the national age and sex distribution. The resulting adjusted mortality rates tell us how excess mortality would differ across racial/ethnic groups if all groups had the same age and sex structures.

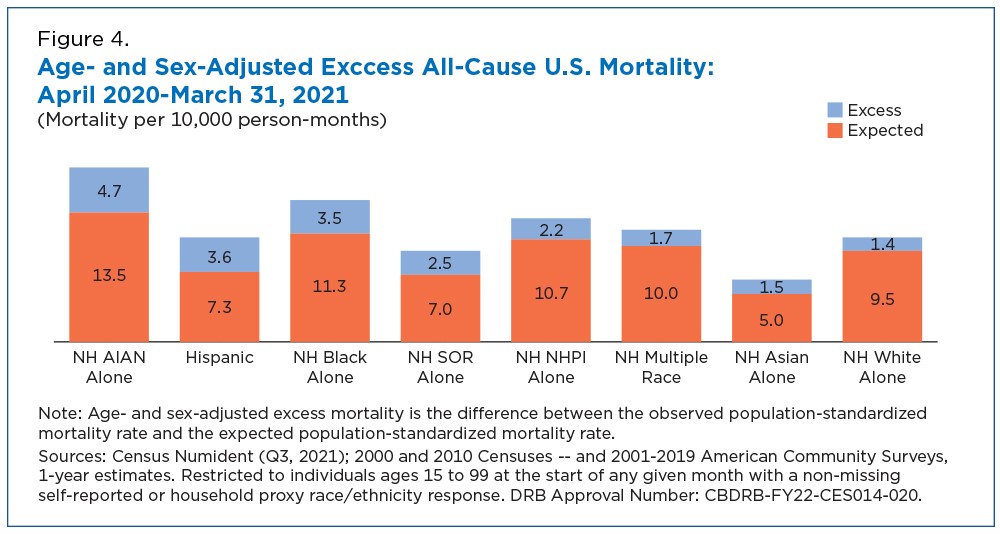
Age- and sex-adjusted mortality rates (Figure 4) show that overall, the non-Hispanic AIAN population experienced the highest rates (4.7 per 10,000 PMs) of excess all-cause mortality during the first year of the pandemic, followed by the Hispanic (3.6 per 10,000 PM) and non-Hispanic Black (3.5 per 10,000 PM) populations.

In contrast, excess mortality was lowest among the non-Hispanic White and non-Hispanic Asian populations (1.4 and 1.5 per 10,000 PM, respectively).

However, the Hispanic population experienced the biggest increase in mortality during the pandemic — 49.1% higher than expected based on pre-pandemic mortality trends.

Excess mortality also rose among the non-Hispanic Some Other Race (35.1%); non-Hispanic AIAN (34.6%); and non-Hispanic Black (31.4%) populations.

The non-Hispanic White population saw the smallest increases (14.6%) relative to expected mortality.

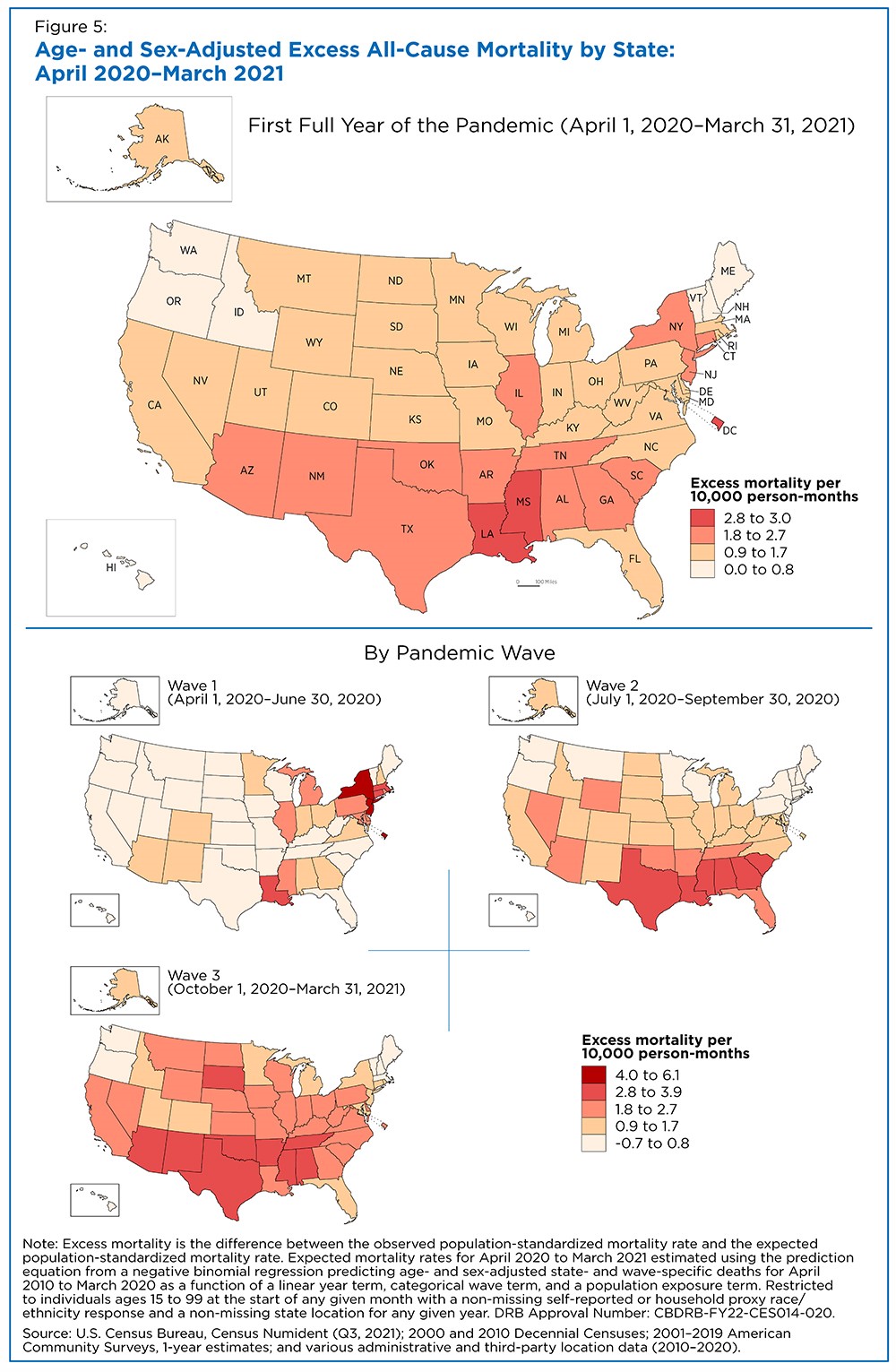
Time and Space Variations

Periodic spikes in excess mortality corresponded with shifts in the geographic dispersal of COVID-19.

During the pandemic’s first entire year, New York, New Jersey, Louisiana, Mississippi, and Washington, D.C. experienced the highest excess mortality (Figure 5).

Much of the excess mortality in New York and New Jersey occurred during the pandemic’s first wave (April 1-June 30, 2020). In the second wave, excess mortality dispersed to the deep South, particularly Mississippi and Louisiana. By wave 3, however, excess mortality was common across the South, had expanded to the Southwest and was also elevated in the Midwest.

Pandemic and Mortality Disparities

In the decade leading up to the pandemic, the national mortality gap between the Black and White populations had narrowed substantially but still favored non-Hispanic White individuals.

The Hispanic population, however, held a long-standing mortality advantage over the non-Hispanic White population.

But the pandemic reversed improvements in the Black-White mortality gap and completely wiped out the Hispanic mortality advantage.

The Black-White and Hispanic-White mortality gaps shifted by an average of 2 deaths per 10,000 PMs in favor of the non-Hispanic White population in virtually all states during the pandemic’s entire first year (Figures 6 and 7).

These findings point to the social and economic determinants of health, which also contributed to racial and ethnic mortality gaps for years before the pandemic began and drove disproportionate increases in excess mortality among racial and ethnic minorities in the pandemic’s first year. 

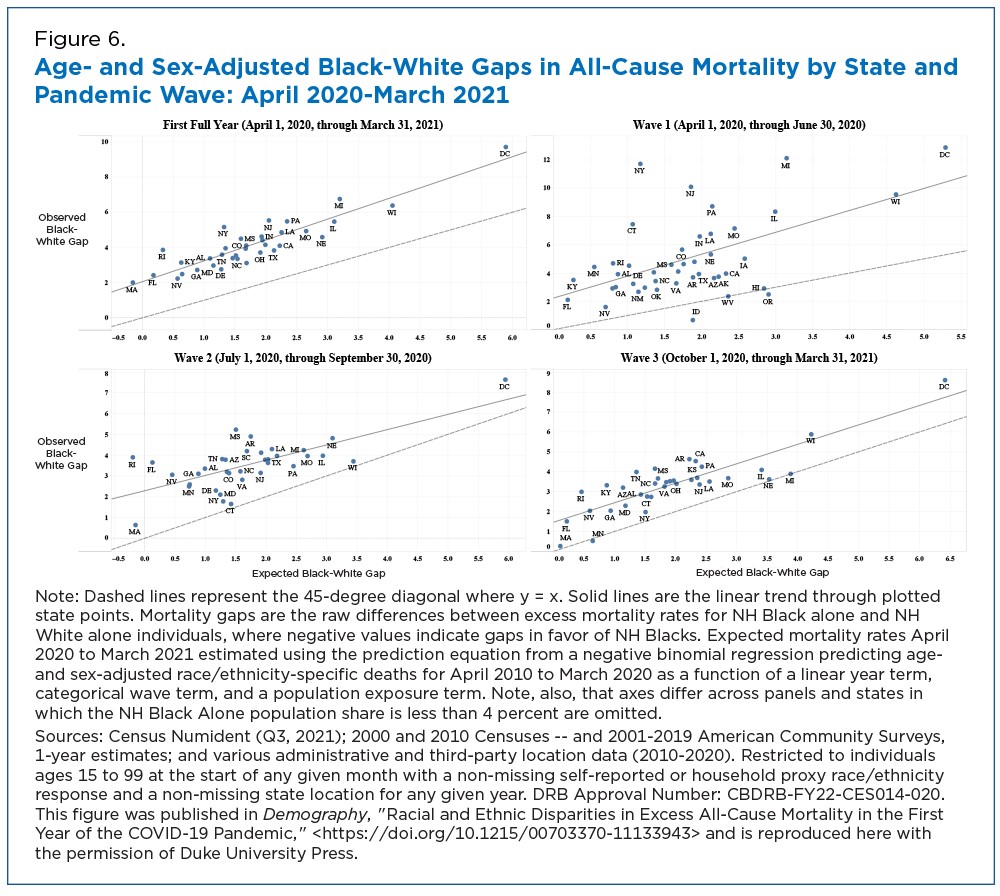
Thomas B. Foster is a senior sociologist in the Census Bureau’s Center for Economic Studies (CES).

Sonya R. Porter is the assistant center chief of the Interdisciplinary Research Area in CES.

Nikolas Pharris-Ciurej is the assistant center chief of the Demographic Research Area in CES.

Related Statistics

Our email newsletter is sent out on the day we publish a story. Get an alert directly in your inbox to read, share and blog about our newest stories.

Contact our  Public Information Office  for media inquiries or interviews.

Related America Counts Stories

More stories.

Some content on this site is available in several different electronic formats. Some of the files may require a plug-in or additional software to view.

The content on this page includes a link to a non-government website. Our linking to these sites does not constitute an endorsement of any products, services or the information found on them. Once you link to another site you are subject to the policies of the new site.

Business | Equal education, unequal pay: Why is there…

Share this:.

• Click to share on Facebook (Opens in new window)
• Click to share on Twitter (Opens in new window)

Baltimore Sun eNewspaper

• Real Estate
• Top Workplaces
• Best Reviews

Business | Equal education, unequal pay: Why is there still a gender pay gap in 2024?

Women still make about 71 cents on the dollar compared with men at the same education level..

By Claire Savage, Associated Press

CHICAGO (AP) — Not even education can close the pay gap that persists between women and men, according to a recent  U.S. Census Bureau report .

Whether women earn a post-secondary certificate or graduate from a top-tier university, they still make about 71 cents on the dollar compared with men at the same education level,  Census Bureau research found .

That difference is coming into stark view on  Equal Pay Day , and in spite of the fact that women comprise  more than half  of college-educated workers and participate in the labor force at  record rates .

Rather than comparing full-time working men to full-time working women, the Feb. 22 Census Bureau report juxtaposes men and women with the same education caliber: graduates of certificate degree programs and those who hold bachelor’s degrees from the most selective universities, explained economist Kendall Houghton, a co-author of the research. The report also includes graduates who may have opted out of the labor force, such as women taking on child care responsibilities.

“The main point here is that there’s a substantial gap at every single level,” added Census Bureau economist and co-author Ariel Binder.

Field of study, choice of occupation and hours account for much of the discrepancy, but not all. Field of study, for instance, contributes to the pay gap much more for top graduates (24.6%), but for less selective degree holders accounted for only a sliver (3.8%). And the number of hours and weeks worked affect the pay gap more for certificate earners (26.4%) than selective bachelor’s degree earners (11.3%), suggesting there is a bigger gender difference in work participation for certificate holders, Binder said.

At the same time, about 31% of the gap for each education level remains unexplained, suggesting less easily measured factors such as gender stereotypes and discrimination may be at play.

Chantel Adams says she isn’t surprised that the gender pay gap persists even among men and women with the same level and quality of education, or that the gap is wider for Black and Hispanic women.

A senior marketing executive who holds an MBA from University of North Carolina’s Kenan-Flagler Business School, Adams said her qualifications aren’t enough to counteract the headwinds she faces in her career as a Black woman.

Despite taking on extra responsibilities and an undisputedly strong performance, Adams said she was turned down for a promotion because she was told that “I was so articulate and sharp that it was intimidating to some people.”

“I have nearly $300,000 of post-high school education. It would be surprising if I weren’t articulate and sharp,” said Adams, who is based in Durham, North Carolina.

She said her peers at the company — one of whom did not have an MBA — were promoted while she was held back two years in a row.

“It’s unreasonable and unfair to hold someone’s strengths against them,” Adams said. “I would consider that as something that is race-based.”

Broadly, younger women are closer to wage parity with younger men, according to Carolina Aragao, who researches social and demographic trends at Pew Research Center. But the gap widens between the ages of 35 and 44, which coincides with when women are most likely to have a child at home.

“That does not play out the same way for men,” Aragao said, adding that there is actually an opposite phenomenon known as  the fatherhood premium , in which fathers tend to earn more than other workers, including men without children at home.

Despite women making vast gains in C-suite and high-earning industry representation, wage gap improvement has  stalled for about 20 years , Aragao said. Uneven child care and household responsibilities, falling  college wage premiums , and overrepresentation in lower-paying occupations are all contributors to why the pay gap stubbornly remains.

For Adams, the best strategy to overcome them has been to keep changing jobs — six times in 10 years, across multiple states in her case.

“I knew that I needed to be intentional and move with urgency as I navigated my career in order to work against that headwind,” she said. “When those opportunities were not afforded me within one company, I’ve gone elsewhere.”

Adams said job coaching, mentorship, and support from Forte Foundation, a nonprofit focused on women’s advancement, have been instrumental to her success, while salary transparency laws — and even salary transparency within social circles — could help alleviate the significant pay gap challenges women of color face.

But corporate diversity initiatives have been subject to a  growing list of lawsuits  ever since the Supreme Court  struck down affirmative action  in college admissions. Adams said she worries that without affirmative action, corporate racial diversity could decrease, too.

“The big question that is looming over my head and probably many other executive leaders is: What does that do to the pipeline of diverse candidates that we may or may not have 10 years from now?” Adams said.

The Associated Press’ women in the workforce and state government coverage receives financial support from Pivotal Philanthropies. AP is solely responsible for all content. Find AP’s  standards  for working with philanthropies, a list of supporters and funded coverage areas at  AP.org .

More in Business

SUBSCRIBER ONLY

Baltimore orioles | fubo, a ‘cable tv replacement product,’ to add masn this season, giving orioles fans another way to watch games.

US lawmakers say TikTok won’t be banned if it finds a new owner. But that’s easier said than done

Business | New Noodles & Co. CEO pledges menu overhaul

Boeing promises changes after getting poor grades in a government audit of manufacturing quality

Equal education, unequal pay: Why is there still a gender pay gap in 2024?

C HICAGO (AP) — Not even education can close the pay gap that persists between women and men, according to a recent U.S. Census Bureau report .

Whether women earn a post-secondary certificate or graduate from a top-tier university, they still make about 71 cents on the dollar compared with men at the same education level, Census Bureau research found .

That difference is coming into stark view on Equal Pay Day , and in spite of the fact that women comprise more than half of college-educated workers and participate in the labor force at record rates .

Rather than comparing full-time working men to full-time working women, the Feb. 22 Census Bureau report juxtaposes men and women with the same education caliber: graduates of certificate degree programs and those who hold bachelor’s degrees from the most selective universities, explained economist Kendall Houghton, a co-author of the research. The report also includes graduates who may have opted out of the labor force, such as women taking on child care responsibilities.

“The main point here is that there’s a substantial gap at every single level,” added Census Bureau economist and co-author Ariel Binder.

Field of study, choice of occupation and hours account for much of the discrepancy, but not all. Field of study, for instance, contributes to the pay gap much more for top graduates (24.6%), but for less selective degree holders accounted for only a sliver (3.8%). And the number of hours and weeks worked affect the pay gap more for certificate earners (26.4%) than selective bachelor’s degree earners (11.3%), suggesting there is a bigger gender difference in work participation for certificate holders, Binder said.

At the same time, about 31% of the gap for each education level remains unexplained, suggesting less easily measured factors such as gender stereotypes and discrimination may be at play.

Chantel Adams says she isn’t surprised that the gender pay gap persists even among men and women with the same level and quality of education, or that the gap is wider for Black and Hispanic women.

A senior marketing executive who holds an MBA from University of North Carolina’s Kenan-Flagler Business School, Adams said her qualifications aren’t enough to counteract the headwinds she faces in her career as a Black woman.

Despite taking on extra responsibilities and an undisputedly strong performance, Adams said she was turned down for a promotion because she was told that “I was so articulate and sharp that it was intimidating to some people.”

“I have nearly $300,000 of post-high school education. It would be surprising if I weren’t articulate and sharp,” said Adams, who is based in Durham, North Carolina.

She said her peers at the company — one of whom did not have an MBA — were promoted while she was held back two years in a row.

“It’s unreasonable and unfair to hold someone’s strengths against them,” Adams said. “I would consider that as something that is race-based.”

Broadly, younger women are closer to wage parity with younger men, according to Carolina Aragao, who researches social and demographic trends at Pew Research Center. But the gap widens between the ages of 35 and 44, which coincides with when women are most likely to have a child at home.

“That does not play out the same way for men," Aragao said, adding that there is actually an opposite phenomenon known as the fatherhood premium , in which fathers tend to earn more than other workers, including men without children at home.

Despite women making vast gains in C-suite and high-earning industry representation, wage gap improvement has stalled for about 20 years , Aragao said. Uneven child care and household responsibilities, falling college wage premiums , and overrepresentation in lower-paying occupations are all contributors to why the pay gap stubbornly remains.

For Adams, the best strategy to overcome them has been to keep changing jobs — six times in 10 years, across multiple states in her case.

“I knew that I needed to be intentional and move with urgency as I navigated my career in order to work against that headwind,” she said. “When those opportunities were not afforded me within one company, I’ve gone elsewhere.”

Adams said job coaching, mentorship, and support from Forte Foundation, a nonprofit focused on women’s advancement, have been instrumental to her success, while salary transparency laws — and even salary transparency within social circles — could help alleviate the significant pay gap challenges women of color face.

But corporate diversity initiatives have been subject to a growing list of lawsuits ever since the Supreme Court struck down affirmative action in college admissions. Adams said she worries that without affirmative action, corporate racial diversity could decrease, too.

"The big question that is looming over my head and probably many other executive leaders is: What does that do to the pipeline of diverse candidates that we may or may not have 10 years from now?" Adams said.

The Associated Press’ women in the workforce and state government coverage receives financial support from Pivotal Ventures. AP is solely responsible for all content. Find AP’s standards for working with philanthropies, a list of supporters and funded coverage areas at AP.org .