methods of problem solving in mathematics

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.

5 Teaching Mathematics Through Problem Solving

Janet Stramel

In his book “How to Solve It,” George Pólya (1945) said, “One of the most important tasks of the teacher is to help his students. This task is not quite easy; it demands time, practice, devotion, and sound principles. The student should acquire as much experience of independent work as possible. But if he is left alone with his problem without any help, he may make no progress at all. If the teacher helps too much, nothing is left to the student. The teacher should help, but not too much and not too little, so that the student shall have a reasonable share of the work.” (page 1)

What is a problem  in mathematics? A problem is “any task or activity for which the students have no prescribed or memorized rules or methods, nor is there a perception by students that there is a specific ‘correct’ solution method” (Hiebert, et. al., 1997). Problem solving in mathematics is one of the most important topics to teach; learning to problem solve helps students develop a sense of solving real-life problems and apply mathematics to real world situations. It is also used for a deeper understanding of mathematical concepts. Learning “math facts” is not enough; students must also learn how to use these facts to develop their thinking skills.

According to NCTM (2010), the term “problem solving” refers to mathematical tasks that have the potential to provide intellectual challenges for enhancing students’ mathematical understanding and development. When you first hear “problem solving,” what do you think about? Story problems or word problems? Story problems may be limited to and not “problematic” enough. For example, you may ask students to find the area of a rectangle, given the length and width. This type of problem is an exercise in computation and can be completed mindlessly without understanding the concept of area. Worthwhile problems  includes problems that are truly problematic and have the potential to provide contexts for students’ mathematical development.

There are three ways to solve problems: teaching for problem solving, teaching about problem solving, and teaching through problem solving.

Teaching for problem solving begins with learning a skill. For example, students are learning how to multiply a two-digit number by a one-digit number, and the story problems you select are multiplication problems. Be sure when you are teaching for problem solving, you select or develop tasks that can promote the development of mathematical understanding.

Teaching about problem solving begins with suggested strategies to solve a problem. For example, “draw a picture,” “make a table,” etc. You may see posters in teachers’ classrooms of the “Problem Solving Method” such as: 1) Read the problem, 2) Devise a plan, 3) Solve the problem, and 4) Check your work. There is little or no evidence that students’ problem-solving abilities are improved when teaching about problem solving. Students will see a word problem as a separate endeavor and focus on the steps to follow rather than the mathematics. In addition, students will tend to use trial and error instead of focusing on sense making.

Teaching through problem solving  focuses students’ attention on ideas and sense making and develops mathematical practices. Teaching through problem solving also develops a student’s confidence and builds on their strengths. It allows for collaboration among students and engages students in their own learning.

Consider the following worthwhile-problem criteria developed by Lappan and Phillips (1998):

• The problem has important, useful mathematics embedded in it.
• The problem requires high-level thinking and problem solving.
• The problem contributes to the conceptual development of students.
• The problem creates an opportunity for the teacher to assess what his or her students are learning and where they are experiencing difficulty.
• The problem can be approached by students in multiple ways using different solution strategies.
• The problem has various solutions or allows different decisions or positions to be taken and defended.
• The problem encourages student engagement and discourse.
• The problem connects to other important mathematical ideas.
• The problem promotes the skillful use of mathematics.
• The problem provides an opportunity to practice important skills.

Of course, not every problem will include all of the above. Sometimes, you will choose a problem because your students need an opportunity to practice a certain skill.

Key features of a good mathematics problem includes:

• It must begin where the students are mathematically.
• The feature of the problem must be the mathematics that students are to learn.
• It must require justifications and explanations for both answers and methods of solving.

Problem solving is not a  neat and orderly process. Think about needlework. On the front side, it is neat and perfect and pretty.

But look at the b ack.

It is messy and full of knots and loops. Problem solving in mathematics is also like this and we need to help our students be “messy” with problem solving; they need to go through those knots and loops and learn how to solve problems with the teacher’s guidance.

When you teach through problem solving , your students are focused on ideas and sense-making and they develop confidence in mathematics!

Mathematics Tasks and Activities that Promote Teaching through Problem Solving

Choosing the Right Task

Selecting activities and/or tasks is the most significant decision teachers make that will affect students’ learning. Consider the following questions:

• Teachers must do the activity first. What is problematic about the activity? What will you need to do BEFORE the activity and AFTER the activity? Additionally, think how your students would do the activity.
• What mathematical ideas will the activity develop? Are there connections to other related mathematics topics, or other content areas?
• Can the activity accomplish your learning objective/goals?

Low Floor High Ceiling Tasks

By definition, a “ low floor/high ceiling task ” is a mathematical activity where everyone in the group can begin and then work on at their own level of engagement. Low Floor High Ceiling Tasks are activities that everyone can begin and work on based on their own level, and have many possibilities for students to do more challenging mathematics. One gauge of knowing whether an activity is a Low Floor High Ceiling Task is when the work on the problems becomes more important than the answer itself, and leads to rich mathematical discourse [Hover: ways of representing, thinking, talking, agreeing, and disagreeing; the way ideas are exchanged and what the ideas entail; and as being shaped by the tasks in which students engage as well as by the nature of the learning environment].

The strengths of using Low Floor High Ceiling Tasks:

• Allows students to show what they can do, not what they can’t.
• Provides differentiation to all students.
• Promotes a positive classroom environment.
• Advances a growth mindset in students
• Aligns with the Standards for Mathematical Practice

Examples of some Low Floor High Ceiling Tasks can be found at the following sites:

• YouCubed – under grades choose Low Floor High Ceiling
• NRICH Creating a Low Threshold High Ceiling Classroom
• Inside Mathematics Problems of the Month

Math in 3-Acts

Math in 3-Acts was developed by Dan Meyer to spark an interest in and engage students in thought-provoking mathematical inquiry. Math in 3-Acts is a whole-group mathematics task consisting of three distinct parts:

Act One is about noticing and wondering. The teacher shares with students an image, video, or other situation that is engaging and perplexing. Students then generate questions about the situation.

In Act Two , the teacher offers some information for the students to use as they find the solutions to the problem.

Act Three is the “reveal.” Students share their thinking as well as their solutions.

“Math in 3 Acts” is a fun way to engage your students, there is a low entry point that gives students confidence, there are multiple paths to a solution, and it encourages students to work in groups to solve the problem. Some examples of Math in 3-Acts can be found at the following websites:

• Dan Meyer’s Three-Act Math Tasks
• Graham Fletcher3-Act Tasks ]
• Math in 3-Acts: Real World Math Problems to Make Math Contextual, Visual and Concrete

Number Talks

Number talks are brief, 5-15 minute discussions that focus on student solutions for a mental math computation problem. Students share their different mental math processes aloud while the teacher records their thinking visually on a chart or board. In addition, students learn from each other’s strategies as they question, critique, or build on the strategies that are shared.. To use a “number talk,” you would include the following steps:

• The teacher presents a problem for students to solve mentally.
• Provide adequate “ wait time .”
• The teacher calls on a students and asks, “What were you thinking?” and “Explain your thinking.”
• For each student who volunteers to share their strategy, write their thinking on the board. Make sure to accurately record their thinking; do not correct their responses.
• Invite students to question each other about their strategies, compare and contrast the strategies, and ask for clarification about strategies that are confusing.

“Number Talks” can be used as an introduction, a warm up to a lesson, or an extension. Some examples of Number Talks can be found at the following websites:

• Inside Mathematics Number Talks
• Number Talks Build Numerical Reasoning

Saying “This is Easy”

“This is easy.” Three little words that can have a big impact on students. What may be “easy” for one person, may be more “difficult” for someone else. And saying “this is easy” defeats the purpose of a growth mindset classroom, where students are comfortable making mistakes.

When the teacher says, “this is easy,” students may think,

• “Everyone else understands and I don’t. I can’t do this!”
• Students may just give up and surrender the mathematics to their classmates.
• Students may shut down.

Instead, you and your students could say the following:

• “I think I can do this.”
• “I have an idea I want to try.”
• “I’ve seen this kind of problem before.”

Tracy Zager wrote a short article, “This is easy”: The Little Phrase That Causes Big Problems” that can give you more information. Read Tracy Zager’s article here.

Using “Worksheets”

Do you want your students to memorize concepts, or do you want them to understand and apply the mathematics for different situations?

What is a “worksheet” in mathematics? It is a paper and pencil assignment when no other materials are used. A worksheet does not allow your students to use hands-on materials/manipulatives [Hover: physical objects that are used as teaching tools to engage students in the hands-on learning of mathematics]; and worksheets are many times “naked number” with no context. And a worksheet should not be used to enhance a hands-on activity.

Students need time to explore and manipulate materials in order to learn the mathematics concept. Worksheets are just a test of rote memory. Students need to develop those higher-order thinking skills, and worksheets will not allow them to do that.

One productive belief from the NCTM publication, Principles to Action (2014), states, “Students at all grade levels can benefit from the use of physical and virtual manipulative materials to provide visual models of a range of mathematical ideas.”

You may need an “activity sheet,” a “graphic organizer,” etc. as you plan your mathematics activities/lessons, but be sure to include hands-on manipulatives. Using manipulatives can

• Provide your students a bridge between the concrete and abstract
• Serve as models that support students’ thinking
• Provide another representation
• Support student engagement
• Give students ownership of their own learning.

Adapted from “ The Top 5 Reasons for Using Manipulatives in the Classroom ”.

any task or activity for which the students have no prescribed or memorized rules or methods, nor is there a perception by students that there is a specific ‘correct’ solution method

should be intriguing and contain a level of challenge that invites speculation and hard work, and directs students to investigate important mathematical ideas and ways of thinking toward the learning

involves teaching a skill so that a student can later solve a story problem

when we teach students how to problem solve

teaching mathematics content through real contexts, problems, situations, and models

a mathematical activity where everyone in the group can begin and then work on at their own level of engagement

20 seconds to 2 minutes for students to make sense of questions

Mathematics Methods for Early Childhood Copyright © 2021 by Janet Stramel is licensed under a Creative Commons Attribution 4.0 International License , except where otherwise noted.

Share This Book

• 1st Grade Math
• 2nd Grade Math
• 3rd Grade Math
• 4th Grade Math
• 5th Grade Math
• 6th Grade Math
• 7th Grade Math
• 8th Grade Math
• Knowledge Base
• Math for kids

10 Strategies for Problem Solving in Math

Created: December 25, 2023

Last updated: January 6, 2024

When faced with problem-solving, children often get stuck. Word puzzles and math questions with an unknown variable, like x, usually confuse them. Therefore, this article discusses math strategies and how your students may use them since instructors often have to lead students through this problem-solving maze.

What Are Problem Solving Strategies in Math?

If you want to fix a problem, you need a solid plan. Math strategies for problem solving are ways of tackling math in a way that guarantees better outcomes. These strategies simplify math for kids so that less time is spent figuring out the problem. Both those new to mathematics and those more knowledgeable about the subject may benefit from these methods.

There are several methods to apply problem-solving procedures in math, and each strategy is different. While none of these methods failsafe, they may help your student become a better problem solver, particularly when paired with practice and examples. The more math problems kids tackle, the more math problem solving skills they acquire, and practice is the key.

Strategies for Problem-solving in Math

Even if a student is not a math wiz, a suitable solution to mathematical problems in math may help them discover answers. There is no one best method for helping students solve arithmetic problems, but the following ten approaches have shown to be very effective.

Understand the Problem

Understanding the nature of math problems is a prerequisite to solving them. They need to specify what kind of issue it is ( fraction problem , word problem, quadratic equation, etc.). Searching for keywords in the math problem, revisiting similar questions, or consulting the internet are all great ways to strengthen their grasp of the material. This step keeps the pupil on track.

Math for Kids

Guess and Check

One of the time-intensive strategies for resolving mathematical problems is the guess and check method. In this approach, students keep guessing until they get the answer right.

After assuming how to solve a math issue, students should reintroduce that assumption to check for correctness. While the approach may appear cumbersome, it is typically successful in revealing patterns in a child’s thought process.

Work It Out

Encourage pupils to record their thinking process as they go through a math problem. Since this technique requires an initial comprehension of the topic, it serves as a self-monitoring method for mathematics students. If they immediately start solving the problem, they risk making mistakes.

Students may keep track of their ideas and fix their math problems as they go along using this method. A youngster may still need you to explain their methods of solving the arithmetic questions on the extra page. This confirmation stage etches the steps they took to solve the problem in their minds.

Work Backwards

In mathematics, a fresh perspective is sometimes the key to a successful solution. Young people need to know that the ability to recreate math problems is valuable in many professional fields, including project management and engineering.

Students may better prepare for difficulties in real-world circumstances by using the “Work Backwards” technique. The end product may be used as a start-off point to identify the underlying issue.

In most cases, a visual representation of a math problem may help youngsters understand it better. Some of the most helpful math tactics for kids include having them play out the issue and picture how to solve it.

One way to visualize a workout is to use a blank piece of paper to draw a picture or make tally marks. Students might also use a marker and a whiteboard to draw as they demonstrate the technique before writing it down.

Find a Pattern

Kids who use pattern recognition techniques can better grasp math concepts and retain formulae. The most remarkable technique for problem solving in mathematics is to help students see patterns in math problems by instructing them how to extract and list relevant details. This method may be used by students when learning shapes and other topics that need repetition.

Students may use this strategy to spot patterns and fill in the blanks. Over time, this strategy will help kids answer math problems quickly.

When faced with a math word problem, it might be helpful to ask, “What are some possible solutions to this issue?” It encourages you to give the problem more thought, develop creative solutions, and prevent you from being stuck in a rut. So, tell the pupils to think about the math problems and not just go with the first solution that comes to mind.

Draw a Picture or Diagram

Drawing a picture of a math problem can help kids understand how to solve it, just like picturing it can help them see it. Shapes or numbers could be used to show the forms to keep things easy. Kids might learn how to use dots or letters to show the parts of a pattern or graph if you teach them.

Charts and graphs can be useful even when math isn’t involved. Kids can draw pictures of the ideas they read about to help them remember them after they’ve learned them. The plan for how to solve the mathematical problem will help kids understand what the problem is and how to solve it.

Trial and Error Method

The trial and error method may be one of the most common problem solving strategies for kids to figure out how to solve problems. But how well this strategy is used will determine how well it works. Students have a hard time figuring out math questions if they don’t have clear formulas or instructions.

They have a better chance of getting the correct answer, though, if they first make a list of possible answers based on rules they already know and then try each one. Don’t be too quick to tell kids they shouldn’t learn by making mistakes.

Review Answers with Peers

It’s fun to work on your math skills with friends by reviewing the answers to math questions together. If different students have different ideas about how to solve the same problem, get them to share their thoughts with the class.

During class time, kids’ ways of working might be compared. Then, students can make their points stronger by fixing these problems.

Check out the Printable Math Worksheets for Your Kids!

There are different ways to solve problems that can affect how fast and well students do on math tests. That’s why they need to learn the best ways to do things. If students follow the steps in this piece, they will have better experiences with solving math questions.

Jessica is a a seasoned math tutor with over a decade of experience in the field. With a BSc and Master’s degree in Mathematics, she enjoys nurturing math geniuses, regardless of their age, grade, and skills. Apart from tutoring, Jessica blogs at Brighterly. She also has experience in child psychology, homeschooling and curriculum consultation for schools and EdTech websites.

After-School Math Program

• Boost Math Skills After School!
• Join our Math Program, Ideal for Students in Grades 1-8!

Kid’s grade

After-School Math Program Boost Your Child's Math Abilities! Ideal for 1st-8th Graders, Perfectly Synced with School Curriculum!

Related posts

December 26, 2023

Exploring Geometry Through Play: Geometry Games for 5th Grade

As students start learning, they have fun with shapes, angles, and puzzles about space. This helps them understand basic geometry. To make learning more fun, it is essential to spice it up with fun videos, games and other interactive activities to boost their understanding of the concept.  Let’s explore some fun geometry games for 5th […]

January 10, 2024

10 Ideas of Fun Last Day of School Activities

The last days of the school year always feel unique to students and teachers. After all, everyone is excited about the deserved sun-drenched summer break and carefree mornings! While being relaxed and looking forward to a few months of leisure, students want to meet friends and play outdoors. They would better leave math classes for […]

December 29, 2023

How to Teach Division – A Simple Step by Step Guide

Division is fourth among the first four basic math operations that a child should learn. These math operations include adding, subtracting, multiplying, and dividing. They form the basis of all math problems. Children do not necessarily need to know the first three operations to understand division, although, as we will see, they are crucial. Teaching […]

We use cookies to help give you the best service possible. If you continue to use the website we will understand that you consent to the Terms and Conditions. These cookies are safe and secure. We will not share your history logs with third parties. Learn More

Or search by topic

Number and algebra

• The Number System and Place Value
• Calculations and Numerical Methods
• Fractions, Decimals, Percentages, Ratio and Proportion
• Properties of Numbers
• Patterns, Sequences and Structure
• Algebraic expressions, equations and formulae
• Coordinates, Functions and Graphs

Geometry and measure

• Angles, Polygons, and Geometrical Proof
• 3D Geometry, Shape and Space
• Measuring and calculating with units
• Transformations and constructions
• Pythagoras and Trigonometry
• Vectors and Matrices

Probability and statistics

• Handling, Processing and Representing Data
• Probability

Working mathematically

• Thinking mathematically
• Mathematical mindsets
• Cross-curricular contexts
• Physical and digital manipulatives

For younger learners

• Early Years Foundation Stage

Advanced mathematics

• Decision Mathematics and Combinatorics
• Advanced Probability and Statistics

Problem Solving, Using and Applying and Functional Mathematics

Problem solving.

The problem-solving process can be described as a journey from meeting a problem for the first time to finding a solution, communicating it and evaluating the route. There are many models of the problem-solving process but they all have a similar structure. One model is given below. Although implying a linear process from comprehension through to evaluation, the model is more of a flow backward and forward, revisiting and revising on the problem-solving journey.

Comprehension

Representation.

• Can they represent the situation mathematically?
• What is it that they are trying to find?
• What do they think the answer might be (conjecturing and hypothesising)?
• What might they need to find out before they can get started?

Planning, analysis and synthesis

Having understood what the problem is about and established what needs finding, this stage is about planning a pathway to the solution. It is within this process that you might encourage pupils to think about whether they have seen something similar before and what strategies they adopted then. This will help them to identify appropriate methods and tools. Particular knowledge and skills gaps that need addressing may become evident at this stage.

Execution and communication

During the execution phase, pupils might identify further related problems they wish to investigate. They will need to consider how they will keep track of what they have done and how they will communicate their findings. This will lead on to interpreting results and drawing conclusions.

Pupils can learn as much from reflecting on and evaluating what they have done as they can from the process of solving the problem itself. During this phase pupils should be expected to reflect on the effectiveness of their approach as well as other people's approaches, justify their conclusions and assess their own learning. Evaluation may also lead to thinking about other questions that could now be investigated.

Using and Applying Mathematics

Aspects of using and applying reflect skills that can be developed through problem solving. For example:

In planning and executing a problem, problem solvers may need to:

• select and use appropriate and efficient techniques and strategies to solve problems
• identify what further information may be required in order to pursue a particular line of enquiry and give reasons for following or rejecting particular approaches
• break down a complex calculation problem into simpler steps before attempting a solution and justify their choice of methods
• make mental estimates of the answers to calculations
• present answers to sensible levels of accuracy; understand how errors are compounded in certain calculations.

During problem solving, solvers need to communicate their mathematics for example by:

• discussing their work and explaining their reasoning using a range of mathematical language and notation
• using a variety of strategies and diagrams for establishing algebraic or graphical representations of a problem and its solution
• moving from one form of representation to another to get different perspectives on the problem
• presenting and interpreting solutions in the context of the original problem
• using notation and symbols correctly and consistently within a given problem
• examining critically, improve, then justifying their choice of mathematical presentation
• presenting a concise, reasoned argument.

Problem solvers need to reason mathematically including through:

• exploring, identifying, and using pattern and symmetry in algebraic contexts, investigating whether a particular case may be generalised further and understanding the importance of a counter-example; identifying exceptional cases
• understanding the difference between a practical demonstration and a proof
• showing step-by-step deduction in solving a problem; deriving proofs using short chains of deductive reasoning
• recognising the significance of stating constraints and assumptions when deducing results
• recognising the limitations of any assumptions that are made and the effect that varying the assumptions may have on the solution to a problem.

Functional Mathematics

Functional maths requires learners to be able to use mathematics in ways that make them effective and involved as citizens, able to operate confidently in life and to work in a wide range of contexts. The key processes of Functional Skills reflect closely the problem solving model but within three phases:

• Making sense of situations and representing them
• Processing and using the mathematics
• Interpreting and communicating the results of the analysis

You may also like

A group activity using visualisation of squares and triangles.

Seven Squares - Group-worthy Task

Choose a couple of the sequences. Try to picture how to make the next, and the next, and the next... Can you describe your reasoning?

• PRO Courses Guides New Tech Help Pro Expert Videos About wikiHow Pro Upgrade Sign In
• EDIT Edit this Article
• EXPLORE Tech Help Pro About Us Random Article Quizzes Request a New Article Community Dashboard This Or That Game Popular Categories Arts and Entertainment Artwork Books Movies Computers and Electronics Computers Phone Skills Technology Hacks Health Men's Health Mental Health Women's Health Relationships Dating Love Relationship Issues Hobbies and Crafts Crafts Drawing Games Education & Communication Communication Skills Personal Development Studying Personal Care and Style Fashion Hair Care Personal Hygiene Youth Personal Care School Stuff Dating All Categories Arts and Entertainment Finance and Business Home and Garden Relationship Quizzes Cars & Other Vehicles Food and Entertaining Personal Care and Style Sports and Fitness Computers and Electronics Health Pets and Animals Travel Education & Communication Hobbies and Crafts Philosophy and Religion Work World Family Life Holidays and Traditions Relationships Youth
• Browse Articles
• Learn Something New
• Quizzes Hot
• This Or That Game New
• Train Your Brain
• Explore More
• Support wikiHow
• About wikiHow
• Log in / Sign up
• Education and Communications
• Mathematics

How to Solve Math Problems

Last Updated: May 16, 2023 Fact Checked

This article was co-authored by Daron Cam . Daron Cam is an Academic Tutor and the Founder of Bay Area Tutors, Inc., a San Francisco Bay Area-based tutoring service that provides tutoring in mathematics, science, and overall academic confidence building. Daron has over eight years of teaching math in classrooms and over nine years of one-on-one tutoring experience. He teaches all levels of math including calculus, pre-algebra, algebra I, geometry, and SAT/ACT math prep. Daron holds a BA from the University of California, Berkeley and a math teaching credential from St. Mary's College. This article has been fact-checked, ensuring the accuracy of any cited facts and confirming the authority of its sources. This article has been viewed 588,133 times.

Although math problems may be solved in different ways, there is a general method of visualizing, approaching and solving math problems that may help you to solve even the most difficult problem. Using these strategies can also help you to improve your math skills overall. Keep reading to learn about some of these math problem solving strategies.

Understanding the Problem

• Draw a Venn diagram. A Venn diagram shows the relationships among the numbers in your problem. Venn diagrams can be especially helpful with word problems.
• Draw a graph or chart.
• Arrange the components of the problem on a line.
• Draw simple shapes to represent more complex features of the problem.

Developing a Plan

Solving the Problem

Expert Q&A

• Seek help from your teacher or a math tutor if you get stuck or if you have tried multiple strategies without success. Your teacher or a math tutor may be able to easily identify what is wrong and help you to understand how to correct it. Thanks Helpful 1 Not Helpful 1
• Keep practicing sums and diagrams. Go through the concept your class notes regularly. Write down your understanding of the methods and utilize it. Thanks Helpful 2 Not Helpful 0

You Might Also Like

• ↑ Daron Cam. Math Tutor. Expert Interview. 29 May 2020.
• ↑ http://www.interventioncentral.org/academic-interventions/math/math-problem-solving-combining-cognitive-metacognitive-strategies
• ↑ http://tutorial.math.lamar.edu/Extras/StudyMath/ProblemSolving.aspx
• ↑ https://math.berkeley.edu/~gmelvin/polya.pdf

About This Article

To solve a math problem, try rewriting the problem in your own words so it's easier to solve. You can also make a drawing of the problem to help you figure out what it's asking you to do. If you're still completely stuck, try solving a different problem that's similar but easier and then use the same steps to solve the harder problem. Even if you can't figure out how to solve it, try to make an educated guess instead of leaving the question blank. To learn how to come up with a solid plan to use to help you solve a math problem, scroll down! Did this summary help you? Yes No

• Send fan mail to authors

Reader Success Stories

Thakgalo Mokalapa

Feb 16, 2018

Did this article help you?

Offor Chukwuemeka

May 17, 2018

Jan 21, 2017

May 3, 2018

Featured Articles

Trending Articles

Watch Articles

• Terms of Use
• Privacy Policy
• Do Not Sell or Share My Info
• Not Selling Info

Don’t miss out! Sign up for

wikiHow’s newsletter

• Prodigy Math
• Prodigy English

From our blog

• Is a Premium Membership Worth It?
• Promote a Growth Mindset
• Help Your Child Who's Struggling with Math
• Parent's Guide to Prodigy
• Assessments
• Math Curriculum Coverage
• English Curriculum Coverage
• Game Portal

How to Solve Math Problems Faster: 15 Techniques to Show Students

Written by Marcus Guido

• Teaching Strategies

“Test time. No calculators.”

You’ll intimidate many students by saying this, but teaching techniques to solve math problems with ease and speed can make it less daunting.

This can also  make math more rewarding . Instead of relying on calculators, students learn strategies that can improve their concentration and estimation skills while building number sense. And, while there are educators who  oppose math “tricks”  for valid reasons, proponents point to benefits such as increased confidence to handle difficult problems.

Here are 15 techniques to show students,  helping them solve math problems faster:

Addition and Subtraction

1. two-step addition.

Many students struggle when learning to add integers of three digits or higher together, but changing the process’s steps can make it easier.

The first step is to  add what’s easy.  The second step is to  add the rest.

Let’s say students must find the sum of 393 and 89. They should quickly see that adding 7 onto 393 will equal 400 — an easier number to work with. To balance the equation, they can then subtract 7 from 89.

Broken down, the process is:

• (393 + 7) + (89 – 7)

With this fast technique, big numbers won’t look as scary now.

2. Two-Step Subtraction

There’s a similar method for subtraction.

Remove what’s easy. Then remove what’s left.

Suppose students must find the difference of 567 and 153. Most will feel that 500 is a simpler number than 567. So, they just have to take away 67 from the minuend — 567 — and the subtrahend — 153 — before solving the equation.

Here’s the process:

• (567 – 67) – (153 – 67)

Instead of two complex numbers, students will only have to tackle one.

3. Subtracting from 1,000

You can  give students confidence  to handle four-digit integers with this fast technique.

To subtract a number from 1,000, subtract that number’s first two digits from 9. Then, subtract the final digit from 10.

Let’s say students must solve 1,000 – 438.  Here are the steps:

This also applies to 10,000, 100,000 and other integers that follow this pattern.

Multiplication and Division

4. doubling and halving.

When students have to multiply two integers, they can speed up the process when one is an even number. They just need to  halve the even number and double the other number.

Students can stop the process when they can no longer halve the even integer, or when the equation becomes manageable.

Using 33 x 48 as an example,  here’s the process:

The only prerequisite is understanding the 2 times table.

5. Multiplying by Powers of 2

This tactic is a speedy variation of doubling and halving.

It simplifies multiplication if a number in the equation is a power of 2, meaning it works for 2, 4, 8, 16 and so on.

Here’s what to do:  For each power of 2 that makes up that number, double the other number.

For example, 9 x 16 is the same thing as 9 x (2 x 2 x 2 x 2) or 9 x 24. Students can therefore double 9 four times to reach the answer:

Unlike doubling and halving, this technique demands an understanding of exponents along with a strong command of the 2 times table.

6. Multiplying by 9

For most students, multiplying by 9 — or 99, 999 and any number that follows this pattern — is difficult compared with multiplying by a power of 10.

But there’s an easy tactic to solve this issue, and  it has two parts.

First, students round up the 9  to 10. Second, after solving the new equation, they subtract the number they just multiplied by 10 from the answer.

For example, 67 x 9 will lead to the same answer as 67 x 10 – 67. Following the order of operations will give a result of 603. Similarly, 67 x 99 is the same as 67 x 100 – 67.

Despite more steps, altering the equation this way is usually faster.

7. Multiplying by 11

There’s an easier way for multiplying two-digit integers by 11.

Let’s say students must find the product of 11 x 34.

The idea is to put a space between the digits, making it 3_4. Then, add the two digits together and put the sum in the space.

The answer is 374.

What happens if the sum is two digits? Students would put the second digit in the space and add 1 to the digit to the left of the space.  For example:

It’s multiplication without having to multiply.

8. Multiplying Even Numbers by 5

This technique only requires basic division skills.

There are two steps,  and 5 x 6 serves as an example. First, divide the number being multiplied by 5 — which is 6 — in half. Second, add 0 to the right of number.

The result is 30, which is the correct answer.

It’s an ideal, easy technique for students mastering the 5 times table.

9. Multiplying Odd Numbers by 5

This is another time-saving tactic that works well when teaching students the 5 times table.

This one has three steps,  which 5 x 7 exemplifies.

First, subtract 1 from the number being multiplied by 5, making it an even number. Second, cut that number in half — from 6 to 3 in this instance. Third, add 5 to the right of the number.

The answer is 35.

Who needs a calculator?

10. Squaring a Two-Digit Number that Ends with 1

Squaring a high two-digit number can be tedious, but there’s a shortcut if 1 is the second digit.

There are four steps to this shortcut,  which 812 exemplifies:

• Subtract 1 from the integer: 81 – 1 = 80
• Square the integer, which is now an easier number: 80 x 80 = 6,400
• Add the integer with the resulting square twice: 6,400 + 80 + 80 = 6,560
• Add 1: 6,560 + 1 = 6,561

This work-around eliminates the difficulty surrounding the second digit, allowing students to work with multiples of 10.

11. Squaring a Two-Digit Numbers that Ends with 5

Squaring numbers ending in 5 is easier, as there are  only two parts of the process.

First, students will always make 25 the product’s last digits.

Second, to determine the product’s first digits, students must multiply the number’s first digit — 9, for example — by the integer that’s one higher — 10, in this case.

So, students would solve 952 by designating 25 as the last two digits. They would then multiply 9 x 10 to receive 90. Putting these numbers together, the  result is 9,025.

Just like that, a hard problem becomes easy multiplication for many students.

12. Calculating Percentages

Cross-multiplication is an  important skill  to develop, but there’s an easier way to calculate percentages.

For example, if students want to know what 65% of 175 is, they can multiply the numbers together and move the decimal place two digits to the left.

The result is 113.75, which is indeed the correct answer.

This shortcut is a useful timesaver on tests and quizzes.

13. Balancing Averages

To determine the average among a set of numbers, students can balance them instead of using a complex formula.

Suppose a student wants to volunteer for an average of 10 hours a week over a period of four weeks. In the first three weeks, the student worked for 10, 12 and 14 hours.

To determine the number of hours required in the fourth week, the student must  add how much he or she surpassed or missed the target average  in the other weeks:

• 14 hours – 10 hours = 4 hours
• 12 – 10 = 2
• 10 – 10 = 0
• 4 hours + 2 hours + 0 hours = 6 hours

To learn the number of hours for the final week, the student must  subtract the sum from the target average:

• 10 hours – 6 hours = 4 hours

With practice, this method may not even require pencil and paper. That’s how easy it is. 

Word Problems

14. identifying buzzwords.

Students who struggle to translate  word problems  into equations will benefit from learning how to spot buzzwords — phrases that indicate specific actions.

This isn’t a trick. It’s a tactic.

Teach students to look for these buzzwords,  and what skill they align with in most contexts:

Be sure to include buzzwords that typically appear in their textbooks (or other classroom  math books ), as well as ones you use on tests and assignments.

As a result, they should have an  easier time processing word problems .

15. Creating Sub-Questions

For complex word problems, show students how to dissect the question by answering three specific sub-questions.

Each student should ask him or herself:

• What am I looking for?  — Students should read the question over and over, looking for buzzwords and identifying important details.
• What information do I need?  — Students should determine which facts, figures and variables they need to solve the question. For example, if they determine the question is rooted in subtraction, they need the minuend and subtrahend.
• What information do I have?  — Students should be able to create the core equation using the information in the word problem, after determining which details are important.

These sub-questions help students avoid overload.

Instead of writing and analyzing each detail of the question, they’ll be able to identify key information. If you identify students who are struggling with these, you can use  peer learning  as needed.  

For more fresh approaches to teaching math in your classroom, consider treating your students to a range of  fun math activities .

Final Thoughts About these Ways to Solve Math Problems Faster

Showing these 15 techniques to students can give them the  confidence to tackle tough questions .

They’re also  mental math  exercises, helping them build skills related to focus, logic and critical thinking.

A rewarding class equals an  engaging class . That’s an easy equation to remember.

> Create or log into your teacher account on Prodigy  — a free, adaptive math game that adjusts content to accommodate player trouble spots and learning speeds. Aligned to US and Canadian curricula, it’s loved by more than 500,000 teachers and 15 million students.

Problem Solving in Mathematics

• Math Tutorials
• Pre Algebra & Algebra
• Exponential Decay
• Worksheets By Grade

The main reason for learning about math is to become a better problem solver in all aspects of life. Many problems are multistep and require some type of systematic approach. There are a couple of things you need to do when solving problems. Ask yourself exactly what type of information is being asked for: Is it one of addition, subtraction, multiplication , or division? Then determine all the information that is being given to you in the question.

Mathematician George Pólya’s book, “ How to Solve It: A New Aspect of Mathematical Method ,” written in 1957, is a great guide to have on hand. The ideas below, which provide you with general steps or strategies to solve math problems, are similar to those expressed in Pólya’s book and should help you untangle even the most complicated math problem.

Use Established Procedures

Learning how to solve problems in mathematics is knowing what to look for. Math problems often require established procedures and knowing what procedure to apply. To create procedures, you have to be familiar with the problem situation and be able to collect the appropriate information, identify a strategy or strategies, and use the strategy appropriately.

Problem-solving requires practice. When deciding on methods or procedures to use to solve problems, the first thing you will do is look for clues, which is one of the most important skills in solving problems in mathematics. If you begin to solve problems by looking for clue words, you will find that these words often indicate an operation.

Look for Clue Words

Think of yourself as a math detective. The first thing to do when you encounter a math problem is to look for clue words. This is one of the most important skills you can develop. If you begin to solve problems by looking for clue words, you will find that those words often indicate an operation.

Common clue words for addition  problems:

Common clue words for  subtraction  problems:

• How much more

Common clue words for multiplication problems:

Common clue words for division problems:

Although clue words will vary a bit from problem to problem, you'll soon learn to recognize which words mean what in order to perform the correct operation.

Read the Problem Carefully

This, of course, means looking for clue words as outlined in the previous section. Once you’ve identified your clue words, highlight or underline them. This will let you know what kind of problem you’re dealing with. Then do the following:

• Ask yourself if you've seen a problem similar to this one. If so, what is similar about it?
• What did you need to do in that instance?
• What facts are you given about this problem?
• What facts do you still need to find out about this problem?

Develop a Plan and Review Your Work

Based on what you discovered by reading the problem carefully and identifying similar problems you’ve encountered before, you can then:

• Define your problem-solving strategy or strategies. This might mean identifying patterns, using known formulas, using sketches, and even guessing and checking.
• If your strategy doesn't work, it may lead you to an ah-ha moment and to a strategy that does work.

If it seems like you’ve solved the problem, ask yourself the following:

• Does your solution seem probable?
• Does it answer the initial question?
• Did you answer using the language in the question?
• Did you answer using the same units?

If you feel confident that the answer is “yes” to all questions, consider your problem solved.

Tips and Hints

Some key questions to consider as you approach the problem may be:

• What are the keywords in the problem?
• Do I need a data visual, such as a diagram, list, table, chart, or graph?
• Is there a formula or equation that I'll need? If so, which one?
• Will I need to use a calculator? Is there a pattern I can use or follow?

Read the problem carefully, and decide on a method to solve the problem. Once you've finished working the problem, check your work and ensure that your answer makes sense and that you've used the same terms and or units in your answer.

• 2nd Grade Math Word Problems
• The Horse Problem: A Math Challenge
• 2020-21 Common Application Essay Option 4—Solving a Problem
• How to Use Math Journals in Class
• The Frayer Model for Math
• Algorithms in Mathematics and Beyond
• "Grandpa's Rubik's Cube"—Sample Common Application Essay, Option #4
• Math Stumper: Use Two Squares to Make Separate Pens for Nine Pigs
• Critical Thinking Definition, Skills, and Examples
• Graphic Organizers in Math
• College Interview Tips: "Tell Me About a Challenge You Overcame"
• Christmas Word Problem Worksheets
• Solving Problems Involving Distance, Rate, and Time
• Innovative Ways to Teach Math
• Study Tips for Math Homework and Math Tests
• 7 Steps to Math Success

Why is important to learn solving a math problem using different methods?

Enhancing Understanding: Different methods provide alternative perspectives on a problem, helping you gain a deeper understanding of its underlying concepts. By exploring various approaches, you can uncover different strategies, techniques, and relationships within the problem. This broader understanding of mathematical concepts can strengthen your overall mathematical ability.

Promoting Flexibility: When you solve a problem using different methods, you develop flexibility in your problem-solving skills. Mathematics is not a one-size-fits-all subject, and different problems may require different approaches. By being familiar with multiple methods, you can adapt your problem-solving strategy to fit various situations. This adaptability is crucial for tackling complex problems that may not have a straightforward solution.

Encouraging Critical Thinking: Exploring different methods encourages critical thinking and analytical reasoning. Each method may involve different steps, logical deductions, and mathematical principles. By comparing and contrasting these methods, you can evaluate their strengths, weaknesses, and underlying assumptions. This analytical thinking helps sharpen your problem-solving skills and improves your ability to assess the validity and efficiency of different approaches.

Finding Multiple Solutions: Some math problems may have multiple valid solutions. By utilizing different methods, you increase your chances of finding alternative solutions. This not only expands your mathematical repertoire but also fosters creativity and innovation in problem-solving. It enables you to think outside the box and consider different perspectives, potentially leading to more elegant or efficient solutions.

Building Mathematical Connections: Different methods often share common principles and connections. By exploring various approaches, you can uncover these connections and deepen your understanding of how different mathematical concepts relate to one another. Recognizing these connections can enhance your problem-solving abilities in other areas of mathematics and enable you to apply knowledge from one domain to another.

Developing Problem-Solving Strategies: Each method you encounter adds to your toolkit of problem-solving strategies. By using different methods, you learn valuable techniques that can be applied to future problems. Over time, these strategies become part of your problem-solving repertoire, empowering you to approach new and unfamiliar problems with confidence and adaptability.

• It enhances understanding, promotes flexibility
• Encourages critical thinking
• Allows for multiple solutions
• Builds mathematical connections
• and develops problem-solving strategies

• Our Mission

6 Tips for Teaching Math Problem-Solving Skills

Solving word problems is tougher than computing with numbers, but elementary teachers can guide students to do the deep thinking involved.

A growing concern with students is the ability to problem-solve, especially with complex, multistep problems. Data shows that students struggle more when solving word problems than they do with computation , and so problem-solving should be considered separately from computation. Why?

Consider this. When we’re on the way to a new destination and we plug in our location to a map on our phone, it tells us what lane to be in and takes us around any detours or collisions, sometimes even buzzing our watch to remind us to turn. When I experience this as a driver, I don’t have to do the thinking. I can think about what I’m going to cook for dinner, not paying much attention to my surroundings other than to follow those directions. If I were to be asked to go there again, I wouldn’t be able to remember, and I would again seek help.

If we can switch to giving students strategies that require them to think instead of giving them too much support throughout the journey to the answer, we may be able to give them the ability to learn the skills to read a map and have several ways to get there.

Here are six ways we can start letting students do this thinking so that they can go through rigorous problem-solving again and again, paving their own way to the solution. 

1. Link problem-solving to reading

When we can remind students that they already have many comprehension skills and strategies they can easily use in math problem-solving, it can ease the anxiety surrounding the math problem. For example, providing them with strategies to practice, such as visualizing, acting out the problem with math tools like counters or base 10 blocks, drawing a quick sketch of the problem, retelling the story in their own words, etc., can really help them to utilize the skills they already have to make the task less daunting.

We can break these skills into specific short lessons so students have a bank of strategies to try on their own. Here's an example of an anchor chart that they can use for visualizing . Breaking up comprehension into specific skills can increase student independence and help teachers to be much more targeted in their problem-solving instruction. This allows students to build confidence and break down the barriers between reading and math to see they already have so many strengths that are transferable to all problems.

2. Avoid boxing students into choosing a specific operation

It can be so tempting to tell students to look for certain words that might mean a certain operation. This might even be thoroughly successful in kindergarten and first grade, but just like when our map tells us where to go, that limits students from becoming deep thinkers. It also expires once they get into the upper grades, where those words could be in a problem multiple times, creating more confusion when students are trying to follow a rule that may not exist in every problem.

We can encourage a variety of ways to solve problems instead of choosing the operation first. In first grade, a problem might say, “Joceline has 13 stuffed animals and Jordan has 17. How many more does Jordan have?” Some students might choose to subtract, but a lot of students might just count to find the amount in between. If we tell them that “how many more” means to subtract, we’re taking the thinking out of the problem altogether, allowing them to go on autopilot without truly solving the problem or using their comprehension skills to visualize it. 

3. Revisit ‘representation’

The word “representation” can be misleading. It seems like something to do after the process of solving. When students think they have to go straight to solving, they may not realize that they need a step in between to be able to support their understanding of what’s actually happening in the problem first.

Using an anchor chart like one of these ( lower grade , upper grade ) can help students to choose a representation that most closely matches what they’re visualizing in their mind. Once they sketch it out, it can give them a clearer picture of different ways they could solve the problem.

Think about this problem: “Varush went on a trip with his family to his grandmother’s house. It was 710 miles away. On the way there, three people took turns driving. His mom drove 214 miles. His dad drove 358 miles. His older sister drove the rest. How many miles did his sister drive?”

If we were to show this student the anchor chart, they would probably choose a number line or a strip diagram to help them understand what’s happening.

If we tell students they must always draw base 10 blocks in a place value chart, that doesn’t necessarily match the concept of this problem. When we ask students to match our way of thinking, we rob them of critical thinking practice and sometimes confuse them in the process. 

4. Give time to process

Sometimes as educators, we can feel rushed to get to everyone and everything that’s required. When solving a complex problem, students need time to just sit with a problem and wrestle with it, maybe even leaving it and coming back to it after a period of time.

This might mean we need to give them fewer problems but go deeper with those problems we give them. We can also speed up processing time when we allow for collaboration and talk time with peers on problem-solving tasks. 

5. Ask questions that let Students do the thinking

Questions or prompts during problem-solving should be very open-ended to promote thinking. Telling a student to reread the problem or to think about what tools or resources would help them solve it is a way to get them to try something new but not take over their thinking.

These skills are also transferable across content, and students will be reminded, “Good readers and mathematicians reread.” 

6. Spiral concepts so students frequently use problem-solving skills

When students don’t have to switch gears in between concepts, they’re not truly using deep problem-solving skills. They already kind of know what operation it might be or that it’s something they have at the forefront of their mind from recent learning. Being intentional within their learning stations and assessments about having a variety of rigorous problem-solving skills will refine their critical thinking abilities while building more and more resilience throughout the school year as they retain content learning in the process. 

Problem-solving skills are so abstract, and it can be tough to pinpoint exactly what students need. Sometimes we have to go slow to go fast. Slowing down and helping students have tools when they get stuck and enabling them to be critical thinkers will prepare them for life and allow them multiple ways to get to their own destination.

Multiple Methods

• Posted April 13, 2015
• By Mary Tamer

Do you remember watching your math teacher solve a problem on the blackboard and then diligently trying to copy her technique to solve the other problems on your worksheet? That’s the way many of us learned math. The problem is, we absorbed some counterproductive messages in the process. As it turns out, there isn’t always one best way to solve a given problem.

In his research, Associate Professor Jon Star is pushing hard to craft some new messages, by showing students how important it is to use multiple strategies when solving math problems.

“Math problems can be approached in many different ways,” says Star, an educational psychologist and former math teacher. “When a teacher insists that there is only one way, or only one best way, to solve a problem, students are missing out. There is great value in allowing them to explore and contrast many different ways to solve problems.”

Star and colleague Bethany Rittle-Johnson of Vanderbilt University have conducted a number of studies over the past decade that demonstrate the benefits of comparing a variety of problem-solving approaches for learning math, especially algebra. And their work has paid off: the US Department of Education’s Institute of Education Sciences echoed their findings in two recent publications by the What Works Clearinghouse : a new problem-solving guide for grades 4-8 and a new algebra practice guide for middle and high school students.

Building on this work, Star, Rittle-Johnson, and colleague  Kristie Newton of Temple University developed a set of curriculum materials  designed to be used in middle and high school algebra classrooms. The goal is to expose students to multiple problem-solving strategies and to build deep and flexible mathematical knowledge.

“In math class, you should have opportunities to talk about different approaches, and comparison helps us to think not only about what works in mathematics, but also about how and why things work,” says Star. “Our materials are designed to be used by algebra teachers to supplement their regular curriculum, to provide a stronger focus on the learning of multiple strategies.“ The curriculum materials were developed with middle and high schoolers in mind, but there are some applications for elementary schoolers as well. Educators can access the curriculum online at no cost.

In several recent studies, Star and his colleagues have studied the impact of teachers’ use of these materials on their students’ learning. He calls the results quite promising.

“Our research suggests that using our curriculum materials was not especially difficult for teachers, and that students enjoyed and benefited from the emphasis on multiple strategies,” says Star. “Many teachers already include multiple strategies for certain topics that they teach; our materials are designed to expand this focus across all topics in algebra.”

Additional Resources

• Read " Developing Flexibility in Math Problem Solving ."
• Visit the  Contrasting Cases website .
• Use the  Contrasting Cases curriculum .
• Teaching Strategies for Improving Algebra Knowledge in Middle and High School Students

Get Usable Knowledge — Delivered Our free monthly newsletter sends you tips, tools, and ideas from research and practice leaders at the Harvard Graduate School of Education. Sign up now .

Usable Knowledge

Connecting education research to practice — with timely insights for educators, families, and communities

Related Articles

Making Math “Almost Fun”

Alum develops curriculum to entice reluctant math learners

Movies, Books, and "The Giver"

What's Worth Learning in School?

35 problem-solving techniques and methods for solving complex problems

Design your next session with SessionLab

Join the 150,000+ facilitators 
using SessionLab.

Recommended Articles

A step-by-step guide to planning a workshop, how to create an unforgettable training session in 8 simple steps, 47 useful online tools for workshop planning and meeting facilitation.

All teams and organizations encounter challenges as they grow. There are problems that might occur for teams when it comes to miscommunication or resolving business-critical issues . You may face challenges around growth , design , user engagement, and even team culture and happiness. In short, problem-solving techniques should be part of every team’s skillset.

Problem-solving methods are primarily designed to help a group or team through a process of first identifying problems and challenges , ideating possible solutions , and then evaluating the most suitable .

Finding effective solutions to complex problems isn’t easy, but by using the right process and techniques, you can help your team be more efficient in the process.

So how do you develop strategies that are engaging, and empower your team to solve problems effectively?

In this blog post, we share a series of problem-solving tools you can use in your next workshop or team meeting. You’ll also find some tips for facilitating the process and how to enable others to solve complex problems.

Let’s get started! 

How do you identify problems?

How do you identify the right solution.

• Tips for more effective problem-solving

Complete problem-solving methods

• Problem-solving techniques to identify and analyze problems
• Problem-solving techniques for developing solutions

Problem-solving warm-up activities

Closing activities for a problem-solving process.

Before you can move towards finding the right solution for a given problem, you first need to identify and define the problem you wish to solve. 

Here, you want to clearly articulate what the problem is and allow your group to do the same. Remember that everyone in a group is likely to have differing perspectives and alignment is necessary in order to help the group move forward. 

Identifying a problem accurately also requires that all members of a group are able to contribute their views in an open and safe manner. It can be scary for people to stand up and contribute, especially if the problems or challenges are emotive or personal in nature. Be sure to try and create a psychologically safe space for these kinds of discussions.

Remember that problem analysis and further discussion are also important. Not taking the time to fully analyze and discuss a challenge can result in the development of solutions that are not fit for purpose or do not address the underlying issue.

Successfully identifying and then analyzing a problem means facilitating a group through activities designed to help them clearly and honestly articulate their thoughts and produce usable insight.

With this data, you might then produce a problem statement that clearly describes the problem you wish to be addressed and also state the goal of any process you undertake to tackle this issue.  

Finding solutions is the end goal of any process. Complex organizational challenges can only be solved with an appropriate solution but discovering them requires using the right problem-solving tool.

After you’ve explored a problem and discussed ideas, you need to help a team discuss and choose the right solution. Consensus tools and methods such as those below help a group explore possible solutions before then voting for the best. They’re a great way to tap into the collective intelligence of the group for great results!

Remember that the process is often iterative. Great problem solvers often roadtest a viable solution in a measured way to see what works too. While you might not get the right solution on your first try, the methods below help teams land on the most likely to succeed solution while also holding space for improvement.

Every effective problem solving process begins with an agenda . A well-structured workshop is one of the best methods for successfully guiding a group from exploring a problem to implementing a solution.

In SessionLab, it’s easy to go from an idea to a complete agenda . Start by dragging and dropping your core problem solving activities into place . Add timings, breaks and necessary materials before sharing your agenda with your colleagues.

The resulting agenda will be your guide to an effective and productive problem solving session that will also help you stay organized on the day!

Tips for more effective problem solving

Problem-solving activities are only one part of the puzzle. While a great method can help unlock your team’s ability to solve problems, without a thoughtful approach and strong facilitation the solutions may not be fit for purpose.

Let’s take a look at some problem-solving tips you can apply to any process to help it be a success!

Clearly define the problem

Jumping straight to solutions can be tempting, though without first clearly articulating a problem, the solution might not be the right one. Many of the problem-solving activities below include sections where the problem is explored and clearly defined before moving on.

This is a vital part of the problem-solving process and taking the time to fully define an issue can save time and effort later. A clear definition helps identify irrelevant information and it also ensures that your team sets off on the right track.

Don’t jump to conclusions

It’s easy for groups to exhibit cognitive bias or have preconceived ideas about both problems and potential solutions. Be sure to back up any problem statements or potential solutions with facts, research, and adequate forethought.

The best techniques ask participants to be methodical and challenge preconceived notions. Make sure you give the group enough time and space to collect relevant information and consider the problem in a new way. By approaching the process with a clear, rational mindset, you’ll often find that better solutions are more forthcoming.  

Try different approaches  

Problems come in all shapes and sizes and so too should the methods you use to solve them. If you find that one approach isn’t yielding results and your team isn’t finding different solutions, try mixing it up. You’ll be surprised at how using a new creative activity can unblock your team and generate great solutions.

Don’t take it personally 

Depending on the nature of your team or organizational problems, it’s easy for conversations to get heated. While it’s good for participants to be engaged in the discussions, ensure that emotions don’t run too high and that blame isn’t thrown around while finding solutions.

You’re all in it together, and even if your team or area is seeing problems, that isn’t necessarily a disparagement of you personally. Using facilitation skills to manage group dynamics is one effective method of helping conversations be more constructive.

Get the right people in the room

Your problem-solving method is often only as effective as the group using it. Getting the right people on the job and managing the number of people present is important too!

If the group is too small, you may not get enough different perspectives to effectively solve a problem. If the group is too large, you can go round and round during the ideation stages.

Creating the right group makeup is also important in ensuring you have the necessary expertise and skillset to both identify and follow up on potential solutions. Carefully consider who to include at each stage to help ensure your problem-solving method is followed and positioned for success.

Document everything

The best solutions can take refinement, iteration, and reflection to come out. Get into a habit of documenting your process in order to keep all the learnings from the session and to allow ideas to mature and develop. Many of the methods below involve the creation of documents or shared resources. Be sure to keep and share these so everyone can benefit from the work done!

Bring a facilitator 

Facilitation is all about making group processes easier. With a subject as potentially emotive and important as problem-solving, having an impartial third party in the form of a facilitator can make all the difference in finding great solutions and keeping the process moving. Consider bringing a facilitator to your problem-solving session to get better results and generate meaningful solutions!

Develop your problem-solving skills

It takes time and practice to be an effective problem solver. While some roles or participants might more naturally gravitate towards problem-solving, it can take development and planning to help everyone create better solutions.

You might develop a training program, run a problem-solving workshop or simply ask your team to practice using the techniques below. Check out our post on problem-solving skills to see how you and your group can develop the right mental process and be more resilient to issues too!

Design a great agenda

Workshops are a great format for solving problems. With the right approach, you can focus a group and help them find the solutions to their own problems. But designing a process can be time-consuming and finding the right activities can be difficult.

Check out our workshop planning guide to level-up your agenda design and start running more effective workshops. Need inspiration? Check out templates designed by expert facilitators to help you kickstart your process!

In this section, we’ll look at in-depth problem-solving methods that provide a complete end-to-end process for developing effective solutions. These will help guide your team from the discovery and definition of a problem through to delivering the right solution.

If you’re looking for an all-encompassing method or problem-solving model, these processes are a great place to start. They’ll ask your team to challenge preconceived ideas and adopt a mindset for solving problems more effectively.

• Six Thinking Hats
• Lightning Decision Jam
• Problem Definition Process
• Discovery & Action Dialogue

Design Sprint 2.0

• Open Space Technology

1. Six Thinking Hats

Individual approaches to solving a problem can be very different based on what team or role an individual holds. It can be easy for existing biases or perspectives to find their way into the mix, or for internal politics to direct a conversation.

Six Thinking Hats is a classic method for identifying the problems that need to be solved and enables your team to consider them from different angles, whether that is by focusing on facts and data, creative solutions, or by considering why a particular solution might not work.

Like all problem-solving frameworks, Six Thinking Hats is effective at helping teams remove roadblocks from a conversation or discussion and come to terms with all the aspects necessary to solve complex problems.

2. Lightning Decision Jam

Featured courtesy of Jonathan Courtney of AJ&Smart Berlin, Lightning Decision Jam is one of those strategies that should be in every facilitation toolbox. Exploring problems and finding solutions is often creative in nature, though as with any creative process, there is the potential to lose focus and get lost.

Unstructured discussions might get you there in the end, but it’s much more effective to use a method that creates a clear process and team focus.

In Lightning Decision Jam, participants are invited to begin by writing challenges, concerns, or mistakes on post-its without discussing them before then being invited by the moderator to present them to the group.

From there, the team vote on which problems to solve and are guided through steps that will allow them to reframe those problems, create solutions and then decide what to execute on. 

By deciding the problems that need to be solved as a team before moving on, this group process is great for ensuring the whole team is aligned and can take ownership over the next stages. 

Lightning Decision Jam (LDJ)   #action   #decision making   #problem solving   #issue analysis   #innovation   #design   #remote-friendly   The problem with anything that requires creative thinking is that it’s easy to get lost—lose focus and fall into the trap of having useless, open-ended, unstructured discussions. Here’s the most effective solution I’ve found: Replace all open, unstructured discussion with a clear process. What to use this exercise for: Anything which requires a group of people to make decisions, solve problems or discuss challenges. It’s always good to frame an LDJ session with a broad topic, here are some examples: The conversion flow of our checkout Our internal design process How we organise events Keeping up with our competition Improving sales flow

3. Problem Definition Process

While problems can be complex, the problem-solving methods you use to identify and solve those problems can often be simple in design. 

By taking the time to truly identify and define a problem before asking the group to reframe the challenge as an opportunity, this method is a great way to enable change.

Begin by identifying a focus question and exploring the ways in which it manifests before splitting into five teams who will each consider the problem using a different method: escape, reversal, exaggeration, distortion or wishful. Teams develop a problem objective and create ideas in line with their method before then feeding them back to the group.

This method is great for enabling in-depth discussions while also creating space for finding creative solutions too!

Problem Definition   #problem solving   #idea generation   #creativity   #online   #remote-friendly   A problem solving technique to define a problem, challenge or opportunity and to generate ideas.

4. The 5 Whys 

Sometimes, a group needs to go further with their strategies and analyze the root cause at the heart of organizational issues. An RCA or root cause analysis is the process of identifying what is at the heart of business problems or recurring challenges. 

The 5 Whys is a simple and effective method of helping a group go find the root cause of any problem or challenge and conduct analysis that will deliver results. 

By beginning with the creation of a problem statement and going through five stages to refine it, The 5 Whys provides everything you need to truly discover the cause of an issue.

The 5 Whys   #hyperisland   #innovation   This simple and powerful method is useful for getting to the core of a problem or challenge. As the title suggests, the group defines a problems, then asks the question “why” five times, often using the resulting explanation as a starting point for creative problem solving.

5. World Cafe

World Cafe is a simple but powerful facilitation technique to help bigger groups to focus their energy and attention on solving complex problems.

World Cafe enables this approach by creating a relaxed atmosphere where participants are able to self-organize and explore topics relevant and important to them which are themed around a central problem-solving purpose. Create the right atmosphere by modeling your space after a cafe and after guiding the group through the method, let them take the lead!

Making problem-solving a part of your organization’s culture in the long term can be a difficult undertaking. More approachable formats like World Cafe can be especially effective in bringing people unfamiliar with workshops into the fold. 

World Cafe   #hyperisland   #innovation   #issue analysis   World Café is a simple yet powerful method, originated by Juanita Brown, for enabling meaningful conversations driven completely by participants and the topics that are relevant and important to them. Facilitators create a cafe-style space and provide simple guidelines. Participants then self-organize and explore a set of relevant topics or questions for conversation.

6. Discovery & Action Dialogue (DAD)

One of the best approaches is to create a safe space for a group to share and discover practices and behaviors that can help them find their own solutions.

With DAD, you can help a group choose which problems they wish to solve and which approaches they will take to do so. It’s great at helping remove resistance to change and can help get buy-in at every level too!

This process of enabling frontline ownership is great in ensuring follow-through and is one of the methods you will want in your toolbox as a facilitator.

Discovery & Action Dialogue (DAD)   #idea generation   #liberating structures   #action   #issue analysis   #remote-friendly   DADs make it easy for a group or community to discover practices and behaviors that enable some individuals (without access to special resources and facing the same constraints) to find better solutions than their peers to common problems. These are called positive deviant (PD) behaviors and practices. DADs make it possible for people in the group, unit, or community to discover by themselves these PD practices. DADs also create favorable conditions for stimulating participants’ creativity in spaces where they can feel safe to invent new and more effective practices. Resistance to change evaporates as participants are unleashed to choose freely which practices they will adopt or try and which problems they will tackle. DADs make it possible to achieve frontline ownership of solutions.

7. Design Sprint 2.0

Want to see how a team can solve big problems and move forward with prototyping and testing solutions in a few days? The Design Sprint 2.0 template from Jake Knapp, author of Sprint, is a complete agenda for a with proven results.

Developing the right agenda can involve difficult but necessary planning. Ensuring all the correct steps are followed can also be stressful or time-consuming depending on your level of experience.

Use this complete 4-day workshop template if you are finding there is no obvious solution to your challenge and want to focus your team around a specific problem that might require a shortcut to launching a minimum viable product or waiting for the organization-wide implementation of a solution.

8. Open space technology

Open space technology- developed by Harrison Owen – creates a space where large groups are invited to take ownership of their problem solving and lead individual sessions. Open space technology is a great format when you have a great deal of expertise and insight in the room and want to allow for different takes and approaches on a particular theme or problem you need to be solved.

Start by bringing your participants together to align around a central theme and focus their efforts. Explain the ground rules to help guide the problem-solving process and then invite members to identify any issue connecting to the central theme that they are interested in and are prepared to take responsibility for.

Once participants have decided on their approach to the core theme, they write their issue on a piece of paper, announce it to the group, pick a session time and place, and post the paper on the wall. As the wall fills up with sessions, the group is then invited to join the sessions that interest them the most and which they can contribute to, then you’re ready to begin!

Everyone joins the problem-solving group they’ve signed up to, record the discussion and if appropriate, findings can then be shared with the rest of the group afterward.

Open Space Technology   #action plan   #idea generation   #problem solving   #issue analysis   #large group   #online   #remote-friendly   Open Space is a methodology for large groups to create their agenda discerning important topics for discussion, suitable for conferences, community gatherings and whole system facilitation

Techniques to identify and analyze problems

Using a problem-solving method to help a team identify and analyze a problem can be a quick and effective addition to any workshop or meeting.

While further actions are always necessary, you can generate momentum and alignment easily, and these activities are a great place to get started.

We’ve put together this list of techniques to help you and your team with problem identification, analysis, and discussion that sets the foundation for developing effective solutions.

Let’s take a look!

• The Creativity Dice
• Fishbone Analysis
• Problem Tree
• SWOT Analysis
• Agreement-Certainty Matrix
• The Journalistic Six
• LEGO Challenge
• What, So What, Now What?
• Journalists

Individual and group perspectives are incredibly important, but what happens if people are set in their minds and need a change of perspective in order to approach a problem more effectively?

Flip It is a method we love because it is both simple to understand and run, and allows groups to understand how their perspectives and biases are formed. 

Participants in Flip It are first invited to consider concerns, issues, or problems from a perspective of fear and write them on a flip chart. Then, the group is asked to consider those same issues from a perspective of hope and flip their understanding.  

No problem and solution is free from existing bias and by changing perspectives with Flip It, you can then develop a problem solving model quickly and effectively.

Flip It!   #gamestorming   #problem solving   #action   Often, a change in a problem or situation comes simply from a change in our perspectives. Flip It! is a quick game designed to show players that perspectives are made, not born.

10. The Creativity Dice

One of the most useful problem solving skills you can teach your team is of approaching challenges with creativity, flexibility, and openness. Games like The Creativity Dice allow teams to overcome the potential hurdle of too much linear thinking and approach the process with a sense of fun and speed. 

In The Creativity Dice, participants are organized around a topic and roll a dice to determine what they will work on for a period of 3 minutes at a time. They might roll a 3 and work on investigating factual information on the chosen topic. They might roll a 1 and work on identifying the specific goals, standards, or criteria for the session.

Encouraging rapid work and iteration while asking participants to be flexible are great skills to cultivate. Having a stage for idea incubation in this game is also important. Moments of pause can help ensure the ideas that are put forward are the most suitable. 

The Creativity Dice   #creativity   #problem solving   #thiagi   #issue analysis   Too much linear thinking is hazardous to creative problem solving. To be creative, you should approach the problem (or the opportunity) from different points of view. You should leave a thought hanging in mid-air and move to another. This skipping around prevents premature closure and lets your brain incubate one line of thought while you consciously pursue another.

11. Fishbone Analysis

Organizational or team challenges are rarely simple, and it’s important to remember that one problem can be an indication of something that goes deeper and may require further consideration to be solved.

Fishbone Analysis helps groups to dig deeper and understand the origins of a problem. It’s a great example of a root cause analysis method that is simple for everyone on a team to get their head around. 

Participants in this activity are asked to annotate a diagram of a fish, first adding the problem or issue to be worked on at the head of a fish before then brainstorming the root causes of the problem and adding them as bones on the fish. 

Using abstractions such as a diagram of a fish can really help a team break out of their regular thinking and develop a creative approach.

Fishbone Analysis   #problem solving   ##root cause analysis   #decision making   #online facilitation   A process to help identify and understand the origins of problems, issues or observations.

12. Problem Tree 

Encouraging visual thinking can be an essential part of many strategies. By simply reframing and clarifying problems, a group can move towards developing a problem solving model that works for them. 

In Problem Tree, groups are asked to first brainstorm a list of problems – these can be design problems, team problems or larger business problems – and then organize them into a hierarchy. The hierarchy could be from most important to least important or abstract to practical, though the key thing with problem solving games that involve this aspect is that your group has some way of managing and sorting all the issues that are raised.

Once you have a list of problems that need to be solved and have organized them accordingly, you’re then well-positioned for the next problem solving steps.

Problem tree   #define intentions   #create   #design   #issue analysis   A problem tree is a tool to clarify the hierarchy of problems addressed by the team within a design project; it represents high level problems or related sublevel problems.

13. SWOT Analysis

Chances are you’ve heard of the SWOT Analysis before. This problem-solving method focuses on identifying strengths, weaknesses, opportunities, and threats is a tried and tested method for both individuals and teams.

Start by creating a desired end state or outcome and bare this in mind – any process solving model is made more effective by knowing what you are moving towards. Create a quadrant made up of the four categories of a SWOT analysis and ask participants to generate ideas based on each of those quadrants.

Once you have those ideas assembled in their quadrants, cluster them together based on their affinity with other ideas. These clusters are then used to facilitate group conversations and move things forward. 

SWOT analysis   #gamestorming   #problem solving   #action   #meeting facilitation   The SWOT Analysis is a long-standing technique of looking at what we have, with respect to the desired end state, as well as what we could improve on. It gives us an opportunity to gauge approaching opportunities and dangers, and assess the seriousness of the conditions that affect our future. When we understand those conditions, we can influence what comes next.

14. Agreement-Certainty Matrix

Not every problem-solving approach is right for every challenge, and deciding on the right method for the challenge at hand is a key part of being an effective team.

The Agreement Certainty matrix helps teams align on the nature of the challenges facing them. By sorting problems from simple to chaotic, your team can understand what methods are suitable for each problem and what they can do to ensure effective results. 

If you are already using Liberating Structures techniques as part of your problem-solving strategy, the Agreement-Certainty Matrix can be an invaluable addition to your process. We’ve found it particularly if you are having issues with recurring problems in your organization and want to go deeper in understanding the root cause. 

Agreement-Certainty Matrix   #issue analysis   #liberating structures   #problem solving   You can help individuals or groups avoid the frequent mistake of trying to solve a problem with methods that are not adapted to the nature of their challenge. The combination of two questions makes it possible to easily sort challenges into four categories: simple, complicated, complex , and chaotic .  A problem is simple when it can be solved reliably with practices that are easy to duplicate.  It is complicated when experts are required to devise a sophisticated solution that will yield the desired results predictably.  A problem is complex when there are several valid ways to proceed but outcomes are not predictable in detail.  Chaotic is when the context is too turbulent to identify a path forward.  A loose analogy may be used to describe these differences: simple is like following a recipe, complicated like sending a rocket to the moon, complex like raising a child, and chaotic is like the game “Pin the Tail on the Donkey.”  The Liberating Structures Matching Matrix in Chapter 5 can be used as the first step to clarify the nature of a challenge and avoid the mismatches between problems and solutions that are frequently at the root of chronic, recurring problems.

Organizing and charting a team’s progress can be important in ensuring its success. SQUID (Sequential Question and Insight Diagram) is a great model that allows a team to effectively switch between giving questions and answers and develop the skills they need to stay on track throughout the process. 

Begin with two different colored sticky notes – one for questions and one for answers – and with your central topic (the head of the squid) on the board. Ask the group to first come up with a series of questions connected to their best guess of how to approach the topic. Ask the group to come up with answers to those questions, fix them to the board and connect them with a line. After some discussion, go back to question mode by responding to the generated answers or other points on the board.

It’s rewarding to see a diagram grow throughout the exercise, and a completed SQUID can provide a visual resource for future effort and as an example for other teams.

SQUID   #gamestorming   #project planning   #issue analysis   #problem solving   When exploring an information space, it’s important for a group to know where they are at any given time. By using SQUID, a group charts out the territory as they go and can navigate accordingly. SQUID stands for Sequential Question and Insight Diagram.

16. Speed Boat

To continue with our nautical theme, Speed Boat is a short and sweet activity that can help a team quickly identify what employees, clients or service users might have a problem with and analyze what might be standing in the way of achieving a solution.

Methods that allow for a group to make observations, have insights and obtain those eureka moments quickly are invaluable when trying to solve complex problems.

In Speed Boat, the approach is to first consider what anchors and challenges might be holding an organization (or boat) back. Bonus points if you are able to identify any sharks in the water and develop ideas that can also deal with competitors!   

Speed Boat   #gamestorming   #problem solving   #action   Speedboat is a short and sweet way to identify what your employees or clients don’t like about your product/service or what’s standing in the way of a desired goal.

17. The Journalistic Six

Some of the most effective ways of solving problems is by encouraging teams to be more inclusive and diverse in their thinking.

Based on the six key questions journalism students are taught to answer in articles and news stories, The Journalistic Six helps create teams to see the whole picture. By using who, what, when, where, why, and how to facilitate the conversation and encourage creative thinking, your team can make sure that the problem identification and problem analysis stages of the are covered exhaustively and thoughtfully. Reporter’s notebook and dictaphone optional.

The Journalistic Six – Who What When Where Why How   #idea generation   #issue analysis   #problem solving   #online   #creative thinking   #remote-friendly   A questioning method for generating, explaining, investigating ideas.

18. LEGO Challenge

Now for an activity that is a little out of the (toy) box. LEGO Serious Play is a facilitation methodology that can be used to improve creative thinking and problem-solving skills. 

The LEGO Challenge includes giving each member of the team an assignment that is hidden from the rest of the group while they create a structure without speaking.

What the LEGO challenge brings to the table is a fun working example of working with stakeholders who might not be on the same page to solve problems. Also, it’s LEGO! Who doesn’t love LEGO! 

LEGO Challenge   #hyperisland   #team   A team-building activity in which groups must work together to build a structure out of LEGO, but each individual has a secret “assignment” which makes the collaborative process more challenging. It emphasizes group communication, leadership dynamics, conflict, cooperation, patience and problem solving strategy.

19. What, So What, Now What?

If not carefully managed, the problem identification and problem analysis stages of the problem-solving process can actually create more problems and misunderstandings.

The What, So What, Now What? problem-solving activity is designed to help collect insights and move forward while also eliminating the possibility of disagreement when it comes to identifying, clarifying, and analyzing organizational or work problems. 

Facilitation is all about bringing groups together so that might work on a shared goal and the best problem-solving strategies ensure that teams are aligned in purpose, if not initially in opinion or insight.

Throughout the three steps of this game, you give everyone on a team to reflect on a problem by asking what happened, why it is important, and what actions should then be taken. 

This can be a great activity for bringing our individual perceptions about a problem or challenge and contextualizing it in a larger group setting. This is one of the most important problem-solving skills you can bring to your organization.

W³ – What, So What, Now What?   #issue analysis   #innovation   #liberating structures   You can help groups reflect on a shared experience in a way that builds understanding and spurs coordinated action while avoiding unproductive conflict. It is possible for every voice to be heard while simultaneously sifting for insights and shaping new direction. Progressing in stages makes this practical—from collecting facts about What Happened to making sense of these facts with So What and finally to what actions logically follow with Now What . The shared progression eliminates most of the misunderstandings that otherwise fuel disagreements about what to do. Voila!

20. Journalists  

Problem analysis can be one of the most important and decisive stages of all problem-solving tools. Sometimes, a team can become bogged down in the details and are unable to move forward.

Journalists is an activity that can avoid a group from getting stuck in the problem identification or problem analysis stages of the process.

In Journalists, the group is invited to draft the front page of a fictional newspaper and figure out what stories deserve to be on the cover and what headlines those stories will have. By reframing how your problems and challenges are approached, you can help a team move productively through the process and be better prepared for the steps to follow.

Journalists   #vision   #big picture   #issue analysis   #remote-friendly   This is an exercise to use when the group gets stuck in details and struggles to see the big picture. Also good for defining a vision.

Problem-solving techniques for developing solutions 

The success of any problem-solving process can be measured by the solutions it produces. After you’ve defined the issue, explored existing ideas, and ideated, it’s time to narrow down to the correct solution.

Use these problem-solving techniques when you want to help your team find consensus, compare possible solutions, and move towards taking action on a particular problem.

• Improved Solutions
• Four-Step Sketch
• 15% Solutions
• How-Now-Wow matrix
• Impact Effort Matrix

21. Mindspin  

Brainstorming is part of the bread and butter of the problem-solving process and all problem-solving strategies benefit from getting ideas out and challenging a team to generate solutions quickly. 

With Mindspin, participants are encouraged not only to generate ideas but to do so under time constraints and by slamming down cards and passing them on. By doing multiple rounds, your team can begin with a free generation of possible solutions before moving on to developing those solutions and encouraging further ideation. 

This is one of our favorite problem-solving activities and can be great for keeping the energy up throughout the workshop. Remember the importance of helping people become engaged in the process – energizing problem-solving techniques like Mindspin can help ensure your team stays engaged and happy, even when the problems they’re coming together to solve are complex. 

MindSpin   #teampedia   #idea generation   #problem solving   #action   A fast and loud method to enhance brainstorming within a team. Since this activity has more than round ideas that are repetitive can be ruled out leaving more creative and innovative answers to the challenge.

22. Improved Solutions

After a team has successfully identified a problem and come up with a few solutions, it can be tempting to call the work of the problem-solving process complete. That said, the first solution is not necessarily the best, and by including a further review and reflection activity into your problem-solving model, you can ensure your group reaches the best possible result. 

One of a number of problem-solving games from Thiagi Group, Improved Solutions helps you go the extra mile and develop suggested solutions with close consideration and peer review. By supporting the discussion of several problems at once and by shifting team roles throughout, this problem-solving technique is a dynamic way of finding the best solution. 

Improved Solutions   #creativity   #thiagi   #problem solving   #action   #team   You can improve any solution by objectively reviewing its strengths and weaknesses and making suitable adjustments. In this creativity framegame, you improve the solutions to several problems. To maintain objective detachment, you deal with a different problem during each of six rounds and assume different roles (problem owner, consultant, basher, booster, enhancer, and evaluator) during each round. At the conclusion of the activity, each player ends up with two solutions to her problem.

23. Four Step Sketch

Creative thinking and visual ideation does not need to be confined to the opening stages of your problem-solving strategies. Exercises that include sketching and prototyping on paper can be effective at the solution finding and development stage of the process, and can be great for keeping a team engaged. 

By going from simple notes to a crazy 8s round that involves rapidly sketching 8 variations on their ideas before then producing a final solution sketch, the group is able to iterate quickly and visually. Problem-solving techniques like Four-Step Sketch are great if you have a group of different thinkers and want to change things up from a more textual or discussion-based approach.

Four-Step Sketch   #design sprint   #innovation   #idea generation   #remote-friendly   The four-step sketch is an exercise that helps people to create well-formed concepts through a structured process that includes: Review key information Start design work on paper,  Consider multiple variations , Create a detailed solution . This exercise is preceded by a set of other activities allowing the group to clarify the challenge they want to solve. See how the Four Step Sketch exercise fits into a Design Sprint

24. 15% Solutions

Some problems are simpler than others and with the right problem-solving activities, you can empower people to take immediate actions that can help create organizational change. 

Part of the liberating structures toolkit, 15% solutions is a problem-solving technique that focuses on finding and implementing solutions quickly. A process of iterating and making small changes quickly can help generate momentum and an appetite for solving complex problems.

Problem-solving strategies can live and die on whether people are onboard. Getting some quick wins is a great way of getting people behind the process.   

It can be extremely empowering for a team to realize that problem-solving techniques can be deployed quickly and easily and delineate between things they can positively impact and those things they cannot change. 

15% Solutions   #action   #liberating structures   #remote-friendly   You can reveal the actions, however small, that everyone can do immediately. At a minimum, these will create momentum, and that may make a BIG difference.  15% Solutions show that there is no reason to wait around, feel powerless, or fearful. They help people pick it up a level. They get individuals and the group to focus on what is within their discretion instead of what they cannot change.  With a very simple question, you can flip the conversation to what can be done and find solutions to big problems that are often distributed widely in places not known in advance. Shifting a few grains of sand may trigger a landslide and change the whole landscape.

25. How-Now-Wow Matrix

The problem-solving process is often creative, as complex problems usually require a change of thinking and creative response in order to find the best solutions. While it’s common for the first stages to encourage creative thinking, groups can often gravitate to familiar solutions when it comes to the end of the process. 

When selecting solutions, you don’t want to lose your creative energy! The How-Now-Wow Matrix from Gamestorming is a great problem-solving activity that enables a group to stay creative and think out of the box when it comes to selecting the right solution for a given problem.

Problem-solving techniques that encourage creative thinking and the ideation and selection of new solutions can be the most effective in organisational change. Give the How-Now-Wow Matrix a go, and not just for how pleasant it is to say out loud. 

How-Now-Wow Matrix   #gamestorming   #idea generation   #remote-friendly   When people want to develop new ideas, they most often think out of the box in the brainstorming or divergent phase. However, when it comes to convergence, people often end up picking ideas that are most familiar to them. This is called a ‘creative paradox’ or a ‘creadox’. The How-Now-Wow matrix is an idea selection tool that breaks the creadox by forcing people to weigh each idea on 2 parameters.

26. Impact and Effort Matrix

All problem-solving techniques hope to not only find solutions to a given problem or challenge but to find the best solution. When it comes to finding a solution, groups are invited to put on their decision-making hats and really think about how a proposed idea would work in practice. 

The Impact and Effort Matrix is one of the problem-solving techniques that fall into this camp, empowering participants to first generate ideas and then categorize them into a 2×2 matrix based on impact and effort.

Activities that invite critical thinking while remaining simple are invaluable. Use the Impact and Effort Matrix to move from ideation and towards evaluating potential solutions before then committing to them. 

Impact and Effort Matrix   #gamestorming   #decision making   #action   #remote-friendly   In this decision-making exercise, possible actions are mapped based on two factors: effort required to implement and potential impact. Categorizing ideas along these lines is a useful technique in decision making, as it obliges contributors to balance and evaluate suggested actions before committing to them.

27. Dotmocracy

If you’ve followed each of the problem-solving steps with your group successfully, you should move towards the end of your process with heaps of possible solutions developed with a specific problem in mind. But how do you help a group go from ideation to putting a solution into action? 

Dotmocracy – or Dot Voting -is a tried and tested method of helping a team in the problem-solving process make decisions and put actions in place with a degree of oversight and consensus. 

One of the problem-solving techniques that should be in every facilitator’s toolbox, Dot Voting is fast and effective and can help identify the most popular and best solutions and help bring a group to a decision effectively. 

Dotmocracy   #action   #decision making   #group prioritization   #hyperisland   #remote-friendly   Dotmocracy is a simple method for group prioritization or decision-making. It is not an activity on its own, but a method to use in processes where prioritization or decision-making is the aim. The method supports a group to quickly see which options are most popular or relevant. The options or ideas are written on post-its and stuck up on a wall for the whole group to see. Each person votes for the options they think are the strongest, and that information is used to inform a decision.

All facilitators know that warm-ups and icebreakers are useful for any workshop or group process. Problem-solving workshops are no different.

Use these problem-solving techniques to warm up a group and prepare them for the rest of the process. Activating your group by tapping into some of the top problem-solving skills can be one of the best ways to see great outcomes from your session.

• Check-in/Check-out
• Doodling Together
• Show and Tell
• Constellations
• Draw a Tree

28. Check-in / Check-out

Solid processes are planned from beginning to end, and the best facilitators know that setting the tone and establishing a safe, open environment can be integral to a successful problem-solving process.

Check-in / Check-out is a great way to begin and/or bookend a problem-solving workshop. Checking in to a session emphasizes that everyone will be seen, heard, and expected to contribute. 

If you are running a series of meetings, setting a consistent pattern of checking in and checking out can really help your team get into a groove. We recommend this opening-closing activity for small to medium-sized groups though it can work with large groups if they’re disciplined!

Check-in / Check-out   #team   #opening   #closing   #hyperisland   #remote-friendly   Either checking-in or checking-out is a simple way for a team to open or close a process, symbolically and in a collaborative way. Checking-in/out invites each member in a group to be present, seen and heard, and to express a reflection or a feeling. Checking-in emphasizes presence, focus and group commitment; checking-out emphasizes reflection and symbolic closure.

29. Doodling Together  

Thinking creatively and not being afraid to make suggestions are important problem-solving skills for any group or team, and warming up by encouraging these behaviors is a great way to start. 

Doodling Together is one of our favorite creative ice breaker games – it’s quick, effective, and fun and can make all following problem-solving steps easier by encouraging a group to collaborate visually. By passing cards and adding additional items as they go, the workshop group gets into a groove of co-creation and idea development that is crucial to finding solutions to problems. 

Doodling Together   #collaboration   #creativity   #teamwork   #fun   #team   #visual methods   #energiser   #icebreaker   #remote-friendly   Create wild, weird and often funny postcards together & establish a group’s creative confidence.

30. Show and Tell

You might remember some version of Show and Tell from being a kid in school and it’s a great problem-solving activity to kick off a session.

Asking participants to prepare a little something before a workshop by bringing an object for show and tell can help them warm up before the session has even begun! Games that include a physical object can also help encourage early engagement before moving onto more big-picture thinking.

By asking your participants to tell stories about why they chose to bring a particular item to the group, you can help teams see things from new perspectives and see both differences and similarities in the way they approach a topic. Great groundwork for approaching a problem-solving process as a team! 

Show and Tell   #gamestorming   #action   #opening   #meeting facilitation   Show and Tell taps into the power of metaphors to reveal players’ underlying assumptions and associations around a topic The aim of the game is to get a deeper understanding of stakeholders’ perspectives on anything—a new project, an organizational restructuring, a shift in the company’s vision or team dynamic.

31. Constellations

Who doesn’t love stars? Constellations is a great warm-up activity for any workshop as it gets people up off their feet, energized, and ready to engage in new ways with established topics. It’s also great for showing existing beliefs, biases, and patterns that can come into play as part of your session.

Using warm-up games that help build trust and connection while also allowing for non-verbal responses can be great for easing people into the problem-solving process and encouraging engagement from everyone in the group. Constellations is great in large spaces that allow for movement and is definitely a practical exercise to allow the group to see patterns that are otherwise invisible. 

Constellations   #trust   #connection   #opening   #coaching   #patterns   #system   Individuals express their response to a statement or idea by standing closer or further from a central object. Used with teams to reveal system, hidden patterns, perspectives.

32. Draw a Tree

Problem-solving games that help raise group awareness through a central, unifying metaphor can be effective ways to warm-up a group in any problem-solving model.

Draw a Tree is a simple warm-up activity you can use in any group and which can provide a quick jolt of energy. Start by asking your participants to draw a tree in just 45 seconds – they can choose whether it will be abstract or realistic. 

Once the timer is up, ask the group how many people included the roots of the tree and use this as a means to discuss how we can ignore important parts of any system simply because they are not visible.

All problem-solving strategies are made more effective by thinking of problems critically and by exposing things that may not normally come to light. Warm-up games like Draw a Tree are great in that they quickly demonstrate some key problem-solving skills in an accessible and effective way.

Draw a Tree   #thiagi   #opening   #perspectives   #remote-friendly   With this game you can raise awarness about being more mindful, and aware of the environment we live in.

Each step of the problem-solving workshop benefits from an intelligent deployment of activities, games, and techniques. Bringing your session to an effective close helps ensure that solutions are followed through on and that you also celebrate what has been achieved.

Here are some problem-solving activities you can use to effectively close a workshop or meeting and ensure the great work you’ve done can continue afterward.

• One Breath Feedback
• Who What When Matrix
• Response Cards

How do I conclude a problem-solving process?

All good things must come to an end. With the bulk of the work done, it can be tempting to conclude your workshop swiftly and without a moment to debrief and align. This can be problematic in that it doesn’t allow your team to fully process the results or reflect on the process.

At the end of an effective session, your team will have gone through a process that, while productive, can be exhausting. It’s important to give your group a moment to take a breath, ensure that they are clear on future actions, and provide short feedback before leaving the space. 

The primary purpose of any problem-solving method is to generate solutions and then implement them. Be sure to take the opportunity to ensure everyone is aligned and ready to effectively implement the solutions you produced in the workshop.

Remember that every process can be improved and by giving a short moment to collect feedback in the session, you can further refine your problem-solving methods and see further success in the future too.

33. One Breath Feedback

Maintaining attention and focus during the closing stages of a problem-solving workshop can be tricky and so being concise when giving feedback can be important. It’s easy to incur “death by feedback” should some team members go on for too long sharing their perspectives in a quick feedback round. 

One Breath Feedback is a great closing activity for workshops. You give everyone an opportunity to provide feedback on what they’ve done but only in the space of a single breath. This keeps feedback short and to the point and means that everyone is encouraged to provide the most important piece of feedback to them. 

One breath feedback   #closing   #feedback   #action   This is a feedback round in just one breath that excels in maintaining attention: each participants is able to speak during just one breath … for most people that’s around 20 to 25 seconds … unless of course you’ve been a deep sea diver in which case you’ll be able to do it for longer.

34. Who What When Matrix 

Matrices feature as part of many effective problem-solving strategies and with good reason. They are easily recognizable, simple to use, and generate results.

The Who What When Matrix is a great tool to use when closing your problem-solving session by attributing a who, what and when to the actions and solutions you have decided upon. The resulting matrix is a simple, easy-to-follow way of ensuring your team can move forward. 

Great solutions can’t be enacted without action and ownership. Your problem-solving process should include a stage for allocating tasks to individuals or teams and creating a realistic timeframe for those solutions to be implemented or checked out. Use this method to keep the solution implementation process clear and simple for all involved. 

Who/What/When Matrix   #gamestorming   #action   #project planning   With Who/What/When matrix, you can connect people with clear actions they have defined and have committed to.

35. Response cards

Group discussion can comprise the bulk of most problem-solving activities and by the end of the process, you might find that your team is talked out! 

Providing a means for your team to give feedback with short written notes can ensure everyone is head and can contribute without the need to stand up and talk. Depending on the needs of the group, giving an alternative can help ensure everyone can contribute to your problem-solving model in the way that makes the most sense for them.

Response Cards is a great way to close a workshop if you are looking for a gentle warm-down and want to get some swift discussion around some of the feedback that is raised. 

Response Cards   #debriefing   #closing   #structured sharing   #questions and answers   #thiagi   #action   It can be hard to involve everyone during a closing of a session. Some might stay in the background or get unheard because of louder participants. However, with the use of Response Cards, everyone will be involved in providing feedback or clarify questions at the end of a session.

Save time and effort discovering the right solutions

A structured problem solving process is a surefire way of solving tough problems, discovering creative solutions and driving organizational change. But how can you design for successful outcomes?

With SessionLab, it’s easy to design engaging workshops that deliver results. Drag, drop and reorder blocks  to build your agenda. When you make changes or update your agenda, your session  timing   adjusts automatically , saving you time on manual adjustments.

Collaborating with stakeholders or clients? Share your agenda with a single click and collaborate in real-time. No more sending documents back and forth over email.

Explore  how to use SessionLab  to design effective problem solving workshops or  watch this five minute video  to see the planner in action!

Over to you

The problem-solving process can often be as complicated and multifaceted as the problems they are set-up to solve. With the right problem-solving techniques and a mix of creative exercises designed to guide discussion and generate purposeful ideas, we hope we’ve given you the tools to find the best solutions as simply and easily as possible.

Is there a problem-solving technique that you are missing here? Do you have a favorite activity or method you use when facilitating? Let us know in the comments below, we’d love to hear from you! 

thank you very much for these excellent techniques

Certainly wonderful article, very detailed. Shared!

Leave a Comment Cancel reply

Your email address will not be published. Required fields are marked *

Going from a mere idea to a workshop that delivers results for your clients can feel like a daunting task. In this piece, we will shine a light on all the work behind the scenes and help you learn how to plan a workshop from start to finish. On a good day, facilitation can feel like effortless magic, but that is mostly the result of backstage work, foresight, and a lot of careful planning. Read on to learn a step-by-step approach to breaking the process of planning a workshop into small, manageable chunks.  The flow starts with the first meeting with a client to define the purposes of a workshop.…

How does learning work? A clever 9-year-old once told me: “I know I am learning something new when I am surprised.” The science of adult learning tells us that, in order to learn new skills (which, unsurprisingly, is harder for adults to do than kids) grown-ups need to first get into a specific headspace.  In a business, this approach is often employed in a training session where employees learn new skills or work on professional development. But how do you ensure your training is effective? In this guide, we'll explore how to create an effective training session plan and run engaging training sessions. As team leader, project manager, or consultant,…

Effective online tools are a necessity for smooth and engaging virtual workshops and meetings. But how do you choose the right ones? Do you sometimes feel that the good old pen and paper or MS Office toolkit and email leaves you struggling to stay on top of managing and delivering your workshop? Fortunately, there are plenty of online tools to make your life easier when you need to facilitate a meeting and lead workshops. In this post, we’ll share our favorite online tools you can use to make your job as a facilitator easier. In fact, there are plenty of free online workshop tools and meeting facilitation software you can…

Design your next workshop with SessionLab

Join the 150,000 facilitators using SessionLab

Sign up for free

Mathematical modeling and problem solving: from fundamentals to applications

• Open access
• Published: 15 March 2024

Cite this article

You have full access to this open access article

• Masahito Ohue 1 ,
• Kotoyu Sasayama 2 &
• Masami Takata 3  

149 Accesses

Explore all metrics

The rapidly advancing fields of machine learning and mathematical modeling, greatly enhanced by the recent growth in artificial intelligence, are the focus of this special issue. This issue compiles extensively revised and improved versions of the top papers from the workshop on Mathematical Modeling and Problem Solving at PDPTA'23, the 29th International Conference on Parallel and Distributed Processing Techniques and Applications. Covering fundamental research in matrix operations and heuristic searches to real-world applications in computer vision and drug discovery, the issue underscores the crucial role of supercomputing and parallel and distributed computing infrastructure in research. Featuring nine key studies, this issue pushes forward computational technologies in mathematical modeling, refines techniques for analyzing images and time-series data, and introduces new methods in pharmaceutical and materials science, making significant contributions to these areas.

Similar content being viewed by others

Optimization Theory

WORHP: Development and Applications of the ESA NLP SOLVER

Optimization

Avoid common mistakes on your manuscript.

The field of machine learning and mathematical modeling is rapidly evolving, significantly impacting diverse research areas. The recent surge in artificial intelligence technologies has further accelerated this trend, highlighting the growing importance of “mathematical modeling and problem solving” in scientific endeavors [ 1 ]. Modeling natural phenomena and engineering systems not only deepens our understanding of fundamental principles but also drives the development of innovative technologies for effective control. These advancements have considerable implications for both industry and academia.

This special issue showcases the latest advancements in mathematical modeling and problem solving across various disciplines. The scope of topics is wide, encompassing everything from foundational research in new matrix operation methods, heuristic search, and constrained optimization techniques to practical research in computer vision, drug discovery, materials science, financial engineering, and mechanical processes.

A key aspect of contemporary mathematical modeling research is its integration with supercomputing, which involves extensive parallel and distributed computing. The sheer volume and augmented data often require rapid computational strategies. The infrastructure, including hardware and software, supporting parallel and distributed computing is thus vital for applied research. This issue includes a selection of research presented at the “Mathematical Modeling and Problem Solving” workshop during the 29th International Conference on Parallel and Distributed Processing Techniques and Applications (PDPTA’23). After a thorough selection process, nine significant studies were chosen as articles on this issue.

Four papers focus on computational technologies foundational to mathematical modeling. Chiyonobu and colleagues enhance the two-sided Jacobi method for singular value decomposition for complex matrices, previously effective only for real matrices [ 2 ]. They incorporate QR decomposition for complex matrix scenarios, offering two distinct implementations for both complex and real matrices. Zhong et al. introduce a novel hyper-heuristic algorithm, the evolutionary multi-mode slime mold optimization (EMSMO), inspired by slime mold behaviors [ 3 ]. This algorithm demonstrates superior performance in benchmarks and engineering problems, outperforming traditional evolutionary and hyper-heuristic algorithms. Zhang et al. unveil the meta-generative data augmentation optimization (MGDAO), a method that advances data augmentation in foundational machine learning for image and natural language processing [ 4 ]. This technique surpasses standard auto-augmentation methods in few-shot image and text classification benchmarks. Matsuzaki and colleagues propose a mixed-integer programming (MIP)-based method for scheduling machining operations in automated manufacturing, considering worker conditions [ 5 ]. They validate this method through computer experiments modeled on real-world machining tasks.

Two papers address applications involving image and time-series data, traditional targets of mathematical modeling. Ishikawa et al. enhance concrete crack detection by using strongly blurred images in training data, improving recognizer accuracy [ 6 ]. Takata et al. develop a method for recommending stock combinations by analyzing price change waveforms, showing potential for diversifying portfolios and minimizing risks [ 7 ].

Last but not least, three papers focus on pharmaceutical and materials science applications. Ueki and Ohue assess AlphaFold2 and binder hallucination techniques for improving antibody binding affinity, indicating a more efficient method than traditional experimental approaches [ 8 ]. Morikawa et al. introduce a machine learning method using graph kernels for predicting metal–organic frameworks (MOFs) combinations, demonstrating accurate MOF structure prediction without physical synthesis [ 9 ]. Furui and Ohue present an enhanced version of the lead optimization mapper (Lomap) algorithm for drug discovery [ 10 ]. This improved algorithm offers a faster approach to create free energy perturbation (FEP) graphs for numerous compounds, while maintaining the quality of the output.

In summary, this special issue represents a significant contribution to the fields of mathematical modeling and application, providing innovative methods to the community. As editors, we extend our gratitude to all researchers who contributed to this collection, paving the way for the next era of mathematical modeling and problem solving.

Yüksel N, Börklü HR, Sezer HK, Canyurt OE (2023) Review of artificial intelligence applications in engineering design perspective. Eng Appl Artif Intell 118:105697

Article   Google Scholar  

Chiyonobu M, Miyamae T, Takata M, Harayama J, Kimura K, Nakamura Y (2024) Singular value decomposition for complex matrices using two-sided Jacobi method. J Supercomput. https://doi.org/10.1007/s11227-024-05903-6

Zhong R, Zhang E, Munetomo M (2024) Evolutionary multi-mode slime mold optimization: a hyper-heuristic algorithm inspired by slime mold foraging behaviors. J Supercomput. https://doi.org/10.1007/s11227-024-05909-0

Zhang E, Dong B, Wahib M, Zhong R, Munetomo M (2024) Meta generative image and text data augmentation optimization. J Supercomput. https://doi.org/10.1007/s11227-024-05912-5

Matsuzaki J, Sakakibara K, Nakamura M, Watanabe S (2024) Large neighborhood local search method with MIP techniques for large-scale machining scheduling with many constraints. J Supercomput. https://doi.org/10.1007/s11227-024-05912-5

Ishikawa S, Chiyonobu M, Iida S, Takata M (2024) Improvement of recognition rate using data augmentation with blurred images. J Supercomput. https://doi.org/10.1007/s11227-024-05901-8

Takata M, Kidoguchi N, Chiyonobu M (2024) Stock recommendation methods for stability. J Supercomput. https://doi.org/10.1007/s11227-024-05902-7

Ueki T, Ohue M (2024) Antibody complementarity-determining region design using AlphaFold2 and DDG Predictor. J Supercomput. https://doi.org/10.1007/s11227-023-05887-9

Morikawa Y, Shin K, Ohshima H, Kubouchi M (2024) Prediction of specific surface area of metal–organic frameworks by graph kernels. J Supercomput. https://doi.org/10.1007/s11227-024-05914-3

Furui K, Ohue M (2024) FastLomap: faster lead optimization mapper algorithm for large-scale relative free energy perturbation. J Supercomput

Download references

This study was partially supported by JSPS KAKENHI (23H04887) (M.O.).

Author information

Authors and affiliations.

Department of Computer Science, School of Computing, Tokyo Institute of Technology, Kanagawa, 226-8501, Japan

Masahito Ohue

Elevator and Escalator Development Department, Mitsubishi Electric Building Solutions Corporation, Aichi, 492-8682, Japan

Kotoyu Sasayama

Research Group of Information and Communication Technology for Life, Nara Women’s University, Nara, 630-8506, Japan

Masami Takata

You can also search for this author in PubMed   Google Scholar

Contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Corresponding author

Correspondence to Masahito Ohue .

Ethics declarations

Conflict of interest.

All authors declare that the research was conducted without any commercial or financial relationships that could be construed as a potential conflict of interest.

Additional information

Publisher's note.

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/ .

Reprints and permissions

About this article

Ohue, M., Sasayama, K. & Takata, M. Mathematical modeling and problem solving: from fundamentals to applications. J Supercomput (2024). https://doi.org/10.1007/s11227-024-06007-x

Download citation

Accepted : 17 February 2024

Published : 15 March 2024

DOI : https://doi.org/10.1007/s11227-024-06007-x

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Mathematical modeling
• Machine learning
• Parallel and distributed computing
• Drug discovery and materials science
• Find a journal
• Publish with us
• Track your research

March 12, 2024

The Simplest Math Problem Could Be Unsolvable

The Collatz conjecture has plagued mathematicians for decades—so much so that professors warn their students away from it

By Manon Bischoff

Mathematicians have been hoping for a flash of insight to solve the Collatz conjecture.

James Brey/Getty Images

At first glance, the problem seems ridiculously simple. And yet experts have been searching for a solution in vain for decades. According to mathematician Jeffrey Lagarias, number theorist Shizuo Kakutani told him that during the cold war, “for about a month everybody at Yale [University] worked on it, with no result. A similar phenomenon happened when I mentioned it at the University of Chicago. A joke was made that this problem was part of a conspiracy to slow down mathematical research in the U.S.”

The Collatz conjecture—the vexing puzzle Kakutani described—is one of those supposedly simple problems that people tend to get lost in. For this reason, experienced professors often warn their ambitious students not to get bogged down in it and lose sight of their actual research.

The conjecture itself can be formulated so simply that even primary school students understand it. Take a natural number. If it is odd, multiply it by 3 and add 1; if it is even, divide it by 2. Proceed in the same way with the result x : if x is odd, you calculate 3 x + 1; otherwise calculate x / 2. Repeat these instructions as many times as possible, and, according to the conjecture, you will always end up with the number 1.

On supporting science journalism

If you're enjoying this article, consider supporting our award-winning journalism by subscribing . By purchasing a subscription you are helping to ensure the future of impactful stories about the discoveries and ideas shaping our world today.

For example: If you start with 5, you have to calculate 5 x 3 + 1, which results in 16. Because 16 is an even number, you have to halve it, which gives you 8. Then 8 / 2 = 4, which, when divided by 2, is 2—and 2 / 2 = 1. The process of iterative calculation brings you to the end after five steps.

Of course, you can also continue calculating with 1, which gives you 4, then 2 and then 1 again. The calculation rule leads you into an inescapable loop. Therefore 1 is seen as the end point of the procedure.

Following iterative calculations, you can begin with any of the numbers above and will ultimately reach 1.

Credit: Keenan Pepper/Public domain via Wikimedia Commons

It’s really fun to go through the iterative calculation rule for different numbers and look at the resulting sequences. If you start with 6: 6 → 3 → 10 → 5 → 16 → 8 → 4 → 2 → 1. Or 42: 42 → 21 → 64 → 32 → 16 → 8 → 4 → 2 → 1. No matter which number you start with, you always seem to end up with 1. There are some numbers, such as 27, where it takes quite a long time (27 → 82 → 41 → 124 → 62 → 31 → 94 → 47 → 142 → 71 → 214 → 107 → 322 → 161 → 484 → 242 → 121 → 364 → 182 → 91 → 274 → ...), but so far the result has always been 1. (Admittedly, you have to be patient with the starting number 27, which requires 111 steps.)

But strangely there is still no mathematical proof that the Collatz conjecture is true. And that absence has mystified mathematicians for years.

The origin of the Collatz conjecture is uncertain, which is why this hypothesis is known by many different names. Experts speak of the Syracuse problem, the Ulam problem, the 3 n + 1 conjecture, the Hasse algorithm or the Kakutani problem.

German mathematician Lothar Collatz became interested in iterative functions during his mathematics studies and investigated them. In the early 1930s he also published specialist articles on the subject , but the explicit calculation rule for the problem named after him was not among them. In the 1950s and 1960s the Collatz conjecture finally gained notoriety when mathematicians Helmut Hasse and Shizuo Kakutani, among others, disseminated it to various universities, including Syracuse University.

Like a siren song, this seemingly simple conjecture captivated the experts. For decades they have been looking for proof that after repeating the Collatz procedure a finite number of times, you end up with 1. The reason for this persistence is not just the simplicity of the problem: the Collatz conjecture is related to other important questions in mathematics. For example, such iterative functions appear in dynamic systems, such as models that describe the orbits of planets. The conjecture is also related to the Riemann conjecture, one of the oldest problems in number theory.

Empirical Evidence for the Collatz Conjecture

In 2019 and 2020 researchers checked all numbers below 2 68 , or about 3 x 10 20 numbers in the sequence, in a collaborative computer science project . All numbers in that set fulfill the Collatz conjecture as initial values. But that doesn’t mean that there isn’t an outlier somewhere. There could be a starting value that, after repeated Collatz procedures, yields ever larger values that eventually rise to infinity. This scenario seems unlikely, however, if the problem is examined statistically.

An odd number n is increased to 3 n + 1 after the first step of the iteration, but the result is inevitably even and is therefore halved in the following step. In half of all cases, the halving produces an odd number, which must therefore be increased to 3 n + 1 again, whereupon an even result is obtained again. If the result of the second step is even again, however, you have to divide the new number by 2 twice in every fourth case. In every eighth case, you must divide it by 2 three times, and so on.

In order to evaluate the long-term behavior of this sequence of numbers , Lagarias calculated the geometric mean from these considerations in 1985 and obtained the following result: ( 3 / 2 ) 1/2 x ( 3 ⁄ 4 ) 1/4 x ( 3 ⁄ 8 ) 1/8 · ... = 3 ⁄ 4 . This shows that the sequence elements shrink by an average factor of 3 ⁄ 4 at each step of the iterative calculation rule. It is therefore extremely unlikely that there is a starting value that grows to infinity as a result of the procedure.

There could be a starting value, however, that ends in a loop that is not 4 → 2 → 1. That loop could include significantly more numbers, such that 1 would never be reached.

Such “nontrivial” loops can be found, for example, if you also allow negative integers for the Collatz conjecture: in this case, the iterative calculation rule can end not only at –2 → –1 → –2 → ... but also at –5 → –14 → –7 → –20 → –10 → –5 → ... or –17 → –50 → ... → –17 →.... If we restrict ourselves to natural numbers, no nontrivial loops are known to date—which does not mean that they do not exist. Experts have now been able to show that such a loop in the Collatz problem, however, would have to consist of at least 186 billion numbers .

The length of the Collatz sequences for all numbers from 1 to 9,999 varies greatly.

Credit: Cirne/Public domain via Wikimedia Commons

Even if that sounds unlikely, it doesn’t have to be. In mathematics there are many examples where certain laws only break down after many iterations are considered. For instance,the prime number theorem overestimates the number of primes for only about 10 316 numbers. After that point, the prime number set underestimates the actual number of primes.

Something similar could occur with the Collatz conjecture: perhaps there is a huge number hidden deep in the number line that breaks the pattern observed so far.

A Proof for Almost All Numbers

Mathematicians have been searching for a conclusive proof for decades. The greatest progress was made in 2019 by Fields Medalist Terence Tao of the University of California, Los Angeles, when he proved that almost all starting values of natural numbers eventually end up at a value close to 1.

“Almost all” has a precise mathematical meaning: if you randomly select a natural number as a starting value, it has a 100 percent probability of ending up at 1. ( A zero-probability event, however, is not necessarily an impossible one .) That’s “about as close as one can get to the Collatz conjecture without actually solving it,” Tao said in a talk he gave in 2020 . Unfortunately, Tao’s method cannot generalize to all figures because it is based on statistical considerations.

All other approaches have led to a dead end as well. Perhaps that means the Collatz conjecture is wrong. “Maybe we should be spending more energy looking for counterexamples than we’re currently spending,” said mathematician Alex Kontorovich of Rutgers University in a video on the Veritasium YouTube channel .

Perhaps the Collatz conjecture will be determined true or false in the coming years. But there is another possibility: perhaps it truly is a problem that cannot be proven with available mathematical tools. In fact, in 1987 the late mathematician John Horton Conway investigated a generalization of the Collatz conjecture and found that iterative functions have properties that are unprovable. Perhaps this also applies to the Collatz conjecture. As simple as it may seem, it could be doomed to remain unsolved forever.

This article originally appeared in Spektrum der Wissenschaft and was reproduced with permission.

Help | Advanced Search

Mathematics > General Mathematics

Title: series for even powers of pi by generalization euler's method for solving the basel problem.

Abstract: The purpose of this paper is to present series expansions for even powers of the number $\pi$. This is accomplished by generalizing Euler's method for solving the Basel Problem, which was published in 1735. We employ elementary symmetric polynomials, transform them into nested sums, and thereby derive nice series formulas for even powers of the number $\pi$ such as \[ \frac{\pi^2}{3!}= \sum_{\ell_1=1}^\infty\frac{1}{\ell_1^2} \;;\quad\quad \frac{\pi^4}{5!} = \sum_{\ell_2=2}^\infty \sum_{\ell_1=1}^{\ell_2-1} \frac{1}{\ell_1^2\cdot\ell_2^2} \;;\quad\quad \frac{\pi^6}{7!}= \sum_{\ell_3=3}^\infty \sum_{\ell_2=2}^{\ell_3-1} \sum_{\ell_1=1}^{\ell_2-1}\frac{1}{\ell_1^2\cdot\ell_2^2\cdot\ell_3^2} \;;\quad\cdots \] Many of these formulas do not seem to be widely known. -- In dieser Abhandlung stellen wir ein Verfahren vor, das die Berechnung von Reihen für geradzahlige Potenzen von $\pi$ ermöglicht. Die Grundidee ist eine Verallgemeinerung des Verfahrens von Euler, mit dem er 1735 das Basler Problem löste. Wir stellen elementar-symmetrische Polynome durch mehrfach verschachtelte Summen dar und leiten davon Reihen für geradzahlige Potenzen der Kreiszahl $\pi$ ab. Die meisten der angegebenen Reihen scheinen nicht so bekannt zu sein.

Submission history

Access paper:.

• Download PDF
• HTML (experimental)
• Other Formats

References & Citations

• Google Scholar
• Semantic Scholar

BibTeX formatted citation

Bibliographic and Citation Tools

Code, data and media associated with this article, recommenders and search tools.

• Institution

arXivLabs: experimental projects with community collaborators

arXivLabs is a framework that allows collaborators to develop and share new arXiv features directly on our website.

Both individuals and organizations that work with arXivLabs have embraced and accepted our values of openness, community, excellence, and user data privacy. arXiv is committed to these values and only works with partners that adhere to them.

Have an idea for a project that will add value for arXiv's community? Learn more about arXivLabs .

• MyU : For Students, Faculty, and Staff

Professor Bernardo Cockburn receives 2024 Frontiers of Science Award in Mathematics

MINNEAPOLIS / ST. PAUL (3/20/2024) – The International Congress of Basic Science recently selected a paper by Distinguished McKnight University Professor Bernardo Cockburn and collaborators for the 2024 Frontiers of Science Award in Mathematics. The paper, entitled  Bridging the Hybrid High-Order and Hybridizable Discontinuous Galerkin Methods , was a collaboration between Professor Cockburn, Daniele A. Di Pietro (Université de Montpellier), and Alexandre Ern (Ecole des Ponts).

Hybrid high-order (HHO) and the hybridizable discontinuous Galerkin (HDG) methods are both used to solve partial differential equations, like those describing diffusion, in a more efficient way than traditional methods.  Bridging the Hybrid High-Order and Hybridizable Discontinuous Galerkin Methods explores ways to build a bridge between HHO and HDG methods in the setting of a model diffusion problem to take advantage of each method’s strengths. Incorporating the HHO method into the HDG framework brings up new, efficient choices of the local spaces and a new, subtle construction of the numerical flux ensuring optimal orders of convergence on meshes made of general shape-regular polyhedral elements.

Cockburn first joined the University of Minnesota as a postdoctoral associate at the Institute for Mathematics and its Applications in 1986. Since joining the faculty the following year, Cockburn’s research has been primarily focused on the devising and analysis of efficient methods for numerically solving linear and nonlinear partial differential equations. He is particularly interested in the development of discontinuous Galerkin methods. For his outstanding research contributions and dedication to the mathematical community, Cockburn was named a Distinguished McKnight University Professor in 2007 and was invited to speak at the International Congress of Mathematicians in 2010.

The Frontiers of Science Award in Mathematics (FSA) was inaugurated in 2023 with support from the International Congress of Basic Sciences (ICBS), and was sponsored by the City of Beijing and the Yanqi Lake Beijing Institute of Mathematical Sciences and Application. An FSA is awarded to a recent paper, recognized for a major breakthrough in its field. FSA recipients are invited to the ICBS to accept the award in person in July 2024, at the Great Hall of People of China in Beijing.  More information can be found here.

Read  Bridging the Hybrid High-Order and Hybridizable Discontinuous Galerkin Methods

Related news releases

• UMN student team wins national data analytics competition
• Professor Michelle Chu selected for McKnight Land-Grant Professorship award
• Duggal, Gomes, Houssou, Kenney, Manivel, and Zhang named Outstanding TAs
• Daniela Ali Beckelhymer receives Dr. Sylvia T. Bozeman Predoctoral Fellowship
• Eleven graduate students recognized with School of Mathematics awards
• Future undergraduate students
• Future transfer students
• Future graduate students
• Future international students
• Diversity and Inclusion Opportunities
• Learn abroad
• Living Learning Communities
• Mentor programs
• Programs for women
• Student groups
• Visit, Apply & Next Steps
• Information for current students
• Departments and majors overview
• Departments
• Undergraduate majors
• Graduate programs
• Integrated Degree Programs
• Additional degree-granting programs
• Online learning
• Academic Advising overview
• Academic Advising FAQ
• Academic Advising Blog
• Appointments and drop-ins
• Academic support
• Commencement
• Four-year plans
• Honors advising
• Policies, procedures, and forms
• Career Services overview
• Resumes and cover letters
• Jobs and internships
• Interviews and job offers
• CSE Career Fair
• Major and career exploration
• Graduate school
• Collegiate Life overview
• Scholarships
• Diversity & Inclusivity Alliance
• Anderson Student Innovation Labs
• Information for alumni
• Get engaged with CSE
• Upcoming events
• CSE Alumni Society Board
• Alumni volunteer interest form
• Golden Medallion Society Reunion
• 50-Year Reunion
• Alumni honors and awards
• Outstanding Achievement
• Alumni Service
• Distinguished Leadership
• Honorary Doctorate Degrees
• Nobel Laureates
• Alumni resources
• Alumni career resources
• Alumni news outlets
• CSE branded clothing
• International alumni resources
• Inventing Tomorrow magazine
• Update your info
• CSE giving overview
• Why give to CSE?
• College priorities
• Give online now
• External relations
• Giving priorities
• Donor stories
• Impact of giving
• Ways to give to CSE
• Matching gifts
• CSE directories
• Invest in your company and the future
• Recruit our students
• Connect with researchers
• K-12 initiatives
• Diversity initiatives
• Research news
• Give to CSE
• CSE priorities
• Corporate relations
• Information for faculty and staff
• Administrative offices overview
• Office of the Dean
• Academic affairs
• Finance and Operations
• Communications
• Human resources
• Undergraduate programs and student services
• CSE Committees
• CSE policies overview
• Academic policies
• Faculty hiring and tenure policies
• Finance policies and information
• Graduate education policies
• Human resources policies
• Research policies
• Research overview
• Research centers and facilities
• Research proposal submission process
• Research safety
• Award-winning CSE faculty
• National academies
• University awards
• Honorary professorships
• Collegiate awards
• Other CSE honors and awards
• Staff awards
• Performance Management Process
• Work. With Flexibility in CSE
• K-12 outreach overview
• Summer camps
• Outreach events
• Enrichment programs
• Field trips and tours
• CSE K-12 Virtual Classroom Resources
• Educator development
• Sponsor an event

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

1.01: Introduction to Numerical Methods

• Last updated
• Save as PDF
• Page ID 126380

Lesson 1: Why Numerical Methods?

Learning objectives.

After successful completion of this lesson, you should be able to: 1) Enumerate the need for numerical methods.

Introduction

Numerical methods are techniques to approximate mathematical processes (examples of mathematical processes are integrals, differential equations, nonlinear equations).

Approximations are needed because

1) we cannot solve the procedure analytically, such as the standard normal cumulative distribution function

\[\Phi(x) = \frac{1}{\sqrt{2\pi}}\int_{- \infty}^{x}e^{- t^{2}/2}{dt} \;\;\;\;\;\;\;\;\;\;\;\;(\PageIndex{1.1}) \nonumber\]

2) the analytical method is intractable, such as solving a set of a thousand simultaneous linear equations for a thousand unknowns for finding forces in a truss (Figure \(\PageIndex{1.1}\)).

In the case of Equation (1), an exact solution is not available for \(\Phi(x)\) other than for \(x = 0\) and \(x \rightarrow \infty\) . For other values of \(x\) where an exact solution is not available, one may solve the problem by using approximate techniques such as the left-hand Reimann sum you were introduced to in the Integral Calculus course.

In the truss problem, one can solve \(1000\) simultaneous linear equations for \(1000\) unknowns without using a calculator. One can use fractions, long divisions, and long multiplications to get the exact answer. But just the thought of such a task is laborious. The task may seem less laborious if we are allowed to use a calculator, but it would still fall under the category of an intractable, if not an impossible, problem. So, we need to find a numerical technique and convert it into a computer program that solves a set of \(n\) equations and \(n\) unknowns.

Again, what are numerical methods? They are techniques to solve a mathematical problem approximately. As we go through the course, you will see that numerical methods let us find solutions close to the exact one, and we can quantify the approximate error associated with the answer. After all, what good is an approximation without quantifying how good the approximation is?

Audiovisual Lecture

Title: Why Do We Need Numerical Methods

Summary : This video is an introduction to why we need numerical methods.

Lesson 2: Steps of Solving an Engineering Problem

After successful completion of this lesson, you should be able to:

1) go through the stages (problem description, mathematical modeling, solving and implementation) of solving a particular physical problem.

Numerical methods are used by engineers and scientists to solve problems. However, numerical methods are just one step in solving an engineering problem. There are four steps for solving an engineering problem, as shown in Figure \(\PageIndex{2.1}\).

The first step is to describe the problem. The description would involve writing the background of the problem and the need for its solution. The second step is developing a mathematical model for the problem, and this could include the use of experiments or/and theory. The third step involves solving the mathematical model. The solution may consist of analytical or/and numerical means. The fourth step is implementing the solution to see if the problem is solved.

Let us see through an example of these four steps of solving an engineering problem.

Problem Description

To make the fulcrum (Figure \(\PageIndex{2.2}\)) of a bascule bridge, a long hollow steel shaft called the trunnion is shrunk-fit into a steel hub. The resulting steel trunnion-hub assembly is then shrunk-fit into the girder of the bridge.

The shrink-fitting is done by first immersing the trunnion in a cold medium such as a dry-ice/alcohol mixture. After the trunnion reaches the steady-state temperature, that is, the temperature of the cold medium, the outer diameter of the trunnion contracts. The trunnion is taken out of the medium and slid through the hole of the hub (Figure \(\PageIndex{2.3}\)).

When the trunnion heats up, it expands and creates an interference fit with the hub. In 1995, on one of the bridges in Florida, this assembly procedure did not work as designed. Before the trunnion could be inserted fully into the hub, the trunnion got stuck. Luckily, the trunnion was taken out before it got stuck permanently. Otherwise, a new trunnion and hub would need to be ordered at the cost of \(\$50,000\) . Coupled with construction delays, the total loss could have been more than a hundred thousand dollars.

Why did the trunnion get stuck? Because the trunnion had not contracted enough to slide through the hole. Can you find out why this happened?

Simple Mathematical Model

A hollow trunnion of an outside diameter \(12.363^{\prime\prime}\) is to be fitted in a hub of inner diameter \(12.358^{\prime\prime}\) . The trunnion was put in a dry ice/alcohol mixture (temperature of the fluid - dry-ice/alcohol mixture is \(- 108{^\circ}\text{F}\) ) to contract the trunnion so that it can be slid through the hole of the hub. To slide the trunnion without sticking, a diametrical clearance of at least \(0.01^{\prime\prime}\) is required between the trunnion and the hub. Assuming the room temperature is \(80{^\circ}\text{F}\) , is immersing the trunnion in a dry-ice/alcohol mixture a correct decision?

To calculate the contraction in the diameter of the trunnion, the thermal expansion coefficient at room temperature is used. In that case, the reduction \(\Delta D\) in the outer diameter of the trunnion is

\[\displaystyle\Delta D = D\alpha\Delta T \;\;\;\;\;\;\;\;\;\;\;\; (\PageIndex{2.1}) \nonumber\]

\[D = \text{ outer diameter of the trunnion,} \nonumber\]

\[\alpha = \text{ coefficient of thermal expansion coefficient at room temperature, and} \nonumber\]

\[\Delta T = \text{change in temperature.} \nonumber\]

Solution to Simple Mathematical Model

\[D = 12.363^{\prime\prime} \nonumber\]

\[\alpha = 6.47 \times 10^{-6}\ \text{in/in/}^{\circ}\text{F} \text{ at } 80{^\circ}\text{F} \nonumber\]

\[\displaystyle \begin{split} \Delta T&= T_{\text{fluid}} - T_{\text{room}}\\ &= - 108 - 80\\ &= - 188{^\circ}\ \text{F}\end{split} \nonumber\]

\[T_{\text{fluid}}= \text{ temperature of dry-ice/alcohol mixture} \nonumber\]

\[T_{\text{room}}= \text{ room temperature} \nonumber\]

the reduction in the outer diameter of the trunnion from Equation \((\PageIndex{2.1})\) hence is given by

\[\begin{split} \Delta D &= (12.363)\left( 6.47 \times 10^{- 6} \right)\left( - 188 \right)\\ &=- 0.01504^{\prime\prime} \end{split} \nonumber\]

So the trunnion is predicted to reduce in diameter by \(0.01504^{\prime\prime}\) . But is this enough reduction in diameter? As per specifications, the trunnion diameter needs to change by

\[\begin{split} \Delta D &= -\text{trunnion outside diameter} + \text{hub inner diameter} - \text{diametric clearance}\\ &= -12.363 +12.358 - 0.01\\ &= - 0.015^{\prime\prime} \end{split} \nonumber\]

So, according to this calculation, immersing the steel trunnion in dry-ice/alcohol mixture gives the desired contraction of greater than \(0.015^{\prime\prime}\) as the predicted contraction is \(0.01504^{\prime\prime}\) . But, when the steel trunnion was put in the hub, it got stuck. Why did this happen? Was our mathematical model adequate for this problem, or did we create a mathematical error?

Accurate Mathematical Model

As shown in Figure \(\PageIndex{2.4}\) and Table 1, the thermal expansion coefficient of steel decreases with temperature and is not constant over the range of temperature the trunnion goes through. Hence, Equation \((\PageIndex{2.1})\) would overestimate the thermal contraction.

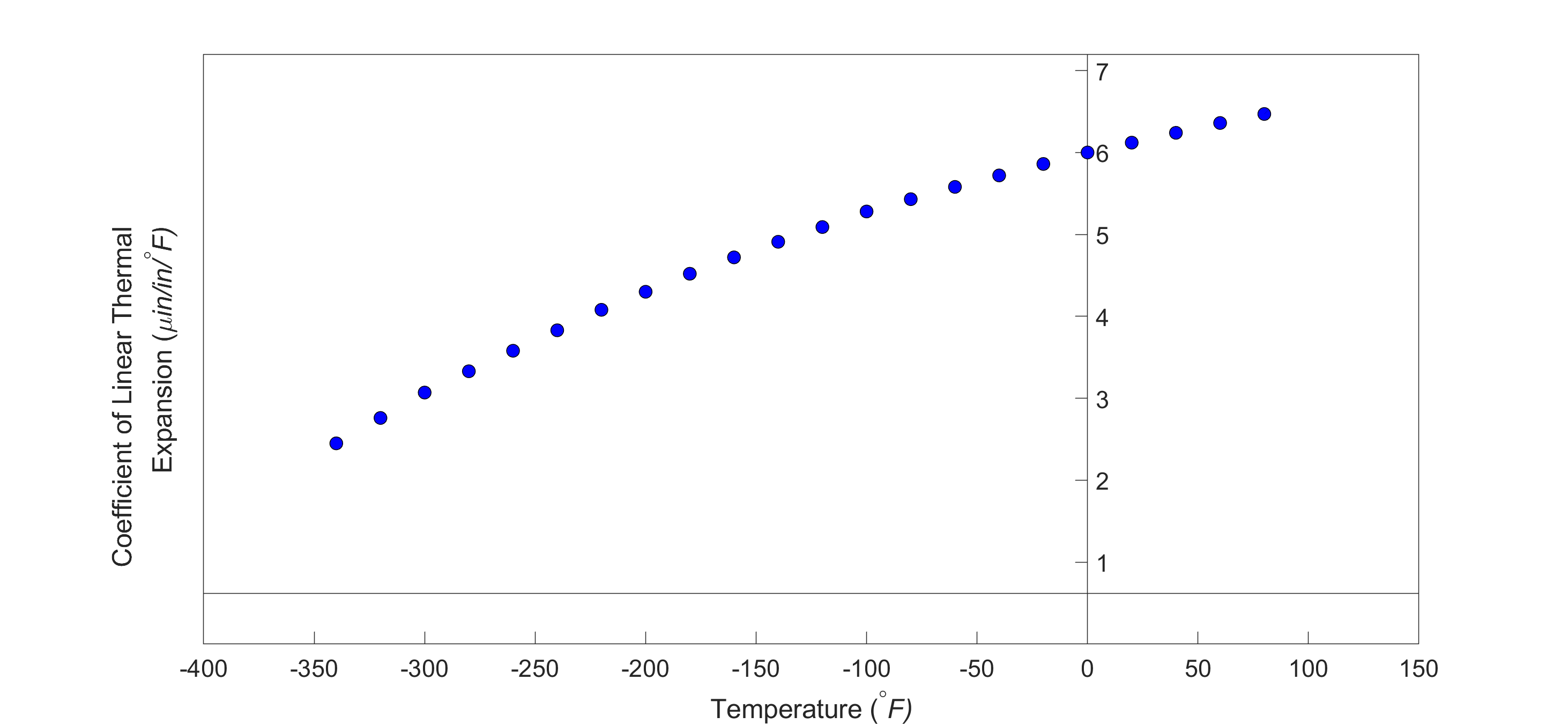
he contraction in the diameter of the trunnion for which the thermal expansion coefficient varies as a function of temperature is given by

\[ \Delta D = D\int_{T_{\text{room}}}^{T_{\text{fluid}}} \alpha dT \;\;\;\;\;\;\;\;\;\;\;\; (\PageIndex{2.2}) \nonumber\]

Solution to More Accurate Mathematical Model

So, one needs to curve fit the data to find the coefficient of thermal expansion as a function of temperature. This curve is found by regression where we best fit a function to the data given in Table 1. In this case, we may fit a second-order polynomial

\[\displaystyle\alpha = a_{0} + a_{1} T + a_{2} T^{2}\;\;\;\;\;\;\;\;\;\;\;\; (\PageIndex{2.3}) \nonumber\]

The values of the coefficients in the above Equation \((\PageIndex{2.3})\) will be found by polynomial regression (we will learn how to do this later in the chapter on Nonlinear Regression). At this point, we are just going to give you these values, and they are

\[\begin{bmatrix} a_{0} \\ a_{1} \\ a_{2} \\ \end{bmatrix} = \begin{bmatrix} 6.0150 \times 10^{- 6} \\ 6.1946 \times 10^{- 9} \\ - 1.2278 \times 10^{- 11} \\ \end{bmatrix} \nonumber\]

to give the polynomial regression model (Figure \(\PageIndex{2.5}\)) as

\[\displaystyle \begin{split} \alpha &= a_{0} + a_{1}T + a_{2}T^{2}\\ &= {6.0150} \times {1}{0}^{- 6} + {6.1946} \times {10}^{- 9}T - {1.2278} \times {10}^{- {11}}T^{2} \end{split} \;\;\;\;\;\;\;\;\;\;\;\; (\PageIndex{2.4}) \nonumber\]

Knowing the values of \(a_{0}\) , \(a_{1}\) , and \(a_{2}\) , we can then find the contraction in the trunnion diameter from Equations \((\PageIndex{2.2})\) and \((\PageIndex{2.3})\) as

\[\begin{split} \displaystyle\Delta D &= D\int_{T_{\text{room}}}^{T_{\text{fluid}}}{(a_{0} + a_{1}T + a_{2}T^{2}}){dT}\\ &= D\left\lbrack a_{0}T + a_{1}\frac{T^{2}}{2} + a_{2}\frac{T^{3}}{3} \right\rbrack\begin{matrix} T_{\text{fluid}} \\ \\ T_{\text{room}} \\ \end{matrix}\\ &= D\lbrack a_{0}(T_{\text{fluid}} - T_{\text{room}}) + a_{1}\frac{({T_{\text{fluid}}}^{2} - {T_{\text{room}}}^{2})}{2}\\ & \ \ \ \ \ + a_{2}\frac{({T_{\text{fluid}}}^{3} - {T_{\text{room}}}^{3})}{3}\rbrack\;\;\;\;\;\;\;\;\;\;\;\;(\PageIndex{2.5}) \end{split} \nonumber\]

Substituting the values of the variables gives

\[\displaystyle \begin{split} \Delta D &= 12.363\begin{bmatrix} 6.0150 \times 10^{- 6} \times ( - 108 - 80) \\ + 6.1946 \times 10^{- 9}\displaystyle \frac{\left( ( - 108)^{2} - (80)^{2} \right)}{2} \\ - 1.2278 \times 10^{- 11}\displaystyle \frac{(( - 108)^{3} - (80)^{3})}{3} \\ \end{bmatrix}\\ &= - 0.013689^{\prime\prime}\end{split} \nonumber\]

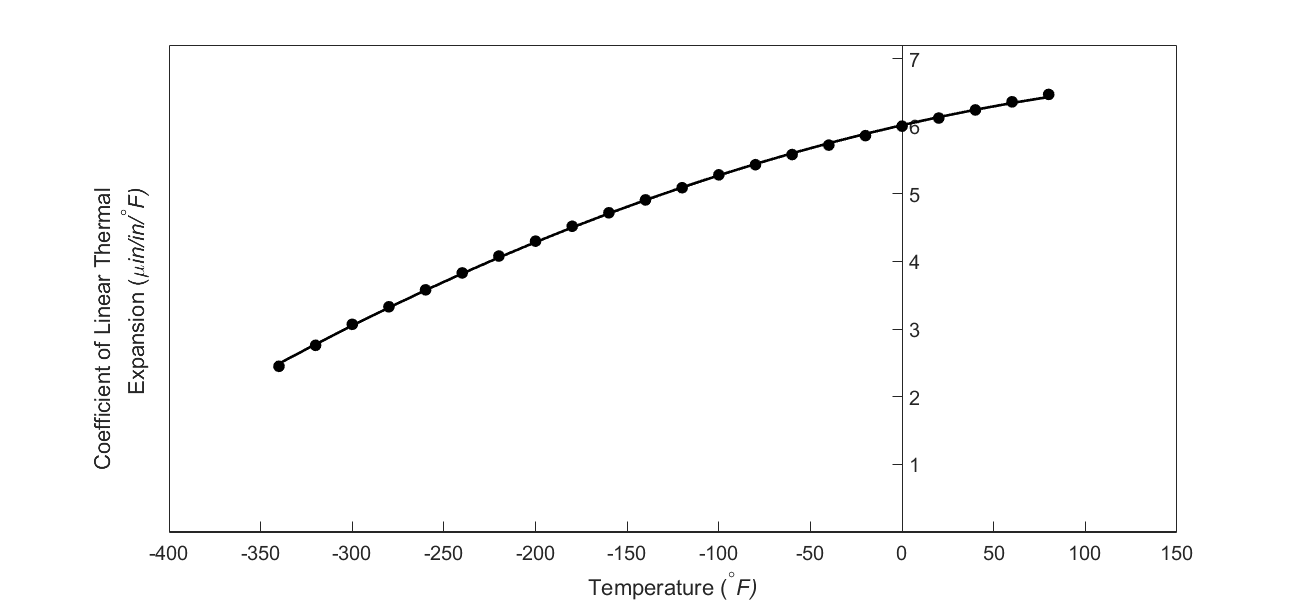
What do we find here? The contraction in the trunnion is not enough to meet the required specification of \(0.015^{\prime\prime}\) .

Implementing the Solution

Although we were able to find out why the trunnion got stuck in the hub, we still need to find and implement a solution. What if the trunnion were immersed in a medium that was cooler than the dry-ice/alcohol mixture of \(- 108{^\circ}F\) , say liquid nitrogen, which has a boiling temperature of \(- 321{^\circ}F\) ? Will that be enough for the specified contraction in the trunnion?

As given in Equation \((\PageIndex{2.5})\)

\[\displaystyle \begin{split} \Delta D &= D\int_{T_{\text{room}}}^{T_{\text{fluid}}}{(a_{0} + a_{1}T + a_{2}T^{2}}){dT}\\ &= D\left\lbrack a_{0}T + a_{1}\frac{T^{2}}{2} + a_{2}\frac{T^{3}}{3} \right\rbrack\begin{matrix} T_{\text{fluid}} \\ \\ T_{\text{room}} \\ \end{matrix}\\ &= D\lbrack a_{0}(T_{\text{fluid}} - T_{\text{room}}) + a_{1}\frac{({T_{\text{fluid}}}^{2} - {T_{\text{room}}}^{2})}{2}\\ & \ \ \ \ \ + a_{2}\frac{({T_{\text{fluid}}}^{3} - {T_{\text{room}}}^{3})}{3}\rbrack\;\;\;\;\;\;\;\;\;\;\;\; (\PageIndex{2.5}-repeated) \end{split} \nonumber\]

which gives

\[\displaystyle \begin{split} \Delta D &= 12.363\begin{bmatrix} 6.0150 \times 10^{- 6} \times ( - 321 - 80) \\ + 6.1946 \times 10^{- 9} \displaystyle\frac{\left( ( - 321)^{2} - (80)^{2} \right)}{2} \\ \ - 1.2278 \times 10^{- 11} \displaystyle\frac{(( - 321)^{3} - (80)^{3})}{3} \\ \end{bmatrix}\\ & \\ &= - 0.024420^{\prime\prime} \end{split} \nonumber\]

The magnitude of this contraction is larger than the specified value of \(0.015^{\prime\prime}\).

So here are some questions that you may want to ask yourself later in the course.

1) What if the trunnion were immersed in liquid nitrogen (boiling temperature \(= - 321{^\circ}\text{F}\) )? Will that cause enough contraction in the trunnion?

2) Rather than regressing the thermal expansion coefficient data to a second-order polynomial so that one can find the contraction in the trunnion OD, how would you use the trapezoidal rule of integration for unequal segments?

3) What is the relative difference between the two results?

4) We chose a second-order polynomial for regression. Would a different order polynomial be a better choice for regression? Is there an optimum order of polynomial we could use?

Title: Steps of Solving Engineering Problems

Summary : This video teaches you the steps of solving an engineering problem- define the problem, model the problem, solve, and implementation of the solution.

Lesson 3: Overview of Mathematical Processes Covered in This Course

1) enumerate the seven mathematical processes for which numerical methods are used.

Numerical methods are techniques to approximate mathematical processes. This introductory numerical methods course will develop and apply numerical techniques for the following mathematical processes:

1) Roots of Nonlinear Equations

2) Simultaneous Linear Equations

3) Curve Fitting via Interpolation

4) Differentiation

5) Curve Fitting via Regression

6) Numerical Integration

7) Ordinary Differential Equations.

Some undergraduate courses in numerical methods may include topics of partial differential equations, optimization, and fast Fourier transforms as well.

Roots of a Nonlinear Equation

The ubiquitous formula

\[ x = \frac{- b \pm \sqrt{b^2 - 4ac}}{2a} \;\;\;\;\;\;\;\;\;\;\;\; (\PageIndex{3.1}) \nonumber\]

of finding the roots of a quadratic equation \(\displaystyle ax^{2} + bx + c = 0\) goes back to the ancient world. But in the real world, we get equations that are not just the quadratic ones. They can be polynomial equations of a higher order and transcendental equations.

Take an example of a floating ball shown in Figure \(\PageIndex{3.1}\), where you are asked to find the depth to which the ball will get submerged when floating in the water.

Assume that the ball has a density of \(600\ \text{kg}/\text{m}^{3}\) and has a radius of \(0.055\ \text{m}\) . On applying the Newtons laws of motion and hence equating the weight of the ball to the buoyancy force, one finds that the depth, \(x\) in meters, to which the ball is underwater and is given by

\[\displaystyle 3.993 \times 10^{- 4} - 0.165x^{2} + x^{3} = 0 \;\;\;\;\;\;\;\;\;\;\;\; (\PageIndex{2}) \nonumber\]

Equation \((\PageIndex{3.2})\) is a cubic equation that you will need to solve. The equation will have three roots, and the root that is between \(0\ \text{m}\) (just touching the water surface) and \(0.11\ \text{m}\) (almost submerged) would be the depth to which the ball is submerged. The two other roots would be physically unacceptable. Note that a cubic equation with real coefficients can have a set of one real root and two complex roots or a set of three real roots. You may wonder, why could such an application be important? Let’s suppose you are filling in this tank with water, and you are using this ball as a control so that when the ball goes all the way to the top that the flow of the water stops – say in a fish tank that needs replenishing while the owner is away for a few weeks. So, we do need to figure out how much of the ball is submerged underwater.

A cubic equation can be solved exactly by radicals, but it is a tedious process. The same is true but even more complicated for a general fourth-order polynomial equation as well. However, there is no closed-form solution available for a general polynomial equation of fifth-order or more. So, one has to resort to numerical techniques to solve polynomial and other transcendental nonlinear equations (e.g., finding the nonzero roots of \(\tan x = x\) ).

Simultaneous Linear Equations

Ever since you were exposed to algebra, you have been solving simultaneous linear equations.

Take this problem statement as an example. Suppose the upward velocity of a rocket (Figure \(\PageIndex{3.2}\)) is given at three different times (Table \(\PageIndex{3.1}\)).

The velocity data is approximated by a polynomial as

\[\displaystyle v\left( t \right) = at^{2} + {bt} + c\ {, 5} \leq t \leq {12}.\;\;\;\;\;\;\;\;\;\;\;\;(\PageIndex{3.3}) \nonumber\]

To estimate the velocity at a time that is not given to us, we can set up the equations to find the coefficients \(a,b,c\) of the velocity profile.

The polynomial in Equation (3) is going through three data points \(\left( t_{1},v_{1} \right),\left( t_{2},v_{2} \right),\) and \(\left( t_{3},v_{3} \right)\) where from Table 1.1.3.1

\[\begin{split} t_{1} &= 5,v_{1} = 106.8\\ t_{2} &= 8,v_{2} = 177.2\\ t_{3} &= 12,v_{3} = 600.0 \end{split} \nonumber\]

Requiring that \(v\left( t \right) = at^{2} + bt + c\) passes through the three data points, gives

\[\begin{split} v\left( t_{1} \right) &= v_{1} = at_{1}^{2} + bt_{1} + c\\ v\left( t_{2} \right) &= v_{2} = at_{2}^{2} + bt_{2} + c\\ v\left( t_{3} \right) &= v_{3} = at_{3}^{2} + bt_{3} + c \end{split} \nonumber\]

Substituting the data \(\left( t_{1},\ v_{1} \right),\ \left( t_{2},\ v_{2} \right),\) and \(\left( t_{3},\ v_{3} \right)\) gives

\[\begin{split} a\left( 5^{2} \right) + b\left( 5 \right) + c = 106.8 \\ a\left( 8^{2} \right) + b\left( 8 \right) + c = 177.2 \\ a\left( 12^{2} \right) + b\left( 12 \right) + c = 600.0 \end{split} \nonumber\]

\[\begin{split} 25a + 5b + c = 106.8 \\ 64a + 8b + c = 177.2 \\ 144a + 12b + c = 600.0 \end{split} \;\;\;\;\;\;\;\;\;\;\;\; (\PageIndex{3.4}) \nonumber\]

Solving a few simultaneous linear equations such as the above set can be done without the knowledge of numerical techniques. However, imagine that instead of three given points, you were given 10 data points. Now the setting up as well as solving the set of 10 simultaneous linear equations without numerical techniques becomes laborious, if not impossible.

Curve Fitting by Interpolation

Interpolation involves that given a function as a set of data points. How does one find the value of the function at points that are not given?. For this, we choose a function, called an interpolant, and make it pass through all the points involved.

You may think that you have already used interpolation in courses such as Thermodynamics and Statistics. After all, it was just taking two points from a table at the back of the textbook or online and finding the value of the function at a point in between by using a straight line.

Take this problem statement as an example. Let’s suppose the upward velocity of a rocket is given at three different times (Table 1.1.3.1).

If one asked you to estimate the velocity at \(7\ \text{s}\) , one might simply use the straight-line formula you are most accustomed to as given below.

Given ( \(t_{1},\ v_{1}\) ) and ( \(t_{2},\ v_{2}\) ), the value of the function \(v\) at \(t\) is given by

\[\displaystyle v = v_{1} + \frac{v_{2} - v_{1}}{t_{2} - t_{1}}(t - t_{1}) \;\;\;\;\;\;\;\;\;\;\;\; (\PageIndex{3.5}) \nonumber\]

Although this is possibly enough for courses such as Thermodynamics and Statistics, there are two questions to ask. Is the value calculated accurately, and how accurate is it? To know that, one needs to calculate at least more than one value. In the above example of a rocket velocity vs. time, one can instead use a second-order polynomial interpolant and set up the three equations and three unknowns to find the unknown coefficients, \(a\) , \(b\) , and \(c\) as given in the previous section.

\[v\left( t \right) = at^{2} + {bt} + c{ ,\ 5} \leq t \leq {12}\;\;\;\;\;\;\;\;\;\;\;\; (\PageIndex{3.6}) \nonumber\]

Then, the resulting second-order polynomial can be used to find the velocity at \(t = 7\ \text{s}\) .

The value obtained from the second-order polynomial (Equation \((\PageIndex{3.6})\)) can be considered to be a new measure of the value of \(v( 7)\) , and the first-order polynomial (Equation \((\PageIndex{3.5})\)) result can be used to determine the accuracy of the results.

Numerical Differentiation

You have taken a semester-long course in Differential Calculus, where you found derivatives of continuous functions. So let’s suppose somebody gives you the velocity of a rocket as a continuous and at least once differentiable function of time and wants you to find acceleration. Indeed for this particular problem, you can use your differential calculus knowledge to differentiate the velocity function to get the acceleration and put in the value of time, \(t = 7\ \text{s}\) . What if the velocity vs. time is not given as a continuous and at least once differentiable function? Instead, let’s say the function is given at discrete data points (Table 1.1.3.1). How are you then going to find out what the acceleration at \(t = 7\ \text{s}\) ? Do we draw a straight line from \((5,106.8)\) to \((8,177.2)\) and use the straight-line slope as the estimate of acceleration? How do we know that this is adequate? We could incorporate all three points and find a second-order polynomial as given by Equation \((\PageIndex{3.6})\). This polynomial can now be differentiated to estimate the acceleration at \(t = 7\ \text{s}\) . Now the two values can be used to evaluate the accuracy of the calculated acceleration.

Curve Fitting by Regression

When we talked about curve fitting by interpolation, the chosen interpolant needs to go through all the points considered. What happens when we are given many data points, and we instead want a simplified formula to explain the relationship between two variables. See, for example, in Figure \(\PageIndex{3.4a}\), we are given the coefficient of linear thermal expansion data for cast steel as a function of temperature. Looking at the data, one may proclaim that a straight line could explain the data, and that is drawn in Figure \(\PageIndex{3.4b}\). How we draw this straight line is what is called regression. It would be based on minimizing some form of the residuals between what is observed (given data points) and what is predicted (straight line). It does not mean that every time you have data given to you, you draw a straight line. It is possible that a second-order polynomial or a transcendental function other than the first-order polynomial will be a better representation of this particular data. So these are the questions that we will answer when we discuss regression. We will also discuss the adequacy of linear regression models.

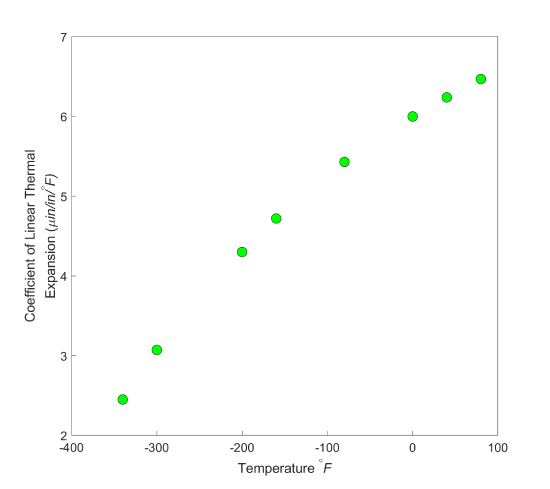
Numerical Integration

You have taken a whole course on integral calculus. Now, why would we need to make numerical approximations of integrals? Just like the standard normal cumulative distribution function

\[\displaystyle\Phi(x) = \frac{1}{\sqrt{2\pi}}\int_{- \infty}^{x}e^{- t^{2}/2}{dt} \;\;\;\;\;\;\;\;\;\;\;\; (\PageIndex{3.7}) \nonumber\]

cannot be solved exactly, or when the integrand values are given at discrete data points, we need to use numerical methods of integration.

In the previous lesson, we looked at the example of contracting the diameter of a trunnion for a bascule bridge fulcrum assembly by dipping it in a mixture of dry ice and alcohol. The contraction is given by

\[\Delta D = D\int_{T_{\text{room}}}^{T_{\text{fluid}}}{\alpha\ dT} \;\;\;\;\;\;\;\;\;\;\;\; (\PageIndex{3.8}) \nonumber\]

\[D = \text{outer diameter of the trunnion,} \nonumber\]

\[\alpha = \text{coefficient of linear thermal expansion that is varying with temperature} \nonumber\]

\[T_{\text{room}}= \text{room temperature} \nonumber\]

\[T_{\text{fluid}}= \text{temperature of dry-ice alcohol mixture.} \nonumber\]

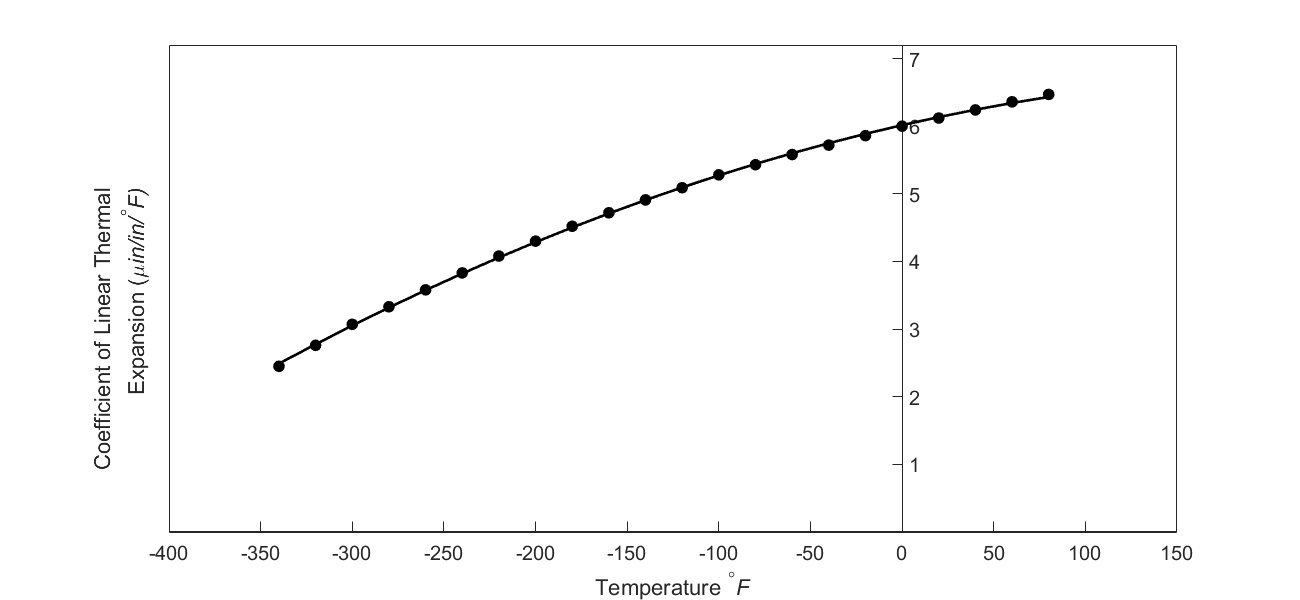
From Figure \(\PageIndex{3.4a}\), one can note that the coefficient of thermal expansion is only given at discrete temperatures and not as a known continuous function that could be integrated exactly. So we have to resort to numerical methods by approximating the data, say, by a second-order polynomial obtained via regression.

In Figure \(\PageIndex{3.6}\), the thermal expansion coefficient of typical cast steel is approximated by a second-order regression polynomial as given by Equation \((\PageIndex{3.9}\)) (how we get this is a later lesson in regression) as

\[\displaystyle\alpha = - 1.2278 \times 10^{- 11}T^{2} + 6.1946 \times 10^{- 9}T + 6.0150 \times 10^{- 6} \;\;\;\;\;\;\;\;\;\;\;\; (\PageIndex{3.9}) \nonumber\]

The contraction of the diameter then is given by

\[\displaystyle\Delta D = D\int_{T_{\text{room}}}^{T_{\text{fluid}}}{\left( - 1.2278 \times 10^{- 11}T^{2} + 6.1946 \times 10^{- 9}T + 6.015 \times 10^{- 6} \right){dT}} \;\;\;\;\;\;\;\; (\PageIndex{3.10}) \nonumber\]

and can now be calculated using integral calculus.

Numerical Solution of Ordinary Differential Equations

Taking the same example of the trunnion being dipped in a dry-ice/alcohol mixture, one could ask the question - What would the temperature of the trunnion be after dipping it in the mixture for 30 minutes? The model is given by an ordinary differential equation for the temperature \(\theta\) as a function of time, \({t.}\)

\[\displaystyle -{hA} \left(\theta - \theta_{a} \right) = {mC} \frac{d \theta}{dt}\;\;\;\;\;\;\;\;\;\;\;\; (\PageIndex{3.11}) \nonumber\]

\[h= \text{the convective cooling coefficient,}\ \text{W/m}^{2} \cdot \text{K} \nonumber\]

\[A = \text{surface area},\ \text{m}^2 \nonumber\]

\[\theta_{a} = \text{ambient temperature of dry-ice/alcohol mixture},\ \text{K} \nonumber\]

\[m = \text{mass of the trunnion, kg} \nonumber\]

\[C = \text{specific heat of the trunnion,}\ \text{J/(kg} \cdot \text{K)} \nonumber\]

The differential Equation \((\PageIndex{3.11})\) can be solved exactly by using the classical solution, Laplace transform, or separation of variables techniques. So, where do numerical methods enter into the picture for this problem? For the temperature range of room temperatures to cold media such as dry-ice/alcohol, several of the variables in Equation \((\PageIndex{3.11})\) are not constant but change with the temperature. These include the convection coefficient \(h\) as well as the specific heat \(C\) . Now, this differential equation has turned nonlinear as follows.

\[\displaystyle -h(\theta)A\left( \theta - \theta_{a} \right) = mC(\theta)\frac{d \theta}{dt} \;\;\;\;\;\;\;\;\;\;\;\; (\PageIndex{3.12}) \nonumber\]

The ordinary differential Equation \((\PageIndex{3.12})\) cannot be solved by exact methods and would need to be solved by a numerical method.

In the above discussion, we have illustrated the need for numerical methods for each of the seven mathematical processes in the course. In the lessons to follow, we will be developing various numerical techniques to approximate the mathematical processes to calculate acceptable accurate values while calculating associated errors.

Title: Overview of Mathematical Processes Covered in This Course

Summary : This lecture shows you four mathematical procedures that need numerical methods - namely, nonlinear equations, differentiation, simultaneous linear equations, and interpolation.

Multiple Choice Test

(1). Solving an engineering problem requires four steps. In order of sequence, the four steps are

(A) formulate, model, solve, implement

(B) formulate, solve, model, implement

(C) formulate, model, implement, solve

(D) model, formulate, implement, solve

(2). One of the roots of the equation \(x^{3} - 3x^{2} + x - 3 = 0\) is

(C) \(\sqrt{3}\)

(3). The solution to the set of equations

\[\begin{split} 25a + b + c &= 25 \\ 64a + 8b + c &= 71\\ 144a + 12b + c &= 155 \end{split} \nonumber\]

most nearly is \(\left( a,b,c \right) =\)

(A) \((1,1,1)\)

(B) \((1,-1,1)\)

(C) \((1,1,-1)\)

(D) does not have a unique solution.

(4). The exact integral of \(\displaystyle \int_{0}^{\frac{\pi}{4}} 2 \cos 2x \ dx\) is most nearly

(A) \(-1.000\)

(B) \(1.000\)

(C) \(0.000\)

(D) \(2.000\)

(5). The value of \(\displaystyle \frac{dy}{dx}\left( 1.0 \right)\) , given \(y = 2\sin\left( 3x \right)\), is most nearly

(A) \(-5.9399\)

(B) \(-1.980\)

(C) \(0.31402\)

(D) \(5.9918\)

(6). The form of the exact solution of the ordinary differential equation \(\displaystyle 2\frac{dy}{dx} + 3y = 5e^{- x},\ y\left( 0 \right) = 5\) is

(A) \(Ae^{- 1.5x} + Be^{x}\)

(B) \(Ae^{- 1.5x} + Be^{- x}\)

(C) \(Ae^{1.5x} + Be^{- x}\)

(D) \(Ae^{- 1.5x} + Bxe^{- x}\)

For complete solution, go to

http://nm.mathforcollege.com/mcquizzes/01aae/quiz_01aae_introduction_answers.pdf

Problem Set

(1). Give one example of an engineering problem where each of the following mathematical procedures is used. If possible, draw from your experience in other classes or from any professional experience you have gathered to date.

a) Differentiation

b) Nonlinear equations

c) Simultaneous linear equations

d) Regression

e) Interpolation

f) Integration

g) Ordinary differential equations

(2). Only using your nonprogrammable calculator, find the root of

\[x^{3} - 0.165x^{2} + 3.993 \times 10^{- 4} = 0 \nonumber\]

by any method. Hint: Find one root by hit and trial, and use long division for factoring the polynomial.

\(0.06237758151,\ 0.1463595047,\ -0.04373708621\)

(3). Solve the following system of simultaneous linear equations by any method

\[\begin{split} 25a + 5b + c &= 106.8\\ 64a + 8b + c &= 177.2\\ 144a + 12b + c &= 279.2 \end{split} \nonumber\]

\(a = 0.2904761905,\ b = 19.69047619,\ c = 1.085714286\)

(4). You are given data for the upward velocity of a rocket as a function of time in the table below. Find the velocity at \(t = 16 \ \text{s}\) .

\(543.0420000\ \text{m/s}\)

(5). Integrate exactly.

\[\int_{0}^{\pi/2}\sin2x \ dx \nonumber\]

\[\frac{dy}{dx}(x = 1.4) \nonumber\]

\[y = e^{x} + \sin(x) \nonumber\]

\(4.225167110\)

(7). Solve the following ordinary differential equation exactly.

\[\frac{dy}{dx} + y = e^{- x}, \ y(0) = 5 \nonumber\]

Also find \(y(0),\ \displaystyle \frac{dy}{dx}\ (0),\ y(2.5),\ \displaystyle\frac{dy}{dx}\ (2.5)\)

\(\displaystyle y(0)=5,\ \frac{dy}{dx}(0)=-4,\ y(2.5)=0.61563,\ \frac{dy}{dx}(2.5)=-0.53355\)