canonical analysis in research methodology

No internet connection.

All search filters on the page have been cleared., your search has been saved..

• All content
• Dictionaries
• Encyclopedias
• Expert Insights
• Foundations
• How-to Guides
• Journal Articles
• Little Blue Books
• Little Green Books
• Project Planner
• Tools Directory
• Sign in to my profile My Profile

• Sign in Signed in
• My profile My Profile

• FOUNDATION ENTRY Chi-Squared Test
• FOUNDATION ENTRY Bonferroni, Carlo Emilio
• FOUNDATION ENTRY Variance Estimation
• FOUNDATION ENTRY Yule, George Udny
• FOUNDATION ENTRY Correlation
• FOUNDATION ENTRY Statistical Significance Problem
• FOUNDATION ENTRY Confidence Intervals
• FOUNDATION ENTRY Canonical Correlation Analysis
• FOUNDATION ENTRY Fisher, Ronald Aylmer
• FOUNDATION ENTRY Bias
• FOUNDATION ENTRY t Test
• FOUNDATION ENTRY Type I and Type II Errors
• FOUNDATION ENTRY Pearson, Karl
• FOUNDATION ENTRY Goodness-of-Fit Measures
• FOUNDATION ENTRY Central Limit Theorem
• FOUNDATION ENTRY Effect Size
• FOUNDATION ENTRY ANOVA and ANCOVA
• FOUNDATION ENTRY Standard Errors

Discover method in the Methods Map

Canonical correlation analysis.

• By: Peter Boedeker & Robin K. Henson | Edited by: Paul Atkinson, Sara Delamont, Alexandru Cernat, Joseph W. Sakshaug & Richard A.Williams
• Publisher: SAGE Publications Ltd
• Publication year: 2020
• Online pub date: January 15, 2020
• Discipline: Anthropology , Business and Management , Communication and Media Studies , Computer Science , Counseling and Psychotherapy , Criminology and Criminal Justice , Economics , Education , Engineering , Geography , Health , History , Marketing , Mathematics , Medicine , Nursing , Political Science and International Relations , Psychology , Social Policy and Public Policy , Science , Social Work , Sociology , Technology
• Methods: Canonical correlation , Independent variables , Dependent variables
• Length: 10k+ Words
• DOI: https:// doi. org/10.4135/9781526421036883301
• Online ISBN: 9781529749182 More information Less information
• What's Next

Canonical correlation analysis (CCA) is a multivariate statistical technique that can be used in research scenarios in which there are several correlated outcomes of interest. Instead of separating analyses of these outcomes into several univariate analyses, a single application of CCA can capture the relationship across variables while honoring the fact that variables are correlated within sets. In CCA, the variability shared between two variable sets is partitioned into independent relationships and these relationships are characterized by the variables that contribute most in their formation. CCA is described here in detail, connecting the multivariate procedure to simple bivariate correlation and multiple regression and highlighting its position in the general linear model. After reviewing the procedure and important terminology, an accessible example is provided. The example is reproducible with data and syntax available online.

Introduction

Canonical correlation analysis (CCA) is a multivariate statistical technique used to investigate the number and nature of independent relationships between two sets of variables where each set contains at least two variables. With multivariate methods such as CCA, correlated outcomes are investigated in concert rather than separately. By taking a multivariate approach, the researcher is able to honor the fact that outcomes of interest may be correlated with one another and that those relationships are relevant in understanding associations between variables deemed to be “predictors” and those labeled “outcomes.” Although one set of variables may be labeled as the “independent variables” or “predictors” and the other the “dependent variables” or “outcomes,” such specifications are not required in CCA because of the method’s correlational nature. The goal in conducting a CCA is to parsimoniously separate the variability that is shared across variable sets into independent relationships. These independent relationships are then characterized by the variables that contribute most to their existence. This entry provides an explanation of CCA as well as the tools and knowledge necessary to conduct a CCA. To that end, this entry proceeds by providing (a) a characterization of CCA as a multivariate method and its position in the general linear model (GLM), (b) details concerning the derivation of important aspects of a CCA, (c) procedures for evaluating the results of a CCA, and (d) a complete example of CCA with simulated data that are available online.

Overview and Statistical Context

Generally, CCA is an appropriate method to use when a researcher is interested in parsimoniously understanding the multivariate pattern of relationships between two sets of variables. The variables within each set have some natural relation to one another and can be measures of the same construct or related constructs. For example, a set of measured variables in an education setting may be reading ability, math ability, and problem-solving ability, where the overall grouping of these variables is made to represent a child’s academic ability. Another set of variables capturing academic soft skills may contain measures of scholastic interest, academic motivation, and persistence. In this context, the researcher may describe the academic soft-skills variable set as the predictor set and the academic ability variable set as the outcome set based on the idea that academic soft skills predict academic outcomes. CCA could then be utilized to investigate the relationship between academic soft skills and academic ability and discover the number and nature of unique relationships within the shared variability of the two sets of variables.

It may be that the overall shared variability between the variable sets can be decomposed into, for example, two unique relationships, each characterized by different variables within sets. The two unique relationships are identified using various methods described in detail later in this entry, but in general the first unique relationship captures the greatest association between variables across sets, thereby accounting for the largest portion of shared variability, and the second accounts for a smaller portion of the total shared variability. The first unique relationship could be primarily defined by the association between scholastic interest from the predictor variable set and reading ability in the outcome variable set. The second unique relationship could then be primarily defined by the association between academic motivation and persistence from the predictor variable set and math ability and problem-solving ability from the outcome variable set. The first relationship extracted (between scholastic interest and reading ability) would be the strongest relationship and therefore the relationship most responsible for producing the noteworthy overall relationship between the two variable sets. The second relationship then would account for a smaller portion of the noteworthy overall effect but still may be itself of interest. By partitioning shared variability in this manner, the analyst can better understand the relationships across variable sets while also honoring the relationships within variable sets.

Multivariate Methods

In the social sciences, for the many predictor variables of interest, there are likely to be several related outcomes. For example, an intervention in an education setting to improve the reading ability of a child may affect more than reading ability. Other outcomes in this scenario may include reading self-efficacy and the child’s motivation to read on his or her own. An intervention may be effective at increasing the reading ability of a child but may also, due to mundane reading drills, reduce the child’s motivation to read. Although the child’s short-term reading ability has increased, the long-term ramification of a decreased motivation to read may inevitably prove that the intervention stymies achievement. Such a result is certainly relevant in the evaluation of an intervention’s effectiveness. Multivariate analyses honor the fact that research in the social sciences is conducted in a world filled with related predictors and related outcomes and that these relationships are relevant when the researcher seeks to understand a phenomenon.

Apart from multivariate methods honoring the multivariate world in which much of social sciences research takes place, multivariate methods are also useful for controlling type I error rates (Fish, 1988). Instead of conducting various t tests to evaluate the difference between two groups on several outcomes, a single omnibus test of a difference across all outcomes can be evaluated using Hotelling’s T 2 . When more than two groups are involved, instead of conducting several univariate analyses of variance (ANOVAs), one for each outcome, the researcher can evaluate group differences across the entire set of outcomes in a multivariate analysis of variance (MANOVA). Finally, if the analyst is interested in the association between a set of predictors and outcomes, instead of using multiple regressions in which each outcome is regressed upon a set of predictors, a single CCA can be conducted that captures the joint relationship between all predictors and outcomes simultaneously. These multivariate methods honor the reality that the outcomes are correlated with one another, thereby providing omnibus tests that can control for type I error.

Canonical Correlation Analysis and the General Linear Model

CCA is found within the GLM, a family of procedures that (a) are correlational by nature, (b) produce r 2 -type effect sizes, and (c) apply weights to observed variables to produce synthetic variables that often become the focus of analysis (Thompson, 1998). Although regression has been shown to be the univariate form of the GLM subsuming all parametric univariate methods (Cohen, 1968), CCA was shown to be the multivariate GLM subsuming both univariate ( t tests, ANOVAs, regression) and multivariate methods (Hotelling’s T 2 , MANOVA; Knapp, 1978). When considering a hierarchy of statistical procedures, where lower level procedures are subsumed as special cases of higher level procedures, CCA is just below structural equation modeling in which measurement error is modelled (Bagozzi, Fornell, & Larcker, 1981; Zientek & Thompson, 2009). CCA therefore has pedagogical relevance to the analyst who is learning about the relationship between statistical methods as well as the substantive researcher seeking a method for investigating relationships between sets of variables.

From Bivariate Correlation to Canonical Correlation

The logic and procedure for CCA can be developed starting with the bivariate correlation and progressing through multiple regression with a single outcome. This “road map” introduces terminology relevant in a discussion of CCA (and therefore relevant throughout the GLM). Foundational in the GLM is the Pearson’s correlation coefficient. The squared correlation coefficient indicates the amount of shared variability between two variables. The squared correlation is an effect size and the statistical significance of this relationship can be evaluated. If a relationship between two variables is found to exist, the source of this relationship is obvious because there are only two variables under consideration.

When this variability is cast in a regression context, the researcher is able to evaluate the shared variability between one or several predictors and a single outcome. In the regression context, the variability shared between the single outcome and the set of predictors is denoted as the R 2 . This squared multiple correlation is the squared bivariate correlation between the outcome and a synthetic variable, often denoted y ^ . This y ^ variable is the predicted outcome based on the observed variables in the model. As a characteristic of GLM analyses, the synthetic y ^ is created by applying weights to the observed variables and becomes of primary focus in the analysis. Utilizing ordinary least squares, coefficients (i.e., the weights applied to observed variables) for each predictor are derived to produce y ^ such that the sum of squared error is minimized and, as a result, the shared variance between the predictors and the outcome ( R 2 ) is maximized.

The contribution of each predictor in making the y ^ variable is evaluated traditionally by investigating the standardized regression coefficients ( β weights) and, although less frequently, squared structure coefficients (Courville & Thompson, 2001). The standardized regression coefficients indicate the number of standard deviations the outcome variable will change given a one standard deviation change in the predictor, holding constant all other predictors in the model. Standardized weights are susceptible to multicollinearity, the condition in which predictors are highly correlated with one another. For example, a predictor with a moderate bivariate correlation with the outcome and high correlation with another predictor in the model may have a near zero β weight, appearing unrelated to the outcome. This result may occur because both predictors are similarly increasing and each could be credited (by assigning a high β weight) with changes in the outcome; however, to assign a high β weight to both predictors would produce a y ^ that is too large. Therefore, predictive credibility that could be attributed to either predictor must be credited to only one of the predictors or divided in some fashion to each. Standardized weights distribute this credibility across correlated predictors, making standardized weights less useful in evaluating predictor importance in a model in which predictors are correlated with one another. The squared structure coefficient for each predictor variable is simply the squared correlation between the predictor and the synthetic y ^ variable. Structure coefficients honor the fact that the focus of the analysis is on y ^ (the predicted score) and allows the analyst to investigate the importance of each predictor in relation to y ^ unconfounded by the presence of other correlated variables in the model. Structure coefficients are then useful when interpreting the importance of a given predictor when predictors are correlated with one another (as often is the case in social sciences research). Therefore, when conducting a multiple regression, the analyst is interested first in evaluating the overall model of predictors and outcome, typically by evaluating the R 2 and its statistical significance, and second in determining which of the predictors are important contributors in the model by investigating standardized weights and structure coefficients.

CCA is a further extension of multiple regression. Although the predictor side of the equation in multiple regression was expanded to include additional predictors (thus making the regression “multiple”), in CCA there are both multiple predictors and multiple outcomes to consider. For example, one set of variables may be broadly defined as Personality and the other Attachment, wherein each variable of Personality is a measure of a specific personality trait and each variable of Attachment is a specific measure of attachment. The variables in the predictor set are linearly combined, using a canonical function, to produce a synthetic canonical variate and the variables in the outcome set are linearly combined, using another canonical function, to produce another synthetic canonical variate. Although in multiple regression y ^ was created to maximize its shared variance with the observed outcome, in CCA the canonical variates are derived to have maximum shared variance with one another. The shared variance in multiple regression is R 2 and is the squared correlation between y ^ and the observed outcome; the shared variance of interest in CCA is the squared canonical correlation ( R C 2 ) and is the squared correlation between the two canonical variates. In CCA, several pairs of canonical functions may be derived, each pair of functions producing two canonical variates that are correlated yielding an R C 2 . The R C 2 for a set of functions captures a portion of the total shared variance between the variable sets. By deriving multiple sets of functions and their variates, the total shared variance between variables across sets is partitioned into unique relationships defined by different linear combinations of the variables in the predictor and outcome sets.

Similar to the y ^ of regression, the canonical variates are created by applying weights to observed variables. The standardized form of these weights are called standardized canonical coefficients and are analogous to β weights in regression. Structure coefficients also exist in CCA and are the bivariate correlation between each observed variable and the respective canonical variate. In CCA, the contribution of each variable is evaluated using the standardized canonical function coefficients and the structure coefficients in a similar manner as would be done in multiple regression. The difference in CCA compared to regression is that there are two equations with weights applied to observed variables for each R C 2 instead of one.

After the first set of canonical functions have been derived, there is potential for the variables in the two sets to still have shared variance that could be explained by a different linear combination of the variables in each variable set. To explain the remaining variability, a new set of functions is derived and a new pair of synthetic canonical variates created. This second set of functions has an R C 2 and its own set of canonical function coefficients and structure coefficients to be evaluated. A variable may do little to contribute to the formation of the canonical variate in the first set of functions but may be a substantial contributor in the second. Because the subsequent sets of functions are used to explain variability left unexplained by the previously extracted set of functions, the variability explained by the second set of functions is uncorrelated with the variability explained by the previous functions. Therefore, each set of functions describes a unique relationship between the sets of variables. There will be as many canonical functions as there are variables in the smallest variable set. For example, if there are three variables in one set and two variables in the other, then there will be at most two sets of canonical functions that can be derived.

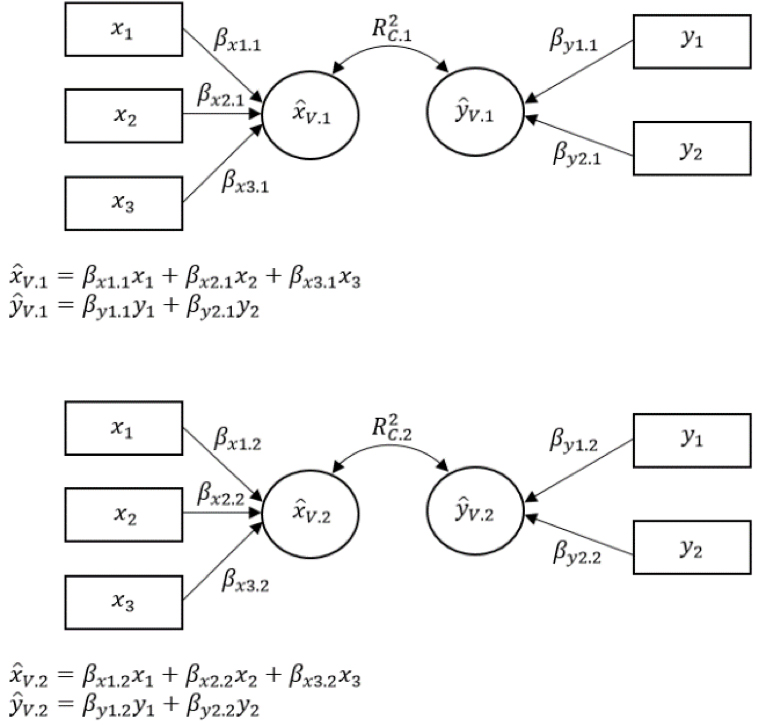
Figure 1 provides a graphic representation of CCA using a path model. In this scenario, there are three X variables and two Y variables. The first set of standardized canonical function coefficients for the X variables ( β x 1.1 , β x 1.2 , β x 1.3 ) are used to produce the canonical variate x ^ V .1 that is maximally correlated (i.e., maximizing R C .1 2 ) with the canonical variate y ^ V .1 , where y ^ V .1 is the result of applying standardized canonical function coefficients ( β y 1.1 , β y 1.2 ) to the observed Y variables. After shared variability between variable sets is explained with the first set of canonical functions, a second set of canonical functions can be derived to produce canonical variates to explain variability left unexplained by the first set of functions. This is shown in the lower half of Figure 1 , as indicated with a “2” subscript that these are coefficients uniquely derived for the second canonical function. The second set of standardized canonical function coefficients are estimated to produce a new pair of canonical variates that maximize R C .2 2 , where R C .2 2 is the squared canonical correlation of shared variability between the two canonical variates. The R C .2 2 captures the variability shared between the variables in the variable sets that was not captured by the first functions and therefore is uncorrelated with the results of the first canonical functions. The canonical variates themselves then are uncorrelated across functions, a condition termed double orthogonality (Sherry & Henson, 2005).

In the first set, the function coefficients beta subscript x 1.1, beta subscript x 2.1, and beta subscript x 3.1 of x subscript 1, x subscript 2, and x subscript 3, respectively, are used to produce x subscript V.1-hat. The function coefficients beta subscript y 1.1 and beta subscript y 2.1 of y subscript 1 and subscript 2, respectively, are used to produce y subscript V.1-hat. X subscript V.1-hat and y subscript V.1-hat are correlated by R squared subscript C .1. X subscript V.1-hat equals beta subscript x 1.1 times x subscript 1 plus beta subscript x 2.1 times x subscript 2 plus beta subscript x 3.1 times x subscript 3. Y subscript V.1-hat equals beta subscript y 1.1 times y subscript 1 plus beta subscript y 2.1 times y subscript 2. In the second set, the function coefficients beta subscript x 1.2, beta subscript x 2.2, and beta subscript x 3.2 of x subscript 1, x subscript 2, and x subscript 3, respectively, are used to produce x subscript V.2-hat. The function coefficients beta subscript y 1.2 and beta subscript y 2.2 of y subscript 1 and subscript 2, respectively, are used to produce y subscript V.2-hat. X subscript V.2-hat and y subscript V.2-hat are correlated by R subscript C .2 squared. X subscript V.2-hat equals beta subscript x 1.2 times x subscript 1 plus beta subscript x 2.2 times x subscript 2 plus beta subscript x 3.2 times x subscript 3. Y subscript V.2-hat equals beta subscript y 1.2 times y subscript 1 plus beta subscript y 2.2 times y subscript 2.

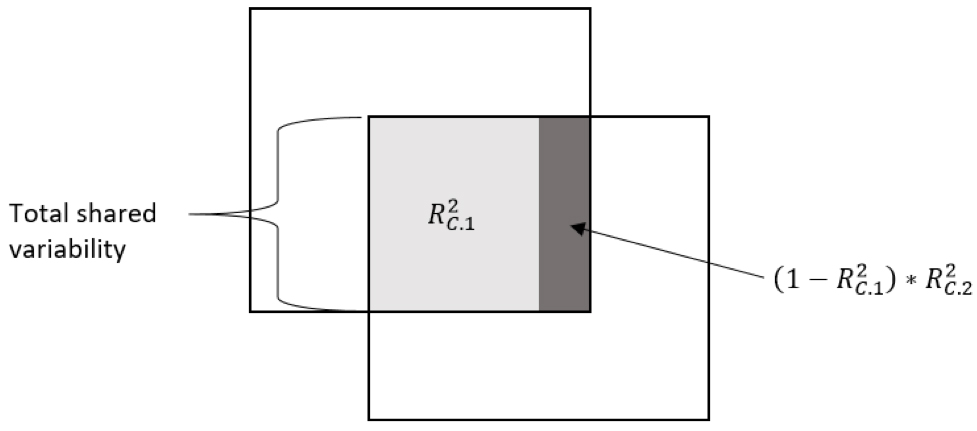
An illustration of the decomposition of the total shared variability between the two sets in relation to each function set’s R C 2 is provided in Figure 2 . The R C .1 2 is the relationship between the canonical variates of the first function and captures a portion of the variability in a set of variables. The next set of functions’ R C .2 2 captures a portion of the shared variability between variables in the two variable sets that remains after the first function has been used to explain as much of the shared variability as possible. The R C .2 2 is the portion explained of the residual variability left unexplained by the first function.

The larger portion on the left side of the smaller square is shaded, and labeled R subscript C .1 squared, total shared variability. The smaller portion on the right side of the larger square is shaded, and labeled 1 minus R subscript C .1 squared times R subscript C .2 squared.

As can be seen, the logic of CCA is the same as that of the bivariate correlation. Instead of a bivariate relationship between two observed variables, however, the relationship of interest is between two synthetic variates, created by applying weights to observed variables. In a CCA, there are at least two variables in each set of variables. If one set was constrained to include only one variable, the analysis could be termed a multiple regression with a single outcome predicted by the variables in the other set. If both sets of variables are each constrained to one variable, then the resulting analysis is a bivariate correlation. The bivariate correlation and multiple regression with a single outcome, as well as other univariate and multivariate tests, are special cases of CCA.

Derivation of Canonical Functions and Canonical Variates

CCA is a multivariate technique that honors the reality that many of the outcomes of interest in social sciences research will be correlated and considering those relationships is essential in properly understanding some phenomenon. A CCA is used to decompose the shared variance between variable sets into unique relationships that can be described by the variables found important in the creation of canonical variates. Although a detailed explanation of the mathematical procedures behind deriving canonical functions and therefore variates are available elsewhere and completed by software, a simple outline of the procedure is provided here to highlight the correlational nature of CCA.

Canonical Functions

Derivation of canonical functions requires the formation of a series of correlation matrices, the use of matrix algebra to multiply these matrices together, and then the mathematics of principal components analysis to consolidate the total shared variability into a reduced number of functions. For example, assume that a CCA is conducted on two variable sets, each set comprised of two variables. The first set contains variables A and B and the second set contains variables S and T. The correlations between these variables are first set into a single correlation matrix which is subsequently divided into four correlation matrices (see Table 1 ).

These four correlation matrices are then multiplied together (after inverting the first and third) to produce a single matrix in the following manner:

The matrix R is then solved for eigenvectors and eigenvalues. The eigenvectors are transformed into canonical functions that are used to combine the original variables into the canonical variates. An eigenvalue is equivalent to the squared canonical correlation between variates produced by canonical functions. By deriving eigenvalues, the variance of a matrix is redistributed and consolidated into composite variates instead of many individual variables (Tabachnick & Fidell, 2013).

The mathematics used for deriving the eigenvalues, eigenvectors, and canonical functions is the same as that which is utilized in principal components analysis. However, in a principal components analysis, components are derived to consolidate the variability in the correlation matrix of the original set of variables; whereas in CCA, functions are derived to consolidate the variability in the R matrix. The result of a principal components analysis with the original variables is a set of uncorrelated components that, depending on the number of components retained, captures all or some of the variability in the original set of variables. In CCA, the result is a set of uncorrelated function pairs that, depending on the number of variables in each set and the number of functions retained, explains all or some of the variability shared across the variable sets. By using the principal components analysis on the R matrix instead of the original correlation matrix, the analyst is able to honor the membership of variables in sets and therefore able to better understand the relationships between variables across sets (Thompson, 1984).

Canonical Variates

Canonical variates are created by multiplying the standardized form of each variable within a set by its standardized canonical coefficient and summing across these products. This is the same as is done in a multiple regression when calculating predicted y ^ values; however, the derivation of weights and subsequent multiplication of these weights by standardized values of the observed variables is done for both sets of variables in the CCA instead of only one. Returning to Figure 1 , the canonical variate for the x -variable set is calculated as

where β x j .1 is the standardized canonical function coefficient in the first canonical function for the x j standardized variable in the x -variable set. The summation is from 1 to 3 because there are three variables in the x -variable set in Figure 1 . Similarly, to calculate the first canonical variate for the y -variable set

where β y j .1 is the standardized canonical function coefficient in the first canonical function for the y j standardized variable in the y -variable set. These standardized canonical function coefficients were derived to maximize R C .1 2 , the squared canonical correlation between the two canonical variates for the first set of retained functions.

Evaluating the Canonical Solution

Evaluating the canonical solution requires first determining whether there is an overall relationship between the two variable sets. If an overall relationship is detected, then the variability can be reasonably partitioned over function pairs, each evaluated using an effect size and statistical significance test. An effect size is a standardized measure of the magnitude of an effect or relationship that can be compared across studies and provides a metric for evaluating the practical significance of the results. A statistical significance test yields a p value, or the probability of observing a result, or a more extreme result, given a null hypothesis of no difference between groups or no relationship between variables is true and (b) the sample size. Considering both statistical significance and effect size is important in general when evaluating statistical results. This is especially true in CCA because the method is a large sample procedure. R. S. Barcikowski and J. P. Stevens (1975) conducted a Monte Carlo study in which they investigated the necessary sample sizes for reliably detecting and interpreting CCA results and found that a minimum sample size to variable ratio of 42:1 is necessary if interpreting the first two sets of functions and 20:1 if only interpreting the first set of functions. With large sample sizes, functions with potentially trivial amounts of explained variability may be deemed statistically significant. Therefore, a balanced perspective on evaluating a result as significant, both statistically and practically, should be employed. For each function found to produce canonical variates with noteworthy shared variance, the contribution of variables within each function may be evaluated to determine which variables characterize the relationship captured in the set of functions.

Evaluating the Total Shared Variability

For many multivariate procedures, such as MANOVA or descriptive discriminant analysis, the overall solution can be evaluated using one of several statistical tests, including Wilk’s λ , Pillai’s trace, Lawley-Hotelling trace, and Roy’s largest (or greatest characteristic) root. For CCA, the most frequently used methods are based on Wilk’s λ and include Bartlett’s χ 2 test and Rao’s F test. Wilk’s λ is a likelihood ratio test evaluating the null hypothesis that the relationship across variable sets is equal to zero. The sampling distribution of the likelihood ratio test is approximately χ 2 , although M. S. Bartlett (1939) proposed an adjustment to improve the chi-square approximation and C. Radhakrishna Rao (1948) derived an F-approximation for testing the same null. A benefit to considering Wilk’s λ is that the λ value itself is a variance-unaccounted for effect size, meaning λ represents the amount of variability that is not shared across the variable sets. As such, 1 – λ is equal to the total shared variance between variable sets and is the variability that is partitioned across function sets in CCA. If found to be noteworthy, this shared variability can then be decomposed across function sets by use of CCA.

Evaluating Canonical Functions

As stated, the maximum number of canonical functions that can be created is equal to the number of variables in the smaller set. Each function is evaluated using a combination of effect size and statistical significance test. The effect size for each set of canonical functions is the R C 2 , and for statistical significance, the Bartlett’s χ 2 test or Rao’s F test approximations for the likelihood ratio test may be used in a sequential, “peel-away” manner.

Statistical Significance

After an initial evaluation of the entire canonical solution, which is essentially a test of all possible functions together, Bartlett’s χ 2 test or Rao’s F test is applied in a sequential or peel-away procedure. Because of the complexity of the underlying sampling distribution theory (Johnson & Wichern, 2007; Kshirsagar,1972), the statistical significance of each R C 2 produced by unique function pairs cannot be tested. Instead, the null hypothesis of the first test is that the canonical correlations across all pairs of canonical variates are equal to zero. This first test is an evaluation of the entire canonical solution if all function sets were retained (and is equivalent to an evaluation of 1 − λ ). The next test is an evaluation of the null hypothesis that after excluding the first canonical correlation, all remaining canonical correlations are equal to zero. Therefore, the first and largest canonical correlation is “peeled-away” from the rest and the results of the remaining functions evaluated together. This is repeated until only the last canonical correlation remains, and this single value is tested against the null that the canonical correlation is zero. For example, if there are three canonical correlations, then the first statistical significance test evaluates the null hypothesis that all three canonical correlations are equal to zero. The next test evaluates the null hypothesis that the smallest two canonical correlations are equal to zero (excluding the largest canonical correlation that is associated with the first set of functions). The final statistical significance test evaluates the third canonical correlation in isolation. This is the only canonical correlation of the three that is evaluated alone. Because not all canonical correlations are evaluated separately, the number of function sets to retain is based on when in the sequential testing the results are no longer statistically significant. If the first test of all three canonical correlations is statistically significant and the second test of the two smallest is not statistically significant, then there is evidence that the first set of canonical functions is worth interpreting and the remaining are not. If instead the first test of all three and the second test of the smallest two were statistically significant but the third test not, then the first two sets of functions are candidate for interpretation based on statistical significance whereas the third is not.

Bartlett’s χ 2 is calculated using

Λ j is the eigenvalue (or equivalently the squared canonical correlation) for the j th set of canonical variates, k y is the number of variables in the Y set, k x is the number of variables in the X set, n is the sample size, and p is the total number of canonical correlations being tested. The degrees of freedom for the χ 2 test is equal to ( k x + 1 − i ) ( k y + 1 − i ) , where i is an indicator for the test number in sequential testing. For example, in the first test of all canonical correlations, the degrees of freedom equals ( k x + 1 − 1 ) ( k y + 1 − 1 ) or simply k x k y . For the next test of all canonical correlations excluding the canonical correlation of the first set of canonical functions, the degrees of freedom is equal to ( k x + 1 − 2 ) ( k y + 1 − 2 ) .

Rao’s approximate F test is found by

This formula holds for all values of k y and k x unless k x 2 k y 2 = 4, in which case s is set equal to 1 (Cohen, 1988). Note that for the first function, where i would equal 1, the numerator of s would then be k x 2 k y 2 − 4; if k x 2 k y 2 = 4 then this would equal zero. In Rao’s F test, the reciprocal of s is used and therefore a zero value in the numerator would result in an undefined exponent, hence setting k x 2 k y 2 equal to 1 to avoid an undefined solution. The d f 1 is found in the same manner as the degrees of freedom for Bartlett’s test and

and all other values are defined as before. Rao’s test has been shown by Monte Carlo simulation to be accurate with data that violates the multivariate normality assumption (assumptions being discussed later), including with variables that are dichotomous (Olson, 1974) with samples of 60 or more. Rao’s F test is generally considered a better test than Bartlett’s (Schuster & Lubbe, 2015), although in many scenarios the two tests will yield the same conclusion.

Effect Size

Similar to the regression R 2 , in CCA, the R C 2 for each set of canonical functions is the effect size of interest. The R C 2 for the first set of functions is the amount of shared variability between the two canonical variates produced by the first set of functions and is a direct measure of the amount of variability in the “outcome” set that is explained or accounted for by variability in the “predictor” set. The second R C 2 is the shared variability between the second set of canonical variates and is the proportion of the variability left unexplained in the outcome set by the first set of functions that is explained by the predictor set using the second set of functions. Returning to Figure 2 , this idea of explaining residual variability is shown. For example, if R C .1 2 , the squared canonical correlation for the first set of canonical functions is .58, then 58% of the variability in the canonical variates is shared. Using one set as a predictor set and one as an outcome set, then 58% of the variability in the set of outcome variables is explained by the predictors using the first set of canonical functions. If R C .2 2 , the squared canonical correlation for a second set of canonical functions, is .29, then 29% of the variability between the canonical variates produced by the second set of functions is shared. This also means that 29% of the 42% of the variability in the outcome variable set left unexplained by the first set of functions is explained by the predictors using the second set of functions. Therefore, the second set of canonical functions is used to explain .29*.42 = .1218, or 12.18% of the variability in the outcome variable set. If a maximum of two function sets could be produced, then the total proportion of variability in the outcome variable set that is explained by the predictor set is equal to R C .1 2 + ( 1 − R C .1 2 ) ( R C .2 2 ) = .7018 (which is also equivalent to 1 − λ ). Understanding that the second canonical correlation is a proportion of the unexplained variability (i.e., the residual variability) rather than of the total variability in the outcome is important, particularly in the scenario in which the R C .2 2 is larger than the R C .1 2 . For instance, if the R C .1 2 for the first set of canonical functions was .58 and the R C .2 2 for the second set was .80, the uninformed analyst may be led to believe that the second set of canonical functions explains a greater proportion of variability in the variables than the first set of canonical functions do. In this scenario, the second set of canonical functions is used to explain .42*.80 = .336 or 33.6% of the total variability in the outcome variable set.

Evaluation of what a meaningful effect size is depends first on a thorough understanding of the substantive area in which the procedure is being applied. Second, rules of thumb can be employed to evaluate whether or not an R C 2 of a certain size is worth interpreting. Jacob Cohen, in Chapter 10 of Statistical Power Analysis for the Behavioral Sciences , offers methods of determining what may be considered small, medium, and large effects in CCA (Cohen calls CCA “set correlation”) by comparison to multiple regression in which small, medium, and large effects were associated with f 2 values of .02, .15, and .35, respectively. To find the R C 2 value associated with a given f 2 from multiple regression, s must be found as detailed in Rao’s F test. After calculating s ,

gives the value of R C 2 associated with a given value of f 2 . For example, if there are three variables in the X set and two variables in the Y set then s = 2 and small, medium, and large values of R C 2 for the first set of functions are approximately .04, .24, and .45, respectively.

The R C 2 estimated from a sample is positively biased, meaning that on average the sample R C 2 will be larger than the actual population R C 2 . This is due to the lower bound of the sample R C 2 being zero. Therefore, if the population R C 2 was actually zero, then the only values that would deviate from the population value would be positive. Cohen (1988) provides a “shrinkage” formula that will result in a less biased estimate of the population squared canonical correlation,

where R C . s h r u n k e n 2 is the shrunken squared canonical correlation, R C 2 is the sample squared canonical correlation, and d f 1 , d f 2 , and s are found as they were in Rao’s F test. The shrunken value can take on negative values. If this occurs, reporting that R C . s h r u n k e n 2 is equal to zero would be appropriate.

Determining the number of functions retained requires a balanced evaluation of statistical significance using Bartlett’s χ 2 or Rao’s F test and the effect size R C 2 for each function set. After the analyst has determined the number of functions to retain, the task is to then describe what these functions tell the researcher with regard to the unique relationships that they identify between the sets of variables. To do this, the individual variables within each set can be evaluated for their contribution in creating their respective variate.

Evaluating Variables

After evaluating each set of canonical functions using statistical significance and effect size, the next step is to determine which variables within each function are most important. The logic for why we are interested in the contribution of variables to the formation of the variates is straightforward. The variates are linear composites of the variables within each set. Therefore, determination of which variable or variables contributed most to the creation of the composite or are most associated with the composite gives the analyst an understanding of which variables within each set contributed most to the identified shared variability between the variates. This is the same process as is followed in a univariate regression, only now with two functions within which to evaluate the contribution of variables instead of only one as in regression. When considering the contribution of variables in CCA to the formation of the canonical variates, it is appropriate to interpret standardized function coefficients and structure coefficients. Additionally, because of the possibility of retaining multiple function pairs and the complexity that may introduce in evaluating variable importance, several other values may be interpreted. The communality coefficient is useful as an aggregate measure of variable importance in the final canonical solution (set of retained functions). Adequacy coefficients describe, on average, how well the canonical variate reproduces the variability of the variables within the variable set used to create the variate. Finally, a procedure not recommended in conjunction with CCA, that of redundancy coefficient analysis, is also possible.

After determining which variables are most important in the formation of the canonical variate within a set of functions, the relationship captured between variable sets and quantified in R C 2 can be named. Those variables that contribute most to the creation of the canonical variate for a given function, and thus responsible for the shared relationship identified in R C 2 , are the variables that are used to characterize the relationship. Variables deemed unimportant in one function set may be the most important variable in another function set. Each R C 2 then represents a unique relationship between variables. In this manner, the partitioning of shared variability across sets of functions allows the analyst to understand what unique relationships exist within the overall relationship identified.

Standardized and Unstandardized Function Coefficients

Both standardized and unstandardized function coefficients exist in a CCA. However, because the interpretation of unstandardized coefficients will be in a metric that is likely not common across variables, the standardized form of the coefficients are generally used in evaluating variable contribution to the canonical variate. Standardized coefficients are multiplied by the standardized form of each variable to produce a canonical variate, so they can indicate how much each variable has contributed to the creation of the variate. However, these coefficients are based on the partial relationship between each variable and the canonical variate after accounting for the variable’s association with other variables in the set. When the variables within a set are correlated with one another (as would be expected in a CCA) this leads the standardized coefficient to potentially misrepresent the relationship between the variable in question and the canonical variate. For example, if two variables could equally be used to create the variate but are correlated with one another, one of the variables may receive the lion’s share of the credibility for making the canonical variate by having a large standardized coefficient while the second variable be assigned a near zero standardized coefficient (Thompson & Borrello, 1985). In this way, the relationship between a variable and the variate could be masked if only using standardized weights to determine variable importance. Therefore, when evaluating the importance of each variable to the formation of the canonical variate, consultation of structure coefficients (and their squared values) is necessary.

Canonical Structure Coefficients

A canonical structure coefficient is the bivariate correlation of a variable and the canonical variate to which the variable contributed. In Figure 1 , the structure coefficient of x 1 in the first function is the correlation between x 1 and x ^ V .1 . The structure coefficient is unaffected by the presence of other variables and gives direct insight into the magnitude of relationship between each variable and its respective canonical variate. The squared canonical structure coefficient is the proportion of shared variability between a given variable and the canonical variate. Large squared structure coefficients indicate that the variable is highly related to the canonical variate and therefore important to consider when evaluating variable importance and when naming relationships identified by function sets.

Variable Importance

When evaluating a variable’s contribution in creating the canonical variate, the determination is made simple when both the standardized canonical function coefficient and the structure coefficient are high in magnitude or low in magnitude. When this is not the case and instead one of these coefficients is near zero or coefficients are of opposite magnitude, interpretational challenges may exist. For example, if the standardized coefficient for a variable is near zero but the structure coefficient is high, then the variable is highly correlated with the variate but does not appear to have any part in the creation of the variate (based on the standardized weight). Such masking of variable importance may occur when variables are correlated with one another. In another scenario, the standardized coefficient may be high but the structure coefficient near zero. This variable is being given credit for the creation of the variate yet does not have a meaningful correlation with the variate it is given credit for creating. This may be the result of suppression, which can occur when a variable is associated with other variables in the model but not directly with the variate. When naming the relationship identified by a set of functions, it is recommended that both standardized weights and structure coefficients be consulted (Sherry & Henson, 2005).

Communalities

A communality is the sum of a variable’s squared structure coefficients across all retained functions and as such is an aggregate measure of a variable’s contribution to the entire canonical solution. The communality of a variable is generally denoted h 2 . For example, if two sets of functions were retained and the squared structure coefficient for a variable in the first set of functions was 0.3 and in the second set of functions was 0.5, then the communality for the given variable would be 0.8. This means that 80% of the variability in the variable was shared with the variates for the retained functions.

Adequacy Coefficients

An adequacy coefficient is the average of the squared structure coefficients of variables within a function. This value represents in a single number how well the canonical variate represents the variability in the variables used to produce it. For example, if a canonical variate is created from a set of three variables, and each variable had a squared structure coefficient of 0.2, 0.5, and 0.5, respectively, the adequacy coefficient for the function would be 0.4. On average, the variate reproduces 40% of the variability in the variables used to create the variate. For each set of variables, an adequacy coefficient can be derived, therefore there are two per retained set of functions.

A redundancy coefficient is found by multiplying the adequacy coefficient for a given function by the squared canonical correlation between a pair of variates. With the adequacy coefficient representing the average variability a variate shares with the variables used to create it and the squared canonical correlation the amount of shared variability between two canonical variates, then the redundancy is the amount of variability in a given set of variables accounted for by the variables in the other variable set. For example, for an adequacy coefficient of 0.4, if the squared canonical correlation between functions was 0.5, then the redundancy coefficient would be 0.2. This would mean that 20% of the variability in the variables used to create a canonical variate could be reproduced by variables in the other canonical function.

Bruce Thompson (1991) and Xitao Fan and Timothy R. Konold (2010) caution against the use of redundancy coefficients with CCA. The rationale for this caution is simple: in CCA, the canonical correlation between two variates is optimized, not the redundancy coefficients. There is little reason to describe the redundancy analysis results in CCA when the goal of CCA is not to optimize redundancy but instead to optimize canonical correlation. Additionally, redundancy coefficients are equivalent to the average of R 2 values resulting from univariate regressions of each variable in one set predicted by all of the variables in the other set. Reverting to the equivalent of multiple univariate analyses when a multivariate analysis was already deemed necessary is counter to the logic of using a multivariate analysis at the start. Therefore, use of redundancy analysis is not recommended with CCA.

Assumptions

There are several assumptions of CCA. First, multivariate normality is necessary for accuracy of statistical significance tests that are developed based on this assumption. However, the assumption of normality is not strict and for mild departures from multivariate normality the statistical tests will still perform well, including the use of Rao’s test with categorical variables. Statistical significance tests for evaluating multivariate normality include Mardia’s tests for skewness and kurtosis (Mardia, 1970; 1974). Mardia’s tests evaluate the null hypotheses that multivariate skewness and kurtosis of the sample are consistent with a multivariate normal distribution; therefore, a nonstatistically significant result to these two tests would indicate that the distribution does not deviate substantially from a multivariate normal distribution. However, given that CCA is a large sample procedure, and statistical significance tests are sensitive to sample size such that larger sample sizes yield statistically significant results even for minor deviations from the null hypothesis, Mardia’s tests may yield statistically significant results even if the deviation from multivariate normality is negligible. A visual inspection of multivariate normality is the plot of the Mahalanobis distance against the associated χ 2 quantile (Henson, 1999). The Mahalanobis distance is the multivariate distance of a case’s responses to the centroid, or point defined in the multivariate space by the average of each variable. Evaluation of plots of distance and the χ 2 quantile follow the same rationale as the Q-Q plots used to evaluate the normality of a single variable. If the points on the plot generally fall along a diagonal, there is evidence that the distribution of variables is approximately multivariate normal.

As shown in the derivation of the canonical functions, the correlation matrix is at the core of CCA. Therefore, the correlation coefficient (a measure of linear relationship) must be an accurate representation of the relationship between variables included in the analysis. This can be evaluated by looking at the bivariate scatterplots of each pair of variables and checking for any potential nonlinear relationships. If a curvilinear relationship is found, an appropriate transformation can be applied. For instance, when a parabolic relationship exists between two variables, including in one set of variables a squared form of the variable could effectively capture the curvilinear relationship.

Finally, the variables should have minimum amounts of measurement error. Herein lies a difference between structural equation modeling and CCA in the hierarchy of analyses. In structural equation modeling, measurement error is included in the modeling of latent constructs. In CCA, each predictor is assumed to perfectly capture the construct or trait in question and therefore no measurement error need be accounted for. In the social sciences where researchers measure such traits as motivation or aptitude, these traits are measured with some degree of error because unlike more tangible characteristics such as height and weight, these latent constructs can only be approximated through a series of related questions. Therefore, when using CCA the instruments used should have minimal measurement error.

Example of CCA

An example is provided here to give some applied context to the previous discussion. In this example, three variables define the X set and three variables define the Y set. To make the example concrete, the scenario is that a researcher is interested in understanding the relationship between academic soft skills and academic ability, such that academic soft skills are predictors and academic ability variables are outcomes. Therefore, the X variable set is comprised of measures of scholastic interest, academic motivation, and persistence, where scholastic interest is a self-report evaluation from the child of their interest in learning in school, academic motivation is a variable describing a child’s general motivation to succeed in school, and persistence is a measure of a child’s willingness to put forth effort to complete complex tasks. The Y variable set contains measures of reading, mathematics, and problem-solving ability, where reading and mathematics ability are measured with end-of-course assessments, and problem-solving ability is a measure of a child’s ability to solve complex problems regardless of whether they are presented as text or in mathematical form. The data for the example are comprised of 80 simulated cases and are available, along with R (R Core Team, 2018) syntax at the open science framework account of Peter Boedeker, the first author of this entry. Although the data are fabricated, the research scenario and grouping of variables are plausible and the use of CCA is appropriate.

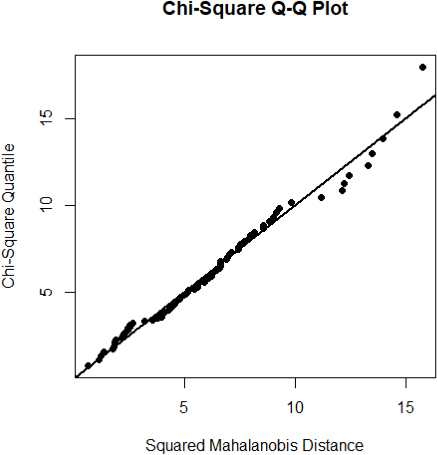
The multivariate normality of the data was evaluated using Mardia’s tests of multivariate skewness and kurtosis (see Table 2 ) as well as by visual inspection of the chi-square Q-Q plot (see Figure 3 ). Results indicated that multivariate normality was not violated to a substantial degree and therefore statistical significance tests of the canonical correlations are permissible. To evaluate the correlation coefficient as an accurate measure of the relationship between variables, the bivariate scatterplots of the data were scrutinized (not shown here). Finally, the traits measured by the variables in this fictitious example have minimal measurement error so we can proceed without modeling measurement error using structural equation modeling.

The horizontal axis is labeled squared mahalanobis distance and ranges from 0 to 15 in increments of 5. The vertical axis is labeled chi-square quantile and ranges from 0 to 15 in increments of 5. The best fit line slopes upward from the origin, through (5, 5), (10, 10), and (15, 15).

Evaluating the Overall Canonical Solution and Functions

The overall canonical solution is evaluated in the first of the peel-away statistical significance tests and the overall shared variability by 1 – λ . The results of the overall and subsequent testing of functions using Rao’s F test are presented in Table 3 . Given the scenario with three variables in the academic soft-skills set and three variables in the academic ability set, up to three sets of canonical functions may be retained. The first test evaluates the statistical significance of the entire canonical solution as if all function sets were retained. This is an evaluation of the overall solution. The λ value for the example scenario was 0.35, indicating that 1 – 0.35 = 0.65 or 65% of the variance is shared across the two sets of variables (or, that 65% of the variability in the outcome variable set could be explained by variability in the predictor variable set). Given that the test of functions 1 through 3 was statistically significant, F (9,180.25) = 10.813, p < .001 and the total shared variability was practically significant, λ = .35, further investigation of functions is warranted.

Using the peel-away procedure to evaluate functions, all results were statistically significant at the .05 level, although the third function (the only function evaluated in isolation) was notably less statistically significant than the previous evaluations. Given the importance of evaluating results using effect sizes, the R C 2 , R C . s h r u n k e n 2 , and the R C 2 values associated with interpretations of small, medium, and large according to Cohen (1988) for each function are presented in Table 4 . The first set of functions yielded an R C 2 of .473 with a shrunken value of .419. According to Cohen’s metric, the squared canonical correlation is between medium and large. The shared variability between the variates formed by the first set of functions is both practically and statistically significant. In this scenario, the first set of functions would be retained for interpretation. The R C 2 of .283 for the second set of functions indicates that 28.3% of the variability in the outcome variable set unexplained by the first set of functions is explained in the second set of functions. With an R C . s h r u n k e n 2 of .244, the relationship between the variates produced by the second set of functions can be considered medium according to Cohen (1988). The proportion of total variability in the outcome variable set explained in the second set of functions is (1 − .473)(.283) = .149. The argument then could be made to retain the second set of functions for interpretation because the shared variability was statistically significant and noteworthy. The third set of functions, however, produced canonical variates with a much smaller amount of shared variability ( R C 2 = .075) and of the total variability in the variable sets, only (1 − .473)(1 − .283)(.075) = .028 or 2.8% of the variability in the outcome is explained in the third set of canonical functions. Although the third set of functions did produce canonical variates with a statistically significant amount of shared variability ( p < .05), this shared variability may not be worth interpreting. Herein the analyst must use judgment and knowledge of the substantive area to make such a determination. In the present example, the third set of canonical functions is not retained for interpretation because they yielded a negligible R C 2 . Therefore, the amount of overall variability between the two variable sets using the two sets of retained functions is .473 + .149 = 0.622 or 62.2%. Notice that this total is 2.8% less than the value of 1 – λ , and that the third set of functions would have explained 2.8%.

Given that only the first two function sets were retained for interpretation, all subsequent discussion of the results will ignore the third set of functions. The standardized function coefficients, structure coefficients, and communalities for each variable and adequacies for each function are shown in Table 5 . Evaluation of variables will take place within each retained function.

If only depending on standardized weights for determining the composition of the canonical variate in the first set of functions, it would appear that for the set of academic soft-skills variables, persistence ( β = −1.040) primarily contributes to the formation of the canonical variate with a secondary contribution from academic motivation ( β = 0.276) and nearly zero contribution from scholastic interest ( β = 0.026). For the academic ability set of variables, relying on standardized weights alone would indicate that math ability ( β = −0.972) carries much of the credit for creating the canonical variate, followed by reading ability ( β = 0.406) and a marginal contribution from problem-solving ability ( β = −0.1). However, the structure coefficients are more useful when determining the composition of the canonical variate when variables are correlated. The structure coefficients of the academic soft-skills variables indicate that persistence ( r s = − .977 ) does have the greatest relationship with the canonical variate, in line with the interpretation of the standardized weights. However, scholastic interest ( r s = − .304 ) has a nearly equivalent relationship with the canonical variate compared to that of academic motivation ( r s = − .297 ), a substantial change from the evaluation of standardized weights. In the academic ability set of variables, mathematics ability ( r s = − .946 ) is still deemed to have the strongest relationship with the canonical variate, but problem-solving ability ( r s = − .675 ) is found to have a substantial relationship as well and reading ability a smaller relationship ( r s = − .188 ). This discrepancy between standardized weights and structure coefficients is due to the correlation between the variables within each set. When such discrepancies occur, interpretation based on structure coefficients is recommended (Thompson, 1984). As such, the noteworthy R C 2 and statistically significant result are primarily due to the relationship between persistence from the academic soft-skills set and both problem-solving ability and math ability from the academic ability set. The variables in the second set of functions can be similarly evaluated.

Note. Coeff = coefficient.

Using the definitions of the education variables and the resulting relationships between variables and canonical variates, the functions can be named. The first set of functions that explains the greatest amount of variability between the variable sets captures primarily the relationship between persistence and mathematics with problem-solving ability contributing as well. This function may be named “Analytical Challenges and Academic Persistence.” The second set of functions captures primarily the relationship between scholastic interest from the soft-skills variable set and reading ability and problem-solving ability from the academic ability variable set. This set of functions could be named “Interest and Complex Reading Tasks.”

If the analyst is interested in determining the sign of the relationship between two variables across sets, the structure coefficients of both variables must be taken into consideration. The structure coefficient is the correlation between the variable and the canonical variate it is used to create. The canonical correlation between variates will always be positive. Therefore, if the structure coefficients of both variables are negative, then the correlation of the variables across sets will be positive. As seen in Table 5 , the variables within each variable set are positively related to one another because they all have negative correlations with their canonical variate. Also, the variables across variable sets are all positively related with one another because all variables are negatively related with their respective canonical variate.

The communality coefficients (labeled h 2 in Table 5 ) indicate the total variability of each variable captured across the retained functions. As such, the communality is useful as an evaluation of a given variable’s contribution to the overall canonical solution. For example, from the academic soft-skills variable set, academic motivation ( h 2 = 0.187) was represented least in the canonical solution whereas persistence ( h 2 = 0.962) was represented most. In the academic ability variable set, the variability in problem-solving ability ( h 2 = 1) was completely represented by the two retained functions.

The adequacy coefficients are the average of the squared structure coefficients within a function for a single set of variables. They communicate, on average, how representative each canonical variate is of the variables used to create it. In this example, the largest adequacy coefficient was 0.462 for the academic ability variable set of the first functions, indicating that on average 46.2% of the variability in the variables is captured by the canonical variate. Adequacy coefficients are useful for evaluating the overall representativeness of the canonical variate. Low values indicate that the canonical variate may not represent all or any of the variables well. In the present example, some of the variables are represented well whereas others are not, for instance, math ability is almost entirely represented in the first set of functions whereas reading ability is not.

Summary of Example

The overall relationship between the variable sets was both practically and statistically significant. The first two sets of functions produced practically significant squared canonical correlations that were statistically significant. Based on the squared structure coefficients between variables and their canonical variates, the first function primarily describes the relationship between persistence and mathematics and problem-solving ability and is therefore named “Analytical Challenges and Academic Persistence.” The second set of functions primarily describes the relationship between scholastic interest and reading ability and problem-solving ability and therefore is named “Interest in Complex Reading Tasks.”

CCA is a multivariate technique that allows the researcher to parse out the shared variability between sets of variables into smaller, distinct, and interpretable relationships. As the highest member analysis in the GLM that does not model measurement error, CCA subsumes many of the parametric analyses that are commonly used in social science research including univariate analyses such as the t test, ANOVA, and regression, as well as other multivariate analyses such as Hotelling’s T 2 and MANOVA. Because of CCA’s position in the GLM, understanding the method is both pedagogically informative and practically applicable. CCA is useful when a researcher plans to investigate independent relationships (via creation of functions) between variables that are logically grouped into variable sets, that have low measurement error, and for which a correlation adequately captures the bivariate relationships. When measurement error must be modeled, structural equation modeling is recommended.

Sign in to access this content

Get a 30 day free trial, more like this, sage recommends.

We found other relevant content for you on other Sage platforms.

Have you created a personal profile? Login or create a profile so that you can save clips, playlists and searches

• Sign in/register

Navigating away from this page will delete your results

Please save your results to "My Self-Assessments" in your profile before navigating away from this page.

Sign in to my profile

Sign up for a free trial and experience all Sage Learning Resources have to offer.

You must have a valid academic email address to sign up.

Get off-campus access

• View or download all content my institution has access to.

Sign up for a free trial and experience all Sage Research Methods has to offer.

• view my profile
• view my lists

User Preferences

Content preview.

Arcu felis bibendum ut tristique et egestas quis:

• Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris
• Duis aute irure dolor in reprehenderit in voluptate
• Excepteur sint occaecat cupidatat non proident

Keyboard Shortcuts

Lesson 13: canonical correlation analysis, overview section  .

Canonical correlation analysis explores the relationships between two multivariate sets of variables (vectors), all measured on the same individual.

Consider, as an example, variables related to exercise and health. On the one hand, you have variables associated with exercise, observations such as the climbing rate on a stair stepper, how fast you can run a certain distance, the amount of weight lifted on a bench press, the number of push-ups per minute, etc. On the other hand, you have variables that attempt to measure overall health, such as blood pressure, cholesterol levels, glucose levels, body mass index, etc.  Two types of variables are measured and the relationships between the exercise variables and the health variables are of interest.

As a second example consider variables measured on environmental health and environmental toxins. A number of environmental health variables such as frequencies of sensitive species, species diversity, total biomass, the productivity of the environment, etc. may be measured and a second set of variables on environmental toxins are measured, such as the concentrations of heavy metals, pesticides, dioxin, etc.

For a third example consider a group of sales representatives, on whom we have recorded several sales performance variables along with several measures of intellectual and creative aptitude. We may wish to explore the relationships between the sales performance variables and the aptitude variables.

One approach to studying relationships between the two sets of variables is to use canonical correlation analysis which describes the relationship between the first set of variables and the second set of variables. We do not necessarily think of one set of variables as independent and the other as dependent, though that may potentially be another approach.

• Carry out a canonical correlation analysis using SAS (Minitab does not have this functionality);
• Assess how many canonical variate pairs should be considered;
• Interpret canonical variate scores;
• Describe the relationships between variables in the first set with variables in the second set.

Research methodology. Part IV: Understanding canonical correlation analysis

• PMID: 8715316

Canonical correlation is presented as a technique to determine how sets of dependent variables are related with sets of independent variables. Canonical correlation reveals the strength of the relationship between the clusters using case data as illustration, three pairs of clusters (factors or profiles) emerged. Interpretation of the clusters are presented. As indicated in the case presentation, Canonical Correlation (CA) is the fourth in a series of methodologies selected for illustration as precursors to advanced statistics and modeling. In this paper, background will be given, a schematic example presented, sample size and CA, SPSS procedure to perform CA, and interpretation of CA and possible uses of CA in nursing research.

• Analysis of Variance
• Cluster Analysis*
• Data Interpretation, Statistical*
• Multivariate Analysis
• Nursing Research
• Predictive Value of Tests
• Statistics, Nonparametric*

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

• View all journals
• My Account Login
• Explore content
• About the journal
• Publish with us
• Sign up for alerts
• Open access
• Published: 05 July 2017

Data analytics using canonical correlation analysis and Monte Carlo simulation

• Jeffrey M. Rickman 1 , 2 ,
• Yan Wang 2 ,
• Anthony D. Rollett 3 ,
• Martin P. Harmer 2 &
• Charles Compson 4  

npj Computational Materials volume  3 , Article number:  26 ( 2017 ) Cite this article

7452 Accesses

17 Citations

2 Altmetric

Metrics details

• Materials science
• Theory and computation

A canonical correlation analysis is a generic parametric model used in the statistical analysis of data involving interrelated or interdependent input and output variables. It is especially useful in data analytics as a dimensional reduction strategy that simplifies a complex, multidimensional parameter space by identifying a relatively few combinations of variables that are maximally correlated. One shortcoming of the canonical correlation analysis, however, is that it provides only a linear combination of variables that maximizes these correlations. With this in mind, we describe here a versatile, Monte-Carlo based methodology that is useful in identifying non-linear functions of the variables that lead to strong input/output correlations. We demonstrate that our approach leads to a substantial enhancement of correlations, as illustrated by two experimental applications of substantial interest to the materials science community, namely: (1) determining the interdependence of processing and microstructural variables associated with doped polycrystalline aluminas, and (2) relating microstructural decriptors to the electrical and optoelectronic properties of thin-film solar cells based on CuInSe 2 absorbers. Finally, we describe how this approach facilitates experimental planning and process control.

Similar content being viewed by others

Smart machine learning or discovering meaningful physical and chemical contributions through dimensional stacking

Lee A. Griffin, Iaroslav Gaponenko, … Nazanin Bassiri-Gharb

Variable Selection in the Regularized Simultaneous Component Analysis Method for Multi-Source Data Integration

Zhengguo Gu, Niek C. de Schipper & Katrijn Van Deun

Principal component analysis

Michael Greenacre, Patrick J. F. Groenen, … Elena Tuzhilina

Introduction

One goal of data analytics is the effective dimensional reduction of large, high-dimensional data sets by the identification of a few low-dimensional axes that are most important. 1 For this purpose, several different strategies are utilized to highlight significant correlations among the relevant variables. One of the most useful such strategies is the principal component analysis (PCA), 2 a multivariate technique in which a linear projection is used to transform data into a smaller set of uncorrelated variables. 3 It is widely applied in pattern classification and is used, for example, in such diverse fields as drug discovery 4 and face recognition. 5 There are also several extensions of PCA that are useful if, for example, one wishes to emphasize some variables over others, such as weighted PCA, 3 , 6 or if a non-linear model of the data is appropriate, such as generalized PCA. 3 , 7

In many cases, one is interested in finding the correlations between two sets of variables. For example, in an engineering application one may wish to find a connection between a set of processing variables (controlled by the engineer) and a set of output variables, the latter characterizing a product. A canonical correlation analysis (CCA) is a very general technique for quantifying relationships between two sets of variables, and most parametric tests of significance are essentially special cases of CCA. 8 In particular, for two paired data sets, a CCA identifies paired directions such that the projection of the first data set along the first direction is maximally correlated with the projection of the second data set along the second direction. 9 A reduction in dimensionality is achieved by identifying a subspace that best represents the data. This process is facilitated in CCA by a ranking of each pair of directions in terms of its associated correlation coefficient.

As noted above, one shortcoming of CCA is that it provides only linear combinations of variables that are maximally correlated. In some cases, non-linear models of the data are more appropriate, but the identification of non-linear combinations of variables is usually not straightforward. In some cases, physical reasoning or even intuition may be invoked to suggest a functional form that reflects the competing effects of the variables of interest. More generally, several ‘‘non-linear” techniques have been employed in recent years to effect a reduction in dimensionality. 2 For example, kernel CCA is a reasonably flexible method for the modeling of nonparametric correlations among variables using classes of smooth functions. The smoothness of these functions is often enforced via an imposed regularization; 10 , 11 however, the results may be sensitive to the regularization parameter. In addition, the so-called ‘‘group method for data handling” is a non-linear regression couched as a neural network model. This approach was among the first deep-learning models and involves the growth and training of neuron layers using regression, followed by the elimination of layers based on a validation set. 12 , 13

In this work, we describe a straightforward, Monte-Carlo (MC)-based methodology for identifying non-linear functions of the variables that lead to strong input/output correlations. It is extremely versatile and can be applied straightforwardly to any number of problems. This methodology is an extension of the CCA to more complex scenarios in which non-linear variable dependencies are likely. For this reason we will denote it as canonical correlation analysis with Monte Carlo simulation (CCAMC). As will be demonstrated below, this approach is easily implemented and provides in many cases, with relatively little computational cost, combinations of variables that are strongly correlated. We validate our approach for two applications, the first establishing correlations among processing and microstructural variables associated with doped polycrystalline aluminas, and the second relating microstructural decriptors to the electrical and optoelectronic properties of thin films used for solar energy conversion.

Canonical correlation analysis

We begin with an overview of the CCA methodology. Suppose that one has a set of input variables \(\left\{ {{x_1},{x_2} \cdots ,{x_{{N_i}}}} \right\}\) and corresponding output variables \(\left\{ {{y_1},{y_2} \cdots ,{y_{{N_{\rm{o}}}}}} \right\}\) , where N i ( N o ) are the number of input (output) variables. One seeks linear combinations (known as canonical variates) \(V = \mathop {\sum}\nolimits_i {{\alpha _i}{x_i}} \) and \(W = \mathop {\sum}\nolimits_i {{\beta _i}{y_i}} \) , where α i and β i are known as canonical weights, such that these combinations are maximally correlated. If one regards these input and output variables as the components of two vectors, \(\vec x\) and \(\vec y\) , respectively, then one can define a covariance matrix whose ( i , j )-th element is cov( x i , y j ). CCA begins with the construction of this matrix (or the associated correlation matrix) Σ. 14 , 15 The matrix elements are estimated from a sample covariance matrix that is calculated from the data from the M experiments. 14 Then, Σ may be written in block form as

The aim of CCA is to determine { α i } and { β i } such that the correlation between W and V is maximized. Since the covariance between W and V is cov ( W , V ) =  \({\vec \beta ^T}\mathop {\sum}\nolimits_{\vec y\vec x} {\vec \alpha } \) , one seeks to maximize the correlation

where the denominator is the product of the variances of W and V , respectively. This may be accomplished by finding the solution of a system of homogeneous equations or, equivalently, by finding the eigenvectors and corresponding eigenvalues of two operators σ 1 and σ 2 . The two operators are constructed from products of matrix blocks of Σ and given by

The eigenvalues of each operator are the same, and the square roots of these eigenvalues are the canonical correlations. Moreover, the corresponding eigenvectors may be used to determine the α i and β i and, thereby, the canonical variates. More specifically, if \({\vec \alpha ^*}\) and \({\vec \beta ^*}\) are eigenvectors of σ 1 corresponding to its maximum eigenvalue, then V * and W * are the desired canonical variates that maximize the correlation. 14

CCA with Monte Carlo simulation (CCAMC)

While the CCA is extremely useful in highlighting linear relationships among input and output variables, it may be that a non-linear model of the data is more appropriate in some circumstances. More formally, one wishes to find some function of the subset of input variables, { x 1 , x 2 …, x n }, where n  <  N i , such that the largest eigenvalue λ max ( x 1 , x 2 , x 3 , x 4 , …, x n ) in the spectrum of σ 1 (or σ 2 ) is maximized. In practice, this is often tedious, especially for n large. With this in mind, we outline here a strategy using Monte Carlo simulation 16 to identify appropriate non-linear combinations of variables for a given problem, and then validate this approach for two test cases below. The CCAMC strategy has the virtue that it can be straightforwardly implemented in most cases with relatively little computational cost. In addition, parallel computations can be performed to explore relatively wide regions of parameter space, as described below.

The procedure is as follows. One identifies, perhaps from a CCA analysis of data, the aforementioned input variables { x 1 , x 2 …, x n }, where n  <  N i , that contribute significantly to the input canonical variate. It may be suspected that some (perhaps non-linear) function of these variables is, in fact, strongly correlated with the output, but the functional form may not be readily apparent. In this case, it is sensible to consider families of trial functions that ideally form a basis in some infinite-dimensional vector space. For example, for the vector space of multivariate polynomial functions one may parametrize the unknown function f ( \(\vec x\) ) in terms of Kolmogorov-Gabor polynomials 17

where c 0 , c i , etc., are unknown expansion coefficients. This expansion is used extensively in, for example, polynomial neural networks to identify non-linear relationships between input and output variables. 12 Alternatively, if variable ratios are more appropriate, one may employ a multivariate generalization of Padé approximants. 18 , 19 , 20 For example, in the trivariate case, one can write

where m is an expansion parameter and the c ijk and d ijk are unknown expansion coefficients. For more than three variables, Eq.  5 can, of course, be generalized.

Upon replacing an input variable by one of the above representations, one then seeks the set of variables that maximize the largest eigenvalue, λ max , of either σ 1 or σ 2 . This may be accomplished by employing Monte Carlo simulation using λ max as an objective function. In brief, one chooses values for the variable set and then calculates λ max from a CCA analysis. These starting values are most conveniently chosen from the representations given in either Eq.  4 or 5 with a set of arbitrary coefficients. This selection and a subsequent CCA analysis leads to a corresponding starting value for λ max . As in a conventional Monte Carlo simulation, one constructs a Markov chain of states. One begins by defining a ‘‘box” in coefficient space for trial variations of the coefficients. For convenience, the size of the box can be chosen so that approximately 50% of the variations are accepted. Such trial variations lead to concomitant changes in the CCA operators given in Eq.  3 , and thereby to changes in their spectra. If a change in the given coefficient set leads to an increase (decrease) in λ max , then this set is retained (rejected). This procedure is repeated for many iterations, usually from a different initial state, and may be performed in parallel. As is intuitively reasonable, the selection of an initial state determines the convergence to the maximum eigenvalue, and the use of many different initial states mitigates against trapping in configuration space. In practice, we have found that convergence is achieved after a few thousand iterations for the examples considered here. In effect, we are performing the analog of a zero-temperature Monte Carlo simulation. It is also possible to define an effective temperature and to perform simulated annealing, as indicated below, if one is still concerned about trapping.

To determine whether a given pair of variates is indeed correlated, one ascertains the significance of the results from a hypothesis test in which one tests the null hypothesis that a given pair of variates is uncorrelated. The results of this test are then quantified in terms of a statistic, such as Wilks lambda, 21 and an associated p -value. For relatively small p -values, there is contrary evidence of a correlation and the corresponding variate pair is acceptable.

In practice, there are several issues to be addressed when implementing this methodology. First, in calculating σ 1 and σ 2 using Eq.  3 one must calculate inverses of the block matrices \({\Sigma _{\vec X\vec X}}\) and \({\Sigma _{\vec Y\vec Y}}\) . In some cases, however, these matrices may be ill-conditioned at some point during the Monte Carlo simulation. To remedy this situation, one can either regularize the block matrices 22 or, alternatively, replace the inverse by the Moore-Penrose pseudoinverse. 23 For a given matrix Ξ and appropriate identity matrix I , the pseudoinverse Ξ + satisfies the relation that the sum of the squares of the matrix elements of ΞΞ +  −  I is a minimum. We have chosen to employ this latter approach and found it to be a satisfactory remedy. Second, it is possible to become trapped near local extrema during the simulation. It is, therefore, advisable to perform many simulations, each comprising approximately 15,000–20,000 iterations, possibly starting from different initial conditions to explore a wide range of parameter space. Such simulations may, of course, be performed in parallel. In addition, simulated annealing may be employed to mitigate this problem. 16 This approach would require the introduction of a fictitious temperature that would permit fluctuations. These fluctuations imply that states that minimize λ max would sometimes be accepted and the system would escape from a local trap. The subsequent extraction of thermal energy would then allow the system to relax to (perhaps) another extremum. We have not employed annealing here as it has not been necessary in the various test cases that we have considered. Third, one may wish to explore the robustness of this methodology. To verify robustness, we have systematically eliminated less impactful input variables from the analysis, and there has been little to no change in the correlation coefficient, etc. Finally, the selection “a priori” of a best functional form (e.g., Eqs.  4 and 5 ) is not crucial here. Given that the CCAMC methodology may be implemented in parallel, it is straightforward to examine many different functional forms (including, of course, others not given here) at the same time to identify which is best. This flexibility is another strength of this methodology.

Applications

To validate the CCAMC methodology outlined above, we consider here two experimental applications of relevance in applied physics and materials science and engineering, namely: (1) quantifying abnormal grain growth (AGG) in ceramic oxides, and (2) relating the detailed microstructural features in CuInSe 2 thin films, the so-called grain-boundary character distribution (GBCD), to the electrical and optoelectronic properties of these films. In each case, one seeks to identify a combination of input variables that is strongly correlated with an observable output.

Application 1: Abnormal grain growth

AGG occurs in a polycrystal when a small group of grains, typically having anisotropic boundary energies or mobilities, becomes relatively large by growing into the surrounding matrix of ‘‘normal” grains. 24 , 25 It is a ubiquitous phenomenon in many systems, especially thin films, and occurs, in some cases, due to the presence of impurity excesses (e.g., Ca or Si in alumina). 26 AGG is found in both metallic and ceramic material microstructures and may have a significant impact on their electromechanical properties. Figure  1 shows a prototypical microstructure, as obtained from electron backscatter diffraction (EBSD), highlighting abnormal grains in a background of ‘‘normal grains” for an alumina sample.

A prototypical microstructure, as obtained from electron backscatter diffraction (EBSD), highlighting abnormal grains in a background of ‘‘normal grains” for an alumina sample. Reprinted with permission from Elsevier, Ltd 27

In a recent paper, Lawrence et al. 27 introduced a series of metrics that are useful in quantifying various microstructural aspects of AGG, and then employed a CCA to highlight the influence of processing variables on these metrics in doped aluminas. 27 These metrics highlight specific features of the joint probability density function (pdf) p ( G , a ) of grain size, G , and aspect ratio, a , for a given microstructure, and, therefore, necessarily focus on grains in the tail of the distribution. More specifically, the metrics reflect the extreme events (i.e., large grains) that determine the shape of the tail in terms of conditional expectation values, and will be denoted here by { ϕ 1 , ϕ 2 , …, ϕ 5 }. The object of the study by Lawrence et al. was to understand how the processing parameters for the doped aluminas, including compositions c (for such dopants as MgO, CaO, Na 2 O, and SiO 2 ), temperature T and time t influence the aforementioned metrics. It should be noted that impurities often segregate to grain boundaries or other defects and may thereby affect thermomechanical and kinetic properties. 28 , 29 , 30

In this study, we wish to identify which (possibly non-linear) combination(s) of processing variables is (are) most correlated with microstructural abnormality. To accomplish this aim, after the spark-plasma sintering of specialty alumina powders, we compiled statistics for microstructures associated with grain growth at some annealing temperature. The original work by Lawrence et al. was based on 33 samples; in this study we have augmented the original data set to obtain 68 independent samples. Each of the 68 independent specialty powders had a unique combination of processing variables, and the final microstructures had grain populations in the range of approximately 1000–9000 grains. For this analysis, it is convenient to define a set of input (i.e., processing) variables, \(\vec x\) , and a set of output (i.e., metric) variables, \(\vec y\) , as

where the composition subscripts denote dopant type.

A CCA was performed using the data set described above. From this analysis, one finds a single pair of canonical variates having a (maximum) correlation coefficient of 0.59 and a p -value of 0.10 for the hypothesis test using Rao’s F-test. 14 In Fig.  2a the corresponding canonical variates, V and W , are plotted for each of the data points, along with the associated regression line.

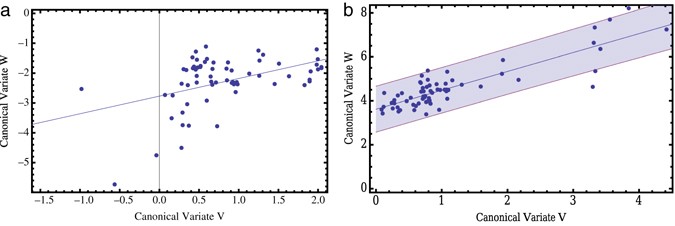
a The canonical variates V and W identified by a canonical correlation analysis of the 68 data points from Application 1. The regression line is also shown. b The same as for part a, except that these results are obtained after Monte Carlo simulation. Also shown are the corresponding regression line and a 95% confidence interval for the data ( shaded region ). The correlation coefficient is 0.86

To find variates having a stronger correlation, one can either use physical intuition to identify a new combination of variables or employ, for example, the CCAMC method. Based on the earlier work of Lawrence et al., one such variable that reflects perceived correlations, and identified via physical intuition, is the ratio \(r = {c_{{\rm{MgO}}}}{\rm{/}}\left( {{c_{{\rm{CaO}}}} + {c_{{\rm{Si}}{{\rm{O}}_2}}}} \right)\) . With this guidance and after augmenting the input variable set with r , a CCA analysis yields a pair of canonical variates having a (maximum) correlation coefficient of 0.69 with a p -value of 0.02. To determine whether the CCAMC procedure can yield further improvement, consider the Padé functional form given in Eq.  5 with the variable set \(\left\{ {{c_{{\rm{MgO}}}},{c_{{\rm{CaO}}}},{c_{{\rm{Si}}{{\rm{O}}_{\rm{2}}}}}} \right\}\) and expansion exponent m  = 1. These approximants replace r . These input variables were identified from the CCA as making significant contributions to the input canonical variate. Moreover, the inverse relationship between some pairs of variables suggests the Padé functional form. After approximately 100 simulations, each comprising 15,000 iterations, expansion coefficients were found yielding a maximum observed correlation coefficient of 0.86 with an associated p -value of 4 × 10 −8 . In Fig.  2b, the corresponding canonical variates are plotted for each of the data points, along with the associated regression line and a 95% confidence interval for the data. Thus, with relatively little computational effort, one can obtain well-correlated canonical variables using a trial function with the CCAMC methodology. These new variables facilitate experimental planning, as described below.

Application 2: Electrical and optoelectronic properties of thin films

Thin-film solar cells, such as those based on, for example polycrystalline CuInSe 2 absorbers, are of considerable technological interest given their relatively high conversion efficiencies. 31 Indeed, many workers have sought to describe the role of grain boundaries in determining device performance in these systems. 32 In a recent paper, Abou-Ras et al. examined the grain-boundary character of these films in relation to their electrical and optoelectronic properties for a relatively large number of grain boundaries. 33 More specifically, EBSD was employed to acquire microstructural data that, in conjunction with an electron-beam-induced current (EBIC) analysis and a cathodoluminescence (CL) image study, permitted the correlation of boundary type with local electrical and optoelectronic properties. Figure  3 shows the distribution of disorientation axes for grain boundaries in polycrystalline CuInSe 2 , in multiples of a random distribution (MRD), presented as stereographic projections.

The distribution of disorientation axes for grain boundaries in polycrystalline CuInSe 2 , in multiples of a random distribution (MRD), presented as stereographic projections. The disorientation angles are a 32°, b 39°, and c 60°. Reprinted with permission from Elsevier, Ltd 33

Several parameters were used to quantify the GBCD as extracted from EBSD maps, including, for a given boundary: the grain-boundary disorientation angle ψ , the three Rodrigues vector \(\overrightarrow R \) components of the disorientation and scalar measures of closeness k to the 〈100〉, 〈110〉, and 〈111〉 crystallographic directions. Our aim here is, as above, to to identify which (possibly non-linear) combination(s) of GBCD variables is (are) most correlated with electrical and optoelectronic properties. For this purpose, it is sensible to define sets of input and output variables, respectively, as

where the subscripts on k denote crystallographic directions and where ebic and cl are the EBIC and CL signals, respectively.

To identify those input and output variables that are most important in connecting microstructure to properties, one first performs a CCA using the variables given in Eq.  7 . For concreteness, we consider a data set comprising 104 samples for non-twin boundaries. From this analysis, one finds a single pair of canonical variates that are maximally, though relatively weakly correlated, having a correlation coefficient of 0.26 and a large p -value of 0.88 for the hypothesis test using Rao’s F-test. 14 (Given this p -value, one cannot reject the possibility that these variables are uncorrelated.) The canonical weights for the input and output variables are given in Table  1 . In Fig.  4a, the corresponding canonical variates, V and W , are plotted for each of the data points, along with the associated regression line.

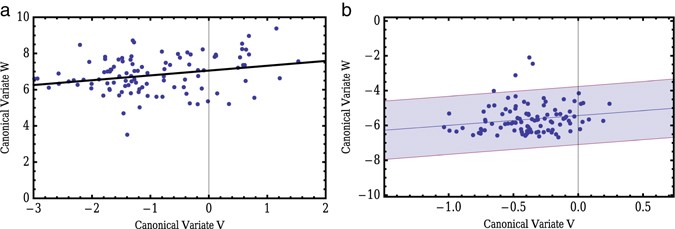
a The canonical variates V and W identified by a canonical correlation analysis of the 104 data points from Application 2. The regression line is also shown. b The same as for part a, except that these results are obtained after Monte Carlo simulation. Note the stronger dependence between the two variates as compared to those shown in a . Also shown are the corresponding regression line and a 95% confidence interval for the data ( shaded region ). The correlation coefficient is 0.56

From Table  1 it is evident that several of the input variables, given their relatively small canonical weights, make little contribution to the input canonical variate. This situation is, in fact, ideally suited to CCAMC as the trial function need only depend on a few input variables. We identify three input variables, namely the components of \(\vec R\) , that have significant canonical weights and ask whether the addition of some (possibly) non-linear function of these variables would lead to a stronger correlation with the output variables. Consider, for example, the Padé functional form given in Eq.  5 with the variable set { R 1 , R 2 , R 3 } and expansion exponent m  = 1. After approximately 150 CCAMC simulations, each comprising 15,000 iterations, expansion coefficients were found yielding a maximum observed correlation coefficient of 0.56 with an associated p -value < 10 −3 . In Fig.  4b, the corresponding canonical variates are displayed for each of the data points, along with the regression line and a 95% confidence interval for the data. Clearly, this procedure has produced canonical variates with a substantially increased degree of correlation; moreover, the corresponding p -value gives one confidence that this correlation is real.

We outlined above a MC-based methodology based on a CCA that permits one to identify non-linear functions of the variables that lead to strong input/output correlations. We then validated this CCAMC approach for two applications of technological relevance. The first application focused on the interdependence of processing and microstructural variables associated with doped polycrystalline aluminas, and the second related microstructural decriptors to the electrical and optoelectronic properties of thin-film solar cells based on CuInSe 2 absorbers. In each case it was found that the CCAMC methodology was extremely useful in highlighting significant input/output correlations. It is expected that this methodology will also be useful in cases where the number of output variables exceeds the number of input variables given that underlying CCA analysis identifies correlated variates irrespective of which variables are labeled ‘‘input” or ‘‘output.’’

Having identified highly correlated variates, the information summarized in Figs  2 and 4 can be used for planning future experiments or for process control. For example, from Fig.  2 one can identify those processing variables (e.g., compositions) in Application 1 that, with a certain confidence, will produce a microstructure having target metrics (i.e., grain-size distributions). This capability greatly reduces the amount of experimentation required to produce microstructures having desirable characteristics.

One important issue that should be considered in applying the CCA or CCAMC technique is the adequacy of sample sizes. While there is no simple procedure for estimating sample size sufficiency, some authors have attempted to quantify the increase in sample size required as the number of variables increases. 21 , 34 In general, the minimum data requirements needed for these techniques depend on the reliability of the data. While relatively large sample sizes are, of course, desirable, and may be necessary in some cases, if there are strong correlations then relatively small samples sizes should detect them. As a practical matter, for Application 1 (AGG), it is very time consuming to perform the required microstructural analysis to obtain sensible grain probability distributions. Hence, we have taken the practical approach of recalculating the maximum eigenvalue and corresponding eigenvectors from CCA as we augmented our data set, starting with 33 samples and ending with 68 samples. The analysis is robust in that the same metrics are identified as contributing significantly to the canonical variates. Thus, we are confident that we are identifying the important factors that dictate AGG.

The CCAMC methodology has, of course, much broader application. Moreover, as noted above, it is readily parallelized, and, therefore, one can explore the parameter space associated with many different functional forms for the input variables. More rapid convergence to local extrema can also be achieved by employing extensions of the usual MC algorithm including, for example, force-biased MC. 35 In this approach transition probabilities are modified by a knowledge of the instantaneous ‘‘force” associated with a configuration that, in this case, corresponds to the numerical derivative of λ max with respect to changes in the input variables. We are currently exploring other applications of the CCAMC methodology, as well as the role of CCAMC in guiding experimental processing in other contexts.

Data availability

The authors will make available, upon request, the data used in both applications described in this work. It is understood that the data provided will not be for commercial use.

Samudrala, S., Rajan, K. & Ganapathysubramanian, B. in Informatics for Materials Science and Engineering (ed. Rajan, K.) (Elsevier, 2013).

Lee, J. A. & Verleysen, M. Nonlinear Dimensionality Reduction (Springer, 2007).

Jackson, J. E. A User’s Guide to Principal Components (John Wiley and Sons, 2003).

Wu, K., Natarajan, B., Morkowchuk, L., Krein, M. & Breneman, C. M. in Informatics for Materials Science and Engineering (ed. Rajan, K.) (Elsevier, 2013).

Huang, W. & Yin, H. in Intelligent Data Engineering and Automated Learning-IDEAL 2009 (eds Corchado, E. & Yin, H.) (Springer-Verlag, 2009).

Meredith, W. & Millsap, R. E. On component analysis. Psychometrika 50 , 495–507 (1985).

Article   Google Scholar  

Gnanadesikan, R. & Wilk, M. B. in Multivariate Analysis II (ed. Krishnaiah, P. R.) (Academic Press, 1969).

Knapp, T. R. Canonical correlation analyis: a general parametric significance-testing system. Psych. Bull 85 , 410–416 (1978).

Burges, C. J. C. Dimension reduction: a guided tour. Found. Trends Mach. Learn. 2 , 275–365 (2009).

Akaho, S. in International Meeting of Psychometric Society (Osaka, Japan, 2001).

Balakrishnan, S., Puniyani, K. & Lafferty, J. Sparse additive functional and kernel CCA, in Proc. 29th International Conference on Machine Learning (Edinburgh, 2012).

Ivakhnenko, A. G. & Ivakhnenko, G. A. The review of problems solvable by algorithms of the group method of data handling (GMDH). Pattern Recogn. Image Anal 5 , 527–535 (1995).

Google Scholar  

Schmidhuber, J. Deep learning in neural networks: an overview. Neural Networks 61 , 85–117 (2015).

Jobson, J. D. Applied Multivariate Data Analysis , Vol. II (Springer-Verlag, 1992).

Gittins, R. Canonical Analysis: A Review With Applications In Ecology (Springer-Verlag, 1985).

Hartmann, A. K. & Weigt, M. Phase Transitions in Combinatorial Optimization Problems: Basics, Algorithms and Statistical Mechanics (Wiley-VCH, 2005).

Dehuri, S., Coello, C., Cho, S. -B. & Ghosh, A. in Swarm Intelligence for Multi-Objective Problems in Data Mining (eds Coello, C., Dehuri, S. and Ghosh, S.) 115–155 (Springer-Verlag, 2009).

Baker, G. A. & Graves-Morris, P. Padé Approximant s 2nd edn, (Cambridge University Press, 1996).

Turut, V. & Bayram, M. Rational approximations for solving Cauchy problems. New Trend. Math. Sci. 4 , 254–262 (2016).

Cuyt, A. A review of multivariate Padé approximation theory. J. Comp. Appl. Math 12,13 , 221–232 (1985).

Thorndike, R. M. Correlational Procedures for Research (Gardner Press, 1978).

Press, W. H., Teukolsky, S. A., Vetterling, W. T. & Flannery, B. P. Numerical Recipes in Fortran: The Art of Scientific Computing 2nd edn, (Cambridge University Press, 1992).

Gentle, J. E. Matrix Algebra: Theory, Computations and Applications in Statistics (Springer, 2007).

Rollett, A. D., Srolovitz, D. J. & Anderson, M. P. Simulation and theory of abnormal grain growth-anisotropic grain boundary energies and mobilities. Acta Metall 37 , 1127–1240 (1989).

Mullins, W. W. & Viñals, J. Linear bubble model of abnormal grain growth. Acta Mater. 50 , 2945–2954 (2002).

Handwerker, C. A., Morris, P. A. & Coble, R. L. Effects of chemical inhomogeneities on grain growth and microstructure in Al 2 O 3 . J. Am. Ceram. Soc. 72 , 130–136 (1989).

Lawrence, A., Rickman, J. M., Harmer, M. P. & Rollett, A. D. Parsing abnormal grain growth. Acta Mater. 103 , 681–687 (2016).

Cho, J., Wang, C. M., Chan, H. M., Rickman, J. M. & Harmer, M. P. Improved tensile creep properties of yttrium- and lanthanum-doped alumina: a solid solution effect. J. Mater. Res. 16 , 425–429 (2001).

Wang, C.-M., Cho, J., Chan, H. M., Harmer, M. P. & Rickman, J. M. Influence of dopant concentration on creep properties of Nd 2 O 3 -doped alumina. J. Amer. Ceram. Soc 84 , 1010–1016 (2001).

Rickman, J. M., LeSar, R. & Srolovitz, D. J. Solute effects on dislocation glide in metals. Acta Mater. 51 , 1199 (2003).

Jackson, P. et al. Effects of heavy alkali elements in Cu(In,Ga)Se 2 solar cells with efficiencies up to 22.6%. Phys. Stat. Sol. (RRL), doi: 10.1002/pssr.201600199 .

Rao, U., Taretto, K. & Siebentritt, S. Grain boundaries in Cu(In,Ga)(Se,S) 2 thin-film solar cells. Appl. Phys. A 96 , 221 (2009).

Abou-Ras, D. et al. Grain-boundary character distribution and correlations with electrical and optoelectronic properties of CuInSe 2 thin films. Acta Metall 118 , 244–252 (2016).

Barcikowski, R. S. & Stevens, J. P. A Monte Carlo study of the stability of canonical correlations, canonical weights and canonical variate-variable correlations. Multivariate Behav. Res. 10 , 353–364 (1975).

Rao, M. & Berne, B. J. On the force-bias Monte Carlo simulation of simple liquids. J. Chem. Phys. 71 , 129–132 (1979).

Download references

Acknowledgements

We wish to thank Almatis, Inc. for kindly supplying the alumina samples for our microstructural analysis and for their guidance during this project. We also wish to thank D. Abou-Ras and colleagues for their data. We also acknowledge support from the Office of Naval Research under grant N00014-11-1-0678.

Author information

Authors and affiliations.

Department of Physics, Lehigh University, Bethlehem, PA, 18015, USA

Jeffrey M. Rickman

Department of Materials Science and Engineering, Lehigh University, Bethlehem, PA, 18015, USA

Jeffrey M. Rickman, Yan Wang & Martin P. Harmer

Department of Materials Science and Engineering, Carnegie Mellon University, Pittsburgh, PA, 15213, USA

Anthony D. Rollett

Almatis Inc., Leetsdale, PA, 15056, USA

Charles Compson

You can also search for this author in PubMed   Google Scholar

Contributions

J.M.R. is the primary author (and guarantor) of this work. He developed the formalism and did most of the analysis. Y.W. also performed some of the analysis, especially the CCA of the Application 1 data. A.D.R., M.P.H., and C.C. provided data and helped in the physical interpretation of the results presented here.

Corresponding author

Correspondence to Jeffrey M. Rickman .

Ethics declarations

Competing interests.

The authors declare that they have no competing financial interests.

Additional information

Publisher’s note.

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/ .

Reprints and permissions

About this article

Cite this article.

Rickman, J.M., Wang, Y., Rollett, A.D. et al. Data analytics using canonical correlation analysis and Monte Carlo simulation. npj Comput Mater 3 , 26 (2017). https://doi.org/10.1038/s41524-017-0028-9

Download citation

Received : 06 March 2017

Revised : 22 May 2017

Accepted : 12 June 2017

Published : 05 July 2017

DOI : https://doi.org/10.1038/s41524-017-0028-9

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

This article is cited by

Autoantibodies targeting gpcrs and ras-related molecules associate with covid-19 severity.

• Otavio Cabral-Marques
• Gilad Halpert
• Yehuda Shoenfeld

Nature Communications (2022)

The network interplay of interferon and Toll-like receptor signaling pathways in the anti-Candida immune response

• Ranieri Coelho Salgado
• Dennyson Leandro M. Fonseca

Scientific Reports (2021)

In Situ Al-TiC Composites Fabricated by Self-propagating High-Temperature Reaction: Insights on Reaction Pathways and Their Microstructural Signatures

• C. W. Reese
• A. Gladstein

Metallurgical and Materials Transactions A (2020)

Materials informatics for the screening of multi-principal elements and high-entropy alloys

• J. M. Rickman
• G. Balasubramanian

Nature Communications (2019)

Austenite Reconstruction Elucidates Prior Grain Size Dependence of Toughness in a Low Alloy Steel

• Chasen Ranger
• Anthony Rollett

Metallurgical and Materials Transactions A (2018)

Quick links

• Explore articles by subject
• Guide to authors
• Editorial policies

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

• © 1985

Canonical Analysis

A Review with Applications in Ecology

• Robert Gittins 0

Department of Plant Sciences, University of Western Ontario, London, Canada

You can also search for this author in PubMed   Google Scholar

Part of the book series: Biomathematics (BIOMATHEMATICS, volume 12)

3767 Accesses

127 Citations

• Table of contents

About this book

Authors and affiliations, bibliographic information.

• Publish with us

Buying options

• Available as PDF
• Read on any device
• Instant download
• Own it forever
• Compact, lightweight edition
• Dispatched in 3 to 5 business days
• Free shipping worldwide - see info

Tax calculation will be finalised at checkout

Other ways to access

This is a preview of subscription content, log in via an institution to check for access.

Table of contents (14 chapters)

Front matter, introduction.

Robert Gittins

Canonical correlations and canonical variates

Extensions and generalizations, canonical variate analysis, dual scaling, applications, general introduction, experiment 1: an investigation of spatial variation, experiment 2: soil-species relationships in a limestone grassland community, soil-vegetation relationships in a lowland tropical rain forest, dynamic status of a lowland tropical rain forest, the structure of grassland vegetation in anglesey, north wales, the nitrogen nutrition of eight grass species, herbivore-environment relationships in the rwenzori national park, uganda, appraisal and prospect, applications: assessment and conclusions, research issues and future developments, back matter.

• plant ecology

Book Title : Canonical Analysis

Book Subtitle : A Review with Applications in Ecology

Authors : Robert Gittins

Series Title : Biomathematics

DOI : https://doi.org/10.1007/978-3-642-69878-1

Publisher : Springer Berlin, Heidelberg

eBook Packages : Springer Book Archive

Copyright Information : Springer-Verlag Berlin Heidelberg 1985

Softcover ISBN : 978-3-642-69880-4 Published: 08 December 2011

eBook ISBN : 978-3-642-69878-1 Published: 06 December 2012

Series ISSN : 0067-8821

Series E-ISSN : 2197-4160

Edition Number : 1

Number of Pages : XVI, 352

Topics : Mathematical and Computational Biology

Policies and ethics

• Find a journal
• Track your research

An official website of the United States government

The .gov means it’s official. Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

The site is secure. The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

• Publications
• Account settings

Preview improvements coming to the PMC website in October 2024. Learn More or Try it out now .

• Advanced Search
• Journal List
• Iran Red Crescent Med J
• v.18(3); 2016 Mar

Application of Canonical Correlation Analysis for Detecting Risk Factors Leading to Recurrence of Breast Cancer

Farahnaz sadoughi.

1 Department of Health Information Management, School of Health Management and Information Sciences, Iran University of Medical Sciences, Tehran, IR Iran

Hadi Lotfnezhad Afshar

2 Department of Health Information Technology, School of Paramedical, Urmia University of Medical Sciences, Urmia, IR Iran

Asiie Olfatbakhsh

3 Breast Cancer Research Center (BCRC), The Academic Center for Education, Culture and Research (ACECR), Tehran, IR Iran

Neda Mehrdad

Background:.

Advances in treatment options of breast cancer and development of cancer research centers have necessitated the collection of many variables about breast cancer patients. Detection of important variables as predictors and outcomes among them, without applying an appropriate statistical method is a very challenging task. Because of recurrent nature of breast cancer occurring in different time intervals, there are usually more than one variable in the outcome set. For the prevention of this problem that causes multicollinearity, a statistical method named canonical correlation analysis (CCA) is a good solution.

Objectives:

The purpose of this study was to analyze the data related to breast cancer recurrence of Iranian females using the CCA method to determine important risk factors.

Patients and Methods:

In this cross-sectional study, data of 584 female patients (mean age of 45.9 years) referred to Breast Cancer Research Center (Tehran, Iran) were analyzed anonymously. SPSS and NORM softwares (2.03) were used for data transformation, running and interpretation of CCA and replacing missing values, respectively. Data were obtained from Breast Cancer Research Center, Tehran, Iran.

Analysis showed seven important predictors resulting in breast cancer recurrence in different time periods. Family history and loco-regional recurrence more than 5 years after diagnosis were the most important variables among predictors and outcomes sets, respectively.

Conclusions:

Canonical correlation analysis can be used as a useful tool for management and preparing of medical data for discovering of knowledge hidden in them.

1. Background

Breast cancer is the most common type of diagnosed and fatal cancers in females of the most areas of the world, especially in Iran ( 1 , 2 ). Iran is located in the western part of Asia where breast cancer in women is the first leading cause of death ( 3 ). In comparison with developed countries, breast cancer is diagnosed nearly one decade sooner in Iran and ages of incidence are often in the range of 40 to 49 years ( 2 , 4 , 5 ).

Identification of important predictors that prognosis (chance of recovery) of breast cancer depends on them, is a challenging task. There are many prognosis variables in paper and computerized medical records of breast cancer patients. Extraction of the most important predictors among them, regarding outcome variable(s), without using a proper statistical technique may be difficult ( 5 , 6 ).

A common statistical technique used to find relationships between predictors and outcome is multiple regression analysis (MRA). This technique is suitable when the outcome side has one variable, but applying of it in the scenarios of more than one variable leads to wrong results ( 7 ). Another important issue that must be concerned in multiple regression models is multicollinearity. Existence of the strong correlations between predictors is a major cause of it. As multicollinearity increases, it will be difficult to assess the importance of individual predictors ( 8 ).

In MRA, identification of important predictors is based on their beta weights. Since beta weights are affected by multicollinearity, using an alternative approach ignoring multicollinearity is necessary. Canonical correlation analysis (CCA) developed by Hotelling (1936) is an approach applying structure coefficients as indices for selecting important predictors. Contrary to beta weights, structure coefficients reflect the direct contribution of one predictor to the outcome variable, regardless of the multicollinearity ( 9 ).

Because breast cancer recurs at any time -mainly during the first five years- after the primary treatment, time is considered as an essential factor in the analysis of breast cancer recurrence ( 6 ). The Cox regression method is a traditional statistical one that is suitable for handling events such as cancer recurrence happening during different times ( 10 ). However, since cancer recurrences have different outcomes, the CCA method is preferable.

2. Objectives

The purpose of this study was to identify the most important risk factors leading to breast cancer recurrence during different time intervals by using the CCA method as a new technique in the clinical domain. The CCA method was applied to data set of breast cancer patients in the capital of Iran (Tehran).

3. Patients and Methods

3.1. data source.

In this cross-sectional study, data of 584 female patients (mean age, 45.9 years) were analyzed anonymously. Data were obtained from Breast Cancer Research Center (BCRC) in Tehran, Iran. This center, located in capital of Iran, has multiple clinics related to breast cancer therapy and research. After consulting with oncologists of the research center and studying the literature in the domain ( 7 , 11 , 12 ), two sets of predictors and outcomes (see Box 1. ) were selected.

Abbreviations: DM, distant metastasis; LN, lymph node; LRR, loco-regional recurrence.

a All periods are time after diagnosis.

3.2. Data Preprocessing

We obtained the data of this study in the format of Excel file from the BCRC in June 2012 anonymously; so, any special ethical certification was not needed. The original file contained demographic and clinical information of 843 breast cancer patients diagnosed in the BCRC. In the current study, only female patients that had been followed-up 5 years after diagnosis were selected as study samples. As mentioned criteria, 4 male patients and 255 ones that had a follow-up period less than 5 years (60 months) were excluded from the study. As a rule of thumb for minimum sample size calculation in the multivariate techniques that CCA is a subcategory of them, at least 30 observations for each variable are often used ( 13 ) that our study has met this criterion (584 > 570).

The raw data were transformed and converted as illustrated in Table 1 . Two variables such as LN positive and LN removed were dichotomized based on their presence or absence in the patients. Other variables, except age, were already categorized. The variable of age, continuous before, was transformed to the dichotomous one.

Abbreviations: BCS, breast conserving surgery; DCIS, ductal carcinoma in situ; IDC, invasive ductal carcinoma; ILC, invasive lobular carcinoma; LCIS, lobular carcinoma in situ; MRM, modified radical mastectomy; P, preservation.

a Values are presented as No. (%).

Although, canonical correlation analysis can accommodate any variable without the strict assumption of normality ( 14 ), the normality tests were done and nonnormal variables (surgery and pathology of tumor) fixed by the log transformation.

Variables with more than 50% of missing values were removed from dataset. Based on this criterion, three variables, age of menopause, tumor margin and Her2 were deleted. Missing values of other variables with less than 50% were substituted using the expectation maximization (EM) algorithm ( 15 ). The EM algorithm is an efficient repetitive procedure to compute the maximum likelihood (ML) estimate in the presence of missing or hidden data. In ML, estimation of the model parameter(s) for which the observed data are the most likely is performed. The E-step and the M-step are two processes that combine iterations of the EM algorithm. The E-step estimates the missing data through the observed data and current estimate of the model parameters and the M-step maximizes the likelihood function under the assumption that the missing data are known ( 16 ).

3.3. Canonical Correlation Analysis

Since two sets of variables existed and outcome set included more than one variable, the CCA method was performed. Figure 1 illustrates the fundamental principle behind CCA. Simply, the variable relationships in a hypothetical CCA with three predictor and two outcome variables have been shown. The combination of the observed variables in both sets into one unobserved variable is essential for evaluating the simultaneous relationship between several predictor and several outcome variables. In CCA, a linear equation is applied separately to the observed predictor and dependent variables to create one unobserved variable for each set. The reason these two equations are generated is that they yield the largest possible correlation between the two unobserved variables. The canonical correlation between the two unobserved variables is the most basic statistic in a CCA and it almost is a Pearson r (see Figure 1 ). Maximization of this simple correlation is the main purpose of the CCA ( 17 ).

Furthermore, in a CCA, the number of canonical functions is equal to the number of variables in the smaller set (e.g., two functions for the example in Figure 1 ). The first canonical correlation is the highest possible correlation between any synthetic predictor variable and synthetic outcome variable and is the most proper candidate for interpretation. The criterion for choosing the important variables in each canonical function is the structure coefficients, the bivariate correlation between an observed variable and a synthetic variable. As a rule of thumb for meaningful structure coefficients, an absolute value equal to or greater than 0.45 is often used ( 17 ).

SPSS version 16 for Windows (Chicago, SPSS Inc.; USA) and NORM software (2.03) ( 18 ) were used for data transformation, running and interpretation of CCA and replacing missing values, respectively.

A canonical correlation analysis was conducted using the thirteen attachment variables as predictors of the 6 outcome variables to evaluate the multivariate shared relationship between the two variable sets. The analysis yielded six functions with squared canonical correlations (R 2 c ) of 0.48, 0.18, 0.1, 0.09, 0.04, 0.02 for each successive function. Collectively, the full model across all functions was statistically significant using the Wilks’s λ = 0.32 criterion, F (192, 3235.78) = 3.57, P < 0.001. Because Wilks’s λ represents the variance unexplained by the model, 1 - λ yields the full model effect size in a r 2 metric. Thus, for the set of six canonical functions, the r 2 type effect size was 0.68 indicating that the full model explained a substantial portion, about 68%, of the variance shared between the variable sets.

The dimension reduction analysis allows the researcher to test the hierarchal arrangement of functions for statistical significance. As noted, the full model (Functions 1 to 6) was statistically significant. Functions 2 to 6 and 3 to 6 were also statistically significant, F (155, 2711.9) = 1.75, P < 0.001. F (120, 2181.04) = 1.26, P < 0.05. Functions 4, 5 and 6, with F (87, 1643.55) = 1.06, P = 0.329, F (56, 1100) = 0.67, P = 0.968 and F (27, 551) = 0.44, P = 0.994 respectively, did not explain a statistically significant amount of shared variance between the variable sets.

Given the R 2 c effects for each function, the first function was considered noteworthy in the context of this study (48% of shared variance). The last five functions only explained 18%, 9.9%, 9.1%, 4.5% and 2.1%, respectively from the remaining variance in the variable sets after the extraction of the prior functions.

Table 2 presents the standardized canonical function coefficients and structure coefficients for Function 1. The squared structure coefficients are also given for each variable. Looking at the coefficients of the outcome set, one sees that important variables were LRR, more than 5 years and LRR, 3 - 5 years, respectively. This conclusion was supported by the squared structure coefficients. These variables also tended to have the larger canonical function coefficients. All of these variables’ structure coefficients had the negative sign, indicating that they were all negatively related.

Abbreviations: Coef, standardized canonical function coefficient; r s , structure coefficient; r s 2 , squared structure coefficient, R 2 c , squared canonical correlations.

a Structure coefficients (r s ) greater than 0.45 are underlined.

Regarding the predictor variable set in Function 1, family history, estrogen receptor, pathology of tumor (LCIS), type of surgery (bilateral BCS), tumor size (> 2), pathology of tumor (IDC), and hormone therapy (combined) had the highest coefficients, respectively. Structure coefficients of all of them were negative, except for variables of estrogen receptor and pathology of tumor (IDC) that had positive sign.

5. Discussion

In this study, applying of the CCA method leads to identification of variables: family history, estrogen receptor, pathology of tumor, type of surgery, tumor size and hormone therapy, as important factors in predicting LRR, more than 5 years and LRR, 3 - 5 years.

Within the general linear models (i.e. CCA), r 2 type effect sizes are the first point for considering ( 19 ). Reporting results only with P values (without effect sizes) has little or no information about the importance of results ( 20 ). Our study’s statistical significance and effect sizes demonstrate that there is a remarkable relationship between our variable sets.

As Sherry ( 17 ), structure coefficients are answer to the question “what variables are contributing to the relationship between the variables set across the functions?” So, they are critical for deciding what variables are useful for the model ( 9 ).

The variable of family history, which got the highest structure coefficient, is a common and important predictor for the prognosis of breast cancer ( 21 , 22 ). The second variable among predictors set (based on its structure coefficient) is estrogen receptor. This variable is a significant one that has an inverse relation with outcome variables. In patients who have ER positive breast cancers local recurrence occurs less common. The estrogen receptor positive cancers, need to estrogen in order to grow and multiply, are less aggressive than negative ones and have better prognosis ( 23 - 25 ). Pathology plays an important part in determining the treatment strategy for women with breast cancer, with the evaluation of breast specimens determining the surgical and the oncological therapeutic options used ( 26 , 27 ). In this study, variable of pathology of tumor values got third and sixth places among predictors. Type of surgery is a pertinent risk factor of breast cancer affecting mortality rate of this disease and has different mental and physical consequences on various age categories of patients ( 28 , 29 ). Tumor size ( 24 , 30 , 31 ) and hormone therapy ( 32 ), were also found to be important predictors in the present study.

Some researchers have detected progesterone receptor as a prognostic factor in predicting breast cancer recurrence, especially in accompanying with estrogen receptor ( 7 , 33 ), whereas this variable did not get enough structure coefficients for reporting as important predictor in our study. Lyman ( 34 ), Paik ( 35 ) and Arvold ( 36 ) have showed that variable of age is an important factor in detecting the breast cancer recurrence, although age has not been determined as an important one in the present study.

Lymph node removed, number of involved LN, LN positive, radiotherapy and tumor grade were not detected as predictors of breast cancer recurrence in this research. Razavi ( 7 ) in a nearly similar study to the current study determined DM during the first four years and LRR during the first two years after diagnosis as outcome variables related to the predictor variables. In our study, LRR between three and five years and LRR more than five years were detected as outcome variables.

Dissimilarities between detected variables in our study and any other similar studies could be due to: geographical difference, nature of population studied and finally the way of data preprocessing.

There are two important limitations in the current study. First, some important variables that probably had great potential to exist among other significant risk factors were removed in our study because they had not enough values for analyzing; so, some valuable information were missed. Second, this study was performed in a single institution and consequently the generalization of its results is weaker than population-based studies.

In this study, the CCA was applied on the variables selected after consulting with experienced clinicians to achieve the medical meaningfulness and identification of most important risk factors leading to breast cancer recurrence during different time intervals.

In the medical complicated cases, for example the breast cancer disease that contains considerable numbers of variables (risk factors) in the predictor set and usually more than one variable in the outcome set, applying CCA as a new solution for detecting important ones in both sets is an appropriate selection. Detected breast cancer risk factors in this study were consistent with clinical guidelines.

Acknowledgments

The author would like to thank Dr Khalkhali (Ph.D. of statistics) for giving valuable comments to us.

Authors’ Contribution: Study concept and design: Farahnaz Sadoughi, and Hadi Lotfnezhad Afshar; acquisition of data: Hadi Lotfnezhad Afshar, Asiie Olfatbakhsh, and Neda Mehrdad; analysis and interpretation of data: Hadi Lotfnezhad Afshar; drafting of the manuscript: Farahnaz Sadoughi, Hadi Lotfnezhad Afshar, and Asieh Olfatbakhsh; critical revision of the manuscript for important intellectual content: Farahnaz Sadoughi, and Asiie Olfatbakhsh; statistical analysis: Hadi Lotfnezhad Afshar; administrative, technical, and material support: Farahnaz Sadoughi; study supervision: Farahnaz Sadoughi.

Funding/Support: This study was funded and supported by Iran university of medical sciences; grant no: 90-04-136-15619.